Assessment of EEG dynamical complexity in Alzheimer’s disease using multiscale entropy

Abstract

Objective

Multiscale entropy (MSE) is a recently proposed entropy-based index of physiological complexity, evaluating signals at multiple temporal scales. To test this method as an aid to elucidating the pathophysiology of Alzheimer’s disease (AD), we examined MSE in resting state EEG activity in comparison with traditional EEG analysis.

Methods

We recorded EEG in medication-free 15 presenile AD patients and 18 age- and sex-matched healthy control (HC) subjects. MSE was calculated for continuous 60-second epochs for each group, concurrently with power analysis.

Results

The MSE results from smaller and larger scales were associated with higher and lower frequencies of relative power, respectively. Group analysis demonstrated that the AD group had less complexity at smaller scales in more frontal areas, consistent with previous findings. In contrast, higher complexity at larger scales was observed across brain areas in AD group and this higher complexity was significantly correlated with cognitive decline.

Conclusions

MSE measures identified an abnormal complexity profile across different temporal scales and their relation to the severity of AD.

Significance

These findings indicate that entropy-based analytic methods with applied at temporal scales may serve as a complementary approach for characterizing and understanding abnormal cortical dynamics in AD.

1. Introduction

Electroencephalography (EEG) has been widely employed as a non-invasive clinical research tool for examining normal and pathologic neurophysiological temporal dynamics at a fine temporal resolution. Since brain activity is regulated by multiple couplings and feedback loops among multiple neuronal populations, its output signals exhibit complex temporal fluctuations, which are not simply attributable to noise but rather reflect nonlinear dynamical processes (Sporns et al., 2000; Tononi et al., 1998). As such, nonlinear EEG complexity analyses have been successfully applied and provide a novel understanding of physiological processes in both healthy and pathological conditions (Stam, 2005).

The neuropathology of Alzheimer's disease (AD) is characterized by generalized neuronal cell loss, neurofibrillary tangles, and senile plaques in different widespread brain regions, and these changes leads to cognitive and behavioral disturbance. How these neurobiological changes translate into functional disturbances can be understood in terms of a neocortical disconnection syndrome (Delbeuck et al., 2003) that results from local neuronal death and deficiency of neurotransmitters (Dringenberg et al., 2000) or altered long cortico-cortical association fibers (Kavcic et al., 2008), rather than by a specific regional alterations. This cortical disconnection is supported by a large number of electrophysiological studies demonstrating a loss of functional interactions using well-established linear (Jeong, 2004) and nonlinear coherence measures (Jeong et al., 2001; Stam et al., 2003). Although this cortical disconnection theoretically could give rise to increased complexity in electrophysiological signals, the nonlinear complexity measurements have been consistently found as complexity loss in EEG signals in AD (Jeong, 2004; Stam, 2005).

Over the past decade, novel nonlinear approaches have addressed many of the methodological limitations of traditional nonlinear approaches, including vulnerability to noise (Grassberger and Procaccia, 1983a) or data set size requirements (Eckmann and Ruelle, 1992). Among others, approximate entropy (ApEn) (Pincus, 1991), and its refined version, sample entropy (SampEn) (Richman and Moorman, 2000) were developed as practically tractable entropy-based measures which can be applied to stochastic, deterministic and composite physiologic processes (Pincus, 1991; Richman and Moorman, 2000). These measures determine the probability of finding specific patterns or resemblance in a time series, thereby examining the irregularity or predictability in a time series. Several studies have demonstrated the utility of ApEn ( Abásolo et al., 2005, 2007) and SampEn (Abásolo et al., 2006) in AD with high sensitivity and specificity. Although these two entropy measures assess temporal dynamics, they are limited in their scope to only short-range temporal dynamics (Costa et al., 2005; Goldberger et al., 2002). In order to investigate the variability in physiological signals across multiple temporal scales, Costa et al. (2002) introduced multiscale entropy (MSE), an extension of SampEn method using temporal coarse-graining procedures, in recognition of the likelihood that dynamical complexity of biological signals may operate across a range of temporal scales. This extension to larger temporal scales may allow the detection of history effects in long-range temporal dynamics i.e., neural dynamics that relate current activity to past activation states that have been stored dynamically through feedbacks loops at multiple, hierarchic levels of cortical processing (Fell et al., 2000). If functional disconnection in AD is originated at multiple, hierarchic levels, complex fluctuation of their neurophysiological output signal need to be characterized by multiple scales. In this context, MSE profiles provide useful insights into the network controlling mechanisms underlying physiological dynamics (Costa et al., 2005) which might be altered in AD due to disconnection syndrome. A few studies have demonstrated the utility of MSE in exploring EEG changes with aging (Takahashi et al., 2009), schizophrenia (Takahashi et al., in press) and AD (Escudero et al., 2006; Park et al., 2007). Escudero et al. (2006) and Park et al. (2007) examined resting state EEG activity of AD using MSE and found that AD patients had less complexity, consistent with previous nonlinear EEG analysis findings in AD. Although the advantage of MSE analysis is based on the utility of examining long-range temporal dynamics, their explorations were limited their scope to examining relatively short-range temporal dynamics using short length epochs.

Our aim was to investigate possible disturbances in the long-range temporal dynamics in EEG signals in AD and examine their relevance to cognitive function. As such, building on previous AD studies using MSE analysis, we widen the scope to examining in larger temporal scales with longer interest epochs in AD patients and their relation to cognitive decline, and explored their relevancy to that of traditional power analysis. Further, we examined patients that were unmedicated and with relatively young presenile onset, thus avoiding the potential confounds of medication effects and other factors associated with aging such as vascular changes. To this end, we examined resting state EEG activity using MSE in medication-free AD subjects.

2. Methods and Materials

2.1. Subjects

The patient group consisted of 15 subjects (10 women) recruited from Kanazawa University Hospital (Table 1). The patients fulfilled the NINCDS – ADRDA work group criteria for probable AD (McKhann et al., 1984) and DSM-IV criteria for primary degenerative dementia, presenile onset. Their mean age (± SD) was 59.1 ± 5.4 years (range, 43 – 66). Their mean age at onset of illness was 56.5 ± 5.8 years (range, 43 – 64). Other medical conditions known to cause dementia were excluded following neurological, serological and neuroimaging (MRI and/or CT) studies. None of the patients were receiving medications acting upon the central nervous system (CNS). Each patient was assessed with the Functional Assessment Stages (FAST) (Reisberg et al., 1986) and a Japanese version of the Mini-Mental State Examination (MMSE) (Folstein et al., 1975). By FAST assessments, 3 patients had mild (FAST 3), 7 moderate (FAST 4), and 5 slightly severe dementia (FAST 5). Their MMSE scores ranged from 10 to 26 (mean ± SD, 15.9 ± 4.5). Age and gender matched 18 healthy control (HC) subjects (11 women), with an average age of 57.5 ± 4.7 years (range, 51 – 67), were recruited into this study (Table 1). All HC subjects were staff members of Kanazawa University Hospital or their family members, who had no personal or family history of psychiatric or neurological diseases. All HC subjects were functioning normally and independently in their daily lives. None of them were taking CNS-active medications. All subjects were medication-free, nonsmokers and nonhabitual drinkers. All subjects were right handed. The protocol of the study was approved by the Ethics Committee of the Kanazawa University. All subjects agreed to participate in the study with full knowledge of the experimental nature of the research. After a complete explanation of the study, written informed consent was obtained from each subject.

Table 1.

Demographic and clinical and demographic data in healthy control subjects and Alzheimer’s disease patients

Group	Healthy controls	Alzheimer’s disease patients
		All subjects	MMSE > 15	MMSE ≤ 15
Total number	18	15	7	8
Male/Female	7/11	5/10	2/5	3/5
Age (range) years	57.5 (51–67)	59.1 (43–66)	57.7 (43–64)	60.4 (55–66)
MMSE	NA	15.9(10–26)	19.7 (16–26)	12.6 (10–15)
Duration of the disease (range) months	NA	32.7 (4–110)	41.6 (4–110)	25.0 (10–46)

Abbreviations: MMSE, Mini-Mental State Examination; NA, not applicable.

2.2 EEG recordings

The subjects were studied while seated in an electrically shielded, soundproof, light-controlled recording room. Standard scalp electrodes were placed in accordance with the International 10–20 System. EEG was recorded with 18-channel electroencephalogram (EEG-4518, Nihon-Koden, Tokyo, Japan) at 16 electrodes sites: Fp1, Fp2, F3, Fz, F4, F7, F8, C3, C4, P3, Pz, P4, T5, T6, O1 and O2, referenced to physically-linked ear lobe electrodes. Eye movements were monitored by means of bipolar electro-oculographic (EOG) derivations. The EEG signals (200 Hz sampling frequency) were recorded with a time constant of 0.3 and a 1.5 to 60 Hz bandpass filter. Since line noise was at 60 Hz, notch filter was not applied in this study. Impedance of electrode/skin conductance was carefully kept less than 5 kΩ for each electrode. EEGs were recorded for 10 – 15 min for each subject with the eyes closed. The subjects were observed via a video monitoring system. State of vigilance was visually inspected with EEG traces during recording session. When the subjects appeared to be drowsy, they were asked to open their eyes and verbally warned to avoid drowsiness. Selection of segments recorded during eyes-closed wakefulness was performed by visual inspection of EEG and EOG recordings. The subject was considered to be fully awake when alpha activity appeared predominantly over the posterior regions, with concurrent fast eye movements in the EOG channel (Wada et al., 1996). The data were stored on a magnetic optical disk for off-line analysis. Other pre-processing steps were not conducted (i.e., filtering, artifacts removal or data reconstruction), because such processing may destroy data’s intrinsic dynamics and we rigorously visually selected epochs without artifacts.

In order to adequately index information regarding long-range temporal dynamics, MSE was calculated on a single, continuous 60-sec (12000 data points) artifact-free epoch during the eyes-closed resting condition selected by an expert electroencephalographer who was blinded to the group identity of the subjects and double-checked by another expert electroencephalographer who was also blinded to the group identity of the subjects.

In order to obtain long-range temporal dynamic’s information, the EEG signals used for MSE analysis corresponded to continuous 60-sec, artifact-free epochs selected from eye-closed resting condition

2.3. Multiscale entropy (MSE)

The MSE method quantifies the degree of complexity of a time series at multiple temporal scales (Costa et al., 2002). Irregularity/unpredictability at each scale can be measured by Kolmogorov-Sinai (KS) entropy, which calculates the rate of information loss (Kolmogorov, 1958). Although KS entropy based measurements, such as K₂ entropy (Grassberger and Procaccia, 1983b) or K₁ entropy, Eckmann and Ruelle entropy (Eckmann and Ruelle, 1985) have been proposed as estimates of KS entropy with reasonable precision, they were not suitable for noisy or short time series. As a refinement of the traditionally used ApEn, which is a K₁ information entropy version of KS entropy, Richman and Moorman (2000) proposed SampEn, as a K₂ correlation entropy version of KS entropy, which is relatively robust to noise and variations in sequence length.

For the extension of SampEn to multiple time scales (i.e., calculation of MSE), the original EEG time series {x₁, x₂,…, x_N} was coarse-grained by the scale factor (SF) τ, with non-overlapping windows as follows:

$$y_j{}^{(\mathrm{\tau })}=(1/\mathrm{\tau }){\displaystyle \sum _{i=(j-1)\mathrm{\tau }+1}^{j\mathrm{\tau }}{x}_i,}1\le j\le N/\mathrm{\tau }$$

τ is the temporal scaling factor (SF) of the time series. At unit SF, τ = 1, the time series {y⁽¹⁾} is simply identical to the original time series which represents short-range temporal scale whereas larger SF represents longer temporal scales. Next, the SampEn was calculated for each series {y^(τ)} with various time scales. Thus, MSE profile consists of determinations of SampEn at each scale value.

Briefly, SampEn, being a measure of regularity, is the negative of the logarithmic conditional probability that two sequences of m consecutive data points are similar to each other (within given tolerance r) will remain similarity at the next point (m + 1) in the data set (N), where N is the length of the time series, m is the length of the sequence to be compared and r is the effective filter for measuring consistency of time series. Considering for any coarse-grained EEG time-series {x₁, x₂,…x_N} as observations of the stochastic variable x, dynamic SampEn is defined as:

$$h_{\text{samp}}(r,m,N)={\text{log}}_{\mathrm{e}}[c_{m+1}(r)/C_m(r)],$$

where C_m (r) = {number of pairs (i, j) with | x^m_i – x^m_j | < r, i ≠ j} / {number of all probable pairs, i.e. (N – m + 1) (N – m)}.

Therein, x^m is a vector of m members time series of (N – m) length, and | x^m_i – x^m_j | denotes the distance (Euclidian distance actually) between points x^m_i and x^m_j in the space of dimension m (for details of the SampEn algorithm see Richman and Moorman, 2000). Various theoretical and clinical applications have shown that m = 1 or 2, and r = 0.1–0.25 of the standard deviation of the original sequence provides good statistical validity for SampEn (Richman and Moorman, 2000). For the present analyses, the calculation of MSE was carried out using self-produced software developed with Mathematica 5.2 (Wolfram Research, Inc.), and we used a time series of length N = 12000 (i.e. 60-sec × 200 Hz) with m = 2, r = 0.2 and SF = 1 – 20, which are values that have been successfully applied in our previous work (Takahashi et al., in press; Takahashi et al., 2009).

2.4. Power analysis

In addition to MSE analysis, we performed power analysis as a comparative conventional EEG measurement using a computer program specifically designed for EEG, ‘BIMUTAS II’ (Kissei-Comtec). A Hanning window was applied to each artifact-free 2.56-s epoch (sampling rate 200 Hz), and the spectral density was calculated using a fast Fourier transform (FFT). From the consecutive 60-s epochs which were used for MSE analyses, a total of 23 artifact-free epochs were selected to calculate absolute EEG power. Then the frequency spectrum was divided into frequency bands of delta (2–6 Hz), theta (6–8 Hz), alpha (8–13 Hz), beta (13–30 Hz) and gamma (30–40 Hz). For each frequency band, we then calculated a measure of relative power change (power in each frequency divided by total power across all frequency bands) for statistical analyses.

2.6. Statistical analysis

Statistical analyses were carried out using SPSS (Windows version 17; SPSS Japan Inc., Tokyo, Japan). SampEn values for each SF were found to have a skewed distribution and were therefore log-transformed to achieve a normal distribution.

For MSE analysis, repeated measures analysis of variance (ANOVA), with group (AD vs. HC) as a between-subject factor, and hemisphere (left vs. right) and SF (τ: 20 scales) as within-subject factors, were used to test differences in MSE analysis for each paired electrode site. For midline electrode sites, repeated measures ANOVA, with group (AD vs. HC) as a between-subject factor, and SF (τ: 20 scales) as within-subject factors, were used to test for group differences in MSE analysis. In the case of significant group-by-SF interaction, post-hoc independent t-tests were used to compare group differences separately for each SF. In order to explore the behavior of MSE in more severe AD, we selected patient subjects (n = 8) with low MMSE scores (MMSE score ≤ 15), and similarly performed ANOVA and post-hoc independent t-tests. Additionally, for the AD subjects, Spearman’s rank-order correlations were performed to evaluate associations between SampEn values and clinical/demographic data (MMSE score, age, age at onset and illness duration).

For relative power analysis, repeated measures ANOVA were performed with group (AD vs. HC) as between-subject factor, and the hemisphere (left vs. right) and frequency band (delta, theta, alpha, beta and gamma) as within-subject factors, were used to test differences for each paired electrode site. For midline electrode sites, repeated measures ANOVA, with group (AD vs. HC) as between-subject factors, and frequency band (delta, theta, alpha, beta and gamma) as within-subject factors, were used to test for group differences. In the case of significant group-by-SF interaction, independent t-tests were used to compare group differences separately for each frequency band and electrode sites.

To explore the relationship between MSE and power analyses, we performed Spearman’s rank-order correlations between relative power and SampEn values for HC and AD subjects.

The Greenhouse-Geisser adjustment was applied to the degrees of freedom for all analyses. A two-tailed α level of 0.01 was considered statistically significant for all analysis (i.e., both for ANOVAs and post-hoc t-tests), in order to avoid type I error.

3. Results

3.1. Multiscale entropy value AD vs. HC

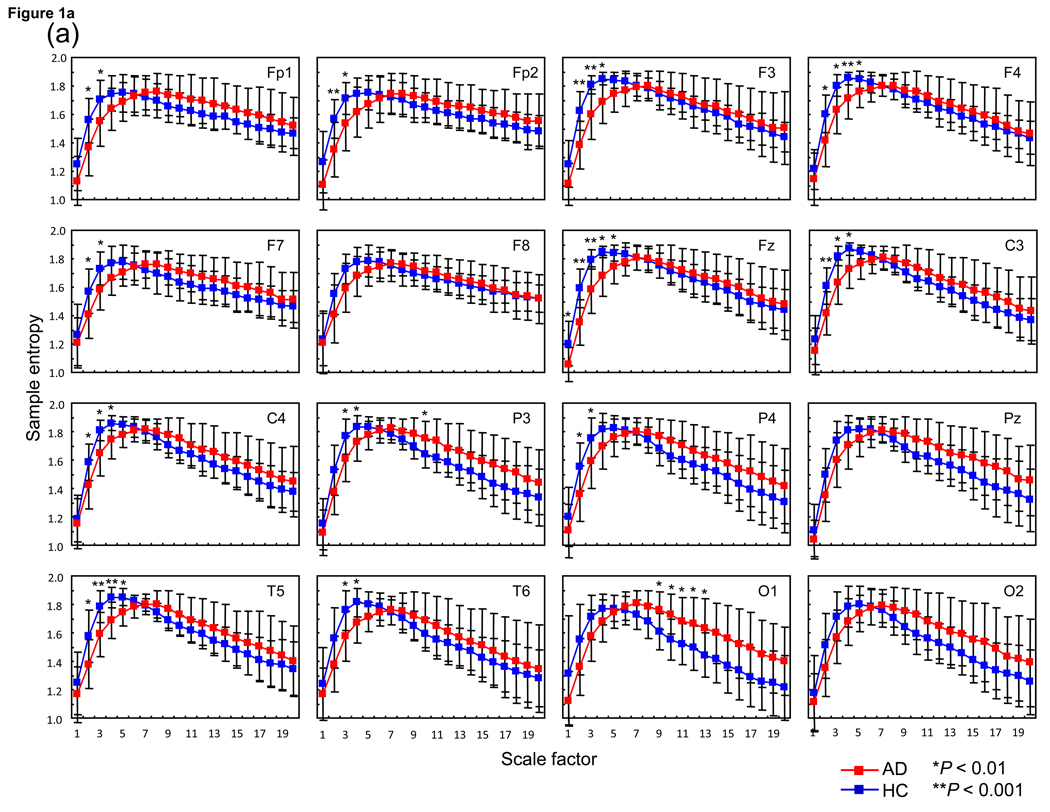
Results of ANOVA testing for group difference between AD and HC revealed no group-by-hemisphere-by-SF interaction and no main effect for hemisphere in any paired electrode sites. However, a significant group-by-SF interaction in Fp1/2 [F(19,589) = 5.7, P = 0.006], P3/4 [F(19,589) = 6.1, P = 0.004] and O1/2 [F(19,589) = 6.6, P = 0.0013], and a trend group-by-SF interaction in F3/4 [F(19,589) = 4.6, P = 0.016], C3/4 [F(19,589) = 4.6, P = 0.016] and T5/6 [F(19,589) = 4.6, P = 0.012] was identified for each paired electrode sites, but not in F7/8 [F(19,589) = 3.1, P = 0.05]. For intermediate electrode sites, a significant and a trend group-by-SF interaction was identified in both Fz [F(19,589) = 5.8, P = 0.007] and Pz [F(19,589) = 5.0, P = 0.012]. Post-hoc t-tests identified significant decreases in SampEn values at smaller SFs around 1–5 in selected electrode sites (i.e., Fp1/Fp2, F3/4, F7, Fz, C3/4, P3/4 and T5/T6), whereas significant increases were identified at larger SFs 9–13 only in O1 in AD patients (Fig. 1a).

Fig. 1.

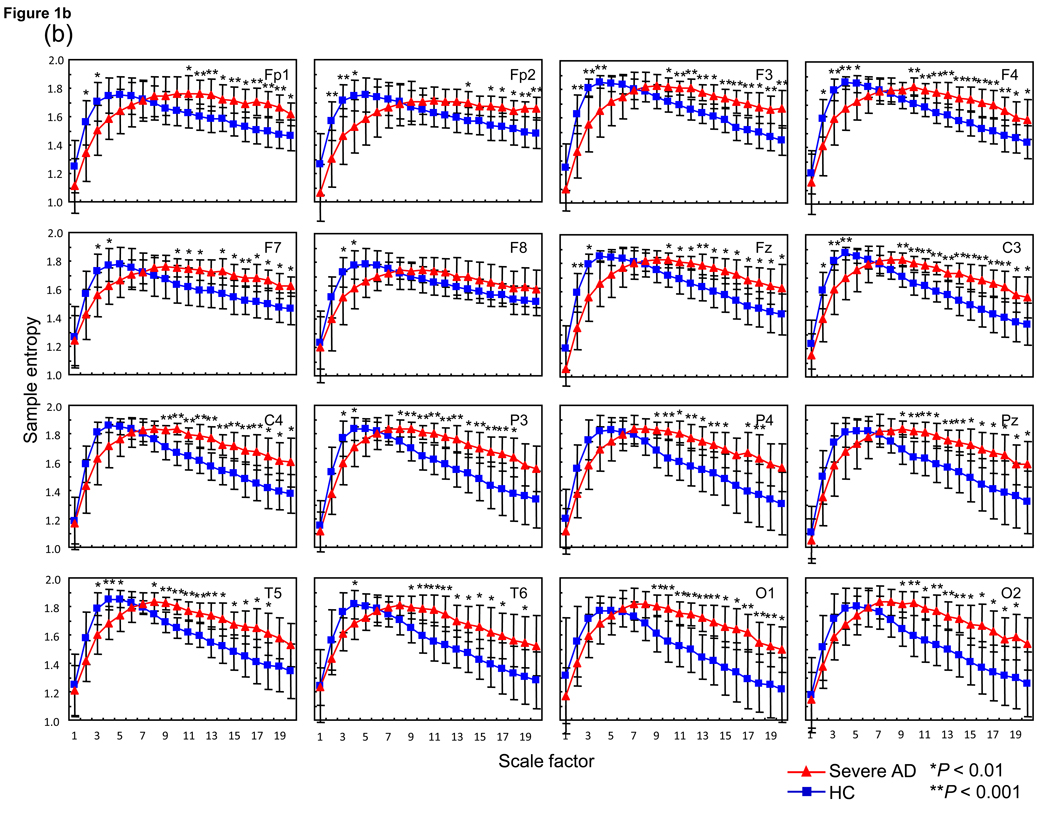
(a) Multiscale entropy (MSE) analysis of 15 Alzheimer’s disease patients (AD) (red square) and 18 healthy control subjects (HC) (blue square) for each site and average of each site. Each panel presents the average of the left and right MSE values. Post-hoc comparisons between AD and HC: ^*P < 0.01, ^**P < 0.001. (b) MSE analysis of 8 severe Alzheimer’s disease patients (AD: Mini-Mental State Examination (MMSE) score ≤ 15) (red triangle) and 18 HC (blue square) for each site and average of each site. Each panel presents the average of the left and right MSE values. Post-hoc comparisons between severe AD and HC: ^*P < 0.01, ^**P < 0.001.

3.2. Multiscale entropy in AD with low MMSE score vs. HC

Results of ANOVA testing for group difference between AD with low MMSE score and HC revealed no group-by-hemisphere-by-SF interaction and main effect for hemisphere in any paired electrode sites. However, a significant group-by-SF interaction was identified in all paired electrode sites (Fp1/2 [F(19,456) = 14.1, P = 0.00002], F3/4 [F(19,456) = 15.2, P = 0.000004], F7/8 [F(19, 456) = 7.2, P = 0.002], C3/4 [F(19, 456) = 12.9, P = 0.00002], P3/4 [F(19, 456) = 11.9, P = 0.00003], T5/6 [F(19, 456) = 10.0, P = 0.0001] and O1/2 [F(19, 456) = 9.7, P = 0.0013]). For intermediate electrode sites, both Fz [F(19, 456) = 14.2, P = 0.00001] and Pz [F(19, 456) = 10.5, P = 0.0001] demonstrated significant group-by-SF interactions. Post-hoc t-tests identified significant decreases in SampEn values at smaller SFs around 2–5 in selected electrode sites (i.e., Fp1/Fp2, F3/4, F7/8, Fz, C3, P3 and T5/6), whereas significant increases were identified at larger SFs around 10–20 in all electrode sites except for F8 in severe AD patients (Fig. 1b).

3.3. Correlations between MSE values with individuals’ clinical and demographic data

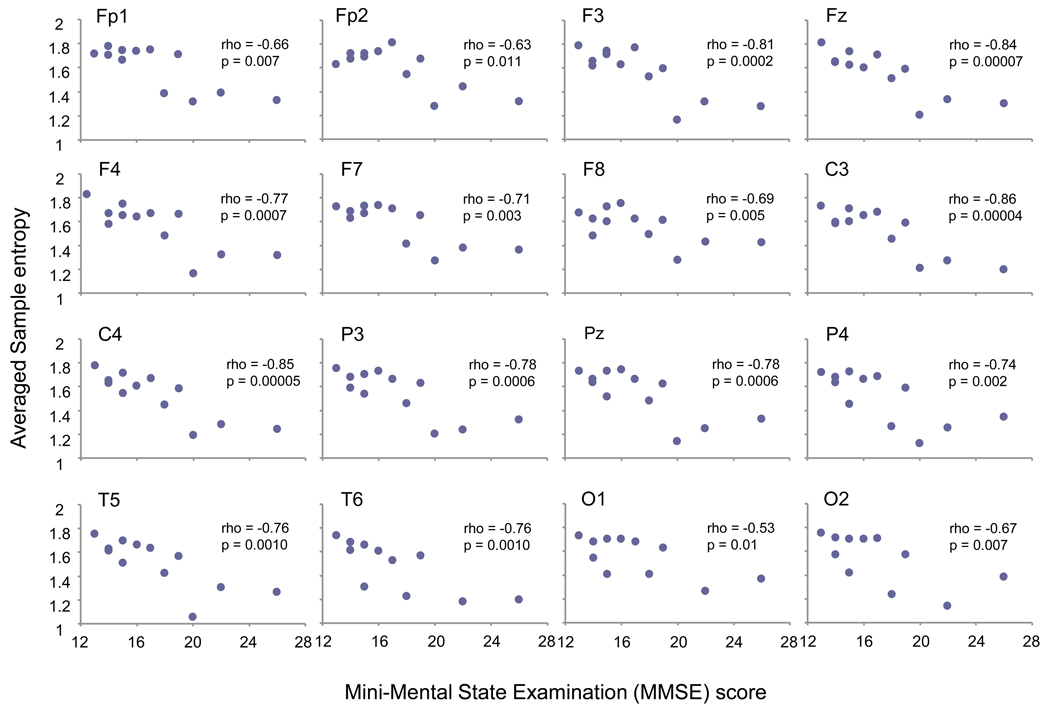
There was no significant correlation between SampEn values and individuals’ clinical/demographic data such as age, age at onset and illness duration. However, MMSE score was negatively correlated with larger SampEn values (from SF 11 to 20) consistently across every site at larger SFs. In order to clarify the possible association of cognitive decline to SampEn value further, we averaged all these SampEn values (10 SFs) into one value for each site. There was a significant negative correlation between MMSE score and averaged SampEn values at all sites (Fig. 2), whereas no significant correlation between MMSE score and SampEn value across small SF (data not presented).

Fig. 2.

Each panel presents association between the Mini-Mental State Examination (MMSE) score and the averaged Sample entropy (SampEn_ave) value for each site. SampEn_ave was calculated as a result of averaging SFs across 11 to 20. Significant negative correlations were observed at any electrode sites.

3.4. Power analysis

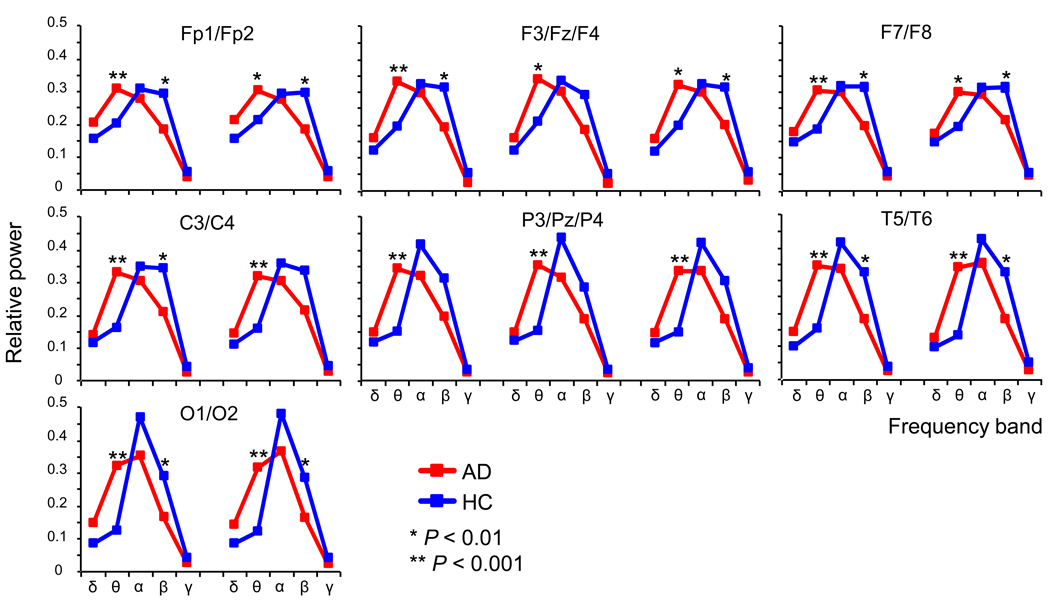
Results of ANOVA testing for group difference between AD and HC revealed no group-by-hemisphere-by-frequency band interaction and no main effect for hemisphere in any paired electrode sites. However, a significant group-by-SF interaction in C3/4 [F(4,124) = 6.1, P = 0.003], P3/4 [F(4,124) = 7.4, P = 0.001], T5/6 [F(4,124) = 5.7, P = 0.004] and O1/2 [F(4,124) = 8.9, P = 0.002] and a trend group-by-SF interaction in Fp1/2 [F(4,124) = 3.9, P = 0.02], F3/4 [F(4,124) = 4.6, P = 0.01] and F7/8 [F(4,124) = 3.8, P = 0.02] was identified for each paired electrode sites. For intermediate electrode sites, both Fz [F(4,124) = 4.5, P = 0.010] and Pz [F(4,124) = 8.1, P = 0.0006] demonstrated significant group-by-SF interactions. Post-hoc independent t-tests showed significant increases in theta and decreases in beta band power in AD, respectively (Fig. 3).

Fig. 3.

Relative power analysis of 18 healthy control (HC) (blue) and 15 Alzheimer’s disease (AD) subjects (red). Each panel presents the paired electrode sites of relative power values. Post-hoc comparisons between HC and AD: *P < 0.05, **P < 0.01.

3.5. Relationship between power and MSE

To investigate the relationship between MSE and power analysis, we collapsed SFs into four components (i.e., SF 1–5, SF 6–10, SF 11–15 and SF 16–20) as a data reduction measure. As a result, complexity at smaller and larger SFs was significantly correlated with the faster and slower frequency’s relative power, respectively. Table 2 and 3 demonstrate examples (Fz) of the correlation matrix between collapsed MSE value and the relative power for HC and AD subjects, respectively.

Table 2.

Correlations between MSE and relative power among healthy control subjects for Fz

Relative power	MSE SF: 1–5	MSE SF: 6–10	MSE SF: 11–15	MSE SF: 16–20
Delta	−0.28	0.28	0.82	0.9
	0.26	0.26	0.00003	0.000001
Theta	−0.046	0.14	0.54	0.57
	0.86	0.59	0.021	0.014
Alpha	−0.28	0.48	−0.21	−0.42
	0.26	0.045	0.41	0.085
Beta	0.29	−0.79	−0.58	−0.43
	0.23	0.0001	0.012	0.076
Gamma	0.51	−0.34	−0.043	0.1
	0.03	0.16	0.86	0.68

Abbreviations: MSE, Multiscale entropy; SF, scale factor.

Upper and lower numbers in each cell represent r -values for correlations between relative frequency power value and averaged MSE value across SFs, and their respective P -values.

Table 3.

Correlations between MSE and relative power among Alzheimer's disease subjects for Fz

Relative power	MSE SF: 1–5	MSE SF: 6–10	MSE SF: 11–15	MSE SF: 16–20
Delta	−0.61	0.04	0.78	0.83
	0.015	0.89	0.0007	0.0002
Theta	−0.61	0.43	0.85	0.84
	0.015	0.11	0.00007	0.0001
Alpha	0.17	0.01	−0.58	−0.75
	0.53	0.97	0.027	0.001
Beta	0.76	−0.43	−0.62	−0.45
	0.001	0.11	0.014	0.090
Gamma	0.62	−0.36	−0.41	−0.24
	0.013	0.18	0.13	0.39

Abbreviations: MSE, Multiscale entropy; SF, scale factor.

Upper and lower numbers in each cell represent r -values for correlations between relative frequency power value and averaged MSE value across SFs, and their respective P -values.

4. Discussion

In this study, we employed MSE analysis to evaluate EEG signal complexity in AD patients. As MSE quantifies the degree of complexity over a range of time scales, we were able to demonstrate that AD may not only be characterized by decreased complexity in EEG signals as reported by previous studies, but also increased complexity at larger temporal scales. Further, these increases in complexity seem to be pathophysiologically meaningful, in that they correlated with measures of cognitive impairment.

Significantly reduced complexity at smaller SFs in frontal regions in our AD group is consistent with a well-established hypothesis that AD is characterized by less complexity in EEG signals (Jeong, 2004; Stam, 2005), with several studies using ApEn (Abásolo et al., 2005, 2007) and SampEn (Abásolo et al., 2006) reporting findings consistent with this hypothesis. With regard to MSE measures, Escudero et al. (2006) and Park et al. (2007) have demonstrated decreased EEG complexity across smaller SFs in AD patients compared to that of age-matched controls, consistent with our findings. In contrast, we also found increased complexity at larger SFs for severe AD patients globally across brain regions, and this abnormally increased complexity was strongly correlated with cognitive decline in all AD patients.

Results from power analysis support the frequently observed findings demonstrating spectral “slowing” in AD. Comparing MSE with power analyses, we found significant associations with fast and slow frequency relative power being correlated with smaller and larger SFs, respectively. As such, detecting increase in complexity in AD might be achieved only by examining larger SFs, that indexes, longer range temporal dynamics.

Our MSE findings at the smaller and larger SFs could be related to the spectral slowing in AD. However, the neurophysiological mechanism for this apparently contradictory finding in complexity difference across SFs remains unclear. Although measurements of complexity in AD have repeatedly found complexity loss (Jeong, 2004; Stam, 2005), these former studies did not consider multiple time scales or frequencies. Some studies have explored the complexity across different frequency bands in AD. van Cappellen van Walsum et al. (2003) explored MEG signal complexity using neural complexity (C_N) and correlation dimension (D₂), finding higher complexity in slower frequency (2 – 8 Hz) and but low complexity not significantly at higher frequencies with C_N, whereas D₂ demonstrated opposite to the results from C_N. Czigler et al. (2008) also demonstrated increased complexity across a wide range of frequency band (0.5–25 Hz) using Omega-complexity, concurrently with slowing of the spectral changes. Furthermore, Jelles et al. (2008) explored the relationship between EEG linear coherence and global complexity using D₂, and suggest that the different frequency bands reflect separate brain dynamical systems. The varying of results of these studies across frequencies, similar to our variable findings across SFs, emphasizes the importance of examining a range of time scales when exploring EEG signal dynamics. In order to explore the relationship of EEG complexity to disconnection in neuronal networks, Friston (1996) assessed the effect of the degree of connectivity within neuronal populations and measures of complexity using synthetic neuronal models, finding that aberrant or reduced connectivity increased EEG signal complexity. Further, the topography of our findings for large vs. small SFs may also shed light on their opposite directionality. The MSE increases at larger SFs in severe AD patients occurred more globally across regions than the decreases at smaller SFs (Fig. 1b). As brain dynamics are influenced by both local dense interconnectivity and long-range excitatory projections (Friston et al., 1995; Tononi et al., 1994), neuronal activity at these two spatial scales may be modulated by separate neuropathophysiological mechanisms in AD. In this context, complexity at different time scale might represent different neuropathophysiological mechanism in AD and our findings of increased complexity at larger SFs may thus reflect abnormal neuronal network connectivity and interpreted in terms of a disconnection syndrome (Delbeuck et al., 2003). As for cognitive decline, we found a significant correlation of MSE values with MMSE score at larger SFs. Considering the fact that the specific frequency bands may have their own different functional roles (Klimesch et al., 2007), we speculate that disturbances in long-range neuronal networks in AD might cause abnormally increased activity in larger temporal scales that could give rise to disturbances in cognitive function. However, it is unclear why significant correlations between MSE and MMSE were not found in smaller SFs, particularly in frontal regions. This could be due to the fact that MMSE is a summary index of that taps multiple cognitive functions and brain regions. Therefore, another index which is more sensitive and specific to frontal cognitive function, such as executive function, may be necessary to clarify this issue. Although this is a limitation of this study, it may also support the generalizability of the results to more conventional cognitive assessment.

The potential effect of gender and severity to the MSE results need to be considered. We additionally performed ANOVA in the AD group, with gender (male vs. female) and severity (FAST: mild, moderate and slightly severe) as a between-subject, and hemisphere (left vs. right) (for paired electrode sites) and SF (τ: 20 scales) as within-subject factors in any of the paired or intermediate electrode sites. As a result, gender and severity did not demonstrate any significant main effects or interactions. However, dividing our 15 patient subjects by severity (3 mild, 7 moderate and 5 slightly severe) would not provide an adequately powered test of the effects of severity. Studies with larger sample sizes are necessary to clarify this issue.

In summary, our study found both decreased complexity in small SFs, consistent with previous literature, but also increased complexity at larger SFs that correlates strongly with cognitive function in AD. This extension of MSE analyses to larger SFs may provide insights into disturbances in long-range network control mechanisms underlying physiological dynamics (Costa et al., 2002, 2005), consistent with the idea of a disconnection syndrome in AD (Delbeuck et al., 2003). In addition to the methodological advantage of MSE, employing patient subjects that were medication-free with presenile onset, afforded interpretive clarity by avoiding medication confounds and other effects associated with aging such as vascular effects. Future studies of possible correlative findings with functional or structural methods, such as fMRI or diffusion tensor imaging techniques, including more precise assessments of cognitive function, and a longitudinal design could strengthen the present findings. However, our findings highlight the potential utility of MSE with a wide-range of time scales, as a complementing powerful approach for understanding the assessment of pathophysiologic processes in AD.