Multivariate-adjusted pharmacoepidemiologic analyses of confidential information pooled from multiple health care utilization databases

SUMMARY

Purpose

Mandated post-marketing drug safety studies require vast databases pooled from multiple administrative data sources which can contain private and proprietary information. We sought to create a method to conduct pooled analyses while keeping information private and allowing for full confounder adjustment.

Methods

We propose a method based on propensity score (PS) techniques. A set of propensity scores are computed in each data-contributing center and a PS-adjusted analysis is then carried out on a pooled basis. The method is demonstrated in a study of the potentially negative effects of concurrent initiation of clopidogrel and proton pump inhibitors (PPIs) in four cohorts of patients assembled from North American claims data sources. Clinical outcomes were myocardial infarction (MI) hospitalization and hospitalization for revascularization procedure. Success of the method was indicated by equivalent performance of our PS-based method and traditional confounder adjustment. We also implemented and evaluated high-dimensional propensity scores and meta-analytic techniques.

Results

On both a pooled and individual cohort basis, we saw substantially similar point estimates and confidence intervals for studies adjusted by covariates and from privacy-maintaining propensity scores. The pooled, adjusted OR for MI hospitalization was 1.20 (95% confidence interval 1.03, 1.41) with individual variable adjustment and 1.16 (1.00, 1.36) with PS adjustment. The revascularization OR estimates differed by <1%. Meta-analysis and pooling yielded substantially similar results.

Conclusions

We observed little difference in point estimates when we employed standard techniques or the proposed privacy-maintaining pooling method. We would recommend the technique in instances where multi-center studies require both privacy and multivariate adjustment.

INTRODUCTION

The need to perform epidemiologic analyses with data drawn from multiple populations is long-established,^1–4 particularly when studies of treatment effects in small patient subgroups or of rare outcomes require very large populations to provide sufficiently precise estimates.⁵ New requirements for a post-marketing data safety surveillance system outlined in the Food and Drug Administration Amendments Act (FDAAA)⁶ have heightened the need for access to large databases. Indeed, the FDAAA requires combined databases covering 25 million lives by 2010 and 100 million lives by 2012.⁷ As no single public or private US health plan can scale to such a number, achieving the goal will necessarily involve pooling data from multiple sources. With these large databases, researchers and regulators hope to speedily analyze drug safety signals in-newly marketed drugs.⁸

Pooling data from multiple sources is optimally done in a manner that allows for adjustment for large numbers of confounding variables and simultaneously protects the information of patients and health plans. Data providers want to preserve the proprietary nature of their data as there are often organizational, research, or business interests at stake, such as an commercial insurer’s case mix. Patient privacy must be maintained^7,9 in a way that goes beyond simple deleting of names and masking of patient identifiers. One solution is to aggregate patients into strata and weight regressions by a stratum-specific count, but large numbers of covariates, rare conditions, or uncommon procedures can easily create single-person cells that identify patients in all ways save for their name.^10,11

Many of the questions to be addressed with pooled analyses involve intended and unintended drug effects for which confounder adjustment is necessary.^12,13 Covariate information must be utilized to the fullest extent possible, but this goal may run contrary to protection of privacy. The propensity score (PS) has found widespread application in pharmacoepi-demiology¹⁴ as a mechanism to summarize many covariates into a single number that does not have covariate-specific meaning. They have certain strengths¹⁵ and limitations.¹⁶ Within levels of a PS, patients can be assumed to be comparable with respect to treatment choice, and PSs allow balancing drug exposure groups with respect to all component variables.^15,17 The summarization removes the detail of individual-level patient information but retains the information’s content. As a result, PS methods can enhance data security and privacy while still adjusting for confounding.

We propose a process which addresses both study validity as well as protection of proprietary and private data. We demonstrate this method by combining data from four healthcare utilization databases to study the recently hypothesized increase in thrombotic events as a consequence of concurrent use of a proton pump inhibitor (PPI) and the anti-platelet agent clopidogrel. We studied patients who had undergone percutaneous coronary intervention (PCI) or who had been hospitalized for MI or unstable angina and subsequently initiated use of clopidogrel. We assessed outcomes of myocardial infarction (MI) hospitalization and the need for revascularization.

DESCRIPTION OF DATA POOLING METHOD

Definitions

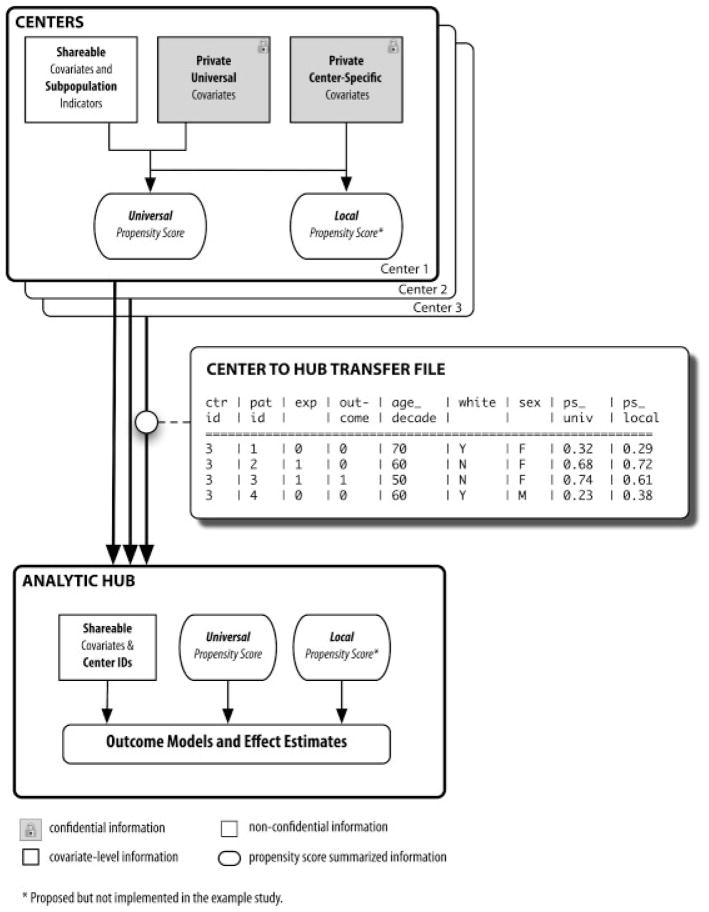
We define a center as an organization that will contribute a cohort of patients to a pooled analysis. Such centers may be private insurers, academic organizations with access to healthcare utilization data, or governmental bodies like state Medicaid programs or the Centers for Medicare and Medicaid Services (CMS). In our taxonomy, centers are responsible for collecting, cleaning, organizing, and transmitting data, locally implementing the overall study design, and estimating PSs within their population. This framework is not unlike the distributed Sentinel system proposed by FDA.⁷ We define the analytic hub as the ‘master center’ in which the data will be pooled and analyzed. The analytic hub may or may not contribute data of its own.

Covariates and propensity scores

To begin, the collaborators perform basic aspects of a study design (Step 1 in Table 1): they target a desired exposure and outcome, identify important covariates, and pre-specify any patient subgroups in which subgroup analysis should be performed.

Table 1.

Outline of proposed data integration process

Step	Procedure
1	Implement basic study design Identify centers and data sources Define cohort entry criteria Define exposure and outcome Define covariates available at each center Pre-define patient subgroups
2	Divide measured covariates into three categories: Shareable (e.g., age in decades, sex, year of cohort entry) Private and available in all centers (“private universal”, e.g., service dates, procedures) Private and not available in all centers (“private center-specific”, e.g., lab values)
3	Estimate propensity scores within each center: Universal propensity score based on shareable and private universal covariates Local propensity score based on shareable, private universal, and private center-specific covariates High-dimensional propensity score (if desired)
4	Create and transmit center-aggregated transfer files containing: Study patient identifier Center identifier Exposure Outcome Shareable covariates Each of the estimated propensity scores Propensity score diagnostics (c-statistics, balance in treatment groups, etc.)
5	Merge each center’s data into a pooled dataset Assess center heterogeneity Perform covariate balancing as desired: Compute decile of propensity score within each center Match on propensity score within each center
6	Perform statistical analysis Estimate treatment effects using one or more of: Logistic models stratified by center Cox proportional hazard models stratified by center Analyses on matched cohorts Fixed- and random-effects meta-analysis

From that point, patient-level information is divided into three categories: shareable, private universal, and private center-specific (Step 2). Shareable information comprises non-confidential covariates that are measured in virtually all patients.⁷ These include age in decades, sex, index date, drug exposure status, outcome status, and event and censoring dates. Private universal information, information that would generally be considered non-disclosable or protected under HIPAA standards and that is measured in all centers,¹⁸ includes more sensitive patient data: prior procedures, diagnoses and drugs; recent diagnosis-related groups (DRGs) and hospitalization discharge diagnoses; nursing home stays; and other confidential information. The specific coding may vary between databases – one center could record diagnoses with ICD-9 codes while another might use ICD-10 – as long as all centers provide equivalent measurement of the underlying condition. Private center-specific information includes those private covariates that only certain centers can provide based on the granularity of their data or their access to electronic medical records (EMRs) or lab values. Examples include socioeconomic status, family history of disease, and troponin or LDL cholesterol levels.

With these covariates, each center estimates and records several PSs (Step 3): first, a PS based on the shareable and private universal information (PS_Univ) and optionally, second, a high-dimensional propensity score (hd-PS).¹⁹ The PS_Univ is estimated by a logistic regression model with exposure as the dependent variable and the covariates as the independent variables.^15,20 The hd-PS is estimated using the published hd-PS algorithm.¹⁹ This algorithm examines all recorded diagnosis, procedure, and drug codes for the cohort’s patients, and then ranks the codes by their potential to bias the exposure/outcome relationship under study. The several hundred highest-ranked codes are combined with all investigator-defined covariates and entered into a single PS model. The hd-PS SAS macro is available at www.drugepi.org.

If the centers vary with respect to the amount of data available – for example, if one center has EMRs but the others do not – a third PS can be estimated. This score, noted PS_Local, is based on the private center-specific information as well as the shareable and private universal information. A PS_Local could be used for adjustment alongside or instead of the PS_Univ, and may convey more complete confounding information than would the PS_Univ alone.

Transfer and analysis of centers’ data

Each center creates an aggregated transfer file (Steps 4 and 5) and transmits the file to the analytic hub, where all of the files are pooled. Each file contains only non-private information: a center identifier, a randomly generated patient identifier, the shareable covariates, and the PSs. The flow of shareable and private information between centers and the analytic hub is displayed in Figure 1.

Figure 1.

Flow diagram of proposed data integration method

The analytic hub can undertake any statistical method suitable for PS analysis (Step 6), including adjusting by quintile or decile of score, or PS matching.²¹ Depending on the study population and analytic plan, the matching can be 1:1 or 1:many,²² and can occur within or among centers. Among-center matching should only be considered if there is very little heterogeneity among patients and coding patterns, as a score of 0.45 in Center 1 may not be equivalent to a score of 0.45 Center 2. Quintiles or deciles of PS are far likelier to be comparable across centers.

EXAMPLE STUDY

Recent literature suggests the potential for a negative interaction between clopidogrel, an anti-platelet agent, and PPIs such as omeprazole.^23,24 The concern has been that PPIs may block the anti-platelet effects of clopidogrel by inhibiting a shared activation enzyme, resulting in more thrombotic events in clopidogrel users who concurrently use PPIs versus those who use clopidogrel alone. We assembled four cohorts of patients who had undergone PCI or who had been hospitalized for MI or unstable angina and who filled an initial prescription for clopidogrel within 7 days of discharge.²⁵ We counted as exposed those patients who used a PPI during those 7 days. Clopidogrel users with no recorded PPI use were counted in the comparator.

Starting at the end of the 7-day run-in period,²⁶ we sought outcomes of hospitalization for MI or revascularization. MI was identified through ICD-9 discharge diagnosis codes; revascularization was determined through ICD-9 and CPT procedure codes. The full design of the example study has been described in other work.²⁷

To demonstrate and test the method, we combined data from four data sources for which we had direct access to covariate-level information. Thus, we served both as the four centers and the analytic hub in order to assess the method in an environment with full visibility into the data elements. Each of our four centers was a health insurance program: Pennsylvania’s (PA) state Pharmaceutical Assistance Contract for the Elderly program, New Jersey’s (NJ) state Pharmaceutical Assistance to the Aged & Disabled program, British Columbia’s (BC) Pharmacare program, and NJ residents covered by commercial insurer Horizon. Details of the centers’ populations are described in other works.^28–31 Among the four centers, we expected meaningful variation in overall health status, plan benefits, and other key drivers of drug utilization patterns and health outcomes.³² The Institutional Review Board of the Brigham and Women’s Hospital approved this study and data use agreements were in place.

We considered age and sex to be shareable information. We estimated the PS_Univ using a logistic regression model dependent on age, sex, and approximately 25 private universal covariates. These covariates included past use of non-selective NSAIDs, coxibs, or statins; history of MI or gastrointestinal (GI) bleed; prior diagnosis of diabetes or hypertension; and number of medications the patient used. An hd-PS was estimated based on the maximum information available at each center: patients’ prior medication usage, diagnoses, and procedures recorded in inpatient settings, outpatient settings, and nursing homes. Based on earlier research,¹⁹ we considered 200 variables per dimension and included the top 400 confounders in the hd-PS. Because each of our centers collected comparable amounts and types of data, we did not implement a PS_Local in our example study.

We performed two main statistical analyses. In the first, we did a cumulative risk analysis using logistic regression to estimate the relative risk of outcome with a fixed 90-day follow-up time. In the second, we did a time-to-event analysis using Cox proportional hazards models to estimate the hazard ratio. Participants were censored at the earliest of 180 days, occurrence of the endpoint, stopping clopidogrel, change in PPI exposure status, or death. We performed these analyses with the PSs and, for validation, with full covariate information. Analyses were carried out both within each center and pooled across all centers. We hypothesized that the score PS-adjusted and covariate-adjusted point estimates and their confidence intervals would be nearly equal.

All pooled models were stratified by center. Pooled PS-adjusted models were adjusted by decile of PS and, separately, with 1:1 greedy matching²¹ within center.²² Greedy matching began at the eighth decimal place and continued to the first. Ninety-five per cent confidence intervals are reported. We also computed a c-statistic for each PS; the c-statistic, a number between 0.5 and 1.0, indicates the area under the receiver operating curve (ROC) and is a broad though imperfect measure³³ of how well the PS predicts the exposure. Finally, to compare pooling against meta-analysis, we performed fixed- and random-effects meta-analyses using point estimates and variances estimated within each center.^2,36

All models were run in SAS version 9.2 using PROCs LOGISTIC and PHREG. Meta-analyses were performed in Stata version 9 using the ‘meta’ add-on.³⁵

RESULTS

There was variation in the patient composition of the four cohorts; the average age ranged from 55 in Horizon to 78 in PA and NJ (Table 2). Prevalence of baseline risk factors for three outcomes also ranged widely: the younger Horizon population had fewer than 1% of patients with a history of hospitalization for GI bleed, while the low-income elderly patients from NJ had a prevalence of 4%. Seventy-one per cent of BC was male while 75% of PA was female.

Table 2.

Characteristics of study participants from four populations. Cohort entry was defined by percuataneous coronary intervention or hospitalization for myocardial infarction or acute coronary syndrome

Variable	British Columbia		Pennsylvania		New Jersey		Horizon		Pooled
	PPI use (n = 2191)	PPI non-use (n = 17788)	PPI use (n = 1352)	PPI non-use (n = 2824)	PPI use (n = 1291)	PPI non-use (n = 2707)	PPI use (n = 822)	PPI non-use (n = 2629)	PPI use (n = 5656)	PPI non-use (n = 25948)
Age	67.99 ± 11.96	64.65 ± 11.83	78.67 ± 6.56	78.29 ± 6.67	78.38 ± 6.90	77.71 ± 6.85	55.04 ± 6.57	54.84 ± 6.76	67.31 ± 12.52	66.50 ± 12.44
Male gender	60.8%	72.3%	21.6%	26.7%	30.9%	36.4%	73.0%	77.2%	60.9%	64.1%
Previous hospitalization for
Myocardial infarction	8.0%	9.4%	4.7%	4.3%	3.8%	3.4%	0.6%	0.2%	6.9%	7.3%
Gastrointestinal bleed	2.1%	0.2%	5.6%	1.9%	6.2%	3.0%	1.5%	0.5%	1.3%	0.7%
Angina	6.6%	7.6%	5.0%	3.6%	4.0%	4.2%	1.2%	1.1%	5.9%	6.1%
Peripheral vascular disease	1.2%	0.7%	2.1%	1.5%	1.9%	2.2%	1.1%	0.6%	1.0%	0.9%
Hemmorhagic stroke	0.5%	0.2%	2.6%	2.0%	2.2%	1.5%	1.2%	0.6%	0.8%	0.6%
Previous use of
Non-selective NSAID	22.4%	19.1%	15.9%	14.4%	17.6%	15.6%	17.8%	15.3%	18.1%	17.9%
Cox-2 inhibitor	11.3%	6.8%	30.0%	21.5%	32.8%	25.7%	13.6%	8.8%	12.5%	10.6%
Diabetes drug	12.0%	12.8%	29.7%	32.6%	28.6%	31.3%	21.9%	19.2%	18.2%	17.5%
Statin	37.1%	40.6%	44.2%	44.5%	44.3%	47.8%	39.7%	39.4%	41.5%	41.7%
Beta blocker	33.2%	36.5%	53.2%	54.4%	49.0%	53.7%	35.6%	33.2%	40.3%	39.9%
ACE/ARB	32.1%	33.7%	48.0%	47.9%	47.9%	48.7%	33.1%	30.7%	37.1%	36.5%
Warfarin	4.8%	3.8%	11.8%	11.4%	12.4%	11.0%	5.5%	2.4%	5.8%	5.2%
Previous diagnosis of
Diabetes	27.0%	24.4%	39.3%	41.5%	37.6%	39.2%	26.5%	26.0%	28.7%	28.0%
Hypertension	58.7%	50.2%	75.9%	74.1%	75.6%	74.8%	57.1%	54.6%	57.7%	55.8%
Peripheral vascular disease	0.5%	0.3%	11.8%	8.0%	17.1%	16.8%	2.1%	2.1%	3.8%	3.1%
Congestive heart failure
Number of generics	3.79 ± 4.30	2.97 ± 3.29	12.67 ± 6.16	10.24 ± 5.29	13.43 ± 7.03	11.40 ± 6.17	9.23 ± 7.44	7.16 ± 6.15	5.75 ± 5.95	5.07 ± 5.37
Number of hospital days	8.97 ± 13.87	5.98 ± 7.82	4.78 ± 9.95	3.25 ± 7.50	5.86 ± 12.51	3.58 ± 8.28	1.25 ± 5.83	0.62 ± 3.48	5.11 ± 8.67	4.89 ± 7.72
Number of office visits	10.91 ± 18.47	9.33 ± 12.81	11.26 ± 8.43	10.34 ± 6.82	12.89 ± 8.38	11.84 ± 8.08	7.82 ± 8.84	6.28 ± 7.08	9.68 ± 11.84	9.39 ± 11.46
Charlson score	2.53 ± 1.82	2.04 ± 1.52	2.82 ± 2.12	2.51 ± 1.96	3.04 ± 2.26	2.74 ± 2.17	1.52 ± 1.49	1.22 ± 1.28	2.17 ± 1.75	2.08 ± 1.67

Including the private universal covariates in each center’s PS model added information and increased c-statistics substantially, with increases in c-statistics of between 0.12 and 0.14. Moving from the universal to high dimensional PS further increased the PSs’ prediction of exposure in all centers: c-statistics increased again by between 0.08 and 0.13, indicating that the addition of the empirical variables identified by the hd-PS positively affected the ability to predict exposure.

Under the fixed-time cumulative risk analysis, the MI hospitalization outcome occurred in 4.3% of the pooled cohort’s PPI user group and 3.3% of its non-user group (Table 3). The crude association between PPI use and MI, pooled HR = 1.52 (1.30, 1.76), was substantially reduced by addition of variables and PSs to the models; the adjusted estimate was HR = 1.20 (1.03, 1.41). Moving to the estimate based on the hd-PS continued the downward trend to HR = 1.11 (0.95, 1.31). There were certain instances in which no center-specific point estimate could be reached due to low event rates; this was true for all odds ratio estimates in the Horizon cohort, and for selected estimates in the NJ cohort.

Table 3.

Point estimates for risk of two study outcomes. Cumulative risk and time-to-event models are shown, each with several methods of covariate adjustment. Models (3) and (4) include the same covariate set—(3) as individual covariates and (4) as components of the propensity score—and should therefore yield substantially similar estimates

Outcome	Within-center analyses				Combined Center Analyses
	British Columbia† (n = 19 979)	Pennsylvania (n = 4176)	New Jersey (n = 3998)	Horizon (n = 3451)	Pooled‡ (n = 31 604)	Meta-analysis§
						Fixed-effects estimate (n = 31 604)	p-value for heterogeneity among centers
Myocardial infarction hospitalization
Cumulative risk analysis (odds ratios)
Number of events (risk) among PPI users	135 (6.2%)	48 (3.6%)	41 (3.2%)	21 (2.6%)	245 (4.3%)	—	—
Number of events (risk) among non-users	669 (3.8%)	85 (3.0%)	64 (2.4%)	46 (1.7%)	864 (3.3%)	—	—
1 Crude	1.68 [1.39, 2.03]	1.19 [0.83, 1.70]	1.35 [0.91, 2.02]	~1.47 [0.87, 2.48]	1.52 [1.30, 1.76]	1.52 [1.31, 1.76]	0.36
2 Adjusted by shareable variables	1.50 [1.23, 1.81]	1.20 [0.84, 1.73]	1.31 [0.88, 1.95]	~1.42 [0.84, 2.40]	1.40 [1.21, 1.63]	1.41 [1.21, 1.64]	0.75
3 Adjusted by shareable and private variables	1.23 [1.00, 1.52]	1.18 [0.80, 1.72]	~1.21 [0.79, 1.86]	~1.05 [0.60, 1.86]	1.20 [1.03, 1.41]	1.20 [1.03, 1.41]	0.96
4 Adjusted by universal PS	1.23 [1.01, 1.50]	1.19 [0.82, 1.74]	1.14 [0.75, 1.71]	~1.11 [0.65, 1.91]	1.16 [1.00, 1.36]	1.20 [1.03, 1.40]	0.98
5 Adjusted by hd-PS	1.15 [0.94, 1.41]	1.03 [0.69, 1.56]	1.27 [0.82, 1.98]	~0.99 [0.55, 1.78]	1.11 [0.95, 1.31]	1.14 [0.97, 1.33]	0.88
Time-to-event analysis (hazard ratios)
1 Crude	1.87 [1.49, 2.35]	2.03 [1.16, 3.56]	1.32 [0.74, 2.36]	1.21 [0.62, 2.33]	1.74 [1.44, 2.11]	1.75 [1.45, 2.12]	0.44
2 Adjusted by shareable variables	1.66 [1.32, 2.09]	2.12 [1.21, 3.71]	1.25 [0.70, 2.22]	1.18 [0.61, 2.27]	1.60 [1.32, 1.94]	1.61 [1.33, 1.95]	0.45
3 Adjusted by shareable and private variables	1.34 [1.06, 1.71]	1.99 [1.11, 3.56]	1.19 [0.65, 2.17]	0.75 [0.37, 1.54]	1.34 [1.10, 1.63]	1.33 [1.09, 1.62]	0.22
4 Adjusted by decile of universal PS	1.35 [1.07, 1.71]	2.11 [1.16, 3.81]	1.22 [0.67, 2.21]	0.88 [0.45, 1.72]	1.32 [1.09, 1.61]	1.35 [1.11, 1.64]	0.28
5 Adjusted by decile of hd-PS	1.28 [1.00, 1.63]	1.95 [1.03, 3.70]	1.05 [0.56, 1.98]	0.78 [0.38, 1.59]	1.22 [0.99, 1.50]	1.25 [1.02, 1.54]	0.28
Hospitalization for revascularization
Cumulative risk analysis (odds ratios)
Number of events (risk) among PPI users	105 (4.8%)	96 (7.1%)	114 (8.8%)	106 (12.9%)	421 (7.4%)	—
Number of events (risk) among non-users	661 (3.7%)	192 (6.8%)	259 (9.6%)	255 (9.7%)	1367 (5.3%)	—
1 Crude	1.30 [1.06, 1.61]	1.05 [0.81, 1.35]	0.92 [0.73, 1.15]	~1.38 [1.08, 1.75]	1.15 [1.02, 1.29]	1.15[1.03, 1.30]	0.05
2 Adjusted by shareable variables	1.35 [1.09, 1.67]	1.05 [0.81, 1.35]	0.94 [0.74, 1.18]	~1.38 [1.08, 1.76]	1.17 [1.04, 1.32]	1.17 [1.04, 1.32]	0.05
3 Adjusted by shareable and private variables	1.23 [0.99, 1.53]	1.02 [0.78, 1.34]	0.96 [0.75, 1.22]	~1.39 [1.09, 1.79]	1.15 [1.02, 1.30]	1.14 [1.01, 1.29]	0.13
4 Adjusted by universal PS	1.27 [1.02, 1.57]	1.03 [0.79, 1.35]	0.94 [0.74, 1.20]	~1.38 [1.07, 1.77]	1.13 [1.00, 1.28]	1.15 [1.02, 1.30]	0.11
5 Adjusted by hd-PS	1.21 [0.97, 1.50]	1.07 [0.81, 1.43]	0.88 [0.68, 1.14]	~1.31 [1.00, 1.71]	1.07 [0.94, 1.21]	1.11 [0.98, 1.26]	0.16
Time-to-event analysis (hazard ratios)
1 Crude	1.41 [1.08, 1.32]	0.96 [0.67, 1.37]	0.77 [0.56, 1.05]	1.34 [1.02, 1.77]	1.12 [0.96, 1.30]	1.14 [0.98, 1.32]	0.01
2 Adjusted by shareable variables	1.50 [1.15, 1.96]	0.95 [0.66, 1.36]	0.78 [0.57, 1.06]	1.34 [1.02, 1.77]	1.14 [0.98, 1.32]	1.16 [1.00, 1.35]	0.01
3 Adjusted by shareable and private variables	1.42 [1.08, 1.87]	0.96 [0.66, 1.39]	0.78 [0.56, 1.07]	1.34 [1.01, 1.78]	1.14 [0.97, 1.32]	1.14 [0.98, 1.33]	0.02
4 Adjusted by universal PS	1.44 [1.10, 1.88]	0.93 [0.64, 1.36]	0.76 [0.55, 1.05]	1.32 [0.99, 1.75]	1.11 [0.95, 1.29]	1.13 [0.97, 1.32]	0.01
5 Adjusted by hd-PS	1.41 [1.07, 1.86]	0.92 [0.62, 1.38]	0.70 [0.50, 0.99]	1.30 [0.96, 1.77]	1.07 [0.91, 1.26]	1.10 [0.94, 1.30]	0.01

PS Propensity score; hd-PS High dimensional propensity score. Universal PS included all shareable and private variables.

PS-adjusted models are adjusted by indicators for decile of PS. PS deciles are computed within each center.

^~Model failed to converge and value is approximate.

^†Within-center odds ratios are estimated by logistic regression.

^‡Pooled odds ratios are estimated by conditional logisitic regression. Pooled hazard ratios are estimated by Cox proportional hazards models. Both are stratified by center.

^§Fixed-effects meta-analysis method. The random effects method yielded nearly identical results which are not displayed.

There were differences among the centers’ odds ratio and hazard ratio point estimates, but for the MI outcome, p-values for heterogeneity were each over 0.05, and in the multivariate-adjusted analyses, each point estimate was within the range of the others’ confidence intervals. There was statistically significant heterogeneity among each of the centers in the time-to-event analysis of the revascularization outcome; the p-value for heterogeneity was below 0.05 in several cases.

Regardless of method employed, we saw substantially similar point estimates and confidence intervals when adjusting by individual covariates (Model 3 in Table 3) versus adjusting by deciles of PS (Model 4). The PS-adjusted OR estimate for MI was 1.16 (1.00, 1.36) versus the variable-adjusted figure of OR = 1.20 (1.03, 1.41). For revascularization, the comparable figures were 1.13 (1.00, 1.28) and 1.15 (1.02, 1.30). We observed similar results in the time-to-event analysis.

For both the odds and hazard ratios, pooling and meta-analysis yielded very similar results; meta-analytic point estimates differed by 0–4% from the associated pooled estimate. Note that in cases where the center-specific logistic regression model did not converge (marked with a tilde in the table), the meta-analysis was based on the best estimate at the time the logistic regression procedure stopped. Fixed and random-effects meta-analyses yielded nearly identical results. Odds and hazard ratios as a result of the 1:1 universal PS matched analysis (Table 4) were also generally similar to their non-matched counterparts; hd-PS-based matching exhibited lower matching frequencies and greater variability than did the matching based on universal PS.

Table 4.

1:1 propensity score matched analysis of outcomes presented in Table 3. Matching was performed with the greedy matching algorithm

Outcome	Within-center analyses				Pooled†
	British Columbia*	Pennsylvania	New Jersey	Horizon
Myocardial infarction hospitalization
Cumulative risk analysis (odds ratios)
Matched by universal PS	1.26 [0.97, 1.62]	1.06 [0.68, 1.64]	1.30 [0.81, 2.08]	0.97 [0.52, 1.78]	1.19 [0.98, 1.44]
Per cent of exposed patients matched	98.4%	91.7%	94.3%	95.0%	95.4%
Matched by hd-PS	1.19 [0.92, 1.54]	1.31 [0.81, 2.11]	1.34 [0.81, 2.20]	1.05 [0.50, 2.17]	1.21 [1.00, 1.48]
Per cent of exposed patients matched	95.6%	74.6%	79.1%	84.8%	85.2%
Time-to event analysis (hazard ratios)
Matched by universal PS	1.24 [0.91, 1.69]	1.59 [0.78, 3.25]	1.64 [0.80, 3.36]	0.81 [0.37, 1.76]	1.26 [0.98, 1.62]
Per cent of exposed patients matched	98.4%	91.7%	94.3%	95.0%	95.4%
Matched by hd-PS	1.22 [0.89, 1.68]	3.30 [1.25, 8.70]	0.91 [0.45, 1.83]	0.52 [0.21, 1.27]	1.17 [0.90, 1.52]
Per cent of exposed patients matched	95.8%	73.5%	77.5%	86.4%	85.0%
Hospitalization for revascularization
Cumulative risk analysis (odds ratios)
Matched by universal PS	1.52 [1.11, 2.06]	1.00 [0.75, 1.34]	0.97 [0.75, 1.27]	1.26 [0.94, 1.68]	1.15 [1.00, 1.33]
Per cent of exposed patients matched	98.4%	91.7%	94.3%	95.0%	95.4%
Matched by hd-PS	1.06 [0.81, 1.40]	1.00 [0.72, 1.37]	0.91 [0.67, 1.22]	1.46 [1.07, 2.00]	1.08 [0.93, 1.26]
Per cent of exposed patients matched	96.3%	74.4%	78.2%	84.9%	85.3%
Time-to event analysis (hazard ratios)
Matched by universal PS	1.47 [1.00, 2.15]	0.85 [0.56, 1.29]	0.80 [0.55, 1.16]	1.26 [0.89, 1.77]	1.07 [0.89, 1.29]
Per cent of exposed patients matched	98.4%	91.7%	94.3%	95.0%	95.4%
Matched by hd-PS	1.48 [1.00, 2.19]	0.88 [0.57, 1.38]	0.73 [0.49, 1.10]	1.58 [1.09, 2.30]	1.14 [0.94, 1.39]
Per cent of exposed patients matched	96.1%	76.0%	78.2%	84.9%	85.6%

PS Propensity score; hd-PS High-dimensional propensity score.

^*Within-center odds ratios are estimated by logistic regression.

^†Pooled odds ratios are estimated by conditional logisitic regression stratified by center.

DISCUSSION

The safe and effective use of medications will increasingly require the deployment of rigorous analytic tools that make it possible to identify risks in very large populations and to execute valid, rapid studies. In this paper, we have proposed a novel approach to combining data from multiple centers. The approach protects patients’ and organizations’ privacy and maintains analytic integrity. In our example study, we observed that pooling individual-level patient data based on a PS resulted in qualitatively similar estimates to pooling based on individual covariates, while not yielding any information that would easily lead to patient identification or health plan case-mix. hd-PS adjustment was as effective or more effective in controlling for confounding than was standard adjustment. We observed little difference between pooled results and results from meta-analysis. In all, we found that in our data, the proposed method of pooling offered many benefits with few drawbacks.

Pooling based on PS is a simple technique that was effective in our example study. PSs allow full conveyance of covariate information.²⁰ They are robust to over-fitting; since a PS is meant to describe the data at hand and is not meant to be generalized beyond the population under study, it is considered ‘safe’ to add numerous confounders to the model.¹⁵ However, the fundamental question of whether pooling out-performs meta-analysis remains, as both achieve the primary goal of increasing statistical power to detect an association between exposure and the outcome of interest.³

The literature generally leans toward pooling individual-level data rather than doing study-level meta-analysis, when possible.^1,2,36 The rationale is partially analytical and partially operational. Analytically, pooling allows for easier assessment of dose–response relationships,¹ though it is certainly possible to evaluate dose–response data meta-analytically if exposures are categorized equivalently across studies. Pooling may also perform better in the context of rare outcomes,² as it may not be possible to generate a center-specific estimate if there are few outcomes in that center. The main benefit ascribed to individual-level pooling is its ability to detect interactions and population heterogeneity. This may be harder when covariates are summarized as PSs, but even with PSs, it is possible to search for interactions of treatment with shareable covariates, shared subgroup indicators, and strata of PS. As in most studies, significance tests for interactions may remain underpowered,³³ but variation in measures of association among centers can indicate effect measure modification.

For the price of somewhat increased operational complexity, pooling provides far more analytic flexibility than does meta-analysis. Analytic exploration of data, matching on factors identified post hoc, and conducting subgroup analyses are each more straightforward with pooled, individual-level data. However, with either pooling or meta-analysis, there is a baseline level of complexity inherent to all multi-center studies: necessary challenges lie in creating datasets with harmonized definitions for exposures, outcomes, and covariates. Meta-analysis may hide these universal challenges – or mask even errors –under the guise of tidy point estimates. One partial remedy may be high dimensional PSs, which are implemented with a downloadable SAS macro and are applicable to either a pooled study or a meta-analysis. The hd-PS technique can reduce some of the complexity of covariate definition by adjusting for hundreds of empirically identified variables alongside a greatly reduced panel of variables identified by the investigators a priori.²¹

Awareness of heterogeneity is a fundamentally important aspect of multi-center analyses; in many studies, centers’ populations are likely to be meaningfully heterogeneous.³² Moreover, there may be ‘information heterogeneity’ among the centers with respect to the quality and quantity of data elements each center is able to measure. The proposed method—when used with both universal and local PSs—will avoid resorting to the ‘lowest common denominator’ of available data. Analyzing the centers’ data twice, once using the universally defined PS_Univ, and again using the maximal information PS_Local, may allow for disentangling population and information heterogeneity. The PS_Local-adjusted estimate may be used to identify the center that had the most complete confounding adjustment and therefore the most valid analysis; deviations from this estimate could indicate residual confounding in the other centers’ estimates.

Investigators using the method we propose need to make certain choices on a study-by-study basis, such as how to handle missing data, which variables to include in the PS, how to assess the possibility of residual confounding, and what statistical methods to employ. The method also has certain limitations. It may add complexity where it may not be needed, or mask problems in covariate definition in the process of summarizing covariates into a single score. It requires a somewhat higher level of analytic expertise at each center in order to create the necessary PSs, though one solution would be for a single party to provide programming macros that could be shared across centers.³⁷ The method would requires extensions to assess dose–response relationships, multiple exposure categories, or time-varying exposures and covariates. One way to address some of these challenges would be to summarize covariates not in a PS but rather in a disease risk score, and then apply the same principle of pooling. Disease risk scores have operational advantages when studying multiple exposures or dose categories as they are estimated as a function of the outcome but independent of the exposure.^38,39 They are less useful, however, when outcomes are rare.

We have presented a simple and, in our example, effective process for pooling private data from multiple sources and performing multivariate-adjusted pharmacoepidemiologic analyses. We combined data first retaining individual covariates and then with only PSs, and in both cases observed substantially similar point estimates and confidence intervals. The PS-based estimates posed little risk of compromise of patient or center privacy. Despite the need for further testing –including on studies with a broad array of negative, positive, and null effects – we feel confident in the method as presented, and have applied it to several large research projects.

KEY POINTS.

• Pooling data from multiple cohorts is a key part of pharamcoepidemiologic studies of large populations, including FDA’s Sentinel Initiative. Pooling must occur in a way that protects patients’ privacy but also allows for full multivariate adjustment.

• We propose a propensity score-based approach to pooling data which allows sharing of cohort data without compromising patient privacy or study validity.

• We demonstrate the method in a four cohort study of a potential interaction between clopidogrel and PPIs. We compare study results using our proposed PS-based method versus the established techniques of covariate-based pooling and meta-analysis.