Broadband Heteronuclear Solid-State NMR Experiments by Exponentially Modulated Dipolar Recoupling without Decoupling

Abstract

We present a novel solid-state NMR method for heteronuclear dipolar recoupling without decoupling. The method, which introduces the concept of exponentially modulated rf fields, provides efficient broadband recoupling with large flexibility with respect to hetero- or homonuclear applications, sample spinning frequency, and operation without the need for high-power ¹H decoupling. For previous methods, the latter has been a severe source of sample heating which may cause detoriation of costly samples. The so-called EXPonentially mOdulated Recoupling Technique (EXPORT) is described analytically and numerically, and demonstrated experimentally by 1D ¹³C spectra and 2D ¹³C-¹⁵N correlation spectra of ¹³C,¹⁵N-labeled samples of GB1, ubiquitin, and fibrils of the SNNFGAILSS fragment of amylin. Through its flexible operation, robustness, and strong performance, it is anticipated that EXPORT will find immediate application for both hetero- and homonuclear dipolar recoupling in solid-state NMR of ¹³C,¹⁵N-labeled proteins and compounds of relevance in chemistry.

Over the past few years solid-state NMR has demonstrated capability to undertake a long-standing need in structural biology, namely resolving atomic-resolution structure and dynamics information for so-called insoluble proteins that reside in, e.g., membranes,^1–7 filaments,⁸ and amyloid fibrils.^9–14 This has been facilitated by development of advanced instrumentation, isotope-labeling procedures,^15–17 and pulse sequences extracting information from isotropic and anisotropic nuclear spin interactions to provide information about molecular structure and dynamics. Particular efforts have been devoted to the design of experiments which combines the high-resolution properties of magic-angle spinning (MAS) and recoupling methods to probe desired nuclear spin interactions while not using excessively long periods of strong rf irradiation.

To reduce sample detoriating effect of high-frequency rf heating focus has recently been devoted to the design of experiments that enable recoupling of dipolar interactions between low-γ nuclei without the need for intense ¹H irradiation for decoupling of dipolar interactions to protons. Until now this has been realized for experiments recoupling homonuclear ¹³C-¹³C couplings, as introduced through the experiments CMAR,¹⁸ RFDR without decoupling,^19,20 and variants of these.²¹ For the important class of heteronuclear recoupling experiments, being fundamental in solid-state NMR relying on ¹³C,¹⁵N-labeled compounds, broadband recoupling under fast MAS and high-field conditions in combination with released demands to decoupling remains a challenge.

In this Letter, we introduce a novel concept for dipolar recoupling taking advantage of multi-axis phase-modulated rf irradiation to enable recoupling of heteronuclear dipolar couplings with (a) extreme broadbandedness even at high field, (b) high efficiency through γ-encoded recoupling,²² (c) compensation for rf inhomogeneity, (d) operation at all relevant spinning frequencies, and (e) realization without high-power ¹H decoupling. This is accomplished by introducing exponentially modulated rf fields which, with inspiration from recent multiple-field-oscillating recoupling methods,^23,24 exploit the effect of two intertwined modulations to facilitate simultaneous ¹³C-¹⁵N (or ¹³C-¹³C) recoupling and ¹H decoupling. The method will be referred to as the EXPonentially mOdulated Recoupling Technique (EXPORT).

The recoupling experiment, illustrated schematically in Fig. 1, is governed by the rf Hamiltonian

$$H_{\mathit{\text{rf}}}=C_I{I}_x+C_S{S}_x+B_I{e}^{\mathit{\text{i̶}}{C}_I{\mathit{\text{tI}}}_x}{I}_y{e}^{i{C}_I{\mathit{\text{tI}}}_x}+B_S{e}^{\mathit{\text{i̶}}{C}_S{\mathit{\text{tS}}}_x}{S}_y{e}^{i{C}_S{\mathit{\text{tS}}}_x}$$ (1)

where I_q and S_q (q=x,y,z) represent Cartesian operators for the I and S spins, respectively, and B_I, B_S, C_I, and C_S amplitudes for the I- and S-spin components of the rf field. Although the method works equally well for homonuclear dipolar recoupling, we here restrict ourselves to the heteronuclear case with I=¹⁵N and S=¹³C. In pratice, the rf fields may be expessed in terms of an amplitude $A_K(t)=\sqrt{C_K^2+{(B_K\text{cos}(C_{K}t))}^2}$ and phase ${\varphi }_K(t)={\text{tan}}^{-1}\left(\frac{B_K\text{cos}(C_{K}t)}{C_K}\right)+\frac{B_K}{C_K}(\text{cos}(C_{K}t)-1)(K=I\text{or}S)$. While the use of different C_K values on the two rf channels offers interesting possibilities to adapt the rf fields most appropriately to the instrumentation and specific desires in terms of broadbandedness, we will for the sake of simplicity assume C=C_I=C_S.

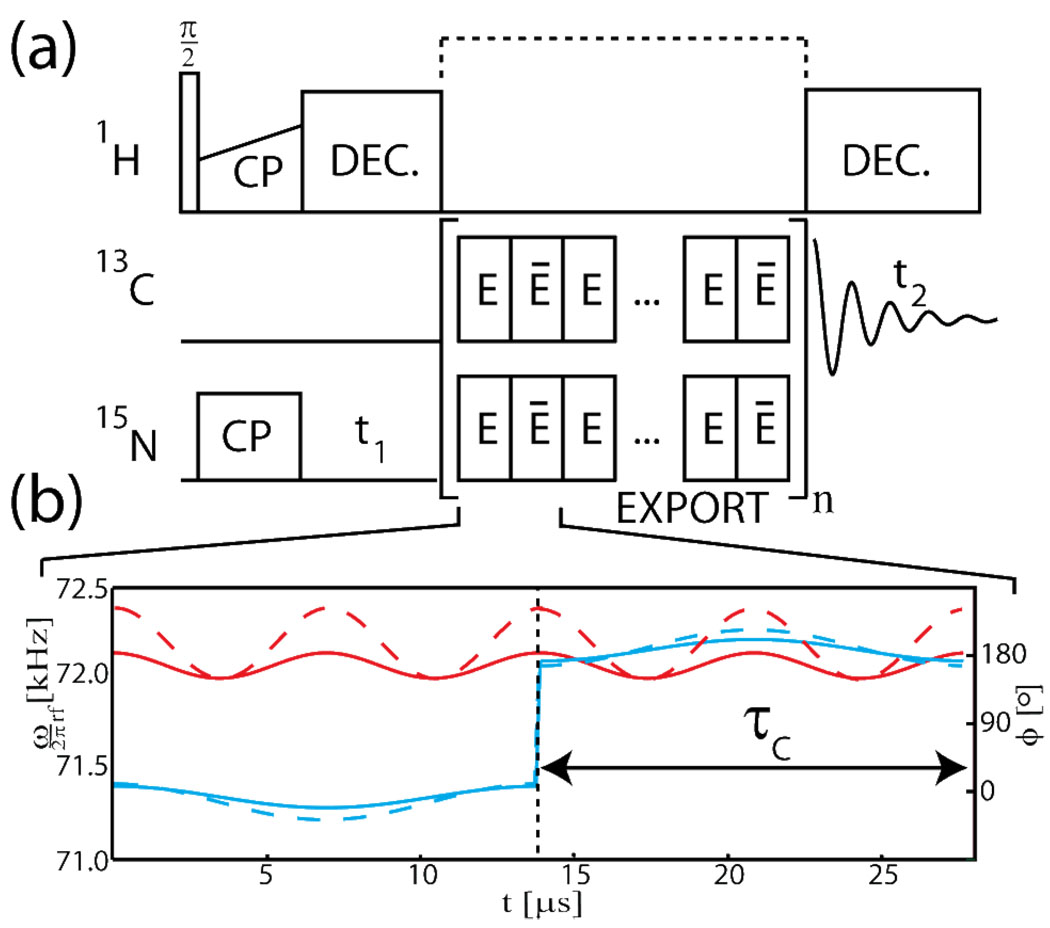
Figure 1.

(a) The EXPORT pulse sequence for heteronuclear dipolar recoupling without decoupling embedded in a typical 2D NCO/NCA chemical shift correlation experiment. (b) The amplitude (red) and phase (blue) modulation schemes of the basic elements with the ¹³C and ¹⁵N fields represented by solid and broken lines, respectively, for EXPORT with C=6ω_r, B_I=3ω_r/8, B_S=5ω_r/8, and ω_r/2π=12 kHz.

The impact of the rf field on chemical shift and dipolar couplings may be described by transforming the Hamiltonians for these interactions, H_K (t) = ω_K (t)K_z and H_IS(t) = ω_IS (t)2I_z S_z, respectively, into the interaction frame of the rf irradiation. By first transforming into the frame of the modulating field C(I_x+S_x) using F̃(t) = e^{iCt(I_x + S_x)}Fe^{−iCt(I_x + S_x)} and subsequently into the frame of the weak rf fields B_II_y and B_SS_y using F͌(t) = e^iB_ItI_x e^iB_StS_x F̃(t)e^{i̶B_S tS_x} e^i̶B_ItI_x one arrives at

$${\stackrel{\approx }{H}}_K(t)={\omega }_K(t)\left[-c_{\mathit{\text{Ct}}}{s}_{B_{K}t}{I}_x+s_{\mathit{\text{Ct}}}{I}_y+c_{\mathit{\text{Ct}}}{c}_{B_{K}t}{I}_z\right]$$ (2)

$${\stackrel{\approx }{H}}_{\mathit{\text{IS}}}(t)=2{\omega }_{\mathit{\text{IS}}}(t)[s_{\mathit{\text{Ct}}}^2{I}_y{S}_y+c_{\mathit{\text{Ct}}}^2\left(c_{B_{I}t}{c}_{B_{S}t}{I}_z{S}_z+s_{B_{I}t}{s}_{B_{S}t}{I}_x{S}_x-c_{B_{I}t}{s}_{B_{S}t}{I}_z{S}_x-s_{B_{I}t}{c}_{B_{S}t}{I}_x{S}_z\right)+s_{\mathit{\text{Ct}}}{c}_{\mathit{\text{Ct}}}\left(c_{B_{I}t}{I}_z{S}_y+c_{B_{S}t}{I}_y{S}_z-s_{B_{I}t}{I}_y{S}_x-s_{B_{S}t}{I}_x{S}_y\right)]$$ (3)

using the shorthand notation c_x=cos(x) and s_x=sin(x). By assuming C>>B_I,B_S,ω_r, it is evident that all linear terms (eq. (2)) – covering chemical shift on the I and S spins as well as dipolar couplings to protons (the Hamiltonian is modified by multiplying with 2H_z, with H_z being the ¹H Zeeman operator, and changing the angular frequency to that of the coupling) vanish to first-order upon averaging over the period 1/C. It can also be shown that the first and third of the three terms within the square bracket in eq. (3) does not lead to recoupling. Using ${\omega }_{\mathit{\text{IS}}}(t)={\displaystyle \sum _{m=-2}^2{\omega }_{\mathit{\text{IS}}}^{(m)}{e}^{\mathit{\text{im}}{\omega }_{r}t}}$ with the Fourier coefficients given elsewhere,²⁵ the second term lead to the first-order average over the period 1/|B_I−B_S|:

$${\overline{\stackrel{\approx }{H}}}_{\mathit{\text{IS}}}(B_I\pm B_S=n{\omega }_r)={\kappa }_n[c_{n{\gamma }_{\mathit{\text{PR}}}}(I_z{S}_z\mathrm{m}{I}_x{S}_x)-s_{n{\gamma }_{\mathit{\text{PR}}}}(I_x{S}_z\mathrm{m}{I}_z{S}_x)]$$ (5)

using ${\kappa }_{\pm 1}=b_{\mathit{\text{IS}}}{s}_{2{\beta }_{\mathit{\text{PR}}}}/(4\sqrt{2})\text{and}{\kappa }_{\pm 2}=-b_{\mathit{\text{IS}}}{s}_{{\beta }_{\mathit{\text{PR}}}}^2/8\text{with}{b}_{\mathit{\text{IS}}}=-{\gamma }_I{\gamma }_S{\mu }_o/(4\pi r_{\mathit{\text{IS}}}^3)$ denoting the dipole-dipole coupling in angular units and β_PR and γ_PR the polar an azimutal angles, respectively, relating the internuclear axis to the rotor axis. It is evident that γ_PR-encoded²² zero- or double-quantum dipolar recoupling (in a frame tilted by π/2 around I_y and S_y) may be obtained by adjusting the sum and difference of the recoupling B_I and B_S field amplitudes to match nω_r (n=±1 or ±2). Efficient cancellation of chemical shift and couplings to protons and avoiding interference with recoupling require that the decoupling field C is substantially larger than the B fields. Effects from rf inhomogeneity may be reduced by phase-alternating ±C for each τ _C=τ_r/C as illustrated by the E and E̅ elements in Fig. 1.

Independent adjustment of the recoupling and decoupling fields opens up the possibility to perform experiments with (small values of C) or without (large values of C) ¹H decoupling with great flexibility on the spinning frequency. This solves a major problem for heteronuclear dipolar recoupling, where typical combinations of recoupling fields at the low-γ spins species and simultaneous need for high-power ¹H decoupling (typical recommendation: ω_rf(¹H) > 2.5ω_rf(I,S)) may lead to excessively strong ¹H rf fields in the regime of medium to fast sample spinning with the inherent risk of sample damage. We note that at very spinning frequencies (>35 kHz), ¹H decoupling with low rf field strengths may be feasible.^26,27

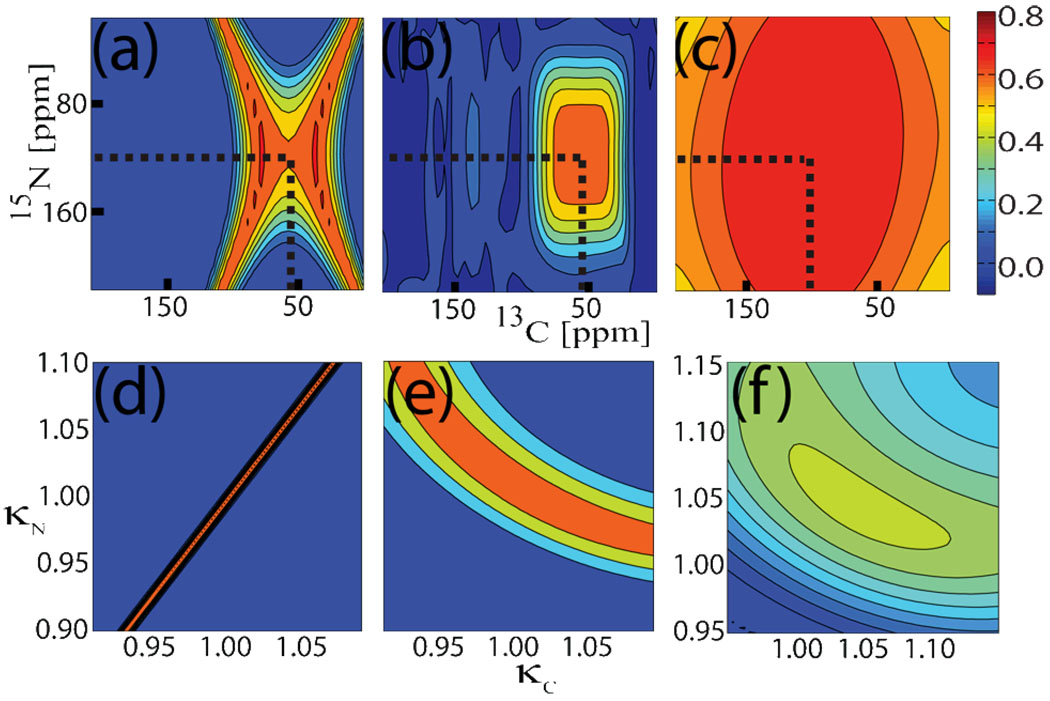
Through numerical simulations of ¹⁵N to ¹³C_α coherence transfer in a typical ¹⁵N-¹³C_α spin-pair system at 16.4 T using MAS with ω_r/2π=12 kHz, Fig. 2c demonstrates that EXPORT (C=6ω_r, B_I=3ω_r/8, and B_S=5ω_r/8) is substantially more robust with respect to resonance offsets than standard double-cross-polarization²⁹ (DCP, ω_rf,N=3ω_r, ω_rf,C=4ω_r) (Fig. 2a) and the deliberately bandselective ^OCNCA experiment (Fig. 2b).²⁸ EXPORT is also superior to previous experiments with respect to rf mismatch (and thereby rf inhomogenity) as illustrated in Figs. 2d–2f by numerical simulations for DCP (Fig. 2d), EXPORT with the rf wave digitized in 100 (Fig. 2e) and 20 (Fig. 2f) steps over each rotor period. Figures 2e and 2f also illustrate an important issue of EXPORT, namely the need for good digitization of the C-field phase modulation. Too low digitization may degrade the sensitivity of the experiment, but conversely improve the robustness towards rf inhomogeneity.

Figure 2.

¹⁵N to ¹³C_α coherence transfer efficiencies calculated for EXPORT using the parameters in Fig. 1b. (a–c) 2D ¹⁵N vs ¹³C offset plots for EXPORT (c), an ^OCNCA optimal control sequence²⁸ (b), and DCP (a)²⁹. (d–f) 2D ¹⁵N vs ¹³C rf field strength plots (scaling factors relative to the nominal values) for DCP (d), EXPORT with high digitization of the rf field (100 points over 1 rotor period) (e), and EXPORT with lower digitization (20 points over 1 rotor period) (f). Simulations were made using SIMPSON²⁵ with parameters³⁰ for a directly bonded ¹⁵N-¹³C_α spin system, powder averaging with 5 γ_CR and 144 REPULSION angles,³¹ and a spinning frequency of 12 kHz at 16.4 T. Broken lines mark carrier frequencies.

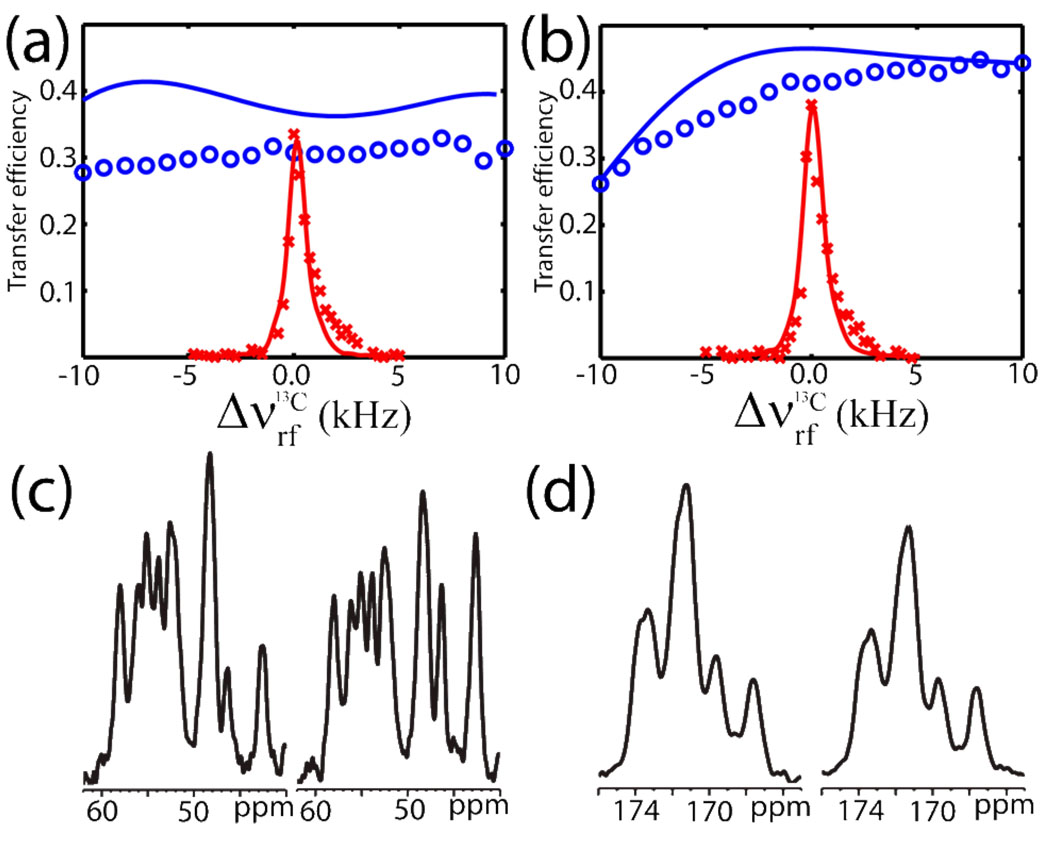
Experimental data in Fig. 3, obtained at 16.4 T for a fibrillar sample of the hIAPP20-29 decapeptide (SNNFGAILSS) of amylin with uniform ¹³C,¹⁵N labeling of the FGAIL stretch using a 1D version of the pulse sequence in Fig. 1 with 11.9 kHz spinning, clearly reinforces that EXPORT in addition to the clear advantage of recoupling without decoupling facilitates experimental realization through robustness towards rf mismatch and inhomogeneity. We note that the doubled number of peaks is a result of antiparallel fibril formation.¹³ Figure 3 illustrates experimentally and numerically the consequences of rf mismatch on the ¹³C rf channel for ¹⁵N to ¹³C_α (NCA, Fig. 3a) and ¹⁵N to ¹³C’ (NCO, Fig. 3b) coherence transfers for EXPORT (open circles; C=7ω_r, B_I=3ω_r/8, B_S=5ω_r/8, no decoupling) and a carefully optimized DCP sequence (crosses; ω_rf,C/(2π) = 50.2 kHz, ω_rf,N/(2π) = 39.3 kHz with 120 kHz CW ¹H decoupling). Both experiments and simulations took into account 5% Lorentzian rf inhomogeneity, which along with a relatively course digitization (time steps of 1.2 µs) reduces the overall transfer to 0.4–0.5 in this specific case. We note that the corresponding homonuclear experiments are considerably less influenced by digitization and rf inhomogeneity effects. Nonetheless, the experiments (including the representative spectra in Figs. 3c and 3d) and the good numerical reproductions clearly highlight the robustness of EXPORT relative to DCP with respect to rf field variations, which removes one of the major drawbacks of DCP, namely the need for very precise calibrations and long-term stability of the involved rf field strengths. It should be mentioned that under the present modest sample-spinning conditions some intensity loss is observed for the methylene groups using EXPORT without decoupling, which is understandable considering the strong couplings present in this system and the associated general difficulties in decoupling of methylene carbons.

Figure 3.

Experimental (signal integrals for the target spin spectral region) and simulated ¹⁵N to ¹³C’ (a) and ¹⁵N to ¹³C_α (b) coherence transfer efficiencies for DCP (experiment: red crosses, simulation: red line) and EXPORT (experiment: blue circles, simulation: blue line) as function of the ¹³C rf field strength mismatch. Experimental spectra were obtained for U-¹³C,¹⁵N-labeled FGAIL in a SNNFGAILSS fibril sample. Representative ¹³C spectra following (c) ¹⁵N to ¹³C_α and (d) ¹⁵N to ¹³C’ transfer for EXPORT (left) and DCP (right). In accord with Fig. 1a, the spectra were recorded using CP for the initial ¹H-¹⁵N transfer and SPINAL-64 decoupling³² (80 kHz) was used during acqusition. All spectra were recorded at 11.9 kHz spinning with carrier frequencies at 120 ppm for ¹⁵N and 50/172 ppm for NCA/NCO transfer. DCP used ω_rf,C/2π = 50.2 kHz, ω_rf,N/2π = 39.3 kHz, and 120 kHz ¹H decoupling. EXPORT used C=7ω_r, B_I=3ω_r/8, B_S=5ω_r/8, and no ¹H decoupling.

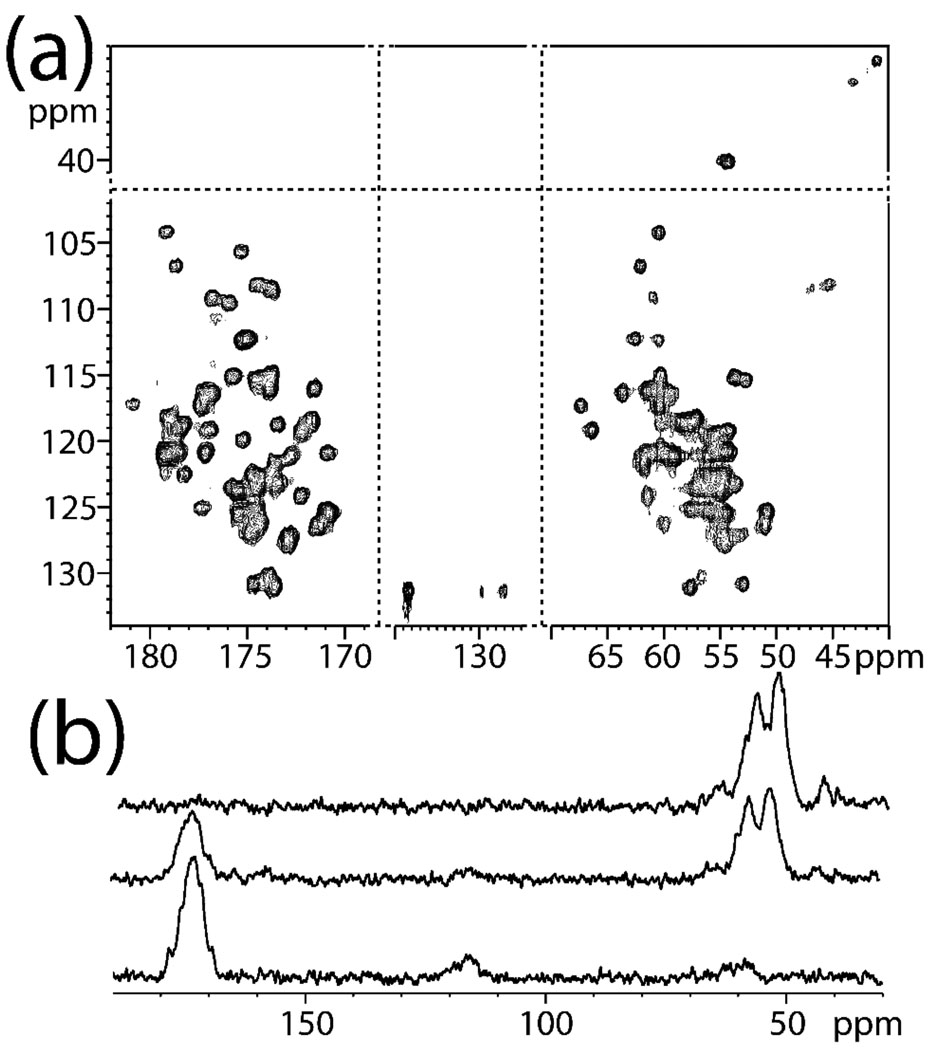
Figure 4a illustrates the use of EXPORT to obtain ¹⁵N-¹³C 2D chemical shift correlation for a uniformly-¹³C,¹⁵N-labelled sample of the β₁-domain of the immunoglobulin binding protein G (GB1)³³ at 23.81 kHz spinning without ¹H decoupling during the ¹³C-¹⁵N mixing. The static fields were adjusted to C=3ω_r (i.e., 71.5 kHz) with the ¹³C rf carrier between the ¹³C_α and ¹³C’ regions leading to efficient transfer to both types of spins. We note that recoupling without decoupling may alternatively be obtained using DCP or adiabatic variants with comparatively strong rf fields on the ¹³C and ¹⁵N channels, although with higher sensitivity towards rf inhomogeneity and mismatch. In Fig. 4b, we experimentally demonstrate the broadband recoupling of ¹³C,¹⁵N dipolar interactions for EXPORT on U-¹³C,¹⁵N-ubiquitin at 10.02 kHz spinning, using C=3ω_r, B_I=3ω_r/8, and B_S=5ω_r/8. By varying the ¹³C carrier frequency, polarization can be directed to both ¹³C_α’s and ¹³C`’s (top) or in a band-selective manner to either <sup>13</sup>C<sub>α</sub>’s (middle) or <sup>13</sup>C`’s (bottom). The spectra were obtained using relatively weak ¹³C,¹⁵N rf fields (~31 kHz) and standard ¹H CW decoupling (90 kHz) during the heteronuclear transfer.

Figure 4.

Experimental spectra for U-¹³C,¹⁵N-labeled samples of (a) GB1 and (b) ubiquitin recorded at 16.4 T using EXPORT for ¹⁵N-¹³C transfer with C =3ω_r, B_I=3ω_r/8, B_S=5ω_r/8, and τ_mix=2.35 ms. In accord with Fig. 1a, the spectra were recorded using CP for the initial ¹H-¹⁵N transfer. SPINAL-64 decoupling (70 kHz) was used in the detection periods. The 2D spectrum (a) used 23.81 kHz sample spinning without ¹H decoupling during EXPORT, 560 points in the indirect and 4096 point in the direct dimensions. The 1D spectra (b) used 10.02 kHz spinning, carrier frequencies at 40 (top), 120 (middle), and 180 (bottom) ppm, and 90 kHz ¹H decoupling during EXPORT.

In conclusion, we have introduced the concept of exponentially modulated dipolar recoupling and demonstrated its strong capabilities to accomplish ¹³C-¹⁵N dipolar recoupling at varying MAS frequencies with or without ¹H decoupling. Through its superior performance relative to previous methods, and the straightforward use of the EXPORT principle in numerous other applications, we anticipate that the presented methods will find widespread applications for solid-state NMR spectroscopy of biological molecules, as well as problems in materials chemistry where heteronuclear correlation experiments have broad applicability.