Abstract
Complex trait variation is likely to be explained by the combined effects of genes, environmental factors, and gene × environment (G × E) interaction. The authors introduce a novel 2-step method for detecting a G × E interaction in a genome-wide association study (GWAS) of case-parent trios. The method utilizes 2 sources of G × E information in a trio sample to construct a screening step and a testing step. Across a wide range of models, this 2-step procedure provides substantially greater power to detect G × E interaction than a standard test of G × E interaction applied genome-wide. For example, for a disease susceptibility locus with minor allele frequency of 15%, a binary exposure variable with 50% prevalence, and a GWAS scan of 1 million markers in 1,000 case-parent trios, the 2-step method provides 87% power to detect a G × E interaction relative risk of 2.3, as compared with only 25% power using a standard G × E test. The method is easily implemented using standard software. This 2-step scan for G × E interaction is independent of any prior scan that may have been conducted for genetic main effects, and thus has the potential to uncover new genes in a GWAS that have not been previously identified.
Keywords: environmental exposure; epidemiologic methods; genetic association studies; genetics; genome-wide association study; models, genetic
Genome-wide association studies (GWAS) have successfully uncovered new genes for complex traits. Most of these genes, however, have only modest effects and explain only a small proportion of the overall trait variation (1). Many complex traits also have established environmental risk factors, but these nongenetic factors also leave much of the trait variation unexplained. Complex trait variation is likely to be due to the combined effect of genes, environmental factors, and their interactions. However, most investigators conducting GWAS do not consider gene × environment (G × E) interactions in their search for new genes. This is partly due to a current lack of efficient statistical methods for detecting interactions in high-volume genetic data.
In a GWAS, a dense panel of single nucleotide polymorphisms (SNPs) spanning the genome are genotyped and each SNP is tested for association with the trait. GWAS of a disease trait are often conducted using either the case-control study design or the case-parent trio study design. In the former, cases and unrelated controls are selected from a source population, and a standard logistic regression analysis can be used to test associations. It is well recognized that population stratification bias (also known as confounding by race/ethnicity) can adversely affect inferences in a case-control design. A number of strategies have been proposed with which to characterize individual ancestry and use this information in the model to adjust for race/ethnicity in the analysis of a case-control sample (2–6). A case-parent trio study, on the other hand, controls for race/ethnicity by design through the collection of data on parental genotypes. For a disease trait, the transmission disequilibrium test (7) can be applied to test for an association between each SNP and disease. Variations of the transmission disequilibrium test have been proposed that allow for the use of sibling genotypes (8), account for missing parental genotypes (9), and provide tests of G × E or G × G interaction (10–14).
For analysis of G × E interaction, an alternative to a case-control or case-parent trio study is the case-only design (15). Here, one simply tests for association between G and E in cases without the use of parental data. The case-only test has been shown to be more powerful than a case-control or case-parent-trio analysis for identifying interactions (16, 17). However, the validity of a case-only analysis depends on an underlying assumption of gene-environment (G-E) independence in the population, which, for many environmental factors, would be untenable across all SNPs being scanned in a GWAS. Population-level G-E dependence can occur if there is a causal association between G and E (e.g., a gene that predisposes a person to smoke) or a noncausal association induced by population stratification, specifically confounding due to differential G and E distributions within subgroups of the source population. Causal G-E association is likely to occur for only a small subset of SNPs. Noncausal G-E associations, on the other hand, are likely to be much more prevalent, particularly for factors such as height or diet that can vary substantially across ethnic subgroups. The case-parent design, on the other hand, requires the weaker assumption that G and E are independent, conditional on parental genotypes (12). While this will not hold for genes with a causal G-E association, it will hold for genes with a noncausal G-E association due to ethnic confounding.
We propose a new procedure with which to screen the genome for G × E interaction in the context of a GWAS of case-parent trios. This method uses G × E interaction information in a trio sample that is not used in standard tests but can be uniquely used in a GWAS to improve efficiency. The method is computationally efficient and can be implemented using standard statistical software. We compare the power of the proposed approach with that of a standard test of interaction over a wide range of underlying models.
MATERIALS AND METHODS
Consider a sample of N diseased persons sampled from a population, and let Dc, c = 1, …, N, denote the disease indicators for these cases. Let Ec denote the exposure of a given case to some environmental factor, where “environment” is loosely defined to include exogenous environmental variables (e.g., sunlight, air pollution), personal exposures (e.g., smoking, dietary fat), or other personal characteristics (e.g., sex, age). We assume that M SNPs spanning the genome are genotyped for each case, and we let the genotype at a given SNP locus for a case be denoted by Gc. We furthermore assume that the same M SNPs are typed for both parents of each case; we denote the genotypes at a given locus for the mothers and fathers by Gm and Gf, respectively, and let Gp = {Gm, Gf}. We let qA denote the frequency of the minor (less common) allele “A” for a given SNP and let “a” denote the more common allele. For use in a statistical model, G will be coded according to an assumed genetic model. In a GWAS, G is often coded according to an additive model, specifically G = 0, 1, or 2 for genotype aa, Aa, or AA, respectively. However, G could also be coded according to a dominant (G indicates AA or Aa genotype), recessive (G indicates AA genotype), or codominant (pair of indicators coding the 3 genotypes) model.
In a sample of case-parent trios, the probability of the data for a given trio can be expressed as
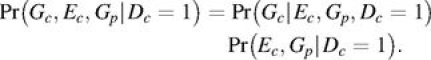 |
(1) |
The first factor in equation 1 is the basis for analysis of G × E interaction that has been previously described (11, 12). For example, Schaid (11) adopted a conditional logistic regression likelihood of the form
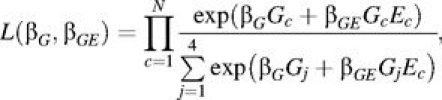 |
(2) |
where the sum in the denominator is taken over the 4 possible genotypes the case could have inherited, conditional on parental genotypes. The maximum likelihood estimates derived from equation 2 are consistent estimators of the corresponding relative risk parameters (11). Specifically, exp(βG) denotes the main effect of G—that is, the increase in the relative risk of disease per 1-unit increase in G for those unexposed (E = 0). The interaction effect exp(βGE) parameterizes the ratio of the genetic relative risks in exposed subjects compared with unexposed subjects. An additional requirement for inference related to interaction effects is that the main-effect model for G is correctly parameterized, which may cause one to choose a codominant coding for G effects. The main effect of E cannot be estimated in a case-parent trio design. As an alternative to conditional logistic regression, Umbach and Weinberg (12) developed a Poisson regression approach that also provides unbiased estimates of the same relative risk parameters, and which has the added advantage that it can naturally handle incomplete trios (9). The general assumptions required for analysis of trios by either the conditional logistic regression approach or the Poisson approach are the same, and are reviewed by Umbach and Weinberg (12). In the context of a GWAS, one can simply apply either the conditional logistic regression model or the Poisson model to each SNP in turn and test the corresponding G × E interaction null hypothesis that βGE = 0. We denote the likelihood ratio test of this null hypothesis as the “standard” test of G × E interaction.
The second factor on the right-hand side of equation 1 is typically assumed not to depend on parameters of interest and is ignored (12). However, in the presence of G × E interaction, there will be an induced association between case exposure and parental genotypes for an ascertained sample of cases. This follows from the known association between G and E in the presence of G × E interaction that is exploited in a case-only analysis (15), coupled with the inheritance-based association between case and parental genotypes. However, as in the case-only analysis, there will also be an induced association between case exposure and parental genotypes in the presence of population-level association (unrelated to disease) between exposure and genotype. Thus, as a means of final inference for testing a specific G × E interaction, use of the second factor in equation 1 can lead to an inflated type I error in the presence of population-level G-E association. For this reason, the G × E information contained in the Ec-versus-Gp association has not been utilized in previously proposed methods (11, 12).
In the context of a GWAS, we propose a 2-step analysis that will exploit all of the information in equation 1 while maintaining valid inference in the presence of population-level G-E association. This 2-step scan of M SNPs for G × E interaction in a case-parent trio sample takes the following form.
Step 1 (G-E association test).
Screen the M SNPs for G × E interaction at a fixed α1 significance level, based on a test of association between case exposures (Ec) and some function of the parental genotypes Gp*.
Step 2 (case-parent trio test).
Apply the conditional logistic regression likelihood in equation 2 to test G × E interaction with the m markers that pass step 1, declaring statistical significance at the α/m level, where α is the desired experiment-wise type I error rate.
The value of α1 should be chosen carefully to maximize the overall power of the 2-step procedure. As α1 increases, the power to pass a true G × E interaction from step 1 to step 2 increases, but m will also be inflated due to additional false positive SNPs' being passed to step 2. On the other hand, decreasing α1 will decrease m and increase power in step 2, but at the possible expense of preventing a true G × E interaction from reaching step 2. We will demonstrate the optimal setting of α1 under a variety of models.
As shown in the Web Appendix (available on the Journal’s Web site (http://aje.oxfordjournals.org/)), the tests from steps 1 and 2 are independent. Because of this independence, the overall type I error rate of the above procedure is ensured, as long as the step 2 test has the correct test size, conditional on the number of SNPs (m) that reach step 2 (18). Intuitively, the independence guarantees that the distribution of the step 2 statistic is unaffected by the outcome of the step 1 screening. If, on the other hand, the tests from steps 1 and 2 were not independent, the noncentrality parameter of the step 2 statistic, conditional on the step 1 statistic's exceeding a given significance threshold, would be nonzero under the null hypothesis of no interaction. This would inflate the type I error of step 2, assuming a zero noncentrality parameter under the null hypothesis.
As noted above, a situation in which the validity of the test is of particular concern is that of a noncausal SNP-E association in the population but no SNP × E interaction in disease risk. Such a SNP will have an increased chance of passing the step 1 screen, but again, because of the independence, this will not affect the validity of the step 2 intrafamily test statistic. Moreover, because the step 2 test has the correct size in the presence of population-level SNP-E association (18), the overall type I error rate in the presence of population-level SNP-E association will be preserved. One may be tempted to use a case-only test of G-E association in the affected offspring to screen the M SNPs in step 1. While it provides greater power to pass a true SNP × E interaction on to step 2, this approach is not desirable, because it produces a correlation in the test statistics between steps 1 and 2 and a corresponding inflation of the false-positive rate in the presence of SNP-E association, for the reason described above.
The second factor on the right-hand side of equation 2 can be expressed as Pr(Ec|Gp, Dc = 1) × Pr(Gp|Dc = 1). Since only the first factor of this expression is informative for G × E interaction, the step 1 screen can be based on a model for the case exposure given parental genotypes. With a binary environmental factor and additive (0, 1, or 2 minor alleles) coding for parental genotypes, one can use a logistic regression model for step 1 with the following form for a single trio:
Assuming that associations with E do not differ between maternal and paternal genotypes, the above can be simplified to
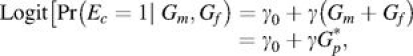 |
(3) |
where Gp* = Gm + Gf. The step 1 test then consists of testing the null hypothesis H0: γ = 0—using a likelihood ratio or score test, for example. In a GWAS setting, it is reasonable to use an additive coding scheme for Gm and Gf, so that Gp* represents the total number of minor alleles carried by parents. However, alternative 1-variable (e.g., dominant) or 2-variable (codominant) coding schemes could be adopted for parental genotypes.
We compare the power of the proposed 2-step method to detect G × E interaction in a GWAS with the power of a standard analysis. We assume that among a collection of M SNPs, there is a true G × E interaction effect on disease between a specific disease susceptibility locus (DSL) and exposure E. In our initial “base” model, we assume that the minor allele frequency for the DSL is qA = 0.15, the genetic model is additive, the exposure prevalence is pE = 0.5, and RG = RE = 1.0—that is, neither the DSL nor exposure has an effect in the absence of the other factor. We set the sample size equal to 1,000 case-parent trios, set M equal to 1 million SNPs, and assume that all SNPs are independent. We also assume in our base model that for each of the 1 million SNPs, there is no SNP-E association in the general population.
Our general approach to computing statistical power is based on direct calculation of the expected noncentrality parameter for the likelihood ratio test of interaction (see Gauderman (19) for additional details). In all calculations, we assume a desired experiment-wise type I error of 0.05 and a 2-sided alternative hypothesis, and we utilize a Bonferroni correction for the m tests in step 2. Statistical power for the 2-step method is computed as the product of the powers of steps 1 and 2, relying on the independence of these 2 steps. In addition to the base model, we compare the power of the 2-step and standard analyses under a range of model parameters and assumptions about population-level SNP-E association. As described above, an important quantity in our 2-step procedure is α1, the significance threshold in step 1. For each model considered, we identify the optimal setting of α1—that is, the value of α1 that yields the greatest power in a 2-step analysis—using a simple search algorithm. We also explore the sensitivity of the 2-step power to the choice of α1.
RESULTS
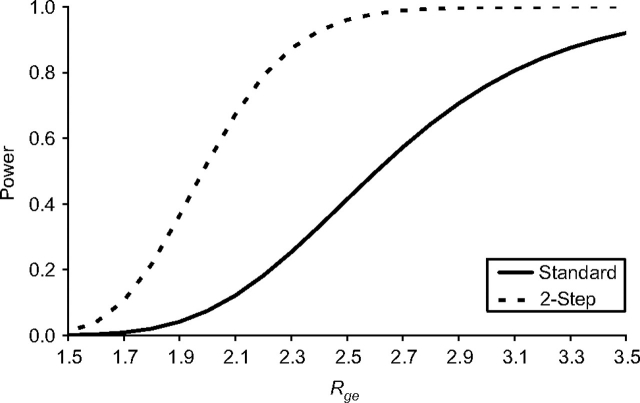
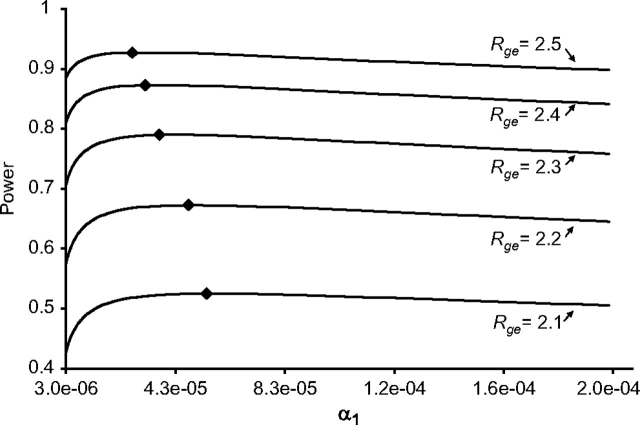
Under our base model parameter settings, the 2-step method provides substantially greater power to detect a G × E interaction with the DSL than a standard analysis across a range of interaction effect sizes (Figure 1). For example, with 1,000 case-parent trios, the 2-step method provides 87% power at the optimal setting of α1 to detect an interaction effect of Rge = 2.3, compared with only 25% power using the standard test. At the commonly used threshold of 80% power, the detectable magnitude of Rge is 2.22 using the 2-step method, compared with 3.10 based on a standard analysis. The optimal step-1 significance threshold is α1 = 5.4 × 10−5 when Rge = 2.1, and it generally declines for greater interaction effect sizes (Figure 2, diamonds). However, Figure 2 also shows that powers for a given magnitude of Rge are quite similar across a range of α1 settings from 1 × 10−5 to 1 × 10−4.
Figure 1.
Statistical power to detect a gene × environment interaction in a genome-wide screen for varying magnitudes of the true interaction effect (Rge). Power for the 2-step method is shown at the optimal setting of α1. All other parameter values are set to those in the base model (see footnote “a” of Table 1).
Figure 2.
Statistical power to detect gene × environment interaction using the 2-step method as a function of the step-1 significance threshold (α1, ranging from 3 × 10−6 to 2 × 10−4) and the magnitude of the interaction (Rge). All other parameter values are set to those in the base model (see footnote “a” of Table 1).
The power to detect G × E interaction for the 2-step method is also substantially greater than that for the standard test across a range of model parameters (Table 1), including different values of the DSL allele frequency (models 2 and 3), exposure prevalence (models 4 and 5), and baseline relative risks (models 6 and 7). The 2-step method also has greater power when the interaction effect is negative (Rge < 1.0, models 8 and 9). Power generally increases as the number of SNPs tested decreases (models 10–12) because of the reduced multiple-testing burden. The latter setting of M = 1,500 demonstrates that the 2-step approach can be effective in smaller-scale genotyping studies, such as might be the case in a post-GWAS follow-up study. Power for the 2-step method is also higher than that for the standard analysis under a dominant model (model 13), but the improvement is not as large under a recessive model (model 14). The relative improvement in power with the 2-step method is similar for alternative settings of α, the experiment-wise type I error rate (models 15 and 16). In most models, the optimal setting for α1 is between 1 × 10−5 and 1 × 10−4. The final column of Table 1 shows that the power achieved by fixing α1 to 1 × 10−4 is nearly identical to the power at the optimal α1 in most situations.
Table 1.
Statistical Power to Detect Gene × Environment Interaction in 1,000 Case-Parent Trios for the Standard Test and the 2-Step Test Across a Range of Models
| Model No. | Model | Standard Test Power | 2-Step Test |
||
| Optimal |
Power at α1 = 1 × 10−4 | ||||
| Power | α1 | ||||
| 1 | Base modela | 0.25 | 0.87 | 3.7 × 10−5 | 0.86 |
| Disease susceptibility locus allele frequency (qA) | |||||
| 2 | 0.05 | 0.01 | 0.15 | 2.9 × 10−5 | 0.15 |
| 3 | 0.25 | 0.54 | 0.97 | 5.9 × 10−5 | 0.97 |
| Exposure frequency (pE) | |||||
| 4 | 0.10 | 0.03 | 0.28 | 7.3 × 10−5 | 0.28 |
| 5 | 0.25 | 0.23 | 0.83 | 5.1 × 10−5 | 0.83 |
| Main effect sizes (Rg, Re) | |||||
| 6 | 1.0, 2.0 | 0.23 | 0.66 | 3.5 × 10−5 | 0.65 |
| 7 | 2.0, 1.0 | 0.10 | 0.97 | 3.0 × 10−6 | 0.89 |
| Negative interaction effect (Rge) | |||||
| 8 | 0.45 | 0.08 | 0.35 | 1.1 × 10−3 | 0.29 |
| 9 | 0.35 | 0.37 | 0.77 | 2.0 × 10−3 | 0.65 |
| No. of single nucleotide polymorphisms (M) | |||||
| 10 | 500,000 | 0.29 | 0.89 | 5.4 × 10−5 | 0.89 |
| 11 | 100,000 | 0.40 | 0.93 | 1.4 × 10−4 | 0.93 |
| 12 | 1,500 | 0.74 | 0.99 | 2.0 × 10−3 | 0.95 |
| Genetic modelb | |||||
| 13 | Dominant | 0.25 | 0.77 | 1.7 × 10−4 | 0.77 |
| 14 | Recessive | 0.25 | 0.40 | 2.4 × 10−2 | 0.16 |
| Experiment-wise type I error rate (α) | |||||
| 15 | 0.01 | 0.17 | 0.82 | 1.5 × 10−5 | 0.78 |
| 16 | 0.10 | 0.29 | 0.89 | 5.4 × 10−5 | 0.89 |
The base model has qA = 0.15, pE = 0.5, Rg = Re = 1.0, Rge = 2.3, M = 1 million single nucleotide polymorphisms, and experiment-wise α = 0.05. Each additional model varies the indicated parameter.
For the dominant model, Rge was increased to 2.6. For the recessive model, qA was increased to 0.43 and Rge to 2.6. These settings provided the same power as the base model for the standard analysis.
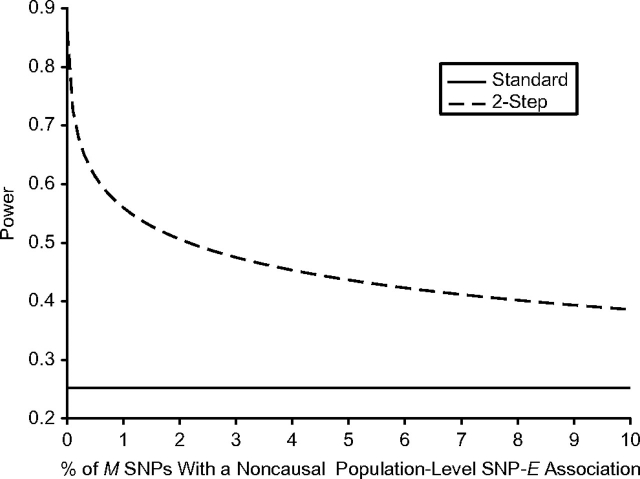
In all of the above models, we assumed no population-level association between E and any of the M SNPs. Under that scenario, we expect that M × α1 false-positive SNPs will pass through the first-step screen. However, it is likely that there will be noncausal E-SNP associations for some fraction of the M SNPs—due to population stratification, for example. We let pge denote the proportion of M SNPs that have a noncausal association with E in the general population. If we conservatively assume that all pge × M of these SNPs pass the step-1 screen, the expected total number of SNPs that pass step 1 is E(m) = M(pge + α1 – pgeα1). As shown in Figure 3, as pge increases, the power of the 2-step method declines sharply but then levels off. Even in the unlikely situation where 100,000 (10%) of 1 million SNPs have a noncausal population-level SNP-E association, the power of the 2-step method is still markedly greater than that of the standard analysis.
Figure 3.
Statistical power to detect gene × environment interaction using the standard and 2-step methods, as a function of the proportion of single nucleotide polymorphisms (SNPs) with a noncausal population-level SNP-environment (E) association. All other parameter values are set to those in the base model (see footnote “a” of Table 1).
DISCUSSION
We have proposed a novel method of screening the genome for G × E interactions in a GWAS. The method uses information from the full likelihood of trio data (equation 1) to substantially increase power relative to use of the standard likelihood for G × E analysis in trios that conditions on parental genotypes. The partitioning of the full likelihood into 2 independent factors gives rise to the proposed 2-step approach. The use of the conditional likelihood in step 2 ensures that the overall procedure has the correct test size in the presence of noncausal population-level association between E and some subset of SNPs. The procedure is complimentary to a genome-wide association scan for main effects, and thus has the potential to uncover novel genetic signals that may otherwise be missed.
Across a wide range of models we considered, the 2-step method was more powerful than a standard analysis for detecting G × E interactions. Coupled with this improvement in power is relative ease of implementation, requiring no specialized software and only a modest increase in computation time in comparison with a standard analysis. Despite the improved efficiency of our 2-step method, the detectable interaction effect size at the 80% power level was still large (>2.0; Figure 1) in our base model with 1,000 trios. Larger sample sizes will be required to detect interaction effects of the magnitude that have been reported for main effects (typically odds ratios < 1.5) in many genome-wide scans. We assumed that the M SNPs were independent in all calculations, which will not generally be the case because of linkage disequilibrium. Although linkage disequilibrium will not change the expected number of SNPs that pass from step 1 to step 2, correlation in the step-2 test statistics due to linkage disequilibrium will make a Bonferroni correction conservative. An alternative multiple-testing correction procedure that accounts for correlated statistics (e.g., see Conneely and Boehnke (20)) could be considered for both the 2-step and standard interaction tests to improve power in the presence of linkage disequilibrium.
We presented our 2-step approach in the context of a binary environmental variable, but it could also be implemented for a quantitative or multicategory exposure. Here one would simply replace the step 1 logistic model in equation 3 with a regression model appropriate for the type of environmental variable—for example, a linear regression model if E is quantitative. One could also consider reversing the roles of G and E (14) in our first-step model (equation 3)—for example, modeling the parental G distribution as a function of E using polytomous logistic regression. This may be preferred when the exposure variable includes some fraction of zero values indicating “nondetectable,” requiring the use of a nonstandard regression model for E in order to obtain a valid test of association. We expect analogous increases in power for the 2-step method relative to the standard approach for alternative types of environmental variables and for alternative forms of the step-1 regression model.
A situation in which the 2-step method can lose power relative to the standard approach is one where there is population-level association between the DSL and E in the opposite direction of the association induced by the G × E interaction. In the unlikely case that this occurs because of a causal DSL-E association (e.g., the DSL increases predisposition for exposure), neither the standard method nor the 2-step method will provide a valid test of G × E interaction. A more likely situation is that of a noncausal DSL-E association due to population stratification, which does not affect the validity of the 2-step method but will affect power. For example, if E is less prevalent in the subpopulation with higher DSL allele frequency, then our first-step test will have reduced power to detect a positive G × E interaction effect. On the other hand, if E is more prevalent in the subpopulation with higher DSL frequency, our first-step test will have enhanced power, albeit for an artifactual reason. It may be possible to modify our first-step logistic model (equation 3) to include standard covariates describing population structure (4, 21) that would identify ethnic subgroups and would therefore adjust for this type of noncausal G-E association. Population stratification will also affect the power of the standard 1-step method, since the distribution of G and E in a sample of trios will depend on the corresponding distributions in the subpopulations. Further study of the impact of population stratification on the power to detect G × E interaction and the impact of including adjustments for population structure in our first-step model are areas for future research.
A standard paradigm in the GWAS setting is to reserve testing of interactions for only those SNPs that are significant genome-wide (e.g., at α = 10−7) in the primary main-effects scan. We certainly advocate testing for G × E interaction with relevant E’s as part of the follow-up of any such genome-wide-significant SNP. However, while some models of G × E interaction induce a strong main effect, there are many interactions that are likely to go undetected by this form of screening (22). One could envision a mixed screening step that passes a SNP on to step 2 G × E testing if it achieves some modest level of significance either in a main-effect test or in the step-1 screen proposed in this paper. Further research is required to investigate the type I error rate and power of such a hybrid approach.
The use of a screening step to improve efficiency in multiple-testing situations has been proposed in other contexts. For example, Van Steen et al. (23) developed an efficient 2-step analysis of trios to detect genetic main effects for a quantitative trait. Millstein et al. (24) proposed a screening step to improve efficiency in the analysis of gene-gene interactions for studies of multiple candidate genes. Murcray et al. (18) described a 2-step analysis for detecting G × E interaction in a GWAS of a case-control sample. A common element in all of these approaches is the coupling of an informative but potentially biased first-step test with an independent and unbiased second-step test to guarantee the overall validity of the procedure. The goal of these procedures is to reduce the multiple-testing burden by using a screening step to eliminate the majority of associations, specifically those that are least likely to be statistically significant in the primary test of interest (i.e., the step 2 test). As with any screening procedure, there is the possibility that a true association will not pass step 1 and thus will not be formally tested in step 2. However, our results and the results of other similarly constructed 2-step procedures demonstrate that the substantial improvement in expected power is likely to be worth this risk.
Of course, scanning the genome for G × E interactions is predicated on the identification of a relevant E for the trait of interest. For example, for lung cancer or cardiovascular disease, scanning for genes involved in a G × smoking interaction might seem natural, given the strong associations that have been reported between these traits and smoking. On the other hand, for traits such as prostate cancer or multiple sclerosis, the choice of a relevant E is less clear. Just as it is important to obtain high-quality SNP data through careful genotyping and rigorous quality control procedures, it will be important in the G × E setting to also obtain well-measured environmental data. In the types of large samples required for a GWAS, one may have to utilize easily obtained measures that are available on all subjects (e.g., ever smoking/never smoking) rather than more detailed and harder-to-measure variables (e.g., pack-years of tobacco exposure) that are available for only a subset of subjects. This may be particularly true in a consortium setting, where several GWAS with varying types of environmental data will be analyzed. Investigators should carefully consider the tradeoff between increasing sample size and introducing possible measurement error when they choose the specific form of E that will be analyzed.
By definition, a complex trait is one that depends on many factors, including both genes and environmental exposures. Direct, main-effect testing of genome-wide panels of SNPs has certainly been successful at identifying new genes of interest for several complex traits. However, there are likely to be many remaining genes, some that may only have detectable levels of effect in the presence or absence of an environmental exposure. Given the high cost of genotyping large numbers of subjects in genome-wide SNP panels, it is essential that investigators fully analyze their data to uncover any detectable associations. We have developed an efficient method with which to utilize available environmental and genetic data in case-parent trios to scan for genes involved in a G × E interaction. Application of this method has the potential to augment an investigator’s list of main-effect “hits” with additional genes that modify or are modified by an environmental factor.
Supplementary Material
Acknowledgments
Author affiliation: Department of Preventive Medicine, Keck School of Medicine, University of Southern California, Los Angeles, California (W. James Gauderman, Duncan Thomas, Cassandra Murcray, David Conti, Dalin Li, Juan Pablo Lewinger).
This work was supported in part by the National Institute of Environmental Health Sciences (grants 5P30ES007048, 5P01ES009581, R826708, RD831861, 5P01ES011627, 5R01ES014447, T32 ES013678, and 5R01ES014708), the National Heart, Lung, and Blood Institute (grants 5R01HL087680, 5R01HL61768, and 5R01HL76647), and the National Genome Research Institute (grant P50 HG 002790-02).
Conflict of interest: none declared.
Glossary
Abbreviations
- DSL
disease susceptibility locus
- G-E
gene-environment
- G × E
gene × environment
- GWAS
genome-wide association study(ies)
- SNP
single nucleotide polymorphism
References
- 1.Hindorff LA, Sethupathy P, Junkins HA, et al. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc Natl Acad Sci U S A. 2009;106(23):9362–9367. doi: 10.1073/pnas.0903103106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55(4):997–1004. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
- 3.Pritchard JK, Donnelly P. Case-control studies of association in structured or admixed populations. Theor Popul Biol. 2001;60(3):226–237. doi: 10.1006/tpbi.2001.1543. [DOI] [PubMed] [Google Scholar]
- 4.Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155(2):945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pritchard JK, Stephens M, Rosenberg N, et al. Association mapping in structured populations. Am J Hum Genet. 2000;67(1):170–181. doi: 10.1086/302959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Price AL, Patterson NJ, Plenge RM, et al. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38(8):904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- 7.Spielman RS, McGinnis RE, Ewens WJ. Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM) Am J Hum Genet. 1993;52(3):506–516. [PMC free article] [PubMed] [Google Scholar]
- 8.Spielman RS, Ewens WJ. A sibship test for linkage in the presence of association: the sib transmission/disequilibrium test. Am J Hum Genet. 1998;62(2):450–458. doi: 10.1086/301714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Weinberg CR. Allowing for missing parents in genetic studies of case-parent triads. Am J Hum Genet. 1999;64(4):1186–1193. doi: 10.1086/302337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Self SG, Longton G, Kopecky KJ, et al. On estimating HLA/disease association with application to a study of aplastic anemia. Biometrics. 1991;47(1):53–61. [PubMed] [Google Scholar]
- 11.Schaid DJ. Case-parents design for gene-environment interaction. Genet Epidemiol. 1999;16(3):261–273. doi: 10.1002/(SICI)1098-2272(1999)16:3<261::AID-GEPI3>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 12.Umbach DM, Weinberg CR. The use of case-parent triads to study joint effects of genotype and exposure. Am J Hum Genet. 2000;66(1):251–261. doi: 10.1086/302707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weinberg CR. Less is more, except when less is less: studying joint effects. Genomics. 2009;93(1):10–12. doi: 10.1016/j.ygeno.2008.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kistner EO, Shi M, Weinberg CR. Using cases and parents to study multiplicative gene-by-environment interaction. Am J Epidemiol. 2009;170(3):393–400. doi: 10.1093/aje/kwp118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Piegorsch WW, Weinberg CR, Taylor JA. Non-hierarchical logistic models and case-only designs for assessing susceptibility in population-based case-control studies. Stat Med. 1994;13(2):153–162. doi: 10.1002/sim.4780130206. [DOI] [PubMed] [Google Scholar]
- 16.Yang Q, Khoury MJ, Flanders WD. Sample size requirements in case-only designs to detect gene-environment interaction. Am J Epidemiol. 1997;146(9):713–720. doi: 10.1093/oxfordjournals.aje.a009346. [DOI] [PubMed] [Google Scholar]
- 17.Gauderman WJ. Sample size requirements for association studies of gene-gene interaction. Am J Epidemiol. 2002;155(5):478–484. doi: 10.1093/aje/155.5.478. [DOI] [PubMed] [Google Scholar]
- 18.Murcray CE, Lewinger JP, Gauderman WJ. Gene-environment interaction in genome-wide association studies. Am J Epidemiol. 2009;169(2):219–226. doi: 10.1093/aje/kwn353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gauderman WJ. Sample size requirements for matched case-control studies of gene-environment interaction. Stat Med. 2002;21(1):35–50. doi: 10.1002/sim.973. [DOI] [PubMed] [Google Scholar]
- 20.Conneely KN, Boehnke M. So many correlated tests, so little time! Rapid adjustment of P values for multiple correlated tests. Am J Hum Genet. 2007;81(6):1158–1168. doi: 10.1086/522036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Reich D, Price AL, Patterson N. Principal component analysis of genetic data. Nat Genet. 2008;40(5):491–492. doi: 10.1038/ng0508-491. [DOI] [PubMed] [Google Scholar]
- 22.Thomas D. Gene-environment-wide association studies: emerging approaches. Nat Rev Genet. 2010;11(4):259–272. doi: 10.1038/nrg2764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Van Steen K, McQueen MB, Herbert A, et al. Genomic screening and replication using the same data set in family-based association testing. Nat Genet. 2005;37(7):683–691. doi: 10.1038/ng1582. [DOI] [PubMed] [Google Scholar]
- 24.Millstein J, Conti DV, Gilliland FD, et al. A testing framework for identifying susceptibility genes in the presence of epistasis. Am J Hum Genet. 2006;78(1):15–27. doi: 10.1086/498850. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.