Particle tracking model of electrophoretic morphogen movement reveals stochastic dynamics of embryonic gradient

Abstract

Some developmental events rely on an electrophoretic force to produce morphogenetic gradients. To quantitatively explore the dynamics of this process, we constructed a stochastic model of an early phase of left-right patterning: serotonin movement through the gap junction-coupled blastomeres of the Xenopus embryo. Particle-tracking simulations showed that a left-right gradient is formed rapidly, quickly reaching a final stable level. The voltage difference was critical for producing a morphogen gradient of the right steepness; gap junctional connectivity and morphogen mass determined the timing of the gradient. Endogenous electrophoresis drives ~50% of the particles across more than one cell width, and ~20% can travel across half the embryo. The stochastic behavior of the resulting gradients exhibited unexpected complexity among blastomeres' morphogen content, and showed how spatiotemporal variability within individual cells resulted in robust and consistent gradients across the embryonic left-right axis. Analysis of the distribution profile of gradient gain values made quantitative predictions about the conditions that result in the observed background level of laterality defects in unperturbed frog embryos. This work provides a general model that can be used to quantitatively analyze the unexpectedly complex dynamics of morphogens in a wide variety of systems.

Introduction

Numerous developmental patterning events are orchestrated by the movements of signaling molecules across embryonic tissues. In the case of morphogens, spatio-temporal gradients of such molecules can establish large-scale pattern during embryogenesis and regeneration (Schiffmann, 1989; Green, 1990; Schiffmann, 1991; Dyson and Gurdon, 1998; Gurdon et al., 1999; Chen and Schier, 2001; Teleman et al., 2001; Green, 2002). Recently, several elegant studies have mathematically modeled the formation, maintenance, and interpretation of morphogenetic gradients (Eldar et al., 2003; Eldar et al., 2004; England and Cardy, 2005; Ashe and Briscoe, 2006; Nakamura et al., 2006; Reeves et al., 2006; Coppey et al., 2007). The mechanistic understanding of the complex, sometimes counterintuitive behavior of biological gradients, as revealed through computer simulations, is an important component of the efforts to synthesize molecular details back into a coherent, predictive, systems-level understanding of pattern formation (French et al., 1976; Lewis, 2008; Barkai and Ben-Zvi, 2009).

Electrophoretic generation of morphogen gradients

While most work has focused on gradients of extracellular proteins, it is now known that intracellular movement of molecule signals among cell groups is also an important component of developmental patterning. One example is the movement of maternal proteins and mRNAs from nurse cells into oocytes in insects through cytoplasmic bridges. Another is the transfer of small molecules through gap junctions (Blomstrand et al., 1999; Bao et al., 2004; Suadicani et al., 2004; Momose-Sato et al., 2005). Gap junctions (GJs) are channels, assembled from connexin, pannexin, or innexin proteins, that allow direct transfer of ions and metabolites from the cytoplasm of one cell into that of its neighbor (Nicholson, 2003; Goldberg et al., 2004; Sohl et al., 2005). GJs exhibit exquisite selectivity and gating control (Francis et al., 1999; Weber et al., 2004), and gap junctional communication (GJC) allows large numbers of cells to act as compartments with respect to select physiological signals during morphogenesis (Schiffmann, 1991; Levin, 2007a). What forces are responsible for establishing intracellular gradients, especially the long-term gradients that must be maintained against diffusion during embryonic patterning?

One interesting example is electrophoresis – the redistribution of charged molecules under the influence of an endogenous electric field created by ion channel and pump activity within cells. Electrophoresis of signaling molecules is a general and powerful mechanism by which endogenous bioelectrical signals, long known to be important regulatory factors in development and regeneration (Lund, 1947; Nuccitelli et al., 1986; Borgens et al., 1989; Adams, 2008), are transduced into morphogenetic events (Poo and Robinson, 1977; Poo et al., 1978; Messerli and Robinson, 1997; Levin, 2007b). Electrophoretic movement of morphogens has previously been proposed (Jaffe et al., 1974; Lange and Steele, 1978; Cooper, 1984; Cooper et al., 1989), and electrophoresis has been shown to be the driving force in both oocyte-nurse cell gradients (Woodruff and Telfer, 1973; Jaffe and Woodruff, 1979; Woodruff and Telfer, 1980; Emanuelsson and Arlock, 1985; Woodruff et al., 1988; Woodruff and Cole, 1997; Anderson and Woodruff, 2001; Brooks and Woodruff, 2004) and in left-right patterning of the frog embryo (Levin, 2006; Levin et al., 2006).

Left-right patterning: electrophoresis of serotonin

Consistent left-right patterning is a fascinating aspect of vertebrate development (Levin, 2005; Speder et al., 2007). In the embryo of the frog and chick, recent work has uncovered a circumferential path of gap-junctional communication around a zone of junctional isolation; both are required for normal LR patterning (Levin and Mercola, 1998; Levin and Mercola, 1999). This circumferential GJ path appears to be the way in which the left and right sides of the early embryo coordinate their identities upstream of asymmetric gene expression (Levin and Palmer, 2007); the LR-relevant signaling is mediated by movement of the neurotransmitter serotonin (Fukumoto et al., 2005a; Fukumoto et al., 2005b) which at least in part is driven by a left-right voltage gradient (Levin et al., 2006). The gradient (Fig. 1) is produced by the coordinated asymmetric function of two ion channels and two ion pumps (Levin et al., 2002; Adams et al., 2006; Aw et al., 2008; Morokuma et al., 2008), whose activity is required for the right-ward accumulation of serotonin (5HT), in a GJ-dependent manner, during the 16-32 cell stage. It is not known whether the gradient of serotonin is interpreted such that different concentration levels result in different positional values along a graded LR axis (the strictest definition of “morphogen”) or whether the presence/absence of serotonin is a binary signal that defines “Right” during early stages through a threshold mechanism.

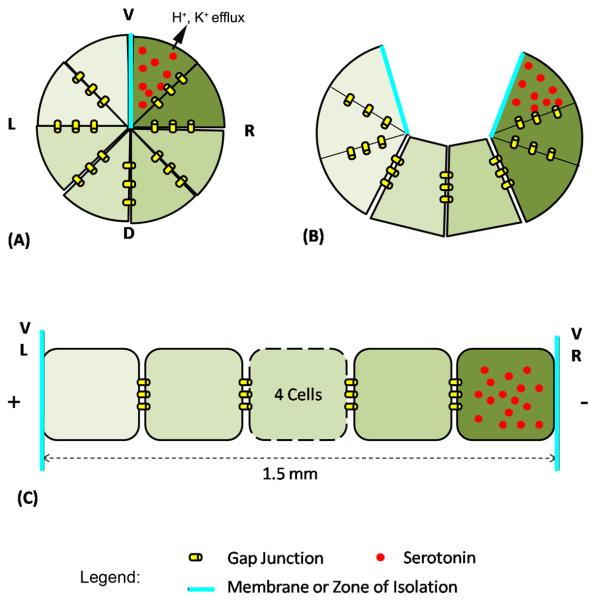
Figure 1. Schematic of serotonin electrophoresis in Xenopus.

(A) The 8 animal-pole cells of the frog embryo comprise an epithelium coupled by gap junctions except across the boundary between the ventral blastomeres; both the GJ coupling and the zone of isolation are crucial for normal LR patterning (Levin and Mercola, 1998). (B) The embryonic architecture can be unwrapped to model it as a linear (Esser et al., 2006), GJ-coupled array of cells bounded by the L and R ventral cells. (C). Our model tracks the movement of serotonin particles (shown in red) towards the right side (Fukumoto et al., 2005b) under a voltage gradient (produced by differential ion exchange with external medium) occurring in the L and R ventral cells (Levin et al., 2002; Adams et al., 2006). V-ventral, D-dorsal, L-left and R-right.

While the identity of the signaling molecule, the gradient path, and the driving force for its redistribution have all been characterized at the molecular level, a number of systems-level questions arose. For example, it was not clear whether it is in fact physically realistic for such a mechanism to generate the observed gradient in the time period available to the embryo. One of the key features of this pathway is that most of the important parameters have now been determined quantitatively. Thus, we developed and analyzed a computer model of this process to understand whether the electrophoretic mechanism was a plausible model of how the serotonin gradient is generated (Esser et al., 2006). This model demonstrated that using realistic estimates of gap junctional connectivity, endogenous bioelectric gradient, the known properties of cytoplasm and serotonin, and the size and geometry of the early frog embryo, an electrophoretic mechanism is indeed able to generate a considerable gradient within the ~1-2 hours available to the embryo before the 32 cell stage.

Remaining open questions

That work modeled the mechanism, at the level of the concentration gradient. It did not reveal the behavior of individual morphogens; thus, it was unable to answer questions about the movement of individual molecules through the embryo. How far do individual serotonin molecules travel in the embryo? Is this a true case of long-range communication via GJ signaling (serotonin molecules traveling across multiple cells) or is the electric field the only long-range signal, and the chemical morphogens only ratchet a short distance right-ward, resulting in an overall gradient but no long-range movement? How do the spatio-temporal dynamics of morphogens' movement through the embryo depend on biological properties of the cells such as voltage gradient, gap junction number, and morphogen size? Which properties of the system are key to understanding the movement of serotonin and other signaling molecules and how might they be modulated to achieve predictable changes in morphogen signaling in applications of regenerative medicine?

Moreover, since the previous model was deterministic, it lacked the element of individual variability that is inherent in biological events and can shed light on the role and influence of randomness in developmental morphogenesis. This is important because it is likely an important source of the variation observed in individual responses to experimental perturbations. Would an analysis at the particle level validate the conclusions of the previous model? How do the vagaries of individual particles' motions give rise to the high overall stability and robustness of the LR pathway? How different are the gradients produced in individual embryos under identical conditions? What quantitative aspects of the process result in the observed low (~1%) level of spontaneous laterality defects in frog embryogenesis?

In order to (1) understand the paths of individual molecules during electrophoresis of intracellular morphogens, (2) study the significance of the variability inherent in this process, and (3) discover the basis for robustness and the specific level of laterality observed in the wild-type frog embryo, we used Langevin's equation – a stochastic differential equation describing the acceleration of a particle with Brownian motion in viscous fluid under electric potential (see Experimental Procedures). We produced a general computer model that can be applied to numerous real biological systems by simply adjusting the relevant parameters (Matlab code is available as Supplement 1). We then used it to study the movement of serotonin during LR patterning in Xenopus by simulating a number of serotonin particles under the influence of collision from other molecules, viscosity of the cytoplasm, and force due to electric potential. The results confirm the main findings of the previous deterministic analysis, and illustrated several surprising new features that suggest direct quantitative experimental predictions. Our simulation revealed a number of fascinating aspects of this epigenetic patterning system (functioning solely on maternal biophysical components, upstream of changes in gene transcription) that shed light on the robustness and dynamics of LR signaling in embryogenesis.

Results

Using the Matlab™ environment, we constructed a computer model that applies Langevin's equation (see Experimental Procedures) – a stochastic differential equation describing the acceleration of a particle with Brownian motion in viscous fluid under electric potential – to the 8 animal-tier blastomeres of the early frog embryo (user-friendly code is available as Supplemental Material). The number of total morphogen molecules remained constant; we neglect degradation or synthesis of serotonin since in the frog embryo, 5HT is maternal and is not synthesized or degraded until after the relevant stages (Fukumoto et al., 2005b).

We first determined the proper values for free simulation parameters, such as time interval, total particle number, and sample size (number of repetitions of each experiment). These are shown in Figure S2. We observed that the Right-left gain values converged, and standard deviation from repeats of in silico experiments were minimized, when tracking 20000 particles with a time interval = 0.01 second, and repeating each experiment 20 times. These parameters were thus used for all subsequent simulations.

We next validated the model by asking whether it reproduced the same serotonin behavior as the very different model of (Esser et al., 2006). Consistent with the correct implementation of both models, analysis (Supplement 3) of the effects of voltage, diffusion constant, gap junction number, and gating probability on the time-course and final value of the morphogen gradient revealed that our stochastic simulation reproduced all of the key results of the deterministic model and confirmed the features of this morphogenetic system that are most important in establishing the properties of observed gradients: voltage, morphogen mass, GJ density, and duration.

Thus, we performed experiments to answer several questions about this system that could not be addressed by the previous deterministic model. We simulated a simple syncitial condition (lack of cell boundaries) as a background on which to overlay different degrees of GJC between blastomeres, and other variables. We utilized the unique features of our new algorithm to track the trajectories of individual particles to determine how far individual serotonin molecules travel in this system and how this behavior depends on critical bioelectric and genetic parameters of the system.

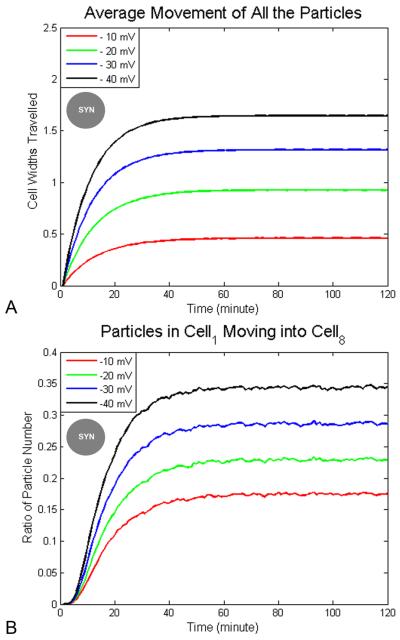
Because signaling molecules can potentially be modified (thus carrying non-cell-autonomous information when entering neighboring cells through GJs), one key question is whether the same serotonin molecule can move considerable distances (perhaps across more than one cell width), or whether the movement is of a ratcheting type, where each molecule moves only a short distance but it is the overall gradient that shifts rightward. In order to determine how far particles driven by electrophoresis in cytoplasm can move, we first investigated how voltage difference effects cell movement under a syncitium state. In Fig. 2, we show particle movement in 2 hours with D_s=3×10⁻¹⁰ m²/s under different voltage differences. The average movement of all the particles (Fig. 2A) has stationary values at 0.09 mm (0.48 cell diwths) at −10 mV, 0.17 (0.91 cell widths) at −20 mV, 0.25 mm (1.33 cell widths) at −30 mV and 0.31 mm (1.65 cell widths) at −40 mV. The final ratios of particles originally in cell₁ (the left-most cell) moving to cell₈ (the right-most cell) (Fig. 2B) are 17% at −10 mV, 23% at −20 mV, 28% at −30 mV and 34% at −40 mV. Though the stationary values differ, they are all reached in about 40 minutes. We conclude the final particle traversal path length is determined by voltage difference, but the time to reach the values is not. The movement of all the particles under −20 mV is about 1 cell width (0.1875 mm), but particles can move beyond 1 cell width and under a voltage gradient of −20 mV across the LR field, a significant number of particles (23% of them) in cell₁ actually move across the whole embryo and reach cell₈. We conclude that electrophoresis does indeed drive individual particles across embryo-wide distances.

Figure 2. Distance traveled by morphogens as a function of voltage difference.

The simulation ran for 2 hours in a syncitial condition. (A) The maximum value of mean movement of all the particles increases with greater LR voltage difference, e.g., 1 cell width under −20 mV and 1.7 cell widths under −40 mV. It takes morphogens about the same time duration, 50 minutes, to reach a maximum distance at all voltage differences tested. (B) The maximum proportion of particles that moved from cell₁ to cell₈ increases with the larger voltage difference, e.g., 17% of the particles move across the whole embryo at −20 mV while 34% of the morphogens do so at −40 mV. The time to reach the maximum value is the same, about 50 minutes, under different voltages. Legend: circle with “SYN” label in the center indicates experiment was made under syncitial conditions.

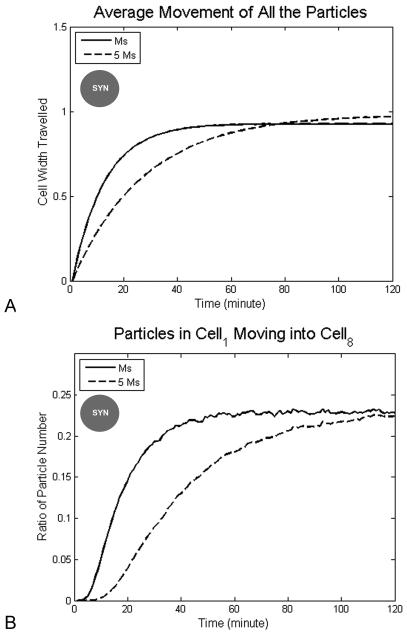
In order to determine how the morphogen mass affects particle movement, we investigated particle behavior in two hours under −20 mV voltage difference but with different diffusion constants in a syncitium state (Fig. 3). Under different diffusion constants, particles reach the same stationary movement (0.17 mm, ~1 cell width, Fig. 3A) and the ratio of particles originally in cell₁ moving to cell₈ have the same value 23% (Fig. 3B), but the time to reach the stationary value is different, about 40 minutes for D_s and 80 minutes for $\mathit{Ds}∕\sqrt{5}$ (for a molecule with five times the molecular mass of serotonin). Thus, particles with fast diffusion reach the stationary value quickly. We conclude that the cytosolic viscosity and mass of particles effect how fast particles can move to their destination, but not how far particles end up moving during the process.

Figure 3. Distance traveled by morphogens as a function of morphogen mass.

Smaller morphogens move to the right side earlier but weight does not change the maximum distance they move or the number of particles moving the whole distance from cell₁ to cell₈. The simulation was run with diffusion constants corresponding to serotonin (Ms) or a molecule with five times the molecular mass of serotonin (5Ms), under −20 mV left-right voltage difference in syncitium condition within 2 hours. (A) The average distance moved by all the particles reaches a maximum, about 1 cell width, and is the same under different diffusion constant. Smaller particles reach the maximum value quickly, in ~50 minutes. More massive morphogens reach the maximum value slowly, in ~80 minutes. (B) The proportion of particles originally in cell₁ (the left-most) moving all the way into cell₈ (the right-most) rises to a maximum value (23% of the morphogen pool), and this is dependent on morphogen mass (50 minutes for serotonin and 80 minutes for a molecule five-fold heavier). Legend: circle with “SYN” label in the center indicates experiment was made under syncitial conditions.

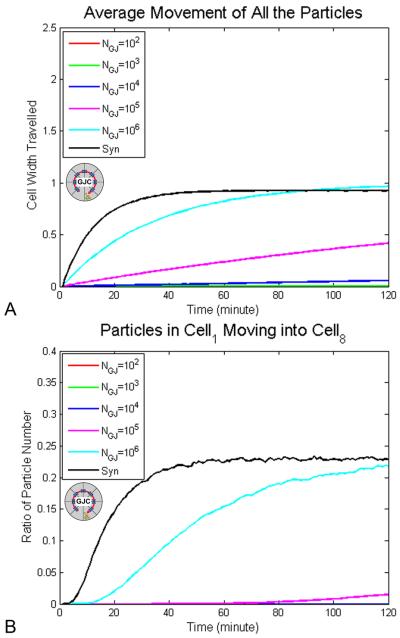
Next, to determine how gap junctions affect particle movement, we studied the average movement of all the particles (Fig. 4A) and the ratios of particles originally in cell₁ moving to cell₈ (Fig. 4B), under different numbers of gap junction channels with D_s=3×10⁻¹⁰ m²/s (a diffusion constant appropriate to the mass of serotonin moving through typical cytoplasm (Mastro et al., 1984)) within 2 hours. Introduction of cell boundaries with GJ channels into the embryonic field did not affect the stationary values of the average movement of all particles (0.17 mm), but the movement of all the particles reaches the stationary state more quickly with greater numbers of gap junctions: 0.17 mm after 80 minutes for gap junction number N_GJ = 10⁶ (Fig. 4A). The ratio of particles in cell₁ moving to cell₈ is about 20% at 120 minutes. We conclude that the maximum movement of particles (Fig. 4A) and ratio of particles traversing all the way from cell₁ to cell₈ are not determined by the number of gap junction channels, gate open probability, or pore size, but the time to reach the final values is strongly affected by these parameters.

Figure 4. Distance profiles of morphogen movement in a GJ-coupled cell field.

(A) At highest gap junction density, N_GJ=10⁶, it takes 80 minutes to reach the maximum of the average distance traveled by all particles (~1 cell width). With fewer gap junctions, N_GJ=10² to 10⁵, the maximum distance is not reached by 2 hours but the average displacement increases during the time period. (B) The Y axis indicates the ratio of the total particles moving from cell₁ to cell₈, normalized to the number of total particles in the cell. The maximum proportion of particles moving all the way from cell₁ into cell₈, 20%, is reached by 120 minutes at N_GJ=10⁶. The maximum number of cells traversing the whole field is not reached in 2 hours period but the proportion of the morphogen pool that moves the entire distance keeps increasing in the two hour period N_GJ≤10⁵. Syn = syncitium. Circle with “GJC” label in the center indicates cellularized condition with gap junctions.

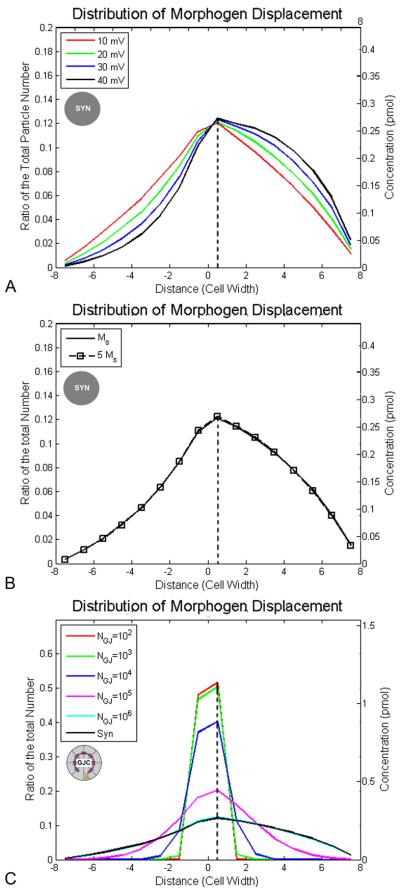
To determine whether electrophoresis provides global, or purely local, chemical signals, we studied the distribution of morphogen molecules' movement under different voltages, diffusion constants and gap junction numbers (Fig. 5). More particles (~60%) move to the right than to the left side (~30%) of the embryo at −20 mV. About 50% of the particles (in the case of serotonin in Xenopus, ~1.1 pmol, or 6.6×10¹¹ serotonin molecules) move to the right a distance greater than 1 cell width, and about 20% move more than 4 cell widths, at −20 mV. Our results predict that increasing the voltage gradient across the LR field would shift the traversal distance profile distribution to the right side (compare the curve of −40 mV with that of −10 mV, Fig. 5A), but the profile does not depend on the strength of the voltage difference (Fig. 5A). The distribution of morphogen traversal path lengths also does not depend on morphogen size or cytoplasm viscosity (Fig. 5B).

Figure 5. Profile of the relationship between distance moved, and the proportion of morphogen molecules that move that distance, as a function of voltage, mass, and GJ density.

In these simulations, the displacement is measured at two hours; movement right-ward (due to the electrophoretic force) is represented as shifts toward positive values along the X axis. Double Y-axes are used to label the proportion of the total particles (left) and absolute molarity of the serotonin pool in Xenopus (right). (A) The distribution of displacement is shifted to the right side with increased voltage (−10 mV to −40 mV): ~50% of the serotonin molecules (1.1 pmol, or 6.6 × 10¹¹ particles) move more than 1 cell width and ~20% (0.44 pmol) move more than 4 cell widths rightward at −20 mV. All curves were derived with serotonin mass and a syncitium condition. (B) The distribution of displacement is not changed by morphogen mass, which is consistent with the previous result that the final concentration of morphogen is not related to the diffusion constant. Both curves were generated at −20 mV and in a syncitium condition. (C) The displacement is entirely (~100% or 2.2 pmol) restricted to ~1 cell width under low gap junction density (N_GJ=10² and 10³), but includes much longer travel by a fraction of individual particles at a high gap junction number (N_GJ=10⁵, 10⁶ and syn = syncitium). All curve were generated under −20 mV and with diffusion constant D_s=3×10⁻¹⁰ m²/s. At high numbers of gap junctions, some molecules move a significant distance to the left, but the net movement (shown as dashed vertical lines) is rightward (positive values). Legend: circle with “SYN” label in the center indicates experiment was made under syncitial conditions; circle with “GJC” label in the center indicates cellularized condition with gap junctions.

More particles move rightward overall at all gap junction numbers, due to the biased driving force from the voltage difference between left and right. The movement is greatly restricted within 1 cell width at low gap junction numbers (N_GJ = 10²−10⁴). With increasing gap junction density however, particles move further towards (± 5 cell widths). The peak of the moving distance is ~1 cell width towards the right at N_GJ = 10²−10⁶ and in the syncitium condition (Fig. 5C).

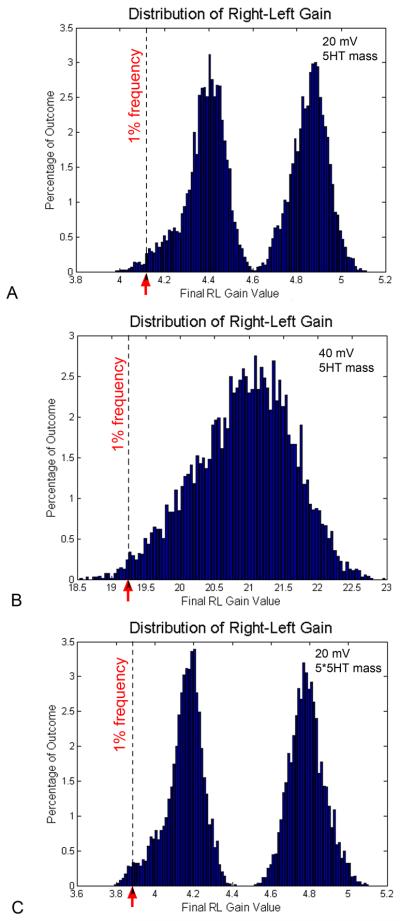
Laterality in Xenopus is a fairly robust process, with about 1% laterality defects (scored as heterotaxia - the reversal of any one or more of heart, gut, or gall-bladder) appearing in unperturbed clutches of eggs. To understand the stochastic properties of the electrophoretic process, and determine how much variability in the gradient exists among embryos under identical conditions, we performed a large number of in silico experiments under the same parameters (the most physiological conditions, as in Table 1), and plotted the frequency at which each final gradient gain value was observed in the dataset (Fig. 6). Surprisingly, in a total of 8000 repetitions, the distribution of final LR gain values was not simply centered around one value, but was bimodal. The most common LR gain values reached by virtual embryos in this set of experiments were 4.4108 and 4.8896 (Fig. 6A). We sought to determine how this distribution profile was related to simulation parameters. Running 7100 repetitions of an experiment where voltage difference was set to 40 mV, the distribution was unimodal, with the most common LR gain value being 21.1131 (Fig. 6B). When a morphogen with a mass of 5-fold that of serotonin was modeled, a bimodal distribution was again observed; in 7700 repetitions, the most common LR gain values in this set were 4.2101 and 4.7761 (Fig. 6C). These data make a prediction about the steepness of the gradient required for normal LR patterning. Setting a cutoff at the observed incidence of background heterotaxia in lab-reared Xenopus laevis embryos, 1%, we can estimate what lower bound of the LR gain range occurs that often in a clutch of identical embryos. The distribution in Fig. 6A reveals that this value is <4.123, suggesting this gain value as the lowest value of a serotonin gradient that can reliably drive the downstream steps that lead to normal, consistent LR patterning.

Table 1.

Values for Parameters of Particle Tracking Model

Parameter	Value
Morphogen Particle
Particle Valence (z)	+2 (Kema et al., 2000)
Particle Radius (rs)	0.3 nm
Particle Molecular Mass (m)	175 Da
Particle Diffusion Constant (Ds)	3×10−10 m2/s (Mastro et al., 1984)
Gap Junctions
Gap Junction Length (LGJ)	16 nm
Gap Junction Pore Radius (rGJ)	0.6 nm
Gap Junction Density (NGJ)	6×1011 m−2 (Hanna et al., 1980; Spray et al., 1981)
Embryo
Embryo Length (L)	1.5 mm
Embryo Temperature (T)	293 K
Embryo Voltage Difference (V)	−20 mV
Cellular Interfacial Area (Acc)	0.15×10−6 m2

Figure 6. Frequency distribution for LR gain values achieved during repeated simulations.

To characterize the stochastic nature of this process, the histograms show distributions of RL gain values obtained in multiple repeats of the same in silico experiment under 3 conditions (the values for parameters are in Table (A) Under the endogenous condition, in a total of 8000 repetitions, the distribution of final LR gain values was bimodal. The most common RL gain values observed were 4.4108 and 4.8896. RL gain values occurring with a frequency of 1% (corresponding to the background degree of laterality defects in normal Xenopus embryos) were those <4.123. (B) When the voltage is increased to 40 mV (7100 repetitions), the distribution was unimodal, centered around the most common RL gain value of 21.1131. Under this condition, values of RL gain occurring at a frequency 1% were those <19.247. (C) When a morphogen with a mass of 5-fold that of serotonin (diffusion constant = Ds/Sqrt(5)), a bimodal distribution was again observed. In 7700 repetitions, the most common RL gain values were 4.2101 and 4.7761. Right-left gains occurring approximately 1% of the time were those <3.883.

Discussion

We built a stochastic model (Supplement 1) to simulate the trajectories of individual morphogen particles during serotonin's electrophoretic movement in LR patterning of Xenopus. We also explored the space of values for free parameters (Supplement 2), uncovering the particle number (20000), experiment repetition number (20), and temporal granularity (0.01 sec.) that lead to optimal convergence in outcomes of multiple experiments with the same parameters (reduce standard deviation of results). Analysis of the in silico experiments identify those key properties of this system that determine the spatio-temporal gradient. While the results obtained by this very different mathematical model validate (and are supported by) the previous deterministic analysis (Esser et al., 2006), this work advances beyond previous deterministic models by enabling analysis of how far individual morphogen models may travel in such a system, and providing surprising information on the variability and robustness inherent in an electrophoretic process.

We analyzed both a syncitial condition (applicable to Xenopus embryos prior to cell division and other systems such as the nurse cell : oocytes cytoplasmic bridge) and the 8 animal-pole cells at the 16-cell stage that incorporated cell boundaries and gap junctions (with a two-state gating mechanism for the GJ channels). We explored the contributions of GJ number, voltage difference across the cell field, and morphogen size to several key properties of this system. The readouts included time to reach final (stationary) gradient, the magnitude of the gradient (defined as the difference between morphogen concentration on the Left and Right, divided by the distance), and the magnitude of the gain (defined as morphogen concentration on the right divided by that on the left; this is related to gradient, but does not reflect system length). The results revealed relationships between these variables, as well as the variability in each, due to the stochastic nature of morphogen movement.

Particle tracking simulation reveals dynamics of morphogen movement in electrophoresis

Our model is a simplification of the real embryo in a number of ways, including neglecting the vegetal pole cells, not incorporating progressive cytokinesis during the electrophoresis time-course, and leaving out the activity of serotonin transporters and enzymes (Fukumoto et al., 2005a). These factors were omitted from the model for reasons of tractability, as well as the desire to make the model as general as possible, so that it is able to shed light on the properties of electrophoretic morphogen movement in general (not restricted to the specifics of 5HT signaling). The data also reveal those aspects of this process that provide a degree of functional redundancy among different conditions, allowing comparison among the dynamics in different systems. For example, doubling the time (from 50 to 100 minutes) to reach a given LR gain value can be achieved by increasing morphogen mass (in the syncitial case, Figure S4B) or equivalently, by changing the GJ density in a cellularized system from 10⁷ to 10⁶ (Figure S7A).

We observed that the magnitude of the voltage difference determines the stationary (endpoint) values of morphogen concentration, the gradient and left-right gain. Morphogen mass and gap junctional connectivity among blastomeres determine the time necessary to reach the stationary values. Analysis of the paths of individual particles in this model revealed the role of stochastic influences the final outcome and demonstrates that electrophoresis can act as a powerful mechanism for the generating pattern via small molecule signals in embryonic systems. While morphogen size and gap junction properties determine how fast the morphogen can traverse large distances through the embryo, the magnitude of voltage difference among cells determines the final path length of long-range chemical signaling. Thus, the expression of ion transporters in early embryonic cells is likely to be a key factor determining the magnitude of morphogen gradients that can be generated by a given cell field during electrophoresis.

Gap junctions and morphogen flow

Gap junctions allow water-soluble morphogens to pass between cell boundaries in a multi-cellular field. Our results illustrate (Fig. S6) that the morphogen concentration, which is initially uniform, becomes ragged at neighboring cells' boundaries first (25 minutes) and then form a final smooth profile (105 minutes). In most conditions, a number of the key parameters, including R-L gain (Fig. S3B), average distance traversed by particles (Fig. 2A), and embryonic gradient (Fig. S5B), have achieved their steady-state maximum values by about 50 minutes. This indicates that the electrophoretic patterning process occurs quite rapidly, and sets an upper bound on a number of the important properties of this process that is a stable point, which cannot be exceeded by simply providing additional developmental time.

The rate at which the right-left gain reaches its maximum value is affected by the number of gap junction channels, and the gain reaches its maximum value at N_GJ=10⁶ within the same time interval as at N_GJ=10⁷ (Fig. S7A,B). Our results predict that morphogen particles accumulate on one side of the cell first and then become transported through the gap junction channel slowly; finally the concentration reaches a stationary smooth profile. This result of the simulation nicely explains the puzzling observation that prior to the completion of serotonin's transport to the right ventral cell, serotonin signal is observed as enriched at cell:cell boundaries in Xenopus (Fig. S9B and immunohistochemistry data in Fig. 1E of (Esser et al., 2006)). Taken together, our results suggest the generalization that in electrophoretic processes, voltage is critical for producing a gradient of the right steepness, while gap junctional connectivity (gap junction number, gating probability and junctional pore size) and diffusion (controlled by both morphogen mass and possible binding factors) are critical for morphogen distribution, gain and gradient to build up at the right time frame.

Electrophoresis as a driving force for morphogen redistribution

An early question suggested by the initial GJ model in LR patterning was whether any individual serotonin molecule actually travels significant distances, or whether each molecule merely moves a bit rightward (a “ratchet” mechanism in which there is no transfer of chemical signal across large distances). This question could not be answered by the existing deterministic model (Esser et al., 2006). We found that at −20 mV, the average movement of serotonin particles would be about 1 cell width right-ward; however, more than 20% of the particles will move from cell₁ all the way across to cell₈. About 50% of the total particles move more than 1 cell width (Fig. 5).

Thus, at least under the boundary conditions existing in the Xenopus embryo, electrophoresis can result in true long-range chemical signaling through the GJ-coupled cell field. This is important because signaling molecules can potentially be modified by cells as they pass through them. Thus, a morphogen arriving in Cell₈ from Cell₇ (under the “every molecule only moves a bit to the right” scenario) may not be the same signal as one carried by a molecule that traverses the whole field from Cell₁ to Cell₈ and is chemically altered along the way (under the long-range movement scenario). Thus, electrophoresis allows morphogens to provide to the target cell additional information (relating to the history of their movement through other cells) beyond merely their presence and concentration.

Electrophoresis provides complex patterning information at cellular and embryonic levels

Importantly, our simulation predicts morphogen gradients at both the cellular and embryonic levels (Fig. S5 and S8). The gradients in individual cells are different (thus presenting different information to each cell, which could be interpreted by the embryo as a true LR axis with discrete positional values, not simply binary R vs. L or medio-lateral information). Moreover, the gradient in individual blastomeres increases and decreases non-monotonically throughout the relevant timeframe, while the overall R-L gradient rises continuously. The surprising complexity of these gradients illustrates the non-trivial patterning information that can be generated at multiple scales of size and organization by electrophoresis through cell fields. The appearance of such gradients, which are not intuitively expected given a simple, homogenous field across identical cells, illustrates the necessity of modeling such systems in silico to truly understand their dynamics.

The local voltage difference is translated to cellular polarization at a global level; the gradients at the left and right cells have different directions with respect to the isolation zone, which may be involved in the breaking of symmetry at the subcellular level. The morphogen concentration (right-left gain) is different at the left and right side of the embryo, which can induce downstream transcriptional effects initiating L- and R-specific gene expression cascades. Our simulation shows that significantly reducing the number of gap junctions does not allow the morphogen gradient to form at the tissue level in the proper time frame (Fig. S9B), explaining the experimental data that confirm that knockdown of GJC leads to randomization of the LR axis (Levin and Mercola, 1998; Levin and Mercola, 1999). Similarly, our simulation explains the dependence of the 5HT gradient and subsequent embryonic organ asymmetry on the function of the bioelectric circuit driving the voltage gradient (Levin et al., 2002; Fukumoto et al., 2005b; Adams et al., 2006; Levin, 2006). This model can be applied to numerous other types of tissue geometry and morphogen type, revealing the pattern formation capabilities of a simple electrophoretic system and facilitating the understanding of which parameters can be experimentally altered to achieve a desired morphogenetic outcome in in vivo or in vitro applications.

Variability and Robustness

A recent analysis indicates that a “perfect sink” is important for scaling and robustness in some morphogenetic systems (Barkai and Ben-Zvi, 2009). Interestingly, this system does include a sink – the degradation of serotonin by monoamine oxidase (Fukumoto et al., 2005a; Fukumoto et al., 2005b). However, MAO does not act until after the observed gradient is generated, leading us to investigate other possible sources of this systems robustness. The LR pathway is quite stable, as less than 1% of frog embryos exhibit any randomization of asymmetry. How does this large-scale stability occur despite the vagaries of individual particle motion? Moving beyond the deterministic model, which quantitatively demonstrated the plausibility of the electrophoresis model in LR patterning, the stochastic model allowed us to incorporate the variability of particle motion, caused by Brownian motion. We found that the stochastic motion of particles leads to the temporal fluctuation of the cellular gradient during the developmental period (2 hours), but does not cause the temporal fluctuation of the embryonic gradient (see Figs. S5B and S8B). These results suggest that the stochastic variation at the molecular and cellular level does not transfer to the tissue level, and reveal how the overall morphogen gradient is reliably formed despite stochastic variations at the cellular level. This may also help explain the differences observed among individual wild-type embryos when staining for serotonin via immunohistochemistry.

Seeking to relate these quantitative predictions to the observed 1% failure of normal LR patterning in unperturbed embryos, we studied the distribution of final R-L gain values among thousands of repeats of identical simulation runs. As expected, the stochastic nature of this system led to a distribution of outcomes in a range (approximately 4.0 to 5.1 for the most physiological set of parameters (Table 1). Surprisingly however, the distribution (Fig. 6A) is bimodal, featuring two values that appear to be attractors for this system, and another value (4.6), which seems to be avoided in almost all instances of the electrophoretic process. The shape of distributions is sensitive to system parameters (Fig. 6B) suggesting that for some values of the electric potential, all embryos will indeed converge around one most common RL gain value, while for others (smaller), the system may tend towards one of two stable points. We are investigating, but do not yet have an explanation for, the shape of the gain distribution. Sensitive, spatially-quantitative analysis of 5HT gradient content in many individuals will be needed to determine whether this feature of the model represents a real phenomenon among groups of embryos or whether this is only a peculiar property of the simulation model itself.

How is the gradient interpreted by subsequent steps in LR patterning? The gradient's robustness is consistent with a threshold model: as long as the right-left gain, varying between 4.4 and 4.9 (Figs. S3B, S4B and S7A), is bigger than a threshold value (4.4, for example), the necessary downstream receptor mechanism could be activated (the nature of the intracellular receptor is not yet known). Interestingly, cellular gradients (Figs. S5B and S8B) are predicted to always be bigger than the embryonic gradient in the right cells and smaller than the embryonic gradient in the left cells. This information may be used by cells to decide their identity relative to the embryonic midline, suggesting alternative models for how serotonin gradients inside cells are interpreted to drive downstream steps.

Since values with a RL gain value <4.123 appeared less than 1% of the time (Fig. 6A), perhaps this is the value below which the gradient is too shallow to drive asymmetric downstream (5HT-dependent) signaling. This model predicts that the observed incidence of heterotaxia in unperturbed embryos is due to 1% of the embryos unable to muster a gradient >4,123 simply by virtue of stochastic events during the electrophoretic redistribution of serotonin. This prediction can be tested biochemically, once the novel intracellular receptors for serotonin are characterized (Levin et al., 2006), and extended to other model species (with very different background heterotaxia levels, such as zebrafish) once their serotonin gradients are characterized.

Future steps

While this model has made a number of predictions that explain several puzzling observed phenomena, it has the potential to make many more precise predictions that could be tested. While we are developing the reagents to do this, the effort is hampered by the fact that immunohistochemistry is not quantitative and cannot be done in vivo (there is no good way to track serotonin particles in living embryos). Fluorescent tags are a possibility we are exploring, but the small size of GJ-permeable morphogens means that any such tag potentially alters the ability of the native molecule to interact with gap junctions and other cellular machinery. New techniques, such as 3-photon microscopy (Maiti et al., 1997) may soon allow the tracking such intracellular morphogens in vivo.

Modeling is a crucial aspect of developmental biology. While molecular-genetic approaches continue to generate mountains of data on the mechanistic details of the pathways driving morphogenesis, it is often impossible to know what pattern (and what temporal dynamics) to expect from a given molecular model by simple inspection of the genetic interaction diagram. The electrophoresis of serotonin in LR patterning represents a quantitatively-tractable, model system with important evolutionary and biomedical endpoints in which to build such models that incorporate genetic, embryological, and biophysical data. Aside from its applicability to the details of serotonin movement in LR patterning, the analysis reveals a number of surprising features of endogenous electrophoresis that may be relevant to numerous patterning systems. Assembling this reductive information into a synthetic system that is able to answer questions about the properties observed at multiple scales is a necessary next step. The construction and analysis of such complex systems is absolutely required to reveal which parameters must be changed, and how, in order to provide specific, instructive signals to a biological system in order to rationally control the morphogenesis during embryonic development or biomedical regeneration (Ingber and Levin, 2007; Adams, 2008).

Experimental Procedures

A particle motion in a fluid can be described by Langevin's equation. In an electric field within a cellular environment, a molecule with a charge (z · q) in an electric field (dV/dx) experiences a force z · q · (dv/dx_i). An equation (Sharp et al., 1987) can be used for numerical simulation, to describe a molecule experiencing random collisions from other molecules, viscous force from the cytoplasm, and the electric force. The particle motion can be described as:

$$x_{i+1}=x_i-z\cdot q\cdot (\mathit{dV}∕{\mathit{dx}}_i)\cdot (D_s\tau ∕k_{B}T)+\mathrm{\Delta }n\cdot {\left(2D_s\tau \right)}^{1∕2},$$ (1)

where x_i+1 is the new position of the molecule from the position x_i after a small time interval τ. κ_B is Boltzmann's constant, T is the absolute temperature, and dV/dx_i is the voltage gradient, here, we use a linear approximation $\mathit{dV}∕{\mathit{dx}}_i=\frac{V}{L}$, assuming that the voltage gradient changes gradually over the distance, V is the electrical potential across the Xenopus embryonic length L. D_s is the morphogen diffusion constant in cytoplasm, and z · q · (dV/dx_i) · (D_sτ/κ_BT) is the displacement due to the balance between electrophoresis driving force and viscosity drag force. Δn is a pseudorandom number from a normal distribution with mean 0 and standard deviation 1. (2D_sτ)^1/2 represents the molecular diffusion length within time τ.

When a membrane separates a cytoplasmic field into two neighboring cells, gap junction channels on the membrane provide aqueous pores permeable for hydrophilic morphogen particles. In this model, we consider the three main factors relevant for a morphogen particle transported through a single gap junction channel: (1) The gating of the channel; opening of the GJ can be regulated by voltage, protein phosphorylation, or pH (Gonzalez et al., 2007; Hirst-Jensen et al., 2007; Moreno and Lau, 2007; Retamal et al., 2007). (2) The conductivity of the channel. (3) The electrochemical potential difference across the channel. (4) The selective permeability of gap junction channels (Goldberg et al., 2004).

We used the Monte Carlo method to simulate the stochastic gating of a two-state (open or closed) gap junction channel. The probability for a single channel to be in the open state is P_o and the probability in the closed state is (1 − P_o). We generated a random number, y, which is uniformly distributed on the interval [0,1], if 0 < y < P_o, the channel is open; if P_o < y < 1, the channel is closed. Thus, for N_GJ gap junctions on the cell membrane, the average number of open channels is N_GJ · P_o. In our model, reducing the number of channels, lowering the open probability, or reducing the pore size are all equivalent with respect to overall conductance for morphogen.

To calculate the channel conductance, we adapted a conventional model for a gap junction channel conductance, assuming that conductance is determined primarily by pore diameter (Hille, 2001). The single gap junction channel conductance G_GJ is estimated from the gap junctional geometrical shape, which is given by the pore radius r_GJ and the gap junction length L_GJ:

$$G_{\mathit{GJ}}=\frac{1}{{\rho }_{\mathit{cyt}}}\cdot \frac{\pi r_{\mathit{GJ}}^2}{\pi r_{\mathit{GJ}}∕2+L_{\mathit{GJ}}},$$ (2)

Here, ρ_cyt is cytosolic resistivity. G_GJ includes both the internal pore resistance and the spreading resistance. For the radius of the gap junction pore r_GJ = 0.6 nm and the gap junction length $L_{\mathit{GJ}}=16\mathit{nm},G_{\mathit{GJ}}=\left(\frac{1}{{\rho }_{\mathit{cyt}}}\cdot \frac{\pi r_{\mathit{GJ}}^2}{L_{\mathit{GJ}}}\right)\cdot \left(\frac{L_{\mathit{GJ}}}{\pi r_{\mathit{GJ}}∕2+L_{\mathit{GJ}}}\right)=G_0\left(\frac{L_{\mathit{GJ}}}{\pi r_{\mathit{GJ}}∕2+L_{\mathit{GJ}}}\right)=0.94G_0,G_0=\left(\frac{1}{{\rho }_{\mathit{cyt}}}\cdot \frac{\pi r_{\mathit{GJ}}^2}{L_{\mathit{GJ}}}\right)$ is the cytoplasm conductance. The difference in diffusion constant is thus very small and we ignored it in the simulation.

For the diffusion constant, D_s,GJ, within single gap junction channels, we consider the frictional steric hindrance of the serotonin molecule with radius r_s within a finite-size gap junction channel. D_s,GJ has the form (Levitt, 1991):

$$D_{s,\mathit{GJ}}=D_s\frac{1-2.1054\lambda +2.0805{\lambda }^3-1.7068{\lambda }^5+0.72603{\lambda }^6}{1-0.75857{\lambda }^5}$$ (3)

here λ = r_s/r_GJ, r_s is the radius of the morphogen and r_GJ is the radius of the gap junction pore. For r_s = 0.3 nm and r_Gj = 0.6 nm, we have D_s,GJ = 0.17 D_s. Thus, diffusion is effectively reduced within the gap junction.

Compared to the “no cell membrane” (syncitium) situation, the chance for a particle to pass through the cell border is N_GJ · A_GJ · P_o/A_cc. Here, N_GJ is the number of gap junctions on the cell membrane, A_GJ is the pore size of the gap junctions, P_o is the probability of a single gap junction to be open, and A_cc is the interfacial area between two neighboring cells. Here, we use a factor, 10³, multiplied by N_GJ · A_GJ · P_o/A_cc, to account for possible static electric attraction on the plasma membrane that would enhance the overall probability (Hille, 1978; Veenstra et al., 1994; Veenstra et al., 1995; Goldberg et al., 2004).

Initial condition and boundary condition

For simplicity, and because this is the cell group for which the most data on bioelectrical properties are available, we modeled 8 cells of the animal pole under a simple electrical filed. In Xenopus embryo, gap junction proteins are expressed as a circumferential pattern around a zone of isolation (Fig. 1A and 1B). The difference in membrane voltage (generated by the left ventral and right ventral cells as a result of differential ion exchange with the outside world) is on the order of 20 mV. We simplified the geometry and modeled the embryo as a linear array of eight cells connected by gap junction channels (Fig. 1B-D) (Esser et al., 2006). The gap junction isolation zone (ventral midline in the embryo) forms the left and right border of the array. The total array length is the medial circumference of Xenopus embryo with 1 mm in diameter. The embryonic temperature was chosen to be 293 K for Xenopus. We further assumed there was no source or sink to produce or degrade morphogen in the embryo (this is true for serotonin in very early frog development) and no morphogen particles moved in or out the embryo (a no-flux boundary condition).

At the initial time point, the cell field has a homogenous distribution of charged morphogen in the embryo. The total morphogen number, N, was chosen to be 20000. The simulation's temporal resolution (time interval τ) was 0.01 second. The simulation was repeated 20 times. These three parameters were determined according to the convergence of the simulation (see supplement 2). The values of the parameters for the simulation are listed in Table 1, unless stated differently for a given experiment.

Output

During embryogenesis, morphogens provide spatial cues that cells utilize in making decisions to divide, grow, migrate and differentiate (Wolpert, 1969; Ashe and Briscoe, 2006; Kerszberg and Wolpert, 2007). Morphogen levels and gradient properties have been described in diverse organisms, such as retinoic acid in the limb of chick and axolotl (Eichele and Thaller, 1987; Scadding and Maden, 1994) and DPP in Drosophila (Ashe et al., 2000). Thus, for the process of electrophoresis, the dynamic spatio-temporal change of morphogen concentration, morphogen right-left gain, and the gradient represent the key readouts. Using the above-described numerical method, we labeled each molecule and were able to quantitatively determine values such as average movement or spatio-temporal distribution of thousands of particles.

When morphogen concentration ceases to change (the morphogen flux is zero, the numbers of particles moving in and out of a region are equal), we report this as the “stationary state”. At this point, particles have achieved their maximum displacement, the morphogen gradient and gain have reached their maximum values, and the ratio of particles traversing from one cell to another remains at its maximum value.

To calculate the concentration, gain and gradient, the whole embryonic length was divided into 40 bins, 5 bins within each cell. The morphogen concentration was calculated as the total particle numbers in each bin and normalized by initial particle number in each bin. Therefore, we were able to show the morphogen concentration at different time points across the whole embryo schematically, averaged over 10 minute intervals. The right-left gain across the embryo was calculated using the time averaged concentration of the right most bin (bin 40) divided by that of the left most bin (bin 1); The gain of a cell was calculated using the time averaged concentration of the right most bin divided by that of the left most bin of the cell. The gradient of the embryo was calculated by the right-left concentration difference of the embryo divided by the total embryonic length; the gradient of a cell was calculated by the right-left concentration difference of the cell divided by the size of the cell. The average distance traveled by all the particles was calculated and the ratio of the particles originally in cell₁ moving all the way around to cell₈ was recorded. We analyzed 5 independent runs in each experiment.

Supplementary Material

Figure S9. Dependence of morphogen concentration profile on morphogen mass and GJ density.

(A) The simulation used −20 mV and a syncitium condition. Very little difference was observed between the results of Ms (for serotonin) and 5Ms, for a molecule with five times the molecular mass of serotonin. (B) The simulation used cell boundaries, and different numbers of gap junction channels under −20 mV the mass and 5 mass of serotonin. The morphogen distribution differs at high (N_GJ=10⁶) and low (N_GJ=10^2-6) gap junction numbers. At low numbers of gap junctions, no embryo-wide gradient forms. The Y axis has no units since it is a dimensionless ratio of total particle numbers in each bin to the initial particle number in that bin. Legend: circle with “SYN” label in the center indicates experiment was made under syncitial conditions; circle with “GJC” label in the center indicates cellularized condition with gap junctions.

Figure S2

(A) The standard deviation (STD) of right-left gain is smallest when using particle number = 20000 for simulations. (B) With increasing time interval, the standard deviation (STD) of right-left gain decreases. The STD is 0.25 at t=0.01 and 0.21 at t=0.1 second. (C) The means of right-left gain at time interval t=0.01 and 0.1 don't obviously differ. (D) The standard deviations (STD) of right-left gain exhibit large fluctuation at time interval t=0.1 second and have smoother change at t=0.01 second. (E) Increasing particle number more than 20000 does not decrease the STD of right-left gain. (F) The standard deviation (STD) of right-left gain doesn't change at 20 mV but does decrease with larger sample size at voltage = 40 mV. The STD also increases with the particle mass. Legend: circle with “SYN” label in the center indicates experiment was made under syncitial conditions.

Figure S3. LR voltage gradient magnitude determines morphogen gradient.

Higher LR differences in transmembrane voltages increase morphogen concentration on the right cells, thus increasing the gradient's right-left gain, which varies in the physiological range. Left-right voltages are −10 mV, −20 mV, −30 mV and −40 mV, with diffusion constant D_s=3×10⁻¹⁰ m²/s and in syncitium condition within two hours. (A) Morphogen concentrations across the whole embryo at about 2 hours (105 minutes). The concentration with greater voltage differential has steeper profile and higher concentration at the right and lower concentration at the left side of the embryo. Vertical dotted lines mark the cells' borders. The Y axis has no units since it is a dimensionless ratio of total particle numbers in each bin to the initial particle number in that bin. (B) The time evolution of mean and standard deviation (error bars, N=20) of morphogen right-left gains. The variation range is [4.4, 4.9] under −20 mV, [9.4, 10.3] under −30 mV and [20.2, 21.6] under −40 mV. The morphogen gradient gain is always greater than 4.4 under a physiological voltage value (−20 mV). Legend: circle with “SYN” label in the center indicates experiment was made under syncitial conditions.

Figure S4. Dependence of morphogen concentration on time and molecular weight.

(A) The time evolution of morphogen concentration across the whole embryo with diffusion constant D_s=3×10⁻¹⁰ m²/s and a voltage difference of −20 mV. The morphogen profile is smooth across the whole embryo and a stationary (maximal) value is reached by about 50 minutes. Vertical dotted lines mark the cells' border. The Y axis has no units since it is a dimensionless ratio of total particle numbers in each bin to the initial particle number in that bin. (B) The time evolution of morphogen right-left gain (mean and standard deviation shown as error bars, N=20), for two different diffusion constants: serotonin mass (“Ms”) and a morphogen of 5-fold greater mass (“5Ms”). Heavier morphogens take longer (100 minutes) to reach the maximum R-L gain. Legend: circle with “SYN” label in the center indicates experiment was made under syncitial conditions.

Figure S5. Temporal variation in morphogen gradients exists at cellular level but not at the level of the embryo in a syncitial condition.

In this experiment, voltage was set to −20 mV, in a syncitium condition within 2 hours. Number of particles in each location is shown as normalized to total morphogen concentration (see pseudocolor scale). (A) Contour plot of morphogen gradients in the whole embryo and individual cells. The embryonic gradient increases smoothly and is apparent very rapidly (within 20 minutes). Surprisingly, gradients in individual cells are complex, and change as a function of time. For example, the gradient in cell₅ increases, decreases, and then increases again. (B) Temporal variation of morphogen gradients in the whole embryo (thick blue line) and individual cells (colored lines). The gradients in left cells (cell₁-cell₄) are lower than the gradient in the whole embryo, while those in the right cells (cell₅-cell₈) are larger than that of the whole embryo. Importantly, though the cellular gradients undergo significant change in gradient throughout the time period, the gradient of the whole embryo increases smoothly. Legend: circle with “SYN” label in the center indicates experiment was made under syncitial conditions.

Figure S6. Morphogen profiles in a GJ-coupled cell field.

The time evolution of the mean morphogen gradient with 10⁶ gap junction channels at each cell:cell boundary within 2 hours has a similar final concentration as in the syncitial condition, but different profiles. At the beginning of the electrophoresis process (5 minutes), the concentration is high at cell boundaries (serotonin accumulating on one side of blastomere membranes) and the profile is not monotonic. At the end (105 minutes), the concentration profile is smooth within the whole embryo with a few more particles at cell-cell boundaries. Vertical dotted lines mark cell borders. The Y axis has no units since it is a dimensionless ratio of total particle numbers in each bin to the initial particle number in that bin. Legend: circle with “GJC” label in the center indicates cellularized condition with gap junctions.

Figure S7. Morphogen right-left gain in a GJ-coupled cell field.

(A) The time evolution of morphogen right-left gains within 2 hours (mean and standard deviation shown as error bars, N=20). The gain varies at its maximum values round [4.5, 5.0] with gap junction number N_GJ=10⁷ after 60 minutes. The gain keeps increasing when N_GJ≤10⁶. The maximum value can not be reached by 2 hours under lower GJ density. Syn = syncitium. (B) Mean morphogen right-left gains at 2 hours as a function of gap junction connectivity. The gain reaches the maximum value, 4.5, at N_GJ=10⁶ after 2 hours. The gain remains very low, 1.3, when there are a few gap junctions (N_GJ≤10⁴). Legend: circle with “GJC” label in the center indicates cellularized condition with gap junctions.

Figure S8. Temporal evolution of morphogen gradient profile in GJ-coupled cell field.

The simulation used −20 mV and N_GJ=10⁶ in two hours. Number of particles in each location is shown as normalized to total morphogen concentration (see pseudocolor scale). As in the syncitial condition, gradients vary at cellular level but not the embryonic level. Left cells have low gradients and right cells have higher gradients. (A) Contour plot of morphogen gradients in Embryo and individual cells. The gradient in the whole embryo increases smoothly (from blue to cyan). The gradients at the cellular level increase in the right cells (cell₃ to cell₈) and decrease in the left cell (cell₁- cell₂) after initial increase. The cellular gradient exhibits small variations, e.g., cell_2-4 and cell₆. (B) Plot of morphogen gradient in the whole embryo and individual cells. The cellular gradients exhibit small variations; the gradients in left cells (cell₁- cell₄) are lower than the gradient in the whole embryo, while those in the right cells (cell₆- cell₈) are larger than that of the whole embryo. The gradient of the whole embryo increases smoothly. Legend: circle with “GJC” label in the center indicates cellularized condition with gap junctions.