AUTOMATIC IDENTIFICATION AND DELINEATION OF GERM LAYER COMPONENTS IN H&E STAINED IMAGES OF TERATOMAS DERIVED FROM HUMAN AND NONHUMAN PRIMATE EMBRYONIC STEM CELLS

Abstract

We present a methodology for the automatic identification and delineation of germ-layer components in H&E stained images of teratomas derived from human and nonhuman primate embryonic stem cells. A knowledge and understanding of the biology of these cells may lead to advances in tissue regeneration and repair, the treatment of genetic and developmental syndromes, and drug testing and discovery. As a teratoma is a chaotic organization of tissues derived from the three primary embryonic germ layers, H&E teratoma images often present multiple tissues, each of having complex and unpredictable positions, shapes, and appearance with respect to each individual tissue as well as with respect to other tissues. While visual identification of these tissues is time-consuming, it is surprisingly accurate, indicating that there exist enough visual cues to accomplish the task. We propose automatic identification and delineation of these tissues by mimicking these visual cues. We use pixel-based classification, resulting in an encouraging range of classification accuracies from 74.9% to 93.2% for 2- to 5-tissue classification experiments at different scales.

1. INTRODUCTION

The biology of embryonic stem (ES) cells holds great potential as a means of a¹dvancing the research of tissue regeneration and repair, the treatment of genetic and developmental syndromes, and drug testing and discovery [1-3]. By understanding the mechanisms through which ES cells differentiate into tissue, we can further our understanding of early development. The qualities of an ES cell that set it apart from other cells are its ability to self-renew, perpetuate indefinitely, and produce the three germ layers from which all tissue is derived (pluripotency). In typical laboratory situations, ES cells are defined by the proteins they express and their behavior in culture. Human and nonhuman primate cells are different in that they cannot be considered ES cells until they are able to produce a teratoma tumor when injected into immunocompromised mice. A teratoma is strictly defined by histological evidence of tissues derived from each of the three primary germ layers of ectoderm, mesoderm, and endoderm. Initial observation of a teratoma, after hematoxylin and eosin (H&E) staining and imaging, reveals a mass of individual germ-layer components whose underlying organization is unclear (see Figure 1 for examples). Quantitative knowledge of the contribution and organization of the germ layers may provide significant insight into normal and abnormal development. To accomplish this task, the tissues present need to be first identified and delineated. While visual identification of these tissues is time-consuming, it is surprisingly accurate, indicating that there exist enough visual cues to accomplish this task. We propose automatic identification and delineation of these tissues by mimicking these visual cues.

Figure 1.

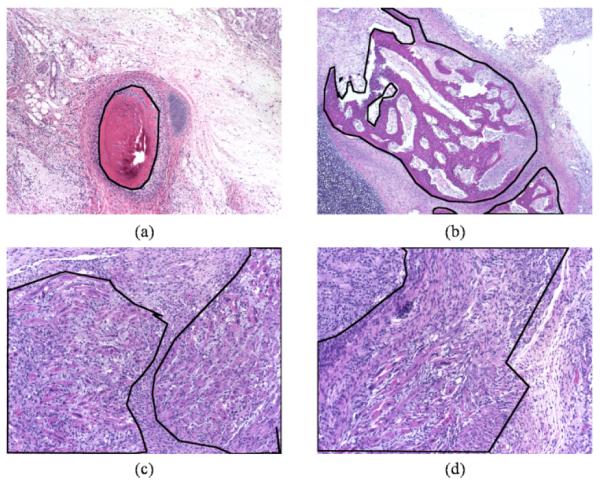
H&E stained teratoma images at different magnifications; outlined in black are specific tissues (a, b) bone at 4X, (c) striated muscle at 10X, and (d) myenteric plexus at 10X.

There is a growing demand for image analysis to aid both clinical and research applications in pathology, such as the determination of the absence or presence and severity of cancers such as breast and prostate cancer. These problems are either binary classification tasks (malignant or benign), or continuous-state assignments (grading of severity of cancer) [4-7], and consider single-class images precluding the need for segmenting the image into regions of interest (ROIs). A less common application is the classification of tissues in normal human systems [8]. Such applications take advantage of the known organization and relationships between different tissues in a given human system.

Our task is significantly more challenging due to the chaotic nature of teratomas. Unlike cancer detection/grading applications, our task is a multi-class problem that requires segmentation of any given image into ROIs, each of which contain only one tissue that must then be identified. Unlike classification of tissues in normal human systems, teratomas do not present any known regular organization or relationships between tissues. As a result, the identification and delineation of tissues in H&E stained images of teratomas is a rather general classification problem.

Other teratoma-specific challenges include occasional low intra-class similarity (one tissue type presents itself in many ways) and high inter-class similarity (multiple tissue types often have similar appearances) as shown in Figure 1. Additionally, since teratomas are masses of maturing tissue, the exact manifestation of a tissue changes depending on the age of the teratoma, introducing within each tissue type a series of subtypes with some common features, but also specific ones unique to the maturation stage.

We propose an algorithm for high-resolution classification of H&E images to automatically identify and delineate tissues. We create a set of scalable image features we term histopathology vocabulary (HV) to mimic the visual cues used by experts to perform this task. We implement these features in a multiscale fashion to describe and classify a given image at any given scale. Given increasingly finer scales, the resulting classifications will provide increasingly sharper delineations of tissues.

Classification of Single-Tissue Images

Our previous work focused on classification of single-tissue images in an effort to gauge the feasibility of developing an automated classification algorithm [9] with accuracy of 88% in a 6-tissue problem. As this algorithm classifies only single-tissue images, it requires segmentation when presented with multiple-tissue images. To automate the entire algorithm, we must automate segmentation as well.

We argue that our problem cannot be solved as segmentation followed by classification, but instead as a joint process. Many segmentation algorithms focus on performing segmentation based on apparent visual similarity or dissimilarity of regions, and are insufficient to segment teratomas into single-tissue ROIs. In addition to visual cues, there are textural and structural cues that must be included to achieve the level of segmentation we require. However, by using these cues, the distinction between segmentation and classification is lost, and thus, accurate segmentation of teratomas into single-tissue ROIs is identical to identification and delineation of tissues present in the teratoma, which is our focus in this work.

2. HIGH-RESOLUTION CLASSIFICATION

We begin by formalizing our notion of high-resolution classification of an image. Given an image I of size M×N, our goal is to assign a label to every one of a set of disjoint regions of size w that partition the image. For simplicity we only consider square regions. We will determine the function

$$f_w(x_n,y_n\mid I)=c_n,$$ (1)

where x_n and y_n are the coordinates of the center of the nth disjoint region of size w in I, while c_n ∈ {1,2, … , C} is the class (tissue) label associated with the region such that

$$f_w(x_{n,i},y_{n,i}\mid I)=c_n,$$ (2)

where x_n,i and y_n,i are the coordinates of all pixels in the nth region, that is, all pairwise combinations of x_n,i ∈ {x_n − w, … , x_n + w} and y_n,i ∈ {y_n − w, … , y_n + w}. The highest possible resolution we can consider is when w = 0 resulting in a separate classification of every pixel and the sharpest delineations of tissues. While we could sacrifice some sharpness by decreasing the resolution to gain computational efficiency and possibly increased resolution-specific accuracy, we choose not to do so as it would require a partitioning of the image into disjoint regions. Such regions may not always align themselves well to the actual contours of the tissue regions and thus reduce the accuracy of our delineation. We refer to high-resolution classification as pixel-level classification.

Typically, pixel-level classification cannot be accomplished by looking at pixels in isolation, but rather with respect to their local neighborhood at a given scale (the size of the neighborhood). We consider multiple scales for many reasons, the most important being that a tissue is a collection of very local organization and appearance, in conjunction with typically medium-scale organization. Thus, we extract features from a pixel using the pixel itself and its local neighborhood; we call these features local features.

We must now determine which local features to use. As we are trying to mimic those visual cues used by experts, it is crucial to agree upon a common set of terms describing the features that are understood by both pathologists and engineers. We address this issue by developing such a set of terms we term histopathology vocabulary (HV), which we discuss next.

Histopathology Vocabulary

The purpose of the HV is to provide a set of terms, understood by both pathologists and engineers, to concisely and accurately describe the cues (visual, structural, etc.) used by pathologists, and thus guide our feature design. Additionally, these features should be robust and accurate mimicking the experts who are able to repeatedly and accurately perform the task.

Creation of the HV is simple and the basic formulation is not limited to this application only. While the formulation below is by no means unique or new, it is rarely used. We now list the basic steps of the HV formulation in the context of our application:

1. The pathologist describes (in as simple terms as possible) and ranks, in order of discriminative ability, the cues (visual, structural, etc.) used to manually identify each tissue type.

2. The engineer takes the pathologist’s descriptions and translates them into terms with a clear computational synonym, but still in terms that are understandable by the pathologist.

3. The engineer describes tissue types using only the translated terms; the pathologist then attempts to identify the tissue types based only on the engineer’s descriptions.

4. Terms that allow the pathologist to identify tissue types are included in the HV.

Using this formulation we have created an HV consisting of the following 10 terms: background/fiber color, lumen density, nuclei color, nuclei density, nuclei shape, nuclei orientation, nuclei organization, macro shape, cytoplasm color, and background texture. We have currently implemented the first 4 terms as local features and the experiments in this work use these 4 local features.

We now briefly describe each of our initial 4 features. Background/fiber color is the apparent/average color of a pixel/region not belonging to nuclei, cytoplasm, or lumen (regions to which none of the H&E stains bonded to), described using RGB values. Lumen density is the percentage of a given area occupied by lumen resulting in a scalar value ranging in value from 0 to 1. Nuclei color is the apparent/average color of a pixel/region belonging to nuclei, again described using RGB values. Nuclei density is analogous to lumen density but now for nuclei. For any given pixel, we will have an HV feature vector of length 8 (3 for each color feature and 1 each for density features) that concisely describes much of the identity of the various tissue types.

HV Features

We now describe the implementation of our HV features. A given image first undergoes H&E stain separation [8] resulting in a hematoxylin-stain image (H) and an eosin-stain image (E). Using these stain images, we create three binary masks representing the portions of the image belonging to nuclei, lumen, and background. Nuclei are identified by simply thresholding H to find sufficiently saturated regions which typically correspond to nuclei. Lumen is identified as regions where there is little contribution from either stain, and background is then determined as those regions not belonging to either nuclei or lumen.

Given these binary masks, we compute the HV features locally and at every pixel location efficiently using filters. We must first consider the size (support) of the neighborhood around each pixel and the weighting we use for each pixel in the neighborhood. Typically, both the support and weighting of the neighborhood are dictated by a single filter. The filter’s nonzero positions and values effectively determine which pixels belong to the neighborhood and how much each contributes to the feature. However, simple filtering of masked images will suffer from inclusion of the artificial effect of the mask itself. For example, when computing the local nuclei color, given a sufficiently large neighborhood, we will likely include in it regions which do not include any nuclei. As it is not desirable to include the effect of these “black” regions on the computed nuclei color, we could iteratively address each nuclei pixel and use values in its neighborhood that are identified as nuclei, at the cost of losing the computational advantages filters offer.

We propose to use a pair of filters to avoid these artifacts. We define a pixel-count filter that merely filters the binary mask of interest (for example, the nuclei mask) with a flat (all 1’s) filter whose spatial support dictates the neighborhood to be considered. The result is an image where the value at any pixel is the number of on (nonzero) pixels in the mask in that neighborhood. Similarly, we filter the masked image (for example, nuclei-only image) with a pixel-value filter whose values specify the spatial weighting to be applied in the neighborhood. The result is an image where the value at any pixel is the spatially-weighted sum of the on values of the masked image. Given these two images, we proceed to perform a pointwise division with the pixel-count result dividing the pixel-value result. The result is an image where each pixel’s value is the spatially-weighted sum of only the on pixels belonging to the mask. Using this formulation, we can quickly extract all 4 HV features for every pixel in the images.

Classifier Training

After generating HV features, we train and test a classifier to evaluate the efficacy of our features in the scope of pixel-level resolution. As the focus of our work is not the design of new classification algorithms, we use available algorithms, specifically, neural networks (NN) trained using backpropagation. Our use of NNs is motivated by our success using them in our previous work [9]. However, it is unclear whether or not existing classification algorithms are sufficiently powerful for this problem.

We now train our selected classifier over a set of training data. Since we are using pixels as our fundamental unit of data we have an over-abundance of data. It is, in fact, computationally infeasible to use all available data while training certain classifiers including NNs. Thus, given a set of training images, we must decide how many and which pixels from each training image to use. This is essentially an issue of overfitting, but not necessarily to the entire dataset but rather to the individual images. If we choose too many pixels from one image we risk learning the specific instances of tissues in that image as opposed to the tissue in general. Conversely, if we choose too few pixels we may not learn enough about the specific instances to account for its particular variations. Moreover, choosing many pixels from one image is not necessarily useful since spatially adjacent pixels are often highly correlated. However, there are instances where neighboring pixels within a tissue present very different appearances and thus potentially discriminative information. We will address this complex issue in future work; here, we choose to use random sampling of pixels within an image to create our training data.

3. EXPERIMENTS AND RESULTS

We now present experiments and results which will evaluate the effectiveness of the overall algorithm while focusing on the influence of the HV features on performance.

Dataset

Teratomas are derived and serially sectioned as in [9], then H&E stained and imaged at 4X magnification resulting in 36 1600×1200 images. 15 tissues appear in these images although the exact number of instances of each tissue varies greatly.

Experimental Setup

We evaluate our algorithm in a series of 2-, 3-, 4-, and 5-tissue/class problems (see Table 1). Bone (B) and cartilage (C) are present in all experiments as they are relatively easily discriminable, while additional classes test the ability of the algorithm to maintain separation as the size of the problem grows.

Table 1.

Best average tissue-specific pixel-level classification accuracies over 10-fold cross-validation for 2-, 3-, 4-, and 5-class problems using bone (B), cartilage (C), immature neuroglial tissue (I), neuroepithelial tissue (N) and fat (F).

Scale	Average accuracy/σ [%]
	B	C	I	N	F
16	81.3/2.4	93.2/0.4
16	85.3/3.2	86.6/1.5	84.7/2.6
16	75.4/5.4	80.7/4.4	64.0/6.2	63.1/10.2
32	71.1/6.4	74.9/8.8	60.2/11.3	64.1/15.3	72.4/4.3

In each problem we choose training and testing sets by first choosing 50% of images with relevant tissues for training. From each of these training images we randomly sample 1% of available pixels from each available relevant tissue. We insure that each tissue is present in at least one training image. The testing set is all available pixels of the relevant images not being used for training. Local HV features are computed for all pixels in the training and testing set. Both the pixel-count and pixel-value filters are flat circular filters of different radii of 4, 8, 16, and 32 pixels. A 2-layer NN is trained and then tested. We perform 10-fold cross-validation and report average accuracy for each experiment.

Results

We present the best results for each experiment (Table 1), differentiated by the particular set of HV features used (different scales), indicating the apparently preferred scale of each tissue. We present the tissue-specific accuracy as all tissues do not have an equal number of available samples and presenting an overall accuracy would misrepresent the performance of the algorithm.

We also present an example confusion matrix from the 5-tissue problem to indicate the scale of the problem and the sources of error in Table 2. To illustrate the delineation of tissues accomplished, Figure 3 shows the labeling of one image from each of the problems.

Table 2.

Example confusion matrix for 5-tissue problem with actual pixel counts at a factor of 10,000 pixels; rows are true labels and columns assigned labels.

	B	C	I	N	F
B	34.25	2.27	7.60	0.77	2.27
C	1.30	129.70	3.81	7.76	14.66
I	7.71	5.50	106.44	5.60	15.95
N	0.10	0.45	2.93	35.67	11.88
F	6.62	60.90	15.59	91.68	264.09

Figure 3.

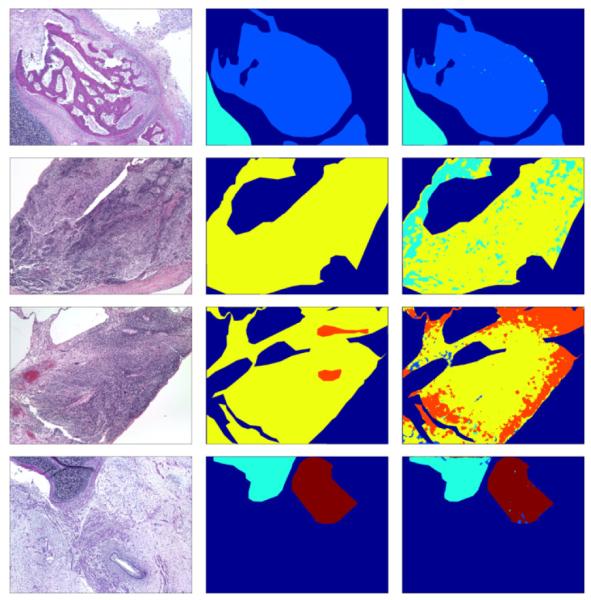
Top to bottom: Example delineations of tissues for 2-, 3-, 4-, and 5-class problems respectively. Left to right: Original image, expert-labeled ground truth, our algorithm’s labeling. Color coding: B (light blue), C (cyan), I (yellow), N (orange), F (maroon), other tissues (dark blue).

4. CONCLUSIONS AND FUTURE WORK

We presented a methodology for automatic identification and delineation of germ-layer components in H&E stained images of teratomas derived from human and nonhuman primate embryonic stem cells. Our results demonstrate that our simple and concise HV features are reasonably sufficient for problems of these sizes, and that given a relatively small amount of training data we are able to characterize a large portion of unseen data. While particular tissues are not as well represented by the 4 HV features, we believe this will be remedied once a full set of 10 HV features is used to cover all structural cues.

In future work, we will focus on developing the full HV set, as well as creating a method with which to choose pixels from a set of training images. Additional classifiers will be tested and formulated in a hierarchical/tree structure that will allow us to perform a type of taxonomic classification of tissues. We will also develop quantitative metrics with which to describe tissues in the pursuit of understanding the underlying biology of ES cells.

Figure 2.

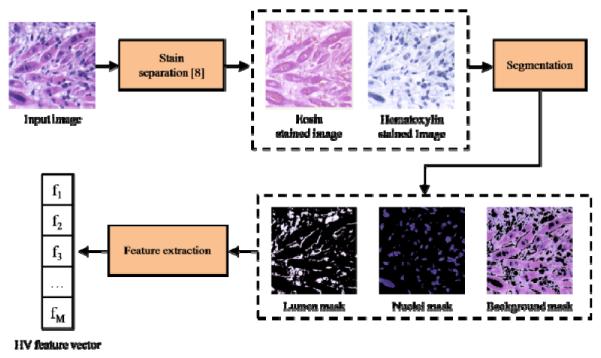
HV feature-extraction methodology.