Abstract
The physiological lag between blood and interstitial fluid (ISF) glucose is a major challenge for non-invasive glucose concentration measurements. This is a particular problem for spectroscopic techniques, which predominantly probe ISF glucose, creating inconsistencies in calibration, where blood glucose measurements are used as reference. To overcome this problem, we present a dynamic concentration correction (DCC) scheme, based on the mass transfer of glucose between blood and ISF, to ensure consistency with the spectral measurements. The proposed formalism allows the transformation of glucose in the concentration domain, ensuring consistency with the acquired spectra in the calibration model. Taking Raman spectroscopy as a specific example, we demonstrate that the predicted glucose concentrations using DCC-based calibration model closely match the measured glucose concentrations, while those generated with the conventional calibration methods show significantly larger deviations from the measured values. In addition, we provide an analytical formula for a previously unidentified source of limiting uncertainty arising in spectroscopic glucose monitoring from a lack of knowledge of glucose kinetics in prediction samples. A study with human volunteers undergoing glucose tolerance tests indicate that this lag uncertainty, which is comparable in magnitude to the uncertainty arising from noise and nonorthogonality in the spectral dataset, can be reduced substantially by employing the DCC in spectroscopic calibration.
1. Introduction
Non-invasive glucose diagnosis has received considerable attention due to its important implications for diabetes management and therapeutics.1, 2 Various techniques ranging from electrochemical assays3, 4 to optical methods5 have been proposed to meet the goals of painless and accurate glucose measurements. Vibrational spectroscopy, notably near infrared (NIR) absorption and Raman spectroscopy, has shown substantial promise in this regard.6 Specifically, NIR Raman spectroscopy has provided successful predictions of glucose at physiologically relevant concentrations in serum,7, 8 whole blood,9 and even in human volunteers.10 However, a clinically accurate and robust algorithm for predicting glucose concentrations in multiple human subjects, or even in the same subject at different times, is currently lacking.11
Researchers have identified factors that degrade the glucose measurement accuracy of Raman spectroscopy by introducing non-analyte specific variance into the calibration model. The predominant factors include sample-to-sample variability in absorption and scattering properties (turbidity),12 tissue autofluorescence and associated quenching,13 and physiological lag between blood and interstitial fluid (ISF) glucose.14–18 Several spectroscopic correction schemes have been implemented to minimize the effect of the first two factors,19–21 but correction for the presence of a lag time has not been demonstrated for transcutaneous glucose monitoring, due to its intricate relationship with the fundamental physiological dynamics. This lag time creates an inconsistency in spectroscopic calibration algorithms, which are based on reference blood glucose concentrations and the acquired tissue spectra. This inconsistency arises from the fact that the spectroscopic techniques primarily probe ISF glucose18, due to the relatively shallow penetration depth (~1mm) of NIR light in tissue and the small density of blood vessels in the superficial layers of the skin.22
This inconsistency in calibration presents a severe hindrance not only for spectroscopy based non-invasive glucose monitoring but also for minimally invasive electrochemical sensors (such as Medtronic/Minimed’s Guardian and FreeStyle Navigator from Abbott Diabetes Care), which base their glucose estimates on interstitial fluid measurements. Indeed, as pointed out by Cengiz and Tamborlane,15 the physiological lag introduces systematic errors during calibration which adversely impact long-term sensor performance, even in the presence of a positive correlation between blood and ISF glucose.23–25 Such diagnostic errors may lead to unnecessary insulin bolus, which significantly increases the risk of hypoglycemia.26, 27 The presence of systematic errors is one of the main reasons that such continuous glucose monitoring sensors need to be re-calibrated against fingerstick measurements at regular intervals.
Typically, for all ISF glucose-based sensors, spectroscopic or otherwise, the underlying assumption is that the blood-to-ISF glucose gradient remains constant over the measurement range.17 However, this assumption fails if the sensor is calibrated during rapid changes in blood glucose, as are encountered during glucose tolerance tests, which provide the most viable protocol for the development of calibration models using spectroscopic techniques.28 Calibration during such non-equilibrium conditions leads to large errors in the developed model. To account for the differences in blood and ISF glucose, Bonnecaze and co-workers established the first substantive models for ISF glucose by considering the ISF and blood glucose to reside in two “compartments”, and performing a mass balance between them.29, 30 Using amperometric glucose sensors implanted in rats, they demonstrated that accurate estimates of blood glucose concentration can be extracted from subcutaneous ISF glucose-based measurements. However, no analogous models exist for development of spectroscopic calibration algorithms, which are inherently more complex because of the multivariate nature of the data.
Furthermore, even if an accurate calibration model can be established by performing all measurements under equilibrium conditions (e.g. by employing glucose clamps), the lack of knowledge of glucose kinetics in prediction samples would introduce an uncertainty in the concentration estimates. Such prediction uncertainties may lead to inappropriate treatments. Previously, several research groups have assessed uncertainty in spectroscopic prediction based on the noise in the spectral and concentration datasets and the non-orthogonality (spectral overlap) of the analyte of interest with the other sample constituents.31–33 However, the uncertainty introduced due to the lag phenomenon in the prediction samples remains unexplored.
This paper presents a new spectroscopic calibration scheme based on “dynamic concentration correction” (DCC), which is based on a two-compartment mass transfer picture of blood and ISF glucose and is designed to provide an accurate estimate of glucose concentrations for non-invasive measurements. These transformations are performed iteratively in conjunction with an implicit calibration method, such as partial least squares (PLS), to form an accurate and consistent regression model. The resulting calibration model can be used on a new set of acquired spectral samples — the prediction set — to calculate the ISF glucose concentrations of the samples. Subsequent application of the DCC model converts the estimated ISF glucose concentrations to the equivalent blood glucose concentrations of the prediction samples.
This work employs Raman spectroscopy as a specific example to demonstrate the effectiveness of the new calibration method, with the understanding that this scheme can be similarly applied to other spectroscopic techniques, such as NIR absorption. Using blood and ISF glucose concentration datasets obtained by Steil et al.34, we first demonstrate that predicted glucose concentrations using the DCC calibration model closely match the measured blood glucose concentrations, whereas those generated solely by the conventional implicit calibration methods show significantly larger deviations from the measured values. These results are further validated on spectral and concentration datasets obtained from clinical studies on human volunteers undergoing glucose tolerance tests.
In addition, we derive analytical expressions for the limiting uncertainty introduced in the concentration predictions due to presence of the physiological lag – with and without application of DCC. Here, limiting uncertainty is defined as the uncertainty in concentration estimate in the case where all modeling noise is disregarded, i.e. where the calibration model is assumed to be completely accurate and noise free. Employing the human volunteer data, we find that the concentration uncertainty due to the lag phenomenon is comparable to that arising from the noise and overlap in the prediction spectra and that this major source of uncertainty can be significantly reduced (approximately six-fold) when DCC is used, providing further motivation for its use in spectroscopy-based transcutaneous blood glucose monitoring.
2. Dynamic concentration correction (DCC) theory
The primary motivation for proposing a new spectroscopic calibration method for blood glucose detection is to establish consistency in the calibration model, which maps the spectral measurements to the glucose concentrations. The conventional linear calibration equation can be written as35:
| (1) |
where b is the spectrum of regression coefficients (also called the regression vector), S is the matrix of calibration spectra and c is the vector of measured concentrations of the analyte of interest in the calibration samples. S* is the appropriate inverse of S, as evaluated by the calibration method of choice. (Lowercase boldface represents a vector and uppercase boldface denotes a matrix.)
As mentioned in Sec.-1, since the spectral measurements are predominantly contributed by ISF glucose, the relevant input concentrations to the implicit calibration method should incorporate the ISF glucose concentrations. However, the ISF glucose concentrations are typically not available in a real-life clinical setting – instead, blood glucose values obtained from frequent blood withdrawals are used as reference concentrations. This creates a regression vector, which is neither based completely on blood glucose nor on ISF glucose, but a mixture of the two contributions. This, in turn, also creates a problem in the prediction step, where the predicted glucose concentration c is obtained by a scalar product of the regression vector b and the spectrum acquired from the prediction sample s:
| (2) |
(Lowercase italics indicates a scalar quantity and the superscript T denotes the transpose of the vector.) In the conventional calibration framework, the predicted glucose concentration is reported as the blood glucose concentration, although this clearly is not an accurate representation.
To correct for this discrepancy, we propose a new calibration methodology (DCC) in which the concentrations are appropriately changed to conform to the spectral measurements. The transformation in the concentration domain is based on a two-compartment mass transfer model, which establishes a well-defined relationship between blood glucose, ISF glucose and the system parameters. Specifically, we perform the following two transformations in DCC:
Pre-calibration DCC (PC-DCC): Transform the blood glucose concentrations in the calibration dataset to their corresponding ISF values before inputting into the implicit calibration method. This ensures that the regression vector is solely based on ISF glucose contributions.
Post-prediction DCC (PP-DCC): Re-transform the predicted ISF glucose concentration, which is determined by Eq. (2), to the corresponding blood glucose value.
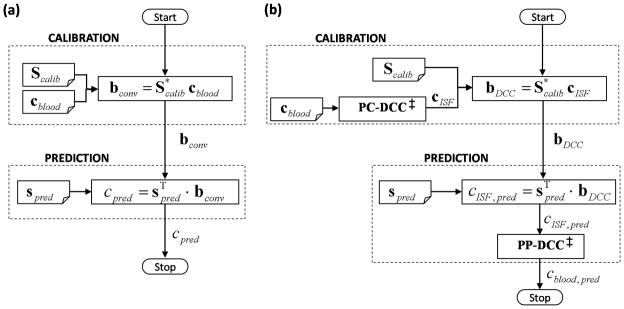
The conceptual differences between the conventional and proposed (DCC-based) calibration methods can be seen in Fig. 1.
Fig. 1.
Flowcharts of (a) the conventional implicit and (b) DCC calibration methods. Scalib, cblood, and spred represent the calibration spectra, reference blood glucose concentrations in the calibration samples, and the spectrum acquired from the prediction sample, respectively. For the conventional calibration method, bconv and cpred give the regression vector and the predicted concentration, respectively. For DCC calibration, bDCC represents the developed regression vector. cISF,pred and cblood,pred are the intermediate ISF glucose estimate and the final blood glucose prediction. PC-DCC is the pre-calibration transformation of blood glucose concentrations into the corresponding ISF glucose values. PP-DCC transforms the predicted ISF glucose concentration into the blood glucose value. Note that the conventional calibration scheme does not differentiate between the blood and ISF glucose concentrations.
‡ Both PP-DCC and PC-DCC require two concentration inputs acquired at a time interval Δt apart for evaluation of Eq. (15) and (16), respectively.
For the subsequent analysis, we assume that the sampling volume (i.e. the volume of tissue probed by the NIR light) is a subset of the interstitial fluid space. This assumption is primarily based on the fact that the ISF constitutes nearly 45% of the volume fraction of the human skin in contrast to the blood vessels which contribute about 5% of the skin volume.36 In Sec.-5, we revisit this assumption and characterize its impact on the proposed calibration model.
Transfer of glucose from the blood to the ISF compartment occurs by passive diffusion across an established concentration gradient.37 The mass transfer rate is affected by several variables, such as the blood flow rate to the site, rate of glucose uptake by the surrounding tissue, and the capillary permeability. Nevertheless, as discussed in the literature,29, 34, 38 a simple two-compartment mass-transfer model can be written for the ISF volume VISF:
| (3) |
where cISF and cBG are the ISF and blood glucose concentrations (mol/cm3) respectively, kM is the glucose mass transfer coefficient (cm/s), A is the effective mass transfer surface area (cm2) and kU is the rate of glucose uptake by the neighboring cells (1/s). The effect of insulin on the uptake term has been ignored. This approximation is consistent with the observed result that the glucose levels in (subcutaneous) ISF are largely unaffected by the local insulin concentration.34 In fact, the uptake term itself has been observed to be very small for subcutaneous glucose sensing.29 This is attributed to the fact that skin tissue, as opposed to muscle or adipose tissue, is unlikely to have significant glucose uptake, even in the presence of high insulin concentration. Consequently, we will ignore the uptake term in further analysis. Eq. (3) can then be simplified to:
| (4) |
where is a lumped mass-transfer parameter having units of time. The parameter α provides a measure of the physiological lag time arising from the diffusion process and is henceforth called the characteristic lag time constant. This equation provides the ability to construct blood glucose estimates based on the spectroscopy-based ISF glucose prediction values and a priori knowledge of the lag time constant in the sample. The numerical evaluation of this equation, which provides the post-prediction (PP-DCC) step, is explained in Appendix I.
The other important portion of the proposed scheme is the pre-calibration (PC-DCC) step. In order to obtain consistency in the calibration model, we need to convert the measured blood glucose concentrations to the corresponding ISF glucose values. To perform this transformation, we write Eq. (4) in its integral form:
| (5) |
where the definite integral is evaluated from time ti to tf. Details of the numerical implementation of this equation are given in Appendix II.
3. Formulation of prediction uncertainty arising from physiological lag
In order to quantify the precision of spectroscopy based calibration models, Lorber and Kowalski derived an elegant prediction error formula, which describes the error propagation for linear multivariate prediction algorithms.31 Our laboratory has previously derived analytical expressions for uncertainty in concentration prediction for the specific case where noise in the prediction dataset (spectra) is the dominant source of error.32, 33 This case is important, as in most biomedical applications constraints on the acquisition time in prediction samples cause the noise in the prediction dataset to be significantly higher than that observed in the calibration dataset (where acquisition times are typically much longer). In such cases, it can be assumed that an accurate calibration model can be achieved by developing it on calibration samples in which sufficiently high signal-to-noise ratio (SNR) can be attained. Under such conditions, the limiting uncertainty in the predicted concentrations arises from the spectral overlap between the analyte of interest and the other tissue constituents, and the measurement noise in the spectra acquired from the prediction samples. Mathematically, the spectroscopic uncertainty for the analyte of interest (glucose) is given by Δcs 33:
| (6a) |
where
| (6b) |
Here, ĉ and c are the estimated and actual analyte concentrations in the prediction sample, respectively and Δs represents the spectral noise in the prediction spectrum s. As the modeling noise is ignored in computation of the limiting uncertainty, b represents the ideal (noise-free) regression vector for glucose. σ is a measure of the noise magnitude in the prediction spectrum, sg quantifies the signal strength of glucose at unit concentration, and olf indicates the amount of overlap between glucose and the other spectral interferents (such as proteins, lipids, and water).
In addition to the spectroscopic uncertainty, there exists a prediction uncertainty for transcutaneous glucose measurements that arises from the physiological lag between blood and ISF glucose levels. Even if the calibration models are developed under conditions in which the blood and ISF glucose concentrations are in equilibrium (such as those obtained by employing glucose/insulin clamps), the predicted concentrations will still contain uncertainties due to the unaccounted physiological lag in the prediction samples. We present an error propagation analysis to determine the limiting uncertainty in concentration prediction due to the physiological lag, with and without DCC. Similar to our laboratory’s previous work,32, 33 we assume that the developed calibration model itself is accurate, i.e. devoid of noise and lag-related errors.
3.1. Limiting uncertainty for conventional calibration
When the modeling noise is ignored, Eq. (6) provides the relationship between the estimated and the actual glucose concentrations. However, for in vivo prediction, there will be a lag between the instantaneous blood and ISF glucose values in the sample, where the latter is measured by the prediction spectrum. Taking this into account, we can re-write Eq. (6) in terms of the estimated (ĉISF) and actual (cISF) ISF glucose concentrations:
| (7) |
Based on the two-compartment model, the actual blood glucose concentration, cBG, can be determined from the actual ISF glucose concentration using Eq. (4), given the correct lag time constant for the prediction sample (αactual). Substituting the value of the actual ISF glucose concentration from Eq. (7) into Eq. (4), we obtain:
| (8) |
However, the conventional models report the estimated ISF glucose concentration as the blood glucose concentration (ĉBG) in the prediction sample:
| (9) |
Substituting Eq. (9) into Eq. (8) and re-arranging, we obtain:
| (10) |
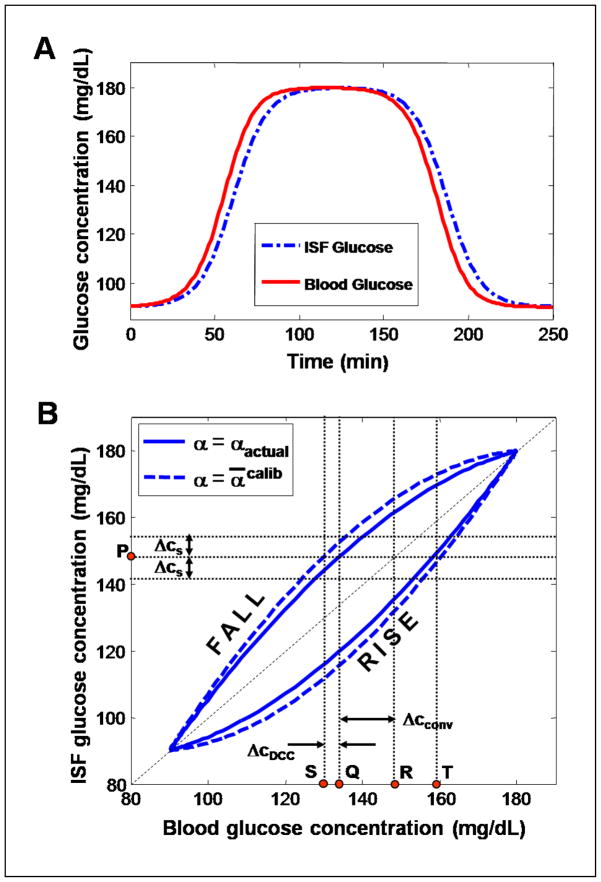
Equation (10) implies that under the conventional calibration framework, the limiting uncertainty in the concentration estimate has two separate contributions: (i) the uncertainty resulting from the measurement noise in the prediction spectrum and the spectral overlap, Δcs and (ii) the uncertainty due to the glucose physiological lag, . While the former (i) is a well-known quantity, the latter uncertainty (ii) has not been examined before. Figure 2 illustrates the two contributing factors of the prediction uncertainty. In this figure, the simulated blood and ISF glucose data in panel (A) (which mimics the glucose profiles obtained from a tolerance test) are plotted against each other to construct the solid line curve in panel (B). It is evident that the physiological lag between the blood and ISF glucose profiles in (A) introduces a hysteresis-like closed loop behavior when blood glucose is plotted against ISF glucose, showing the lack of a one-to-one correspondence between the glucose concentrations in the two compartments. For example, we observe that given an ISF concentration of 148 mg/dl at point P, the actual blood glucose concentration could be either 132 mg/dl (Q) or 158 mg/dl (T). However, conventional methods that have the underlying assumption of a constant blood-to-ISF glucose gradient would predict 148 mg/dl (R), giving rise to a significant error in prediction. Specifically, when the glucose levels are increasing, the blood glucose concentrations are greater than the corresponding ISF glucose concentrations. This set of values is represented by the points on the concave upwards curve (labeled “RISE”). Similarly, the set of values obtained during the falling phase is represented by the concave downwards curve (labeled “FALL”). The lag uncertainty Δcconv in the predicted blood glucose concentration for the conventional calibration model is given by the distance between points Q and R. The uncertainty due to the noise and spectral overlap in the prediction spectrum is marked as Δcs.
Fig. 2.
(A) A schematic representation of blood and ISF glucose concentration profiles, similar to those obtained during a typical tolerance test. (B) Plot of the ISF vs. blood glucose concentrations shown in panel (A). The solid line curve shows the lack of one-to-one correspondence between the actual ISF and blood glucose relationship, while the dotted line curve represents the approximate relationship estimated by the DCC model. Further details are provided in the text.
3.2. Limiting uncertainty for DCC calibration
In contrast to the conventional model, the DCC scheme explicitly accounts for the physiological glucose dynamics. Specifically, the post-prediction equation (PP-DCC) is used to transform the spectroscopy-based ISF glucose estimate (ĉISF) to a corresponding blood glucose value (ĉBG), and this step needs to be considered in evaluating the limiting uncertainty. As the correct lag time constant in the prediction sample is unknown in a real clinical setting, some uncertainty due to the physiological lag is introduced via the PP-DCC step. As explained in Sec.-3.1, we employ the (ensemble) average of the lag time constants obtained from the calibration samples to approximate the actual lag time constant in the prediction sample. Based on this approximation, the PP-DCC equation can be re-written as:
| (11) |
where ᾱcalib refers to the average value of α computed from the calibration samples.
Substituting Eq. (7), into Eq. (11), we obtain:
| (12) |
The deviation of ᾱcalib from the actual lag time constant in the prediction sample, αactual can be written as:
| (13) |
where Δα is the error (uncertainty) in the estimation of the lag time constant.
Substituting Eq. (13) into Eq. (12) and re-writing the first term of the above equation as cBG, we get:
| (14) |
Equation (14), which is analogous to Eq. (10) for the conventional calibration model, implies that even with DCC, the net uncertainty is a combination of the uncertainties arising from the spectral noise and overlap (Δcs) and the physiological lag ( ). However, the primary difference between the two cases – with and without DCC – lies in the magnitude of uncertainty introduced due to the physiological lag. The lag uncertainty for the conventional calibration model case (which is proportional to αactual) is significantly larger than that observed for DCC calibration (which is proportional to Δα). This can be visualized in Fig. 2(B). The dashed line curve of Fig. 2(B) connects the points whose coordinates are given by the model estimated blood and ISF glucose concentrations (in contrast to the solid line curve that represents the points whose co-ordinates are given by the blood and ISF glucose concentrations in Fig. 2(A)). Since the exact lag time constant of the prediction sample is unknown, the estimated blood glucose concentrations will differ from the actual blood glucose concentrations by the product of the rate of change in glucose concentration and the estimation uncertainty of the lag time ( ). It is worth noting that the dashed (DCC estimated) curve is computed using Eq. (11), whereas the blood and ISF glucose concentrations of the solid curve are related by Eq. (4). From the figure, it is evident that ΔcDCC, the distance between points Q and S, is substantially smaller than Δcconv, the distance between points Q and R, as long as the lag time constant used in the DCC model provides a reasonably close approximation to the actual lag time constant. A quantitative comparison of the two lag uncertainties and the spectroscopic uncertainty is performed in Sec.-5.2.
4. Materials and Methods
We performed numerical simulations and experimental studies to: (1) demonstrate the improvement in prospective prediction performance of the calibration model on application of DCC and (2) estimate the distribution of the lag time constant in a human population and characterize the prediction uncertainty introduced due to the physiological lag. To accomplish (1), a numerical simulation study was undertaken (Sec.-4.1). In this study, ISF and blood glucose concentration datasets, described by Steil et al.,14, 34 were used to generate tissue Raman spectra for calibration and prediction. The simulations were also used to understand the relationship between the SNR in the spectral dataset and performance of the conventional and DCC calibration models. In order to investigate the lag time distribution in a human population (2), datasets obtained from our laboratory’s clinical studies on human volunteers were employed. Additionally, the human volunteer study was used to determine the limiting uncertainty arising from the physiological glucose dynamics, as described in Sec.-4.2.
4.1. Numerical simulations
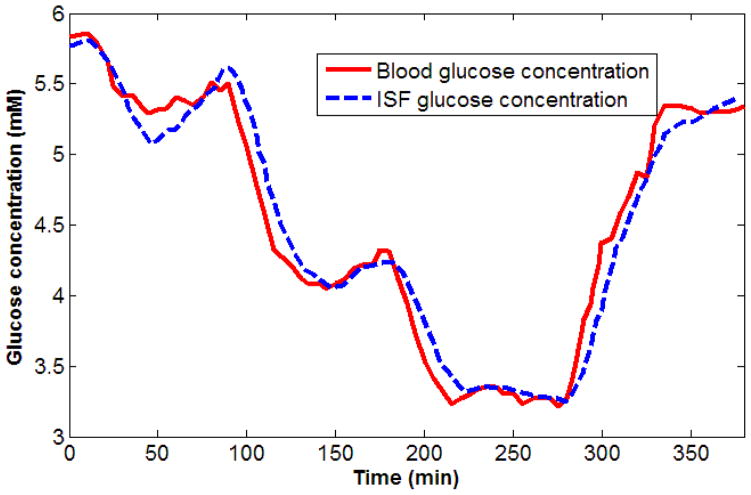
The dataset used in our numerical simulations was based on blood and ISF glucose concentrations originally measured by Steil et al. 34 In their studies, Steil and co-workers monitored blood and ISF glucose concentrations in non-diabetic human subjects during glucose clamping. After 10–12 hours of overnight fasting, glucose was sequentially clamped at approximately 5, 4.2 and 3.1 mM (1 mM of glucose ≈ 18 mg/dL) for 90 minutes each by insulin and glucose infusion, and subsequently allowed to return to euglycemic levels. ISF glucose was measured by two MiniMed (Medtronic, Inc.) subcutaneous amperometric glucose sensors. Blood was withdrawn at regular intervals for blood glucose measurements using a clinical glucose analyzer. Our analysis uses the blood and ISF glucose concentrations from 90 to 380 minutes after initial insulin and glucose infusion, as shown in Fig. 3. The simulated spectra and corresponding blood glucose concentrations is divided into calibration (dataset spanning from 90 to 220 min) and prediction (dataset from 230 to 380 min) sets, respectively.
Fig. 3.
Blood and ISF glucose concentration time profiles measured from a normal human volunteer during insulin-induced hypoglycemia.34 Glucose was clamped at 5, 4.2 and 3.1 mM and subsequently allowed to return to normoglycemic levels. It is observed that the ISF glucose, measured by subcutaneous amperometric sensors, consistently lags blood glucose concentrations during both rising and falling phases. In contrast, they have nearly identical values during the clamping phases.
In our study, simulated Raman spectra are generated by forming weighted linear combinations of the constituent Raman spectra of glucose, creatinine, and urea (as measured by our laboratory Raman system19). The weights assigned for glucose (the analyte of interest) are determined by the experimentally measured ISF glucose concentrations of the Steil dataset. The other two constituents (spectral interferents) are assigned weights that randomly varied within 2% of a constant value, in order to mimic the small changes observed in these constituents during typical glucose tolerance and clamping tests. To simulate normal experimental conditions, zero-mean Gaussian white noise is added to the mixture spectra at varying levels of SNR (20–40 dB) to study its effect on prediction performance of the calibration models. The uniform noise across the spectra and the SNR range are consistent with typical Raman spectra of biological samples.
In contrast to the conventional PLS calibration strategy, where the number of loading vectors are optimized, in the DCC calibration the number of loading vectors as well as the lag time constant, α, need to be optimized. To accomplish this, we initially assign default values to α (0 minutes) and the number of loading vectors (2) employed, respectively. Prior to constructing the leave-one-out calibration model, all but one of the reference blood glucose concentrations are converted to the corresponding ISF glucose values using PC-DCC (Eq. (5)). This allows the creation of a calibration model based purely on ISF glucose. The developed calibration model, in conjunction with the spectrum of the excluded data point (which constitutes the validation data), is then used to predict the ISF glucose concentration at that point. Subsequently, PP-DCC (Eq. (4)) is used to re-transform the predicted ISF glucose concentration to the blood glucose value. This process is repeated till each data point is used once as the validation data. The resultant blood glucose estimates are compared with the actual blood glucose values to give the root-mean-squared error of cross-validation (RMSECV). The whole procedure is iterated for appropriate ranges of α (0 to 20 min) and number of loading vectors (LV) (2 to 10) to determine the optimal combination of parameters (αopt, LVopt) that yields the minimum RMSECV. This combination of parameters is then used to obtain the PLS regression vector, bopt. Prospective prediction on a separate portion of the data set was performed by taking the scalar product of the prediction spectra with bopt (Eq. (2)). The ISF glucose predictions are re-converted to the blood glucose values using PP-DCC, where αopt is used in place of α in Eq. (4). The root-mean-squared error of prediction (RMSEP) is computed from the predicted blood glucose concentrations and the reference blood glucose values.
Conventional PLS calibration and prediction is also performed on the same dataset to compare the relative performance with the DCC model. For further comparison, a fixed time delay is also incorporated into the standard PLS analysis as a second control. This involves shifting the measured blood glucose concentrations with respect to the spectral acquisitions by a specified amount comparable to the time lag reported in the literature. Twenty simulations are carried out for each value of SNR in the spectral dataset (both calibration and prediction) to establish the mean and standard deviation of the prospective prediction errors.
4.2. Experimental studies on human subjects
To investigate the lag time distribution in a human population, clinical datasets consisting of blood glucose concentrations and tissue Raman spectra are used. The acquisition of the clinical data was described in one of our laboratory’s previous publications 11. Briefly, Raman spectra were collected from the forearms of healthy Caucasian and Asian human volunteers undergoing OGTT. The age of the tested human volunteers’ was in the range of 21–29, with a mean of 24.5. For the excitation source, an 830 nm diode laser (Process Instruments) was used at an average power of ~300 mW in a ~1 mm2 spot. A f/1.8 spectrograph (Kaiser Optical Systems) was coupled to a liquid nitrogen-cooled CCD (1340×1300 pixels, Roper Scientific) for spectral dispersion and acquisition, respectively. For each volunteer, OGTT was initiated by the ingestion of a glucose-rich solution, and Raman spectra were collected every 5 minutes over a two-hour period. Concurrently, the reference blood glucose concentrations were measured every 10 minutes from blood samples using a clinical glucose analyzer (HemoCue, Inc.), and spline interpolation was used to correlate the measured blood glucose concentrations with the spectra collected at intermediate time points. This study protocol was approved by MIT Committee On the Use of Humans as Experimental Subjects.
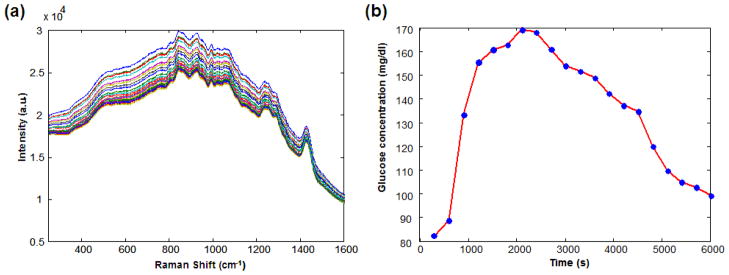
Datasets from volunteers exhibiting motional artifacts, inadequate SNR in the acquired spectra, and impaired glucose tolerance characteristics are excluded from further analysis. A representative set of tissue Raman spectra and the corresponding blood glucose concentration profile acquired from one of the human volunteers are shown in Fig. 4. For the selected volunteer datasets, DCC calibration is performed using a leave-one-out cross-validation routine on the measured Raman spectra and reference blood glucose concentrations to determine the optimal value of α for each individual. In addition, conventional PLS calibration is also performed on the same datasets to compare the resultant cross-validation errors. The cross-validation procedures in both cases remain the same as that described in Sec.-4.1, except that experimentally measured Raman spectra are used in place of the simulated Raman spectra. The mean and standard deviation of α determined from the human subjects are used to approximate αactual and Δα for the quantification of uncertainty due to physiological lag for the DCC and conventional calibration schemes respectively (Sec.-3). These uncertainty estimates are also compared with the spectroscopic uncertainty, Δcs.
Fig. 4.
(a) Representative Raman spectra acquired from a human volunteer during OGTT.
(b) Blood glucose concentration profile measured over the same time.
5. Results and discussion
5.1. Numerical simulations
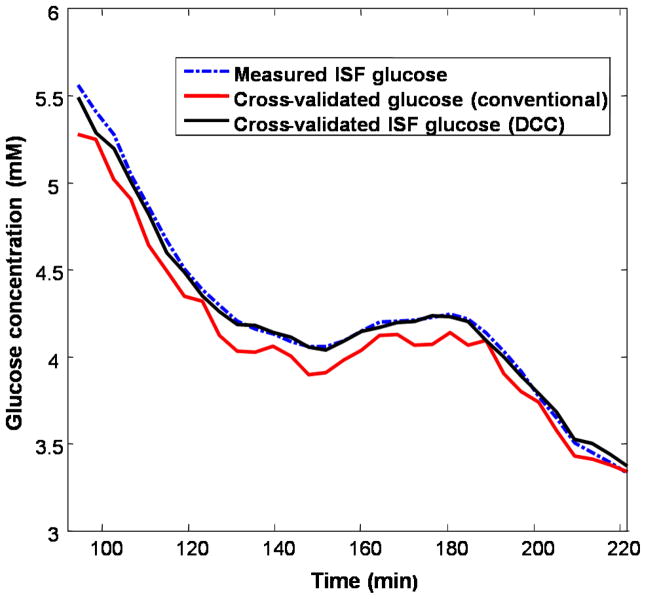
Numerical simulations were used to compare the prospective prediction capability of the conventional and DCC calibration models. DCC implementation was found to reduce the RMSECV of the simulated dataset from 0.15 mM to 0.04 mM, when the measured ISF glucose concentrations were used for computing the cross validation errors. The RMSECV for fixed timed delay PLS processing was computed to be 0.07 mM. These simulation results were obtained for a SNR of 40 dB. Figure 5 shows the measured ISF glucose concentrations plotted together with cross-validated glucose concentrations from the conventional and DCC calibration models. It is evident that the ISF glucose concentration profile generated with DCC closely matches the measured ISF glucose concentrations, while that generated without DCC shows significantly larger deviations. The cross-validation routine also optimized the lag time constant for the DCC calibration model and the number of loading vectors for both models. For this dataset, the characteristic lag time constant αopt was determined to be 6.1 minutes, in agreement with the experimentally observed values of 6–8 minutes.34
Fig. 5.
Cross-validation results of conventional (red) and DCC (black) calibration methods applied on the simulated dataset. The measured ISF glucose concentration values are given by the blue dotted line. In the DCC calibration process, the lag time constant αoptimal was optimized to be 6.1.
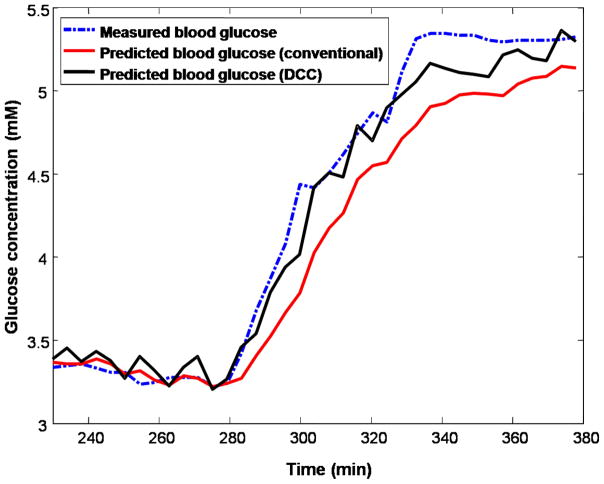
When the calibration models were applied prospective to the prediction dataset, the DCC model (RMSEP = 0.14 mM) exhibited significantly improved prediction accuracy compared with the conventional PLS scheme (RMSEP = 0.28 mM). In comparison, the fixed time delay PLS processing provides an RMSEP of 0.26 mM, which is a slight improvement over conventional PLS implementation, but it is still significantly poorer than the DCC performance. Figure 6 shows the results of prospective prediction, in which the measured blood glucose concentration profile is plotted alongside of the prediction profiles, with and without DCC. This demonstrates how calibration during non-equilibrium conditions leads to systematic errors giving rise to much higher prediction errors (Fig. 6) than estimated during cross-validation (Fig. 5). The presence of systematic errors is further evidenced by the relative performance of the fixed time delay processing in cross-validation (approximately 50% improvement over conventional PLS processing) and prospective prediction (approximately 7% improvement over conventional PLS processing), respectively. In fact, in the presence of such errors, the predicted glucose concentration may have no statistically significant correlation with the actual glucose concentrations during rapidly rising and declining glucose concentrations. Potentially, one could achieve an even closer correlation with the measured blood glucose concentration profile by smoothing out the noisy fluctuations observed in the concentration profile of the DCC prediction of Fig. 6. However, such smoothing algorithms were not employed as they might introduce artifacts and additional delays to the concentration profile that are unrelated to glucose equilibration.34
Fig. 6.
Prospective prediction results of conventional (red) and DCC-based (black) calibration methods applied on the simulated dataset. The measured blood glucose concentration values are given by the blue dotted line.
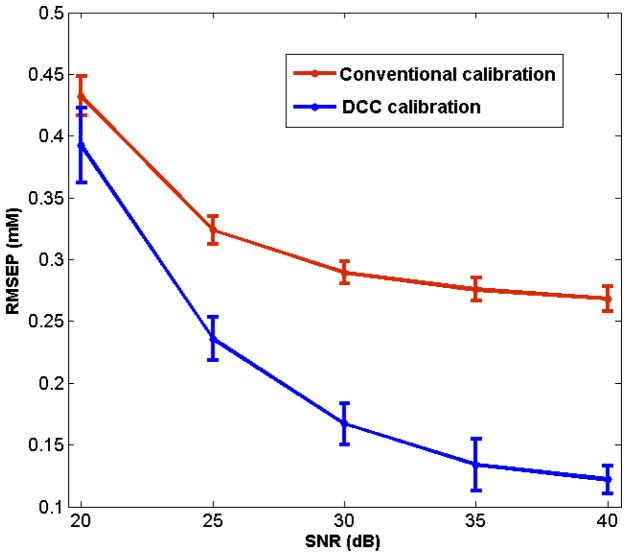
The accuracy of blood glucose concentration prediction with and without DCC was also compared at varying levels of SNR in the spectral dataset. Figure 7 shows a plot of the RMSEP of blood glucose prediction with conventional and DCC calibration models as a function of SNR. In both cases, increase in noise level corresponded to an increase in error values, as expected. However, under all tested values of SNR, the prediction error of DCC calibration models was consistently smaller compared to that of the conventional PLS models. It was also observed that the mean αopt was essentially noise-insensitive, although the variations from the mean αopt were larger for lower SNR (e.g. standard deviation in α was computed to be 0.05 and 0.5 min at 40 and 20 dB, respectively).
Fig. 7.
Plot of RMSEP obtained for conventional (red) and DCC (blue) calibration models, applied on the simulated dataset, as a function of increasing SNR. The error bars represent the standard deviation of RMSEP for 20 iterations.
Clearly for DCC implementation, a time series of glucose measurements (such as those obtained from glucose tolerance tests) are required from human subjects included in the calibration study for characterization of the glucose kinetics. It is not possible to develop a consistent calibration model based only on single spectroscopic measurements from multiple human subjects, as such measurements do not provide information on the glucose kinetics.
It is also worth noting that application of an enhanced calibration scheme, such as support vector machines39 or hybrid calibration methods,40, 41 alone would not alleviate inconsistencies in the calibration models as they do not address the lack of one-to-one correspondence between the ISF and blood glucose concentrations (Fig. 2). Nevertheless, when used in conjunction with DCC, such calibration schemes may potentially further improve the prediction accuracy.
5.2. Experimental studies on human subjects
Table 1 lists the results of the leave-one-out cross-validation on the dataset from each human subject, using DCC calibration as well as the conventional PLS routine. We observe that, on average, the RMSECV for the blood glucose concentrations of the human subjects reduces on application of DCC by 15.5%, with a maximum reduction of 28.6%. This demonstrates the applicability of DCC in clinical situations, where the number of tissue components probed is vastly greater than the three constituents (glucose, creatinine and urea) employed in our simulations.
Table 1.
Summary of cross-validation results of conventional and DCC calibration models applied on the human volunteer data (Sec.-4.2).
| Volunteer | No. of data points | DCC Model | Conventional Model | % change in RMSECV | |
|---|---|---|---|---|---|
| α_opt (min) | RMSECV (mM) | RMSECV (mM) | |||
| 1 | 25 | 9.5 | 0.87 | 1.07 | 19.10 |
| 2 | 26 | 11.5 | 0.52 | 0.72 | 27.56 |
| 3 | 26 | 10.5 | 0.70 | 0.97 | 28.62 |
| 4 | 30 | 11.1 | 1.02 | 1.08 | 5.74 |
| 5 | 25 | 8.4 | 0.68 | 0.79 | 13.35 |
| 6 | 26 | 8.4 | 0.64 | 0.82 | 22.00 |
| 7 | 25 | 7.5 | 0.42 | 0.51 | 17.61 |
| 8 | 29 | 8.1 | 0.76 | 0.87 | 12.44 |
| 9 | 31 | 8.3 | 0.96 | 1.00 | 3.41 |
| 10 | 27 | 12 | 0.50 | 0.53 | 5.25 |
As mentioned in Sec.-2, in formulating DCC, it has been assumed that the sampling volume is a subset of the interstitial fluid space. This assumption was based on: (i) NIR light has a penetration depth of ~1 mm in skin tissue and (ii) the blood vessels contribute only 5% to the total skin volume,36 with the outermost epidermis being completely avascular. However, a small fraction of the inelastically scattered (Raman) light arises from the glucose residing in the blood compartment. This results in a reduction in the value of the lag time constant α, as determined by our DCC model. Nevertheless, our results demonstrate that DCC successfully models the clinical human volunteer data, even though a small Raman contribution from the blood glucose component is present. This shows that the DCC approach is effective in improving consistency in the calibration model and thus in prospective prediction, as long as the spectral contribution of blood glucose is small compared to that of ISF glucose.
The results also suggest that the value of the lag time is fairly constant for the tested human volunteer population. This is established by the lag time distribution obtained from the clinical data, where the mean of α, 9.5 min, is significantly larger than the standard deviation, 1.6 min. The relative constancy of α indicates that the mean lag time of the calibration set provides a fairly accurate approximation to the lag time of any prospective subject, on whom the algorithm has not been applied before. To the best of our knowledge, this is the first time that the lag time distribution in a human population has been measured by optical techniques. Previous attempts with subcutaneous amperometric sensors have been observed to have significant sensor specific lag, which obscures the precision of the physiological lag measurements.14 In addition to the sensor specific lag of the sub-cutaneous amperometric monitors, the difference in lag time constants observed from the numerical simulations using the Steil dataset (6.1 min) and our clinical studies on human volunteers (9.5±1.6 min) can be attributed to: (a) the difference in the composition of glucose (i.e. the proportion of blood and ISF) sampled by the spectroscopic and amperometric sensors and (b) the variations in the population demographics studied in the two cases.
Although most current research including our own study on human subjects reported above indicates a reasonably constant value of α, some research groups have previously suggested that the response times between blood and ISF glucose may be different for the rising and falling phases. These groups claim to have demonstrated that ISF glucose falls in advance of blood glucose during the time of declining glucose levels.42–44 In such situations, a modified DCC model can be implemented by employing two distinct α’s during the rising and falling phases through a piece-wise application of Eq. (4) and (5).
The mean and standard deviation of α obtained on the human volunteer dataset were also employed in determining the physiological lag uncertainties for the DCC and conventional calibration schemes. For the conventional schemes, the uncertainty is calculated as , where the mean α of the human volunteers is used for αactual. At times of reasonably rapid increase in glucose levels, the concentration of glucose in either compartment may change by ~2 mg/dL/min (0.11 mM/min).15 Plugging in these values, we find that for conventional calibration, the prediction uncertainty due to lag amounts to approximately 1.06 mM. For the DCC model, the uncertainty due to lag can be computed by , where Δα is approximated by the standard deviation of α obtained from the human volunteer dataset. Based on this value of Δα, we obtain a lag uncertainty of 0.18 mM for the DCC calibration method. The calculated values project to an approximately six-fold reduction in the lag uncertainty on application of DCC.
Previously, we had estimated using tissue phantom studies that the spectroscopic uncertainty for glucose using our Raman instrument was 1.04 mM (obtained for σ=61.03 (photon counts), sg=83.74 (photon counts/mM) and olfg=1.43 in Eq. (6b)).19 Prior to this work, this spectroscopic uncertainty was considered to be the limit of detection, i.e. the smallest concentration at which glucose could be detected in the tissue. For the specific case of non-invasive glucose detection this does not provide the full picture, as it ignores the lag uncertainty. For example, when conventional calibration schemes are employed, our results suggest that the uncertainty due to lag (1.06 mM) is comparable to the spectroscopic uncertainty (1.04 mM), especially at times of rapid changes in glucose levels. Consequently, the resultant limit of detection, which is sum of the uncertainties arising from spectroscopic considerations and physiological lag (2.1 mM), may be nearly twice that of the previously accepted value (1.04 mM). On the other hand, the net uncertainty on application of DCC (1.22 mM) predominantly arises from spectroscopic considerations (SNR and spectral overlap) and the glucose kinetics plays only a minor role.
6. Conclusion
The presence of a physiological lag between glucose in the blood and ISF compartments must be considered in developing an accurate spectroscopy-based calibration model for predicting blood glucose concentrations. We have presented a mass transfer model based correction scheme that explicitly accounts for the glucose kinetics. The proposed dynamic concentration correction (DCC) enables us to employ the reference concentrations that are appropriate for the acquired spectra in developing the calibration model – a key step which has not been previously considered. In particular, the resulting improvement in blood glucose estimates should enhance the spectroscopic ability to correctly determine hypoglycemia and even predict impending hypoglycemia based on the rate of change in glucose concentration. Furthermore, we have demonstrated that the prediction uncertainty due to physiological lag, which is comparable in magnitude to the uncertainty arising from noise and non-orthogonality in the spectral dataset, can be reduced substantially by employing DCC.
We are currently performing a clinical study to characterize the glucose kinetics in a larger population of human subjects of different ages and ethnicities, both with and without diabetes. It is well-known that inadequate glycemic control causes microvascular and macrovascular changes,45 which may in turn affect the physiological lag time. We expect that this study will provide further details about such changes and the ability of spectroscopy to diagnose similar diabetes-related complications. In addition, the clinical study across a larger and more diverse population would lead to a better understanding of the applicability of the DCC model as well as the variation of the lag time across different population segments. This clinical study is also expected to shed light on tissue site selection for spectroscopic sensing, based on a combination of skin heterogeneity and glucose kinetics parameters. In addition, our future research will focus on combining DCC with non-linear and hybrid regression schemes to develop more robust and accurate calibration models.
Acknowledgments
This research was supported by the NIH National Center for Research Resources (grant P41-RR02594) and a grant from Bayer Health Care. One of the authors, IB, was supported by the Lester Wolfe fellowship.
Appendix I
A first-order accurate estimate of the blood glucose concentration can be obtained by using a finite difference approximation for the derivative term of Eq. (4):
| (15) |
where Δt is the time interval at which spectroscopic measurements (and thus, ISF glucose concentration estimates) are obtained. The above equation gives the discrete transformation equation of the post-prediction (PP-DCC) step, which can be applied in real-time. There are a couple of points worth noting about the application of Eq. (15). Firstly, it is evident from the above equation that at least two spectroscopic predictions of ISF glucose (at t and t −Δt) are necessary in order to determine the blood glucose concentration at time t. In practice, it is beneficial to perform multiple spectroscopic acquisitions so that the corresponding blood glucose estimates can be averaged to ensure less fluctuations in the predicted blood glucose value. Secondly, the time interval Δt, at which the spectroscopy based ISF glucose predictions should be performed, needs to be ascertained. Although spectroscopic acquisitions can be performed rapidly, having a very small Δt is not too useful as it may fail to capture the changes in the glucose levels due to the slow diffusion kinetics – thereby rendering the DCC approach ineffective. On the other hand, too large a time interval would introduce substantial errors in the derivative term. Using these limiting cases as guidelines, one might optimize the value of Δt with a starting point given by a fraction of the typical physiological lag time (~5–10 min).
Appendix II
After employing integration by parts for the second term of Eq. (5), numerical integration was performed by using Simpson’s rule to get the following equation:
| (16a) |
where
| (16b) |
Here, refers to the derivative of cBG evaluated at t. This equation can be readily evaluated by approximating via a first-order finite difference approximation similar to that employed in Eq. (15) for the PP-DCC step (Appendix I). The resultant discretized version of Eq. (16) gives the necessary transformation equation for the PC-DCC step. The primary challenge in the evaluation of this equation lies in having a priori knowledge of the initial ISF glucose value, i.e. at the start of the time window [ti, tf]. Generally, such information is not available for an arbitrary time window. However, during a spectroscopic calibration study such as glucose clamp or tolerance test, one can ensure that the ISF glucose and blood glucose values are completely in equilibrium at the start of the experiment by restricting the glucose intake of the subject prior to the measurements. For example, a typical oral glucose tolerance test (OGTT) protocol stipulates that the patient must fast for 8–14 hours before the study.46 This initial condition enables successful evaluation of Eq. (16) for the first time window. For each subsequent evaluation, the ISF glucose value at time tf for the previous window is inputted as the initial value (at time ti) for the current window. Evidently, the shorter the time window over which the evaluation is performed, the higher the accuracy of the determined ISF glucose concentrations. Nevertheless, the time window cannot be shortened below a lower bound, governed by the maximum permissible frequency of blood withdrawal from a human subject. Most research laboratories, for example, sample blood glucose at time intervals ranging from 2.5–10 minutes.14, 34, 47 To determine the values of the concentrations and their derivatives at intermediate points, spline interpolation is employed.
References
- 1.Khalil OS. Clinical Chemistry. 1999;45:165–177. [PubMed] [Google Scholar]
- 2.Khalil OS. Diabetes Technology & Therapeutics. 2004;6:660–697. doi: 10.1089/dia.2004.6.660. [DOI] [PubMed] [Google Scholar]
- 3.Heller A. Annual Review of Biomedical Engineering. 1999;1:153–175. doi: 10.1146/annurev.bioeng.1.1.153. [DOI] [PubMed] [Google Scholar]
- 4.Tierney MJ, Tamada JA, Potts RO, Jovanovic L, Garg S. Biosensors & Bioelectronics. 2001;16:621–629. doi: 10.1016/s0956-5663(01)00189-0. [DOI] [PubMed] [Google Scholar]
- 5.Tuchin VV. Tissue optics: light scattering methods and instruments for medical diagnosis. SPIE Press; Bellingham, Wash: 2000. Society of Photo-optical Instrumentation Engineers. [Google Scholar]
- 6.Arnold MA, Small GW. Analytical Chemistry. 2005;77:5429–5439. doi: 10.1021/ac050429e. [DOI] [PubMed] [Google Scholar]
- 7.Qu JNY, Wilson BC, Suria D. Applied Optics. 1999;38:5491–5498. doi: 10.1364/ao.38.005491. [DOI] [PubMed] [Google Scholar]
- 8.Rohleder D, Kiefer W, Petrich W. Analyst. 2004;129:906–911. doi: 10.1039/b408927h. [DOI] [PubMed] [Google Scholar]
- 9.Enejder AMK, Koo TW, Oh J, Hunter M, Sasic S, Feld MS, Horowitz GL. Optics Letters. 2002;27:2004–2006. doi: 10.1364/ol.27.002004. [DOI] [PubMed] [Google Scholar]
- 10.Chaiken J, Finney W, Knudson PE, Weinstock RS, Khan M, Bussjager RJ, Hagrman D, Hagrman P, Zhao YW, Peterson CM, Peterson K. Journal of Biomedical Optics. 2005;10 doi: 10.1117/1.1922147. [DOI] [PubMed] [Google Scholar]
- 11.Enejder AMK, Scecina TG, Oh J, Hunter M, Shih WC, Sasic S, Horowitz G, Feld MS. Journal of Biomedical Optics. 2005;10:031114. doi: 10.1117/1.1920212. [DOI] [PubMed] [Google Scholar]
- 12.Aarnoutse PJ, Westerhuis JA. Analytical Chemistry. 2005;77:1228–1236. doi: 10.1021/ac0401523. [DOI] [PubMed] [Google Scholar]
- 13.Zeng H, MacAulay C, McLean DI, Palcic B, Lui H. Photochemistry and Photobiology. 1998;68:227–236. [PubMed] [Google Scholar]
- 14.Boyne MS, Silver DM, Kaplan J, Saudek CD. Diabetes. 2003;52:2790–2794. doi: 10.2337/diabetes.52.11.2790. [DOI] [PubMed] [Google Scholar]
- 15.Cengiz E, Tamborlane WV. Diabetes Technology and Therapeutics. 2009;11:S-11–16. doi: 10.1089/dia.2009.0002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kulcu E, Tamada JA, Reach G, Potts RO, Lesho MJ. Diabetes Care. 2003;26:2405–2409. doi: 10.2337/diacare.26.8.2405. [DOI] [PubMed] [Google Scholar]
- 17.Rebrin K, Steil GM. Diabetes Technology and Therapeutics. 2000;2:461–472. doi: 10.1089/15209150050194332. [DOI] [PubMed] [Google Scholar]
- 18.Thennadil SN, Rennert JL, Wenzel BJ, Hazen KH, Ruchti TL, Block MB. Diabetes Technology and Therapeutics. 2001;3:357–365. doi: 10.1089/15209150152607132. [DOI] [PubMed] [Google Scholar]
- 19.Barman I, Singh GP, Dasari RR, Feld MS. Analytical Chemistry. 2009;81:4233–4240. doi: 10.1021/ac8025509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Matousek P, Towrie M, Stanley A, Parker AW. Applied Spectroscopy. 1999;53:1485–1489. [Google Scholar]
- 21.Lieber CA, Mahadevan-Jansen A. Applied Spectroscopy. 2003;57:1363–1367. doi: 10.1366/000370203322554518. [DOI] [PubMed] [Google Scholar]
- 22.McGrath JA, Eady RA, Pope FM. Rook’s Textbook of Dermatology. Blackwell Publishing; 2004. [Google Scholar]
- 23.Bolinder J, Ungerstedt U, Arner P. Diabetologia. 1992;35:1177–1180. doi: 10.1007/BF00401374. [DOI] [PubMed] [Google Scholar]
- 24.Reach G, Wilson GS. Analytical Chemistry. 1992;64:381A–386A. doi: 10.1021/ac00030a001. [DOI] [PubMed] [Google Scholar]
- 25.Lonnroth P, Jansson PA, Smith U. Am J Physiol. 1987;253:E228–E231. doi: 10.1152/ajpendo.1987.253.2.E228. [DOI] [PubMed] [Google Scholar]
- 26.The Diabetes Control and Complications Trial Research Group. New England Journal of Medicine. 1993;329:977–986. [Google Scholar]
- 27.The Diabetes Control and Complications Trial Research Group. Diabetes Care. 1995;18:1415–1427. doi: 10.2337/diacare.18.11.1415. [DOI] [PubMed] [Google Scholar]
- 28.Heise HM, Marbach R, Koschinsky TH, Gries FA. Artificial Organs. 1994;18:439–447. doi: 10.1111/j.1525-1594.1994.tb02230.x. [DOI] [PubMed] [Google Scholar]
- 29.Schmidtke DW, Freeland AC, Heller A, Bonnecaze RT. Proc Natl Acad Sci. 1998;95:294–299. doi: 10.1073/pnas.95.1.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Freeland AC, Bonnecaze RT. Annals of Biomedical Engineering. 1999;27:525–537. doi: 10.1114/1.196. [DOI] [PubMed] [Google Scholar]
- 31.Lorber A, Kowalski B. Journal of Chemometrics. 1988;2:93–109. [Google Scholar]
- 32.Berger AJ, Feld MS. Applied Spectroscopy. 1997;51:725–732. [Google Scholar]
- 33.Šcepanovic OR, Bechtel KL, Haka AS, Shih WC, Koo TW, Berger AJ, Feld MS. Journal of Biomedical Optics. 2007;12:064012. doi: 10.1117/1.2815692. [DOI] [PubMed] [Google Scholar]
- 34.Steil GM, Rebrin K, Hariri F, Jinagonda S, Tadros S, Darwin C, Saad MF. Diabetologia. 2005;48:1833–1840. doi: 10.1007/s00125-005-1852-x. [DOI] [PubMed] [Google Scholar]
- 35.Brereton RG. Applied Chemometrics for Scientists. John Wiley & Sons Ltd; Chichester, West Sussex, England: 2007. [Google Scholar]
- 36.Roe JN, Smoller BR. Critical Reviews in Therapeutic Drug Carrier Systems. 1998;15:199–241. [PubMed] [Google Scholar]
- 37.Zierler K. American Journal of Physiology. 1999;276:E409–E426. doi: 10.1152/ajpendo.1999.276.3.E409. [DOI] [PubMed] [Google Scholar]
- 38.Rebrin K, Steil GM, van Antwerp WP, Mastrototaro JJ. American Journal of Physiology. 1999;277:E561–E571. doi: 10.1152/ajpendo.1999.277.3.E561. [DOI] [PubMed] [Google Scholar]
- 39.Thissen U, Ustun B, Melssen WJ, Buydens LMC. Analytical Chemistry. 2004;76:3099–3105. doi: 10.1021/ac035522m. [DOI] [PubMed] [Google Scholar]
- 40.Berger AJ, Koo TW, Itzkan I, Feld MS. Analytical Chemistry. 1998;70:623–627. doi: 10.1021/ac970721p. [DOI] [PubMed] [Google Scholar]
- 41.Shih WC, Bechtel KL, Feld MS. Analytical Chemistry. 2007;79:234–239. doi: 10.1021/ac060732v. [DOI] [PubMed] [Google Scholar]
- 42.Sternberg F, Meyerhoff C, Mennel FJ, Mayer H, Bischof F, Pfeiffer EF. Diabetologia. 1996;39:609–612. doi: 10.1007/BF00403309. [DOI] [PubMed] [Google Scholar]
- 43.Aussedat B, Thome-Duret V, Reach G, Lemmonier F, Klein JC, Hu Y, Wilson GS. Biosens Bioelectron. 1997;12:1061–1071. doi: 10.1016/s0956-5663(97)00083-3. [DOI] [PubMed] [Google Scholar]
- 44.Thome-Duret V, Reach G, Gangnerau MN, Lemonnier F, Klein JC, Zhang Y, Hu Y, Wilson GS. Analytical Chemistry. 1996;68:3822–3826. doi: 10.1021/ac960069i. [DOI] [PubMed] [Google Scholar]
- 45.Reusch JEB. J Clin Invest. 2003;112:986–988. doi: 10.1172/JCI19902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.American Diabetes Association. Diabetes Care. 2009;32:S13–S61. doi: 10.2337/dc09-S013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Maruo K, Oota T, Tsurugi M, Nakagawa T, Arimoto H, Tamura M, Ozaki IY, Yamada Y. Applied Spectroscopy. 2006;60:441–449. doi: 10.1366/000370206776593780. [DOI] [PubMed] [Google Scholar]