Skip to main content
PMC home page
Molecular Biology and Evolution logoLink to Molecular Biology and Evolution
. 2010 Mar 15;27(8):1912–1922. doi: 10.1093/molbev/msq077

Detecting Positive and Purifying Selection at Synonymous Sites in Yeast and Worm

Tong Zhou 1,2, Wanjun Gu 3, Claus O Wilke 1,2,4,*
PMCID: PMC2915641  PMID: 20231333

Abstract

We present a new computational method to identify positive and purifying selection at synonymous sites in yeast and worm. We define synonymous substitutions that change codons from preferred to unpreferred or vice versa as nonconservative synonymous substitutions and all other substitutions as conservative. Using a maximum-likelihood framework, we then test whether conservative and nonconservative synonymous substitutions occur at equal rates. Our approach replaces the standard rate of synonymous substitutions per synonymous site, dS, with two new rates, the conservative synonymous substitution rate (dSC) and the nonconservative synonymous substitution rate (dSN). Based on the ratio dSN/dSC, we find that 0.05% of all yeast genes and none of worm genes show evidence of positive selection at synonymous sites (dSN/dSC > 1). On the other hand, 9.44% of all yeast genes and 5.12% of all worm genes show evidence of significant purifying selection on synonymous sites (dSN/dSC < 1). We also find that dSN correlates strongly with gene expression level, whereas the correlation between expression level and dSC is very weak. Thus, dSN captures most of the signal of selection for translational accuracy and speed, whereas dSC is not strongly influenced by this selection pressure. We suggest that the ratio dN/dSC may be more appropriate than the ratio dN/dS to identify positive or purifying selection on amino acids.

Keywords: codon usage bias, preferred codon, positive selection, synonymous substitution rate, translational selection

Introduction

The rate of evolution in protein-coding genes is commonly assessed with the two quantities dN (rate of nonsynonymous substitutions per nonsynonymous site, also called Ka) and dS (rate of synonymous substitutions per synonymous site, also called Ks). If synonymous evolution is neutral, then the ratio of dN/dS identifies the type of selection pressure acting on a gene. dN/dS≪1 indicates strong purifying selection, dN/dS≫1 indicates positive selection, and dN/dS∼1 implies that amino acids evolve largely neutrally (Nielsen and Yang 1998, Suzuki and Gojobori 1999, Hurst 2002, Koonin and Rogozin 2003, Bustamante et al. 2005, Yang et al. 2005, Petersen et al. 2007). But synonymous substitutions are not neutral. Selection for translational efficiency and accuracy operates from bacteria to mammals and shapes codon usage bias (Ikemura 1981, Sharp et al. 1986, Akashi 1994, Stenico et al. 1994, Drummond et al. 2006, Stoletzki and Eyre-Walker 2007, Drummond and Wilke 2008, Higgs and Ran 2008, Zhou et al. 2009). Other selective pressures on synonymous sites relate to splicing (Chamary and Hurst 2005a, Dewey et al. 2006, Parmley et al. 2006, Warnecke and Hurst 2007) and to DNA and messenger RNA (mRNA) secondary structure and stability (Vinogradov 2003, Chamary and Hurst 2005b, Hoede et al. 2006, Stoletzki 2008).

Because selection on synonymous sites is widespread, several authors have developed methods to infer the strength of selection on synonymous sites and/or to correct dN/dS ratios for selection on synonymous sites. McVean and Vieira (2001) proposed a maximum-likelihood method to infer the strength of selection on different codons within each codon family. More recently, Yang and Nielsen (2008) developed a similar but more general approach that can estimate selection pressures on both synonymous and nonsynonymous mutations at the same time. The downside to their approach is that a large number of parameters are being estimated from the data. Thus, reliable estimates can be obtained only for very large data sets. An alternative approach, proposed by Nielsen et al. (2007), takes into account prior knowledge on codon bias and estimates only the overall strength of selection against unpreferred codons. Other approaches include comparing dS with the substitution rate in introns, dI (Resch et al. 2007), regressing dS against codon bias (Hirsh et al. 2005) or using other corrections based on codon usage frequencies (Liberles 2001) or testing the asymmetry between high- and low-expression genes (Higgs et al. 2007).

Here, we develop a novel method to both assess the amount of selection on synonymous sites and to derive improved dN/dS estimates that are less affected by selection on synonymous sites. We introduce two novel evolutionary rates, the rate of conservative synonymous substitutions per conservative synonymous site, dSC, and the rate of nonconservative synonymous substitutions per nonconservative synonymous site, dSN. Conservative synonymous substitutions are synonymous substitutions that connect two preferred or two unpreferred codons. All other synonymous substitutions are nonconservative. Our approach provides two novel ratios, dSN/dSC as a measure of selection on synonymous sites and dN/dSC as a measure of selection on nonsynonymous sites. We apply our model to two species known to experience strong selection for codon usage, Saccharomyces cerevisiae and Caenorhabditis elegans. We also consider Drosophila melanogaster, but because fly violates some of our model assumptions (see Discussion), all fly results are relegated to Supplementary Material online.

Our approach is related to the method of Nielsen et al. (2007), but there are three differences: 1) We treat selection on synonymous and nonsynonymous sites conceptually the same by calculating evolutionary rate ratios for both; Nielsen et al. (2007) calculated a selection coefficient for the former and an evolutionary rate ratio for the latter; 2) we assume that selection favors the preservation of codon status (either preferred or nonpreferred), whereas Nielsen et al. (2007) assumed that selection unconditionally favors specific codons over others; 3) the selection coefficient of Nielsen et al. (2007) for synonymous selection is affected by nonconservative nonsynonymous substitutions, whereas all nonsynonymous substitutions contribute only to nonsynonymous selection in our model. We discuss the implications of these differences below.

Materials and Methods

Model

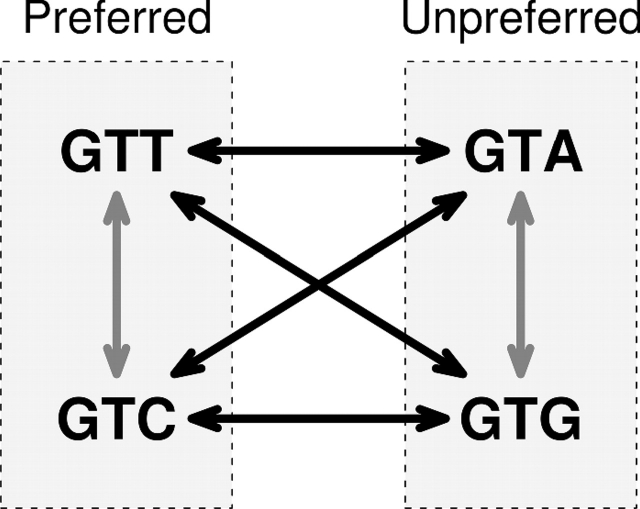
We assume that all the codons for each amino acid can be subdivided into two groups, preferred codons and unpreferred codons. We further assume that there is some selection pressure that keeps codons in the preferred or unpreferred state. Under this assumption, a synonymous substitution leading from a preferred codon to another preferred codon or from an unpreferred codon to another unpreferred codon does not experience this selection pressure, whereas a synonymous substitution leading from a preferred codon to an unpreferred codon or vice versa will experience it. We refer to the former type of synonymous substitution as conservative and to the latter as nonconservative (fig. 1).

FIG. 1.

FIG. 1.

Open in a new tab

Illustration of conservative and nonconservative synonymous substitutions for the amino acid valine in yeast. The black arrows represent all possible nonconservative synonymous substitutions and the grey arrows represent all possible conservative synonymous substitutions.

We use a codon-based continuous-time Markov model to compute the rates of conservative and nonconservative synonymous substitutions. Because there are 61 sense codons, the transition matrix of our model is 61 × 61. We define the instantaneous substitution rate from codon i to codon j (i ≠ j) as

graphic file with name molbiolevolmsq077fx1_ht.jpg (1)

Here, ψ and ω capture selection on synonymous and nonsynonymous substitutions, respectively, and the πj and αikjk reflect the mutation process. As usual, ω < 1 implies purifying selection at the peptide level and ω > 1 suggests positive selection at the peptide level. Similarly, ψ < 1 implies purifying synonymous selection and ψ > 1 suggests positive selection at synonymous sites. The mutation process is fully described by the equilibrium frequency of codons, given by πj, and the relative substitution rates between nucleotides, given by αikjk. Here, ik and jk represent the nucleotides at position k in codons i and j (ik,jk∈{A, C, G, T}). We use the general time-reversible mutation model (αikjk = αjkik) and therefore have six free mutation rate parameters (αAC,αAG,αAT,αCG,αCT,andαGT).

The substitution process between two sequences separated by t time units is described by the matrix P(t) = exp(Qt), where Q = {qij} as defined above. We normalize the Q matrix so that one substitution is expected to occur in one time unit (∑i≠jπiqij = 1) (Goldman and Yang 1994, Yang2006). The numbers of nonsynonymous (Nd) and synonymous (Sd) substitutions per codon are as follows:

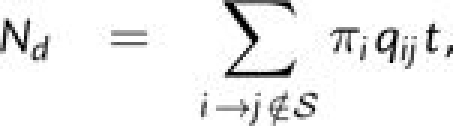graphic file with name molbiolevolmsq077fx2_ht.jpg (2)
graphic file with name molbiolevolmsq077fx3_ht.jpg (3)

Here, 𝒮 is the set of all possible synonymous substitutions. The numbers of conservative (SdC) and nonconservative (SdN) synonymous substitutions per codon are

graphic file with name molbiolevolmsq077fx4_ht.jpg (4)
graphic file with name molbiolevolmsq077fx5_ht.jpg (5)

Here, 𝒞 is the subset of 𝒮 for which codon preference remains unchanged between i and j and 𝒩 is the subset of 𝒮 for which codon preference changes between i and j. We calculate evolutionary rates according to the physical-site definition. We count a nondegenerate site as one nonsynonymous site, a 2-fold degenerate site as one-third synonymous and two-third nonsynonymous site, a 3-fold site as two-third synonymous and one-third nonsynonymous site, and a 4-fold site as one synonymous site (Yang 2006). Similarly, synonymous sites are also divided into fractional conservative synonymous and nonconservative synonymous sites according to the proportion of possible changes at a site that are either conservative or nonconservative. For example, for codon GTT, the third nucleotide position is a synonymous site. One possible nucleotide substitution at this site leads to a conservative synonymous codon change (GTC), whereas the other two possible substitutions are nonconservative (GTA and GTG) (fig. 1). Thus, the third nucleotide position of GTT is counted as one-third of a conservative synonymous site and two-third of a nonconservative synonymous site. We average these counts over all codons in the sequence to obtain the average number of synonymous, nonsynonymous, conservative synonymous, and nonconservative synonymous sites per codon, represented by S, N, SC, and SN. We then define evolutionary rates by dN = Nd/N, dS = Sd/S, dSC = SdC/SC, and dSN = SdN/SN.

Model Fitting

We implemented our model in the software package HyPhy (Kosakovsky Pond et al. 2005). We estimated the parameters ψ, ω, and αrs by maximum likelihood, but estimated codon frequencies πj from the nucleotide frequency at the three codon positions (model F3×4). HyPhy scripts to carry out this analysis can be downloaded from http://openwetware.org/images/5/52/Zhou-Gu-Wilke-synonymous-selection.zip. For comparison, we also fitted our model with a fixed ψ = 1. Throughout this manuscript, all parameters obtained under this setting are indicated with a superscript 1, as in ω1, dN1, and dS1.

Data Sources

We obtained genomic sequences and orthologs from the following sources: the Saccharomyces Genome Database (ftp://genome-ftp.stanford.edu/) for yeast (S. cerevisiae vs. S. bayanus) and the WormBase (http://www.wormbase.org) for worm (C. elegans vs. C. briggsae). For each pair of orthologs, we aligned the peptide sequences using MUSCLE (Edgar 2004) and then translated the peptide sequences back to restore the original nucleotide sequences. We only retained complementary DNAs with 80% of alignment to their orthologs and at least 100 codons. We also excluded all genes for which HyPhy could not fit the model with an optimization precision of 0.001 within 105 likelihood function evaluations. This procedure yielded 4,047 genes for yeast and 5,623 for worm.

We used previously published expression data for yeast (Holstege et al. 1998) and worm (Hill et al. 2000). Multiple signals for the same transcript were averaged. After combining the expression data with the genomic data, we ended up with 3,816 genes for yeast and 4,711 for worm.

Inferring Preferred Codons

We calculated the adjusted effective number of codons (ENC′) for each gene, according to the method developed by Novembre (2002), which corrects for nucleotide content. We then compared the codon usage pattern between the gene groups showing the lowest 5% and highest 5% ENC′ in each species. We defined codons as “preferred” if they showed a statistically significant increase in frequency in the lowest ENC' group, as determined by a chi-square test (supplementary table S1, Supplementary Material online). The codon usage patterns of the orthologous species are quite similar (Supplementary fig. S1, Supplementary Material online) with several exceptions: For S. bayanus, the codon ATT for Ile is assigned as unpreferred, whereas the codon CGT for Arg is assigned as preferred. For C. briggsae, the codon ACT for Thr and the codon GTT for Val are assigned as unpreferred while the codon AGA is assigned as preferred for Arg. The codon preference for the 2-fold degenerate amino acid Glu is reversed between the two worm species. The preferred codons we identified corresponded to transfer RNAs (tRNAs) with increased gene copy number (Supplementary fig. S2, Supplementary Material online).

Results

Conservative and Nonconservative Synonymous Evolutionary Rates

Our method makes the assumption that certain codons in a codon family are either preferred or unpreferred and that there is a selection pressure to keep codons in the preferred or unpreferred state. We make no a priori assumptions about why a specific codon is preferred or unpreferred, but in general, preferred codons will be the ones that are efficiently and rapidly translated because their cognate tRNAs are highly abundant. Codons with highly abundant cognate tRNAs have increased translation speed and/or accuracy, and these properties tend to confer a selective advantage to the gene in which they occur (Ikemura 1981, Sharp et al. 1986, Akashi 1994, Drummond and Wilke 2008, Zhou et al. 2009). At the same time, there is evidence that unpreferred codons are selected for at specific sites, presumably to aid in cotranslational protein folding (Thanaraj and Argos 1996, Komar et al. 1999, Cortazzo et al. 2002, Kimchi-Sarfaty et al. 2007, Widmann et al. 2008, Zhang et al. 2009).

To identify preferred and unpreferred codons, we selected the 5% of genes with the strongest codon usage bias (lowest ENC') and the 5% of genes with the weakest codon usage bias (highest ENC') and identified codons as preferred if they were significantly enriched in the low-ENC' group (see Materials and Methods). We then defined substitutions from a preferred codon to another preferred codon coding for the same amino acid or from a unpreferred codon to another unpreferred codon coding for the same amino acid as “conservative synonymous substitutions.” We defined all other synonymous substitutions as “nonconservative.”

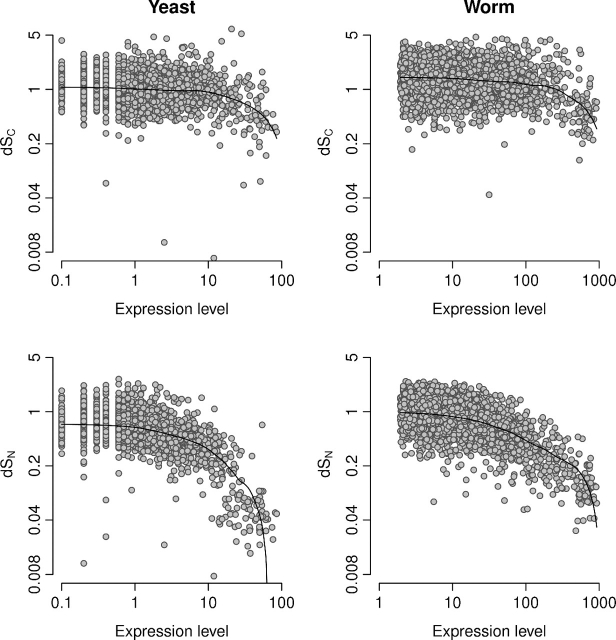
We fitted our model to coding sequences of yeast and worm and calculated conservative and nonconservative evolutionary rates dSC and dSN. Because translational selection is strong in these species (Drummond and Wilke 2008), we calculated the correlation of both dSC and dSN with gene expression level (fig. 2 and table 1). We found that dSN correlates strongly with expression level in yeast and worm. By contrast, the correlation between dSC and expression level, even though statistically significant, is very weak: Gene expression level accounts only for 1.8% of the variation in dSC in yeast and 1.3% of the variation in dSC in worm.

FIG. 2.

FIG. 2.

Open in a new tab

Evolutionary rates dSC and dSN versus expression level for yeast (left) and worm (right). Solid lines show lowess smoothed data.

Table 1.

Spearman Correlations of Expression Level with dSC, dSN, dS, dS1, dN, dN1, dN/dSC, and dSN/dSC.

Variable Yeast
 Worm
ρ P ρ P
dSC – 0.135 5.7 × 10−17 – 0.116 1.2 × 10−15
dSN – 0.441 2.6 × 10−181 – 0.400 1.2 × 10−176
dS – 0.400 8.3 × 10−147 – 0.343 7.8 × 10−130
dS1 – 0.434 8.9 × 10−175 – 0.364 1.5 × 10−147
dN – 0.522 1.7 × 10−265 – 0.290 4.4 × 10−92
dN1 – 0.523 3.8 × 10−267 – 0.280 7.1 × 10−86
dN/dSC – 0.447 1.1 × 10−186 – 0.232 1.2 × 10−58
dSN/dSC – 0.293 1.8 × 10−76 – 0.301 6.1 × 10−99
Open in a new tab

As is well known from prior work (Drummond and Wilke 2008), both dN and dS as calculated by traditional methods correlate strongly with expression level in yeast and worm. We found that the same is true for dN and dS calculated from our model (table 1). Moreover, the correlation coefficients of dS expression level and dSN expression level are comparable, and the correlation between dS and dSN (Spearman's ρ = 0.812,P≪10 − 100 for yeast and ρ = 0.889,P≪10 − 100 for worm) is stronger than that between dS and dSC (Spearman's ρ = 0.643,P≪10 − 100 for yeast and ρ = 0.702,P≪10 − 100 for worm). The correlation between dSN and dSC is much weaker (Spearman's ρ = 0.176,P≪10 − 100 for yeast and ρ = 0.361,P≪10 − 100 for worm). These observations show that the variation in dS due to translational selection is largely captured in dSN and removed from dSC. Therefore, dSC is a suitable neutral baseline to which we can compare both dN and dSN.

To obtain an independent verification that our model works as expected, we also devised a counting model based on the method by Nei and Gojobori (1986) (see Supplementary Material online for details). We computed the proportion of conservative (PSC) and nonconversitive (PSN) synonymous differences for each gene and repeated the same analyses as with dSC and dSN. We obtained largely the same results as we did with the maximum-likelihood method (Supplementary fig. S3, Supplementary Material online).

Hirsh et al. (2005) proposed an adjusted measure of dS, denoted dS′, which takes the relationship between codon bias and synonymous divergence into account. We thus analyzed dS′, dSN, and dSC in yeast (dS′ data obtained from Hirsh et al. 2005). We found that the correlation between dS′ and dSN (Spearman's ρ = 0.501,P≪10 − 100) does not differ greatly from the correlation between dS′ and dSC (Spearman's ρ = 0.449,P≪10 − 100). The correlation between dS′ and expression level (Spearman's ρ = − 0.168,P = 2.1×10 − 19) is comparable but slightly stronger than the one between dSC and expression level (table 1). Thus, our method seems to work at least as well in controlling for effects of translational selection as the method of Hirsh et al. (2005), with the added benefit that our model is based on mechanistic model of molecular evolution formulated in a coherent maximum-likelihood framework.

Selection Restricts Nonconservative Synonymous Substitutions

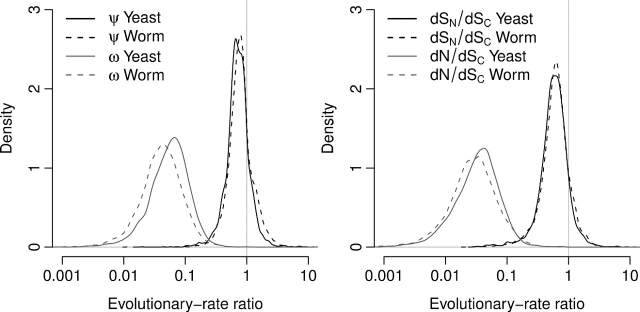
In the previous subsection, we found that the conservative synonymous substitution rate (dSC) is a reasonably neutral baseline of evolutionary variation. Therefore, we can use the parameter ψ to estimate the amount and type of selection on synonymous sites. Under positive selection, we expect ψ to be larger than 1, whereas under purifying selection, ψ should be less than 1. The distributions of ψ in yeast and worm are very similar (fig. 3), and they are slightly shifted to the left of 1 (t-test: P≪10 − 100 for yeast and P≪10 − 100 for worm). Thus, there is some purifying selection at synonymous sites in both species. Interestingly, the distributions of ω are approximately an order of magnitude further to the left than the distributions of ψ (fig. 3). Averaged over all sites in a gene, nonsynonymous substitutions accumulate approximately an order of magnitude slower than nonconservative synonymous substitutions.

FIG. 3.

FIG. 3.

Open in a new tab

Distribution of evolutionary rate ratios. Left panel: distribution of the ratios ω and ψ. Right panel: distribution of the ratios dN/dSC and dSN/dSC. The y axes are scaled such that the area under the curves equals 1.

A comparison of the right and left panel of figure 3 shows that we found very similar results when considering the ratios dN/dSC and dSN/dSC (based on physical sites) instead of the ratios ω and ψ (based on mutational opportunity). Throughout the remainder of the manuscript, we will focus on the physical site–based ratios for genome-wide correlation studies, as these ratios tend to perform more reliably for those kinds of studies (Bierne and Eyre-Walker 2003). We will, however, use ω and ψ for statistical tests of positive or purifying selection in individual genes because the likelihood-ratio test provides us with a straightforward means to test for the null hypotheses ω = 1 and ψ = 1.

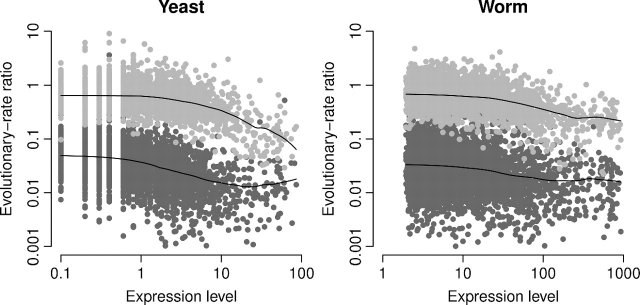
We next studied the correlation of both dN/dSC and dSN/dSC with expression level. We found that both quantities decline as the gene expression level increases (fig. 4 and table 1). Because the correlation of dSC with expression level is very weak and negative (table 1), this result shows that the amount of purifying selection on both synonymous and nonsynonymous sites increases with expression level in both species. Results were similar for ω and ψ, but the correlations were slightly weaker (Supplementary fig. S4, Supplementary Material online). Interestingly, dN/dSC starts increasing again for the genes with the highest expression levels in yeast. This effect may be caused by very strong selection on synonymous sites in those genes. Even though dSC is largely independent of expression level, it does decrease for genes with very high expression level (fig. 2).

FIG. 4.

FIG. 4.

Open in a new tab

Evolutionary rate ratios dN/dSC (dark points) and dSN/dSC (light points) versus expression level for yeast (left) and worm (right). Both ratios decline with increasing expression levels. Solid lines show lowess smoothed data.

We also determined all genes with ψ significantly above or below 1 by testing for the null hypothesis ψ = 1 using a likelihood-ratio test. We found 18 genes in yeast and 41 in worm with ψ > 1 at P < 0.05. These numbers correspond to 0.44% and 0.73% of the genomes of yeast and worm, respectively. After applying a false discovery rate correction for multiple testing (Benjamini and Hochberg 1995) and allowing for a false discovery rate of 5%, only two genes (0.05%) remained significant in yeast and no gene remained significant in worm. On the other hand, we found 1,076 yeast genes (26.59% of the genome) and 1,164 worm genes (20.70% of the genome) with ψ < 1 at P < 0.05. But only 382 (9.44%) and 288 (5.12%) genes survived the correction for multiple testing.

Because selection on preferred codons is generally associated with the translation process and increases with expression level, we compared the number of genes with ψ < 1 and corrected P < 0.05 between the top 10% highest expressed and the bottom 10% lowest expressed genes. In yeast, we found 96 such genes of 374 in the high expression group but only 13 of 152 in the low expression group. These fractions are significantly different (Fisher's exact test, P = 4.9×10 − 6). The group sizes differ because numerous genes had identical expression levels, preventing us from choosing exactly equal-sized groups. In worm, we found 45 significant genes of 472 in the high expression group and 15 of 469 in the low expression group. These fractions are also significantly different (Fisher's exact test, P = 8.1×10 − 5). Thus, highly expressed genes are more likely to experience purifying synonymous selection.

In our model, the parameter ψ measures the extent of selection on synonymous sites. Nielsen et al. (2007) proposed a similar model that estimates the overall strength of selection (S) against unpreferred codons. To compare their model with our model, we implemented a variant of their model and fitted it to our data sets. The one modification we made to the model of Nielsen et al. (2007) is that we used the same general time-reversible mutation model we used for our models. We calculated the selection coefficient S for each gene in yeast and worm. Although S and ψ were correlated, the correlations were weak (Spearman's ρ = − 0.155,P = 2.6×10 − 23 for yeast and ρ = − 0.130,P = 1.8×10 − 22 for worm).

Application for Detecting Selection on Protein Sequence

A large dN/dS is usually interpreted as signal for positive selection at nonsynonymous sites. In our model, the traditional dN/dS ratio (without selection on synonymous sites) is reflected by ω1 (ω estimated under a constant ψ = 1), whereas our ω value corresponds to the ratio between dN and dSC. Under strong purifying synonymous selection, dS should be small, whereas dSC is not necessarily small. In this case, ω1 would overestimate the amount of nonsynonymous divergence. Similarly, for a gene under positive synonymous selection, dS might be inflated and ω1 would underestimate the amount of nonsynonymous divergence. Table 2 lists the genes with either ω or ω1 significantly larger than 1 (P < 0.05 under the null hypothesis ω = 1 or ω1 = 1, respectively) in our data set. We found the strongest effect for yeast gene YDR133C for which we may greatly underestimate the dN/dS value without considering the effect caused by selection at synonymous sites (ω = 5.118 and ω1 = 0.648).

Table 2.

Comparison between ω and ω1.

Gene ω P ω1 P
Yeast YDR133C 5.118 5.0 × 10−2 0.648 3.0 × 10−1
YDR433W 26.253 4.2 × 10−4 12.096 3.0 × 10−5
YJL009W 4.055 3.2 × 10−2 3.048 1.3 × 10−2
Open in a new tab

NOTE.—Only genes with ω or ω1 significantly larger than 1 (P < 0.05) were listed.

We also correlated the ω values with ψ. We found that, in both species, there is a significant correlation between ω and ψ (Spearman's ρ = 0.343,P≪10 − 100 for yeast and ρ = 0.366,P≪10 − 100 for worm) (Supplementary fig. S5, Supplementary Material online). This result most likely reflects the increasing strength of selection on both synonymous and nonsynonymous sites with increasing expression level, as seen by the correlation of both ω and ψ with expression level (Supplementary fig. S4, Supplementary Material online).

An Alternative Definition for Selection on Synonymous Sites

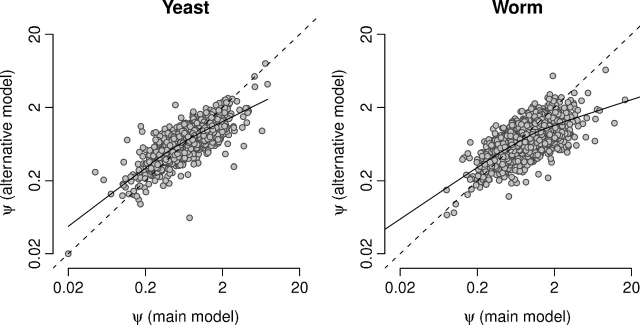
All results we reported in the preceding subsections were obtained with a model in which synonymous selection happens only within codon families. We refer to this model also as the “main model.” We also considered an alternative model in which the rate of nonsynonymous mutations that change codon preference also differs by a factor ψ from the rate of nonsynonymous mutations that do not change codon preference (see Supplementary Material online for details). By and large, the main model and the alternative model produced comparable results (fig. 5 and Supplementary figs. S6–S9, supplementary table S2, and supplementary text, Supplementary Material online), and all results were consistent among yeast and worm. The largest deviations between the two models arise for ψ and dSC. For ψ, the values derived from the main model explain only 51%, and 48% of the variance in the values derived from the alternative model for yeast and worm, respectively (supplementary table S2, Supplementary Material online). For dSC, the amount of variance explained is 73% and 76% in yeast and worm, respectively (supplementary table S2, Supplementary Material online). For comparison, for dSN, the variance explained is above 90% in both species (supplementary table S2, Supplementary Material online).

FIG. 5.

FIG. 5.

Open in a new tab

Evolutionary rate ratio ψ for the model described in the main text and for the alternative model described in the Supplementary Material online for yeast (left) and worm (right). The Spearman correlations for the two data sets are 0.715 (P≪10 − 100) for yeast and 0.694 (P≪10 − 100) for worm. The solid lines show lowess smoothed data and the dashed lines indicate exact agreement between the two models.

It makes intuitive sense that ψ would be more strongly affected by the change in the model definition than ω. Most of the selection on nonsynonymous substitutions is likely due to amino acid–level constraints and not to selection on codon preference. Therefore, ω should be largely the same regardless of which of the two model definitions we use. By contrast, ψ measures a much weaker and more subtle effect, and thus, even a small selection pressure on codon preference among amino-acid families would have a noticeable effect on ψ.

In general, we found that ψ as estimated under the alternative model indicates weaker synonymous selection than ψ as estimated under the main model. The former ψ is consistently closer to 1; it tends to be smaller than the latter ψ when the latter ψ is large, and it tends to be larger than the latter ψ when the latter ψ is small (fig. 5). We interpret this result as follows: The selection pressure among codon families is dominated by amino acid–level effects; codon preference plays only a minor role when the amino acid is changed. However, when the amino acid remains unchanged, codon preference is important. The main model, by disregarding synonymous selection pressures among codon families, can fully measure the synonymous selection pressure within codon families. In the alternative model, on the other hand, ψ gets diluted by the weak selection pressure on codon preference among codon families.

Consistent with this interpretation, the correlation between dSC and expression level is slightly stronger for the alternative model than for the main model in yeast and worm (Spearman's ρ = − 0.143,P = 3.5×10 − 19 for yeast and ρ = − 0.133,P = 3.0×10 − 24 for worm, see also Supplementary fig. S7, Supplementary Material online, and table 1). Under the alternative model, dSC is likely somewhat confounded by amino acid–level selection pressures mediated by expression level.

A Model with Four Synonymous Rates

As a generalization of our main model, we also developed a model in which each type of synonymous substitution (from either preferred or unpreferred to either preferred or unpreferred codon) can occur at an independent rate for a total of four different synonymous rates. We added two additional parameters (η and θ) into our main model (see Supplementary Material online for details). In this model with four rates, η measures the ratio between the substitution rates from unpreferred to preferred codons and from preferred to unpreferred codons, whereas θ measures the ratio between the substitution rates from preferred codons to preferred codons and from unpreferred codons to unpreferred codons. All other parameters in the model have exactly the same meaning as before. On the basis of ψ, η, and θ, we calculated the synonymous substitution rates for preferred to unpreferred codon change (dSPU), unpreferred to preferred codon change (dSUP), unpreferred to unpreferred codon change (dSUU), and preferred to preferred codon change (dSPP).

We tested for correlations between expression level and the four synonymous rates. We considered first the two substitution rates associated with conservative synonymous substitutions. For dSUU, we found that it did not correlate significantly with expression level (Spearman's ρ = − 0.020,P = 0.280 for yeast and ρ = − 0.033,P = 0.076 for worm). For dSPP, we found a moderate negative correlation in yeast (ρ = − 0.248,P = 3.0×10 − 40) and none in worm (ρ = − 0.038,P = 0.038). For nonconservative substitutions, we found that dSPU was negatively correlated with expression level (Spearman's ρ = − 0.541,P≪10 − 100 for yeast and ρ = − 0.491,P≪10 − 100 for worm), whereas the correlation between dSUP and expression level was positive (Spearman's ρ = 0.314,P≪10 − 100 for yeast and ρ = 0.330,P≪10 − 100 for worm). We also correlated both η and θ with expression level. We found that η increased with gene expression level (Spearman's ρ = 0.538,P≪10 − 100 for yeast and ρ = 0.486,P≪10 − 100 for worm). The correlations between θ and expression level were much weaker (Spearman's ρ = 0.034,P = 0.075 for yeast and ρ = 0.167,P≪10 − 100 for worm). Overall, these results support our approach of considering conservative synonymous mutations largely free of expression-related selection pressures, whereas nonconservative synonymous mutations are not.

To assess whether we were justified in combining the two conservative rates and the two nonconservative rates into a single rate each in the main model, we considered the distributions of η and θ. We found that they were very similar across species (Supplementary fig. S10, Supplementary Material online) and nearly centered around 1. The distribution of η was shifted slightly to the right of 1 (t-test: P≪10 − 100 for both species), whereas the distribution of θ was shifted slightly to the left of 1 (t-test: P≪10 − 100 for both species). That both these distributions were nearly centered around 1 supports our approach of using only two synonymous evolutionary rates in the main model. At the same time, the small but statistically significant shifts to the right and left of 1 indicate that the four-rate model is not superfluous but can instead resolve subtle second-order effects that are not visible under the main model.

Discussion

We have developed a statistical method to identify positive and purifying selection at synonymous sites in yeast and worm. We tested whether synonymous substitutions from preferred to unpreferred codons or vice versa happen more or less frequently than expected by chance. If the rate of synonymous substitutions is independent of codon preference, then the conservative synonymous substitution rate (dSC) should equal the nonconservative rate (). If synonymous substitutions tend to conserve codon preference, we expect dSN < dSC (ψ < 1), whereas if they tend to change codon preference, we expect dSN > dSC (ψ > 1). By testing for the null hypothesis ψ = 1, we found that 0.05% of the yeast genes and no worm genes were positively selected at synonymous sites (assuming a 5% false discovery rate). On the other hand, we found 9.44% of yeast genes and 5.12% of worm genes to undergo significant purifying synonymous selection. The percentage of positively selected genes we found is substantially lower than what Resch et al. (2007) found for mammals using a different method (comparing the synonymous rate to the rate of divergence in introns). They found that roughly 12% of the genes (without correction for multiple testing) have undergone positive synonymous selection in mouse–rat orthologs.

By correlating dS, dSN, and dSC with gene expression level, we found that much of the signal of translational selection commonly found in dS (Drummond et al. 2006, Drummond and Wilke 2008) is captured by dSN, whereas dSC is largely unaffected by expression level. The correlation between dSC and expression level, although significant, is very weak. The amount of variance explained is on the order of 2% (yeast) or less (worm). For this reason, we propose that dSC may be a better measure of neutral variation than dS and that the ratio dN/dSC may be more appropriate to detect positive selection than the ratio dN/dS.

We do not claim, however, that dSC is free from any selection pressure. Our model is fundamentally based on the concept of codon bias and of preferred and unpreferred codons. Any selection pressure that acts on the DNA or mRNA level, such as selection pressures related to transcription (Xia 1996), splicing (Chamary and Hurst 2005b, Dewey et al. 2006, Parmley et al. 2006, Warnecke and Hurst 2007), expression regulation (Parmley and Huynen 2009), protein structure (Xie and Ding 1998, Gu et al. 2004, Clarke and Clark 2008), DNA secondary structure (Vinogradov 2003, Hoede et al. 2006), or mRNA secondary structure and stability (Chamary and Hurst 2005a, Stoletzki 2008) will likely affect dSC as much as it affects dS. The relative strength of such selection pressures compared with translational selection in organisms that experience strong translational selection, as is the case with yeast and worm, is not well understood at present and deserves future study.

A common use of the dN/dS method is to identify individual branches in a larger phylogeny that have experienced altered selection pressures. We here applied our model only to species pairs, but our maximum-likelihood approach allows us also to use our model in more complex settings and to test, for example, whether specific branches have experienced particularly strong purifying or positive synonymous selection. Such an analysis makes only sense, however, if the preferred codons remain largely unchanged throughout the phylogeny. We believe that this condition will often be satisfied for species that are not too distantly related. For example, beyond S. cerevisiae and S. bayanus, we found a very similar set of preferred codons in five further Saccharomyces species (S. paradoxus, S. mikatae, S. kudriavzevii, S. castellii, and S. kluyveri), as well as in Kluyveromyces lactis. Even the distantly related Schizosaccharomyces pombe had only minor differences in preferred codon usage. As the number of fully sequenced species is only going to increase in the future, we expect that there will be many situations where our approach may be useful.

Our model differs in three ways from previous work by Nielsen et al. (2007). First, Nielsen et al. (2007) used an explicit selection term for synonymous substitutions in their model and thus estimated a selection strength S rather than an evolutionary rate ratio. Although obtaining a direct estimate for the strength of selection on synonymous sites is desirable, we believe that there are advantages to our approach. Under our approach, ψ and ω are both evolutionary rate ratios measured in comparable units. We can directly compare ψ and ω to assess the relative strength of selection on synonymous and nonsynonymous substitutions. By contrast, it is not obvious how to compare the estimated S to the estimated ω in the model of Nielsen et al. (2007).

Second, the selection term of Nielsen et al. (2007) also assumes that preferred (or unpreferred, for S < 0) codons have systematically higher fitness than the other type of codon. This assumption is different from our assumption, which states that selection tends to preserve codon status, regardless of whether the codon status is preferred or unpreferred. Our assumption is based on the observations that unpreferred codons are selected for at specific sites (Thanaraj and Argos 1996, Komar et al. 1999, Cortazzo et al. 2002, Kimchi-Sarfaty et al. 2007, Widmann et al. 2008, Zhang et al. 2009) and that codon usage bias is highly regulated even in genes that are not encoded primarily by preferred codons (Dong et al. 1996). We believe that the difference in assumption about how selection acts on synonymous codons is the main reason why S and ψ correlate only weakly.

Third, in our model, ψ is purely a measure for the difference in conservative and nonconservative substitutions within codon families. In principle, a substitution from a preferred codon in one codon family to a unpreferred codon in another codon family could experience both a selective effect because the amino acid and the codon preference were changed. We absorbed the latter effect into ω in our model and thus counted it as a nonsynonymous selection pressure as well. We proceeded in this manner because a priori it is not clear that selection pressures on synonymous sites can be compared across codon families. For example, the translational efficiency of a unpreferred codon in one codon family could be higher than the translational efficiency of a preferred codon in another codon family simply because all codons of the first family have higher translational efficiency than all codons of the second family. Nielsen et al. (2007) made a different choice and included a term representing synonymous selection into all substitutions that connected preferred with unpreferred codons or vice versa. To determine to what extent our results were affected by this choice, we also fitted a model in which all substitutions that connected preferred with unpreferred codons or vice versa received a factor ψ in the transition matrix. We found that our main model and our alternative model gave by-and-large similar results. However, the alternative model tended to predict weaker selection on synonymous sites than the main model. This observation shows that selection for preferred or unpreferred codons is not a major force among codon families, and it justifies our approach of disregarding synonymous selection among codon families.

In our model with four synonymous rates, we categorized both conservative and nonconservative substitutions into two subgroups, respectively. The two rates dSUU and dSPP were not strongly correlated with expression level. This finding supports our strategy in the main model to combine these two rates into dSC and use the latter as a baseline to estimate the pace of the neutral evolutionary process. Interestingly, the two rates dSPU and dSUP were both significantly correlated with expression level, but the correlation was negative for dSPU and positive for dSUP. This result suggests that highly expressed genes experience positive selection to increase their number of preferred codons. This result also implies that the effects of dSUP and dSPU may partly cancel each other when we combine these two rates into dSN. Therefore, dSN may actually underestimate the amount of selection on synonymous sites.

We fitted all models we developed to both yeast and worm, with largely identical results. However, when applied to fly, our models gave somewhat comparable results to yeast and worm but also produced some differences (see Supplementary Material online for details). These observations beg the question of how generally applicable our models are to other systems. Our models are valid if two conditions are met: First, codons need to separate clearly into preferred and nonpreferred ones. For organisms for which a clear distinction cannot be made, for example, because codon preference is better described on a continuous scale from preferred to nonpreferred and everything in between, our models would not be appropriate. Indeed, in fly, preferred and nonpreferred codons do not separate as cleanly as they do in yeast or worm. Second, the mutation process needs to be reversible. Although this assumption is commonly made when fitting evolutionary models to sequence data, the assumption is not always justified. In particular, the evolution of the D. melanogaster line relative to other Drosophila species did likely not follow a time-reversible process (Nielsen et al. 2007). In summary, there are likely many more systems than just yeast and worm for which our models may be useful, but one should not assume that any species with strong codon bias is a suitable candidate for our approach.

Supplementary Material

Supplementary text, tables S1 and S2, and figures S1–S9 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).

Supplementary Material

[Supplementary Data]
msq077_index.html (699B, html)

Acknowledgments

This work was supported by the National Institute of Health grant R01 AI065960 to C.O.W. and by a grant from the National Natural Science Foundation of China (No. 30900836) to W.G. We would like to thank David Liberles for helpful comments and suggestions on this work.

References

  1. Akashi H. Synonymous codon usage in Drosophila melanogaster: natural selection and translational accuracy. Genetics. 1994;136:927–935. doi: 10.1093/genetics/136.3.927. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc Series B. 1995;57:289–300. [Google Scholar]
  3. Bierne N, Eyre-Walker A. The problem of counting sites in the estimation of the synonymous and nonsynonymous substitution rates: implications for the correlation between the synonymous substitution rate and codon usage bias. Genetics. 2003;165:1587–1597. doi: 10.1093/genetics/165.3.1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bustamante CD, Fledel-Alon A, Williamson S, Nielsen R, Hubisz MT, Glanowski S, Tanenbaum DM, White TJ, Sninsky JJ, Hernandez RD, et al. 14 co-authors. Natural selection on protein-coding genes in the human genome. Nature. 2005;437:1153–1157. doi: 10.1038/nature04240. [DOI] [PubMed] [Google Scholar]
  5. Chamary JV, Hurst LD. Biased codon usage near intron-exon junctions: selection on splicing enhancers, splice-site recognition or something else? Trends Genet. 2005a;21:256–259. doi: 10.1016/j.tig.2005.03.001. [DOI] [PubMed] [Google Scholar]
  6. Chamary JV, Hurst LD. Evidence for selection on synonymous mutations affecting stability of mRNA secondary structure in mammals. Genome Biol. 2005b;6:R75. doi: 10.1186/gb-2005-6-9-r75. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Clarke TFIV, Clark PL. Rare codons cluster. PLoS One. 2008;3 doi: 10.1371/journal.pone.0003412. e3412. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cortazzo P, Cervenansky C, Marin M, Reiss C, Ehrlich R, Deana A. Silent mutations affect in vivo protein folding in. Escherichia coli. Biochem Biophys Res Commun. 2002;293:537–541. doi: 10.1016/S0006-291X(02)00226-7. [DOI] [PubMed] [Google Scholar]
  9. Dewey CN, Rogozin IB, Koonin EV. Compensatory relationship between splice sites and exonic splicing signals depending on the length of vertebrate introns. BMC Genomics. 2006;7:311. doi: 10.1186/1471-2164-7-311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Dong H, Nilsson L, Kurland CG. Co-variation of tRNA abundance and codon usage in Escherichia coli at different growth rates. J Mol Biol. 1996;260:649–663. doi: 10.1006/jmbi.1996.0428. [DOI] [PubMed] [Google Scholar]
  11. Drummond DA, Raval A, Wilke CO. A single determinant dominates the rate of yeast protein evolution. Mol Biol Evol. 2006;23:327–337. doi: 10.1093/molbev/msj038. [DOI] [PubMed] [Google Scholar]
  12. Drummond DA, Wilke CO. Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution. Cell. 2008;134:341–352. doi: 10.1016/j.cell.2008.05.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Edgar RC. Muscle: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–1797. doi: 10.1093/nar/gkh340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Goldman N, Yang Z. A codon-based model of nucleotide substitution for protein-coding DNA sequences. Mol Biol Evol. 1994;11:725–736. doi: 10.1093/oxfordjournals.molbev.a040153. [DOI] [PubMed] [Google Scholar]
  15. Gu W, Zhou T, Ma J, Sun X, Lu Z. The relationship between synonymous codon usage and protein structure in Escherichia coli and. Homo sapiens. Biosystems. 2004;73:89–97. doi: 10.1016/j.biosystems.2003.10.001. [DOI] [PubMed] [Google Scholar]
  16. Higgs PG, Hao W, Golding GB. Identification of conflicting selective effects on highly expressed genes. Evol Bioinform. 2007;3:1–13. [PMC free article] [PubMed] [Google Scholar]
  17. Higgs PG, Ran W. Coevolution of codon usage and tRNA genes leads to alternative stable states of biased codon usage. Mol Biol Evol. 2008;25:2279–2291. doi: 10.1093/molbev/msn173. [DOI] [PubMed] [Google Scholar]
  18. Hill AA, Hunter CP, Tsung BT, Tucker-Kellogg G, Brown EL. Genomic analysis of gene expression in C. elegans. Science. 2000;290:809–812. doi: 10.1126/science.290.5492.809. [DOI] [PubMed] [Google Scholar]
  19. Hirsh AE, Fraser HB, Wall DP. Adjusting for selection on synonymous sites in estimates of evolutionary distance. Mol Biol Evol. 2005;22:174–177. doi: 10.1093/molbev/msh265. [DOI] [PubMed] [Google Scholar]
  20. Hoede C, Denamur E, Tenaillon O. Selection acts on DNA secondary structures to decrease transcriptional mutagenesis. PLoS Genet. 2006;2 doi: 10.1371/journal.pgen.0020176. e176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Holstege FCP, Jennings E, Wyrick JJ, Lee TI, Hengartner CJ, Green MR, Golub TR, Lander ES, Young RA. Dissecting the regulatory circuitry of a eukaryotic genome. Cell. 1998;95:717–728. doi: 10.1016/s0092-8674(00)81641-4. [DOI] [PubMed] [Google Scholar]
  22. Hurst LD. The Ka/Ks ratio: diagnosing the form of sequence evolution. Trends Genet. 2002;18:486. doi: 10.1016/s0168-9525(02)02722-1. [DOI] [PubMed] [Google Scholar]
  23. Ikemura T. Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes: a proposal for a synonymous codon choice that is optimal for the E. coli translational system. J Mol Biol. 1981;151:389–409. doi: 10.1016/0022-2836(81)90003-6. [DOI] [PubMed] [Google Scholar]
  24. Kimchi-Sarfaty C, Oh JM, Kim IW, Sauna ZE, Calcagno AM, Ambudkar SV, Gottesman MM. A “silent” polymorphism in the mdr1 gene changes substrate specificity. Science. 2007;315:525–528. doi: 10.1126/science.1135308. [DOI] [PubMed] [Google Scholar]
  25. Komar AA, Lesnik T, Reiss C. Synonymous codon substitutions affect ribosome traffic and protein folding during in vitro translation. FEBS Lett. 1999;462:387–391. doi: 10.1016/s0014-5793(99)01566-5. [DOI] [PubMed] [Google Scholar]
  26. Koonin EV, Rogozin IB. Getting positive about selection. Genome Biol. 2003;4:331. doi: 10.1186/gb-2003-4-8-331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kosakovsky Pond SL, Frost SDW, Muse SV. HyPhy: hypothesis testing using phylogenies. Bioinformatics. 2005;21:676–679. doi: 10.1093/bioinformatics/bti079. [DOI] [PubMed] [Google Scholar]
  28. Liberles DA. Evaluation of methods for determination of a reconstructed history of gene sequence evolution. Mol Biol Evol. 2001;18:2040–2047. doi: 10.1093/oxfordjournals.molbev.a003745. [DOI] [PubMed] [Google Scholar]
  29. McVean GA, Vieira J. Inferring parameters of mutation, selection and demography from patterns of synonymous site evolution in. Drosophila. Genetics. 2001;157:245–257. doi: 10.1093/genetics/157.1.245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Nei M, Gojobori T. Simple methods for estimating the numbers of synonymous and nonsynonymous nucleotide substitutions. Mol Biol Evol. 1986;3:418–426. doi: 10.1093/oxfordjournals.molbev.a040410. [DOI] [PubMed] [Google Scholar]
  31. Nielsen R, DuMont VLB, Hubisz MJ, Aquadro CF. Maximum likelihood estimation of ancestral codon usage bias parameters in Drosophila. Mol Biol Evol. 2007;24:228–235. doi: 10.1093/molbev/msl146. [DOI] [PubMed] [Google Scholar]
  32. Nielsen R, Yang Z. Likelihood models for detecting positively selected amino acid sites and applications to the HIV-1 envelope gene. Genetics. 1998;148:929–936. doi: 10.1093/genetics/148.3.929. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Novembre JA. Accounting for background nucleotide composition when measuring codon usage bias. Mol Biol Evol. 2002;19:1390–1394. doi: 10.1093/oxfordjournals.molbev.a004201. [DOI] [PubMed] [Google Scholar]
  34. Parmley J, Chamary J, Hurst L. Evidence for purifying selection against synonymous mutations in mammalian exonic splicing enhancers. Mol Biol Evol. 2006;23:301–309. doi: 10.1093/molbev/msj035. [DOI] [PubMed] [Google Scholar]
  35. Parmley JL, Huynen MA. Clustering of codons with rare cognate tRNAs in human genes suggests an extra level of expression regulation. PLoS Genet. 2009;5 doi: 10.1371/journal.pgen.1000548. e1000548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Petersen L, Bollback JP, Dimmic M, Hubisz M, Nielsen R. Genes under positive selection in. Escherichia coli. Genome Res. 2007;17:1336–1343. doi: 10.1101/gr.6254707. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Resch AM, Carmel L, Mariño-Ramírez L, Ogurtsov AY, Shabalina SA, Rogozin IB, Koonin EV. Widespread positive selection in synonymous sites of mammalian genes. Mol Biol Evol. 2007;24:1821–1831. doi: 10.1093/molbev/msm100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Sharp PM, Tuohy T, Mosurski K. Codon usage in yeast: cluster analysis clearly differentiates highly and lowly expressed genes. Nucleic Acids Res. 1986;14:5125–5143. doi: 10.1093/nar/14.13.5125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Stenico M, Lloyd AT, Sharp PM. Codon usage in Caenorhabditis elegans: delineation of translational selection and mutational biases. Nucleic Acids Res. 1994;22:2437–2446. doi: 10.1093/nar/22.13.2437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Stoletzki N. Conflicting selection pressures on synonymous codon use in yeast suggest selection on mRNA secondary structures. BMC Evol Biol. 2008;8:224. doi: 10.1186/1471-2148-8-224. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Stoletzki N, Eyre-Walker A. Synonymous codon usage in Escherichia coli: selection for translational accuracy. Mol Biol Evol. 2007;24:374–381. doi: 10.1093/molbev/msl166. [DOI] [PubMed] [Google Scholar]
  42. Suzuki Y, Gojobori T. A method for detecting positive selection at single amino acid sites. Mol Biol Evol. 1999;16:1315–1328. doi: 10.1093/oxfordjournals.molbev.a026042. [DOI] [PubMed] [Google Scholar]
  43. Thanaraj TA, Argos P. Ribosome-mediated translational pause and protein domain organization. Protein Sci. 1996;5:1594–1612. doi: 10.1002/pro.5560050814. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Vinogradov AE. DNA helix: the importance of being GC-rich. Nucleic Acids Res. 2003;31:1838–1844. doi: 10.1093/nar/gkg296. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Warnecke T, Hurst LD. Evidence for a trade-off between translational efficiency and splicing regulation in determining synonymous codon usage in. Drosophila melanogaster. Mol Biol Evol. 2007;24:2755–2762. doi: 10.1093/molbev/msm210. [DOI] [PubMed] [Google Scholar]
  46. Widmann M, Clairo M, Dippon J, Pleiss J. Analysis of the distribution of functionally relevant rare codons. BMC Genomics. 2008;9:207. doi: 10.1186/1471-2164-9-207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Xia X. Maximizing transcription efficiency causes codon usage bias. Genetics. 1996;144:1309–1320. doi: 10.1093/genetics/144.3.1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Xie T, Ding D. The relationship between synonymous codon usage and protein structure. FEBS Lett. 1998;434:93–96. doi: 10.1016/s0014-5793(98)00955-7. [DOI] [PubMed] [Google Scholar]
  49. Yang Z. Computational molecular evolution. Oxford: Oxford University Press; 2006. [Google Scholar]
  50. Yang Z, Nielsen R. Mutation-selection models of codon substitution and their use to estimate selective strengths on codon usage. Mol Biol Evol. 2008;25:568–579. doi: 10.1093/molbev/msm284. [DOI] [PubMed] [Google Scholar]
  51. Yang Z, Wong WSW, Nielsen R. Bayes empirical bayes inference of amino acid sites under positive selection. Mol Biol Evol. 2005;22:1107–1118. doi: 10.1093/molbev/msi097. [DOI] [PubMed] [Google Scholar]
  52. Zhang G, Hubalewska M, Ignatova Z. Transient ribosomal attenuation coordinates protein synthesis and co-translational folding. Nat Struct Mol Biol. 2009;16:274–280. doi: 10.1038/nsmb.1554. [DOI] [PubMed] [Google Scholar]
  53. Zhou T, Weems M, Wilke CO. Translationally optimal codons associate with structurally sensitive sites in proteins. Mol Biol Evol. 2009;26:1571–1580. doi: 10.1093/molbev/msp070. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
msq077_index.html (699B, html)
msq077_1.pdf (7.7MB, pdf)

Articles from Molecular Biology and Evolution are provided here courtesy of Oxford University Press

RESOURCES