Computational Mutation Scanning and Drug Resistance Mechanisms of HIV-1 Protease Inhibitors

Abstract

The drug resistance of various clinically available HIV-1 protease inhibitors has been studied using a new computational protocol, i.e. computational mutation scanning (CMS), leading to valuable insights into the resistance mechanisms and structure-resistance correction of the HIV-1 protease inhibitors associated with a variety of active site and non-active site mutations. By using the CMS method, the calculated mutation-caused shifts of the binding free energies linearly correlate very well with those derived from the corresponding experimental data, suggesting that the CMS protocol may be used as a generalized approach to predict drug resistance associated with amino acid mutations. As it is essentially important for understanding the structure-resistance correlation and for structure-based drug design to develop an effective computational protocol for drug resistance prediction, the reasonable and computationally efficient CMS protocol for drug resistance prediction should be valuable for future structure-based design and discovery of anti-resistance drugs in various therapeutic areas.

Introduction

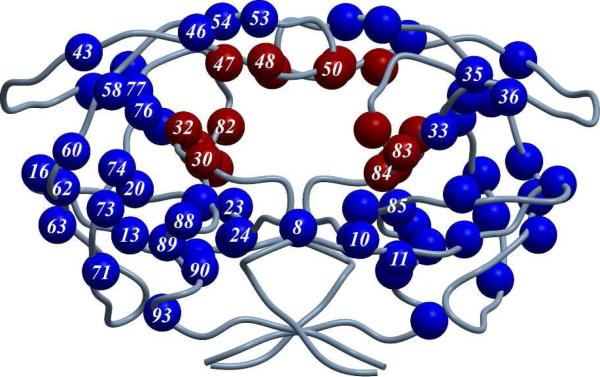
As well known, human immunodeficiency virus type 1 (HIV-1) is one of the most dangerous viruses for humans. The wide and rapid spread of HIV-1 virus causing the acquired immune deficiency syndrome (AIDs) has evolved into a global health problem with the infection number increasing at an explosive rate.^1,2 HIV-1 protease is essential for replication and assembly of the virus, and the inhibition of the HIV-1 protease leads to the production of noninfectious viral particles.³ Therefore, HIV-1 protease inhibitors become one of the key components in the chemotherapy of HIV-1 infection. Various HIV-1 protease inhibitors have been approved by FDA, including saquinavir (SQV), ritonavir (RTV), indinavir (IDV), nelfinavir (NFV), amprenavir (APV), lopinavir (LPV), atazanavir (ATV), tipranavir (TPV), and darunavir (DRV).^4,5 However, despite their great success in the market, all these inhibitors confront with severe drug resistance problem associated with the protease mutations. For example, DRV, as the most hopeful anti-resistance HIV-1 protease inhibitor approved in 2006 by FDA which showed excellent anti-resistance ability to the existing resistance mutations,⁶ still suffered from new drug-resistance mutations after its clinical use for only one year.⁷ To date, at least 37 mutation sites (residues) including active site and non-active site residues have been identified within the HIV-1 protease as shown in Figure 1.⁸

Figure 1.

Structural distribution of the identified mutation sites (residues) of the HIV-1 protease (active site residues in red and non-active site residues in blue).

The discovery of HIV-1 protease inhibitors has been one of the most exciting stories of structure-based drug design in history. Structure-based drug design has increasingly become part of many routine approaches in drug discovery today, due to the technical improvement in crystallography and the increasing computational power. In most cases, the key point that researchers have mainly considered is the binding affinity of a ligand with the target protein. As a consequence, various techniques have been developed and employed to optimize the non-covalent interactions between the protein and ligand, such as H-bond and π-π stacking interaction, with the aim to obtain a number of candidates with a nanomolar, or even picomolar, inhibition potency. However, a lot of clinically available drugs, including those discovered via structure-based design approach, usually encounter resistance, an intractable problem for the global public health. Among the known resistance mechanisms,^9,10 in particular, the target mutation which alters the interactions between the drug molecules and their target protein is the most severe situation, because drugs will become ineffective once a certain mutation on its target protein occurs. Therefore, it is an interesting task and urgent demand for structure-based drug discovery to develop effective methods for drug resistance prediction, which will help to reduce the resistance risk of a new drug discovered by structure-based design approach.

Three computational methods have been used for the drug resistance prediction. The first one is the evolutionary simulation model that evaluates the fitness for millions of mutant strains of enzymes and estimates the binding energies by measuring the volume complementarities between inhibitors, substrates, and the mutant enzymes.¹¹ The second one is the machine learning model constructed based on the structural features of enzyme-drug complexes or the sequence data of various drug-resistant mutants.^12,13 Both the first and second methods can be used only for the systems with lots of experimental data available. In addition, the purely empirical results given by these methods cannot be used to explore the drug resistance mechanism. The third one is the molecular structure based drug resistance prediction, in which molecular docking or molecular dynamics (MD) simulations are carried out.^14-16 Unfortunately, this method also suffers from some problems. For example, the MD simulations followed by accurate binding free energy calculations on a large number of mutants are time-consuming. Therefore, it is highly desirable to develop and test an accurate and rapid computational protocol for drug resistance prediction.

For computational prediction of drug resistance of a compound (ligand) against a target protein, one first needs to computationally determine the free energies of binding of the ligand with the wild-type and mutant forms of the target protein. Kollman et al. developed an approach to evaluate the nucleic acid conformation-dependent free energies.¹⁷ After that, Kollman et al further developed a method, known as Computational Alanine Scanning (CAS),¹⁸ to rapidly estimate the changes of the binding free energies resulted from the mutations on amino acid residues. Because this method reasonably relies on the resemblance assumption between the structures of wild-type (WT) and mutant-type (MT) and adequacy of the conformational sampling, since then, the CAS method has been widely applied in the noncovalent intermolecular interactions, including receptor-ligand and receptor-receptor interactions.^19,20 Nevertheless, the CAS method also suffers from some difficulties including evaluation of the entropy change and its large standard deviations. Besides, it is assumed that the structural perturbations associated with mutations of amino acid residues to alanine are relatively small and the mutations to alanine can be considered as removing side chain interactions beyond the β-C atom. So, the CAS method only considers the mutation of a residue to alanine and, therefore, the CAS method cannot be used to predict the drug resistance associated with the mutations to other amino acids.

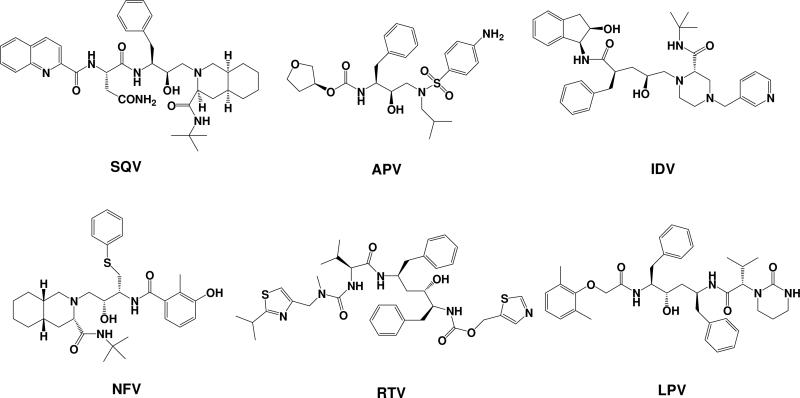
In the present study, we aimed to have a detailed understanding of the drug resistance mechanisms and the structure-resistance correlation of clinically available HIV-1 protease inhibitors by testing a new computational protocol in prediction of the drug resistance associated with target protein mutations. For this purpose, we have extended the CAS method to the mutations between any natural amino acids to predict drug resistance by introducing a rapid geometry refinement and reasonable entropy calculation. The extended method, which may be called Computational Mutation Scanning (CMS), has been used to evaluate the binding free energies of representative, clinically available inhibitors binding with HIV-1 protease and its various mutants. SQV, RTV, IDV, NFV, APV, and LPV, as shown in Scheme 1, were chosen for the present study because these inhibitors were discovered by structure-based design and their resistance spectrum associated with HIV-1 protease mutations have been comprehensively studied.^21,22 Crystallographic structures of the complexes (PDB codes: 1HXB (SQV),²³ 1HXW (RTV),²⁴ 1HSG (IDV),²⁵ 1OHR (NFV),²⁶ 1HPV (APV),²⁷ and 1MUI (LPV)²⁸ were used as the initial structures for our computational simulations. We have computationally modeled 25 most frequently occurred mutants of HIV-1 protease, including single and double mutations, and evaluated the effects of these mutations on the binding free energies. The computationally determined mutation-caused shifts of the binding free energies linearly correlate very well with those derived from the corresponding experimental data, leading to valuable insights into the drug resistance mechanisms of HIV-1 protease inhibitors. The reasonable correlation between the computational and experimental data also suggests that the computational protocol tested in this study might be valuable for predicting drug resistance associated with amino acid mutations on target proteins in future structure-based drug design.

Scheme 1.

Molecular structures of HIV-1 protease inhibitors used in the present study

Methods

The computational protocol used in this study is a combination of MD simulation and free energy perturbation (FEP)-based mutation scanning. For predicting the mutation-caused shift of the binding free energy for a MT protein-ligand complex from that of the corresponding WT, we first performed MD simulation on the unperturbed system (with the WT protein) to obtain the dynamically stable initial structure required for performing the FEP-based CMS calculations. Below, we describe how we carried out the MD and CMS calculations.

1. Molecular dynamics simulation

Prior to MD simulations, geometries of the inhibitors were optimized by performing ab initio quantum mechanics (QM) calculations at the HF/6-31+G* level using the Gaussian03 program.²⁹ With the optimized geometries, the electrostatic potential and partial atomic charges were determined by performing the electrostatic potential (ESP) fitting according to the Merz–Singh–Kollman scheme^30,31 so that the calculated electrostatic potential values surround ligands were well reproduced by using the obtained partial atomic charges.³² The RESP fitting was carried out by using the standard RESP protocol^33,34 implemented in the Antechamber module of the Amber8 program.³⁵ The determined RESP charges for the inhibitors were used in the energy minimizations, MD simulations, and binding free energy calculations described below.

The starting structures of HIV-1 protease-ligand complexes were taken from the protein data bank (PDB). To carry out the MD simulations, the topology and coordinate files of the complexes were built with the Leap module of the Amber8 package. Energy minimizations and MD simulations were performed using the Sander module of the Amber8 program. The AMBER ff03 force field was used as the parameters for amino acid residues,³⁶ and the general AMBER force field (gaff)³⁷ was used for ligands. The counter ions (Cl^- ions) were added to the most electropositive areas around the protein to neutralize the system. All molecules were solvated by a rectangular box of TIP3P waters extended at least 10 Å in each direction from the solute.³⁸ The cutoff distance for the long-range electrostatic interaction which was treated with particle mesh Ewald (PME)^39,40 and for the van der Waals (vdW) energy terms was set at 10.0 Å. SHAKE algorithm was used to constrain all covalent bonds involving hydrogen atoms.⁴¹ The energy minimization was achieved in three stages. First, movement was allowed only for the water molecules and ions. Next, the backbone atoms of the protein were fixed and the other atoms were allowed to move. Finally, all atoms were permitted to move freely. In each stage, the energy minimization was executed by using the steepest descent method for the first 2000 steps and the conjugated gradient method for the subsequent 3000 steps. Then, the MD simulation was performed according to the following steps. First, the solvent molecules were equilibrated for 10 ps to make sure that the simulated solvent system was in an equilibrated condition. Then the system was gradually heated from 10 to 300 K over 20 ps. Finally, to make sure that we obtained a stable MD trajectory for each of the simulated structures, the production MD simulation was kept run for 3 ns or longer at 1 atm and 300 K with applying periodic boundary conditions in the NPT ensemble to avoid edge effects. The time step used for the MD simulations was 2.0 fs. To obtain the best possible binding mode for each ligand, the key intermolecular hydrogen bonds formed after the energy minimization were restrained during the heating and the first 500 ps of the MD simulation at 300 K, and then the whole complex was relaxed to obtain a stable MD trajectory. During the MD simulation, atomic coordinates were collected every 1 ps.

The protonation states of catalytic aspartates D25 and D25' vary depending on different binding ligands. Hence, the appropriate protonation states of the catalytic aspartates which were already determined in previous studies^42,43 must be set for all the ligands before the MD simulations.

2. Computational mutation scanning

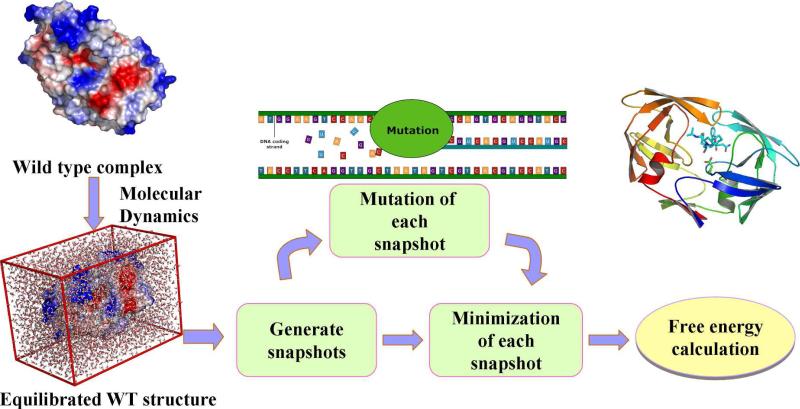
A free energy perturbation approach, such as the CAS, can be used to estimate the free energy shift caused by a small structural change. The CAS method has widely been used to study protein-protein/ligand interactions, but it can only be applied to the mutation changing a residue to alanine and the entropy effects have not been taken into consideration. Here, we describe our CMS protocol which may be regarded as an extension of the CAS method. Depicted in Figure 2 is the work flow of the CMS calculations in detail: (1) Performing MD simulation for the WT protein-ligand complex in explicit solvent. (2) Collecting 100 snapshots of the MD trajectory at regular intervals in order to obtain a representative ensemble of the binding structures. (3) Converting the complex structure of the WT protein for each snapshot to that of the mutant under consideration. (4) Refining the converted complex structures of the mutant associated with all of the 100 snapshots. (5) Calculating the Gibbs binding free energy between the protein and ligand for each snapshot by carrying out the molecular mechanics-Poisson Boltzmann surface area (MM-PBSA) energy analysis on the enthalpy term along with the entropy calculation using a computer program developed in our own laboratory.⁴⁴ The final binding free energy is the average of the calculated values associated with the 100 snapshots.

Figure 2.

Workflow of the computational mutation scanning.

For each MD-simulated enzyme-inhibitor complex, the MM-PBSA calculations were performed on the equally distributed 100 snapshots extracted from the last 1 ns of the stable MD trajectory with a time interval of 10 ps. The mutation was performed automatically on each snapshot with a modified version of MMTSB Tool Set package.⁴⁵ The orientation of the substituted side chain was determined according to the backbone-dependent side chain rotamer library and a repulsive steric energy term imbedded in this program. Furthermore, in order to calculate the binding free energy for inhibitor binding with a mutant, all force field parameters in the topology files for the residue(s) to be mutated were replaced with the parameters of the corresponding new residue(s). To refine the structure of the mutant, the positions of side chain atoms of all residues were energy-minimized in vacuum by using the Sander module of Amber8 program via a combined use of the steepest descent/conjugate gradient algorithms, with a convergence criterion of 0.2 kcal mol^-1 Å^-1 which was appropriate for the desirable computational accuracy. We tried to use different energy minimization methods for the geometry refinement of the snapshot structures and found little difference for the final energetic results between them (data not shown). Some test calculations with a higher convergence criterion (0.01 and 0.1 kcal mol^-1 Å^-1) suggested that the energy minimizations with the convergence criterion of 0.2 kcal mol^-1 Å^-1 were adequate, as further increasing the convergence criterion could no longer really improve the calculated results.

3. Free energy calculation

In the MM-PBSA method, the free energy of the receptor/protein-inhibitor binding, ΔG_bind, is obtained from the difference between the free energies of the receptor/protein-ligand complex (G_cpx) and the unbound receptor/protein (G_rec) and ligand (G_lig) as following:

$$\Delta G_{\text{bind}}=G_{\mathrm{cpx}}-(G_{\mathrm{rec}}+G_{\mathrm{lig}})$$ (1)

The binding free energy (ΔG_bind) is evaluated as a sum of the changes in the molecular mechanical (MM) gas-phase binding energy (ΔE_MM), solvation free energy (ΔG_sol), and entropic contribution (-TΔS):

$$\Delta G_{\text{bind}}=\Delta E_{\text{bind}}-T\Delta S$$ (2)

$$\Delta E_{\text{bind}}=\Delta E_{\mathrm{MM}}+\Delta G_{\text{sol}}$$ (3)

ΔE_MM is calculated by using the following equation:

$$\Delta E_{\mathrm{MM}}=\Delta E_{\mathrm{ele}}+\Delta E_{\mathrm{vdw}}$$ (4)

where, ΔE_ele and ΔE_vdw are respective electrostatic and van der Waals (vdW) interaction energies between a ligand and a protein. These energies are computed using the same parameters used in the MD simulation.

The solvation free energy ΔG_sol consists of two parts:

$$\Delta G_{\mathrm{sol}}=\Delta G_{\mathrm{PB}}+\Delta G_{\mathrm{np}}$$ (5)

The electrostatic contribution to the solvation free energy ( ΔG_PB ) is calculated by Poisson-Boltzmann (PB) method using the MM_PBSA module of Amber8 program. ΔG_np is the nonelectrostatic contribution to the solvation free energy determined as a function of the solvent accessible surface area (SASA).⁴⁶ Further, the entropic contribution to the binding free energy can be divided into two parts:⁴⁷

$$\Delta S=\Delta S_{\mathrm{sol}}+\Delta S_{\mathrm{conf}}$$ (6)

in which ΔS_sol is the solvation entropy change and ΔS_conf is the conformational entropy change. The solvation entropy is gained by the tendency of water molecules to minimize their contacts with hydrophobic groups in protein, whereas the conformational entropy change is related to the change of the number of rotatable bonds during the binding process. The computational procedure used to evaluate the entropic contribution (-TΔS) to the binding free energy is the same as that described in our recent publication.⁴⁴ As we described previously, the solvation entropy change is calculated by using the standard parameters that have been documented in literature.⁴⁸ The contribution to the binding free energy from the conformational entropy change is proportional to the number (ΔN_rot) of the lost rotatable bonds during the binding:

$$-T\Delta S_{\mathrm{conf}}=w\left(\Delta N_{\text{rot}}\right)$$ (7)

in which w is a scaling factor. Thus we have

$$\Delta G_{\text{bind}}=\Delta F_{\mathrm{MM}}+\Delta G_{\mathrm{sol}}-T\Delta S_{\mathrm{solv}}+w\left(\Delta N_{\text{rot}}\right).$$ (8)

This scaling factor, w, was set to be 1 kcal/mol for our MM-PBSA calculations on all the complexes in the present study. The w value of 1 kcal/mol used in the present study is the same as that used previously for the HIV-1 protease calculations by other researchers.⁴⁹ All of the other parameters used in our MM-PBSA calculations are the standard parameters reported in literature or the default parameters of the Amber8 program.

The binding free energy difference between the mutant and WT complexes is defined as:

$$\Delta \Delta G=\Delta G\left(\mathrm{MT}\right)-\Delta G\left(\mathrm{WT}\right)$$ (9)

According to Eq.(9), a positive ΔΔG value means the decrease in the binding affinity, whereas a negative ΔΔG value indicates favorable improvement of the corresponding interactions between enzyme and inhibitor. So, a positive ΔΔG value means resistance, whereas a negative ΔΔG valuemeans no resistance.

The experimental binding free energy changes are derived from the reported resistance ratio, K_i(MT)/K_i (WT), by using the following equation:

$$\Delta \Delta G_{\exp }=-RT\ln \frac{K_i\left(\mathrm{MT}\right)}{K_i\left(\mathrm{WT}\right)}$$ (10)

in which K_i (WT) and K_i(MT) are the dissociation constants for the inhibitor binding with wild-type HIV-1 protease and its mutant, respectively.

To theoretically estimate the reliability of the calculated ΔΔG values, we evaluated the standard error (SE) of the CMS-calculated binding free energy shifts. The SE value is dependent on both the number (N) of snapshots chosen in the CMS calculations and the root-mean-square fluctuation (RMSF) of the calculated ΔΔG values associated with all snapshots:⁵⁰

$$\mathrm{SE}=\frac{\mathrm{RMSF}}{\sqrt{\mathrm{N}}}.$$ (11)

According to Eq.(11), with a given RMSF value, the larger the N, the smaller the SE value is. In the present study, N = 100 and, thus, we have SE = RMSF/10.

Results and Discussion

1. Computational model construction

First of all, it is essential to ensure that all of the MD simulations were thoroughly equilibrated. Obtaining a stable MD trajectory is crucial for subsequent analysis. So, the plot of root-mean-square deviation (RMSD), d_RMS, of the protein backbone and inhibitor atoms in the whole process of the MD simulation must be shown to examine their convergence. Some detailed data about the MD trajectories are provided in Supporting Information (Figure S1). Briefly, the d_RMS of the protein backbone and inhibitor atoms stabilized around 1 Å and persisted more than 1 ns in all systems. To further validate the equilibrium, we also analyzed some key hydrogen bond distances during the MD simulations as seen in Supporting Information (Figure S1). It was found that the six vital hydrogen bonds revealed by X-ray diffraction analysis were maintained during the equilibration stage. These data clearly suggest that we obtained a stable MD trajectory for each of the MD simulations.

Secondly, before the computational mutation scanning, we calculated the binding free energies of the six drug molecules by using a modified MM-PBSA method. For each protein-ligand binding, the energy calculations were performed based on a single-trajectory MD simulation which was carried out on the protein-ligand complex.^51-54 Further, computational mutation scanning and mutation-caused shifts of the binding free energies were evaluated for all of the protein-ligand binding complexes. The calculated binding free energy shifts are summarized in Table 1 in comparison with those derived from available experimental resistance data. The detailed energetic results are provided as Supporting Information (Tables S1 to S9).

Table 1.

Calculated binding free energy shifts (kcal/mol) in comparison with those derived from available experimental data. The original experimental data from literature are summarized in Supporting Information. The values in parentheses are the binding free energy shifts (ΔΔG_corr) predicted by using the obtained linear correlation relationships for the corresponding drugs.

Mutation types	SQV		RTV		IDV		NFV		APV		LPV
	ΔΔGcal [SE]b	ΔΔGexpa (ΔΔGcorr)c	ΔΔGcal [SE]	ΔΔGexp (ΔΔGcorr)	ΔΔGcal [SE]	ΔΔGexp (ΔΔGcorr)	ΔΔGcal [SE]	ΔΔGexp (ΔΔGcorr)	ΔΔGcal [SE]	ΔΔGexp (ΔΔGcorr)	ΔΔGcal [SE]	ΔΔGexp (ΔΔGcorr)
R8Q			2.75 [0.15]	1.86 (2.02)	3.91 [0.32]	1.25 (2.78)
L10F	0.05 [0.14]	0.33 (0.45)			0.00 [0.12]	0.82 (0.69)			0.02 [0.11]	-0.11 (0.24)
L10F/I50V	2.08 [0.23]	2.09 (1.40)							1.75 [0.37]	2.43 (1.44)
L10F/I84V	2.25 [0.26]	1.81 (1.47)			1.06 [0.16]	1.89 (1.25)			1.69 [0.16]	1.78 (1.40)
L10I/L90M											-0.19 [0.10]	0.20 (0.15)
V32I	0.74 [0.17]	0.28 (0.77)	1.54 [0.17]	0.73 (1.28)	1.94 [0.18]	1.23 (1.73)
V32I/I84V	2.98 [0.20]	1.57 (1.82)	3.88 [0.22]	2.46 (2.72)	3.12 [0.20]	2.60 (2.36)
M46I	0.15 [0.11]	0.00 (0.49)	-0.15 [0.08]	0.38 (0.23)	-0.21 [0.12]	0.82 (0.57)			-0.07 [0.09]	-0.41 (0.17)
M46I/I54V											0.08 [0.10]	0.24 (0.24)
M46I/I84V	2.50 [0.28]	0.89 (1.59)	2.04 [0.15]	1.33 (1.59)	0.78 [0.16]	1.82 (1.10)
I47V	-1.62 [0.13]	-0.41 (-0.34)			-0.82 [0.20]	0.65 (0.25)			-0.70 [0.17]	-0.24 (-0.26)
G48V	7.09 [0.48]	3.01 (3.74)	3.14 [0.21]	2.52 (2.26)	0.52 [0.24]	0.95 (0.97)	1.63 [0.15]	0.65 (0.91)	1.59 [0.25]	0.82 (1.33)
G48V/L90M	7.18 [0.51]	4.44 (3.78)	3.27 [0.20]	2.67 (2.35)	0.57 [0.25]	1.18 (0.99)	1.67 [0.17]	0.82 (0.93)	1.56 [0.26]	1.42 (1.30)
I50V	2.18 [0.21]	1.89 (1.44)			1.13 [0.23]	1.37 (1.29)			1.95 [0.35]	2.48 (1.58)
I54M	0.31 [0.14]	0.95 (0.57)
I54V	0.11 [0.12]	1.61 (0.47)
A71T/V82A	0.37 [0.16]	0.25 (0.60)			0.56 [0.15]	0.74 (0.99)
V82A	0.48 [0.14]	0.30 (0.65)	2.36 [0.13]	1.43 (1.78)	0.74 [0.12]	0.59 (1.08)	1.36 [0.14]	0.86 (0.79)	0.40 [0.13]	0.33 (0.50)	0.77 [0.14]	0.79 (0.45)
V82A/I84V											3.02 [0.16]	1.20 (1.16)
V82F			3.19 [0.25]	2.67 (2.30)	3.12 [0.36]	2.63 (2.36)	3.77 [0.30]	1.61 (1.88)	2.50 [0.28]	-0.62 (1.96)	1.86 [0.29]	0.62 (0.79)
V82F/I84V			5.50 [0.30]	3.89 (3.72)	4.08 [0.35]	2.88 (2.87)	5.20 [0.30]	2.64 (2.52)	4.40 [0.28]	2.73 (3.27)
V82I	1.45 [0.18]	1.18 (1.10)	2.67 [0.26]	1.59 (1.97)	2.02 [0.18]	1.15 (1.77)	2.94 [0.17]	1.70 (1.50)	2.05 [0.14]	0.71 (1.64)
V82T											1.41 [0.16]	0.60 (0.65)
I84V	2.64 [0.31]	1.68 (1.66)	2.21 [0.15]	2.09 (1.69)	1.12 [0.12]	1.24 (1.29)	1.86 [0.16]	1.20 (1.02)	1.64 [0.12]	1.86 (1.36)
L90M	-0.08 [0.13]	0.59 (0.38)	-0.06 [0.08]	0.95 (0.29)	-0.29 [0.14]	0.20 (0.53)	-0.03 [0.14]	0.41 (0.16)	0.05 [0.12]	0.65 (0.26)

^aThe original experimental data from literature are summarized in Supporting Information.

^bThe values in square brackets are the standard error of the calculation.

^cThe values in parentheses are the binding free energy shifts (ΔΔG_corr) predicted by using the obtained linear correlation relationships for the corresponding drugs.

Indicated also in Table 1 are the SE values of the CMS binding free energy shift calculations, ranging from 0.08 to 0.51 kcal/mol; the average SE value is 0.20 kcal/mol. It is interesting to note that the average SE value of the CMS binding free energy shift calculations is significantly smaller than the average SE value of the corresponding individual MM-PBSA binding free energy calculations. For example, the average SE value of the calculated binding free energies for all of the wild-type HIV-1 protease-inhibitor complexes examined in this study is 0.41 kcal/mol, and the average SE value of the calculated binding free energies for all of the mutant protease-inhibitor complexes examined in this study is 0.45 kcal/mol.

The absolute values of the binding free energies (ΔG_bind) obtained from the MM-PBSA calculations were -33.88, -40.23, -26.26, -18.30, -22.55, and -26.48 kcal/mol for HIV-1 protease binding with SQV, RTV, IDV, NFV, APV, and LPV, respectively. The binding free energies (ΔG_exp) derived from available experimental data are -14.32, -14.92, -13.14, -12.24, -12.60, and -14.30 kcal/mol for HIV-1 protease with SQV, RTV, IDV, NFV, APV, and LPV, respectively.^55-57 These data show that the MM-PBSA calculations largely overestimated the absolute values of the binding free energies. Nevertheless, the relative order of the ΔG_bind values is completely consistent with the experimentally-derived binding free energies (ΔG_exp). Both the ΔG_bind and ΔG_exp values consistently reveal that the relative order of the binding affinities of the inhibitors is always RTV > SQV > LPV > IDV > APV > NFV (from the highest binding affinity to the lowest).

2. Drug resistance

Drug resistance mutations can be classified into different categories according to the amino acid size, polarity, location and so on. First of all, based on the size (the amino acid size may be roughly characterized by the number of heavy atoms), mutations can be divided into several types: from large to small (L-S), from small to large (S-L), and from equivalent to equivalent (E-E). Secondly, 20 natural amino acids can be divided into nonpolar (NP), polar (P), acidic (A), and basic (B) groups. Hence, mutations can be divided on the basis of the polarity. Besides, mutations can also be sorted in terms of its location in the target enzyme: active site (AS) mutation or non-active site (NAS) mutation. In this work, we collected from literature most of the single and double mutations, including the mutations between residues that are different in size, polarity, and location. All of the experimental data were collected from literatures.^58-70 The studies on different types of mutations could also help us to understand the applicability of the CMS method and common characters of the drug resistance mechanisms in detail. We only investigated the single and double mutations in this work due to the huge number of combinations of multiple mutations.

It was assumed that the mutation to any amino acid except for proline⁷¹ would only lead to local changes of the protein structure and would not significantly change the backbone structure of protein. To verify this assumption, we superimposed the X-ray crystal structures of the wild-type and all available mutant structures of HIV-1 protease in complex with a representative inhibitor, i.e. SQV.^72-76 As shown in Figure S2 and Table S10 of Supporting Information, all these complexes had a similar backbone shape with RMSD less than 0.7 Å. In addition, the L-S and E-E mutations might not change the general binding mode of inhibitors. However, the S-L mutations or mutations between amino acids of different polarity might probably change the general binding mode of inhibitors,⁷⁷ because these types of mutations often cause local spatial bump or property mismatch with the original binding mode of the ligand.

Based on the above assumptions, making a mutation scanning between any two amino acids is reasonable and can be realized through using an appropriately designed computational procedure. The main challenge is to determine a reasonable conformation of the side chain of the mutated amino acid residue. This procedure preserves the backbone coordinates and the side chain coordinates of residues that are not mutated. It only needs to rebuild the structure of the side chain of the mutated residue starting from the space occupied by the side chain of the original residue. It may lead to reasonable structures based on the backbone-dependent side chain rotamer library and a repulsive steric energy term, but further energy minimization is desirable in order to improve the structure of the mutant. Technically, using the CMS method for a mutation, one only needs to deal with the topology and coordinate files of the Amber program. We note that other scanning methods, such as the CAS and Fluorine Scanning, resulted in correct conformational sampling of protein mutants.^78,79

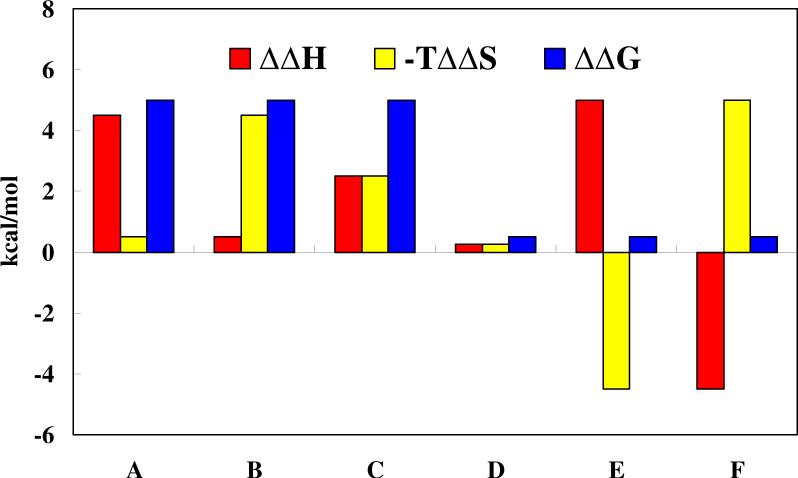
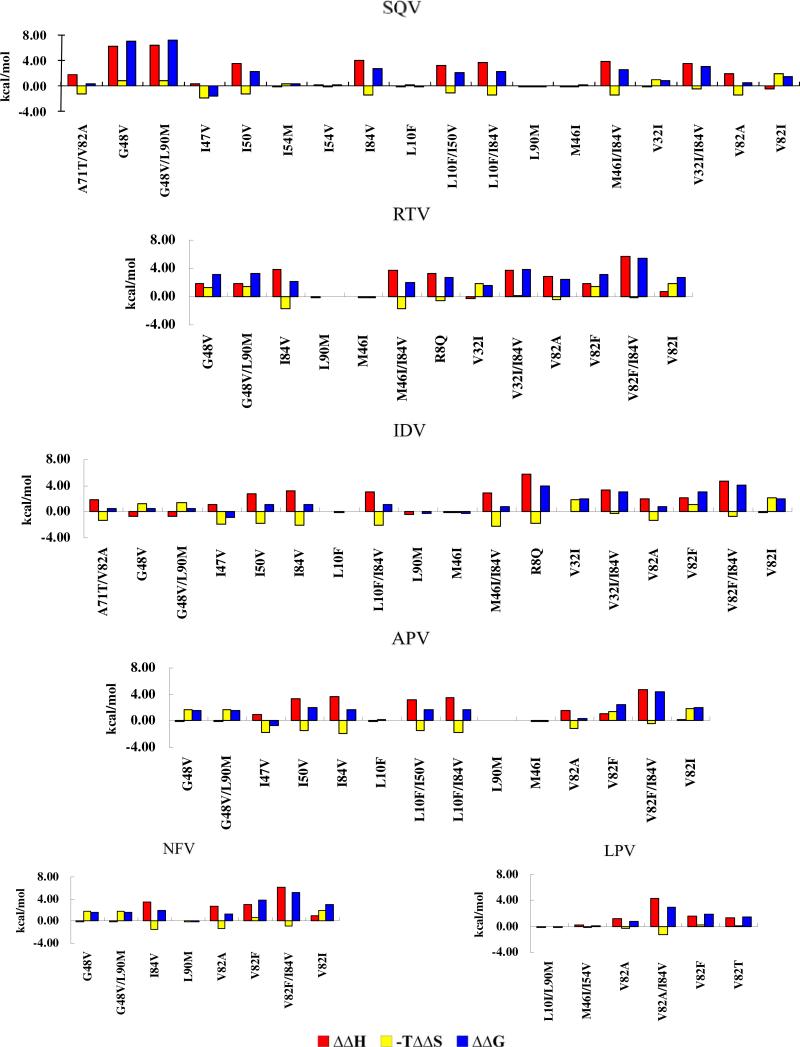
Generally speaking, the resistance mechanism of the target mutation can be divided into six groups in the view of thermodynamic rules as shown in Figure 3: decrease in the enthalpy contribution to the binding affinity (A-type), decrease in the entropic contribution to the binding affinity (B-type), decrease in both the enthalpy and entropic contributions (C-type), no significant change in the enthalpy and entropic contribution (D-type), decrease in the enthalpy contribution compensated with increase in the entropic contribution (E-type), decrease in the entropic contribution compensated with increase in the enthalpy contribution (F-type). The first three groups (A-, B-, and C-types) always lead to high level of resistance, whereas the last three groups (D-, E-, and F-types) always lead to no resistance or low resistance. Understanding the resistance mechanisms is undoubtedly of great interest for the anti-resistance drug design.

Figure 3.

Six possible mechanisms for drug resistance: decrease in the enthalpy contribution to the binding affinity (A-type), decrease in the entropic contribution to the binding affinity (B-type), decrease in both the enthalpy and entropic contributions (C-type), no significant change in the enthalpy and entropic contribution (D-type), decrease in the enthalpy contribution compensated with increase in the entropic contribution (E-type), decrease in the entropic contribution compensated with increase in the enthalpy contribution (F-type). Enthalpy and entropy changes reflect different types of interactions. Thus these signals provide valuable clues for the rational design of anti-resistance drugs.

For convenience, here the drug resistance is defined to have three different levels: low, middle, and high levels. The low resistance level means less than 10-fold resistance, the middle resistance level means less than 100-fold but higher than 10-fold resistance, and the high resistance level means higher than 100-fold resistance. Equation ΔG = -RTln(1/K_i) can be used to predict the resistance level of each mutation by the value of ΔΔG = ΔG(WT) − ΔG(MT). Thus, a positive ΔΔG value of less than 1.37 kcal/mol will result in low level of resistance, a ΔΔG value between 1.37 and 2.73 kcal/mol will result in middle level of resistance, and a ΔΔG value of higher than 2.73 kcal/mol will result in high level of resistance.

Below we discuss the detailed results and insights into the resistance mechanisms for each of the six drugs, followed by a discussion on the overall performance of the CMS calculations.

2.1 Resistance to SQV

The 18 mutants examined include six double mutants and 12 single mutants. These mutants involve mutations on a total of 11 residues including six active site residues (V32, I47, G48, I50, V82, and I84) and five non-active site residues (L10, M46, I54, A71, and L90). In addition, all of these mutants belong to the mutations from nonpolar to nonpolar residue except for A71T, a non-active site mutation from nonpolar to polar residue.

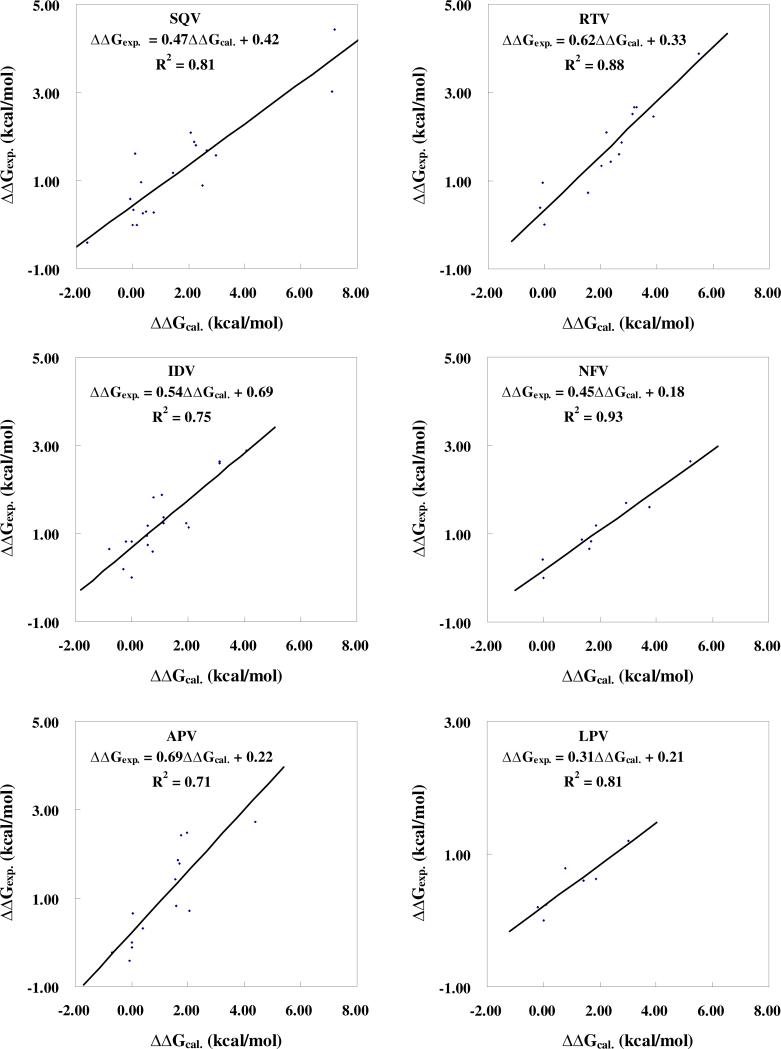
We calculated the binding free energy changes from the WT to the MT for 18 mutant complexes. As shown in Table 1, the calculated binding free energy shifts (ΔΔG_cal) range from -1.62 to 7.18 kcal/mol. The G48V/L90M and I47V mutants are associated with the highest and lowest resistance levels, respectively. As shown in Figure 4, the ΔΔG_cal values linearly correlate very well with the ΔΔG_exp values with a correlation coefficient of r² = 0.81. Neglecting the entropic contribution, ΔΔG_cal becomes ΔΔE_cal (see Supporting Information for the ΔΔE_cal values) and we obtained r² = 0.65 for the linear correlation relationship between the ΔΔE_cal and ΔΔG_exp values. These results indicate that the entropic effects can significantly affect the accuracy of drug resistance prediction and should not be neglected.

Figure 4.

Linear correlation between the calculated and experimental binding free energy shifts for each of the six drugs in clinical use.

Further, the excellent linear correlation relationship between the ΔΔG_cal and ΔΔG_exp values can be used to more accurately predict the binding free energy shifts. The binding free energy shift corrected by using the linear relationship between the ΔΔG_cal and ΔΔG_exp values is denoted by ΔΔG_corr for convenience. The obtained ΔΔG_corr values are also listed in Table 1 for comparison with the corresponding experimental data (ΔΔG_exp). When we consider various levels/catagories of drug resistance in terms of the high resistance, middle resistance, low resistance, and no resistance defined above, the ΔΔG_corr values are qualitatively consistent with the corresponding ΔΔG_exp values for all of the mutants, except for M46I/I84V and I54V, as one can see in Table 1. The hit rate is ~89% (16 out of 18). Considering the two exceptions, ΔΔG_corr = 1.59 kcal/mol and ΔΔG_exp = 0.89 kcal/mol for the M46I/I84V mutant, and ΔΔG_corr = 0.47 kcal/mol and ΔΔG_exp = 1.56 kcal/mol for the I54V mutant; the ΔΔG_corr values are also reasonably close to the corresponding ΔΔG_exp values. Sometimes, one may only consider whether the binding free energy shift (ΔΔG) has a plus or minus sign, because the sign indicates whether there exists the drug resistance (ΔΔG > 0) or not (ΔΔG ≤ 0). When we only concern with the sign of ΔΔG, the ΔΔG_corr values are qualitatively consistent with the corresponding ΔΔG_exp values for all of the mutants (100%).

We further analyzed the drug resistance mechanisms associated with the mutations. As seen in Table 1, all of the mutations, except for M46I and I47V, should result in resistance due to the positive binding free energy shifts. According to the above definitions of the resistance levels, two mutants (G48V and G48V/L90M) are associated with the high-resistance mutations, six mutants (I50V, I54V, I84V, L10F/I50V, L10F/I84V, and V32I/I84V) with the middle-resistance mutations, and eight mutants (L10F, V32I, I54M, V82A, V82I, L90M, M46I/I84V, and A71T/V82A) with the low-resistance mutations. In addition, as shown in Figure 5, several mutations (G48V, V32I/I84V, and G48V/L90M) leading to the drug resistance may be attributed to A-type mechanism, because they share a common characteristic that the decrease in the enthalpy contribution is mainly responsible for the binding affinity decrease. The V32I, I54M, and V82I mutants are associated with B-type resistance mechanism. Besides, four mutants (L10F, M46I, I54V, and L90M) are associated with D-type mechanism, and the I47V, I50V, V82A, I84V, L10F/I50V, L10F/I84V, M46I/I84V, and A71T/V82A mutants are associated with E-type mechanism.

Figure 5.

Thermodynamic representation of the drug resistance mechanism for each drug associated with each mutant of HIV-1 protease.

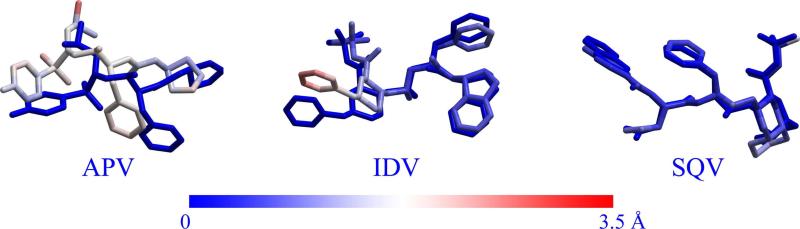
Kollman et al. demonstrated that the CAS method was capable of reasonable conformational sampling. In order to examine whether the CMS method is also capable of reasonable conformational sampling, we randomly selected the I54M mutant for SQV to perform MD simulation. Some plots for the RMSD and distance analysis are provided in the Supporting Information (Figure S3). As shown in Table S3, the ΔG_bind was estimated to be -33.57 kcal/mol based on the CMS model and -34.26 kcal/mol using the MD-based computational model. As shown in Figure 6, the conformational comparison indicates that the CMS method can produce almost the same conformation as the MD simulation for the I54M for SQV with RMSD of 0.92 Å. These results clearly indicate that, compared with the MD simulation, the CMS method is also capable of reasonable conformational sampling with the characteristic of time-saving.

Figure 6.

Superimposition of the MD-simulated molecular structures of APV, IDV, and SQV with the corresponding structures obtained from the CMS calculations. The superimposition was carried out on the backbone atoms of the protein. The structures obtained from the MD simulations are shown as colored sticks, whereas those from the CMS calculations are shown in deep blue. The color shown in the bottom bar refers to the magnitude of the RMSD.

2.2 Resistance to RTV

The 13 mutants examined for RTV include nine single mutants and four double mutants. These mutants involve mutations on a total of seven residues, including four active site residues (V32, G48, V82, and I84) and three non-active site residues (R8, M46, and L90). In addition, all of these mutants belong to the mutations from nonpolar to nonpolar residue, except R8Q which is a non-active site mutation from a basic residue to a neutral polar one.

We calculated the binding free energy changes (ΔΔG_cal) from the WT to the MT for 13 mutant complexes. As shown in Table 1, the calculated binding free energy changes (ΔΔG_cal) range from -0.15 to 5.50 kcal/mol. The M46I and V82F/I84V mutants are associated with the lowest and highest resistance levels, respectively. As shown in Figure 4, the ΔΔG_cal values linearly correlate very well with the ΔΔG_exp values, with a correlation coefficient r² = 0.88. However, r² = 0.55 for the linear relationship between the ΔΔE_cal and ΔΔG_exp values. So, the linear correlation between the computational and experimental binding affinity shifts can significantly be improved when the entropic contribution is accounted for.

As one can see in Table 1, the binding free energy shifts (ΔΔG_corr) predicted by using the linear relationship between the ΔΔG_cal and ΔΔG_exp values are qualitatively consistent with the corresponding ΔΔG_exp values for all of the mutants, except for the V82I mutant discussed above, in terms of the qualitative predictions of the drug resistance levels (high, middle, low, or no resistance). The hit rate is ~92% (12 out of 13). For the exception (V82I mutant), the ΔΔG_corr value of 1.59 kcal/mol is actually very close to the corresponding ΔΔG_exp value 1.33 kcal/mol. When we only consider whether there exist the drug resistance (ΔΔG > 0) or not (ΔΔG ≤ 0), the ΔΔG_corr values are qualitatively consistent with the corresponding ΔΔG_exp values for all of the mutants (100%).

As shown in Table 1, the V82F/I84V mutant is associated with the high-resistance mutation, eight mutants (R8Q, G48V, V82A, V82F, V82I, I84V, G48V/L90M, and V32I/I84V) are associated with the middle-resistance mutations, and four other mutants (V32I, M46I, L90M, and M46I/I84V) with the low-resistance mutations. As shown in Figure 5, among these mutations, four mutants (R8Q, V82A, V32I/I84V, and V82F/I84V) leading to resistance are associated with A-type mechanism because of their significant change in the enthalpy contribution to the binding affinity (ΔΔE_cal > 1.0 kcal/mol), whereas the V32I and V82I mutants are associated with B-type mechanism due to their relatively larger change in the entropic contribution to the binding affinity. In addition, three mutants (G48V, V82F, and G48V/L90M) leading to drug resistance are associated with C-type mechanism, because of their changes in both the enthalpy and entropic contributions to the binding affinity. The M46I and L90M mutants leading to low resistance belong to D-type mechanism. Finally, the I84V and M46I/I84V mutants are associated with E-type mechanism, as the enthalpy change is compensated by the increase in the entropic contribution.

2.3 Resistance to IDV

The 18 mutants examined for IDV include 12 single mutants and six double mutants. These mutants involve the mutations on six active site residues (V32, I47, G48, I50, V82, and I84) and five non-active site residues (R8, L10, M46, A71, and L90). In addition, most of these mutants belong to the mutations from nonpolar to nonpolar residue, except R8Q (a non-active site mutation from a basic to a neutral polar residue) and A71T (a non-active site mutation from a nonpolar to a neutral polar residue).

As shown in Table 1, the calculated binding free energy shifts (ΔΔG_cal) from the WT to the MT for the 18 mutant complexes range from -0.82 kcal/mol to 4.08 kcal/mol. The V82F/I84V and I47V mutants are associated with the highest and lowest resistance, respectively. We obtained r² = 0.59 for the linear correlation between the ΔΔG_cal and ΔΔG_exp values and r² = 0.36 (figure not shown) for the linear relationship between the ΔΔE_cal and ΔΔG_exp values. The linear correlation between the ΔΔG_cal and ΔΔG_exp values for IDV is still reasonable, but is not as good as the aforementioned linear correlation relationships obtained for SQV and RTV. In order to understand why this is the case, we carefully checked the data and found that the CMS calculations overestimated the resistance level associated with the R8Q mutation. Compared with the experimental data, the ΔΔG_cal value for the R8Q mutant overestimated the binding free energy shift by ~2.66 kcal/mol, suggesting that the R8Q mutant might result in a significant conformational change of the IDV in the binding pocket or, in other words, the change in the binding mode of IDV (see below). After discarding the R8Q mutant from the data set, as shown in Figure 4, the linear correlation between the ΔΔG_cal and ΔΔG_exp values was significantly improved to r² = 0.75, whereas the linear relationship between the ΔΔE_cal and ΔΔG_exp was improved to r² = 0.49.

As seen in Table 1, the binding free energy shifts (ΔΔG_corr) predicted by using the linear relationship between the ΔΔG_cal and ΔΔG_exp values are qualitatively consistent with the corresponding ΔΔG_exp values for most of the mutants (13 out of 18) in terms of the qualitative predictions of the drug resistance levels (high, middle, low, or no resistance). The hit rate is ~72%. Concerning the five exceptions, ΔΔG_corr = 2.78 kcal/mol and ΔΔG_exp = 1.25 kcal/mol for the R8Q mutant, ΔΔG_corr = 1.25 kcal/mol and ΔΔG_exp = 1.89 kcal/mol for the L10F/I84V mutant, ΔΔG_corr = 1.73 kcal/mol and ΔΔG_exp = 1.23 kcal/mol for the V32I mutant, ΔΔG_corr = 1.10 kcal/mol and ΔΔG_exp = 1.82 kcal/mol for the M46I/I84V mutant, and ΔΔG_corr = 1.77 kcal/mol and ΔΔG_exp = 1.15 kcal/mol for the V82I mutant. Even the differences between the ΔΔG_cal and ΔΔG_exp values for these exceptions are not really very large. When we only consider whether there exist the drug resistance (ΔΔG > 0) or not (ΔΔG ≤ 0), the ΔΔG_corr values are qualitatively consistent with the corresponding ΔΔG_exp values for all of the mutants (100%).

As shown in Table 1, of the 18 mutants, only the V82F/I84V belongs to the high resistance mutation, five mutants (I50V, V82F, L10F/I84V, V32I/I84V, and M46I/I84V) belong to the middle resistance, and 12 mutants (R8Q, L10F, V32I, M46I, I47V, G48V, V82A, V82I, I84V, L90M, G48V/L90M, and A71T/V82A) belong to the low resistance. Data obtained from the resistance mechanism analysis for these 18 mutants are depicted in Figure 5. According to the computational data, the V32I/I84V and V82F/I84V mutants are associated with A-type mechanism, the V32I and V82I mutants with B-type mechanism, the V82F mutant with C-type mechanism, the L10F, M46I, and L90M mutants with D-type mechanism, the I47V, I50V, V82A, I84V, L10F/I84V, M46I/I84V, and A71T/V82A mutants with E-type mechanism, and the G48V and G48V/L90M mutants with F-type mechanism. Because the R8Q mutation likely results in the binding mode change of IDV, the mechanism of the drug resistance associated with the R8Q mutant for IDV will be discussed later (see below) with some further simulation.

2.4 Resistance to NFV

The eight mutants examined for NFV include six single mutants and two double mutants. These involve mutations on three active site residues (G48, V82, and I84) and one non-active site residue (L90). All of the mutations belong to those from nonpolar to nonpolar residue.

As one can see in Table 1, the calculated binding free energy changes (ΔΔG_cal) from the WT to the mutants range from -0.03 to 5.20 kcal/mol. The highest and lowest resistance levels are associated with the V82F/I84V and L90M mutants, respectively. As shown in Figure 4, an excellent linear correlation (r² = 0.93) was found between the ΔΔG_cal and ΔΔG_exp values. The linear correlation would reduce to r² = 0.67 when the entropy contributions were ignored. As seen in Table 1, the binding free energy shifts (ΔΔG_corr) predicted by using the linear relationship between the ΔΔG_cal and ΔΔG_exp are qualitatively consistent with the corresponding ΔΔG_exp values for all of the mutants in terms of the qualitative predictions of the drug resistance levels (high, middle, low, or no resistance). The hit rate is 100% for NFV.

As shown in Table 1, all of these mutations result in the middle or low resistances. The V82F, V82I, and V82F/I84V mutations lead to the middle resistance, whereas the G48V, V82A, I84V, L90M, and G48V/L90M mutations lead to the low resistance. As seen in Figure 5, the V82F and V82F/I84V mutants are associated with A-type mechanism due to a large change in the enthalpy with a small change in the entropic contribution. In addition, the G48V and G48V/L90M mutants are associated with B-type mechanism, and the V82I mutant with C-type mechanism. Of the other three mutants with the low resistance, only the L90M mutant is associated with D-type mechanism, whereas the V82A and I84V mutants are associated with E-type mechanism.

2.5 Resistance to APV

The 14 mutants examined for APV include 10 single mutants and four double mutants. These mutants involve mutations on five active site residues (I47, G48, I50, V82, and I84) and three non-active site residues (L10, M46, and L90). All of these belong to the mutations from nonpolar to nonpolar residue.

As shown in Table 1, the calculated binding free energy shifts range from -0.70 to 4.40 kcal/mol. The highest and lowest resistance levels were observed with the V82F/I84V and I47V mutants, respectively. Abnormally, the linear correlation (r² = 0.59) between the ΔΔE_cal and ΔΔG_exp was a little higher than that (r² = 0.43) between the ΔΔG_cal and ΔΔG_exp. Through a detailed analysis of the energetic data, the V82F mutant was identified as an outliner with the binding free energy change overestimated by ~3.12 kcal/mol. This implies that the V82F mutant might cause an unusually large conformational change of APV in the binding pocket or a significant change of the binding mode (see below for further discussion). After discarding the V82F mutant from the data set, as shown in Figure 4, the linear correlation between the ΔΔG_cal and ΔΔG_exp values was significantly improved to r² = 0.71, and the linear relationship between the ΔΔE_cal and ΔΔG_exp was also improved to r² = 0.66.

As one can see in Table 1, the binding free energy shifts (ΔΔG_corr) predicted by using the linear relationship between the ΔΔG_cal and ΔΔG_exp values are qualitatively consistent with the corresponding ΔΔG_exp values for most of the mutants (8 out of 13 mutants other than V82F) in terms of the qualitative predictions of the drug resistance levels (high, middle, low, or no resistance). The hit rate is ~62% for APV. The five mutants with the incorrect qualitative predictions are the L10F (ΔΔG_corr = 0.24 kcal/mol and ΔΔG_exp = -0.11 kcal/mol), M46I (ΔΔG_corr = 0.17 kcal/mol and ΔΔG_exp = -0.41 kcal/mol), G48V/L90M (ΔΔG_corr = 1.30 kcal/mol and ΔΔG_exp = 1.42 kcal/mol), V82I (ΔΔG_corr = 1.64 kcal/mol and ΔΔG_exp = 0.71 kcal/mol), and I84V (ΔΔG_corr = 1.36 kcal/mol and ΔΔG_exp = 1.86 kcal/mol). When we only consider whether there exist the drug resistance (ΔΔG > 0) or not (ΔΔG ≤ 0), the ΔΔG_corr values are qualitatively consistent with the corresponding ΔΔG_exp values for 11 mutants (~85%, or ~79% if the aforementioned V82F mutant is also counted in).

Of the 14 mutants, eight are associated with the low or no resistance mutations (L10F, M46I, I47V, G48V, V82A, V82F, V82I, and L90M), five with the middle resistance mutations (I50V, I84V, L10F/I50V, L10F/I84V, and G48V/L90M), and one with the high resistance mutation (V82F/I84V). As shown in Figure 5, only V82F/I84V mutant is associated with A-type mechanism. The G48V, V82I, and G48V/L90M mutants are associated with B-type mechanism. For the low resistance mutations, the L10F, M46I, and L90M are associated with D-type mechanism. The I47V, I50V, V82A, I84V, L10F/I50V, and L10F/I84V mutants are associated with E-type mechanism. The resistance mechanism of the V82F mutant will be discussed with further MD simulation and calculations (see below).

2.6 Resistance to LPV

Only six mutants, including three single and three double mutants, were examined for LPV, as we have found experimental drug resistance data only for these six mutants. These mutants involve mutations on two active site residues (V82 and I84) and four non-active site residues (L10, M46, I54, and L90). All of the mutations belong to those from nonpolar to nonpolar residue, except the V82T which is a mutation from a nonpolar residue to a neutral polar one.

As seen in Table 1, the calculated binding free energy shifts (ΔΔG_cal) from the WT to MT for the six mutant complexes range from -0.19 to 3.02 kcal/mol. The highest and lowest resistances are associated with the V82A/I84V and L10I/L90M mutants, respectively. As shown in Figure 4, ΔΔG_exp linearly correlates with both ΔΔG_cal and ΔΔE_cal very well. We obtained r² = 0.81 for the linear correlation between the ΔΔG_cal and ΔΔG_exp values, and r² = 0.86 for the linear correlation between the ΔΔE_cal and ΔΔG_exp values. These results show that the entropic effects are not important for the relative order of the drug resistances of this particular inhibitor although the entropic effects are important for the aforementioned other inhibitors.

As seen in Table 1, the binding free energy shifts (ΔΔG_corr) predicted by using the linear relationship between the ΔΔG_cal and ΔΔG_exp values are qualitatively consistent with the corresponding ΔΔG_exp values for all of the mutants in terms of the qualitative predictions of the drug resistance levels (high, middle, low, or no resistance). The hit rate is ~100% for LPV.

As shown in Figure 5, the V82F and V82T mutants are associated with A-type mechanism, the L10I/L90M and M46I/I54V mutants with D-type mechanism, and the V82A and V82A/I84V mutants with E-type mechanism.

2.7 Overall performance of the CMS method

The above discussion indicates that the CMS method can reasonably predict the relative drug resistance levels for each of the six drugs associated with a variety of mutations on the target protein. Overall, six clinically available drugs with various mutants of HIV-1 protease have been examined, giving a total of 77 drug-mutant combinations (including all of the exceptions discussed above). The binding free energy shifts (ΔΔG_corr) predicted by using the linear correlation relationships between the ΔΔG_cal and ΔΔG_exp values obtained for individual drugs are qualitatively consistent with the corresponding ΔΔG_exp values for 63 drug-mutant combinations in terms of the qualitative predictions of the drug resistance levels (high, middle, low, or no resistance). The overall hit rate is ~82% (63 out of 77). When we only consider whether there exist the drug resistance (ΔΔG > 0) or not (ΔΔG ≤ 0), the ΔΔG_corr values are qualitatively consistent with the corresponding ΔΔG_exp values for 74 mutants (~96%).

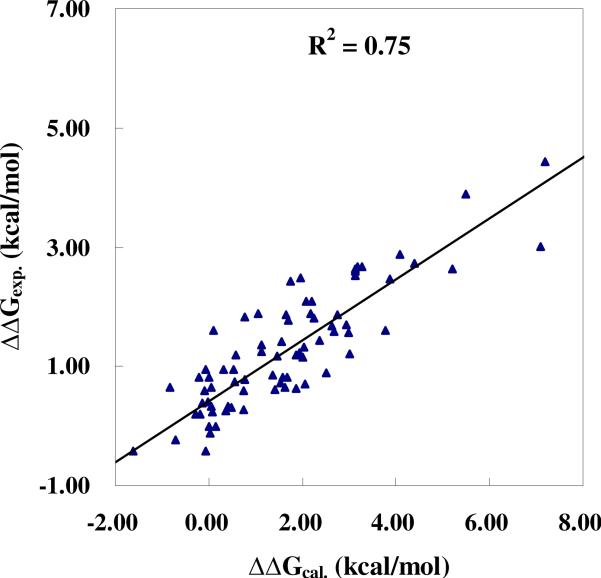
To better assess the predictability of the CMS method, we also examined the overall linear correlation between the calculated and experimental binding free energy shifts for all of the six drugs associated with all of the examined mutants of the target protein, except for the R8Q mutant with IDV and V82F mutant with APV (see below for discussion on these exceptions). Depicted in Figure 7 is the linear correlation. We have r² = 0.75 for the linear correlation between the ΔΔG_cal and ΔΔG_exp values and r² = 0.57 for the linear correlation between the ΔΔE_cal and ΔΔG_exp values. These data further suggest that the overall linear correlation between the ΔΔG_cal and ΔΔG_exp values for all of these drugs is also satisfactory and that the entropy effects are significant for the drug resistance prediction. The binding free energy shifts (ΔΔG_corr) predicted by using the overall linear relationship between the ΔΔG_cal and ΔΔG_exp values are qualitatively consistent with the corresponding ΔΔG_exp values for 57 drug-mutant combinations in terms of the qualitative predictions of the drug resistance levels (high, middle, low, or no resistance). The hit rate is ~74% (57 out of 77, including the aforementioned R8Q mutant with IDV and V82F mutant with APV). When we only consider whether there exist the drug resistance (ΔΔG > 0) or not (ΔΔG ≤ 0), the ΔΔG_corr values predicted by using the overall linear relationship between the ΔΔG_cal and ΔΔG_exp values are qualitatively consistent with the corresponding ΔΔG_exp values for 73 mutants (~95%).

Figure 7.

The overall linear correlation between the calculated and experimental binding free energy shifts for all of the six clinical available drugs with various mutants of the HIV-1 protease.

It should be pointed out that the CMS method can be considered as an extension of the CAS method. But the CMS method is not perfect because it also has a limitation because the binding structure between the mutant and ligand might have not been relaxed fully during the energy minimization process. It could significantly overestimate the binding free energy shift for an inhibitor binding with a mutant when the mutation causes a considerable change in the binding mode. Such cases include the R8Q mutant with IDV and the V82F mutant with APV, in which the calculated binding free energy shifts are considerably larger than the corresponding experimental shifts. R8Q belongs to the mutation from basic to neutral polar residue, and V82F belongs to the mutation from small to large residue. Just like the precondition for using the CAS method, a precondition for using the CMS method is that the mutation does not considerably change the binding mode of the drug molecule. Therefore, in order to check whether the R8Q or V82F mutation significantly changes the binding mode of drug molecule, we carried out additional MD simulations on these two complexes. Some plots for the RMSD and distance analysis are provided in the Supporting Information (Figure S3). As expected, IDV took a large conformational change in the binding pocket after the R8Q mutation (Figure 6). The calculated binding free energy for the MD-simulated R8Q mutant complex, as shown in Table S9, was -26.35 kcal/mol, about 4.01 kcal/mol lower than that (-22.34 kcal/mol) obtained from the CMS calculation. The calculated binding free energy shift based on the MD simulation is closer to the experimental value. Thus, after the R8Q mutation, the original mode of inhibitor IDV binding with the enzyme becomes very unfavorable. But inhibitor IDV can significantly change its binding mode in the binding pocket of the mutant to compensate the binding. Based on the data summarized in Table S9, the binding mode change does not significantly influence the entropy change, but the new binding mode helps to decrease the desolvation penalty and improve the electrostatic interaction. As a result, the overall binding affinity is improved with the binding mode change. Thus, without appropriately simulating the unusually large change of the binding mode, the CMS calculations significantly overestimated the binding free energy shift for IDV binding with the R8Q mutant. According to the MD simulation and the corresponding energetic results, the resistance for IDV with the R8Q mutant should be associated with E-type mechanism. Similarly, the V82F mutation also causes a considerable conformational change of APV in the binding pocket of the enzyme as shown in Figure 6. However, unlike the R8Q mutant with IDV, the change in the enthalpic contribution for the V82F mutant complex was underestimated by only ~0.95 kcal/mol with the CMS method, while its entropic contribution was overestimated by ~3.68 kcal/mol with the CMS method. Overall, the calculated binding free energy for the MD-simulated V82F mutant complex was -22.78 kcal/mol (see Table S9), about 2.73 kcal/mol lower than that (-20.05 kcal/mol) obtained from the CMS calculation. Therefore, without appropriately simulating the unusually large change in the binding mode, the CMS method also overestimated the binding free energy change for APV with the V82F mutant. Hence, the resistance of APV with the V82F mutation should be associated with the E-type, rather than C-type, mechanism, according to the MD simulation and the corresponding energetic results.

Further, in light of the computational results for IDV with the R8Q mutant and APV with the V82F mutant, one might expect that a better, anti-resistance inhibitor could have a good conformational flexibility to adapt the conformational change of the binding pocket upon amino acid mutations, because a conformationally flexible inhibitor could adjust its own conformation and thus reach the best possible mode of interaction with the amino acid residues in the binding pocket to compensate the binding free energy.

Conclusion

Drug resistance problems of various clinically available HIV-1 protease inhibitors associated with a variety of active site and non-active site mutations on the protease have been studied by using a new computational protocol, i.e. the computational mutation scanning (CMS). The computational studies using the CMS protocol have led to a detailed understanding of the drug resistance mechanisms and the structure-resistance correction of the clinically available HIV-1 protease inhibitors associated with the active site and non-active site mutations on the target protein. The computationally determined mutation-caused shifts of the binding free energies are reflected by various resistance mechanisms (A- to F-types). The drug resistance mechanisms are remarkably different for different inhibitors and for different mutations on the target protein (HIV-1 protease).

The CMS method tested in this study may be considered as a reasonable and computationally efficient protocol for evaluating the effects of amino acid mutations of protein on protein-inhibitor interactions. The CMS protocol requires the MD equilibration of wild-type protein-inhibitor complex, followed by performing site-mutation for each snapshot sampling from the MD trajectory at regular time intervals. As an extension of the well-known computational alanine scanning (CAS) method, the CMS protocol includes a fast geometry refinement process and, thus, may be used to deal with both mutations from large residues to smaller ones and those from small residues to the ones with a larger or similar size, so long as the mutations do not cause considerable changes on the orientation of the ligand in the binding pocket of the protein. For another remarkable difference between the CMS and CAS methods, the CMS accounts for entropic contributions in the MM-PBSA binding free energy calculations such that the CMS can be used to reasonably predict the binding free energy changes caused by the mutations on the protein. By using the CMS protocol, the computationally determined mutation-caused shifts of the binding free energies linearly correlate very well with those derived from the corresponding experimental data. Based on the linear correlation, the calculated binding free energy shifts caused by the mutations can reasonably reproduce the experimental data concerning the drug resistance.

Further, the reasonable linear correlation between the computational and experimental shifts of the binding free energies also suggests that the CMS protocol may be used as a generalized computational approach to predict drug resistance associated with amino acid mutations on target proteins. It is essentially important for understanding drug resistance mechanisms and for structure-based drug design to develop an effective computational protocol for drug resistance prediction. Previously used methods suffer from various drawbacks, such as time-consuming, low accuracy, and neglect of entropy contribution. The reasonable and efficient CMS protocol for drug resistance prediction should be valuable for future structure-based design and discovery of anti-resistance drugs in various therapeutic areas. For an ideal drug molecule, in addition to the desirable high potency, high selectivity, and good adsorption, distribution, metabolism, and excretion (ADME) profile, a lower drug resistance risk should also be one of the fundamental characteristics. It is very important to take drug resistance risk into full account during the process of structure-based drug design, as drug resistance has become one of the most serious problems in current drug discovery and development. Therefore, it is essentially important for structure-based drug discovery to have a reasonable computational protocol like the CMS for drug resistance prediction.