Temporal context calibrates interval timing

Abstract

We use our sense of time to identify temporal relationships between events and to anticipate actions. How well we can exploit temporal contingencies depends on the variability of our measurements of time. We asked humans to reproduce time intervals drawn from different underlying distributions. As expected, production times were more variable for longer intervals. Surprisingly however, production times exhibited a systematic regression towards the mean. Consequently, estimates for a sample interval differed depending on the distribution from which it was drawn. A performance-optimizing Bayesian model that takes the underlying distribution of samples into account provided an accurate description of subjects’ performance, variability and bias. This finding suggests that the central nervous system incorporates knowledge about temporal uncertainty to adapt internal timing mechanisms to the temporal statistics of the environment.

From simple habitual responses to complex sensorimotor skills, our behavioral repertoire exhibits a remarkable sensitivity to timing information. To internalize temporal contingencies, and to put them to use in the control of conditioned and deliberative behavior, our nervous systems must be equipped with central mechanisms to process time.

Among the elementary aspect of temporal processing, and one that has been the focus of many psychophysical studies of time perception, is the ability to measure the duration between events; i.e., interval timing¹. A common feature associated with repeated estimation (or production) of a sample interval is that the standard deviation of the estimated (or produced) intervals increases linearly with their mean, a property that is termed scalar variability^2–4. While previous work has demonstrated how suitable forms of internal noise might lead to scalar variability^5–8, we do not know whether and how the nervous system can make use of this lawful relationship to improve timing behavior.

Scalar variability implies that measurements of relatively longer intervals are less reliable and thus more uncertain. The question we address is whether subjects have knowledge about this uncertainty, and how they might exploit it to improve estimation and production of time intervals. This question is particularly important when one has prior expectations of how long an event might last. For instance, if one measures an interval to be ~1.5 s but, based on experience, expects it to be closer to 1.2 s, then s/he may conclude that the true interval was probably somewhere between 1.2 and 1.5 s. More generally, knowledge about the distribution of time intervals one may encounter – which we refer to as temporal context – could help reduce uncertainty. The extent to which temporal context should inform temporal judgments depends on how unreliable measurements of time are. While a metronome need not rely on temporal context to stay on the beat, a piano player may well use the tempo of a musical piece to coordinate finger movements in time. Thus, to make use of the oft-present temporal context, the brain must have knowledge about the reliability of its own measurements of time.

The question of how knowledge about temporal context may improve measurements of elapsed time can be posed rigorously in the framework of statistical inference. In this framework, to estimate a sample interval, the observer may take advantage of two sources of information: (1) the likelihood function, which quantifies the statistics of sample intervals consistent with a measurement, and (2) the prior probability distribution function of the sample intervals the observer may encounter. One possibility is for the observer to ignore the prior distribution, and to choose the most likely value directly from the likelihood function, a strategy known as the maximum-likelihood estimation (ML)⁹. Alternatively, a Bayesian observer would combine the likelihood function and the prior, and use some statistic to map the resulting posterior probability distribution onto an estimate. Common mapping rules are the maximum a posteriori (MAP) and Bayes Least Squares (BLS), which correspond to the mode and the mean of the posterior respectively.

To understand how humans evaluate their measurements of elapsed time in the presence of a temporal context, we asked subjects to estimate and subsequently reproduce time intervals in the sub-second to seconds range that were drawn from three different prior distributions. Subjects’ production times showed a clear dependence on both the sample intervals and the prior distribution from which they were drawn. We fitted subjects’ responses to various observer models such as ML, MAP and BLS and found that a Bayesian observer associated with the BLS could account for the bias, variability and overall performance of every subject in all three prior conditions. This suggests that subjects have implicit knowledge of the reliability of their measurements of time, and can use this information to adjust their timing behavior to the temporal regularities of the environment. Furthermore, our observer model shows that this sophisticated Bayesian behavior can be accounted for by a nonlinear transformation that simply and directly maps noisy measurement of time to optimal estimates.

Results

The Ready-Set-Go paradigm

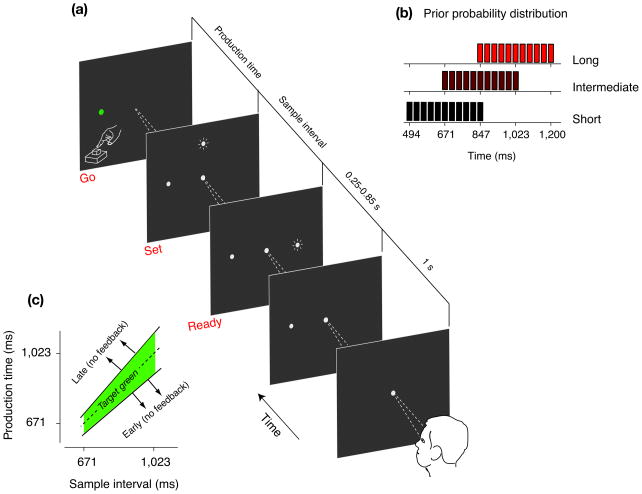
Subjects had to measure, and immediately afterwards reproduce different sample intervals. A sample interval, t_s, was demarcated by two brief flashes, a “Ready” cue followed by a “Set” cue. The corresponding production time, t_p, was measured from the time of the “Set” cue to when subjects proactively responded via a manual key press (Fig. 1a). Subjects received feedback for sufficiently accurate production times (Fig. 1c).

Figure 1.

The Ready-Set-Go time reproduction task. (a) Sequence of events during a trial. Appearance of a central spot indicated the start of the trial. Subjects were instructed to fixate the central spot and maintain fixation throughout the trial. A white “feedback” spot was visible to the left of the fixation point. After a random delay (0.25 to 0.85 s), two briefly flashed cues – “Ready” and “Set” – were presented in sequence. Subjects were instructed to estimate the sample interval demarcated by the time between the “Ready” and “Set” cues and to reproduce it immediately afterwards. The production times were measured from the time of “Set” to the time subjects responded via a key-press. When production times were within an experimentally adjusted window around the target interval (see Methods), the feedback spot turned green to provide positive feedback. (b) Distribution of sample intervals. In each session, sample intervals were drawn randomly from one of three partially overlapping discrete Uniform prior distributions (i.e., “Short”, “Intermediate”, and “Long”) shown by the black, dark red and light red bar charts. Subsequent figures use the same color convention to show results associated with these prior conditions. (c) Feedback schedule. The width of the window for which production times were positively reinforced (green area) scaled with the sample interval (see Methods). No feedback was provided for early and late responses. The plot shows an example schedule for the “Intermediate” prior condition.

In each session, sample intervals were drawn from a discrete uniform prior distribution. For each subject, three partially overlapping prior distributions (“Short”, “Intermediate” and “Long”) were tested (Fig. 1b). The main data for each prior condition were collected after an initial learning stage (typically 500 trials) to ensure subjects had time to adapt their responses to the range of sample intervals presented.

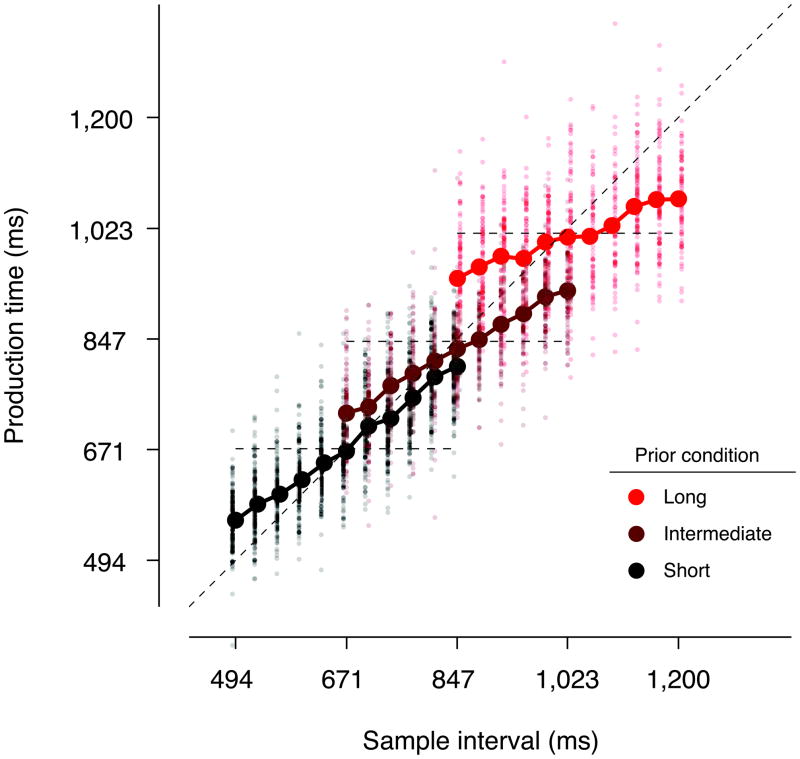
Subjects’ timing behavior exhibited three characteristic features (Fig. 2). First, production times monotonically increased with sample intervals. Second, for each prior condition, production times were systematically biased towards the mean of the prior as evident from their tendency to deviate from sample intervals (diagonal dashed line) and gravitate towards the mean interval (horizontal dashed line)^10–12. Consequently, mean production times associated with a particular t_s were differentially biased for the three prior conditions. Third, production time biases were more pronounced in the “Intermediate”, and more so, in the “Long” prior conditions, indicating that longer sample intervals were associated with progressively stronger prior-dependent biases. Similarly, within each prior condition, the magnitude of the bias was larger for the longest sample interval compared to the shortest sample interval (Supplementary Fig. S1).

Figure 2.

Time reproduction in different temporal contexts. Individual production times for every trial (small dots), and their averages for each sample interval (large circles connected with thick lines) are shown for three prior conditions for a typical subject. Average production times deviated from the line of equality (diagonal dashed line) towards the mean of the priors (horizontal dashed lines). Prior-dependent biases were strongest for the “Long” prior condition. Color conventions are the same as in Fig. 1b.

Scalar variability implies that the measurement of longer sample intervals engender more uncertainty. According to Bayesian theory, for these more uncertain measurements, subjects’ performance would improve if they rely more on their prior expectation (Supplementary Fig. S2). This is consistent with the observed increases in prior-dependent biases associated with longer sample intervals and suggests that subjects might have adopted a Bayesian strategy to reproduce time intervals. We thus developed probabilistic observer models to evaluate these observations quantitatively and to understand the computations from which they might arise.

The observer model

The observer model is presented with a sample interval, t_s. Due to measurement noise, the measured interval, t_m, may differ from t_s. The observer must use t_m to compute an estimate, t_e, for the sample interval, t_s. To do so, the observer may use an estimator that relies on probabilistic sources of information such as the likelihood function and the prior distribution. Importantly however, the estimator itself is fully characterized by a deterministic function, f, that maps a measurement, t_m, to an estimate, t_e; i.e. t_e = f(t_m). Finally additional noise during the production phase may cause the production time, t_p, to differ from t_e (Fig. 3a).

Figure 3.

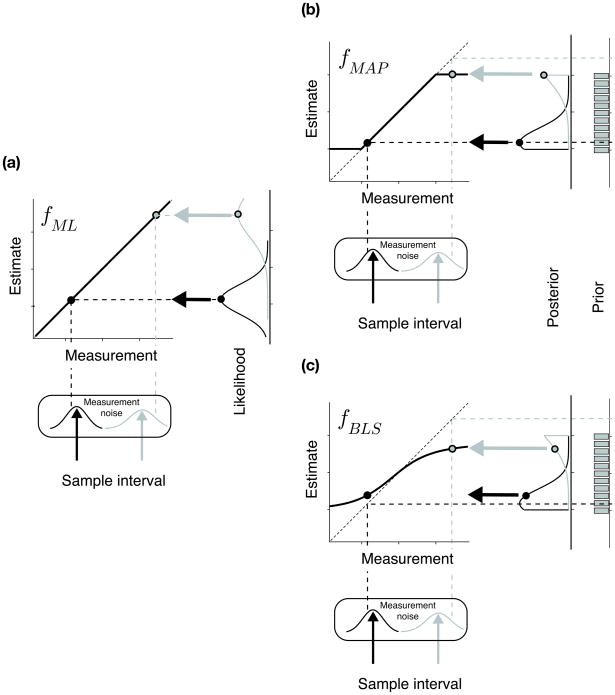
The observer model for time reproduction. (a) The three-stage architecture of the model. In the first stage, the sample interval, t_s, is measured. The relationship between the measured interval, t_m, and t_s is characterized by measurement noise, p(t_m|t_s) which was modelled as a zero-mean Gaussian function whose standard deviation grows linearly with t_s (i.e. scalar variability). The second stage is the estimator; i.e., the deterministic function, f(t_m), that maps measurement t_m to estimate t_e. The third stage uses t_e to produce interval t_p. The conditional dependence of t_p on t_e, p(t_p|t_e), was characterized by production noise, which was modelled by a zero-mean Gaussian distribution whose standard deviation scales linearly with t_e. (b–d) The deterministic mapping functions associated with the ML, MAP and BLS models respectively.

To formulate the model mathematically, we need to specify the relationship between the sample interval, t_s, the measured interval, t_m, the estimate, t_e, and the production time, t_p. The relationship between t_m and t_s can be quantified by the conditional probability distribution, p(t_m|t_s), the probability of different measurements for a specific sample interval. This distribution also specifies the likelihood function, λ_tm (t_s), a statistical description of the different sample intervals associated with a fixed measurement. We modelled p(t_m|t_s) as a Gaussian distribution centered at t_s, and motivated by the scalar variability of timing, assumed that the standard deviation of p(t_m|t_s) grows linearly with its mean (Fig. 3a). The distribution of measurement noise was thus fully characterized by the ratio of the standard deviation to the mean of p(t_m|t_s), which we will refer to as the Weber fraction associated with the measurement, w_m. With the same arguments in mind, we assumed that the distribution of t_p conditioned on t_e, p(t_p|t_e) is also Gaussian, is centered at t_e, and is associated with a constant Weber fraction, w_p.

Finally, the relationship between t_m and t_e was modelled by a deterministic mapping function, f, which we will refer to as the estimator. Different estimators are associated with different mapping rules. Among them, we focused on the ML, MAP and BLS because of their well-known properties, and because they were most germane to the development of our arguments with respect to the psychophysical data. We denote the corresponding estimators by f_ML, f_MAP, and f_BLS respectively (Fig. 3b–d).

The f_ML estimator assigns t_e to the peak of the likelihood function (Fig. 4a). In our model, with a Gaussian-distributed measurement noise and a constant Weber fraction, t_e would be proportional to t_m (see Methods). The f_MAP and f_BLS estimators, on the other hand, rely on the posterior distribution, which is proportional to the product of the prior distribution and the likelihood function. Because the prior distribution we used was uniform, the posterior was a scaled replica of the likelihood function within the domain of the prior and zero elsewhere. The MAP rule extracts the mode of the posterior, which would correspond to the peak of the likelihood function except when the peak falls below/above the prior distribution’s shortest/longest sample interval. Thus, f_MAP is the same as f_ML with the difference that its range is limited to the domain of the prior (Fig. 4b). For BLS, which is associated with the mean of the posterior, the estimator, f_BLS, is a sigmoid function of t_m (Fig. 4c).

Figure 4.

ML, MAP and BLS estimators. The three panels schematically represent how ML, MAP and BLS estimates are computed respectively. Upward arrows in black and gray show two example sample intervals. Vertical dashed lines represent the noise-perturbed measurements associated with those sample intervals. Measured intervals differ from the corresponding samples as shown by the misalignment between the upward arrows and their corresponding vertical dashed lines. The likelihood functions associated with the two measurements are shown on far right of each panel (rotated 90 degree). These likelihood functions are plotted with respect to the measurements as shown by the reflection of the measured interval on the diagonal (horizontal dashed lines). (a) ML estimator. The peak of the likelihood function determines the estimate (filled circles, thick left arrow). The corresponding mapping function, f_ML, for all possible measurements is shown by the solid black line with the two example cases superimposed. Because the likelihood function is Gaussian and centered on the measurements, this function is the identity function. (b) MAP estimator. On the right side of the panel, the posterior distributions (truncated Gaussian functions) for the two measurements are computed by multiplying their associated likelihood functions by the prior (gray bar chart). MAP estimates are computed from the mode of the posterior (filled circles). The corresponding mapping function, f_MAP, is the identity function limited by the domain of the prior. (c) BLS estimator. Same as panel b except that for BLS, the mean of the posterior determines the estimate. The resulting mapping function, f_BLS, is sigmoidal in shape.

Note that since the specification of these estimators does not invoke any additional free parameters, the observer model associated with each estimator was fully characterized by two free parameters only: w_m and w_p.

Comparing experimental data with the observer model

Our psychophysical data consisted of pairs of sample intervals and production times (t_s and t_p), but the observer model we created to relate t_s to t_p relies on two intervening and unobservable (hidden) variables, t_m and t_e. We thus expressed these two hidden variables in terms of their probabilistic relationship to the observable variables t_s and t_p (see Methods), and derived a direct relationship between production times and sample intervals. This formulation was then used to examine which of the three observer models described human subjects’ responses best.

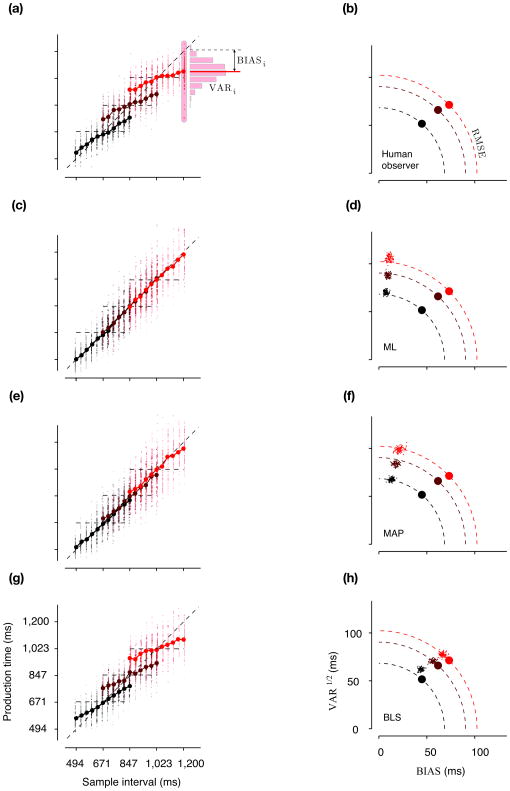
To compare human subjects’ responses to those predicted by the observer models, we quantified production times with two statistics, their variance (VAR), and their bias (BIAS) (Fig. 5a), which together partition the overall root mean squared error (RMSE) as follows:

$${\text{RMSE}}^2=\text{VAR}+{\text{BIAS}}^2$$

Figure 5.

Time reproduction behavior in humans and model observers. (a) For each sample interval (referred to by subscript i) in each prior condition, we computed two statistics: BIAS_i and VAR_i. BIAS_i is the average difference between the production times and the sample interval, and VAR_i as the corresponding variance. As an example, the plots shows how the BIAS_i and VAR_i were computed for the largest sample interval associated with the “Long” prior condition for one subject (same format as in Fig. 2). For this distribution of production times (histogram), BIAS_i is the difference between the solid horizontal red line and the horizontal dashed line, and VAR_i is the corresponding variance. For each prior condition, we computed two summary statistics: BIAS is the root mean square of BIAS_i, and VAR as the average of VAR_i across sample intervals. (b) VAR^1/2 versus BIAS for three prior conditions for the same subject as in panel a. On a plot of VAR^1/2 against BIAS, the locus of a constant root-mean-square-error (RMSE) value is a quarter circle. Dashed quarter circles show the loci of RMSE values associated with the VAR^1/2 and BIAS derived from the subject’s production times. (c) Simulated production times from the best-fitted ML model to the data in a. (d) The scatter of VAR^1/2 and BIAS of the best-fitted ML model for three prior conditions (small dots) computed from 100 simulations like the one shown in c. The VAR^1/2 and BIAS of the subject are plotted for comparison (same as in b). (e,f), and (g,h) are in the same format as in (c,d) and show results for the best-fitted MAP and BLS models respectively. Color conventions are the same as in Fig. 1b.

This relationship, which highlights the familiar trade off between the VAR and BIAS, when written as the sum of squares, becomes the standard equation of a circle:

$${\text{RMSE}}^2={{\text{(VAR}}^{\text{1}/\text{2}}\text{)}}^{\text{2}}+{\text{BIAS}}^2$$

This geometric description indicates that in a plot of VAR^1/2 versus BIAS, a continuum of values along a quarter circle would lead to the same RMSE (Fig. 5b). It also provides a convenient graphical description for how a larger RMSE represented by a quarter circle with a larger radius may arise from increases in VAR^1/2, BIAS or both. We used this plot to summarize the statistics of production times, and also to evaluate the degree to which different observer models could capture those statistics.

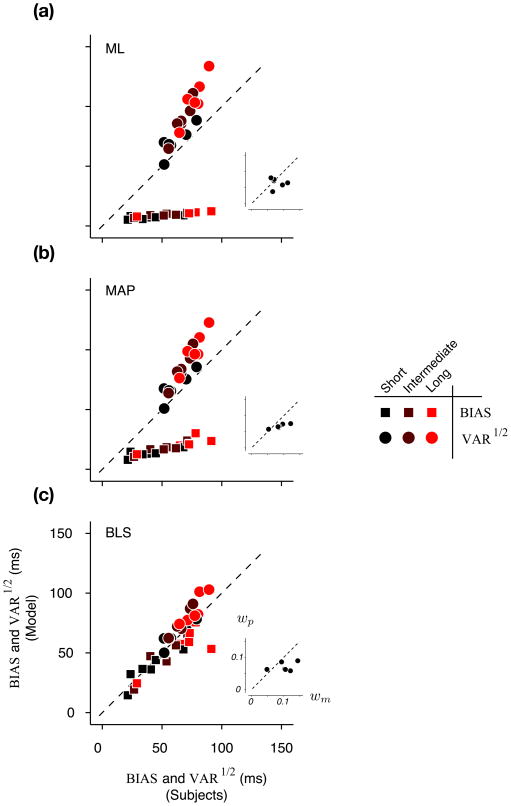
We fitted the parameters of the ML, MAP and BLS models (w_m and w_p) for each subject, based on the production times in the three prior conditions (Fig. 6a–c inset). We then simulated each subject’s behavior using the fitted observer models, and compared each model’s predictions to the actual responses using the BIAS, VAR^1/2, and RMSE statistics (Fig. 5c,e,g).

Figure 6.

Time reproduction behavior in humans and model observers – model comparison. (a) Average BIAS (squares) and VAR^1/2 (circles) computed from 100 simulations of the best-fitted ML model as a function of BIAS and VAR^1/2 computed directly from psychophysical data for all 6 subjects and all 3 prior conditions. The inset shows the Weber fraction of the measurement and production noise (w_p versus w_m) of the best-fitted ML model for the six subjects. (b,c) Same as in a for the MAP, and BLS models respectively. In each panel, each subject contributed 6 data points; i.e. 3 prior condition (black, dark red, and light red) × 2 metrics (BIAS and VAR^1/2).

The ML model did not exhibit the prior-dependent biases present in production times (Fig. 5c,d), because the ML estimator does not take the prior into account. This failure cannot be attributed to an unsuccessful fitting procedure or a misrepresentation of the likelihood function. The fact that subjects’ production times depended on the prior condition would render any estimator that neglects the prior (e.g. ML) inadequate, the parametric form of the likelihood function notwithstanding. The MAP model was slightly better than the ML model at capturing the trade-off between BIAS and VAR (Fig. 5e,f), but it also underestimated the bias of the production times and overestimated their variance for all subjects (Fig. 6b). The BLS model on the other hand, mimicked the bias and variance of the production times quite well (Fig. 5g). It captured the overall RMSE as well as the trade off between the VAR and the BIAS (Fig. 5h), and was statistically superior to both ML and MAP estimators across our subjects (Fig. 6c).

We evaluated several variants of the BLS model by incorporating different assumptions concerning the measurement and production noise. In our main model (Fig. 4c), we fit Weber fractions for both sources of noise (w_m and w_p), consistent with the observation that, for all subjects, the standard deviation of the production times was roughly proportional to the mean (Supplementary Fig. S4). We also considered the possibility that the standard deviation of either the measurement noise or the production noise scales with the base interval, whereas the other noise source has constant standard deviation (Supplementary Table S2). For all subjects, the original BLS model outperformed the model in which the measurement noise had a constant standard deviation, and for 5 out of 6 subjects, it outperformed the alternative in which the production noise had a constant standard deviation (Akaike Information Criterion, Supplementary Table S1). Moreover, a BLS model in which Weber fractions were assumed identical (w_m= w_p) was inferior to the original BLS model (log likelihood ratio test for nested models; p< 0.03 for one subject and p<1e–7 for others). The importance of the measurement and production Weber fractions in accounting for the bias and variability of production times was also evident in model simulations (Supplementary Fig. S5).

Because our observer models were described by two parameters only (w_m and w_p), and all models used the same number of parameters, we were reasonably confident that the success of the BLS rule was not due to over-fitting. Nonetheless, we tested for this possibility by fitting the model to data from the “Short” and “Long” prior conditions. The fits captured the statistics of the “Intermediate” prior condition equally well. Finally, we note that the fits for the BLS and MAP rules did not differ systematically (Fig. 6a–c, insets). Therefore, the success of the BLS model cannot be attributed to the constraints inherent to our fitting procedure, but rather to its superior description of the estimator subjects adopted in this task.

Discussion

Our central finding is that humans can exploit the uncertainty associated with measurements of elapsed time to optimize their timed responses to the statistics of the intervals they encounter. This conclusion is based on the success of a Bayesian observer model that accurately captured the statistics of subjects’ production times in a simple time reproduction task.

A characteristic feature of subjects’ production times was that they were systematically biased towards the mean of the distribution of sample intervals. This observation is consistent with the ubiquitous central tendency of psychophysical responses in categorical judgment and motor production^10–14. Previous work, such as the adaptation-level theory¹⁴, and range-frequency theory¹³ attributed these so-called range effects to subjects’ tendency to evaluate a stimulus based on its relation to the set of stimuli from which it is drawn. These theories, however, did not offer an explanation for what gives rise to such range effects in the first place, and whether or not they are of any value. In contrast, our work suggests that it is subjects’ (implicit) knowledge of their temporal uncertainty that determines the strength of the range effect. Moreover, the Bayesian account of range effects suggest that production time biases help — not harm — subjects’ overall performance (Supplementary Fig. S2,6). In what follows, we explain the novel aspects of our Bayesian model, and then discuss its implications for the neurobiology of interval timing.

Bayesian interval timing

Bayesian models have had great success in describing a variety of phenomena in vision and sensorimotor control^15–18, as well as interval timing^{19, 20}. Symptomatic to these models are prior-dependent biases whose magnitude increases for progressively less reliable measurements²¹. Motivated by the observation of such biases in our subjects’ behavior, and the success of a previous Bayesian model of coincidence timing¹⁹, we set out to formulate a Bayesian model for time reproduction.

The model consisted of three stages. The first stage emulated a noisy measurement process that quantified the probabilistic relationship between the sample intervals and the corresponding noise-perturbed measurements²². In the second stage, a Bayesian estimator computed an estimate of the sample interval from the measurement. Finally, a noisy production stage converted estimates to production times^{23, 24}. In line with previous work on interval timing, the measurement and production noise exhibited scalar variability^{2, 3, 5, 7}.

The estimator in the second stage of the model defines a deterministic mapping of measurements to estimates, and its functional form is determined precisely from the likelihood function, the prior distribution, and the cost (loss) function. The success of a Bayesian estimator thus depends on how well the likelihood, the prior and the cost function are constrained.

In psychophysical settings, because sensory measurements are not directly accessible, the likelihood function must be inferred from behavior and suitable assumptions about the distribution of noise. For example, cue combination studies make the reasonable assumption that measurements are perturbed by additive zero-mean Gaussian noise, and infer the width of the likelihood function from psychophysical thresholds^{25, 26}. Alternatively, it is possible to model the likelihood function based on the uncertainty associated with external noise in the stimulus^{16, 27, 28}. We modelled the likelihood based on the assumption that the distribution of measurements associated with a sample interval was Gaussian, was centered on the sample interval and had a standard deviation that scaled with the mean (see Methods).

To tease apart the roles of the likelihood function and the prior, it is important to be able to vary them independently. To manipulate likelihoods, one common strategy is to control factors that change psychophysical thresholds, such as varying the external noise in the stimulus^{16, 27}. In our work, we exploited the scalar variability of timing to manipulate likelihoods. This property which arises from internal noise only and is known to hold across tasks and species^2–4 for the range of times we used¹⁰ allowed us to manipulate the likelihood function simply by changing the sample interval. To manipulate the prior independently, we collected data using three discrete Uniform prior distributions. The priors were partially overlapping so that certain sample intervals were tested for two or three different priors, which enabled us to evaluate the effect of the prior independent of the likelihood function.

To convert the posterior distribution to an estimate, we needed to specify the cost function associated with the estimator. We considered two possibilities: (i) a cost function that penalizes all erroneous estimates similarly, which corresponds the mode of the posterior (MAP), and (ii) a cost function that penalizes errors by the square of their magnitude, which corresponds to the mean of the posterior (BLS). We also considered a non-Bayesian ML estimator that ignores the prior altogether, and chooses the peak of the likelihood function for the estimate. To decide which of these estimators better described subjects’ behavior, it proved essential to consider both the bias and the variability of production times. This technique, which was originally introduced to estimate internal priors from psychophysical data²², provided a powerful constraint in the specification of the estimator’s mapping function.

We used our three-stage model to estimate the measurement and production Weber fractions, and to decide which of the three mapping rules (ML, MAP, or BLS) better captured production times²⁹. The ML estimator clearly failed to capture the pattern of prior-dependent biases evident in every subject’s production times, as expected from any estimator that neglects the prior. By incorporating the prior, both the MAP and BLS estimators exhibited contextual biases, but the BLS consistently outperformed the MAP model in explaining the trade off between the trial-to-trial variability and bias across our subjects (Fig. 6b,c). It is important to emphasize that, had we ignored the trial-to-trial variability, both BLS and MAP as well as a variety of other Bayesian models could have accounted for the prior-dependent biases in our data.

We also considered variants of the BLS model in which either the measurement or production noise were modelled as Gaussian with a fixed standard deviation (not scalar). Overall, our original model outperformed these alternatives (Supplementary Table S1) because the measurement and production Weber fractions played relatively independent roles in controlling the increasing bias and variance of production times with sample interval (Supplementary Fig. 5). The degrading effect of formulating noise with a fixed standard deviation was more severe for the measurement stage than it was for the production stage (Supplementary Table S1).

Despite the success of our modelling exercise, further validation is required to substantiate the role of a BLS mapping in interval timing. Four considerations deserve scrutiny. First, formulation of the likelihood function might take into account factors other than scalar variability that could alter measurement noise. For example, task difficulty or reinforcement schedule (Supplementary Fig. S3) could motivate subjects to pay more attention to certain intervals, and to measure them more reliably, which could in turn strengthen the role of the likelihood function relative to the prior. Therefore, it is important to consider attention and other related cognitive factors as an integral part of how the nervous system could balance the relative effects of the likelihood function and the prior. Second, knowledge of the prior is itself subject to uncertainty, and the internalized prior distribution may differ from the one imposed experimentally. Third, the feedback subjects receive is likely to interact with the mapping rule they adopt. Our feedback schedule did not encourage the use of BLS rule, but we cannot rule out the possibility that it influenced subjects’ behavior. Fourth, although the operation of a Bayesian estimator is formulated deterministically, its neural implementation is likely subject to biological noise. These different sources of variability must be parsed out before the estimator can be characterized definitively. These considerations, which concern all Bayesian models of psychophysical data, highlight the gap between ‘normative’ descriptions and their biological implementation.

We referred to our model as a Bayesian observer, and not a Bayesian observer-actor because our formulation was only concerned with making optimal estimates. But since the full task of the observer was to reproduce those estimated intervals, we can formulate a Bayesian observer-actor whose objective is to directly optimize production times, and not the intervening estimates. This model has to take into account both the measurement and production uncertainty and integrate them with prior to compute the probability of every possible pair of sample and production interval. It would then use this joint posterior to minimize the cost of producing erroneous intervals. The derivations associated with the Bayesian observer-actor model are more involved and beyond the scope of the present work. Yet, we note that under suitable assumptions, the two models would behave similarly (see Methods).

Context-dependent central timing

Our finding suggests that the brain takes into account knowledge of temporal uncertainty and adapts its time keeping mechanisms to temporal statistics in the environment. What neural computations may lead to such sophisticated behavior? One possibility is that the brain implements a formal Bayesian algorithm. For example, populations of neurons might maintain an internal representation of the prior distribution and the likelihood function, multiply them to represent a posterior and produce an estimate by approximating its expectation. Related variants of this scheme are also conceivable. For instance, our results could be accommodated by an ML strategy if the prior would exert its effect indirectly by changing the statistics of noise associated with measurements. Another more attractive possibility that obviates the need for explicit representations of the likelihood function and the prior is for the brain to learn the sensorimotor transformation that would map measurements onto their corresponding Bayesian estimates directly³⁰. This is what our observer model exemplifies: it establishes a deterministic nonlinear mapping function to directly transform measurements to estimates. Evidently, this form of learning must incorporate knowledge about (1) scalar variability, and (2) prior distribution.

Electrophysiological recordings from sensorimotor structures in monkeys have described computations akin to those our observer model utilizes. For instance, parietal association regions and subcortical neurons in Caudate have been shown to reflect flexible sensorimotor associations^{31, 32}. The time course of activity across sensorimotor neurons is believed to represent sensory evidence³³, its integration with the prior information³⁴, and the preparatory signals in anticipation of instructed and self-generated action^35–37. The importance of sensorimotor structures in time reproduction is further reinforced by their consistent activation in human neuroimaging studies that involve time sensitive computations^38–41.

A variety of models have been proposed to explain the perception and use of an interval of time. Information theoretic models attribute the sense of time to the accumulation of tics from a central clock^{11, 42, 43}; physiological studies have noted a general role for rising neural activity for tracking elapsed time in the brain^{36, 37, 44–48}, and biophysical models have been developed that suggest that time may be represented through the dynamics of neuronal network⁴⁹. Our work, which does not commit to a specific neural implementation, suggests that the internal sense of elapsed time in the sub-second to seconds range may arise from a plastic sensorimotor process that enables us to operate efficiently in different temporal contexts.

Methods

Psychophysical procedures

Six human subjects aged 19 to 40 yr participated in this study after giving informed consent. All had normal or corrected-to-normal vision, and all were naïve to the purpose of the experiment. Subjects viewed all stimuli binocularly from a distance of 52 cm on an 17-inch iiyama AS4311U LCD monitor at a resolution of 1024×768 driven by a Intel Macintosh G5 computer at a refresh rate of 85 Hz in a dark, quiet room.

In a “Ready-Set-Go” time reproduction task, subjects measured certain sample intervals demarcated by a pair of flashed stimuli, and reproduced those intervals by producing time-sensitive manual responses. Each trial began with the presentation of a central fixation point (FP) for 1 s, followed by the presentation of a warning stimulus at a variable distance to the left of the FP. After a variable delay ranging from 0.25 to 0.85 s drawn randomly from a truncated exponential distribution, two 100 ms flashes separated by the sample interval, t_s, were presented. The first flash, which signified the “Ready” stimulus, was presented at the same distance as the warning stimulus but to the right of the FP. The “Set” stimulus was presented t_s ms afterwards and 5 deg above the FP (Fig. 1a). Subjects were instructed to measure and reproduce the sample interval by pressing the space bar on the keyboard t_s ms after the presentation of the “Set”. Production times, t_p, were measured from the center of the “Set” flash (i.e. 50 ms after its onset) to when the key was pressed. When t_p was sufficiently close to t_s, the warning stimulus changed from white to green to provide positive feedback and encourage stable performance.

All stimuli were circular in shape and were presented on a dark grey background. Except for FP that subtended 0.5 deg of visual angle, all other stimuli were 1.5 deg. To ensure that subjects could not use the layout of the stimuli to adopt a spatial strategy for the time reproduction task (e.g. track an imaginary moving target), we varied the distance of the “Ready” and the warning stimulus from the FP on each trial (range 7.5 to 12.5 deg).

For each subject, three experimental conditions were tested separately. These conditions were the same in all respects except that, for each condition, the sample intervals were drawn from a different prior probability distribution. All priors were discrete Uniform distributions with 11 values, ranging from 494 to 847 ms for the “Short”, 671 to 1023 ms for the “Intermediate”, and 847 to 1200 ms for “Long” prior condition. Note that to help tease apart the effects of prior condition from sample interval, the priors were chosen to be partially overlapping.

For each subject, the order in which the three prior conditions were tested was randomized. For each prior condition, subjects were tested after they completed an initial learning stage. Learning was considered complete when the variance and bias of the production times had stabilized (less than 10% change between sessions). The main data for each prior condition were collected in two sessions after leaning for that condition was complete. Learning for each subsequent prior condition started after testing for the preceding prior condition was completed. For 5 out of 6 subjects, the learning was completed by the end of the first session (less than 10% change between first and second sessions). For one subject, learning of the first prior condition was completed after 4 sessions. For this subject, the 5^th and 6^th sessions provided data for the first prior condition. For the other two prior conditions, similar to other subjects, responses stabilized after one practice session. All subjects typically participated in 3 sessions per week, and each sessions lasted ~45 minutes (i.e. nearly 500 trials).

Subjects received positive feedback for responses that fell within a specified window around t_s (i.e., “correct” trials). To compensate for the increased difficulty associated with longer sample intervals – a natural consequence of scalar timing variability^2–4 – the width of this window was scaled with the sample interval with a constant of proportionality, k. To ensure that the performance was comparable across different prior conditions, the value of k was controlled by an adaptive one-up one-down procedure which added/subtracted 0.015 to/from k for each “miss”/“correct” trial. As such, every subject’s performance for every session yielded approximately 50% positively reinforced trials (mean = 51.7%; std=1.33%). For each prior condition, the maximum (minimum) number of “correct” trials corresponded to the intermediate (extreme) sample intervals (Supplementary Fig. S3).

The Bayesian estimator

The noise distribution associated with the measurement stage of the model, determines the distribution of t_m for a given t_s, p(t_m|t_s). From the perspective of the observer who makes a measurement t_m but does not know t_s, this relationship becomes a function of t_s known as the likelihood function, λ_tm(t_s) ≡ p(t_m|t_s) in which t_m is fixed. We modelled p(t_m|t_s) as a Gaussian distribution with mean t_s, and standard deviation w_mt_s that scaled linearly with t_s (scalar variability) with a constant coefficient of variation, w_m.

$${\lambda }_{t_m}(t_s)\equiv p(t_m\mid t_s)=\frac{1}{\sqrt{2\pi {(w_m{t}_s)}^2}}{e}^{\frac{-{(t_s-t_m)}^2}{2{(w_m{t}_s)}^2}}$$ (1)

Similarly, the production noise distribution, p(t_p|t_e), was assumed to be Gaussian with zero mean and a constant coefficient of variation, w_p:

$$p(t_p\mid t_e)=\frac{1}{\sqrt{2\pi {(w_p{t}_e)}^2}}{e}^{\frac{-{(t_p-t_e)}^2}{2{(w_p{t}_e)}^2}}$$ (2)

To simplify derivations, we modelled the discrete uniform prior distributions used in the experiment as continuous. For each prior condition, we specified the domain of sample intervals between $t_s^{min}$ and $t_s^{max}$ based to the minimum and maximum values used in the experiment.

$$\pi (t_s)=\{\begin{array}{ll}\frac{1}{t_s^{max}-t_s^{min}}\hfill & \text{for}{t}_s^{min}\le t_s\le t_s^{max}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (3)

The resulting posterior, π(t_s|t_m), is the product of the prior multiplied by the likelihood function and appropriately normalized:

$$\pi (t_s\mid t_m)=\frac{\pi (t_s)p(t_m\mid t_s)}{\int \pi (t_s)p(t_m\mid t_s){dt}_s}=\{\begin{array}{ll}\frac{p(t_m\mid t_s)}{{\int }_{t_s^{min}}^{t_s^{max}}p(t_m\mid t_s)d{t}_s}\hfill & \text{for}{t}_s^{min}\le t_s\le t_s^{max}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (4)

The Bayesian estimator computes a single estimate, t_e, from the posterior by considering an objective cost function, l(t_e, t_s), that quantifies the cost of erroneously estimating t_s as t_e. The Bayesian estimate minimizes the posterior expected loss, which is the integral of the cost function for each t_s, weighted by its posterior probability, π(t_s|t_m):

$$t_e=f_l(t_m)=\underset{t_e}{argmin}\left[\int l(t_e,t_s)\pi (t_s\mid t_m)d{t}_s\right]$$ (5)

Notice that the optimal estimate, t_e, is a deterministic function of the measured sample, f_l(t_m) in which the subscript l reflects the particular cost/loss function.

For the ML model, the estimator f_ML(t_m ) is associated with the sample interval that maximizes the likelihood function, which can be derived from Equation (1):

$$f_{ML}(t_m)=\underset{t_s}{argmax}{\lambda }_{t_m}(t_s)=t_m\left[\frac{-1+\sqrt{1+4w_m^2}}{2w_m^2}\right]$$ (6)

The ML estimate is proportional to measurement. For a plausible range of values for w_m, the constant of proportionality would be less than one, and thus the ML would systematically underestimate the sample. For instance, for 0.1< w_m < 0.3, the constant of proportionality would vary between 0.99 and 0.92.

For the MAP rule, the cost function is −δ(t_e−t_s), where δ(.) denotes the Dirac delta function. The corresponding estimator function, f_MAP(t_m ), is specified by the mode of the posterior as follows:

$$f_{\mathit{MAP}}(t_m)=\underset{t_s}{argmax}\pi (t_s\mid t_m)=\{\begin{array}{lll}{t}_s^{min}\hfill & \text{for}\hfill & t_s\le t_s^{min}\hfill \\ f_{ML}(t_m)\hfill & \text{for}\hfill & t_s^{min}\le t_s\le t_s^{max}\hfill \\ t_s^{max}\hfill & \text{for}\hfill & t_s\ge t_s^{max}\hfill \end{array}$$ (7)

For the BLS rule, the cost function is the squared error, (t_e−t_s)², and the estimator function, f_BLS(t_m) corresponds to the mean of the posterior:

$$f_{\mathit{BLS}}(t_m)=\frac{{\int }_{t_s^{min}}^{t_s^{max}}{t}_{s}p(t_m\mid t_s)d{t}_s}{{\int }_{t_s^{min}}^{t_s^{max}}p(t_m\mid t_s)d{t}_s}$$ (8)

The Bayesian observer model

The Bayesian estimator specifies a deterministic mapping from a measurement, t_m to an estimate, t_e. But our psychophysical data consists of pairs of sample interval, t_s and production time, t_p. Accordingly, we augmented the estimator with a measurement stage and a production stage, which together with the estimator, provide a complete characterization of the relationship between t_s and t_p. The model however relies on two intermediate variables t_m and t_e that are psychophysically unobservable (i.e. hidden variables). To remove these variables from the description of the model, we took advantage of a trick common to Bayesian inference, which is to integrate out the hidden variables (i.e. marginalization). Specifically, using the chain rule, we decomposed the joint conditional distribution of variables t_m, t_e, and t_p to three intervening conditional probabilities:

$$p(t_p,t_e,t_m\mid t_s,w_m,w_p)=p(t_p\mid t_e,t_m,t_s,w_m,w_p)p(t_e\mid t_m,t_s,w_m,w_p)p(t_m\mid t_s,w_m,w_p)$$ (9)

We used the serial architecture of our model (Fig. 3a) to simplify the dependencies in the right hand side of Equation (9). In the first term, because the conditional probability of t_p is fully specified by t_e and w_p (from Equation (2)), we can safely omit the other conditional variables (t_m, t_s and w_m). In the second term, the only relevant conditional variable is t_m since it specifies t_e deterministically. And for the third term, w_p has no bearing on t_m. Incorporating these simplifications, the joint conditional distribution can be rewritten as follows:

$$p(t_p,t_e,t_m\mid t_s,w_m,w_p)=p(t_p\mid t_e,w_p)p(t_e\mid t_m)p(t_m\mid t_s,w_m)$$ (10)

Moreover, because t_e is a deterministic function of t_m; i.e., t_e= f(t_m), the conditional probability p(t_e|t_m ) can be written as a Dirac delta function as follows:

$$p(t_p,t_e,t_m\mid t_s,w_m,w_p)=p(t_p\mid t_e,w_p)\delta \left[t_e-f(t_m)\right]p(t_m\mid t_s,w_m)$$ (11)

We can eliminate the dependence on the two hidden variables t_m and t_e by marginalization:

$$\begin{array}{l}p(t_p\mid t_s,w_m,w_p)=\iint p(t_p,t_e,t_m\mid t_s,w_m,w_p)d{t}_{m}d{t}_e\\ =\iint p(t_p\mid t_e,w_p)\delta \left[t_e-f(t_m)\right]p(t_m\mid t_s,w_m)d{t}_{m}d{t}_e\\ =\int p(t_p\mid f(t_m),w_p)p(t_m\mid t_s,w_m)d{t}_m\end{array}$$ (12)

The integrand is the product of the conditional probability distributions associated with the measurement and production stages. By substituting these distributions from Equations (1) and (2), and f(t_m) from Equation (6), (7), or (8) (depending on the estimator of interest), Equation (12) provides the conditional probability of t_p for a given t_s as a function of the model parameters, w_m and w_p.

The Bayesian observer-actor model

The observer model described in the previous section obtains an estimate that minimizes a cost built around the estimate and the actual time interval. It was formulated to minimize the expected loss associated with erroneous estimates, not production times. A more elaborate Bayesian “observer-actor” model would seek to minimize expected loss with respect to the ensuing production times (and not the intervening estimates). This elaboration demands two considerations. First, the uncertainty associated with both the measurement and the production phases must be taken in to account. As such, the relevant probability distribution would be the joint posterior of the sample interval and production time conditioned on the measurement, π(t_p, t_s|t_m). Second, the definition of the cost function should concern the sample interval and production time; i.e., l(t_p, t_s). The appropriate posterior expected loss could then be minimized as follows:

$$t_e=f_l(t_m)=\underset{t_e}{argmin}\left[\iint l(t_p,t_s)\pi (t_p,t_s\mid t_m)d{t}_{s}d{t}_p\right]$$ (13)

The Delta and least squares cost functions in this optimization problem do not correspond to the mode and mean of the joint posterior, and derivation of the optimal solution is more involved and beyond the scope of this manuscript. Nonetheless, we note that the corresponding estimators for the Bayesian observer-actor are qualitatively similar to those we derived for the MAP and BLS mapping rules in our simplified Bayesian observer model.

Fitting the model to the data

We assumed that t_p values associated with any t_s were independent across trials, and thus expressed the joint conditional probability of individual t_p values across all N trials, and across the three prior conditions, by the product of their individual conditional probabilities:

$$p(t_p^1,t_p^2,t_p^3,\text{K},t_p^N\mid t_s,w_m,w_p)=\prod _{i=1}^{N}p(t_p^i\mid t_s,w_m,w_p)$$ (14)

The products change to sums by taking the logarithm of both sides:

$$logp(t_p^1,t_p^2,t_p^3,\text{K},t_p^N\mid t_s,w_m,w_p)=\sum _{i=1}^{N}logp(t_p^i\mid t_s,w_m,w_p)$$ (15)

Each term in the sum was derived from Equation (12), after substituting f(t_m) with the appropriate estimator function (Equation (6), (7) or (8)).

We used this equation to maximize the likelihood of model parameters, w_m and w_p, across all t_s and t_p values measured psychophysically. The maximization was done using ‘fminsearch’ command in MATLAB software, which incorporates the Nelder-Mead downhill simplex optimization method. Integrals of Equations (8) and (12) are not analytically solvable and were thus approximated numerically using the trapezoidal rule. We evaluated the success of the fitting exercise by repeating the search with different initial values; the likelihood function near the fitted parameters was highly concave, and the fitting procedure was stable with respect to initial values.