Abstract
Background
Exercise and QT dynamics during ambulatory monitoring impact mortality in a variety of populations. Heart rate recovery (HRR) after exercise is a known strong predictor of mortality.
Objective
We assessed the independent, prognostic significance of the QT response to changing heart rate (QT dynamics) during recovery from exercise.
Methods
The cohort included patients referred for treadmill exercise stress over a 5 year period. Patients had to have at least 4 ECG tracings within 5 minutes of peak exercise. One had to be recorded 60 seconds into recovery to calculate the HRR. Linear regression of the QT-RR relation during recovery was used to predict QT interval at cycle lengths of 500 and 600 ms (QT-500 and QT-600). Only studies with an R2≥0.9 (72%) were retained. Optimal binary cutpoints were chosen. All-cause mortality was determined from either the Social Security death index or hospital records.
Results
2,994 patients met inclusion criteria. 228 (7.6%) died during an average follow-up of 7.6±1.9 years. Abnormal QT-500 (>316 ms) was the strongest univariate QT dynamics predictor in a Cox proportional hazards model (hazard ratio=2.13, p<0.001). It remained an independent predictor of mortality after adjustment for age, exercise capacity, medications, SPECT defects, and abnormal (<12 bpm) HRR (hazard ratio=1.46, p=0.014).
Conclusions
An abnormal predicted QT interval at 500 ms (120 beats/min) during recovery from exercise independently predicts all-cause mortality. Because QT dynamics in recovery incorporates information on both repolarization and autonomic responsiveness, its role in risk prediction for sudden cardiac death should be further explored.
Keywords: QT dynamics, mortality, exercise stress test, heart rate recovery, prognosis
INTRODUCTION
SCD remains a major cause of mortality with an estimated 184,000 to 462,000 cases occurring annually in the United States.1 Although patients with marked left ventricular dysfunction have the highest risk of SCD, they represent only a minority of the total.2 Even within populations for whom ICD devices have been shown to improve survival,3 many patients treated with an ICD do not experience SCD.4 Given the cost, procedural risk, and complications associated with ICDs, a continued need exists to improve the identification of individuals at increased risk for SCD.
Exercise and the post-exercise recovery period are associated with a markedly increased relative risk of SCD, ranging from 11 in individuals who regularly exercise to 74 in those who do not.5 Dramatic physiologic changes occur during this time, with sympathetic excitation and parasympathetic withdrawal during exercise and then their reversal during recovery. One-minute HRR is a simple index that is reflective of these changes and has been shown to be highly predictive of mortality.6
Prolongation of the QT interval in normal7 and diseased8 populations without the long QT syndrome carries prognostic information. The QT interval varies with heart rate, requiring correction using a variety of proposed formulae that all have significant limitations.9 Characterizing the rate dependence of the QT interval by measuring the slope of the QT interval versus the RR interval as it varies naturally, so-called QT dynamics, during ambulatory monitoring has been shown to predict all-cause and arrhythmic death.10
Emerging data suggests that QT dynamics during recovery from exercise may provide an integrative measure of autonomic balance under conditions of stress.11 Because of the increased risk of death during and after the exercise period5 and the risk imparted by abnormal QT dynamics during ambulatory monitoring,10 we hypothesized that abnormal QT dynamics during exercise recovery would independently predict all-cause mortality.
METHODS
Patient population and clinical data
The Institutional Review Board approved this study. An historical cohort was drawn from consecutive patients referred for a treadmill exercise stress study with SPECT imaging. Inclusion criteria were age at least 18 years, a study performed between August 1998 and December 2003 (to ensure availability of archived and decipherable digitized ECG waveforms), 4 ECG tracings within 5 minutes of peak exercise (in addition to 1 at peak exercise), and 1 ECG tracing recorded 60 seconds into recovery (to compute the HRR6). Exclusion criteria were missing demographic information, a prior included study (only the first of multiple studies was included), or an increase in heart rate of more than 10% between serial tracings during recovery.
Demographic, clinical, and Bruce protocol variables were recorded. In contrast to prior work,6 our exercise laboratory does not employ a formal two minute cool-down period, although patients continue on the treadmill for approximately 30 seconds after peak exercise before the belt stops. There is no laboratory policy to continue or discontinue beta-blocker medications uniformly, and this decision is left to the referring physician. Rest, stress, and recovery 12-lead ECGs were interpreted using standard criteria.12
The vast majority of SPECT studies used a single-day dual isotope protocol.13 Rest images were acquired using intravenous thallium-201, and stress images with technetium-99m sestamibi. A minority of studies used a two-day, high dose Tc-99m sestamibi protocol in patients over 350 pounds to improve image quality. Images were interpreted using a 20-segment scoring system in which 0=normal tracer activity and 4=no tracer activity.13 Total scores for the stress and rest images determined the SSS and SRS, respectively. The majority of stress SPECT images was ECG-gated to yield the EF, although arrhythmia limited gating in a minority.
QT dynamics
ECG waveforms in digital format were extracted from our Marquette MUSE database using custom software. Tracings provide 10 seconds of data in standard 12-lead arrangement, giving 4 groups of 3 simultaneous leads with 2.5 seconds of data each. Marquette software records the heart rate, from which the RR interval in milliseconds (ms) was calculated.
Automated QRS onset was detected using single lead data via the auxiliary signal method.14 Two QRS onsets detected within 200 ms of each other were assumed to represent the same QRS complex and were treated as such. Automated T wave offsets were determined by using the publicly available ECGPUWAVE.15 For each set of 3 simultaneous leads (I, II, and III, for example), 2 were chosen for analysis by ECGPUWAVE. Leads I, aVL, V1, and V6 were not used in an attempt to provide the algorithm with uniphasic and high-amplitude T waves. Two T wave offsets detected within 300 ms of each other were assumed to represent the same T wave and were treated as such. QT intervals were calculated as differences between the QRS onset and T wave offset for each beat. The QT interval for the ECG tracing as a whole was taken as the average of the 25th and 75th percentile of all intervals. Tracings from 30 patients (total of 150 tracings) were analyzed manually for QRS onset and T wave offset. QT intervals from these tracings were compared to QT intervals determined by the automated QRS onset and T wave offset.
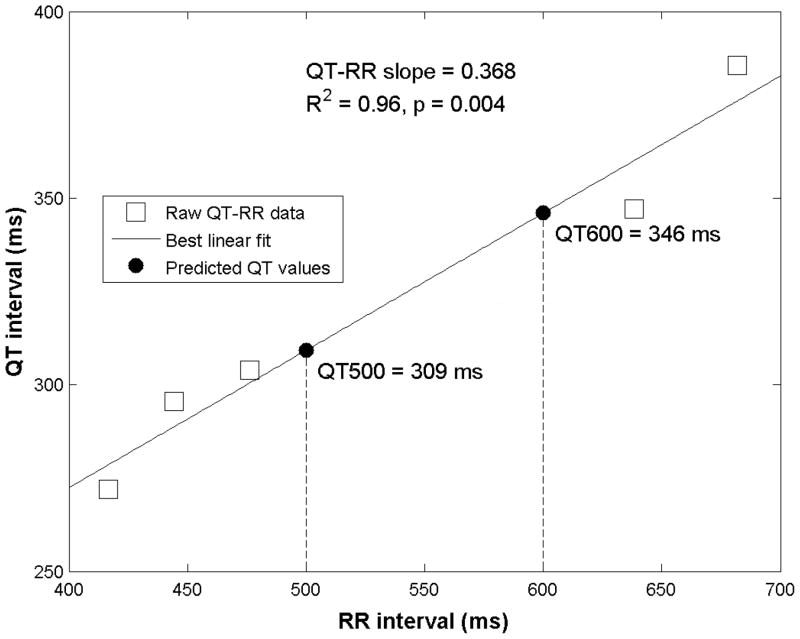
Linear regression analysis was performed on the QT-RR interval pairs (minimum of 5) obtained at peak exercise and during recovery for each subject. The QT-RR relationship has often been characterized by the slope.10 However, this characterization is less complete as it excludes the intercept.11 To incorporate both components of the QT-RR relationship and provide standardized QT intervals that could be evaluated in the population, predicted QT intervals were calculated from the linear regression formula for cycle lengths of 500 ms (QT-500) and 600 ms (QT-600), corresponding to heart rates in the 100–120 bpm range, using individual slope and intercept results from the regression analysis. QT-500 and QT-600 were defined as: QT-500 (or -600)=intercept + slope × 500 (or 600) ms.
Figure 1 shows raw data, results of the linear regression analysis, and the calculated QT-500 and QT-600 values for an individual patient from our cohort.
Figure 1.
Example of QT-RR analysis for an individual patient
The QT-RR relationship in recovery is highly linear with a mean R2 value approaching 0.9.11 Because this is the initial evaluation of QT dynamics in recovery for prognosis, to maximize the specificity of the results our primary analysis incorporated only studies with R2≥0.9 and a positive QT-RR slope. However, a second analysis using R2≥0.7 was performed to determine the robustness of the findings.
Using the peak exercise tracing and the tracing recorded at 60 seconds, HRR was calculated as the difference between the two heart rates.
Survival
All-cause mortality was determined from either the Social Security Administration’s Death Master File16 or our hospital records of inpatient mortality. Length of survival was computed as the number of days between the treadmill exercise stress test and the date of death or the end of December 2008, whichever came first.
Statistical analysis
All statistical tests were performed using STATA version 10.1 (StataCorp, College Station, Texas). The primary analysis for this study evaluated the QT-RR slope, QT-500, and QT-600. Our methods sought to facilitate exploratory data analysis, as these variables have no established cutoff values. Therefore, each variable was optimally dichotomized into normal and abnormal groups by maximizing the log likelihood ratio from a Cox proportional hazards model with the limitation that each subgroup had at least 10% of the cohort.17 This dichotomization simplified tabular, graphical, and statistical comparison of abnormal versus normal subgroups, which seemed most appropriate for this initial exploration of these novel parameters. We also sought to maintain physiologic applicability, as the QT dynamics variables are derived from the slope and intercept values obtained by linear regression. Therefore the arbitrary, but physiologically motivated, QT-500 and QT-600 were employed instead of entering both QT-RR slope and intercept as separate variables into models.
Of these variables, QT-500 proved to be most predictive. An exploratory Cox model with both QT-RR slope and intercept determined their optimal weighting. This showed both variables to be simultaneously significant (p<0.001) with an optimal weighting corresponding to a cycle length of 487 ms, further supporting the choice of QT-500. The data are therefore displayed by normal or abnormal QT-500 subgroups.
Continuous variables were compared using a t-test. Categorical variables were compared using the chi-square or Fisher exact test. The unadjusted incidence of all-cause death used the incidence density, as follow-up differed for each patient. A Kaplan-Meier survival analysis by QT-500 and HRR subgroups used the log-rank test. All applicable tests were two-tailed, and a p<0.05 was considered to be statistically significant.
A Cox proportional hazards model used abnormal QT-500 and then added abnormal HRR. More complex model building proceeded by first identifying all important (p<0.25) univariate predictors for inclusion in a preliminary effects model. Abnormal QT-500 and HRR were also included due to their centrality to our hypothesis. This multivariable model was then reduced in a backward elimination fashion by only retaining variables that remained significant (p<0.05) in the composite model, in addition to abnormal QT-500 and HRR. Schoenfeld residuals tested the assumption of proportional hazards and found no significant deviation in any model.
Cross validation using random subsets was performed to test reproducibility. For each repetition, the entire cohort was randomly split into two distinct cohorts of equal size. The first (derivation) cohort was used to select optimal, binary cutoffs for QT-500 and HRR using the technique described above. These cutoffs were then applied to the second (validation) cohort to build univariate and multivariable models using the technique described above. In total 100 repetitions were performed, and optimal cutoffs as well as univariate and multivariable hazard ratios for QT-500 and HRR were recorded. These distributions were examined using mean±standard deviation. The frequency of p<0.05 for the hazard ratios was recorded for QT-500 and HRR.
RESULTS
Cohort selection and mortality
Between August 1998 and December 2003, our laboratory performed 12,780 stress SPECT studies. Of these, 6,768 (53.0%) utilized treadmill exercise stress. Further studies were excluded: 2,257 who did not have an ECG tracing at 60 seconds or fewer than 4 tracings within 5 minutes of peak exercise or whose heart rate increased by more than 10% between serial tracings, 284 repeat studies on patients already included, 22 with missing social security numbers, 68 with missing demographic information, 6 under 18 years of age, and 3 whose QT-RR slope was negative. Of the remaining 4,128 studies, 1,134 had least squares regression R2<0.9 and were not included in the primary analysis.
The final cohort consisted of 2,994 patients, which represented 44.2% of all treadmill exercise studies during this period. A total of 228 deaths (7.6%) occurred over an average of 7.6±1.9 years of follow-up. Only 34 patients (1.1%) reported taking an antiarrhythmic medication. A chart review found 39 patients (1.3%) had an ICD upon entry into the cohort.
QT interval algorithm
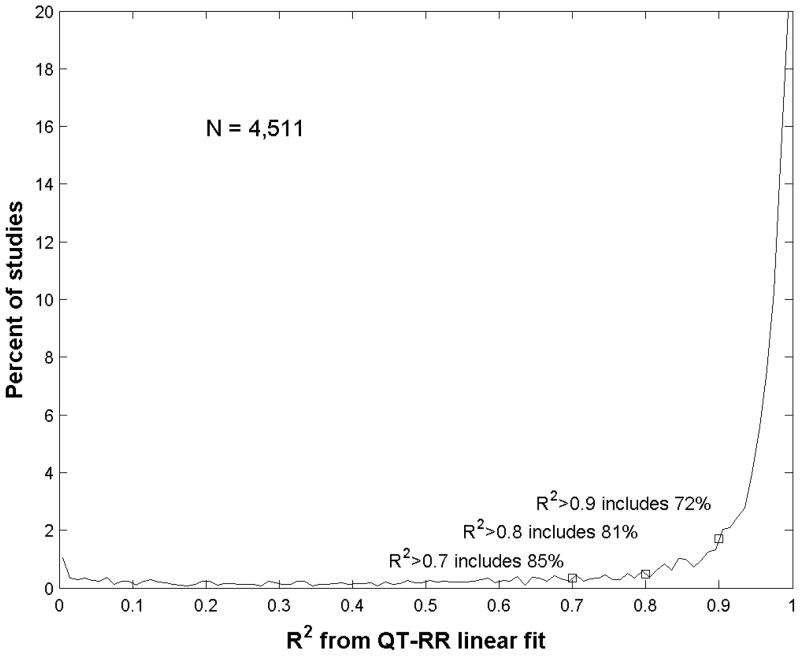
A total of 150 tracings were processed both manually and in automated fashion. Automated QT interval measurements agreed with manual measurements with an overestimation of less than 2% (QT_automated = 1.015 * QT_manual, R2=0.998, p<0.01). Figure 2 shows the cumulative distribution of R2 values for a linear fit to the QT-RR relationship, including all 4,511 studies as above. The vast majority have a QT-RR relationship accounted for in large part by a linear model: 85% had an R2>0.7 and 72% had an R2>0.9.
Figure 2.
Histogram of R2 distribution for QT-RR fit by linear model
Univariate QT dynamics predictors
Table 1 summarizes the results of QT dynamics and HRR univariate predictors and provides their optimal cutpoints. Our HRR cutoff of <12 bpm is nearly identical to the cutoff of ≤12 bpm presented in the original study of its prognostic power.6
Table 1.
Binary QT dynamics and HRR predictors
| Kaplan-Meier | Cox proportional hazards | |||||
|---|---|---|---|---|---|---|
| Variable | Abnormal cutpoint | p by log-rank | χ2 | Hazard Ratio | 95% CI | p |
| QT at 500 ms | >316 ms | <0.0001 | 28.1 | 2.13 | 1.60–2.84 | <0.001 |
| QT at 600 ms | >354 ms | <0.0001 | 17.1 | 1.78 | 1.35–2.35 | <0.001 |
| QT-RR slope | <0.292 | 0.0001 | 15.7 | 1.85 | 1.36–2.52 | <0.001 |
| HRR | <12 bpm | <0.0001 | 64.8 | 2.99 | 2.26–3.96 | <0.001 |
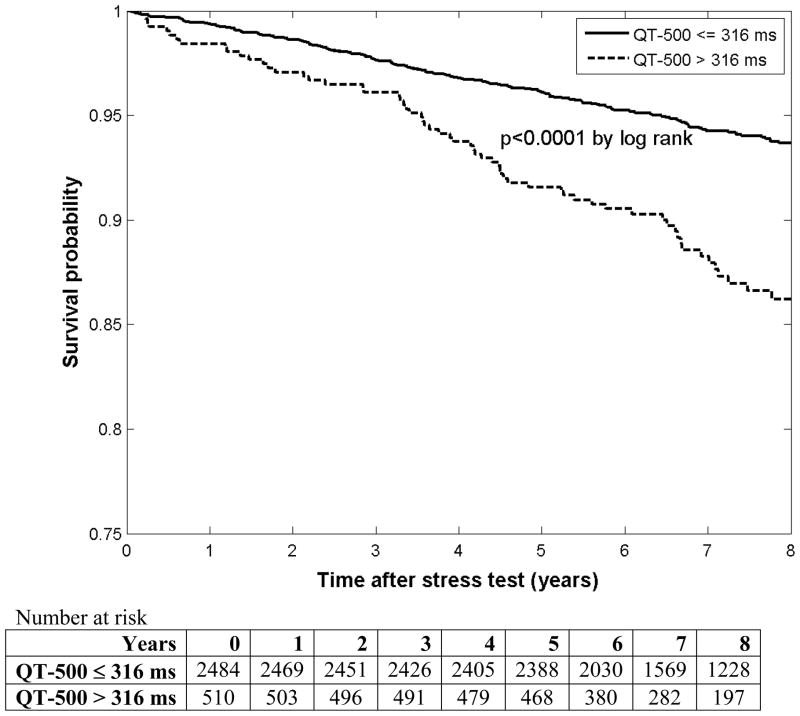
While all QT dynamics variables were significant predictors of survival by both models, QT-500 had the largest hazard ratio so it was selected as the best single variable to represent QT dynamics in our population. Figure 3 shows Kaplan-Meier survival curves for QT-500 subgroups, demonstrating poorer survival among those with a longer QT-500.
Figure 3.
Kaplan-Meier survival curves by QT-500 subgroups
Table 2 shows baseline characteristics for the entire cohort and by QT-500 subgroup. In general, abnormal QT-500 status associates with markers of worse prognosis. Table 3 details the outcomes by QT-500 quartile. Note that the mortality increase clusters in the highest quartile, suggesting an abnormal threshold below which QT-500 has a smaller prognostic gradient.
Table 2.
Clinical features by QT-500 subgroup
| All | QT-500≤316 ms | QT-500>316 ms | p | |
|---|---|---|---|---|
| N | 2,994 | 2,484 | 510 | N/A |
| QT at 500 ms | 305 ± 16 | 300 ± 11 | 330 ± 14 | N/A |
| QT at 600 ms | 344 ± 20 | 338 ± 14 | 372 ± 19 | <0.0001 |
| QT-RR slope | 0.387 ± 0.105 | 0.381 ± 0.087 | 0.419 ± 0.165 | <0.0001 |
| Age (years) | 56.1 ± 11.6 | 55.8 ± 11.5 | 57.5 ± 12.3 | 0.0041 |
| Male | 1763 (58.9%) | 1484 (59.7%) | 279 (54.7%) | 0.035 |
| BMI (kg/m2)* | 28.5 ± 6.0 | 28.2 ± 5.8 | 29.6 ± 6.7 | <0.0001 |
| Diabetes | 380 (12.7%) | 264 (10.6%) | 116 (22.7%) | <0.001 |
| Family history of CAD | 759 (25.4%) | 641 (25.8%) | 118 (23.1%) | NS |
| Hyperlipidemia | 1251 (41.8%) | 1038 (41.8%) | 213 (41.8%) | NS |
| Hypertension | 1191 (39.8%) | 936 (37.7%) | 255 (50.0%) | <0.001 |
| Tobacco use | 443 (14.8%) | 357 (14.4%) | 86 (16.9%) | NS |
| Known CAD | 592 (19.8%) | 449 (18.1%) | 143 (28.0%) | <0.001 |
| s/p CABG | 240 (8.0%) | 167 (6.7%) | 73 (14.3%) | <0.001 |
| s/p MI | 255 (8.5%) | 190 (7.6%) | 65 (12.7%) | <0.001 |
| s/p PCI | 344 (11.5%) | 276 (11.1%) | 68 (13.3%) | NS |
| Resting HR (bpm)** | 71.0 ± 12.0 | 70.8 ± 11.8 | 72.6 ± 13.4 | 0.0062 |
| 60s HRR (bpm) | 21.1 ± 9.7 | 22.4 ± 9.3 | 15.2 ± 9.6 | <0.0001 |
| No CV Medications | 987 (33.0%) | 863 (34.7%) | 124 (24.3%) | <0.001 |
| Antiplatelets | 1042 (34.8%) | 853 (34.3%) | 189 (37.1%) | NS |
| Beta-blockers | 745 (24.9%) | 575 (23.1%) | 170 (33.3%) | <0.001 |
| ACE-I | 468 (15.6%) | 369 (14.9%) | 99 (19.4%) | 0.01 |
| Anticholesterol agents | 1049 (35.0%) | 833 (33.5%) | 216 (42.4%) | <0.001 |
| CCB | 375 (12.5%) | 296 (11.9%) | 79 (15.5%) | 0.026 |
| Diuretics | 365 (12.2%) | 268 (10.8%) | 97 (19.0%) | <0.001 |
| Exercise time (min) | 9.9 ± 3.3 | 10.1 ± 3.2 | 8.9 ± 3.4 | <0.0001 |
| Peak HR* SBP*** | 28015 ± 5429 | 28273 ± 5236 | 26504 ± 6245 | <0.0001 |
| Gated EF (%)**** | 58.7 ± 10.2 | 59.0 ± 9.9 | 57.4 ± 11.6 | 0.0048 |
| Summed stress score (SSS) | 2.9 ± 5.7 | 2.6 ± 5.3 | 4.3 ± 7.0 | <0.0001 |
| Summed rest score (SRS) | 1.0 ± 3.4 | 0.8 ± 3.1 | 1.7 ± 4.6 | <0.0001 |
| SDS=SSS-SRS | 1.9 ± 3.9 | 1.8 ± 3.7 | 2.6 ± 4.6 | <0.0001 |
BMI only available for 2,940 (98.2%) patients (Normal=2442, Abnormal=498)
resting HR only available for 2,712 (90.6%) patients (Normal=2318, Abnormal=394)
peak HR*SBP only available for 2,719 (90.8%) patients (Normal=2323, Abnormal=396)
gated EF only available for 2,240 (74.8%) patients (Normal=1829, Abnormal=411)
Table 3.
Survival by QT-500 quartile
| Q1 | Q2 | Q3 | Q4 | p | |
|---|---|---|---|---|---|
| QT at 500 ms | 288 ± 10 | 299 ± 2 | 307 ± 3 | 325 ± 14 | N/A |
| N | 749 | 748 | 749 | 748 | |
| Dead | 46 | 44 | 52 | 86 | <0.001 |
| Mortality (%) | 6.1 | 5.9 | 6.9 | 11.5 | |
| Length of survival (years) | 7.7 ± 1.9 | 7.6 ± 1.8 | 7.6 ± 1.8 | 7.3 ± 2.0 | 0.0005 |
| Incidence (per 1000 patient years) | 8.0 | 7.7 | 9.1 | 15.7 |
Multivariable models
Table 4 explores progressive Cox proportional hazards models. Model 1 includes abnormal QT-500 as a univariate predictor and is the same as the first line of Table 1. Model 2 adjusts for abnormal HRR.
Table 4.
Cox proportional hazard models including abnormal QT-500
| Model | QT-500 Hazard ratio | 95% CI | p |
|---|---|---|---|
| 1: QT-500 only | 2.13 | 1.60–2.84 | <0.001 |
| 2: QT-500 and HRR | 1.64 | 1.21–2.22 | 0.001 |
| 3: final model* | 1.46 | 1.08–1.97 | 0.014 |
adjusted for abnormal QT-500 and HRR, age, exercise time, SSS, and ACE-I medications
The preliminary effects model includes all univariate predictors with a p<0.25, in addition to abnormal QT-500 and HRR: age, male sex, diabetes, family history, hypertension, tobacco use, known CAD, s/p CABG, s/p MI, s/p PTCA, resting HR, all medication variables, exercise time, peak double product, EF, SSS, and SRS. Model 3 (final model) retains only those variables from the preliminary effects model with p<0.05 when included simultaneously (age, exercise time, SSS, and ACE-inhibitor medications), in addition to abnormal QT-500 and HRR. Even after accounting for these predictors of survival, abnormal QT-500 remains a significant, independent variable. Forcing the covariates diabetes, s/p MI, and EF into this final model did not significantly alter the findings (hazard ratio 1.36, 95% confidence interval 1.01–1.85, p=0.045).
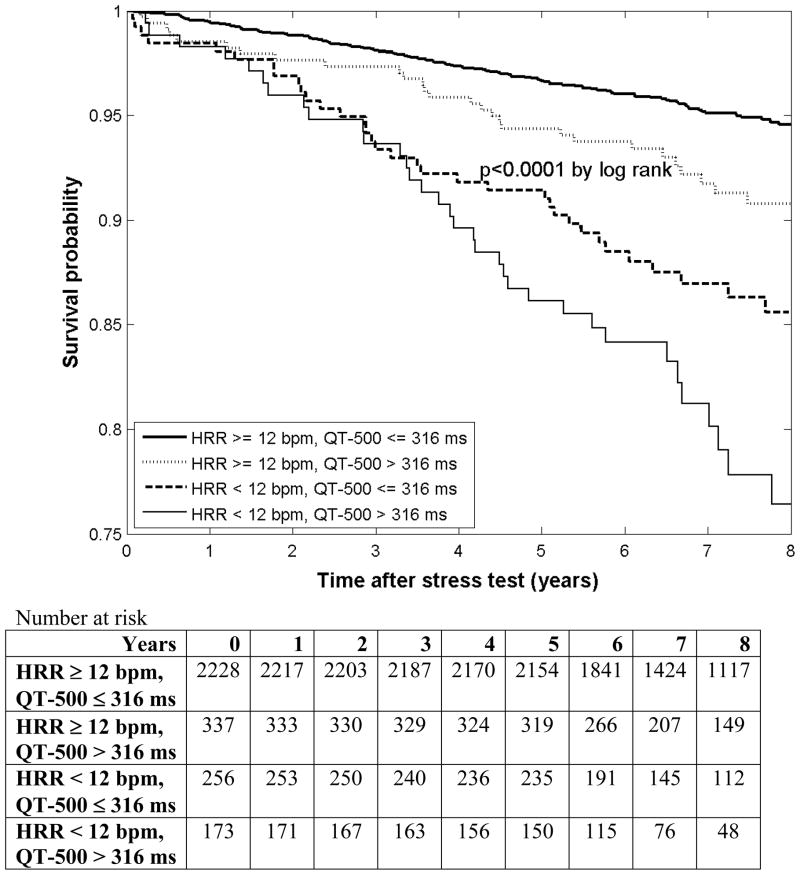
Figure 4 shows Kaplan-Meier survival curves for QT-500 and HRR subgroups. Patients with both normal QT-500 and HRR had the best survival, while patients with both abnormal QT-500 and HRR had the worst survival. Those with normal QT-500 but abnormal HRR had a worse prognosis than patients with an abnormal QT-500 but normal HRR.
Figure 4.
Kaplan-Meier survival curves by QT-500 and HRR subgroups
Sensitivity analysis for R2≥0.7
To determine the robustness of QT dynamics, we expanded our original analysis by including all patients with R2≥0.7 instead of the original criterion of R2≥0.9. This increased the cohort size from 2,994 to 3,505 patients and the number of deaths from 228 to 309. The same analysis as described above was carried out. The results were essentially unchanged. Specifically, the hazard ratio for model 1 was 2.48 (p<0.001), 1.71 (p<0.001) for model 2, and 1.42 (p=0.014) for model 3.
Cross-validation using random subsets
The univariate hazard ratio for QT-500 in the derivation cohorts was 2.32±0.33 compared to 1.82±0.29 in the validation cohorts, and its adjusted hazard ratio in the validation cohorts was 1.27±0.26. This compares to a univariate hazard ratio for QT-500 in the entire cohort of 2.13±0.31 (68% confidence limit to facilitate comparison with standard deviation) and an adjusted hazard ratio of 1.46±0.23. The univariate hazard ratio for QT-500 had a p<0.05 in 83% of the repetitions; the adjusted hazard ratio had a p<0.05 in 10%. The derivation cohort cutoff was 314±8 ms.
The univariate hazard ratio for HRR in the derivation cohorts was 2.85±0.49 compared to 2.70±0.42 in the validation cohorts, and its adjusted hazard ratio in the validation cohorts was 1.62±0.38. This compares to a univariate hazard ratio for HRR in the entire cohort of 2.99±0.43 and an adjusted hazard ratio of 1.81±0.29. The univariate hazard ratio for HRR had a p<0.05 in 100% of the repetitions; the adjusted hazard ratio had a p<0.05 in 50%. The derivation cohort cutoff was 13±2 bpm.
DISCUSSION
We found that QT dynamics during recovery from treadmill exercise, as reflected by the predicted QT interval at 500 ms (QT-500), stratified subsequent all-cause mortality. The predictive power of an abnormal QT-500 remained significant after adjustment for abnormal 60-second HRR and important clinical variables. An abnormal QT-RR slope during the early recovery phase from exercise, which is often used to describe the QT-RR relationship, was a less significant predictor. This suggests that, at least in the recovery phase from exercise, the predominantly linear QT-RR relationship is better described by the full linear regression information incorporating both the slope and the intercept.
Existing literature
Several studies have shown that resting QT dynamics predict outcome, although QT dynamics have been quantified using several metrics, including QT-RR slope, intercept, diurnal slope, and variability ratio. After a myocardial infarction, abnormal resting QT dynamics carries a higher risk of arrhythmia, SCD, and all-cause mortality.18–20 Work in patients with both ischemic21–22 and nonischemic23 cardiomyopathy has demonstrated abnormal resting QT dynamics as a risk factor for arrhythmia or SCD.
Our work extends the existing literature on resting QT dynamics into the new area of stress QT dynamics. One prior work has explored the QT-RR relationship during exercise in patients with exercise-induced ventricular tachycardia (VT) compared to normals.24 However our results are the first, to our knowledge, to study the impact of stress QT dynamics on survival in an unselected group of patients undergoing stress tests.
QT dynamics
The QT interval measures the period of ventricular depolarization and repolarization. Repolarization abnormalities can play an important role in arrhythmogenesis.25 However, there are a number of technical factors that limit the utility of the raw QT interval. First, the QT interval is highly dependent on heart rate, for which rate correction formulae have been developed. None are optimal and they are particularly prone to error at extremes of heart rate, as might be observed during exercise.26 Second, there may be direct autonomic effects on the QT interval. To compensate for these issues, assessment of the QT-RR slope has emerged as a reliable and reproducible method to quantify QT dynamics.10 The prognostic significance of QT-RR slope has been demonstrated in studies using Holter monitoring in which the heart rate varies naturally throughout the day.
Exercise, in contrast, is an established stimulus that alters the heart rate (and consequently repolarization) and has also been shown to be associated with an increased risk for SCD. Therefore, there is pathophysiologic rationale to evaluate whether exercise-induced abnormalities in repolarization are predictive of SCD. In fact, other parameters of repolarization during exercise, such as T-wave alternans, have been shown to predict SCD.1 However, that test requires that the target heart rate be achieved with regular R-R intervals, which renders a significant percentage of tests indeterminate. In addition, the test requires special electrodes and recording equipment.
Studying the QT interval during exercise requires some adjustment for the heart rate. Measures such as the QT-RR slope or QT-500 allow for individualized analysis and make fewer assumptions about the QT-RR relationship than do standard correction methods such as Bazett’s formula. Using a population-based formula to adjust the QT interval will be limited by the substantial variability among even healthy subjects.27 In particular, correction formulae may be less reliable at high heart rates.26
The present study demonstrates that the QT-RR relationship in recovery is predominantly linear. While QT-RR slope has been shown to provide important prognostic information when obtained under non-exercise conditions,10 the QT-RR slope measured in recovery was not an independent predictor in our cohort after adjusting for covariates. As QT-RR slope does not fully characterize the entire QT-RR relationship, use of the linear regression formula to generate a predicted QT interval at a fixed cycle length improved prognostic power in our cohort. Importantly, the predicted QT interval incorporates both the slope and intercept information from the linear regression.
Limitations
Several limitations in our study should be noted. First, all-cause mortality does not distinguish arrhythmic or cardiac death from other mechanisms. Abnormal QT dynamics would be expected to manifest clinically by sudden cardiac death, although our data could not test this association directly.
Second, we assumed a linear model of QT dynamics during the exercise recovery period. The complete relationship between the QT and RR intervals is complex, and a linear model is only one of several possibilities.27 However, the generally high R2 values in Figure 2 support the concept that most of the QT-RR relationship in early exercise recovery can be explained by a linear relationship. Additionally, the same results hold in Table 4 if a cutoff of R2≥0.7 is chosen instead.
Third, the 60-second heart rate recovery is much simpler to compute than QT dynamics and has already been validated as an important prognostic factor during exercise recovery.6 Further studies will need to evaluate the relative contributions of these parameters for risk prediction of SCD and cardiac-specific mortality.
Fourth, we were not able to include baseline QRS duration in our analysis. Our laboratory strongly encourages adenosine stress in patients with a baseline left bundle branch block (LBBB) or pacemaker activity, due to the rate of false positive SPECT defects in the septum. Only 17 patients (0.6%) had a baseline LBBB or pacemaker. However, QT interval dependence on the QRS duration may have been affected by other intraventricular conduction delays.
Fifth, we do not have a large, independent cohort to validate our findings. The cutoff values and hazard ratios in the cross-validation cohorts have a similar distribution to the cutoff value and estimated hazard ratio from the cohort when taken as a whole. The lower adjusted hazard ratio in the validation cohorts and less frequent p<0.05 for the hazard ratio in any repetition are expected due to the smaller size of the cohort and resulting loss of events, which is a well-known and inherent drawback to cross-validation by random subsets. This is seen more prominently for QT-500 than for HRR, as QT-500 is a weaker predictor than HRR in both univariate and adjusted models.
Finally, only 3.1% of the population had an EF≤40% and 1.0% had heart failure. Thus, the predictive value of the QT-500 in these generally higher risk groups will need to be further assessed.
CONCLUSION
As risk for SCD is dramatically increased during exercise and recovery,5 and repolarization abnormalities have also been related to SCD,28 a strong rationale exists for evaluating exercise-induced abnormalities in repolarization as a predictor of mortality and/or SCD. This is the first large-scale evaluation of QT dynamics during recovery from exercise. We found that QT dynamics during recovery from treadmill exercise stress as reflected by an abnormal predicted QT interval at 500 ms (QT-500) independently stratified subsequent all-cause mortality.
Further work is necessary to evaluate whether abnormal QT dynamics in recovery are more predictive of sudden versus non-sudden death. In addition, exercise QT dynamics should be applied to populations enriched for SCD such as those with left ventricular dysfunction.
Acknowledgments
FUNDING SOURCES: Supported in part by 1 RO1 HL 70179-01A2 from the National Heart, Lung, and Blood Institute.
ABBREVIATIONS
- CAD
Coronary artery disease
- ECG
Electrocardiogram
- EF
Ejection fraction
- HRR
Heart rate recovery at 1 minute
- ICD
Implantable cardioverter-defibrillator
- SCD
Sudden cardiac death
- SDS
Summed difference score
- SPECT
Single photon emission computed tomography
- SRS
Summed rest score
- SSS
Summed stress score
Footnotes
DISCLOSURES: Jeffrey Goldberger is the Director, Path to Improved Risk Stratification (not- for-profit think tank on risk stratification for sudden cardiac death).
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Goldberger JJ, Cain ME, Hohnloser SH, et al. AHA/ACCF/HRS scientific statement on noninvasive risk stratification techniques for identifying patients at risk for sudden cardiac death. Circulation. 2008;118:1497–1518. [PubMed] [Google Scholar]
- 2.Sticker EC, Vickers C, Waltz J, et al. Population-based analysis of sudden cardiac death with and without left ventricular systolic dysfunction: two-year findings from the Oregon Sudden Unexpected Death Study. J Am Coll Cardio. 2006;47:1161–1166. doi: 10.1016/j.jacc.2005.11.045. [DOI] [PubMed] [Google Scholar]
- 3.Epstein AE, Dimarco JP, Ellenbogen KA, et al. ACC/AHA/HRS 2008 Guidelines for device- based therapy of cardiac rhythm abnormalities. Heart Rhythm. 2008;5:e1–62. doi: 10.1016/j.hrthm.2008.04.014. [DOI] [PubMed] [Google Scholar]
- 4.Tung R, Zimetbaum P, Josephson ME. A critical appraisal of implantable cardioverter-defibrillator therapy for the prevention of sudden cardiac death. J Am Coll Cardio. 2008;52:1111–1121. doi: 10.1016/j.jacc.2008.05.058. [DOI] [PubMed] [Google Scholar]
- 5.Albert CM, Mittleman MA, Chae CU, Lee IM, Heinekens CH, Manson JE. Triggering of sudden death from cardiac causes by vigorous exertion. N Engl J Med. 2000;343:1355–1361. doi: 10.1056/NEJM200011093431902. [DOI] [PubMed] [Google Scholar]
- 6.Cole CR, Blackstone EH, Pashto FJ, Sander CE, Lauer MS. Heart-rate recovery immediately after exercise as a predictor of mortality. N Engl J Med. 1999;341:1351–1357. doi: 10.1056/NEJM199910283411804. [DOI] [PubMed] [Google Scholar]
- 7.Schouten EG, Dekker JM, Meppelink P, Kok FJ, Vandenbroucke JP, Pool J. QT interval prolongation predicts cardiovascular mortality in an apparently healthy population. Circulation. 1991;84:1516–1523. doi: 10.1161/01.cir.84.4.1516. [DOI] [PubMed] [Google Scholar]
- 8.Schwartz PJ, Wolf S. QT interval prolongation as predictor of sudden death in patients with myocardial infarction. Circulation. 1978;57:1074–1077. doi: 10.1161/01.cir.57.6.1074. [DOI] [PubMed] [Google Scholar]
- 9.Funk-Brentano C, Jaillon P. Rate-corrected QT interval: techniques and limitations. Am J Cardio. 1993;72:17B–22B. doi: 10.1016/0002-9149(93)90035-b. [DOI] [PubMed] [Google Scholar]
- 10.Zareba W, Bayes de Luna A. QT dynamics and variability. Ann Noninvasive Electrocardiol. 2005;10:256–262. doi: 10.1111/j.1542-474X.2005.10205.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sandarac S, Carnation M, Polite K, Kadish AH, Goldberger JJ. Autonomic effects on QT-RR interval dynamics after exercise. Am J Physiology Heart Circ Physiol. 2008;294:H490–H497. doi: 10.1152/ajpheart.00046.2007. [DOI] [PubMed] [Google Scholar]
- 12.Gibbons RJ, Balady GJ, Bricker JT, et al. ACC/AHA 2002 guideline update for exercise testing: summary article. Circulation. 2002;106:1883–92. doi: 10.1161/01.cir.0000034670.06526.15. [DOI] [PubMed] [Google Scholar]
- 13.Imaging guidelines for nuclear cardiology procedures, part 2. American Society of Nuclear Cardiology. J Nucl Cardio. 1999;6:G47–G84. [PubMed] [Google Scholar]
- 14.Marquez AI, Zhang Q. An algorithm for QRS onset and offset detection in single lead electrocardiogram records. Conf Proc IEEE Eng Med Biol Soc. 2007;2007:541–544. doi: 10.1109/IEMBS.2007.4352347. [DOI] [PubMed] [Google Scholar]
- 15.Costa M, Moody GB, Henry I, Goldberger AL. PhysioNet: an NIH research resource for complex signals. J Electrocardiol. 2003;36 (Suppl):139–144. doi: 10.1016/j.jelectrocard.2003.09.038. [DOI] [PubMed] [Google Scholar]
- 16.Cowper DC, Kubal JD, Maynard C, Hynes DM. A primer and comparative review of major US mortality databases. Ann Epidemiology. 2002;12:462–468. doi: 10.1016/s1047-2797(01)00285-x. [DOI] [PubMed] [Google Scholar]
- 17.Williams BA, Mandrake JN, Mandrake SJ, Cha SS, Furth AF. Department of Health Sciences Research, Technical Report Series #79. Mayo Clinic; Rochester, Minnesota: Jun, 2006. Finding Optimal Cutpoints for Continuous Covariates with Binary and Time-to-Event Outcomes. [Google Scholar]
- 18.Chevalier P, Burri H, Adeleine P, et al. QT dynamicity and sudden death after myocardial infarction: results of a long-term follow-up study. J Cardiovasc Electrophysiol. 2003;14:227–233. doi: 10.1046/j.1540-8167.2003.02431.x. [DOI] [PubMed] [Google Scholar]
- 19.Jensen BT, Abildstrom SZ, Larroude CE, et al. QT dynamics in risk stratification after myocardial infarction. Heart Rhythm. 2005;2:357–364. doi: 10.1016/j.hrthm.2004.12.028. [DOI] [PubMed] [Google Scholar]
- 20.Szydlo K, Trusz-Gluza M, Wita K, et al. QT/RR relationship in patients after remote anterior myocardial infarction with left ventricular dysfunction and different types of ventricular arrhythmias. Ann Noninvasive Electrocardiol. 2008;13:61–66. doi: 10.1111/j.1542-474X.2007.00201.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pathak A, Cornier D, Forbade J, et al. QT dynamicity: a prognostic factor for sudden cardiac death in chronic heart failure. Eur J Heart Fail. 2005;7:269–275. doi: 10.1016/j.ejheart.2004.10.016. [DOI] [PubMed] [Google Scholar]
- 22.Millie P, Leenhardt A, Maisonblanche P, et al. Usefulness of ventricular repolarization dynamicity in predicting arrhythmic deaths in patients with ischemic cardiomyopathy. Am J Cardio. 2005;95:821–826. doi: 10.1016/j.amjcard.2004.11.047. [DOI] [PubMed] [Google Scholar]
- 23.Iacoviello M, Forleo C, Guide P, et al. Ventricular repolarization dynamicity provides independent prognostic information toward major arrhythmic events in patients with idiopathic dilated cardiomyopathy. J Am Coll Cardio. 2007;50:225–231. doi: 10.1016/j.jacc.2007.02.071. [DOI] [PubMed] [Google Scholar]
- 24.Gill JS, Baszko A, Xia R, Ward DE, Camm AJ. Dynamics of the QT interval in patients with exercise-induced ventricular tachycardia in normal and abnormal hearts. Am Heart J. 1993;126:1357–1363. doi: 10.1016/0002-8703(93)90534-g. [DOI] [PubMed] [Google Scholar]
- 25.Yan GX, Lankipalli RS, Burke JF, Masco S, Kowey PR. Ventricular repolarization components on the electrocardiogram: cellular basis and clinical significance. J Am Coll Cardio. 2003;42:401–409. doi: 10.1016/s0735-1097(03)00713-7. [DOI] [PubMed] [Google Scholar]
- 26.Milne JR, Ward DE, Spurrell RA, Camm AJ. The ventricular paced QT interval--the effects of rate and exercise. Pacing Clin Electrophysiol. 1982;5:352–358. doi: 10.1111/j.1540-8159.1982.tb02242.x. [DOI] [PubMed] [Google Scholar]
- 27.Mali M, Färbom P, Batchvarov V, Hnatkova K, Camm AJ. Relation between QT and RR intervals is highly individual among healthy subjects: implications for heart rate correction of the QT interval. Heart. 2002;87:220–228. doi: 10.1136/heart.87.3.220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lemming H, Holm E, Jun L, et al. The prognostic value of the QT interval and QT interval dispersion in all-cause and cardiac mortality and morbidity in a population of Danish citizens. Eur Heart J. 1998;19:1391–1400. doi: 10.1053/euhj.1998.1094. [DOI] [PubMed] [Google Scholar]