Abstract
We present an implicit solvent model based on the extended reference interaction site model (XRISM) integral equation theory, which is a molecular theory of solvation. The solvation free energy is composed of additive potentials of mean force (PMF) of various functional groups. The XRISM theory is applied to determine the PMF of each group in water and NaBr electrolyte solutions. The method has been coupled to Brownian dynamics (BD) and is illustrated here on alanine dipeptide. The results of the method are compared with those obtained by explicit water simulations and other popular implicit solvent models for detailed discussion. The comparison of our model with other methods indicates that the intramolecular correlation and the solvation structure influence the stability of the PII and αR conformers. The results of NaBr electrolyte solutions show that the concentration of electrolyte also has a substantial effect on the favored conformations.
Molecular dynamics (MD) simulation has been a powerful tool to study the structure, dynamics, and function of proteins in atomic detail. However, the accessible time scales of typical MD simulations are up to hundreds of nanoseconds. A major computational burden comes from the treatment of solvent molecules, which constitute a large part of the system. For this reason, Brownian dynamics (BD) simulation with implicit solvation models has been used for the longer simulation(1) of biological systems. Recent progress(2) has enhanced the possibility of BD simulation as an alternative to explicit simulation. In general, the result of BD simulation is sensitive to the choice of the implicit solvation model. A successful implicit solvation model with high accuracy, versatility, and low computational cost is, therefore, an important key to successful BD simulation. Because the potential of mean force (PMF) includes the static solvation effect, which is deeply related to the hydration structure around a macromolecule, the solvation term of PMF should be treated carefully. The solvation term of the PMF for N-particle interaction Wsol(RN) can be decomposed into single-body, pairwise, and nonpairwise terms
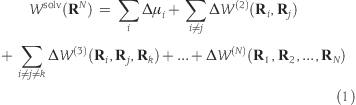 |
where Δμi is the excess chemical potential of ith particle, ΔW(i) corresponds to the ith-order term, RN = (R1, R2, ...,RN), and Ri is the ith atom coordinate of a macromolecule. The sophisticated calculation of eq 1 leads to the establishment of the accurate implicit solvation model. The generalized Born and surface area (GB/SA) model(3) is the most commonly used implicit solvation model. To reduce the computational cost, the surface area approximation is applied to the nonpairwise contribution. Recent studies of the MD simulation indicate that the triplet term in eq 1 can be described qualitatively by molecular surface area.4,5 The reference interaction site model (RISM) is a versatile method for calculating the PMF in terms of the solute−solute radial distribution function (RDF).(6) In this approach, the properties of the hydration structure, which are not considered in the GB/SA model, can refine the PMF in terms of the microscopic theory. Henceforward, superscripts “u” and “v” denote the solute and solvent species, respectively. According to the RISM theory, Wsolv can be expressed as follows(6)
where kBT is the Boltzmann constant times the absolute temperature, rij =|Rj − Ri|, tijuu(r) = hij(r) − cijuu(r), hij(r) and cijuu(r) are the site−site total and direct pair correlation function, respectively, and bij is the bridge function. Pioneering simulation based on eq 2 was carried out by Pettitt and Karplus,(6) and the conformation of alanine dipeptide in water was discussed in their article. They solved the extended RISM (XRISM) equations for a monatomic solute at infinite dilution to obtain tij(r)
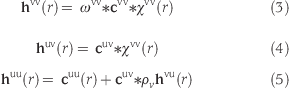 |
where the asterisk denotes the convolution integral, ρv is the density of pure solvent, χijvv(r) = ωij(r) + ρvhijvv(r) is the site−site density pair correlation function, and ωij(r) = δ(r − lij)/4πr2 (where lij is the distance between sites i and j) is the intramolecular correlation function. The hypernetted chain (HNC) closure was employed as the second equation that relates hij(r) and cijuu(r), and the bridge function was neglected in their article. From the viewpoint of the liquid state theory, all nonpairwise terms in eq 1 are renormalized into the bridge function by integrating the multibody correlation functions. Whether the bridge function is considered is, therefore, the central problem for the accuracy of the RISM theory. Recently, the promising bridge function in which the four-body correlations are projected has been proposed by Perkyns et al.(7) By employing this bridge function, the theoretical deficiency might be filled up. A more direct and accurate manner is the RISM calculation with an individual peptide at each time step. If a solute molecule is small, the calculation of the RISM at every integration step is comparably expensive. In contrast, for a giant molecule that has more than 100 000 atoms, the RISM calculation with individual molecular configuration has to handle the 100 000 × 100 000 matrix of the intramolecular correlation function. Therefore, the computational cost is not comparabe but far more expensive. To make matters worse, the convergence of the RISM calculation at each step would be very poor because of the large anisotropy of a macromolecule. This is the reason why the three-dimensional RISM (3DRISM) theory is widely used for a giant molecular system.(8) However, the coupling of the 3DRISM with MD (3DRISM/MD), which is proposed by Miyata and Hirata,(9) is not a promising approach. Who would want to use the slower and far more expensive “implicit” solvation model rather than the explicit water MD? Additionally, their approach does not include the dynamic properties of the solvent such as viscosity. Most people, therefore, would prefer the explicit water MD to the 3DRISM/MD. For these reasons, we extend the approximation of Pettitt and Karplus to the class of groups.
Here, to extract the multibody correlation without correcting the bridge function, we apply the classes of atoms or groups that are defined by Ooi and coworkers(10) to eq 2, namely, (I) aliphatic groups, (II) aromatic groups, (III) hydroxyl groups, (IV) amide and amine groups, (V) carboxyl and carbonyl groups, and (VI) sulfur atoms and thiol groups. For group molecules at infinite dilution, the corresponding eqs 4 and 5 can be expressed as follows
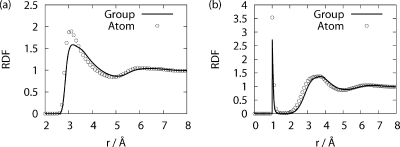
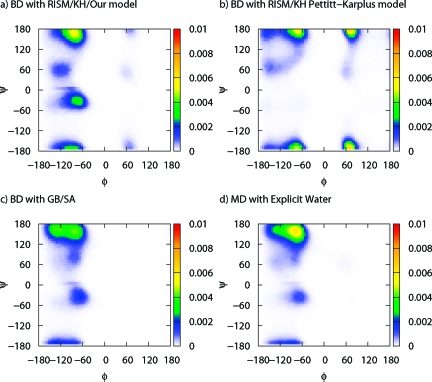
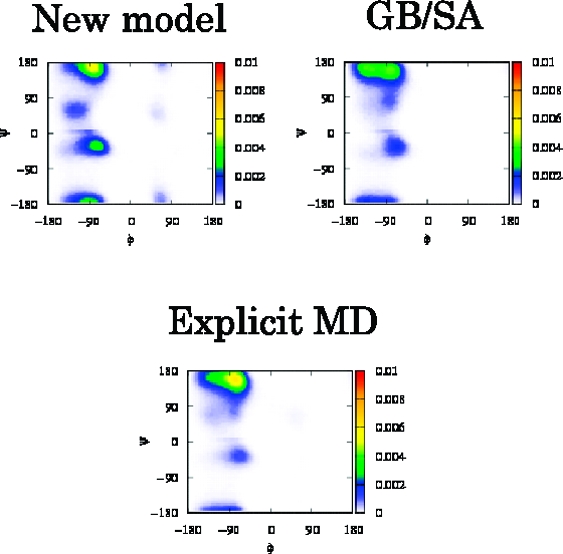
In eqs 6 and 7, the multibody correlations are approximated as the product of ωuu and cuu at the level of Kirkwood superposition approximation. Representation of alanine dipeptide with the above definitions is shown in Figure 1. The XRISM equations are complemented with the Kovalenko−Hirata (KH) closure for effective convergence of the calculation.(11) The theoretical framework and analytical expression of Δμi for KH closure can be found elsewhere. The XRISM/KH results of Δμ for isolated groups of alanine dipeptide in water (T = 298K, ρ = 0.03334 Å−3) are listed in Table 1. The positive values of Δμ for CH3 and CH groups indicate that the hydrophobicity of aliphatic groups in water is reproduced thanks to the multibody correlations of eq 6. RDF between the carbon atom of CH3 and water atoms is plotted in Figure 2. The solid and circle lines are the result of eqs 4 and 6, respectively. As is clearly seen, the oxygen distribution of our model is slightly lower than that of the monatomic model because of the steric effect of CH3. The Ramachandran plots of aqueous alanine dipeptide, which are calculated from the BD with the above-mentioned implicit solvation models and explicit water MD, are shown in Figure 3. The fractions of PII and αR are listed in Table 2. The result of our model shows the stability of the PII (−105° ≤ ϕ ≤ −65°, 140° ≤ ψ ≤ 180°) conformers, which is in good agreement with MD results. Other models are somewhat less satisfactory. The improvement of monatomic model is, therefore, achieved by the renormalization of the multibody correlation in eqs 6 and 7. The result of GB/SA model agrees with the MD result, except for the PII conformer. From this result, the changes of the solvation structure are deeply related to the PII conformer. However, our model produces a less broadened population around the PII conformer and overestimates the population of αR (−100° ≤ ϕ ≤ −60°, −70° ψ ≤ −30°) conformer in contrast with the GB/SA model. Because they are not also observed in Figure 3b, these conformers are sensitive to the approximations of the XRISM theory. The computational cost of each model is also listed in Table 2. The CPU time of the explicit MD is normalized.
Figure 1.
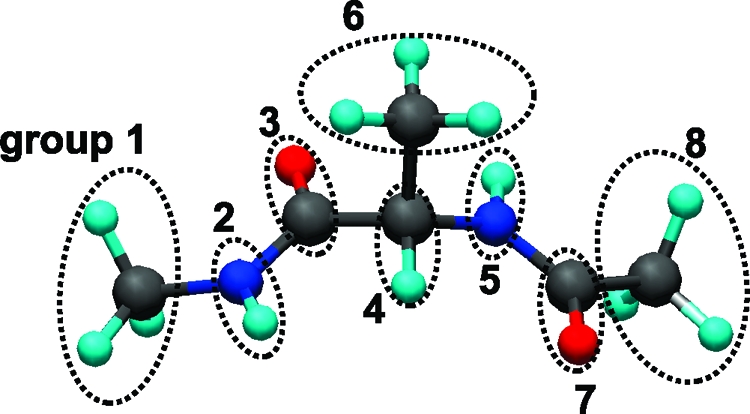
Representation of alanine dipeptide with groups.
Table 1. Excess Chemical Potential Δμ (kilocalories per mole) of Isolated Groups of Alanine Dipeptide in Water.
| group | Δμ [kcal/mol] |
|---|---|
| CH3 (group 1) | 10.562 |
| NH (group 2) | −9.083 |
| CO (group 3) | −4.819 |
| CH (group 4) | 7.595 |
| NH (group 5) | −9.083 |
| CH3 (group 6) | 11.655 |
| CO (group 7) | −4.819 |
| CH3 (group 8) | 11.681 |
Figure 2.
Radial distribution functions (a) between carbon atom of CH3 group and water oxygen and (b) between carbon atom of CH3 group and water hydrogen. The solid and circle lines denote the XRISM/KH result for isolated CH3 group molecule and carbon atom of CH3 group in water, respectively.
Figure 3.
Ramachandran plot of aqueous alanine dipeptide calculated from (a) Brownian dynamics (BD) with XRISM/KH our model, (b) BD with XRISM/KH Pettitt−Karplus model, (c) BD with GB/SA, and (d) molecular dynamics (MD) with explicit water.
Table 2. Fraction of Conformers and CPU Time Ratio.
| method | PII [%] | αR [%] | CPU time ratio |
|---|---|---|---|
| our model | 22.12 | 10.62 | 4.38 × 10−5 |
| Pettitt and Karplus | 17.58 | 0.29 | 4.38 × 10−5 |
| GB/SA | 18.75 | 6.37 | 5.03 × 10−5 |
| explicit MD | 26.18 | 4.52 | 1 |
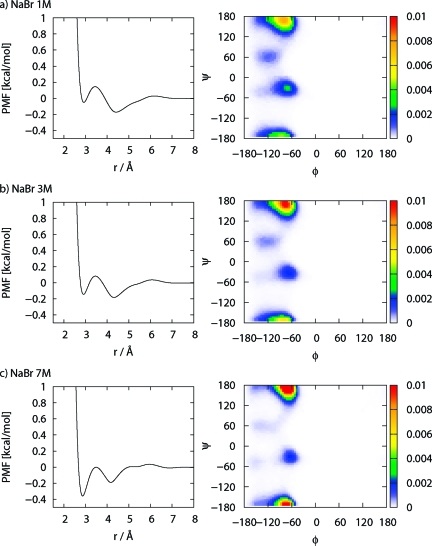
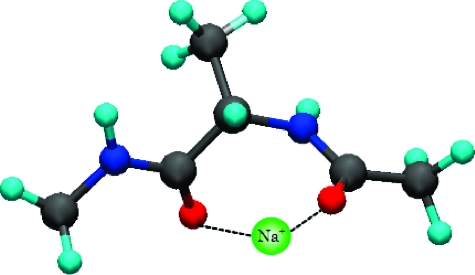
Salt effects on the conformation of biomolecules have been an important problem because the function of protein is deeply related to the salt concentrations in technological as well as physiological settings. To demonstrate the applicability of our model, we briefly discuss the salt effect on the conformation map of alanine dipeptide. By applying eq 3 to an electrolyte mixture, we can easily include the salt effect in the PMF. The PMFs between the amide carbonyl oxygens at each mole concentration with our model are plotted on the l.h.s of Figure 4. The Ramachandran plots are also shown on the r.h.s of these Figures. From the results of PMFs, it appears possible that at high Na+ concentration a Na+ ion may tend to coordinate the two amide carbonyl oxygens, favoring the PII conformer. This result indicates that the PMF between sodium ion and the amide carbonyl oxygen overcomes the repulsive interaction between oxygens (Figure 5). To improve our approach, we will apply the dielectric consistent RISM (DRISM)12−14 to our model and report on it in an upcoming article.
Figure 4.
Left column: PMFs between the amide carbonyl carbons of (a) 1, (b) 3, and (c) 7 M NaBr electrolyte solutions. Right column: Ramachandran plot of alanine dipeptide of (a) 1, (b) 3, and (c) 7 M NaBr electrolyte solutions.
Figure 5.
Schematic view of the stabilized PII conformer by sodium ion.
Method
OPLS-AA force field parameters15−21 and the TIP3P model(22) are employed for potentials of alanine dipeptide and water, respectively. The first-order Ermak and McCammon algorithm(1) is implemented in BD simulations
where dt is a time step, Di is the diffusion coefficient of atom i, and Xi is a random noise vector obtained from a standard normal distribution. The diffusion coefficients of individual atoms are assigned according to
where σi is the van der Waals radius and η is the solvent viscosity: the experimental values of η for pure water and NaBr solution are employed.(23) Time steps of BD simulations are set to 10 fs, and trajectories of 300 ns are generated. We obtained the result of explicit-water MD simulation by carrying out the NVT ensemble simulation including 491 water molecules. The time step of MD simulation is set to 2 fs, and trajectories of 100 ns are generated. The potential parameters and thermal conditions used for all simulation are unified. As was reported,(24) the Ramachandran plot of alanine dipeptide strongly depends on the force field parameters.
Acknowledgments
This work has been partially supported by NSF, NIH, HHMI, CTBP, NBCR, and the NSF Supercomputer Center. We thank Prof. Fumio Hirata for stimulating discussions.
Funding Statement
National Institutes of Health, United States
References
- Ermak D. L.; McCammon J. A. Brownian Dynamics with Hydrodynamic Interaction. J. Chem. Phys. 1978, 69, 1352–1360. [Google Scholar]
- Shen T.; Wong C. F.; McCammon J. A. Atomistic Brownian Dynamics Simulation of Peptide Phosphorylation. J. Am. Chem. Soc. 2001, 123, 9107–9111. [DOI] [PubMed] [Google Scholar]
- Qiu D.; Shenkin P. S.; Hollinger F. P.; Still W. C. The GB/SA Continuum Model for Solvation. A Fast Analytical Method for the Calculation of Approximate Born Radii. J. Phys. Chem. A 1997, 101, 3005–3014. [Google Scholar]
- Czaplewski C.; Ripoll D. R.; Liwo A.; Rodziewicz-Motowidlo S.; Wawak R. J.; Scheraga H. A. Can Cooperativity in Hydrophobic Association Be Reproduced Correctly by Implicit Solvation Model. Int. J. Quantum Chem. 2002, 88, 41–55. [Google Scholar]
- Shimizu S.; Chan H. S. Anti-Cooperativity and Cooperativity in Hydrophobic Interaction: Three-Body Free Energy Landscapes and Comparison With Implicit-Solvent Potential Functions for Proteins. Proteins: Struct., Funct., Genet. 2002, 48, 15–30. [DOI] [PubMed] [Google Scholar]
- Pettitt B. M.; Karplus M. The Potential of Mean Force Surface for the Alanine Dipeptide in Aqueous Solution: A Theoretical Approach. Chem. Phys. Lett. 1985, 121, 194–201. [Google Scholar]
- Perkyns J. S.; Lynch G. C.; Howard J. J.; Pettitt B. M. Protein Solvation from Theory and Simulation: Exact Treatment of Coulomb Interactions in Three-Dimensional Theories. J. Chem. Phys. 2010, 132, 064106–064118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molecular Theory of Solvation, 1st ed.; Hirata F., Ed.; Kluwer Academic: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Miyata T.; Hirata F. Combination of Molecular Dynamics Method and 3D-RISM Theory for Conformational Sampling of Large Flexible Molecules in Solution. J. Comput. Chem. 2008, 29, 871–882. [DOI] [PubMed] [Google Scholar]
- Ooi T.; Oobatake M.; Nemethy G.; Scheraga H. A. Accessible Surface Areas As a Measure of the Thermodynamic Parameters of Hydration of Peptides. Proc. Natl. Acad. Sci. U.S.A. 1987, 84, 3086–3090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovalenko A.; Hirata F. Self-Consistent Description of a Metal−Water Interface by the Kohn−Sham Density Functional Theory and the Three-Dimensional Reference Interaction Site Model. J. Chem. Phys. 1999, 110, 10095–10112. [Google Scholar]
- Perkyns J. S.; Pettitt B. M. A Dielectrically Consistent Interaction Site Theory for Solvent−Electrolyte Mixtures. Chem. Phys. Lett. 1992, 190, 626–630. [Google Scholar]
- Prabhu N. V.; Perkyns J. S.; Blatt H. D.; Smith P. E.; Pettitt B. M. Comparison of the Potentials of Mean Force for Alanine Tetrapeptide between Integral Equation Theory and Simulation. Biophys. Chem. 1999, 78, 113–126. [DOI] [PubMed] [Google Scholar]
- Prabhu N. V.; Perkyns J. S.; Pettitt B. M.; Hurby V. J. Structure and Dynamics of α-MSH Using DRISM Integral Equation Theory and Stochastic Dynamics. Biopolymers. 1999, 50, 255–272. [DOI] [PubMed] [Google Scholar]
- Maxwell D. S.; Tirado-Rives J.; Jorgensen W. L. A Comprehensive Study of the Rotational Energy Profiles of Organic Systems by Ab Initio MO Theory, Forming a Basis for Peptide Torsional Parameters. J. Comput. Chem. 1995, 16, 984–1010. [Google Scholar]
- Jorgensen W. L.; McDonald N. A. Development of an All-Atom Force Field for Heterocycles. Properties of Liquid Pyridine and Diazenes. THEOCHEM 1998, 424, 145–155. [Google Scholar]
- McDonald N. A.; Jorgensen W. L. Development of an All-Atom Force Field for Heterocycles. Properties of Liquid Pyrrole, Furan, Diazoles, and Oxazoles. J. Phys. Chem. B. 1998, 102, 8049–8059. [Google Scholar]
- Rizzo R. C.; Jorgensen W. L. OPLS All-Atom Model for Amines: Resolution of the Amine Hydration Problem. J. Am. Chem. Soc. 1999, 121, 4827–4836. [Google Scholar]
- Price M. L. P.; Ostrovsky D.; Jorgensen W. L. Gas-Phase and Liquid-State Properties of Esters, Nitriles, and Nitro Compounds with the OPLS-AA Force Field. J. Comput. Chem. 2001, 22, 1340–1352. [Google Scholar]
- Udier-Blagovi M.; Tirado P. M. D.; Pearlman S. A.; Jorgensen W. L. Accuracy of Free Energies of Hydration Using CM1 and CM3 Atomic Charges. J. Comput. Chem. 2004, 25, 1322–1332. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Ulmschneider J. P.; Tirado-Rives J. Free Energies of Hydration from a Generalized Born Model and an All-Atom Force Field. J. Phys. Chem. B 2004, 108, 16264–16270. [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
- Goldsack D. E.; Franchetto R. The Viscosity of Concentrated Electrolyte Solutions. I. Concentration Dependence at Fixed Temperature. Can. J. Chem. 1977, 55, 1062–1072. [Google Scholar]
- Drozdov A. N.; Grossfield A.; Pappu R. V. Role of Solvent in Determining Conformational Preferences of Alanine Dipeptide in Water. J. Am. Chem. Soc. 2004, 126, 2574–2581. [DOI] [PubMed] [Google Scholar]