Structure-based kernels for the prediction of catalytic residues and their involvement in human inherited disease

Abstract

Motivation: Enzyme catalysis is involved in numerous biological processes and the disruption of enzymatic activity has been implicated in human disease. Despite this, various aspects of catalytic reactions are not completely understood, such as the mechanics of reaction chemistry and the geometry of catalytic residues within active sites. As a result, the computational prediction of catalytic residues has the potential to identify novel catalytic pockets, aid in the design of more efficient enzymes and also predict the molecular basis of disease.

Results: We propose a new kernel-based algorithm for the prediction of catalytic residues based on protein sequence, structure and evolutionary information. The method relies upon explicit modeling of similarity between residue-centered neighborhoods in protein structures. We present evidence that this algorithm evaluates favorably against established approaches, and also provides insights into the relative importance of the geometry, physicochemical properties and evolutionary conservation of catalytic residue activity. The new algorithm was used to identify known mutations associated with inherited disease whose molecular mechanism might be predicted to operate specifically though the loss or gain of catalytic residues. It should, therefore, provide a viable approach to identifying the molecular basis of disease in which the loss or gain of function is not caused solely by the disruption of protein stability. Our analysis suggests that both mechanisms are actively involved in human inherited disease.

Availability and Implementation: Source code for the structural kernel is available at www.informatics.indiana.edu/predrag/

Contact: predrag@indiana.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Enzymes are critically important macromolecules that accelerate chemical reactions with high efficiency and rate enhancement (Wolfenden and Snider, 2001). Driven by accumulating structural and functional data as well as by increasing computational power, various general mechanisms to account for the molecular basis of enzyme catalysis have been proposed (Benkovic and Hammes-Schiffer, 2003; Garcia-Viloca et al., 2004). Despite this, many enzymes have still not been functionally annotated and many aspects of enzyme catalysis remain unclear, including the precise details of reaction chemistry or the geometry of the active sites (Benkovic et al., 2008; Gutteridge and Thornton, 2005). Thus, computational methods for the identification of active sites and their catalytic residues have the potential to identify novel catalytic pockets, aid the design of more efficient enzymes and in some instances predict the molecular basis of disease.

Catalytic residues are typically defined as amino acid residues directly involved in the chemistry of catalysis (Bartlett et al., 2002; Zvelebil and Sternberg, 1988). Hence, those residues involved in substrate binding and protein stability, or simply supporting the geometry of the active site are not regarded as catalytic residues sensu stricto, despite being vital for catalytic function. Aided by the growing number of annotated enzymes (Porter et al., 2004), the signatures of catalytic sites have been extensively studied, yielding new insights into protein structure-to-function principles (Gutteridge and Thornton, 2005). Catalytic residues are known to be enriched in polar residues and depleted in hydrophobic residues, but most are not directly exposed to water (83%), resulting in below-average relative accessible surface areas and B-factors (Bartlett et al., 2002). Catalytic residues have also been highly conserved over evolutionary time, both structurally and sequence-wise (Bartlett et al., 2002; Youn et al., 2007). As a result, their disruption is expected to result in greatly reduced or complete loss of catalytic activity.

Various computational methods have been proposed to facilitate the task of predicting catalytic residues from protein structure. The earliest published work employed spherical neighborhoods around catalytic residues to define structural neighborhoods, and used conservation of both sequence and structure to investigate the properties of catalytic residues (Zvelebil and Sternberg, 1988). Although this study was only based on the structures of 17 proteins (36 catalytic residues), its conclusions were supported by subsequent work. Indeed, to this end, other groups have exploited the increasing number of annotated catalytic residues and more advanced computational techniques (Alterovitz et al., 2009; Gutteridge et al., 2003; Ondrechen et al., 2001; Ota et al., 2003; Petrova and Wu, 2006; Sankararaman et al., 2010; Tang et al., 2008; Tong et al., 2008, 2009; Torrance et al., 2005; Youn et al., 2007). These methods are all based on vector representations of various sequence, structural and evolutionary features, from which a machine learning model is trained.

Catalytic residue prediction is bound up with the broader issue of residue function prediction from protein structures; therefore, in principle, other approaches can also be used for this task. Most of these methods can be categorized into template-based (Wallace et al., 1996), residue microenvironment-based (Gregory et al., 1993), or graph-theoretic methods (Grindley et al., 1993). In addition, structural alignment programs can provide baseline annotation of catalytic sites. Such methods can readily incorporate the structural similarity of larger and non-spherical neighborhoods. However, they may be less sensitive to evolutionary conservation or to changes in physicochemical properties than the geometry of the sites. Finally, whole-molecule protein function prediction algorithms (Pazos and Sternberg, 2004), combined with methods for predicting functional residues in general (Elcock, 2001), can also be exploited.

From the machine learning perspective, kernel-based methods have recently gained importance in computational biology, in part because of their solid theoretical foundations (Schölkopf et al., 2004). In kernel-based methods, a similarity function is created between pairs of objects such as amino acid sequences (Leslie and Kuang, 2004), secondary structure elements (Borgwardt et al., 2005) or residue neighborhoods (Vacic et al., 2010), and then used in a supervised learning scenario. Kernel methods can be advantageous in cases where a relationship between pairs of objects can be hypothesized to explicitly incorporate prior knowledge into the similarity function. In contrast, non-kernel-based classification models (e.g. neural networks) typically construct features that are considered important for the prediction step. These models do not naturally permit the explicit encoding of prior knowledge such as pairwise object similarities. Furthermore, kernel-based approaches can benefit from the large-margin classification algorithms such as support vector machines (SVMs), but can also be used in combination with simpler methods such as k-nearest neighbors.

In this study, we developed a novel kernel-based approach for the prediction of catalytic residues, and functional sites in general. The predictor was extensively evaluated against established approaches and used to identify instances where the loss or gain of catalytic residue activity could plausibly represent the molecular basis of disease. Our results suggest that the loss, and interestingly also the gain of catalytic residues, may be actively involved in human-inherited disease.

2 METHODS

For the purposes of this analysis, we have assumed that local residue environments contain sufficient information to allow the recognition of catalytic residues and that protein crystal structures provide an adequate representation of their in vivo counterparts. Our goal has been to construct a classification model that outputs a posterior probability that a given residue is catalytic.

2.1 Structure-based residue environments

To exploit the information present in the 3D neighborhood of a potential functional site, we first define a residue environment as a sphere centered around the C_α atom. The directionality of this structural environment is determined by transforming the original atomic coordinates from the Protein Data Bank (PDB) files into the new coordinates using the positions of three backbone atoms with C_α as the origin. The z-axis direction is formed from the vector connecting the amide nitrogen (N) with the carbonyl carbon (C); the y-axis direction is defined as the cross product of the unit vector with direction from C_α to C and the unit vector with direction from C_α to N; finally, the x-axis is formed as the direction of the cross product between the y-axis and the z-axis. This residue-based coordinate system is similar to that proposed by Grossman et al. (1995).

To facilitate similarity calculations, the coordinate system is further transformed to the spherical coordinates. A point with coordinates (x, y, z) is represented by a vector (r, φ, θ), where 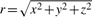, φ=arctan(y/x) and θ=arccos(z/r), with φ ∈ [0, 2π) and θ ∈ [0, π). In the spherical coordinate system, each local environment is divided into cells defined by a vector (Δr, Δφ, Δθ). The total number of cells in the residue environment is n=⌈r/Δr⌉ · ⌈2π/Δφ⌉ · ⌈π/Δθ⌉ + 1, where 1 represents a special cell for the residue whose structural neighborhood is considered and includes only the origin of the coordinate system. Note that the cells are of non-uniform volume since their size progressively increases with distance from the origin. Finally, a residue is considered to be in a cell if its C_α atom resides within the cell's boundaries.

2.2 Structure-based kernel function

The kernel function K(x, y) between two residue neighborhoods, x and y, represented by the contents of their respective cells, is calculated as

(1)

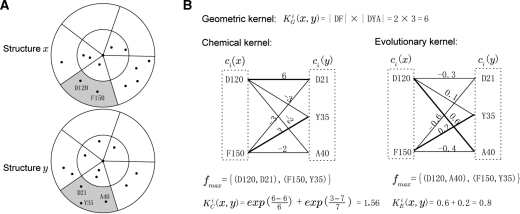
where K_G(x, y) is a geometric kernel, K_C(x, y) is a chemical kernel and K_E(x, y) is an evolutionary kernel between the two neighborhoods. Each of the kernel functions is defined below and a detailed example of a calculation for a 2D situation is provided in Figure 1.

Fig. 1.

An example of kernel calculation. (A) Two 2D structural neighborhoods x and y divided into cells. (B) calculation of the geometric, chemical and evolutionary kernel values for cell c_i (shaded in grey). K_Gⁱ(x, y) = |c_i.(x.|·|c_i.(y.)| represents part of the inner product in the definition of K_G(x, y) corresponding to the cell c_i. The bold lines indicate mappings of the f_max used to calculate K_Cⁱ(x, y) and K_Eⁱ(x, y).

Let 𝒜 be the set of all amino acids. Also, let c_i(x) ⊆ 𝒜 × ℤ⁺ be a set of pairs of amino acids and their protein positions in cell c_i of neighborhood x. To define geometric similarity between x and y, K_G(x, y), we first introduce vector c(x) as

(2)

where |c_i(x)| represents the number of residues from neighborhood x in cell c_i. Then, K_G(x, y) is computed as an inner product between the two respective vectors of counts c(x) and c(y) as

(3)

Calculating chemical similarity between two neighborhoods is more complex due to the possibility that |c_i(x)| ≠ |c_i(y)|. To address this, we first construct a partial matching from the smaller set to the larger set of amino acids and consequently define a similarity function using the matched residues only. More formally, let us consider cell c_i in neighborhoods x and y and let c_ℓ and c_s be the cells with the larger and smaller number of elements, respectively, with an arbitrary assignment if |c_i(x)| = |c_i(y)|. Let also f : c_s → c_ℓ be some 1–1 mapping between two non-empty cell contents c_s and c_ℓ. Then, we define the best mapping f_max between cell contents c_s and c_l as

(4)

where s(A, B) is a symmetric similarity function that depends upon the difference in physicochemical properties between residues in A and B, but ignores their positions. An example of such a function is the BLOSUM62 matrix.

To take advantage of the substitution matrix as a similarity measure between amino acids, we make the following transformation

(5)

which maintains matrix symmetry and generates a positive semi-definite matrix for a number of scoring matrices (e.g. BLOSUM50, BLOSUM62, BLOSUM80, PAM120 and PAM250). This can be easily verified by computing the matrix eigenvalues.

We can now define a chemical similarity function between neighborhoods x and y in cell c_i as

(6)

The chemical kernel between neighborhoods x and y can be expressed as

(7)

The evolutionary kernel for cell c_i is defined as

(8)

where p(A) is an evolutionary profile vector for the amino acid at its protein position j. The evolutionary profile is calculated from the j-th column (p_j) of the position-specific scoring matrix normalized by its length, i.e. p(A) = p_j / ‖p_j‖. The evolutionary kernel between structural neighborhoods x and y can be computed as

(9)

Function K_G(x, y) is a kernel because the inner product matrix is positive semi-definite (Schölkopf et al., 2004). Functions K_Cⁱ(x, y) and K_Eⁱ(x, y) belong to a class of optimal assignment kernels (Fröhlich et al., 2005). Such kernels have shown good performance in practice (Boughorbel et al., 2004; Fröhlich, 2006), but are not positive semi-definite in the general sense (Vert, 2008). While it is an open question under which precise conditions optimal assignment kernels will be positive semi-definite, we note that a symmetric matrix K can always be transformed into a positive semi-definite kernel K′ using the following transformation: K′ ← K − λ_minI, where λ_min is the smallest eigenvalue of K, and I is the identity matrix (Fröhlich, 2006). In our experiments, this transformation was unnecessary since K_C and K_E, which are summations of optimal assignment kernels, were always positive semi-definite. Under the above-mentioned conditions, K(x, y) defined in (1) is a kernel owing to the fact that the kernel property is closed under addition and multiplication (Schölkopf et al., 2004).

2.3 Datasets

Data from the Catalytic Site Atlas (CSA) v2.2.10 (http://www.ebi.ac.uk; (Porter et al., 2004)) were downloaded but only literature-supported catalytic residues were included as positive examples. Sites in sequences with > 40% identity were considered to be redundant and were removed using the ASTRAL40 v1.73 database as a filter. The negative sites were collected from PDB chains, where at least one positive site with the same amino acid was reported. Out of 7125 catalytic residues in CSA, the final non-redundant set used for training comprised 986 catalytic and 112 851 non-catalytic residues. In total, the dataset contained 314 protein chains associated with 339 families, 248 superfamilies and 189 folds. Note that the family, superfamily and fold classification were defined in terms of protein domains; thus, a multi-domain chain can be associated with more than one family (superfamily and fold). Family, superfamily and fold classifications were based on SCOP (Murzin et al., 1995).

To examine the contribution of inherited disease mutations giving rise to the gain or loss of catalytic residues, the public version of the Human Gene Mutation Database (HGMD; http://www.hgmd.org) was analyzed (Stenson et al., 2009). Mutations in HGMD were first mapped to PDB structures in order to obtain their 3D environments. For each mutation site, a 51 residue long sequence centered around the wild-type amino acid at the mutation position was aligned against the PDB sequences. Mutation sites without an exact match were excluded from the further study. An exact match was required because we intended to analyze the influence of single amino acid substitutions. Another set of putatively neutral inherited polymorphisms was downloaded from the Swiss-Prot database and used to provide statistical confidence for the prediction of gains and losses of catalytic residues. Of 31 139 missense mutations acquired from HGMD, 7225 were successfully mapped to PDB structures. Similarly, of 29 346 polymorphisms from Swiss-Prot, 1370 were mapped to PDB structures. Polymorphisms matching HGMD mutations were removed prior to mapping.

2.4 Training and evaluation of classification models

For a given set of training examples D = {(x, d)}, where d ∈ {−1, +1} is the class label (+1 if catalytic; −1 otherwise), a kernel matrix K can be calculated by computing all the pairwise similarity functions K(x_i, x_j). We used the SVM^light package (Joachims, 2002), with a default value for the capacity parameter C, to train a classification model for a given K. After the calculation of the support vectors by the SVM optimizer, the prediction score for an unseen example x can be computed as score(x) = ∑_iα_id_iK(x_i, x), where x_i is the i-th support vector and α_i the i-th Lagrange multiplier calculated during the SVM optimization process. Since score(x) ∈ (−∞, +∞), it is commonly converted into a probability value using a sigmoid function.

Predictor evaluation was carried out as a 10-fold cross-validation in four different scenarios: (i) per chain; (ii) per family; (iii) per superfamily; and (iv) per fold. Thus, in each of the 10 cross-validation steps, 1/10-th of protein chains (families, superfamilies and folds) were included in the test set, while the remaining proteins were used for training. The original dataset was randomly split into 10 non-overlapping partitions based on protein chain, family, superfamily and fold information for each residue. Thus, all residues from any single chain (family, superfamily and fold) were either in the training set or the test set. To obtain stable estimates of classifier performance, each 10-fold cross-validation was repeated 10 times with different random partitions and the results were averaged across the 10 runs.

We estimated sensitivity (sn), specificity (sp), precision (pr) and the area under the ROC curve (AUC) to characterize the performance of the classifiers. For a given decision threshold, sensitivity (also called recall, rc), is defined as the fraction of positive examples correctly predicted, specificity is defined as the fraction of negative examples correctly predicted, while precision is the fraction of all positive predictions that were correct.

2.5 Comparative evaluation

Comparative assessment of methods proposed for catalytic residue prediction is difficult due to prior evaluations on several different datasets using several different evaluation strategies and metrics. Thus, we decided to test our model against well-established methods for which the software was either available or possible for us to implement. This scenario guaranteed training and testing on the same data, using the same evaluation protocol. We downloaded FEATURE (Wu et al., 2008) and also implemented the method by (Gutteridge et al., 2003) using exactly the same features as described by the authors (we refer to the latter model as the GBT algorithm, based on the initials of authors' surnames). However, some other recent methods such as ResBoost (Alterovitz et al., 2009) and Discern (Sankararaman et al., 2010) could not have been obtained and tested at this time (K. Sjölander, personal communication). A positive to negative class prior ratio of 1 : 6 was used in training, as proposed previously (Gutteridge et al., 2003).

We note that FEATURE is based solely on residue microenvironments, constructed from the concentric spheres around each residue of interest. Its representation includes counts of atom types and their properties, counts of residue types and their properties, counts of various chemical groups and secondary structure information. In addition to the various sequence- and structure-based features, the GBT method also uses evolutionary information. It includes six types of features: conservation, relative solvent accessibility, residue depth, cleft information, secondary structure type and residue type (Gutteridge et al., 2003).

2.6 Prediction of the gain and loss of catalytic residues

We defined the probability of the gain and loss of a catalytic residue for mutations based on the probabilities that the residue is catalytic in the wild-type protein (p_wt) and the mutant (p_mt). The probability of loss of a catalytic residue was calculated as p_loss = p_wt·(1 − p_mt), while the probability of gain of a catalytic residue was calculated as p_gain = p_mt·(1 − p_wt). This method assumes that the event of catalysis in the wild-type molecule is independent of the event in the mutant protein, since the two proteins are physically different molecules. To control for false positives, we used the set of putatively neutral polymorphisms, which provide a score distribution of amino acid substitutions that are unlikely to affect protein function. An empirical P-value can be calculated from this null distribution and used to assess the significance of scores for the disease-associated mutations. Thus, scores in the set of disease-associated mutations that were above 95% of the scores in the putatively neutral set would yield P ≤ 0.05.

3 RESULTS

3.1 Parameter optimization

The set of cells in the structural neighborhood was defined by four tunable parameters (r, Δr, Δφ and Δθ), where r was the radius of the sphere. The cysteine subset, i.e. a set of all neighborhoods centered around cysteines, was chosen for parameter optimization because it was a dataset with an approximately average number of positive examples over all catalytic residues. The best-performing parameter set was then used on the whole dataset. This approach significantly reduced the time necessary for parameter selection and the potential for overfitting. We performed a grid-like search by selecting: {(r, Δr, i)| r=6, 7,…, 18; Δr=1, 2,…, 6; i=1, 2, 3, 4} with 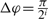and 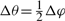. The parameter set with the best performance accuracy was: r=12 Å, Δr=4 Å, Δφ=π/2 and Δθ=π/4.

3.2 Performance evaluation

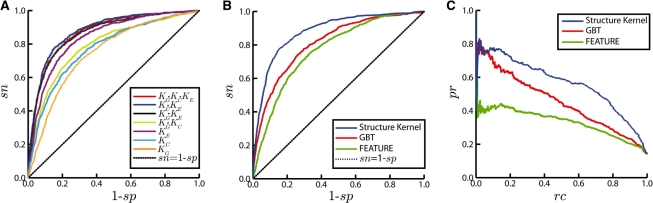
Using the parameters selected above, we used per-chain cross-validation to evaluate the performance accuracy of the three kernels individually (K_G, K_C and K_E), as well as of their various combinations (Fig. 2). As expected, the geometric kernel (AUC = 0.748) was individually inferior to the chemical (AUC = 0.774) and evolutionary kernels (AUC = 0.841). A combination of the geometric and chemical kernels (AUC = 0.791) outperformed any of the two individual components, but was still inferior to the evolutionary kernel. This is consistent with other studies that identified evolutionary conservation as the most important feature for predicting catalytic residues (Gutteridge et al., 2003; Youn et al., 2007). Interestingly, the geometric kernel improved the performance of both chemical (AUC = 0.791) and evolutionary kernels (AUC = 0.864). We believe that this is because chemical and evolutionary kernels do not penalize mismatches in the number of residues in each cell. The performance of the products of the two kernels containing K_E or all three kernels was very similar, with the kernel K_C · K_E (AUC = 0.879) slightly outperforming K_G · K_C · K_E (AUC = 0.873). However, in the most important part of the ROC curve, for false positive rates (fpr) <0.1, there was no difference in their performance. The area with the low fprs (fpr = 1− sp) is of greater interest because of the large imbalance between positive and negative examples (1 : 114 in the full dataset). Therefore, we used the product of all three kernels as our final model. The performance accuracy on the entire dataset (AUC = 0.873) was very similar to that without cysteine residues (AUC = 0.874) thereby ruling out overfitting due to parameter optimization.

Fig. 2.

(A) ROC curves for various structure kernels. (B) ROC curves for the structure kernel compared with FEATURE and GBT. (C) Precision–recall curve for the structure kernel compared with FEATURE and GBT. The black dotted line represents a uniformly random model. ROC and precision–recall curves were estimated using a per-chain 10-fold cross-validation on the same dataset.

The structure-based kernel was also evaluated against FEATURE and the GBT method (Fig. 2B and C). In terms of AUC, the structure kernel outperformed FEATURE by 13.8% and the GBT method by 7.6% (Fig. 2B). However, at the fpr level of 0.05, the structure kernel had a significantly higher sensitivity (sn = 0.453) than either FEATURE (sn = 0.209) or GBT (sn = 0.340), as shown in Table 1. It should be noted that since FEATURE does not use evolutionary information, it should also be compared to the K_C · K_G kernel. In this case, we observed an increase in AUC of 3.1% and an increase in sensitivity of 44.5% for the fpr of 0.05. Although FEATURE uses both amino acid and atomic data representation, we believe that the structure kernel has an increased accuracy due to the use of oriented structural neighborhoods and the selection of a kernel function.

Table 1.

Performance comparison between the three methods of catalytic residue prediction when evaluation was carried out per chain, family, superfamily and fold

	FEATURE		GBT		Structure Kernel
	AUC	sn	AUC	sn	AUC	sn
Fold	76.4	0.20	80.4	0.34	86.1	0.40
Superfamily	76.5	0.20	80.8	0.34	86.1	0.40
Family	76.7	0.21	80.7	0.34	86.8	0.42
Chain	76.7	0.21	81.1	0.34	87.3	0.45

Methods were evaluated on the same dataset using 10-fold cross-validation. The sensitivity sn is shown for sp = 0.95.

All methods were also evaluated by exclusion of particular protein families, superfamilies and folds, as shown in Table 1 (a list of families, superfamilies and folds on which the structure-based kernel performed well or poorly is listed in Supplementary Material). In all experiments, the residues of multidomain proteins were allowed to be split across training and test sets. However, all residues belonging to one chain, family, superfamily or fold were still required to be in either training or test partitions (a stricter experiment that did not allow for a protein to be split across partitions provided nearly identical results; data not shown). The results indicate that there is very little variation between the four different evaluation scenarios, suggesting that the dataset filtered using ASTRAL40 was sufficiently diverse to prevent the model from overfitting. In addition, these results emphasize that the signatures of catalytic residues are inherently local, rather than influenced by families, superfamilies or folds of entire chains. A similar trend was previously reported by Youn et al. (2007) using the S-BLEST method.

3.3 Loss and gain of catalytic residue activity in inherited disease

Catalytic residue predictors were applied in the context of missense mutations causing inherited disease in an attempt to identify those mutations responsible for the loss or gain of catalytic residue activity. The probabilities of loss or gain of catalytic residues were calculated from the probabilities that the residue is catalytic in the wild-type molecule (p_wt) and the mutant (p_mt). Using the putatively neutral polymorphisms to form the empirical null distribution (Noble, 2009), two sets of thresholds, corresponding to 1% and 5% fprs for p_loss and p_gain, respectively, were used to select mutations with relatively confident predictions of loss/gain of catalytic residue activity. At the 1% fpr level, we found that 3.5% of disease-associated mutations were predicted to give rise to a loss of a catalytic residue (P = 2.0 × 10⁻⁸; Fisher's exact test). At the 5% level, 11.4% of disease mutations had scores greater than the threshold (P = 7.0 × 10⁻¹⁵). Similarly, for the gain of catalytic residues, 3.5% (P = 1.0 × 10⁻⁸) and 10.4% (P = 1.1 × 10⁻¹¹) of disease mutations were predicted to be positives at fpr levels of 1% and 5%, respectively. These results indicate significant differences in the distributions of potential/putative catalytic site mutations between the neutral polymorphisms and disease-associated mutations. They also suggest that the gain and loss of catalytic residues are important mechanisms of inherited disease. In practical terms, the differences in the right tails of the score distributions also allow for the estimation of the false discovery rate (fdr) for a particular decision threshold (Noble, 2009). For example, at the 1% fpr level, we estimate fdr = 1/3.5 = 0.286 for both the loss and gain of catalytic activity. At the 5% fpr level, we estimate fdr = 5/11.4 = 0.439 for the loss and fdr = 5/10.4 = 0.481 for the gain of catalytic residue activity.

We searched the literature for experimental evidence to support our predictions. Two such cases are discussed below.

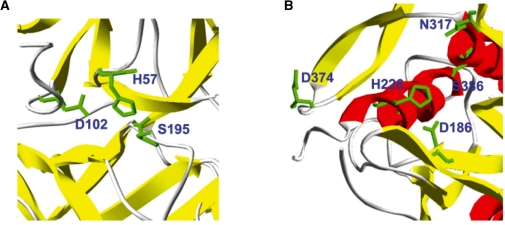
1. Loss of catalytic residue in coagulation factor IX (F9): F9 is activated in response to injury of the blood vessel and has a key role in blood clot formation. F9 itself is a precursor protein that becomes activated to a serine protease through post-translational cleavage. Its catalytic triad consists of H221, D269 and S365 residues (Porter et al., 2004) in activated F9 (Fig. 3A). Mutations in F9 give rise to the X-linked recessive disorder, hemophilia B. Mutation H221R has the probability of loss p_loss = 0.274, which is above the 5% fpr threshold of 0.255. Due to ASTRAL40 filtering, the triple (H221, D269 and S365) was not part of our training set.

2. Gain of catalytic residue in proprotein convertase subtilisin/kexin type 9 (PCSK9): PCSK9 is a member of the proteinase K subfamily of subtilases that reduces the number of LDL receptors (LDLRs) in liver through a hitherto undefined post-transcriptional mechanism. Lagace et al. (2006) have shown that purified PCSK9 added to the medium of HepG2 cells reduces the number of cell-surface LDLRs in a dose- and time-dependent manner. This activity was approximately 10-fold greater for a gain-of-function mutant, PCSK9(D374Y), that causes hyper-cholesterolemia (Lagace et al., 2006). Our prediction of gain of catalytic activity p_gain for D374Y is 0.262 (greater than the fpr = 0.05 threshold of 0.252). Recently, it was also shown that D374H was as potent as D374Y in reducing cell-surface LDLR (Fasano et al., 2009), with our score p_gain = 0.261. The authors also suggested that D129N, R496W and N425S were more potent than the wild-type protein, but less potent than the D374 mutants; our predicted p_gain scores were 0.229, 0.220 and 0.177, respectively. The trend indicates that the predicted scores can provide a quantitative measure of the magnitude of the gain of catalytic function. The predicted catalytic pocket for PCSK9 is shown in Figure 3B.

Fig. 3.

Three-dimensional visualization of structures with predicted gain and loss of catalytic residues. (A) F9 protein (1rfn; residues H57, D102 and S195 in PDB structure correspond to H221, D269 and S365 in F9 sequence) where substitution H221R leads to the loss of catalytic activity. (B) PCSK9 protein (2qtw; D186, H226, N317 and S386 are annotated catalytic residues in CSA with evidence code PSIBLAST) where substitution D374Y leads to a 10-fold increase in catalytic activity.

4 DISCUSSION

In this work, we introduced a novel kernel method for the prediction of functional residues in protein structures. The kernel function is a product of three kernels, each addressing a separate aspect of protein function: (i) the geometric kernel addresses the shape similarity; (ii) the chemical kernel addresses the similarity in physicochemical properties; and (iii) the evolutionary kernel addresses the evolutionary similarity of conservation patterns for the residues in two structural neighborhoods. Our approach was successfully applied to catalytic residue prediction and was favorably evaluated against two of the leading alternative approaches, FEATURE and GBT, on the same dataset. We showed that a construction of oriented structural neighborhoods and separation of the neighborhood volume into cells provides a good alternative to such approaches. The use of oriented neighborhoods was possible due to a very small coefficient of variation (2% in our dataset) between the bond angles of the backbone atoms.

Owing to its simplicity, the proposed kernel can be extended to incorporate a wider array of features. It may incorporate an atomic view of protein structure, or a view that exploits larger structural elements such as pockets, clefts or secondary structure elements. The structure of the kernel as a product of three kernel functions also provided insight into the relative importance of shape, physicochemical properties, and conservation for the prediction of catalytic residues. For example, the importance of evolutionary conservation for catalytic residue prediction was reported previously (Gutteridge et al., 2003; Youn et al., 2007) and confirmed in this work. The geometry of the catalytic residue environments evaluated well as an individual predictor and improved performance of the models based on evolutionary information and physicochemical similarities alone, but not together. This suggests that the site geometry is a distinct feature of catalytic residues, but also that evolutionary and chemical kernels already contain sufficient information about the site geometry, since they are also based on the division of the neighborhood into cells. Thus, for orphan proteins and proteins whose evolutionary history cannot be confidently inferred, a combination of the geometric and chemical kernel will still provide useful performance. Finally, we note that in addition to the product kernel, we also examined a linear combination of the three kernels (with equal weights) as well as a kernel where a combined similarity value was calculated in each cell, before adding them over all cells. These kernels had slightly lower accuracy than the product kernel.

Despite good performance, the machine learning model proposed herein is limited by several basic assumptions. For instance, because the protein structure was considered to be fixed, natural residue fluctuations and movements among alternative conformations will not have been allowed for. An additional constraint is the dependency of protein structures on experimental conditions used for crystallization, such as pH or temperature (Mohan et al., 2009).

The application of our structure-based kernel on known disease-associated mutations and putatively neutral polymorphisms serves to demonstrate that structure-based statistical inference methods can be successfully used to infer the molecular basis of disease. We assumed that the structure of the wild-type protein and its mutant counterpart were identical because the disruption of protein structure or stability can be addressed using alternative approaches (Capriotti et al., 2005). However, these approaches cannot address loss of function events without loss of structure. Wang and Moult (2001) constructed a rule-based model to infer the molecular cause of disease from protein structures and later extended it to SVM-based approaches (Yue and Moult, 2006; Yue et al., 2005). These models cannot, however, predict functional residues such as catalytic residues or post-translational modifications.

It is important to mention that the gain or loss of a catalytic residue does not necessarily result in the gain or loss of enzymatic activity. The gain of a catalytic residue is most likely to be observed in already existing catalytic pockets, where the correct geometry and favorable chemistry are already present. Hence, the gain of catalytic residues may change the rate of the catalytic reaction, as discussed in Section 3.3, but will only very rarely generate catalytic pockets or enzymes de novo. Similarly, the loss of a catalytic residue does not necessarily result in the complete loss of enzymatic function. Thus, when assigning scores for the gain and loss of catalytic residue activity, we assigned the same priors to these events. Until such a time as the estimates of the likelihoods of such events can be precisely ascertained, we believe that this approach is justified.

We have previously proposed sequence-based methods to infer the molecular cause of disease, associating disease mutations with the loss or gain of protein structure and function (Li et al., 2009; Mort et al., 2010; Radivojac et al., 2008). However, for those proteins whose structures have been solved or can be accurately modeled, it is important to improve the statistical inference methods in order for them to be subsequently utilized in translational research.