Abstract
Motivation: Designing mathematical tools that can formally describe the dynamics of complex intracellular processes remains a challenge. Live cell imaging reveals changes in the cellular states, but current simple approaches extract only minimal information of a static snapshot.
Results: We implemented a novel approach for analyzing organelle behavior in live cell imaging data based on hidden Markov models (HMMs) and showed that it can determine the number and evolution of distinct cellular states involved in a biological process. We analyzed insulin-mediated exocytosis of single Glut4-vesicles, a process critical for blood glucose homeostasis and impaired in type II diabetes, by using total internal reflection fluorescence microscopy (TIRFM). HMM analyses of movie sequences of living cells reveal that insulin controls spatial and temporal dynamics of exocytosis via the exocyst, a putative tethering protein complex. Our studies have validated the proof-of-principle of HMM for cellular imaging and provided direct evidence for the existence of complex spatial-temporal regulation of exocytosis in non-polarized cells. We independently confirmed insulin-dependent spatial regulation by using static spatial statistics methods.
Conclusion: We propose that HMM-based approach can be exploited in a wide avenue of cellular processes, especially those where the changes of cellular states in space and time may be highly complex and non-obvious, such as in cell polarization, signaling and developmental processes.
Contact: kresimir.letinic@yale.edu; derek.toomre@yale.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Both fixed and live cell imaging studies often employ only visual inspection or very limited statistical analysis (such as comparisons of means) based on the expected effects of some treatment. In static imaging, a variable of interest is compared under different conditions at a single or few time points. Live fluorescence microscopy has the potential to reveal dynamic changes in a given variable at multiple time points and under different treatments. The resulting temporal sequence of data points extracted from a movie sequence is the starting point for understanding the dynamics of a cellular process. With the advantages of lower background disturbance and higher temporal resolution, total internal reflection fluorescence microscopy (TIRFM) has been widely used for investigating the dynamics of membrane trafficking events, such as exocytosis of secretory vesicles (Deng et al., 2009). During exocytosis, a vesicle generated inside a cell fuses with the plasma membrane. This process is essential for the delivery of membrane receptors and secreted substances to the cell surface and thus critical for normal cellular function in all eukaryotic cells.
Live cell imaging generates data sequences of such complexity that a precise and meaningful description of a biological process necessitates a dynamic quantitative approach (Patterson et al., 2008; Phair and Misteli, 2001; Ronneberger et al., 2008; Sebastian et al., 2006; Talaga, 2007; Wang et al., 2006). Characterization of organelle behavior by visual inspection is hampered by the lack of unique criteria for (and thus user bias in) defining putative ‘functional cellular states’ and low sampling. It is common to attempt to formulate these criteria based on measurements of a variable of interest. To illustrate, in live cell imaging one may wish to determine how direction and rate of displacement of an organelle changes over time. A natural approach is to assume that some arbitrary observed rates or directionalities represent ‘real’ cellular states; e.g. plus-end motion of a vesicle along a microtubule corresponding to a kinesin motor and minus-end motion to a dynein. Due to an inherent variability in noisy biological systems, a manual assignment of two states will lack flexibility and precision and may fail to characterize unclear patterns, e.g. if an organelle pauses due to competing motors. Applying subjective criteria may also result in overlooking important aspects of system's dynamics, which are difficult to observe by naked eye, precluding complete characterization of the underlying molecular mechanisms. Robust methods are needed that can deal with data uncertainty, determine correctly the number of states and reveal the timing of state transitions; such methods have the potential to precisely describe spatial and temporal dynamics of biological processes. In our previous work, we focused on the spatial aspect of exocytosis (Keller et al., 2001; Letinic et al., 2009; Sebastian et al., 2006): by using end-point analysis, we were able to obtain a static description of the distribution of exocytic events on the cell membrane. Typically, we mapped all fusion events that we observed and then applied tests to determine whether they were distributed randomly or clustered into hotspots. While such static analyses are useful, we are often interested in how biological processes evolve over time as a result of dynamic changes in cellular environment. The ability to quantitate dynamic changes in cells and subcellular organelles is extremely important in both basic research and clinical studies.
In this study, we demonstrate that dynamic probabilistic networks called hidden Markov Models (HMMs) can uncover the dynamics of cellular states based on the sequence of outcomes of an observable variable, which conveys information about organelle behavior. Markov and hidden Markov chains can be used to describe processes whose state changes over time in a probabilistic manner (Rabiner, 1989). While in a regular Markov chain model, the states are directly observable, in a hidden Markov chain model, the only observable variable is the one that has an outcome influenced by the hidden states. Since hidden states have a probability distribution over possible outcomes of the observed variable, the sequence of observations contains information about the sequence of hidden states; thus, an algorithm can uncover hidden states. HMMs, first described by Baum and others in the 1960s (Baum et al., 1970), have been used in speech recognition, robotics and later in the analysis of DNA sequence and some single molecule fluorescence studies (Rabiner, 1989; Talaga, 2007).
From previous biophysical studies we have identified possible states of the system, though they are not directly observable, they are hidden. Two clues will help us uncover the sequence of hidden states: (i) rules that probabilistically link the outcomes of the observable variable to a particular state; and (ii) rules that probabilistically relate the states to one another (e.g. State 2 is more likely to be directly preceded by State 1). These clues are outcome and transitional probabilities, respectively, the parameters of HMM. Outcome probabilities determine the observable outcomes generated by hidden states, while transitional probabilities determine state transitions.
Our approach consists of several steps during which we will: (i) design ‘observable’ data sequences as the input for HMM; (ii) estimate multiple model's parameters (assuming 1–10 states) via HMM algorithms; (iii) get an indication of the optimal HMM via model selection methods; and (iv) reveal the trends/patterns in resulting Markov chain state-paths via statistical tools of logistic and ordinal logit regression. Expectation–maximization (EM) algorithms are methods for finding maximum likelihood estimates that are applicable to many statistical problems, including hidden Markov chains (Baum et al., 1970; Dellaert, 2002; Dempster et al., 1977; Rabiner, 1989). EM is a description of a class of related algorithms, not a specific algorithm; the Baum–Welch algorithm is an EM algorithm applied to HMMs (Baum et al., 1970). It can compute maximum likelihood estimates and posterior mode estimates for the transitional and outcome probabilities of an HMM, when given only observed sequence of points as training. A dynamic programming algorithm called the Viterbi algorithm is used for finding the most likely sequence of hidden states, called the Viterbi path, given the model parameters uncovered via EM algorithm and given the sequence of observed events (Rabiner, 1989; Viterbi, 1967).
The object of this study is to find dynamic changes in membrane trafficking events induced by insulin, the hormone critical for normal glucose metabolism. Glut4 is an insulin-responsive glucose transporter, expressed in insulin-responsive tissues such as muscle and fat; Glut4 is responsible for insulin-regulated glucose uptake into these tissues (Larance et al., 2008; Muretta et al., 2008; Watson and Pessin, 2007). In the last decade, the insulin-regulated Glut4 translocation to the plasma membrane has been a major focus in the diabetes field, as dysregulation can cause type II diabetes, the most common type. While various modes of insulin signaling have been implicated in Glut4 translocation, traditional assays were unable to resolve discrete steps in Glut4 vesicle trafficking, including membrane tethering and fusion steps of vesicles carrying Glut4. Several studies proposed that an octameric protein complex, the exocyst, previously suggested to direct secretory vesicles to specialized sites at the plasma membrane in various cell types (Matern et al., 2001; Munson and Novick, 2006; Wang and Hsu, 2006), mediates the effect of insulin by tethering Glut4 vesicles to the plasma membrane (Chen et al., 2007; Inoue et al., 2003). Resolving how insulin signaling and the exocyst could control the spatial–temporal dynamics of where and when Glut4 vesicle fuse is a critical issue in the diabetes field. In this study, we tested whether insulin acting through the exocyst complex can dynamically regulate the spatial sites and/or the rate of Glut4 vesicle exocytosis. Using TIRF microscopy and the HMM mathematical approach, we provide direct evidence for such regulation. HMM was critical in that it allowed us to dissect the number of states involved and real-time kinetics of the exocytic process before and after insulin stimulation. Specifically, we modeled dynamic changes in the spatial distances and time intervals between consecutive fusion events. For each imaged cell, we obtained a sequence of spatial distances and another sequence of time intervals from the sequence of movie frames. We inputed these observed sequences into an HMM and obtained two sets of parameters, one for the spatial and other for the temporal model. Based on these parameters, we extracted spatial and temporal Markov chain, respectively, that represents the uncovered sequence of ‘hidden’ states, each of which gives rise to a unique range of outcomes (i.e. spatial distances or time intervals). Essentially, by using HMMs, we were able to address precisely the hidden states that regulate trafficking in adipocytes and its regulation by insulin.
2 METHODS
2.1 Cell culture and RNAi treatment
3T3-L1 Glut4-GFP cells were cultured, differentiated and stimulated as previously described. Briefly, 3T3-L1 preadipocytes were grown to confluence in dulbecco's modified eagle's medium (DMEM) containing 10% fetal bovine serum (FBS), l-Glutamine and Pen/Strep (Medium A) at 37○C in 5% CO2. Two-day post-confluence (Day 0) differentiation was induced with methylisobutylxanthine (0.5 mM), dexamethasone (0.25 μM) and insulin (1 μg/ml). After 3 days, cells were replated on Mattek dishes, serum starved overnight and switched to an imaging buffer (NaCl, 2.5 mM; KCl, 2 mM; CaCl2, 1.3 mM; MgCl2, 10 mM; HEPES, 7.4). We targeted Sec8 using RNAi; three different siRNAs (25mer double-stranded ‘stealth’ design, Invitrogen) were first evaluated by double transfecting 293 cells with rat Sec8-GFP and siRNAs. siRNAs that decreased the newly synthesized Sec8-GFP (exogenous) were then screened by western blotting for knockdown of endogenous Sec8 in adipocytes. Quantification showed around 70% knockdown. For RNAi experiments, cells were transfected twice (3 and 1 days before differentiation) as preadipocytes, with Sec8 or scrambled RNAi (100 nM).
2.2 TIRF imaging
TIRFM images were acquired using an inverted microscope equipped with a 1.45 NA 60 × TIRFM lens (Olympus, Center Valley, PA), back-illuminated electron-multiplying charge-coupled device camera (512 × 512, 16-bit; iXon887; Andor Technologies) and controlled by Andor iQ software (Andor Technology, South Windsor, CT). Excitation was achieved using a 488 nm line of argon laser, under continuous exposure and acquired at 2 Hz. The calculated evanescent field depth was 100 nm. Cells were imaged before and after insulin stimulation (0.4 μM final concentration) at 37○C for around 15 min. TIRFM data were uploaded into a customized Matlab-based software (Natick, MA) for the detection of exocytic vesicles. All vesicle information (time, position) was stored and used to generate temporal and spatial maps of vesicle docking and fusion.
2.3 Statistical modeling
2.3.1 Data sequences
For every cell, different exocytosis (events) are manually recorded from the image sequences. In our analysis, each exocytosis event is defined by its location at the plasma membrane and its occurrence time. If N fusions are observed during the time interval [0, T], our data are represented by the set X = {(xi, yi, ti)}1,…,N. The data are post-processed to obtain new sequences composed of measured spatial (Euclidean) distance and time interval (inter-arrival time, t), respectively, between fusion events. For temporal analysis (first sequence), we measured inter-arrival times between consecutive fusion events, i.e. Ot = (Xt+1 − Xt)1,…,N−1. We then averaged in groups of 10 consecutive events to minimize the impact of outliers, obtaining a new sequence yt = ∑k=t−9tOk / 10. In the same way for spatial analysis (second sequence), we averaged the distances between a designated arbitrary event and 10 events that immediately preceded it. The resulting sequence contained (N−10) terms for a total of N events recorded (typically >200–300 events per sequence). Thus, the first 10 events represent a ‘warming interval’ and the observed sequence {y}x starts with the event 11. Once we obtained the sequence of distances or inter-arrival times, the range of values was divided into 10 bins, such that the smallest range of values was in bin 1. In this way, each hidden state can assign probability to 10 possible outcomes ( = bins).
2.3.2 The HMM
We considered a hidden Markov chain model for (X, Y) = (X0,…, Xn, Y0,…, Yn), where positive real numbers Yi represent either the observed quantized values of spatial distances or inter-arrival times, respectively, between fusion events, and the random variables Xi are hidden cellular states. Y-sequences were generated as described in the previous section. X-sequence of hidden states was uncovered from the Y-sequence using HMM algorithms.
The model was parameterized by the parameter space θ = (ξ, A, B); ξ is the distribution of X0, matrix A is the probability transition matrix of the hidden chain X (with elements A(k, l) = P{Xi+1 = l | Xi = k}, k, l ∈ S, S is the state space of X); matrix B describes the transitions from Xi to Yi (with elements B(k, l) = P{Yi = l|Xi = k}, k ∈ S, l ∈ Q, Q is the state space of Y). The parameters of the model were determined using an EM algorithm that iteratively searches for θ that maximizes the likelihood function L (θ) = pθ(y), i.e. the probability of data as a function of the parameters of the model {ξ, A, B}. The sequence of hidden states was then reconstructed using the Viterbi algorithm.
2.3.3 EM algorithm
The goal of the algorithm is to find θ maximizing L(θ). An EM algorithm produces a sequence of θ1, θ2,…, θn that increase in likelihood (L(θ0) ≤ L(θ1) ≤ … ≤ L(θn)) (for EM steps, including forward–backward algorithm, see Rabiner, 1989). The obtained model parameters represent the expected values of A and B matrix elements conditional on the data. Starting with θ0, the new parameter was taken to be the θ1 and the procedure was repeated 200 times. The whole cycle was repeated 50 times to minimize the danger of converging to a local instead of global maximum of the likelihood function (the confidence intervals for transitional probabilities were obtained). We calculated standard errors of the transitional probabilities by using the values of transitional probabilities for all the cells included in the analysis. Confidence intervals were obtained from standard errors of these parameters.
We compared HMMs that assume different numbers of states using AIC (Akaike information criterion). AIC can be seen as the goodness of fit minus the complexity of the model and it gives a good indication of the optimal model. AIC measures the fit of an estimated model and is defined as log(Lk) − |k|, where log(L) is the log-likelihood of the model evaluated at the MLE (maximum likelihood estimator) and k is the number of the degrees of freedom. The value of log(L) is given in the output of the HMM, while the value of k represents the number of free elements in the matrices ξ, A and B. Clearly, k increases as the number of hidden states increases. We chose the model with the maximal AIC (see Supplementary Table 1).
2.3.4 The Viterbi algorithm
Once we selected the best HMM, we obtained the most likely sequence of hidden states that generated the observed outcomes sequence. Multiple sequences of states (paths) can lead to a given state, but one is the most likely path to that state, called the ‘survivor path’. This is a fundamental assumption of the algorithm because the algorithm will examine all possible paths leading to a state and only keep the one most likely. The best sequence of hidden states maximizes the joint probability of hidden states and observations, P(X, y) = Pθ (X0 = x0, X1 = x1,…, Xn = xn, Y0 = y0, Y1 = y1,…,Yn = yn). For steps of the algorithm, see Rabiner (1989).
In the current study, the hidden path represents Markov chain that best describes the spatial and temporal changes of vesicle fusion events in any particular cell. In particular, Markov chain includes changes in the cellular states induced by insulin, specifically at 0.4 μM final concentration. The moment of insulin addition within each Viterbi path is indicated by an arrow. In the spatial chain, different states give rise to different ranges of distances between fusion events. In the temporal chain, different states give rise to different ranges of time intervals between fusion events. Logistic and ordinal logit regression were used to estimate the odds ratios for Markov chain state paths (implemented in R).
2.3.5 Spatial statistical methods
We previously developed an approach based on spatial statistics methods for use in live cell imaging (Sebastian et al., 2006). The central concept is distinguishing between a spatial Poisson process, in which the probability of an event is the same at all locations, and a clustered process, in which the location of points depends on the location of nearby points. The relevant statistic is the Ripley K-function, or K(r) (Diggle, 2003; Ripley, 1981, 1988). We used L(r), because it is a variance-stabilized version of K(r). To test how far the observed distribution of fusion events is from Poissonian, we compared the L-plot of an observed process to the range (envelopes) of L plots of ∼1000 Poisson processes generated by Monte Carlo simulations using R statistical program. The Monte Carlo simulation produced a random pattern of fusion event locations across the cell area using the observed spatial intensity estimate (number of events per area). The L-function was then calculated for the observed cell and each simulated Poisson process. The algorithm positions a circle with radius r on any given event and counts the neighboring events inside the circle; it repeats this for different radius sizes and then calculates and plots L(r) as a function of r. The higher the level of clustering, the higher the value of L(r) will be. L-plots of cells with spatial clustering will be located above the L-plots of cells with Poissonian distributions of events. A bootstrap method was used for estimating standard errors and confidence intervals and for the comparison of different groups.
3 RESULTS AND DISCUSSION
The methodology described has been applied to the study of a complex problem in live cell imaging, the study of insulin-regulated exocytosis (Larance et al., 2008; Watson and Pessin, 2007). The goal was to use our HMM methodology to characterize precisely the spatial temporal dynamics of membrane trafficking events controlled by insulin. Insulin regulates the number of Glut4 glucose transporters on the cell surface by stimulating Glut4 vesicles to exocytose at the plasma membrane (Larance et al., 2008; Watson and Pessin, 2007), a process facilitated by the exocyst protein complex (Chen et al., 2007; Inoue et al., 2003; Matern et al., 2001; Munson and Novick, 2006; Wang et al., 2006).
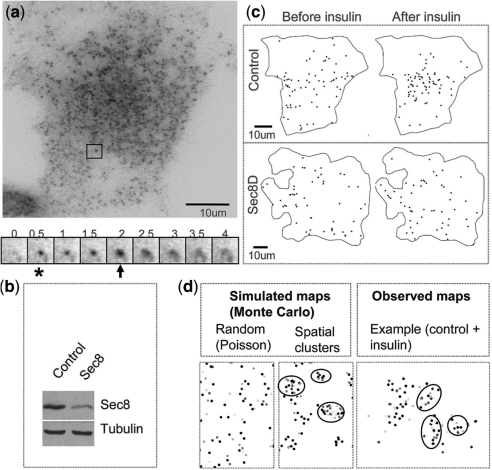
Rigorous analysis requires monitoring and analyzing exocytosis at a single vesicle level. We used an adipocyte cell line that stably expresses myc-Glut4-GFP and TIRFM to visualize single vesicle fusion (Fig. 1a). A custom-Matlab program was developed to facilitate the identification of vesicle fusion at the plasma membrane by an expert. Spatial–temporal maps of vesicle fusion sites were recorded for control cells and cells in which we knocked down a major exocyst subunit, Sec8 (Fig. 1b). The observed data Oi was a tuple Oi = xi, ti of position and fusion time over the imaged sequence. Visual inspection of cumulative fusion maps suggested that the distribution of fusion events changes from relatively dispersed to more clustered upon insulin stimulation (Fig. 1c). Nonetheless, these observations did not account for time evolution, which makes it difficult to assess the sample since the total number of fusions increases over time.
Fig. 1.
Imaging of exocytosis in adipocytes. (a) TIRFM image of an adipocyte (above). An example of a Glut4 vesicle is framed. A sequence of images shows a fusion event (below). Numbers are shown in seconds. When a vesicle enters the evanescent field and tethers to the membrane (asterisk), it increases in fluorescence intensity and appears as a bright spot. As it fuses (arrow), the dye increases in intensity and rapidly spreads, yielding a characteristic flash. (b) A western blot shows an expected decrease of Sec8 by RNAi knockdown on the level of endogenous Sec8 protein (tubulin serves as a loading control). (c) Spatial maps of fusion events in a control and a Sec8-depleted (Sec8D) cell. (d) Point processes simulated using Monte Carlo methods and an example of clusters observed in the control cells after insulin stimulation (on right). Fusion events appear in different shades of gray because the time axis (removed because it was not relevant) was color-coded. The observed clusters resemble simulated spatial clusters. Several visually apparent clusters are circled.
As a proof-of-principle study of the power and utility of HMM in live cell imaging of an important topical issue, we applied HMM to insulin-regulated exocytosis (Larance et al., 2008; Watson and Pessin, 2007). The goal of the present study was to characterize the number and evolution of underlying hidden spatial and temporal states of Glut4 vesicle trafficking events controlled by insulin and exocyst complex protein, Sec8.
To validate and quantize these changes in real time, we designed an HMM approach (Fig. 2). In general, our approach consists of the following steps: (i) calculation of the observed sequence; (ii) EM algorithm for identifying model parameters, which maximize the likelihood of the observed sequence; (iii) AIC-based model selection method to suggest the optimal number of states in the model; and (iv) the Viterbi algorithm to reveal the most likely sequence of hidden states.
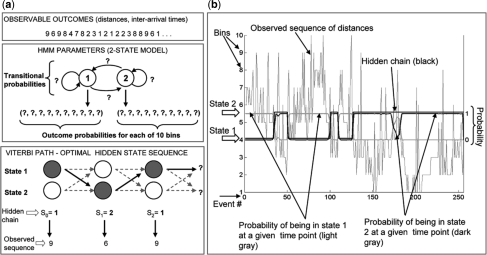
Fig. 2.
A diagram of the approach to model dynamics of exocytosis via HMM. (a) The algorithm: in the first step, a map of fusion events is obtained by using a custom-made Matlab program. The ‘observed’ sequence of Euclidean distances is derived from the spatial coordinates of mapped fusion events. This sequence served as input into the EM algorithm, which revealed the most likely model parameters, outcome and transitional probabilities. Finally, the Viterbi algorithm revealed the most likely sequence of hidden states, based on the model parameters discovered in the previous step. (b) Two-state HMM of a control adipocytes: HMM output (the hidden chain and probabilities of being in State 1 and 2 at any time point) is superimposed on the observed sequence of spatial distances. X-axis shows fusion events ordered in temporal sequence. Bins 1–10 (Y-axis on the left side of the graph) represent subranges of the observed spatial distances between consecutive fusions. There are 10 bins, with bin 1 representing the shortest distances and bin 10 the longest distances. The posterior probabilities (probability of chain being in State 1 or 2, given the observed sequence) are shown with the corresponding Y-axis on the right side of the graph that ranges from 0 to 1. Notice that when the probability that the chain is in State 2 equals zero, the probability that the chain is in State 1 equals one. This makes sense since the chain cannot be in both states simultaneously. In addition, notice that for the most part, the hidden chain is in State 2 when the probability that the chain is in State 2 is bigger than the probability that the chain is in State 1.
We first focused on the spatial distribution of Glut4 vesicle exocytosis and its change upon insulin stimulation. A critical issue and starting point for this analysis were conceiving an observable variable that conveys information about the spatial distribution of vesicle fusion. As more vesicle events occur over time, the distance between neighboring events decreases. This could significantly distort the data if we looked at the distance between a new event and its nearest neighbor. Instead, we considered the distance between a given event and a small fixed number of preceding events (Section 2); this metrics does not depend on the overall density of events. When spatial distribution fluctuates between less and more clustered, this parameter fluctuates between larger and smaller values, respectively. We then focused on the rate of Glut4 vesicle exocytosis and its change upon insulin stimulation. The parameter of interest was inter-arrival time, or time interval between consecutive events, which becomes shorter when the rate of exocytosis increases (Section 2). In the case of both spatial distances and inter-arrival times, we binned the obtained values of parameters into 10 bins (bin 1 = shortest subrange of values; bin 10 = longest subrange of values; this gave 10 possible outcomes of observable variables distance and time interval). Hidden states will assign some probability between 0 and 1 to each of these bins/outcomes. An observed sequence and its associated hidden Markov chain is shown in Figure 2.
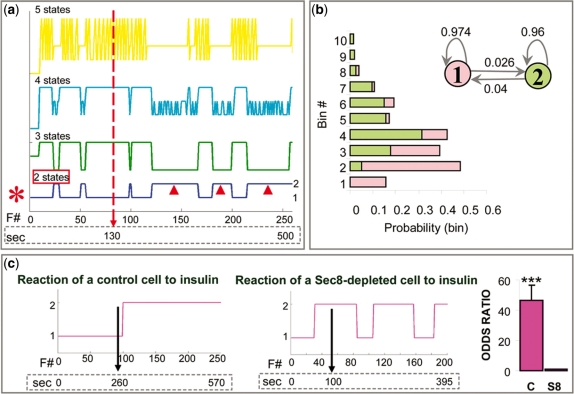
We started our analysis with the spatial data. In many biological processes, the correct number of hidden states is unknown, even though one may hypothesize different models based on accumulated knowledge. We hypothesized that insulin recruits the exocyst at the cell membrane and thus facilitates tethering of Glut4 vesicles to specialized hot spots, which are active zones near insulin receptors. The simplest model would be a two-state model, in which one state reflects random distribution and another state reflects more clustered spatial distribution of events (hot spots). Alternatively, spatial regulation could involve additional molecular mechanisms and thus more than two states. We ran several models, assuming 1–10 states (Fig. 3a). For each model (number of states), we tried dividing the observed values into different number of bins (2–20 bins; Supplementary Table 1). Smaller numbers of bins resulted in higher AIC values; however, the choice of binning did not affect the selection of the optimal number of hidden states. Model selection criterion (AIC) indicated that the two-state model is the optimal one (Supplementary Tables 1 and 2), regardless of the number of bins, so we focused specifically on the parameters of that model (Fig. 3b). We decided to work with 10 bins because 10 bins provide sufficient detail about the distribution of outcomes of hidden states. Even though AIC values are the highest when only two bins are used, two bins results in only two outcomes, which is a very crude representation of the observed values of spatial distances. We calculated the following parameters: (i) transitional probabilities indicated a relatively small probability of switching between the two states; (ii) outcome probabilities indicated that ‘State 1’ favors, or gives more probability to bins with larger spatial distances (we call it unclustered or ‘UC’ state), while ‘State 2’ favors bins with small values of distances (we call it clustered or ‘CL’ state, as clusters become visible after insulin). Thus, at time points when a cell is in UC state, we will observe longer distances between consecutive fusion events and when a cell is in CL state, we will observe shorter distances and clustering of events. We calculated confidence intervals for the transitional probabilities, especially because of the small values obtained for the probabilities of switching between the states and the possibility that the intervals contain zero probability of switching. Equivalently, we wanted to exclude the possibility that confidence intervals for the probabilities of staying in the same state, i.e. not switching, include 1, which is 100%. The mean probability of not switching from UC state was 96.2% (at α = 0.001, the confidence interval is 94.1–98.4%). The mean probability of not switching from CL state is 94.2% (at α = 0.001, the confidence interval is 90.8-−97.7%). These findings strongly support that the two states of the Markov chain communicate with each other.
Fig. 3.
HMM of Glut4-exocytosis: spatial regulation. (a) HMMs assuming 1 (dark green), 2 (blue), 3 (light green), 4 (cyan) or 5 (yellow) states, from a control cell. Plots of hidden Markov chain state paths corresponding to each model are shown. The x-axis contains both the fusion event number (F # ) and time in seconds; the vertical arrow shows the time of insulin addition. The individual states of the optimal model (red asterisk), i.e. a two-state model, are labeled on the right of the plot. Arrowheads mark portions of the state-path when the chain is in State 2, the dominant state after insulin stimulation. (b) Parameters of the two-state model shown in (a). The two states and their transitional probabilities are shown in the upper right corner. The graph on the left shows probabilities that the two states assigns to different bins (graph bars and states of the model are color-coded). (c) State-paths of representative control and Sec8-depleted cells. The vertical arrow shows the moment of insulin addition. The graph on the far right shows the odds ratios, i.e. the factor by which the odds of being in ‘State 2’ change when we add insulin to cells. The odds ratio for control cells is around 46 for control (C) cells and ∼1 for Sec8-depleted (S8) cells.
Finally, we obtained the sequence of hidden states for the two-state model and compared hidden chains of control and Sec8-depleted cells. Remarkably, the probability that the hidden chain is in ‘State 2’ dramatically increases, from 5.2% to 72%, after insulin stimulation (equivalently, the odds of being in State 2 highly significantly increase, P < 0.001; Fig. 3c). This switch occurs rather rapidly, within a few seconds after the stimulation, and commonly persists for up to ∼10 min (i.e. until the end of the movie), although in some cases there is a switch back to ‘State 1’, possibly because the effect of insulin is transient. Sec8 depletion abolishes this effect, as the odds that the hidden chain is in ‘State 2’ do not change significantly after insulin stimulation (P = 0.8; Fig. 3c). This indicated that Sec8 and thus the exocyst play a role in the spatial regulation of Glut4 exocytosis by insulin and that the effect of insulin is rapid and transient.
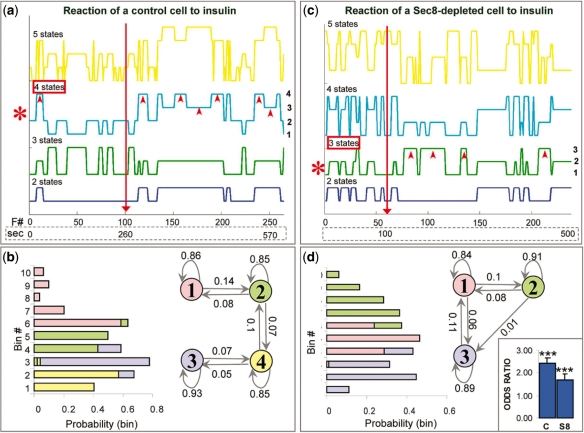
We next analyzed the temporal data. Insulin plays a role in the release of vesicles from the intracellular pool, allowing them to travel toward the cell membrane where they fuse. Insulin also recruits the exocyst at the cell membrane and presumably facilitates tethering of Glut4 vesicles to the membrane. The simplest model would be a two-state model, in which one state reflects a slow rate of events (mostly before insulin) and another state reflects a faster rate (mostly after insulin). However, a more realistic model would take into account several levels of regulation. We hypothesized at least two insulin-induced states, both favoring relatively fast rate of fusion events (fast rate = short intervals). The kinetics of the molecular switch activated by insulin at the cell membrane (presumably the exocyst) differs from the kinetics of the switch activated deep inside the cell (Muretta et al., 2008; Watson and Pessin, 2007). The complex interplay between these two mechanisms should allow us to dissect several insulin-induced states. We ran several HMMs, as before (Fig. 4a and b). Model selection methods indicated that in control cells, a four-state model was optimal (Supplementary Table 2) so we focused specifically on the parameters of that model (Fig. 4c). Transitional probabilities indicated relatively small probabilities of switching between any pair states, but they were still higher than those observed in the spatial model. Outcome probabilities indicated that States 1 and 2 favor larger values of time intervals, i.e. slower fusion rates (State 1 being the slowest), while States 3 and 4 favor smaller values of time intervals and thus faster rates (State 4 being the fastest). Upon insulin stimulation, the odds of any combination of states favoring shorter intervals (e.g. State 4) versus the remaining states (States 1–3) are ∼2.4 greater (P < 0.001; Fig. 4d). This is in agreement with the notion that insulin stimulates Glut4 vesicle fusion. As in the case of spatial regulation, this switch occurs rather rapidly, within a few seconds after the stimulation, and commonly persists for up to ∼10 min. Interestingly, Sec8 depletion did not completely abolish the effect of insulin, as it did in the case of spatial regulation. The effect of Sec8-depletion was two-prong. First, the optimal model had only three states: State 2 favored the longest time intervals, i.e. the slowest rates, State 1 favored the medium-range intervals and State 3 favored the shortest intervals and thus the fastest rate (state numbers are arbitrary). Secondly, the odds of any combination of states favoring shorter intervals (e.g. States 1 and 3 combined) versus the remaining states (State 2) were only ∼1.7 greater, suggesting smaller impact of insulin than in control cells. The two effects strongly suggest that the exocyst plays an important role in the regulation of Glut4 vesicle fusion rate. The loss of one state presumably corresponds with the loss of one site of insulin action, i.e. at the cell membrane. In conclusion, HMM was able to dissect various steps of the temporal process, including the loss of one such step in treated cells, based on a single observable variable, i.e. the time interval.
Fig. 4.
HMM of Glut4-exocytosis: temporal regulation. (a and b) HMMs assuming 2 (blue), 3 (green), 4 (cyan) or 5 (yellow) states, from a control cell (a) and a Sec8-depleted cell (b). Plots of state-paths corresponding to various models are shown (axes/labels are as in previous figure). The individual states of the optimal model (red asterisk) are labeled on the right of the plot (a four-state model for the control cell and a three-state model for the Sec8-depleted cell). In both cases, arrowheads point to states which favor short intervals between events and which are dominant after insulin. (c and d) Parameters of the four-state model (c) and the three-state model (d), shown in (a) and (b), respectively. In both cases, Markov model with the states involved and their transitional probabilities is shown on the right and the graph with the outcome probabilities is on the left (graph bars and model states are color-coded). The graph on the far right shows the odds ratios, i.e. the factor by which the odds of being in states that favor shorter intervals increase when we add insulin to cells (see main text).
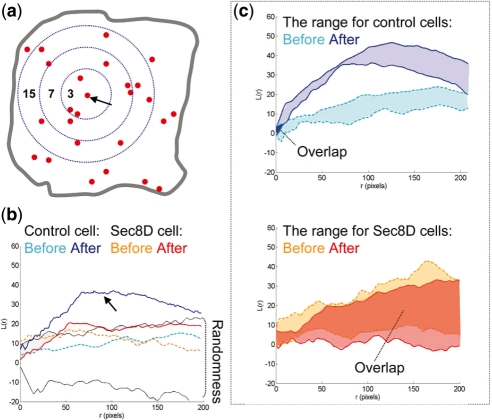
To corroborate our findings obtained using HMM, we used spatial statistical methods based on L-function (Diggle, 2003; Ripley, 1988) that we applied to the problem of exocytosis in previous work (Sebastian et al., 2006). We analyzed cumulative spatial maps of fusion events obtained by plotting separately all events before and after insulin stimulation, respectively. In this case, we disregarded the temporal information and only considered spatial coordinates of fusion events. Using Monte Carlo methods, we compared the obtained maps with simulated maps having completely random distribution of points. We established that the exocytic spatial point process before insulin stimulation is similar to random/Poisson process (Fig. 5), in which the probability of an event is the same at all locations and there is no spatial dependence among events. However, insulin causes prominent spatial clustering (L-function plots become significantly different from random/Poisson; bootstrap P-value = 0.01). Sec8-depletion prevents insulin-induced spatial clustering (most L-plots after insulin stimulation have a random/Poisson distribution, and are not significantly different; bootstrap P-value is 0.96) (Fig. 5). Static end-point analysis of spatial maps thus supports the notion of spatial clustering induced by insulin. Such regulation of fusion sites presumably links insulin-receptor signaling at the membrane to membrane trafficking events. The physiological significance of spatial regulation remains to be established, but it may promote the fidelity of insulin response since exocyst disturbance impairs glucose uptake.
Fig. 5.
A comparison of L-curves of control and Sec8-depleted cells. (a) The scheme illustrates the principle of L-function estimation. The numbers are counts of events within distance r from an arbitrary event (marked by the arrow). The number increases as the radius increases. This counting is repeated for every fusion event. L-function values are estimated for each radius size. (b) L-curves obtained from the control and Sec8-depleted cells shown in Figure 1 (plotted as a function of radius r). The lined area delimits the range of L-function values obtained from a set of simulated random/Poisson point processes (labeled randomness). There are two curves for each cell, one obtained before and one obtained after insulin stimulation. Insulin promotes an upward shift of the L-curve above the envelopes of randomness only in the control cells (arrow). (c) The range of L-function values for control and Sec8-depleted cells before and after insulin stimulation. Notice that ‘before’ and ‘after’ areas do not overlap in the control, but they mostly overlap in the Sec8-depleted group [the overlaps are labeled with dark blue (control) and dark red (sec8-depleted) solid colors, respectively].
Since the goal of this work was to validate a new approach based on HMMs, we chose a system in which we could make expectations about the behavior of the hidden process (hidden chain), as the moment of insulin addition served as an external reference point. We summarize the benefits of using HMMs for analyzing ‘subcellular’ dynamics:
We replace subjective arbitrary criteria with a precise statistical model for identifying functional cellular states.
We replace noisy sequence of observations, in which it may be hard to discern any obvious pattern, with a model with defined number of states, thus making rigorous analysis possible.
We can quantitatively interpret real-time dynamics of cellular processes, while common statistical approaches analyze only end-points of an experiment.
We can link distinct molecules to different aspects of the same process. For example, we showed that manipulating Sec8 affects the behavior of the spatial and temporal Markov chains in different ways.
We can correlate hidden Markov chains of more than one process (e.g. in multi-color imaging) and uncover previously unknown links between various processes.
4 CONCLUSIONS
We presented here a methodology based on HMMs and applied it to the problem of insulin-regulated exocytosis. The method provided new insight into the spatial and temporal regulation of Glut4 vesicle exocytosis and exocyst role in determining vesicle fusion sites at the plasma membrane. While the rainbow of fluorescent proteins has revolutionized the exploration of biology, the extraction and analysis of rich live cell datasets remains a new expanding area. Our results show that HMMs are beneficial in relatively simple cellular systems and their usefulness in other, more complex processes remains to be validated. We suggest that HMM can be exploited in a wide avenue of cellular processes, especially those where the changes of a state in space, time or both may be ill-defined by conventional criteria, such as those that occur in cell polarization, signaling and developmental processes.
AUTHOR CONTRIBUTIONS
K.L. and D.T. designed research, K.L. and A.B. designed and implemented the HMM, K.L. and R.S. did statistical data analysis, K.L. wrote the article with input from A.B. and D.T.
Supplementary Material
ACKNOWLEDGEMENTS
We thank A. Barron, P. Rakic, T. Koleske and Inhee Chung for helpful discussions, J. Bogan for suggestions on the paper and experimental work and for providing the cell line, members of J. Bogan's lab for their help with adipocyte protocols, all members of D. Toomre's lab for suggestions, S.C Hsu for providing antibodies against exocyst proteins and R.H. Scheller for providing Sec8-GFP. In addition to the papers in the reference list, the authors also referred Prof. J. Cheng's manuscript in preparation, ‘Stochastic Processes’. K.L. is a predoctoral fellow of the Howard Hughes Medical Institute.
Funding: National Institute of Health Award (1DP2OD002980-01 and YALE DERC pilot grant to D.T.).
Conflict of Interest: Patents are being filed on these method.
REFERENCES
- Baum L, et al. A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. Ann. Math. Stat. 1970;41:164–171. [Google Scholar]
- Chen X.-W, et al. Activation of rala is required for insulin-stimulated glut4 trafficking to the plasma membrane via the exocyst and the motor protein myo1c. Dev. Cell. 2007;13:391–404. doi: 10.1016/j.devcel.2007.07.007. [DOI] [PubMed] [Google Scholar]
- Dellaert F. Technical report. College of Computing, Georgia Institute of Technology; 2002. The expectation maximization algorithm, git-gvu-02-20. [Google Scholar]
- Dempster AP, et al. Maximum likelihood from incomplete data via the em algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977;39:1–38. [Google Scholar]
- Deng N, et al. Image processing for fusion identification between the glut4 storage vesicles and the plasma membrane. J. Signal Process. Syst. 2009;54:115–125. [Google Scholar]
- Diggle P. Statistical Analysis of Spatial Point Patterns. 2. Arnold, London; 2003. [Google Scholar]
- Inoue M, et al. The exocyst complex is required for targeting of glut4 to the plasma membrane by insulin. Nature. 2003;422:629–633. doi: 10.1038/nature01533. [DOI] [PubMed] [Google Scholar]
- Keller P, et al. Multicolour imaging of post-Golgi sorting and trafficking in live cells. Nat. Cell. Biol. 2001;3:140–149. doi: 10.1038/35055042. [DOI] [PubMed] [Google Scholar]
- Larance M, et al. The glut4 code. Mol. Endocrinol. 2008;22:226–233. doi: 10.1210/me.2007-0282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Letinic K, et al. Exocyst is involved in polarized cell migration and cerebral cortical development. Proc. Natl Acad. Sci. USA. 2009;106:11342–11347. doi: 10.1073/pnas.0904244106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matern HT, et al. The sec6/8 complex in mammalian cells: characterization of mammalian sec3, subunit interactions, and expression of subunits in polarized cells. Proc. Natl Acad. Sci. USA. 2001;98:9648–9653. doi: 10.1073/pnas.171317898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munson M, Novick P. The exocyst defrocked, a framework of rods revealed. Nat. Struct. Mol. Biol. 2006;13:577–581. doi: 10.1038/nsmb1097. [DOI] [PubMed] [Google Scholar]
- Muretta JM, et al. Insulin releases glut4 from static storage compartments into cycling endosomes and increases the rate constant for glut4 exocytosis. J. Biol. Chem. 2008;283:311–323. doi: 10.1074/jbc.M705756200. [DOI] [PubMed] [Google Scholar]
- Patterson GH, et al. Transport through the golgi apparatus by rapid partitioning within a two-phase membrane system. Cell. 2008;133:1055–1067. doi: 10.1016/j.cell.2008.04.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phair RD, Misteli T. Kinetic modelling approaches to in vivo imaging. Nat. Rev. Mol. Cell Biol. 2001;2:898–907. doi: 10.1038/35103000. [DOI] [PubMed] [Google Scholar]
- Rabiner LR. A tutorial on hidden Markov models and selected applications in speech recognition. IEEE J. Proc. 1989;77:257–286. [Google Scholar]
- Ripley B. Spatial Statistics. Chichester: Wiley; 1981. [Google Scholar]
- Ripley B. Statistical Inference for Spatial Processes. Cambridge: Cambridge University Press; 1988. [Google Scholar]
- Ronneberger O, et al. Spatial quantitative analysis of fluorescently labeled nuclear structures: problems, methods, pitfalls. Chromosome Res. 2008;16:523–562. doi: 10.1007/s10577-008-1236-4. [DOI] [PubMed] [Google Scholar]
- Sebastian R, et al. Spatio-temporal analysis of constitutive exocytosis in epithelial cells. IEEE/ACM Trans. Comput. Biol. Bioinform. 2006;3:17–32. doi: 10.1109/TCBB.2006.11. [DOI] [PubMed] [Google Scholar]
- Talaga DS. Cocis: Markov processes in single molecule fluorescence. Curr. Opin. Colloid Interface Sci. 2007;12:285–296. doi: 10.1016/j.cocis.2007.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viterbi A. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE J. IT. 1967;13:260–269. [Google Scholar]
- Wang S, Hsu S. The molecular mechanisms of the mammalian exocyst complex in exocytosis. Biochem. Soc. Trans. 2006;34:687–690. doi: 10.1042/BST0340687. [DOI] [PubMed] [Google Scholar]
- Wang Y, et al. From imaging to understanding: frontiers in live cell imaging, Bethesda, MD, April 19–21, 2006. J. Cell. Biol. 2006;174:481–484. doi: 10.1083/jcb.200607097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watson RT, Pessin JE. Glut4 translocation: the last 200 nanometers. Cell Signal. 2007;19:2209–2217. doi: 10.1016/j.cellsig.2007.06.003. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.