Abstract
In this paper we present a high-throughput system for detecting regions of carcinoma of the prostate (CaP) in HSs from radical prostatectomies (RPs) using probabilistic pairwise Markov models (PPMMs), a novel type of Markov random field (MRF). At diagnostic resolution a digitized HS can contain 80K×70K pixels — far too many for current automated Gleason grading algorithms to process. However, grading can be separated into two distinct steps: 1) detecting cancerous regions and 2) then grading these regions. The detection step does not require diagnostic resolution and can be performed much more quickly. Thus, we introduce a CaP detection system capable of analyzing an entire digitized whole-mount HS (2×1.75 cm2) in under three minutes (on a desktop computer) while achieving a CaP detection sensitivity and specificity of 0.87 and 0.90, respectively. We obtain this high-throughput by tailoring the system to analyze the HSs at low resolution (8 µm per pixel). This motivates the following algorithm: Step 1) glands are segmented, Step 2) the segmented glands are classified as malignant or benign, and Step 3) the malignant glands are consolidated into continuous regions. The classification of individual glands leverages two features: gland size and the tendency for proximate glands to share the same class. The latter feature describes a spatial dependency which we model using a Markov prior. Typically, Markov priors are expressed as the product of potential functions. Unfortunately, potential functions are mathematical abstractions, and constructing priors through their selection becomes an ad hoc procedure, resulting in simplistic models such as the Potts. Addressing this problem, we introduce PPMMs which formulate priors in terms of probability density functions, allowing the creation of more sophisticated models. To demonstrate the efficacy of our CaP detection system and assess the advantages of using a PPMM prior instead of the Potts, we alternately incorporate both priors into our algorithm and rigorously evaluate system performance, extracting statistics from over 6000 simulations run across 40 RP specimens. Perhaps the most indicative result is as follows: at a CaP sensitivity of 0.87 the accompanying false positive rates of the system when alternately employing the PPMM and Potts priors are 0.10 and 0.20, respectively.
Keywords: Markov Random Fields, Prostate Cancer Detection, Histology, Digital Pathology
1. Introduction
Prostate cancer poses a serious health problem for men: the American Cancer Society (ACS) estimates that in 2009 over 192,000 men will be diagnosed with carcinoma of the prostate (CaP) and 27,000 will die from it. Prostate cancer is typically detected (in the U.S.) through routine screening which includes a digital rectal exam and prostate-specific antigen test. If these tests reveal abnormalities, current screening protocol requires a trans-rectal ultrasound guided biopsy to remove tissue for histological examination. If this histological analysis reveals the presence of cancer, a surgeon may perform a radical prostatectomy (RP), excising the entire gland. Following prostatectomy, the prostate is sliced into histological sections (typically whole or quarter sections). The analysis of these histological sections (HSs) is important for several reasons: The spatial extent of CaP, as established by the analysis of HSs, can be registered to other modalities (eg. MRI), providing a “ground truth” for the evaluation of computer-aided diagnosis (CAD) systems that operate on these modalities (Madabhushi et al., 2005; Tiwari et al., 2009). Most importantly, grading (e.g. Gleason grading (Gleason, 1966)) the HSs helps determine patient prognosis and treatment (Heidenreich et al., 2008).
Though the grading of HSs1 is currently performed by clinicians, the advantages of automation have motivated the development of computerized systems (Naik et al., 2007; Tabesh et al., 2007; Doyle et al., 2008; Huang and Lee, 2009; Smith et al., 1999; Farjam et al., 2007). These advantages are as follows: 1) automated systems offer a viable means for analyzing the vast amount of the data present in HSs, a time-consuming task currently performed by pathologists, 2) the extraction of reproducible, quantifiable features can help refine our own understanding of prostate histopathology, thereby helping doctors improve performance and reduce variability in grading (Doyle et al., 2007; Montironi et al., 2005; Epstein et al., 2006), and 3) the data mining of quantified morphometric features may provide means for biomarker discovery, facilitating, for example, the identification of aggressive cancers, i.e. those cancers associated with a high likelihood of metastasis or post-treatment recurrence (Donovan et al., 2008; Cordon-Cardo et al., 2007).
Grading HSs, whether performed by a clinician or a machine, requires high-resolution images: the current clinical standard for Gleason grading (Epstein et al., 2006) recommends magnifications of 20× or 40× which correspond to resolutions of 0.5 µm and 0.25 µm per pixel, respectively. Unfortunately, at 0.25 µm per pixel a typical 2×1.75 cm2 digitized whole-mount histological section (WMHS) contains 80K×70K pixels — approximately 500 times the number pixels in a digital mammogram. Clearly, the automated grading of such an image in a reasonable time is untenable. Consequently, previous automated schemes have restricted their analysis to selected regions of the HSs. Typically, theses regions constitute less than 1/1000 of a WMHS. For example, Tabesh et al. (Tabesh et al., 2007) used textural features to Gleason grade tissue micro-arrays (TMAs) digitized at 20× magnification, yielding 1600 × 1200 images. In (Jafari-Khouzani and Soltanian-Zadeh, 2003) the authors used multi-wavelets to grade selected tissue samples at 100× magnification. Though the specific sizes were not mentioned, their illustrations suggest the samples were much smaller than TMA cores. Using fractal analysis, Huang et al. (Huang and Lee, 2009) graded 512×384 images with a resolution of approximately 0.25 µm per pixel (exact specifications were not provided). Farjam et al. (Farjam et al., 2007) constructed a biologically motivated system to grade small tissue samples imaged at 100× magnification. Smith et al. (Smith et al., 1999) performed Gleason grading on tissue samples digitized at 10× magnification, producing 64×64 images.
Data volume precludes the application of current Gleason grading algorithms directly to HSs. Fortunately, the grading procedure for HSs is inherently different than that for selected tissue samples such as TMA cores: only a small portion of each HS will, on average, contain cancer. Thus, grading can be separated into two distinct steps: 1) detecting CaP regions and 2) grading these detected regions. Therefore, if detection can be performed more quickly than grading, the execution time of entire process can be reduced. Though others have considered automated CaP detection (Roula et al., 2002; Diamond et al., 2004), no current system is capable of rapidly detecting cancer in an entire WMHS. In previous systems CaP detection was viewed as the end goal, and not as a possible precursor to further analysis; and consequently, high-throughput was not a priority. For example, Diamond et al. (Diamond et al., 2004) identified CaP in a WMHS digitized at 40× magnification. Dividing the WMHS into small 100×100 patches, they classified each patch individually using a single Haralick feature. However, the algorithm required manual segmentation and classification of the glands. Additionally, the processing time for the digitized WMHS (58K×42K pixels) was 5.5 hours.
In this paper we introduce a system for rapidly detecting CaP regions in hematoxylin and eosin (H&E) stained histological sections from radical prostatectomies. We envision this system constituting the initial stage of a comprehensive, hierarchical algorithm that quickly detects cancerous regions at lower resolutions, and then refines and ultimately Gleason grades these regions at higher resolutions. Our CaP detection system requires less than three minutes to process an entire WMHS (2×1.75 cm2) on a standard desktop computer (2.4 GHz Intel Core 2 processor, 4GB RAM). We achieve this high throughput by tailoring the algorithm to accurately analyze the HSs at low resolution (8 µm per pixel). For even at low resolution, gland size and morphology remain noticeably different in cancerous and benign regions (Kumar et al., 2004). This motivates the following algorithm: Step 1) glands are identified and segmented, Step 2) the segmented glands are classified as malignant or benign, and Step 3) the malignant glands are consolidated into continuous regions indicating the spatial extent of CaP.
Consistent with our goal of minimizing execution time, the classification of individual glands (Step 2) leverages two simple, but effective, features of biological relevance: 1) glands size and 2) the tendency for proximate glands to share the same class. The second feature describes a spatial dependency that exists among the glands. Accordingly, we choose to model this dependency using a Markov prior distribution, i.e. the glands will be modeled as a Markov random field. The merits of using MRFs to incorporate spatial dependencies have been demonstrated in a variety of computer vision tasks such as clustering (Pappas, 1992), denoising (Besag, 1986; Figueiredo and Leitao, 1997), and texture synthesis (Paget and Longstaff, 1998; Zalesny and Gool, 2001). MRFs are also prevalent in several medical imaging applications: detecting tumors in mammography (Li et al., 1995), identifying cancer in prostate MR imaging (Liu et al., 2009), and segmenting MR images of the brain (Zhang et al., 2001; Awate et al., 2006) and lung (Farag et al., 2006).
MRF priors are established through the construction of local conditional probability density functions (LCPDFs). These LCPDFs — one centered about each site — describe the local inter-site dependencies of a random process. In combination, these LCPDFs can establish a joint probability density function (JPDF) relating all sites. (This JPDF is the Markov prior.) However, only LCPDFs of certain functional forms will reconstitute a valid JPDF. Specifically, the Gibbs-Markov equivalence theorem (Besag, 1974) states that the JPDF will be valid if (and only if) it, and transitively the LCPDFs, can be represented as Gibbs distributions. That is, representing the JPDF as a Gibbs distribution guarantees that the attendant LCPDFs satisfy the Markov property and form a viable JPDF. However, since Gibbs distributions are expressed as a product of potential functions, tailoring LCPDFs to model a specific process devolves into the selection of these functions. Unfortunately, potential functions are mathematical abstractions, lacking intuition and physical meaning. Consequently, constructing LCPDFs through their selection becomes an ad hoc procedure, usually resulting in generic and/or heuristic models such as the prevalent Potts (Potts, 1952) prior.
Consequently, an important contribution of this work is the introduction of an intuitive MRF model — called a probabilistic pairwise Markov model (PPMM) — whose performance exceeds that of the Potts. In place of potential functions, PPMMs formulate the LCPDFs in terms of pairwise probability density functions (PDFs), each of which models the interaction between two neighboring sites. This formulation facilitates the creation of relatively sophisticated LCPDFs (and hence priors), increasing our ability to model complex processes.
To demonstrate the efficacy of our CaP detection system and assess the advantages of using a PPMM prior instead of the Potts, we alternately integrate both Markov priors into our algorithm and then conduct over 6000 simulations to rigorously evaluate system performance with respect to accuracy and computation time. We perform this evaluation across a cohort of 40 HSs obtained from 20 patients across two separate clinics. Thirteen are WMHSs, while the remaining 27 are quarter sections. The HSs predominately contain Gleason grade three and/or four tumors, as do over 80% of all specimens from RPs (Kattan et al., 1999; Stephenson et al., 2005; Roehl et al., 2004). These grades draw the most interest from researchers as they are the grades for which the predictive value of Gleason score is least effective (Andrn et al., 2006), and consequently, for which additional prognostic markers must be identified. In fact, current research indicates that several such prognostic markers reside in the morphological and architectural signatures of the glands, and yet, are not captured by the Gleason grade (Donovan et al., 2008; Cordon-Cardo et al., 2007).
The remainder of the paper proceeds as follows: We begin with a brief review of MRFs in Section 2. This review provides the context necessary for developing the PPMMs and discussing the glandular classification procedure. Section 3 then explicates our novel PPMM model. In Section 4 we present our comprehensive CaP detection system. A quantitative and qualitative evaluation of the detection algorithm is provided in Section 5. Concluding remarks are presented in Section 6.
2. Review of Markov Random Fields
2.1. Random Field Nomenclature
We first establish the general MRF terminology and notation that will be used throughout the paper. Let the set S = {1, 2,…,N} reference N sites to be classified. Each site s ∈ S has two associated random variables: Xs ∈ Λ indicating its state (class) and Ys ∈ ℝD representing its D-dimensional feature vector. Particular instances of Xs and Ys are denoted by the lowercase variables xs ∈ Λ and ys ∈ ℝD. Let X = (X1, X2,…,XN) and Y =(Y1, Y2,…,YN) refer to all random variables Xs and Ys in aggregate. The state spaces of X and Y are the Cartesian products Ω = ΛN and ℝD×N. Instances of X and Y are denoted by the lowercase variables x =(x1, x2,…,xN) ∈ Ω and y = (y1, y2,…,yN) ∈ ℝD×N. See Table 1 for a list and description of the commonly used notations and symbols in this paper.
Table 1.
List of notation and symbols commonly employed in this paper.
| Symbol | Description | Symbol | Description |
|---|---|---|---|
| S | Set referencing N sites | X ∈ Ω | Collection of all Xs : X =(X1, X2,…,XN) |
| E | Set of edges connecting sites | x ∈ Ω | Instance of X: x =(x1, x2,…,xN) |
| D | Number of dimensions in feature space | Ω | Domain of X and x: Ω = ΛN |
| Λ | Domain of Xs and xs | Y ∈ ℝD×N | Collection of all Ys : Y =(Y1, Y2,…,YN) |
| Xs ∈ Λ | Random variable indicating state at site s | y ∈ ℝD×N | Instance of Y: y =(y1, y2,…,yN) |
| xs ∈ Λ | Instance of Xs | ηs | Set of sites that neighbor s ∈S |
| Ys ∈ ℝD | Random variable indicating feature vector at site s | x−s | States of all sites r ∈S except s |
| ys ∈ ℝD | Instance of Ys | xηs | States of all sites such that r ∈ ηs |
| c | Clique, i.e. any fully connected subset of G | 𝒞s | {c ∈ 𝒞 : s ∈ c} |
| 𝒞 | Set containing all cliques | Vc | Potential function on clique c |
Let G = {S, E} establish an undirected graph structure on the sites, where S and E are the vertices (sites) and edges, respectively. A clique c is any subset of S which constitutes a fully connected subgraph of G, i.e. each site in c shares an edge with every other site. The set 𝒞 contains all possible cliques. A neighborhood ηs is the set containing all sites that share an edge with s, i.e. ηs = {r : r ∈ S, r ≠ s, {r, s} ∈ E}. If P is a probability measure defined over Ω then the triplet (G, Ω, P) is called a random field.
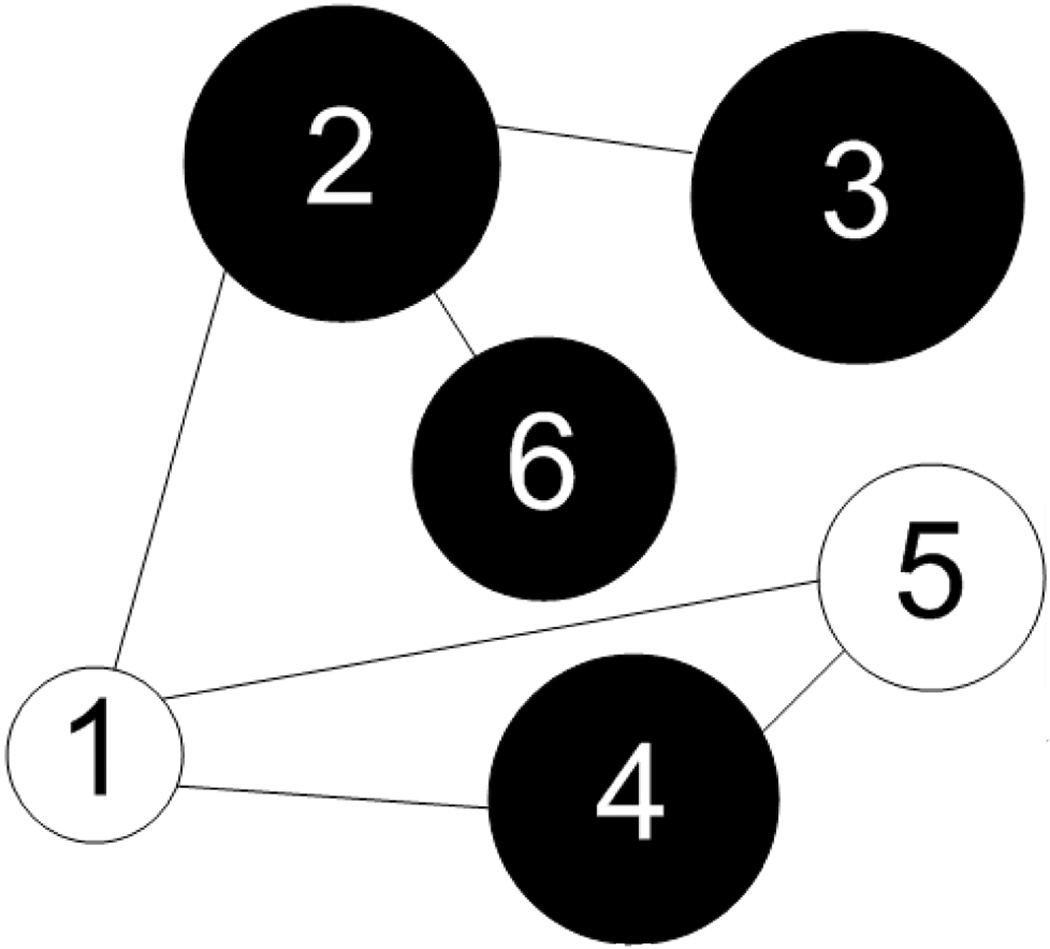
These concepts are best understood in the context of an example. The graph in Figure 1 has sites S = {1,2,3,4,5,6} and edges E = {{1,2} , {1,4}, {1,5}, {2,3}, {2,6}, {4,5}}. The neighborhood of site 5, for example, is η5 = {1,4}. There are six one-element cliques 𝒞1 = {{1}, {2}, {3}, {4}, {5}, {6}}, six two-element cliques 𝒞2 = E, and one three-element clique 𝒞3 = {{1,4,5}}. The set 6 is the union of 𝒞1, 𝒞2, and 𝒞3. The set of possible states for each Xs is Λ= {b,w}, where b and w represent black and white, respectively. The diameter of site s reflects the magnitude of the random variable Ys ∈ ℝ. For this example we have x = (w, b, b, b, w, b) and y = (0.9, 1.5, 1.6, 1.4, 1.1, 1.3).
Figure 1.
Graph with six sites and different binary states. Each site has an associated feature Ys ∈ ℝ. This is illustrated graphically by varying the diameter of each circle in accordance with the magnitude of its associated feature.
We also establish a convention for representing probabilities. Let P(·) indicate the probability of event {·}. For instance, P(Xs = xs) and P(X = x) signify the probabilities of the events {Xs = xs} and {X = x}. Whenever appropriate we will simplify such notations by omitting the random variable, e.g. P(x) ≡ P(X = x). Let p(·) represent a probability density function (PDF)2; for example, pg might indicate a Gaussian PDF. The notations P(·) and p(·) are useful in differentiating P(xs) which indicates the probability that {Xs = xs} from pg(xs) which refers to the probability that a Gaussian random variable assumes the value xs.
2.2. Maximum a Posteriori Estimation
Given an observation of the feature vectors Y, the objective is to estimate the states X. The preferred method is maximum a posteriori (MAP) estimation (Duda et al., 2001), which entails maximizing the following quantity over all x ∈ Ω:
| (1) |
The first term in (1) reflects the influence of the feature vectors. It can be simplified by assuming that all Ys are conditionally independent and identically distributed given their associated Xs. This assumption implies that if the class Xs of site s is known then 1) the classes and features of the remaining sites provide no additional information when estimating Ys and 2) the conditional distribution of Ys is identical for all s ∈ S. As a result we have
| (2) |
where the use of the single PDF pf indicates that P(ys|xs) is identically distributed across S. The second term in (1) — the prior distribution — reflects the expected homogeneity or texture pattern of the labels. In general, modeling this high-dimensional PDF is intractable. However, if the Markov property is assumed its formulation simplifies. This topic is discussed next.
2.3. Gibbs-Markov Equivalence
The random field (G, Ω, P) is a Markov random field (MRF) if all of its local conditional probability density functions (LCPDFs) satisfy the Markov property: P(xs|x−s)= P(xs|xηs), where x−s = (x1,…,xs−1, xs+1,…,xN), xηs = (xηs(1),…,xηs(|ηs|)), ηs(i) ∈ S is the ith element of the set ηs, and |ηs| is the cardinality of the set ηs. Thus, the Markov property simplifies the forms of the LCPDFs.
The connection between the Markov property and the joint probability density function (JPDF) of X is revealed by the Hammersley-Clifford (Gibbs-Markov equivalence) theorem (Besag, 1974). This theorem states that a random field (G, Ω, P) with P(x) > 0 for all x ∈ Ω satisfies the Markov property if, and only if, it can be expressed as a Gibbs distribution:
| (3) |
where Z = ∑x∈Ω Πc∈𝒞 Vc(x) is the normalizing constant and Vc are positive functions, called clique potentials, that depend only on those xs such that s ∈ c. The following reveals the simplified forms of the LCPDFs:
| (4) |
where 𝒞s represents {c∈ 𝒞: s ∈ c} and Zs = Σxs∈Λ ∏c∈𝒞s Vc(x). For proofs of all preceding Markov formulations and theorems, see Geman (Geman, 1991).
2.4. Potts Models
Though (3) and (4) provide the requisite forms of the JPDF and LCPDFs for any MRF, they offer little insight into means for selecting potential functions that will adequately model a given random process. To facilitate the selection of these potential functions, two simplifying assumptions are typically invoked. First, we assume that only the pairwise interactions among sites are significant. Second, we assume that the LCPDFs are stationary, i.e. P (xs|xηs) is identical for each site s ∈ S having |ηs| neighbors. Mathematically, these assumptions equate to the following simplification of (4):
| (5) |
where V1 and V2 are the site-invariant potential functions for one- and two-element cliques, respectively. Furthermore, V2 is symmetric in the sense that V2(xs,xr) = V2(xr,xs); this symmetry is needed to ensure the stationarity of P(xs|xηs).
Even with this simplification, the means for selecting V1 and V2 are not obvious. This lack of clarity has lead to the prevalence of the simplistic Potts model (Potts, 1952), whose potential functions are V1(x) ≡ 1 and
| (6) |
where β > 0. Since typically β > 1, neighboring sites with identical states will contribute more to the JPDF (and their respective LCPDFs) than neighboring pixels with differing states. The degree of contribution is a function of β, with greater values of β producing “smoother” solutions. To see this, consider the MAP estimation in (1). Increasing β increases the weight of the second term, further encouraging neighboring sites to share the same label.
3. Probabilistic Pairwise Markov Models
To arrive at more complex and intuitive MRF models we recognize that (5) can be expressed in terms of PDFs, instead of potential functions:
| (7) |
where p0 is the PDF describing the stationary site s and p1|0 represents the conditional PDF describing the pairwise relationship between site s and its neighboring site r. The numbers 0 and 1 replace the letters s and r to indicate that the probabilities are identical across all sites, i.e. the MRF is stationary. Furthermore, p0 and p1|0 are related in the sense that they are a marginal and conditional distribution of the joint distribution p0,1, i.e. p0,1(xs,xr) = p0(xs)p1|0(xr,xs). The single caveat is that p0,1 must be symmetric to ensure stationarity. We refer to MRFs whose LCPDFs can be expressed using (7) as probabilistic pairwise Markov models (PPMMs).
Below we provide a proof to show that the LCPDFs given in (7) are consistent in the sense that they define a unique and valid JPDF, i.e. they combine to form a Gibbs distribution.
Theorem 1. Let (G, Ω, P) be a random field such that P (X = x) > 0 for all x ∈ Ω. If p0,1(xs,xr) is a PDF such that p0,1(xs,xr)= p0,1(xr,xs) and
for all s ∈ S, then X is a MRF.
Proof 1. It suffices to show that (7) can be expressed in the form given by (5). Consider the following one- and two-element potential functions:
and
where the symmetry of p0,1 ensures that V2 is also symmetric. Inserting these into (5) yields
The significance of PPMMs lies is their ability to formulate the LCPDFs in terms of a single PDF instead of potential functions. Unlike V1 and V2 which have little intuitive value, p0,1(xs,xr) describes the probability that two neighboring sites s and r have states xs and xr. Or, perhaps even more insightful is p1|0(xr|xs), which indicates the probability that r has state xr given site s has state xs3.
On a final note, it is worth pointing out that the Potts model can be reformulated as a PPMM as follows:
| (8) |
Notice that probability function p0,1 has the required symmetry. We will further discuss the significance of this formulation in Section 4.4.
4. Detecting Cancer in Histological Sections
In this section we present our novel classification system for detecting CaP on digitized histological sections of the prostate. We first provide a basic outline of the algorithm and then discuss each component in detail.
4.1. Algorithm Overview
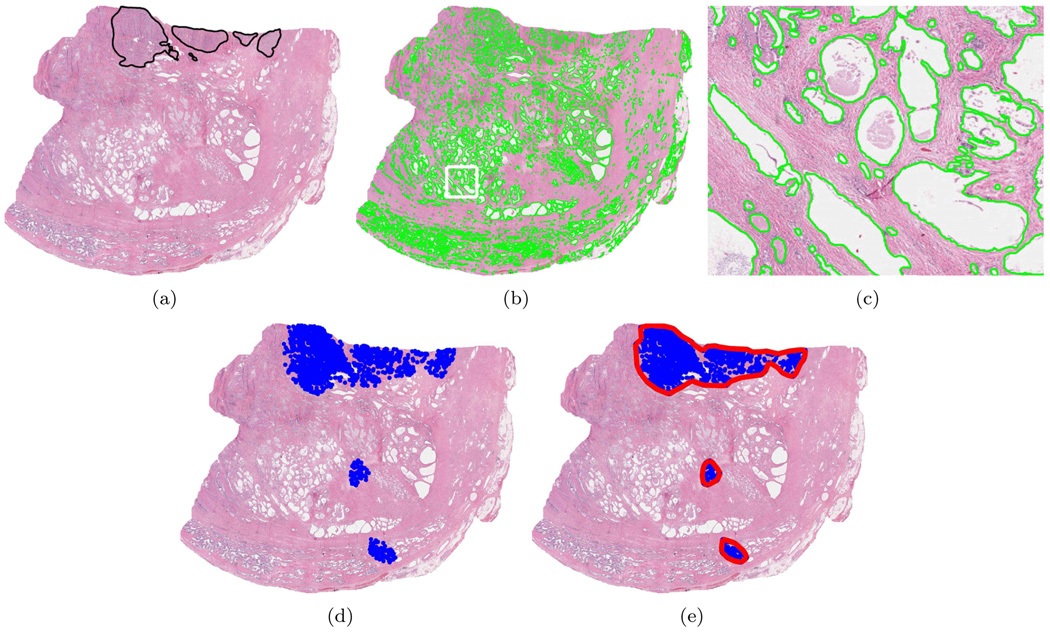
Figure 3(a) illustrates an H&E stained prostate histological (tissue) section. The hematoxylin colors the nucleic material blue, while eosin stains the cytoplasmic structures and extracellular matrix red. The superimposed black line delimits the spatial extent of CaP as determined by a pathologist. The numerous white regions are the gland lumens, i.e. cavities in the prostate through which fluid flows. Our system identifies CaP by leveraging two biological properties: 1) cancerous glands (and hence their lumens) tend to be smaller in cancerous than benign regions and 2) malignant/benign glands tend to be proximate to other malignant/benign glands (Kumar et al., 2004).
Figure 3.
(a) H&E stained prostate histology section; superimposed black ink mark provided by pathologist indicates CaP extent. (b) Gland segmentation boundaries. (c). Magnified view of white box in (b). (d) Centroids of glands labeled as cancerous. (e) Continuous regions formed by gland consolidation.
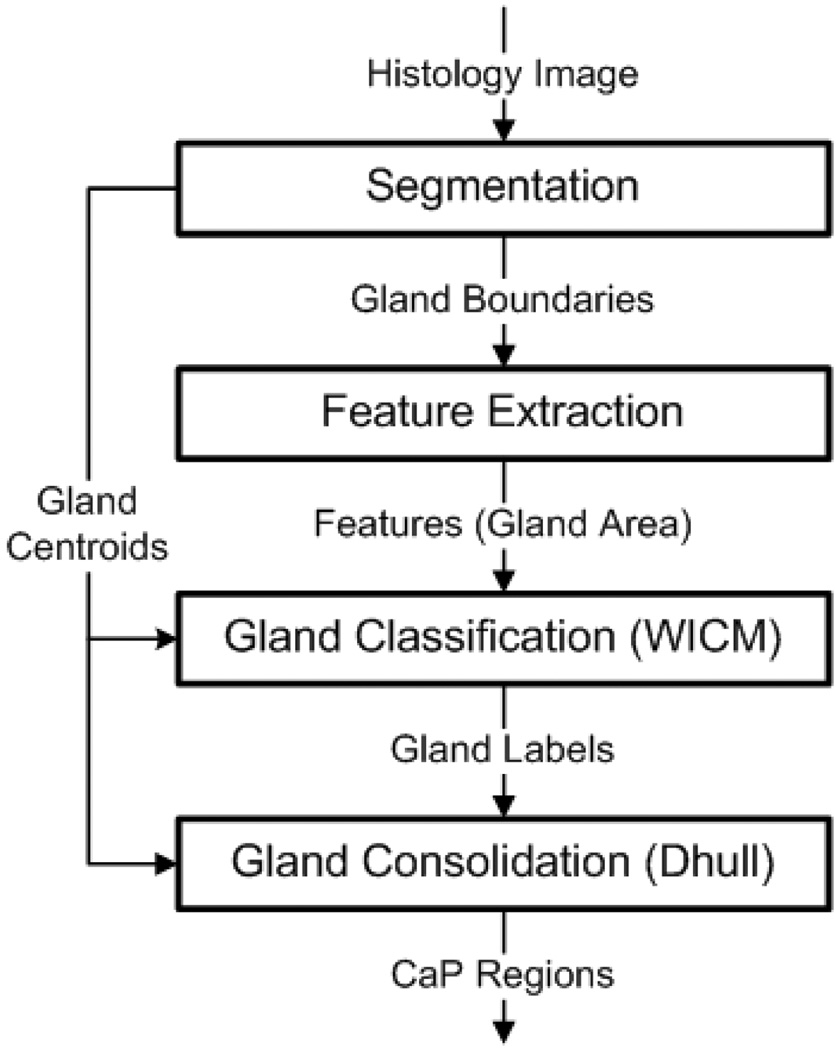
The basic algorithm, illustrated in Figure 2, proceeds as follows: Step 1) The glands (or, more precisely, the gland lumens) are identified and segmented. Figure 3(b) illustrates the segmented gland boundaries in light green. Figure 3(c) shows a magnified view of the white box in Figure 3(b). Step 2) Morphological features are extracted from the segmented boundaries. Currently, we consider only one feature: glandular area. Step 3) Using this feature and an MRF prior (PPMM or Potts) which encourages neighboring glands to share the same label, a Bayesian estimator classifies each gland as either malignant or benign. The blue dots in Figure 3(d) indicate the centroids of those glands classified as malignant. Step 4) The cancerous glands are consolidated into continuous regions. The red polygons in Figure 3(e) depict the regions resulting from the consolidation process.
Figure 2.
Overview of classification algorithm for detecting CaP regions from digitized WMHSs
Before describing each component in detail, we recapitulate the gland classification problem in terms of the MRF nomenclature in Section 2. Let the set S = {1, 2,…,N} reference the N segmented glands in the HS. The random variable Ys ∈ ℝ indicates the square root of the area of gland s. The label Xs of gland s corresponds to one of two possible classes: Xs ∈ Λ ≡ {ω1,ω2}, where ω1 and ω2 indicate malignancy and benignity. Two glands are neighbors if the distance between their centroids is less than R.
4.2. Gland Segmentation
Since color information is not needed to identify gland lumens on digitized HSs, all segmentation is performed using the luminance channel in CIE Lab color space. The CIE Lab color space is known to be more perceptually uniform than the RGB color space (Jain, 1989). In the luminance images glands appear as regions of contiguous, high intensity pixels circumscribed by sharp, pronounced boundaries. Our procedure to segment these glands proceeds as follows: The luminance image is convolved with a Gaussian kernel at multiple scales σg ∈ {0.2, 0.1, 0.05, 0.025}mm to account for varying gland size. Peaks (maxima) in the smoothed images are considered candidate gland centers. These single pixel peaks serve as seeds for the following region growing procedure (which operates on the original image) (Hojjatoleslami and Kittler, 1998):
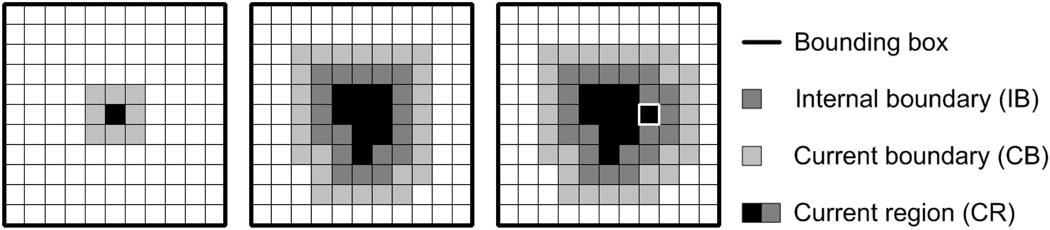
Step 1: Initialize the current region (CR) to the specified seed pixel and establish a 12σg × 12σg bounding box centered about it. Initialize the current boundary (CB) to the 8-connected pixels neighboring CR (Figure 4(a)).
Figure 4.
Region growing examples. (a) Seed pixel with CB. (b) IB, CB, and CR at step j in the growing procedure. (c) IB, CB, and CR at step j + 1. The white box indicates the aggregated pixel.
Step 2: Identity the pixel in CB with the highest intensity. Remove this pixel from CB and add it to CR. Revise CB to include all 8-connected neighbors of the aggregated pixel which are not in CR (Figures 4(b) and (c)).
Step 3: Define the internal boundary (IB) as all pixels in CR that are 8-connected with the pixels in CB (Figure 4). Compute the current boundary strength which is defined as the mean intensity of the pixels in IB minus the mean intensity of the pixels in CB.
Step 4: Repeat steps 2 and 3 until the algorithm attempts to add a pixel outside the bounding box.
Step 5: Identify the iteration step at which the maximum boundary strength was attained. Define the optimal region as CR at this step.
The final segmented regions may overlap; this is resolved by discarding the region with the lower boundary strength. Figure 3(b) illustrates the gland boundaries (light green) after segmentation. A magnified view of the white box in Figure 3(b) is shown in Figure 3(c).
4.3. Feature Extraction and Modeling
4.3.1. Modeling Gland Area
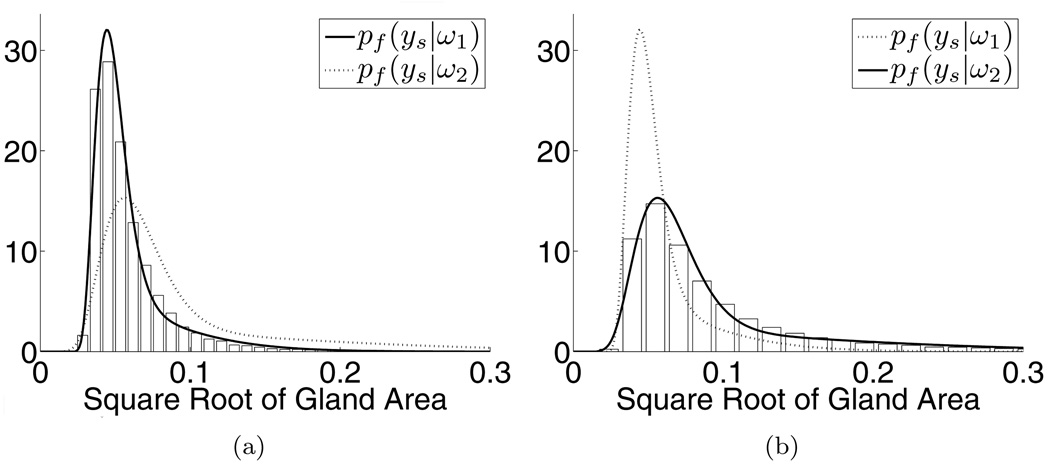
Gland area is a feature known to discriminate benign from malignant glands (Kumar et al., 2004). The MRF framework, specifically Equation (2), requires estimates of the conditional PDFs of gland area for both malignant ω1 and benign ω2 glands. Using the equivalent square root of gland area (SRGA) which is easier to model parametrically, the PDFs pf (ys|ω1) and pf (ys|ω2) can be accurately fit with a mixture of Gamma distributions (Papoulis, 1965):
| (9) |
where y > 0 is the SRGA, α ∈ [0,1] is the mixing parameter, k1, k2 > 0 are the shape parameters, θ1, θ2 > 0 are the scale parameters, and Γ is the Gamma function (Papoulis, 1965). Figure 5 illustrates the normalized histograms (i.e. their areas sum to one) for the malignant (5(a)) and benign (5(b)) glands. The solid lines superimposed over each histogram represent their corresponding fits with the mixtures of Gamma distributions. For reference, we also include the mixtures of Gamma distributions for the opposing classes (dotted lines). All distributions were fit using maximum likelihood estimation.
Figure 5.
Normalized histograms for the malignant (a) and benign (b) glands overlaid with corresponding mixtures of Gamma distributions (solid lines). Dotted lines represent mixtures of Gamma distributions for opposing classes.
4.3.2. Homogeneity of Neighboring Glands
We now discuss the formulation of the Markov prior which encourages neighboring glands to share the same label. We propose to model this PDF using a PPMM. Accordingly, the most general forms of p0 and p1|0 for binary classes (i.e. malignant/benign) are as follows:
| (10) |
and
| (11) |
The required symmetry of p0,1 necessitates that c(1−a) = (1−c) b, yielding c = b/(1+b−a). Values for a and b are obtained from training data. Though (11) and (10) are nonparametric distributions in the sense that there is no assumed model, the limited degrees of freedom allow the use of parametric estimation techniques. Since maximum likelihood estimation (MLE) is numerically untenable for MRFs, maximum pseudo-likelihood estimation (MPLE) (Geman and Graffigne, 1986; Besag, 1986) is the preferred alternative. MPLE maximizes the product of the LCPDFs over all samples, and unlike MLE, does not require computing the intractable normalizing factor Z in (3). A detailed discussion of our MPLE implementation can be found in Appendix A.
Since we will be comparing the performance of our CaP detection system when alternately incorporating the PPMM and the Potts priors, it is instructive to present the formulation of the Potts model for binary classes (expressed as a PPMM):
| (12) |
and
| (13) |
The following assumptions are implicit when using the Potts formulation to model gland interactions: First, p0 is uniform, indicating that both benign and malignant glands should occur with equal frequency. Second, the symmetry of p1|0 implies that malignant glands are just as likely to neighbor benign glands as benign glands are to neighbor malignant glands. Both of these assumptions seem at odds with the true behavior of glands in a HS. In fact, we will show that employing the Potts model instead of the more general PPMM degrades the accuracy of our CaP detection system.
4.4. Gland Classification
In Section 2.2 we defined the optimal states x (i.e. classes for the glands) as those that maximize the a posteriori probability in (1). The literature provides several means for performing this maximization (Szeliski et al., 2006; Dubes et al., 1990; Geman and Geman, 1984). We have selected iterated conditional modes (Besag, 1986) (ICM), a deterministic (as opposed to stochastic) relaxation technique. ICM is popular because of its rapid convergence, which can be an order of magnitude less than other popular methods such as simulated annealing (Geman and Geman, 1984) or maximum posterior marginals (Marroquin et al., 1987).
Since our system requires the ability to favor certain classification results (e.g. misclassifying a malignant gland might be more serious than misclassifying a benign one), we must slightly adapt ICM. Before discussing this adaptation we review the basic ICM algorithm. ICM is based on the following reformulation of (1):
| (14) |
Increasing the first term of (14) necessarily increases P(x|y). Since this term depends only on s and its neighborhood, it can be easily evaluated. This suggests a global optimization strategy that sequentially visits each site s ∈ S, determining the label xs ∈ Λ that maximizes the first term of (14). In the case of binary classes this reduces to the following decision:
| (15) |
where τicm = 1/2. Note that P(ω1|xηs, ys) ∝ P(ys|xs) P(xs|xηs). ICM, after several iterations, converges to a local maximum of (1). This local maximum is a function of the initial labels, which we determine using MLE (i.e. assuming non-informative priors). Using MLE to provide an initial labeling is a commonly accepted procedure, and we have empirically confirmed its effectiveness for our application.
An examination of (15) immediately suggests varying τicm as a means of favoring one class over the other. As τicm decreases, (15) will increasingly prefer ω1. By contrast, increasing τicm will favor ω2. Since the value of τicm implicitly weights the importance of each class, we refer to the modified algorithm as weighted iterated conditional modes (WICM). Figure 3(d) illustrates the result of applying WICM with τicm = 0.825. (The MRF prior was modeled using PPMMs.) It is worth noting that the WICM algorithm can be derived in a more general and mathematically rigorous fashion using Bayesian cost functions (Monaco et al., 2009). However, such analysis is beyond the scope of this paper. For a general discussion of Bayesian risk analysis see (Duda et al., 2001).
4.5. Consolidation of Gland into Regions
The final stage of the algorithm consolidates the malignant glands into continuous regions. This process involves two steps. First, the glands are separated into distinct groups. Two glands are defined as belonging to the same group if the distance between their centroids is less than R. This R is the same R used in Section 4.1 to determine if two glands are neighbors. Thus, two glands belong in the same group if they are neighbors. This definition naturally partitions the glands. The second step combines each group of glands into a single continuous region. One method for performing this encapsulation might be to form the convex hull of the gland centroids. Unfortunately, since the true spatial extent of the CaP rarely forms convex hulls, using such an algorithm will typically overestimate the sizes of the regions. To rectify this we introduce the distance-hull or Dhull, a novel extension of the convex hull that better conforms to the contours of the CaP. Figure 3(e) illustrates the three continuous regions that result from first grouping the malignant glands in Figure 3(d) and then finding the Dhulls of their centroids. The remainder of this section describes the general Dhull algorithm.
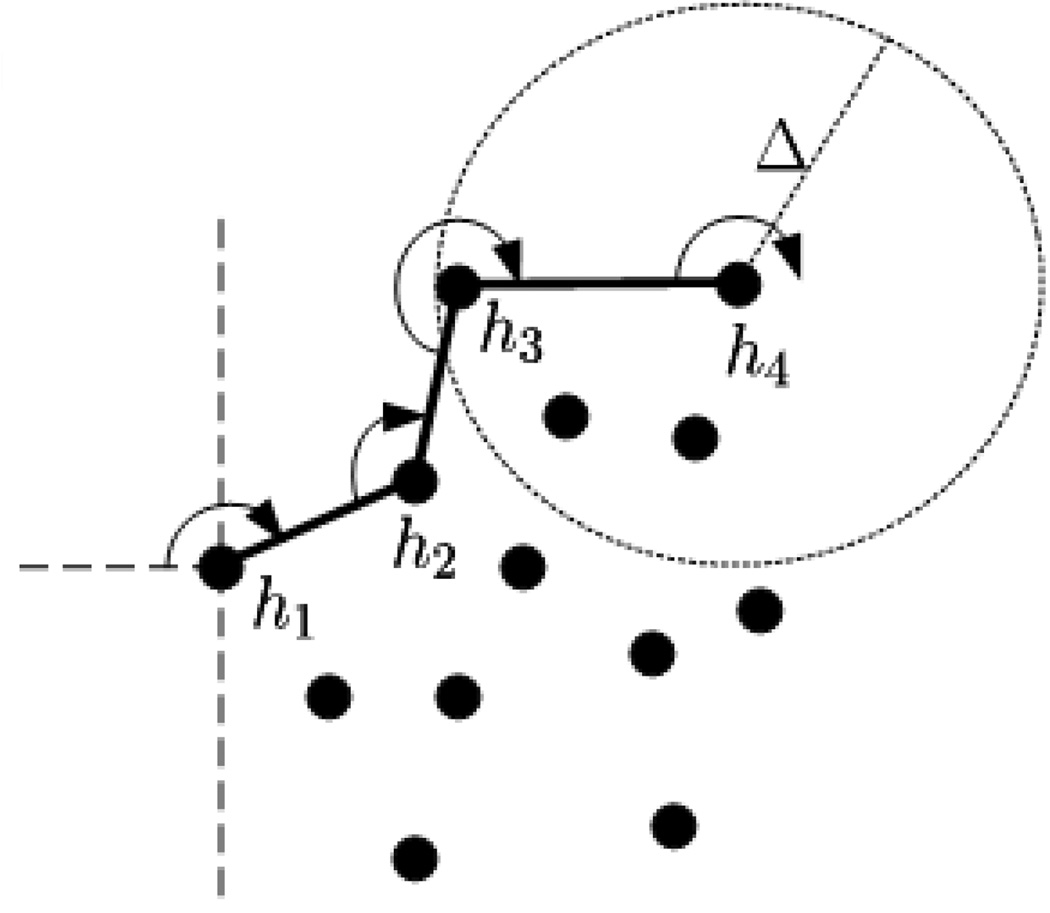
Dhull performs a modified version of the Jarvis march (Jarvis, 1973) (gift-wrapping algorithm) used to find convex hulls. This modification is as follows: whereas a convex hull places no restriction on the distance between consecutive points on the hull, Dhull allows a maximum distance of Δ. More formally, let Z = {z1,…,zK} represent a set containing K points that satisfy the following path constraint: for every zi, zj ∈ Z there exists one or more paths zizm…zlzj for which the distance between any two consecutive points is less than or equal to R. Let H = {h1,…,hM} be an ordered set indicating the points in Z that constitute the Dhull. The following steps, using the terminology in (Jarvis, 1973), detail the Dhull algorithm; Figure 6 provides a graphical interpretation.
Figure 6.
Graphical illustration of Dhull algorithm. Black dots represent the points to encapsulate. h1−h4 indicate the first four points added to the Dhull.
Step 1: Arbitrarily choose an exterior point z ∈ Z (e.g. the left-most point). This is the first point on the hull: h1 = z.
Step 2: Extend a radial arm of length Δ beginning at h1, and extending away from the remaining points (e.g. horizontal line to the left). Rotate the radial arm in an arbitrary direction (e.g. clockwise) until it intersects with another point z ∈ Z. This is next point on the Dhull: h2 = z.
Step 3: Let hi indicate the last point added to the the hull. Extend a radial arm of length Δ in the direction of the vector . Rotate the radial arm — using the direction established in Step 2 — until it intersects with a point z ∈ Z that satisfies the following: the line segment (hi, z) does not intersect with any previous Dhull line segment (hj, hj−1), where j ∈ {1,…,i−1} and (·, ·) indicates the exclusive interval. The next point on the Dhull is hi+1 = z.
Step 4: Repeat Step 3 until every point lies within the Dhull.
In order to guarantee that Dhull will enclose all points in Z, we must have . This can be seen by constructing the Dhull of four points that form the vertices of a quadrilateral whose diagonals are perpendicular (i.e. a diamond shape) and of length R, and whose edge lengths ensure the satisfaction of the path constraint. On a final note, if Δ is infinite then Dhull produces a convex hull.
5. Results and Discussion
5.1. Preliminaries
5.1.1. Description of Data
The dataset consists of 40 H&E stained histological sections from radical prostatectomies obtained from 20 patients at two separate institutions (University of Pennsylvania and Queens University in Canada). Thirteen of the HSs are whole-mounts, while the remaining 27 are quarter sections. The HSs primarily contain CaP with Gleason scores ranging from six to eight.
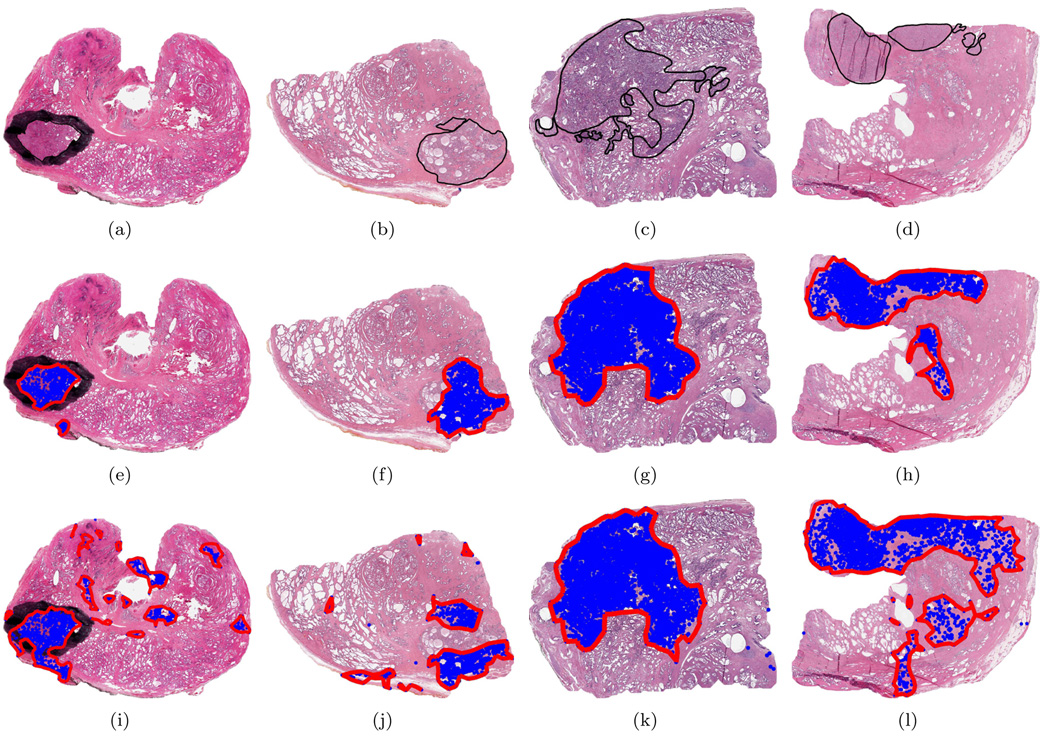
The gold standard defining the spatial extent of CaP was determined as follows: For the 13 WMHSs a pathologist circumscribed the cancerous regions on the physical slides. All 40 slides were then digitized at 40× magnification (0.25 µm per pixel) with an Aperio scanner. Thus, the annotations (for the 13 WMHSs) were necessarily captured in the digital images as illustrated in Figure 8(a). Following digitization, a second pathologist delineated the cancerous regions in all 40 digitized images using the ImageScope software package from Aperio. ImageScope produces digital annotations that are overlaid on the image for viewing, but are not present during automated analysis. The delineations from the first pathologist (for the 13 WMHSs) were used only as a guide. Finally, to ensure the fidelity of these annotations a third pathologist reexamined all 40 images along with their associated annotations. If errors or omissions were detected the annotations were corrected appropriately4. These final delineations are considered the gold standard by which CAD performance is assessed. An example of a digital annotation is shown in Figure 8(b). (Note that Figure 8(a) also contains a digital annotation; however, since it overlays the black ink mark, it is difficult to see.)
Figure 8.
Results from CaP detection algorithm. (a) H&E stained WMHS. Black ink mark delineating CaP extent is an indelible part of the image. (b)-(d) H&E stained quarter HSs. Superimposed black lines delineate CaP extent. PPMM ((e)-(h)) and Potts ((i)-(l)) results with sensitivity adjusted to 87%. This sensitivity corresponds to the thresholds τicm = 0.455 and τicm = 0.715 for the Potts and PPMM models, respectively.
The Aperio scanner provides a multiresolution image pyramid for each digitized HS. The CAD procedure processes the single image whose pixel width is 8 µm. This resolution is 1/32 of that available to the pathologist during “ground truthing.” That is, the images analyzed by the pathologist contain 1024 times more pixels than those considered by the CAD system. Furthermore, the automated system only processes the luminance channel in the CIE Lab color space as discussed in Section 4.2.
5.1.2. Training
The training procedure begins by segmenting the glands in each training image and then calculating their areas and centroids. Segmented glands whose centroids fall within the pathologist provided truth are labeled malignant; otherwise they are labeled benign. A MLE procedure uses these labeled samples to estimate the parameters for the mixtures of Gamma distributions used to model pf, the PDF describing the glandular area (see Section 4.3). The graph structure connecting the glands is determined from the gland centroids: two glands share an edge if the distance between their centroids is less than R. A MPLE procedure (see Appendix A) uses the graph structure and gland labels to estimate parameters for both the PPMM (a and b) and Potts model (β).
5.1.3. Testing
For each test image the algorithm segments the glands and then extracts their areas and centroids. Using these area measurements, a maximum likelihood estimator assigns an initial label to each gland. These classification results are passed to the MRF estimator — weighted iterated conditional modes. A graph structure over the glands is established using the identical methodology described in the training procedure. In addition to this graph structure, the WICM algorithm requires the threshold τicm and the conditional distribution P(xs|xηs). The value selected for τicm determines the sensitivity/specificity of the gland classification, and transitively, the entire algorithm. The distribution P(xs|xηs) is provided by either the PPMM or Potts model. Consequently, we will have two CaP detection systems, which we will refer to simply as PPMM and Potts. After gland classification, the centroids of the malignant glands are consolidated into continuous regions; the Dhull algorithm uses the value .
5.2. Quantitative Results
5.2.1. Accuracy of Cancerous Regions
We begin by defining several measures. Let the true positives (TP) indicate the area of the HSs denoted as cancerous by both the expert pathologist and the CAD system. Let the true negatives (TN) indicate the area of the HSs denoted as benign by both the pathologist and the CAD system. Let the false positives (FP) indicate the area of the HSs denoted as benign by the pathologist and malignant by the CAD system. Let the false negatives (FN) indicate the area of the HSs denoted as malignant by the pathologist and benign by the CAD system. Having established these terms, we define two additional measures: the true positive rate TP/(TP+FN) and the false positive rate FP/(TN+FP). These are synonymous with the sensitivity and one minus the specificity, respectively.
All preceding measures are influenced by four factors: τicm, the radius R, the composition of the test/training sets, and the Markov prior (Potts/PPMM). Varying τicm from zero to one alters system performance, yielding receiver operator characteristic (ROC) curves (i.e. plots of the true positive rate versus the false positive rate). In practice we construct each ROC curve by assessing sensitivity/specificity at certain discrete values of τicm, specifically τicm = 0, 0.025, 0.05,…1; intermediate performance measures (i.e. those falling in between the samples) are linearly interpolated. The total area under the ROC curve (AUC) provides a performance measure that is independent of τicm. To account for differences in training/test sets we will assess the mean and standard error of the AUC over 15 trials using randomized 3-fold cross-validation.
To determine the effect of varying the radius R we perform the following: for each prior (PPMM/Potts) and for each R ∈ {0.5, 0.7, 0.9, 1.1, 1.3} we compute the mean and standard error of the AUCs generated from the 15 trials. (Thus, we generate a total of 2×5×15= 150 ROC curves5.) The results are presented as Table 2. Let indicate the mean AUC at radius R using the PPMM and Potts priors, respectively. Measuring statistical significance using a paired t-test with a significance level of 0.01, we can conclude the following: 1) for all R ∈ {0.5, 0.7, 0.9, 1.1, 1.3} the value is statistically significant under the null hypothesis that ΦR = 0, 2) if R2 > R1 and R1, R2 ∈ {0.5, 0.7, 0.9} then both are statistically significant under the null hypotheses that , and 3) if R2 > R1 and R1, R2 ∈ {0.9, 0.1, 1.3} then both are not statistically significant under the null hypotheses that . It is worth recapitulating these statements less formally: 1) at each radius the mean AUC using the PPMM prior exceeds that of the Potts, 2) each increase in radius from 0.5 mm to 0.9 mm increases the mean AUC of both priors, and 3) increasing the radius beyond 0.9 mm offers no improvement in mean AUC for either prior.
Table 2.
Mean plus/minus standard error of AUC for PPMM and Potts systems over 15 trials using randomized 3-fold cross-validation.
| Radius R | 0.5 mm | 0.7 mm | 0.9 mm | 1.1 mm | 1.3 mm |
|---|---|---|---|---|---|
| PPMM | 0.891 ± .004 | 0.919 ± .006 | 0.930 ± .006 | 0.934 ± .006 | 0.935 ± .007 |
| Potts | 0.885 ± .004 | 0.905 ± .005 | 0.911 ± .006 | 0.914 ± .006 | 0.916 ± .006 |
5.2.2. Computation Time
We measured the execution time of the four major components of the algorithm: gland segmentation, feature extraction, classification, and consolidation. These measurements were obtained using the following system configuration: training/test sets established using a leave-one-out strategy, PPMM used for the Markov prior, sensitivity set to 0.87, and R = 0.9 mm. The execution times for each component, averaged over all quarter and whole-mount HSs, are provided in Table 3. All timing was performed using a 2.40 GHz Intel Core2 processor with 4 GB of RAM. Note that over 90% of the computation time is dedicated to gland segmentation; and consequently, varying the Markov prior, radius R, and/or value of τicm has little impact on overall timing.
Table 3.
Mean execution time for CaP detection algorithm over 13 WMHSs and 27 quarter HSs using a 2.40 GHz Intel Core2 processor with 4 GB of RAM.
| Segmentation | Feature Extraction | Classification | Consolidation | Total | |
|---|---|---|---|---|---|
| Whole-mounts | 156 sec | 1.76 sec | 6.11 sec | 1.28 sec | 165 sec |
| Quarters | 63 sec | 0.76 sec | 1.43 sec | 0.64 sec | 66 sec |
5.3. Qualitative Results
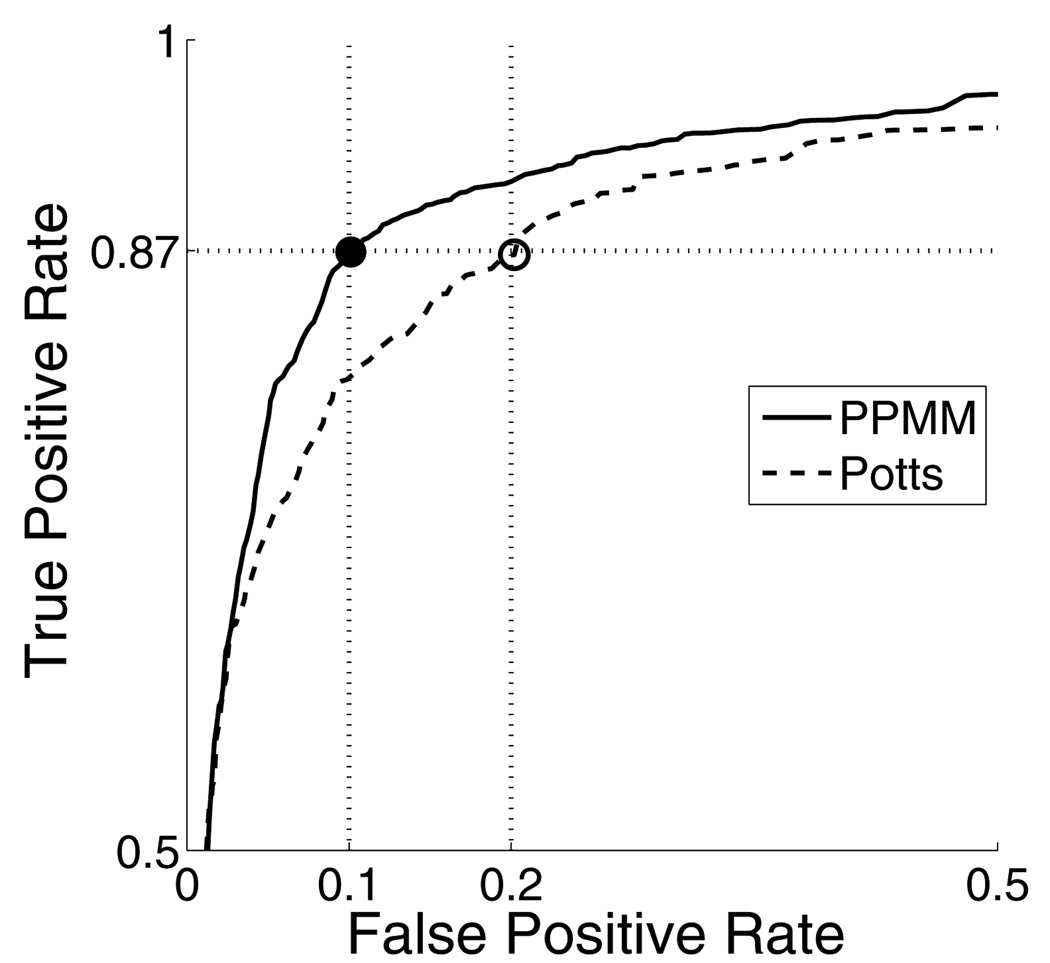
The training and test sets were established using a leave-one-out strategy with R = 0. 9 mm. The performances of the systems (i.e. PPMM/Potts) were varied by adjusting τicm (for each algorithm independently) until their respective sensitivities equaled 0.87. That is, when τicm = 0.715 the PPMM detected 87% of the malignant glands; to achieve the same sensitivity, the Potts required τicm = 0.455. At these sensitivities the corresponding false positive rates for the PPMM and Potts systems were 0.10 and 0.20, respectively. This is depicted graphically in Figure 7 using ROC curves.
Figure 7.
Partial receiver operator characteristic (ROC) curves for PPMM (solid) and Potts (dashed) algorithms determined using leave-one-out cross-validation with R = 0.9 mm. The black and white circles indicate the points where the PPMM and Potts systems attain a true positive rate of 0.87.
Figures 8(a)–(d) show four histological sections, the first of which is a whole-mount histological section. The black lines enclose the spatial extent of the CaP. The blue dots in Figures 8(e)–(h) indicate the centroids of those glands labeled as malignant after classification using the PPMM model; the boundaries resulting from consolidation are also shown. Figures 8(i)–(l) provide the comparable results using the Potts system. Clearly, the PPMM provides superior specificity when the sensitivity of both systems are equivalent.
5.4. Discussion
As previously stated, the primary goal of this algorithm is to eliminate regions that are not likely to be cancerous, thereby reducing the computational load of further, more sophisticated analyses. Consequently, the algorithm should necessarily operate at a high sensitivity (true positive rate), ensuring that very little CaP is discarded. The concomitant specificity then indicates the expected reduction in computational load at any later stage. Accordingly, when determining the qualitative and computational results reported in Sections 5.3 and 5.2.2 we adjusted the sensitivity to 0.87 — a relatively high value. At this sensitivity the accompanying false positive rates for the PPMM and Potts systems were 0.10 and 0.20, respectively. Thus, with the PPMM prior the CaP detection system eliminates 90% of the benign regions; using the Potts prior this percentage falls to 80.
Finally, it is interesting to examine the specific values assigned to the pairwise PDFs p0 and p1|0 for the PPMM and Potts model (see Section 4.3.2). These values were determined using MPLE (see Appendix A) over the entire dataset. For the PPMM we have the following:
| (16) |
and
| (17) |
The Potts model yields
| (18) |
and
| (19) |
The marginal distribution in (16) indicates that, as expected, the occurrence of benign glands is more frequent than malignant glands. Compare this with the (necessarily) uniform distribution of Potts in (18). Also, note the asymmetry in the conditional distribution of the PPMM in (17). This asymmetry allows malignant and benign glands to affect their neighbors differently. The (necessarily) symmetric conditional distribution for the Potts in (19) does not possess this capability.
It is worth discussing why no explicit evaluation of the gland segmentation and classification procedures was presented. As mentioned previously, the ultimate goal of this system is to identify cancerous regions, and not cancerous glands. Thus, the performances of intermediate steps such as gland segmentation and classification become irrelevant in and of themselves. That is, such steps are effective only to the degree to which they help to detect CaP regions. Consequently, their efficacy is measured implicitly — and most appropriately — by assessing the system’s ability to identify these cancerous regions.
Finally, we would like to note that our automated system can operate at any image resolution. In general, the higher the resolution, the longer the computation time and the greater the detection accuracy. Consequently, the appropriate resolution is a function of the processing speed of the hardware, allowable execution time, and desired detection accuracy. For the specific goals of this paper, 8 µm per pixel proved most advantageous. This conclusion was reached from the following procedure: We visually inspected images at different resolutions to ascertain the lowest resolution that qualitatively preserved the salient glandular morphology, and then validated the choice by confirming a satisfactory algorithm performance. In future work, we will methodically investigate the relationship between computational complexity, system performance, and resolution. It should be noted that even with specialized hardware, the analysis of an entire WMHS at maximum resolution (0.25 µm per pixel) will be prohibitive for the foreseeable future. At present this analysis (with our algorithm) requires nearly two days using a high-performance desktop computer.
6. Concluding Remarks
In this work we introduced the first system for rapidly detecting CaP regions in a whole-mount (or quarter) histological section. Specifically, we demonstrated that our system can process an entire WMHS (2×1.75 cm2) in an average of 165 seconds. We achieved this high throughput by tailoring the algorithm to operate at 8 µm per pixel. At this resolution the primary visible structure are the glands. Consequently, we constructed a system that first segments glands, then classifies them, and finally consolidates the malignant glands into continuous regions. We extensively evaluated the algorithm, performing over 6000 simulations across a dataset of 40 HS from 20 patients. Most notably, we demonstrated that at an appropriate operating point our system detects CaP regions with a sensitivity of 0.87 and a specificity of 0.90.
To effectively model the tendency of nearby glands to share the same class, we introduced probabilistic pairwise Markov models. Unlike typical MRF formulations which express local conditional probability functions in terms of clique potentials, PPMMs represent the LCPDFs using probability functions. These probability functions immediately provide insight into the expected behavior of the resulting MRF and suggest means for creating more sophisticated models. Incorporating PPMMs into our CaP detection system we demonstrated their superiority to the ubiquitous Potts model. Specifically, when the two models were alternately integrated into the algorithm, the AUC of the system employing the PPMM prior exceeded that of the Potts (by a margin that statistically significant) in every experiment. Most significantly, when the detection sensitivity was adjusted to 0.87, employing the PPMM prior resulted in a false positive rate less than half that of the Potts.
The construction the CaP detection system required the development of two additional novel contributions: weighted iterated conditional modes and Dhull. WICM, a deterministic estimation procedure for MRFs, provides a means for varying the performance of MRF-based systems, a capability previously absent from the MRF literature. This capability is essential for systems, such as ours, which require the ability to adjust their sensitivity with respect to a specified class. The Dhull algorithm, a novel extension of the Jarvis march used to construct convex hulls, offers a quick method for enclosing points in a hull. Most importantly, the resulting boundary, unlike the convex hull, conforms well to the contours established by the points.
Clearly, operating at a resolution of 8 µm per pixel, we can not hope to perform as well as a pathologist with access to an image digitized at 0.25 µm per pixel. Nevertheless, to be of clinical value the sensitivity of our algorithm would likely need to be increased. Fortunately, since our system follows the methodology supported by clinicians (i.e. it considers glandular morphology and architecture), additional means for improving performance are already well established in the medical literature (Epstein et al., 2005; Kumar et al., 2004). These include the consideration of gland shape, variation in gland size, and the architectural arrangement of the glands. Fortunately, both the gland segmentation and the MRF framework make incorporating these features relatively straightforward. Additionally, the computational load of extracting glandular features is insignificant compared to the burden of segmentation. Thus, we can expect little difference in execution time with the incorporation of such features.
It is important to mention possible limitations of our system. First, some advanced tumors (i.e. some Gleason grade five) completely disrupt normal glandular formations, and thus, the system may have difficulty identifying them. However, studies suggest that less than two percent of radical prostatectomy specimens exhibit such cancers (Kattan et al., 1999; Stephenson et al., 2005; Roehl et al., 2004). Nonetheless, we will consider adding the capability of detecting these Gleason grade five tumors in the future. Second, since tears in the HSs, like glandular lumens, manifest as holes in the tissue, the algorithm can mistakenly detect and segment them as glands. However, unless the prevalence of such tears approaches that of the glands, we would not expect them to impact performance. We have yet to encounter any problems due to tears.
On a final note we reiterate that we do not consider the system presented in this paper as an end in and of itself. Instead, we envision this system as the initial stage of a comprehensive, hierarchical algorithm that quickly detects cancerous regions at lower resolutions, and then refines and ultimately Gleason grades these regions at higher resolutions.
A. Maximum Pseudo-Likelihood Estimation
We consider estimation of the PPMMs for binary classes using maximum pseudo-likelihood estimation (MPLE). Specifically, we wish to determine a, b, and c in (10) and (11). MPLE maximizes the product of the LCPDFs:
| (20) |
The direct maximization of (20) can be computationally expensive and numerically unstable when |S| is large. These problems can be mitigated with the proper reformulation. The following simplification, similar to that of Levada (Levada et al., 2008), provides a tractable means for estimating a and b (c is a function of a and b) using the logarithm of (20):
| (21) |
where
| (22) |
m = maxs |ηs|, and is the number of sites s ∈ S that have the following properties: xs = ωk, i = |{r : r ∈ ηs, xr = ω1}|, and j = |{r : r ∈ ηs, xr = ω2}|. For example, is the number of sites with label ω1 that have three neighbors, two of which are labeled ω1 and one of which is labeled ω2. The quantity in (21) can be optimized using a constrained nonlinear numerical maximization procedure (Baldick, 2006).
Since the Potts model can be expressed as a PPMM, estimating its β parameter proceeds similarly. We have a = eβ/(1+eβ), b = 1/(1+eβ), and b =1−a. After substituting these equalities into (22) and maximizing (21) over a we can recover β as follows: β = ln [a/(1−a)].
Acknowledgment
This work was made possible via grants from the Wallace H. Coulter Foundation, New Jersey Commission on Cancer Research Post-doctoral Fellowship (4-27275), National Cancer Institute (R01CA136535-01, ARRA-NCI-3 R21 CA127186-02S1, R21CA127186-01, R03CA128081-01), the Society for Imaging Informatics in Medicine (SIIM), the Cancer Institute of New Jersey, and the Life Science Commercialization Award
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
When we refer to a histological section (HS) we will always be implying a quarter or whole-mount section from a radical prostatectomy.
For convenience, we will refer to all the probability functions as densities, whether or not the domains of the functions are discrete or continuous.
Note that p0,1(xs,xr) is not precisely equal to the probability of the event {Xs = xs, Xr = r} unless X is a strong MRF (Paget, 2004). However, pragmatically this interpretation is acceptable.
The kappa value measuring the inter-rater agreement between the second and third pathologists was κ = 0.9921.
Since generating each ROC requires running the algorithm for each of the 41 different values of τicm, the total number of simulations is 41 × 150 = 6150.
References
- Andrn O, Fall K, Franzn L, Andersson S-O, Johansson J-E, Rubin MA. How well does the gleason score predict prostate cancer death? a 20-year followup of a population based cohort in sweden. J Urol. 2006 Apr;175(4):1337–1340. doi: 10.1016/S0022-5347(05)00734-2. URL http://dx.doi.org/10.1016/S0022-5347(05)00734-2. [DOI] [PubMed] [Google Scholar]
- Awate S, Tasdizen T, Whitaker R. Unsupervised texture segmentation with nonparametric neighborhood statistics. Computer Vision ECCV. 2006:494–507. [Google Scholar]
- Baldick R. Applied Optimization. Cambridge University Press; 2006. [Google Scholar]
- Besag J. Spatial interaction and the statistical analysis of lattice systems. Journal of the Royal Statistical Society. Series B (Methodological) 1974;36(2):192–236. URL http://www.jstor.org/stable/2984812. [Google Scholar]
- Besag J. On the statistical analysis of dirty pictures. Journal of the Royal Statistical Society. Series B (Methodological) 1986;48(3):259–302. URL http://www.jstor.org/stable/2345426. [Google Scholar]
- Cordon-Cardo C, Kotsianti A, Verbel D, Teverovskiy M, Capodieci P, Hamann S, Jeffers Y, Clayton M, Elkhettabi F, Khan F, Sapir M, Bayer-Zubek V, Vengrenyuk Y, Fogarsi S, Saidi O, Reuter V, Scher H, Kattan M, Bianco F, Wheeler T, Ayala G, Scardino P, Donovan M. Improved prediction of prostate cancer recurrence through systems pathology. J Clin Invest. 2007 Jul;117(7):1876–1883. doi: 10.1172/JCI31399. URL http://dx.doi.org/10.1172/JCI31399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diamond J, Anderson NH, Bartels PH, Montironi R, Hamilton PW. The use of morphological characteristics and texture analysis in the identification of tissue composition in prostatic neoplasia. Hum Pathol. 2004 Sep;35(9):1121–1131. doi: 10.1016/j.humpath.2004.05.010. [DOI] [PubMed] [Google Scholar]
- Donovan MJ, Hamann S, Clayton M, Khan FM, Sapir M, Bayer-Zubek V, Fernandez G, Mesa-Tejada R, Teverovskiy M, Reuter VE, Scardino PT, Cordon-Cardo C. Systems pathology approach for the prediction of prostate cancer progression after radical prostatectomy. J Clin Oncol. 2008 Aug;26(24):3923–3929. doi: 10.1200/JCO.2007.15.3155. URL http://dx.doi.org/10.1200/JCO.2007.15.3155. [DOI] [PubMed] [Google Scholar]
- Doyle S, Agner S, Madabhushi A, Feldman M, Tomaszewski J. Automated grading of breast cancer histopathology using spectral clustering with textural and architectural image features. Proc. 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro ISBI 2008. 2008 May 14–17;:496–499. [Google Scholar]
- Doyle S, Hwang M, Shah K, Madabhushi A, Feldman M, Tomaszeweski J. Automated grading of prostate cancer using architectural and textural image features. ISBI. 2007 April 12–15;:1284–1287. [Google Scholar]
- Dubes R, Jain A, Nadabar S, Chen C. Mrf model-based algorithms for image segmentation. Proceedings of the10th International Conference on Pattern Recognition. 1990;Vol. i:808–814. vol.1. [Google Scholar]
- Duda R, Hart P, Stork D. Pattern Classification. John Wiley & Sons; 2001. [Google Scholar]
- Epstein J, Allsbrook WC, Amin MB, Egevad LL, Committee ISUPG. The 2005 international society of urological pathology (isup) consensus conference on gleason grading of prostatic carcinoma. Am J Surg Pathol. 2005 Sep;29(9):1228–1242. doi: 10.1097/01.pas.0000173646.99337.b1. [DOI] [PubMed] [Google Scholar]
- Epstein JI, Allsbrook WC, Amin MB, Egevad LL. Update on the gleason grading system for prostate cancer: results of an international consensus conference of urologic pathologists. Adv Anat Pathol. 2006 Jan;13(1):57–59. doi: 10.1097/01.pap.0000202017.78917.18. URL http://dx.doi.org/10.1097/01.pap.0000202017.78917.18. [DOI] [PubMed] [Google Scholar]
- Farag A, El-Baz A, Gimel’farb G. Precise segmentation of multimodal images. IEEE Transactions on Image Processing. 2006 April;15(4):952–968. doi: 10.1109/tip.2005.863949. [DOI] [PubMed] [Google Scholar]
- Farjam R, Soltanian-Zadeh H, Jafari-Khouzani K, Zoroofi RA. An image analysis approach for automatic malignancy determination of prostate pathological images. Cytometry B Clin Cytom. 2007 Jul;72(4):227–240. doi: 10.1002/cyto.b.20162. URL http://dx.doi.org/10.1002/cyto.b.20162. [DOI] [PubMed] [Google Scholar]
- Figueiredo MAT, Leitao JMN. Unsupervised image restoration and edge location using compound gaussmarkov random fields and the mdl principle. IEEE Transactions on Image Processing. 1997 Aug.6(8):1089–1102. doi: 10.1109/83.605407. [DOI] [PubMed] [Google Scholar]
- Geman D. Lecture Notes in Mathematics. Vol. 1427. Springer-Verlag; 1991. Random fields and inverse problems in imaging; pp. 113–193. [Google Scholar]
- Geman S, Geman D. Stochastic relaxation, gibbs distribution, and the bayesian restoration of images. IEEE Transactions on Pattern Recognition and Machine Intelligence. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Geman S, Graffigne C. Markov random field image models and their applications to computer vision. Proceedings of the International Congress of Mathematicians. 1986:1496–1517. [Google Scholar]
- Gleason D. Classification of prostatic carcinomas. Cancer chemotherapy reports. 1966;50:125–128. [PubMed] [Google Scholar]
- Heidenreich A, Aus G, Bolla M, Joniau S, Matveev VB, Schmid HP, Zattoni F, of Urology EA. Eau guidelines on prostate cancer. Eur Urol. 2008 Jan;53(1):68–80. doi: 10.1016/j.eururo.2007.09.002. [DOI] [PubMed] [Google Scholar]
- Hojjatoleslami S, Kittler J. Region growing: a new approach. IEEE Trans. on Image Processing. 1998 July;7(7):1079–1084. doi: 10.1109/83.701170. [DOI] [PubMed] [Google Scholar]
- Huang P-W, Lee C-H. Automatic classification for pathological prostate images based on fractal analysis. IEEE Trans Med Imaging. 2009 Jul;28(7):1037–1050. doi: 10.1109/TMI.2009.2012704. URL http://dx.doi.org/10.1109/TMI.2009.2012704. [DOI] [PubMed] [Google Scholar]
- Jafari-Khouzani K, Soltanian-Zadeh H. Multiwavelet grading of pathological images of prostate. IEEE Transactions on Biomedical Engineering. 2003 June;50(6):697–704. doi: 10.1109/TBME.2003.812194. [DOI] [PubMed] [Google Scholar]
- Jain AK. Fundamentals of Digital Image Processing. Prentice Hall; 1989. [Google Scholar]
- Jarvis RA. On the identification of the convex hull of a finite set of points in the plane. Information Processing Letters. 1973;2(1):18–21. URL http://www.sciencedirect.com/science/article/B6V0F-45FKW8B-6K/2/696a870b28b58d8279c52a9077473931. [Google Scholar]
- Kattan MW, Wheeler TM, Scardino PT. Postoperative nomogram for disease recurrence after radical prostatectomy for prostate cancer. J Clin Oncol. 1999 May;17(5):1499–1507. doi: 10.1200/JCO.1999.17.5.1499. [DOI] [PubMed] [Google Scholar]
- Kumar V, Abbas A, Fausto N. Robbins and Cotran Pathologic Basis of Disease. Saunders. 2004 [Google Scholar]
- Levada A, Mascarenhas N, Tannus A. Pseudolikelihood equations for potts mrf model parameter estimation on higher order neighborhood systems. IEEE Geoscience and Remote Sensing Letters. 2008 July;5(3):522–526. [Google Scholar]
- Li H, Kallergi M, Clarke L, Jain V, Clark R. Markov random field for tumor detection in digital mammography. Medical Imaging, IEEE Transactions on. 1995 Sep;14(3):565–576. doi: 10.1109/42.414622. [DOI] [PubMed] [Google Scholar]
- Liu X, Langer D, Haider M, Yang Y, Wernick M, Yetik I. Prostate cancer segmentation with simultaneous estimation of markov random field parameters and class. Medical Imaging, IEEE Transactions on. 2009 June;28(6):906–915. doi: 10.1109/TMI.2009.2012888. [DOI] [PubMed] [Google Scholar]
- Madabhushi A, Feldman MD, Metaxas DN, Tomaszeweski J, Chute D. Automated detection of prostatic adenocarcinoma from high-resolution ex vivo mri. IEEE Transactions on Medical Imaging. 2005 Dec.24(12):1611–1625. doi: 10.1109/TMI.2005.859208. [DOI] [PubMed] [Google Scholar]
- Marroquin J, Mitter S, Poggio T. Probabilistic solution of ill-posed problems in computational vision. Journal of the American Statistical Association. 1987;82(397):76–89. URL http://www.jstor.org/stable/2289127. [Google Scholar]
- Monaco J, Viswanath S, Madabhushi A. Weighted iterated conditional modes for random fields: Application to prostate cancer detection. Workshop on Probabilistic Models for Medical Image Analysis (in conjunction with MICCAI) 2009 [Google Scholar]
- Montironi R, Mazzuccheli R, Scarpelli M, Lopez-Beltran A, Fellegara G, Algaba F. Gleason grading of prostate cancer in needle biopsies or radical prostatectomy specimens: contemporary approach, current clinical significance and sources of pathology discrepancies. BJU Int. 2005 Jun;95(8):1146–1152. doi: 10.1111/j.1464-410X.2005.05540.x. URL http://dx.doi.org/10.1111/j.1464-410X.2005.05540.x. [DOI] [PubMed] [Google Scholar]
- Naik S, Doyle S, Madabhushi A, Tomaszewski J, Feldman M. Gland segmentation and gleason grading of prostate histology by integrating low-, high-level and domain specific information. Workshop on Microscopic Image Analysis with Applications in Biology. 2007 [Google Scholar]
- Paget R. Strong markov random field model. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2004 March;26(3):408–413. doi: 10.1109/TPAMI.2004.1262338. [DOI] [PubMed] [Google Scholar]
- Paget R, Longstaff ID. Texture synthesis via a noncausal nonparametric multiscale markov random field. IEEE Transactions on Image Processing. 1998 June;7(6):925–931. doi: 10.1109/83.679446. [DOI] [PubMed] [Google Scholar]
- Papoulis A. Probability, Random Variables, and Stochastic Processes. New York, NY: McGraw-Hill, Inc.; 1965. [Google Scholar]
- Pappas TN. An adaptive clustering algorithm for image segmentation. IEEE Transaction on Signal Processing. 1992 April;40(4):901–914. [Google Scholar]
- Potts RB. Some generalised order-disorder transformations. Proceedings of the Cambridge Philosophical Society. 1952;48:106–109. [Google Scholar]
- Roehl KA, Han M, Ramos CG, Antenor JAV, Catalona WJ. Cancer progression and survival rates following anatomical radical retropubic prostatectomy in 3,478 consecutive patients: long-term results. J Urol. 2004 Sep;172(3):910–914. doi: 10.1097/01.ju.0000134888.22332.bb. URL http://dx.doi.org/10.1097/01.ju.0000134888.22332.bb. [DOI] [PubMed] [Google Scholar]
- Roula M, Diamond J, Bouridane A, Miller P, Amira A. A multispectral computer vision system for automatic grading of prostatic neoplasia. Proc. IEEE International Symposium on Biomedical Imaging. 2002 July 7–10;:193–196. [Google Scholar]
- Smith Y, Zajicek G, Werman M, Pizov G, Sherman Y. Similarity measurement method for the classification of architecturally differentiated images. Comput. Biomed. Res. 1999;32(1):1–12. doi: 10.1006/cbmr.1998.1500. [DOI] [PubMed] [Google Scholar]
- Stephenson AJ, Scardino PT, Eastham JA, Bianco FJ, Dotan ZA, DiBlasio CJ, Reuther A, Klein EA, Kattan MW. Postoperative nomogram predicting the 10-year probability of prostate cancer recurrence after radical prostatectomy. J Clin Oncol. 2005 Oct;23(28):7005–7012. doi: 10.1200/JCO.2005.01.867. URL http://dx.doi.org/10.1200/JCO.2005.01.867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szeliski R, Zabih R, Scharstein D, Veksler O, Kolmogorov V, Agarwala A, Tappen M, Rother C. A comparative study of energy minimization methods for markov random fields. ECCV. 2006:16–29. doi: 10.1109/TPAMI.2007.70844. [DOI] [PubMed] [Google Scholar]
- Tabesh A, Teverovskiy M, Pang H-Y, Kumar VP, Verbel D, Kotsianti A, Saidi O. Multifeature prostate cancer diagnosis and gleason grading of histological images. IEEE Transactions on Medical Imaging. 2007 Oct.26(10):1366–1378. doi: 10.1109/TMI.2007.898536. [DOI] [PubMed] [Google Scholar]
- Tiwari P, Rosen M, Madabhushi A. A hierarchical spectral clustering and nonlinear dimensionality reduction scheme for detection of prostate cancer from magnetic resonance spectroscopy (mrs) Medical Physics. 2009;36(9):3927–3939. doi: 10.1118/1.3180955. URL http://link.aip.org/link/?MPH/36/3927/1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesny A, Gool LJV. SMILE Workshop. London, UK: SpringerVerlag; 2001. A compact model for viewpoint dependent texture synthesis; pp. 124–143. [Google Scholar]
- Zhang Y, Brady M, Smith S. Segmentation of brain mr images through a hidden markov random field model and the expectation-maximization algorithm. IEEE Transactions on Medical Imaging. 2001 Jan;20(1):45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]