Oriented Single-Crystal Nuclear Resonance Vibrational Spectroscopy of [Fe(TPP)(MI)(NO)]: Quantitative Assessment of the trans Effect of NO

Abstract

This paper presents oriented single-crystal Nuclear Resonance Vibrational Spectroscopy (NRVS) data for the six-coordinate (6C) ferrous heme-nitrosyl model complex [⁵⁷Fe(TPP)(MI)(NO)] (1; TPP²⁻ = tetraphenylporphyrin dianion; MI = 1-methylimidazole). The availability of these data enables for the first time the detailed simulation of the complete NRVS data, including the porphyrin-based vibrations, of a 6C ferrous heme-nitrosyl, using our quantum chemistry centered normal coordinate analysis (QCC-NCA). Importantly, the Fe-NO stretch is split by interaction with a porphyrin-based vibration into two features, observed at 437 and 472 cm⁻¹. The 437 cm⁻¹ feature is strongly out-of-plane (oop) polarized and shows an ¹⁵N¹⁸O isotope shift of 8 cm⁻¹, and is therefore assigned to ν(Fe-NO). The admixture of Fe-N-O bending character is small. Main contributions to the Fe-N-O bend are observed in the 520 – 580 cm⁻¹ region, distributed over a number of in-plane (ip) polarized porphyrin-based vibrations. The main component, assigned to δ_ip(Fe-N-O), is identified with the feature at 563 cm⁻¹. The Fe-N-O bend also shows strong mixing with the Fe-NO stretching internal coordinate, as evidenced by the oop NRVS intensity in the 520 – 580 cm⁻¹ region. Very accurate normal mode descriptions of ν(Fe-NO) and δ_ip(Fe-N-O) have been obtained in this study. These results contradict previous interpretations of the vibrational spectra of 6C ferrous heme-nitrosyls where the higher energy feature at ~550 cm⁻¹ had usually been associated with ν(Fe-NO). Furthermore, these results provide key insight into NO binding to ferrous heme active sites in globins and other heme proteins, in particular with respect to (a) the effect of hydrogen bonding to the coordinated NO, and (b) changes in heme dynamics upon NO coordination. [Fe(TPP)(MI)(NO)] constitutes an excellent model system for ferrous NO adducts of myoglobin (Mb) mutants where the distal histidine (His64) has been removed. Comparison to the reported vibrational data for wild-type (wt) Mb-NO then shows that the effect of H-bonding to coordinated NO is weak, and mostly leads to a polarization of the π/π* orbitals of bound NO. In addition, the observation that δ_ip(Fe-N-O) does not correlate well with ν(N-O) can be traced back to the very mixed nature of this mode. The Fe-N(imidazole) stretching frequency is observed at 149 cm⁻¹ in [Fe(TPP)(MI)(NO)], and spectral changes upon NO binding to five-coordinate ferrous heme active sites are discussed. The obtained high-quality force constants for the Fe-NO and N-O bonds of 2.57 and 11.55 mdyn/Å can further be compared to those of corresponding 5C species, which allows for a quantitative analysis of the σ trans interaction between the proximal imidazole (His) ligand and NO. This is key for the activation of the NO sensor soluble guanylate cyclase. Finally, DFT methods are calibrated against the experimentally determined vibrational properties of the Fe-N-O subunit in 1. DFT is in fact incapable of reproducing the vibrational energies and normal mode descriptions of the Fe-N-O unit well, and thus, DFT-based predictions of changes in vibrational properties upon heme-modification or other perturbations of these 6C complexes have to be treated with caution.

Introduction

Nitric oxide (NO), a poisonous and corrosive diatomic, plays a crucial role in mammals both as a signaling molecule and as a means of immune defense against pathogens.¹ For the purpose of signaling, NO is produced by endothelial (e−) or neuronal (n−) nitric oxide synthase (NOS), which are enzymes of the cytochrome P450 family.² Here, NO is produced by the stepwise oxidation of L-arginine to citrulline, which is accompanied by the generation of one molecule of NO. The important cardiovascular or neuronal regulation by NO is then mediated by soluble guanylate cyclase (sGC).³ This enzyme serves as the general biological NO sensor/receptor in mammals. In its active form, sGC contains a five-coordinate (5C) ferrous heme with proximal histidine (His) coordination, which exhibits a very high affinity for NO.⁴ Upon binding of NO, a six-coordinate ferrous heme-nitrosyl is believed to form as an intermediate. Due to the strong σ trans interaction between NO and the axial His ligand,^5,6,7,8,9 the Fe(II)-N_His bond is broken, leading to the corresponding 5C ferrous heme NO complex. This is accompanied by large structural changes of the enzyme, which activates the catalytic site of sGC for the conversion of guanosine triphosphate (GTP) into the secondary messenger cyclic guanosine monophosphate (cGMP), which leads to the relaxation of vascular smooth muscle tissue, and nerve signal transduction.¹⁰ Besides its central role in mammalian physiology, nitric oxide is also an important intermediate in bacterial and fungal dissimilatory denitrification.¹¹ Here, NO is produced by the reduction of nitrite, and then reduced to nitrous oxide by the NO reductase family of enzymes.¹² Many of the important biological functions and transformations of NO involve heme active sites, leading to the formation of ferrous and ferric heme-nitrosyl complexes and intermediates.^13,14,15 Because of this, NO binding to deoxy-hemoglobin (Hb) and -myoglobin (Mb) and corresponding model complexes has been studied in much detail over the years to elucidate the properties of ferrous heme-nitrosyls, and how these properties are mediated in heme proteins by the choice of the axial ligand, and effects of the substrate binding pocket.^14,15 With respect to the former, it has been shown that the presence of imidazole (Im), for example in His, as a proximal ligand producing the six-coordinate (6C) species [Fe(Porphyrin)(Im)(NO)] weakens both the Fe-NO and N-O bonds, and changes the distribution of the unpaired electron of NO in the complex.^{7,8,9, 15,16,17} This finding could be the key for the activation of NO in bacterial NO reductase.⁷ In addition, the active-site vibrations of proteins often relate to their functional dynamics,¹⁸ for example in cooperativity of small-molecule binding, but quantitative analyses of changes in vibrational dynamics due to small molecule binding are often times lacking. This aspect is further addressed here.

On the other hand, the question of how hydrogen bonding from the distal His in globins influences the properties of bound NO is an open and puzzling problem. The presence of the distal H-bond is important for regulating the properties of bound ligands, most notably O₂,¹⁹ but whether this hydrogen bond also influences bound NO is not clear. Vibrational spectroscopy is a great method to gain insight into these questions, but application of vibrational methods to 6C ferrous heme-nitrosyls has been hampered by the fact that the assignment of the Fe-NO stretching and Fe-N-O bending modes, ν(Fe-NO) and δ_ip(Fe-N-O), has been very controversial for a long time.^20,21,22 Recently, it has been shown that ν(Fe-NO) and δ_ip(Fe-N-O) for wild-type (wt) Mb-NO are observed at 443 and 547 cm⁻¹,²³ whereas previously, the vibration at ~550 cm⁻¹ had been associated with the Fe-NO stretch. This revised assignment with the bending mode being at higher energy than ν(Fe-NO) is also in agreement with our preliminary results for [Fe(TPP)(MI)(NO)] (1; note that MI = 1-methylimidazole, whereas Im = a general imidazole-type ligand).^7c In this work, we further resolve this long-standing controversy.

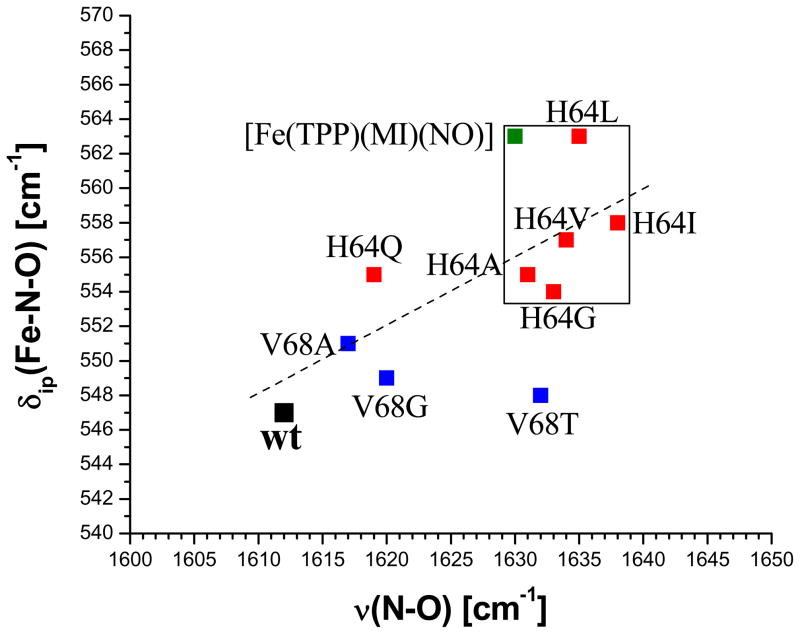
Curiously, if the distal His (His64) in wt Mb is replaced by leucine or isoleucine, ν(N-O) shifts from 1613 to 1635 – 1640 cm⁻¹ and δ_ip(Fe-N-O) moves from 547 to ~560 cm⁻¹, but unfortunately, the change in ν(Fe-NO) is not known.²² In addition, if the energy of δ_ip(Fe-N-O) is plotted against ν(N-O) for ferrous NO adducts with proximal imidazole-type ligands of a variety of heme proteins, a quite poor correlation is observed, where δ_ip(Fe-N-O) and ν(N-O) span ranges of 540 – 580 and 1600 – 1660 cm⁻¹, respectively.¹⁵ If δ_ip(Fe-N-O) would be a pure bending mode, then it should not be strongly affected by small changes in Fe-NO and N-O bond strengths that might be caused by the presence or absence of the H-bond. Importantly, our preliminary results show that the complex studied in this work, [Fe(TPP)(MI)(NO)], is a very good model system for the hydrogen-bond free mutants of Mb (His64X, where X is a bulky amino acid like Leu or Ile). Hence, the detailed analysis of the high-quality single-crystal vibrational data of this complex presented here in comparison to wt Mb-NO provides key insight into the effect of the hydrogen-bond on the coordinated NO in globins, and elucidates why δ_ip(Fe-N-O) shows a quite arbitrary response to changes in heme environment when correlated with ν(N-O). The latter observation can be explained based on the high-quality descriptions of the Fe-NO stretching and Fe-N-O bending vibrations in 6C ferrous heme-nitrosyls obtained in this work.

In order to achieve this, we have applied Nuclear Resonance Vibrational Spectroscopy (NRVS)²⁴ to elucidate the vibrational properties of the model complex [Fe(TPP)(MI)(NO)] in detail. NRVS has the advantage compared to resonance Raman spectroscopy that it does not suffer from the potential photolability of transition metal nitrosyl complexes under laser irradiation,^7c,25 since NRVS is a nuclear scattering technique.²⁶ In addition, due to the different selection rules, metal-ligand stretching vibrations are often very intense in NRVS (see Results and Analysis),²⁶ and correspondingly, this method has successfully been applied to ferrous heme-nitrosyls^{7c,23,27,28,29,30} and -carbonyls.³¹ However, despite these successes, reliable assignments of the complete NRVS spectra of 6C ferrous heme-nitrosyls have not been achieved. This is due to the fact that in our preliminary work, the NCA simulations of the vibrational data were based on the porphine approximation. This has severe consequences for the vibrations of the [Fe(Porphyrin)] core. In particular, (a) no assignments of porphyrin-based vibrations could have been obtained, (b) small NO isotope shifts observed for other NRVS features of 1 could not be explained, (c) the absolute NRVS intensities of ν(Fe-NO) and δ_ip(Fe-N-O) could not be simulated and the mixing between the corresponding internal coordinates could not accurately be determined, (d) the mixing between the Fe-N-O modes and porphyrin vibrations could not be incorporated in the simulation, and (e) the Fe-N_Im (Im = imidazole) stretching mode contributes to multiple porphyrin-based vibrations of complex character.²⁹ The latter are sensitive probes of the Fe-N_Im bond strength²⁹ that directly relates to the cooperativity of NO binding in hemoglobin. This has been shown to be of key importance for the kinetics of NO generation and release in hypoxic sensing.³²

This work demonstrates how reliable assignments of the NRVS data of ferrous heme-nitrosyls can be obtained. For this purpose, the previously published NRVS powder spectra of model complex 1 and of the corresponding ¹⁵N¹⁸O labeled complex are utilized^7c together with in-plane and out-of-plane oriented single-crystal NRVS data.²³ This is the first time that a complete set of single-crystal NRVS data that includes both in- and out-of-plane polarized spectra are simulated using NCA. To improve the reliability of the NCA results, our quantum chemistry centered NCA (QCC-NCA) scheme was applied where the large majority of force constants are not guessed in an empirical refinement procedure, but taken from high-level DFT calculations.^7c,33 In this way, we were able to obtain a very good fit of the NRVS data of 1, and address all the questions (a) – (e) posed above. The biological implications of our results, in particular with respect to NO binding to globins and sGC, are then discussed. Finally, DFT methods are calibrated with respect to their ability to accurately predict the vibrational properties of 6C ferrous heme-nitrosyls.

Experimental and Computational Procedures

Reactions were performed applying Schlenk techniques using carefully purified solvents. Single crystals of the complex [⁵⁷Fe(TPP)(MI)(NO)] (1; TPP²⁻ = tetraphenylporphyrin dianion, MI = 1-methylimidazole, whereas Im = a general imidazole-type ligand) were prepared using ⁵⁷Fe and crystallized as described previously.⁹ The IR spectrum of [⁵⁷Fe(TPP)(MI)(NO)] shows the NO stretching vibration ν(N-O) at 1630 cm⁻¹, indicative of the formation of 1. In addition, the NRVS spectrum obtained for this complex is identical to the one published before by us.^7c,23

Nuclear Resonance Vibrational Spectroscopy (NRVS)

NRVS data were collected as described in ref. 26 at beam line 3-ID-XOR of the Advanced Photon Source (APS) at Argonne National Laboratory. This beamline provides about 2.5·10⁹ photons/sec in ~1 meV bandwidth (= 8 cm⁻¹) at 14.4125 keV in a 0.5 mm(vertical) × 0.5 mm (horizontal) spot. This is achieved using a water-cooled diamond double crystal monochromator with 1.1 eV bandpass, followed by a high resolution monochromator consisting of two asymmetrically cut Si (4 0 0) and two asymmetrically cut Si (10 6 4) crystals, respectively.³⁴ Delayed nuclear fluorescence and Fe K fluorescence were detected using a single avalanche photodiode.³⁵ For the single-crystal measurements, a crystal of 1 was mounted so that the rotation axis of a eucentric goniometer head was exactly parallel to the (0 0 1) plane of the crystal system. This leads to an experimental orientation in which all porphyrin planes lie 13.8° from this plane. The out-of-plane (oop) orientations thus slightly deviate from ideality and the measurements have 6% contribution from the other orientation. Spectra were recorded between −50 and 80 meV in steps of 0.25 meV. Each scan took ~60 min, and all scans were normalized to the intensity of the incident beam and added. The single-crystal and powder data presented in Figure 1 represent averages of 4 scans and 7 scans, respectively. During the NRVS measurements, the samples remained at cryogenic temperatures using a liquid nitrogen cyocooler. Adequate Stokes and anti-Stokes intensities were obtained from the measurements, which allowed us to determine the sample temperatures to 119 K for the in-plane and 112 K for the out-of-plane data sets. Comparison of initial and final scans confirms the absence of spectroscopic changes due to radiation damage. The NRVS raw intensities were converted to the Vibrational Density of States (VDOS) using the program Phoenix.^26a Difficulties in the calculation of the VDOS were sometimes encountered due to problems with the resolution function. However, this affects mostly the background around the central (Mössbauer) line of the spectrum, and hence, the intensities of very low-energy vibrations < 10 cm⁻¹, which are not considered here.

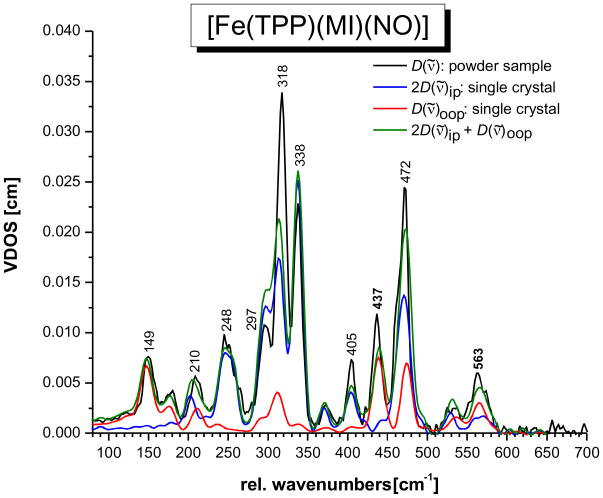
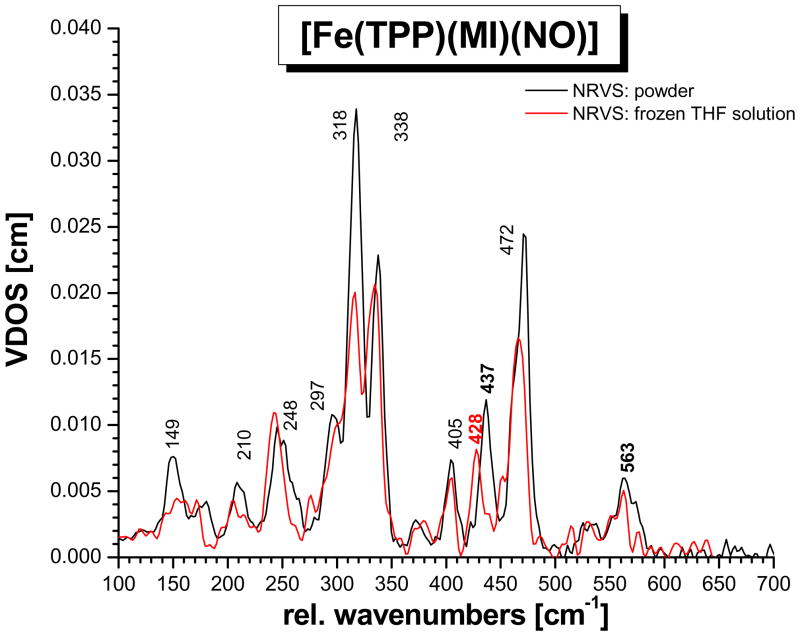
Figure 1.

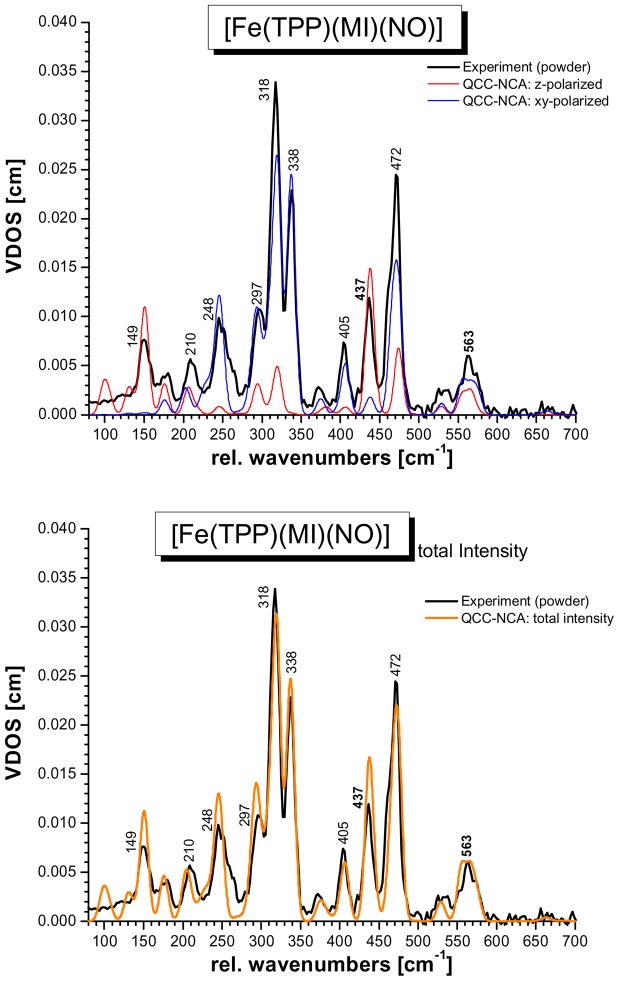
NRVS VDOS spectra of [⁵⁷Fe(TPP)(MI)(NO)] (1). Black: powder spectrum; blue and red: normalized single-crystal in-plane (blue) and out-of-plane (red) polarized spectra; green: predicted powder spectrum calculated by adding the in-plane and out-of-plane polarized contributions (total NRVS VDOS: D(ν̃) = D(ν̃)_oop + 2 D(ν̃)_ip).

Density Functional Theory (DFT) Calculations and Quantum Chemistry Centered Normal Coordinate Analysis (QCC-NCA)

The structure of the model complex [Fe(TPP)(MI)(NO)] (S = 1/2) was fully optimized without simplifications using the functionals BP86 and B3LYP together with the basis sets LanL2DZ* and TZVP. Vibrational frequencies were calculated for all optimized structures obtained this way showing no imaginary frequencies. The LanL2DZ basis set applies Dunning/Huzinaga full double zeta (D95) ³⁶ basis functions on first row and Los Alamos effective core potentials plus DZ functions on all other atoms.³⁷. The LanL2DZ* basis set consists of LanL2DZ plus polarization functions from TZVP on all non-hydrogen atoms (G98 implementation).^7a,28 TZVP corresponds to Ahlrich’s triple-ζ valence polarization basis set.³⁸ All calculations were performed using Gaussian 03.³⁹

In order to simulate the experimental NRVS spectra, we used our quantum chemistry centered normal coordinate analysis (QCC-NCA) package.^7b Here, the cartesian force field from G03 (for the BP86/TZVP calculation) was first transformed into internal coordinates using a modified version of Allouche’s program Redong (QCPE 628).⁴⁰ In the next step, we used our modified NCA programs, based on QCPE 576 by M.R. Peterson and D.F. McIntosh, to calculate the NRVS VDOS spectra.^7c This software was subsequently used to fit the NRVS data of 1. This approach, designed for the NCA of large molecules, is termed quantum chemistry centered NCA (QCC-NCA), because ≫ 99% of the force constants remain purely computational in the NCA simulations, which are focused on a small subset only of the total number of vibrations of the molecule.³³

In the first step of the NCA simulations performed here, the force constants of the Fe-N-O subunit previously determined (with the porphine approximation)^7c were substituted into the calculated force field for 1 (‘adjusted’ BP86/TZVP result). This was first followed by manual adjustments of diagonal force constants of the porphyrin core to approximately reproduce the vibrational frequencies, isotope shifts, and NRVS VDOS intensities of the observed vibrational features. Since not much information is available for the modes of the phenyl substituents, the corresponding force constants were left unchanged. Finally, the vibrational frequencies and isotope shifts were fitted against the experimental data using residual mean deviations as fit criterion. The quality of the calculated NRVS spectrum was included in the fit by qualitative comparison with the experimental spectrum. Further details of the fit, in particular with respect to the exact force constants included in the NCA simulation, are presented in Section C of the Results & Analysis. Table S1 lists all force constants that were adjusted in the fit of the NRVS spectrum of 1; a selection of important force constants of the Fe-N-O unit is provided in Table 1. The complete force field (including definitions of internal coordinates) is provided in the Supporting Information.

Table 1.

Selected force constants of the Fe-N-O subunit invoked in the fit of the NRVS VDOS data of [Fe(TPP)(MI)(NO)] (1) using the QCC-NCA approach. A complete list of force constants is provided in Table S1. Definitions of internal coordinates are included in the Supporting Information.

Force Constant a	BP86/TZVP	QCC-NCA
Fe-NO [1]	3.2408	2.574 [2.55 – 2.60] b
N-O [2]	12.219	11.55
Fe-N-O [60]	0.6944	0.773 [0.76 – 0.78]
Fe-NO/N-O	0.7387	0.336
Fe-NO/Fe-N-O	0.3385	0.399 [0.37 – 0.40]
N-O/Fe-N-O	0.3110	0.403
Fe-NIm [7]	0.5635	0.7835
τ(Fe-NO) [162]	0.0252	0.0275
τ(Fe-NIm) [163]	0.0453	0.0133
[162]/[163]	0.0003	0.0041

^aNumbers in square brackets refer to the number of the corresponding internal coordinate in the force field of complex 1 provided in the Supporting Information.

^bNumbers in square brackets provide a range in the QCC-NCA fit for the corresponding force constant

Results and Analysis

A. Single-Crystal Nuclear Resonance Vibrational Spectroscopy (NRVS) on [Fe(TPP)(MI)(NO)] (1)

Introduction to NRVS

Nuclear Resonance Vibrational Spectroscopy (NRVS) measures the inelastic scattering that is observed upon excitation of the ⁵⁷Fe nucleus at the 14.4125 keV Mössbauer line. NRVS is advantageous for the identification of metal-ligand stretching and bending vibrations, since NRVS intensities are proportional to the amount of iron motion of a normal mode.²⁶ Hence, metal-ligand stretching vibrations are often very intense in NRVS, and correspondingly, this method has recently been successfully applied to ferrous heme-nitrosyls and carbonyls as described in the Introduction. As shown by Sturhahn, the NRVS raw intensity can be converted into the Vibrational Density of States (VDOS),²⁶ in the case of which the integral intensity of a vibrational band is directly proportional to the normalized square of the amount of iron motion, ${\text{e}}_{\text{Fe}}^2$, of the corresponding normal mode (i.e. the kinetic energy fraction of Fe):

$$D(\stackrel{\sim }{\nu })=\sum _{\alpha =1}^{3N-6}{\text{e}}_{\text{Fe},\alpha }^2·\mathrm{\Gamma }(\stackrel{\sim }{\nu }-{\stackrel{\sim }{\nu }}_{\alpha })(\text{total}\text{VDOS})$$ (1)

$$D_k(\stackrel{\sim }{\nu })=\sum _{\alpha =1}^{3N-6}{\left(\overrightarrow{k}·{\overrightarrow{\text{e}}}_{\text{Fe},\alpha }\right)}^2·\mathrm{\Gamma }(\stackrel{\sim }{\nu }-{\stackrel{\sim }{\nu }}_{\alpha })(\text{VDOS}\text{in}\text{direction}k;k=x,y,z)$$ (2)

where D(ν̃) is the VDOS, the sum over α runs over all normal modes of the molecule (3N−6 for non-linear molecules; N = number of atoms), e⃗_Fe,α is the normalized displacement vector of iron for normal mode α with energy h·c·ν̃_α, and Γ(ν̃ − ν̃_α) is a normalized spectroscopic line shape function. The integrated NRVS intensity for a given normal mode corresponds therefore directly to ${\text{e}}_{\text{Fe}}^2$, which is readily obtained from NCA using the atomic displacement matrix together with the equation:^27b

$${\text{e}}_{\text{Fe}}^2=\frac{m_{\text{Fe}}{r}_{\text{Fe}}^2}{{\displaystyle \sum _{\text{i}}}{m}_{\text{i}}{r_{\text{i}}}^2}$$ (3)

where the sum over i runs over all atoms of the molecule, and r_i is the absolute length of the mass-weighted atomic displacement vector for atom i for a given normal mode from NCA. Hence, the NRVS VDOS can be easily obtained from NCA simulations. In the following, we will take advantage of this and calculate in-plane and out-of-plane polarized NRVS spectra using our QCC-NCA method.^7b,c

NRVS data of [⁵⁷Fe(TPP)(MI)(NO)]

In previous work, the NRVS powder spectrum of the complex [⁵⁷Fe(TPP)(MI)(NO)]^7c,23 and of the corresponding ¹⁵N¹⁸O substituted derivative^7c have been reported. Figure 1 (black) shows the NRVS VDOS of this complex with natural abundance NO. Table 2 provides the vibrational energies and observed isotope shifts (¹⁵N¹⁸O data is not included in Figure 1; see ref. 7c). From these data, two strongly ¹⁵N¹⁸O isotope sensitive features are identified at 437 and 563 cm⁻¹, which have been assigned in preliminary work to the Fe-NO stretch ν(Fe-NO) and the Fe-N-O in-plane bend δ_ip(Fe-N-O), respectively.^7c Other isotope sensitive features are observed at 472, 338, and 209 cm⁻¹. These belong to porphyrin-based vibrations, and hence, the reasons for the observed isotope shifts are unclear. This is due to the fact that the NCA simulations in ref. 7c are based on the porphine approximation, i.e. model system [Fe(P)(MI)(NO)], and hence, no assignments of porphyrin-based vibrations could have been made. In addition, the absolute NRVS intensities of the 437 and 563 cm⁻¹ features could not be simulated (only their NRVS VDOS intensity ratio).

Table 2.

Vibrational assignments for [Fe(TPP)(MI)(NO)] (1) based on the QCC-NCA simulation of the oriented single-crystal NRVS data of this complex.

Experiment		QCC-NCA b				Literature (Exp.) e
ν [cm−1] (Δ) a	Polarization	ν [cm−1]	Sym/Int c	Polarization	Assignment d	[Fe(TPP)(MI)(CO)]
		575		ip	18% δip(Fe-N-O) + γCαCM + 11% ν(Fe-NO)
563 (−12)	ip/oop = 2:3	568		ip/oop = 1:1	6% δip(Fe-N-O) + γCαCM + γ(Ph) + 5% ν(Fe-NO)
		566		ip/oop = 1.3:1	13% δip(Fe-N-O) + γCαCM + Pyr.rot + γ(Ph) + 11% ν(Fe-NO)
		555		ip/oop = 1.6:1	18% δip(Fe-N-O) + γCαCM + Pyr.fold + 16% ν(Fe-NO)
530	ip/oop = 1:1	530/528	Eu	ip/oop = 1.3:1	γ(Ph) + δip(N-Fe-N) + Pyr.trans
472 (−3) (two components)	ip/oop = 2:1	474	Eu/s	ip/oop = 3:1	Pyr.rot + 21% ν(Fe-NO) + 9% ν(Fe-NPyr) (ν49/ν50)	471/470, Eu, ν49/ν53
		466			Pyr.rot + 7% ν(Fe-NPyr) (ν49/ν50)
		445	/w	oop	Pyr.rot
437 (−8)	oop	438	/s	oop	35% ν(Fe-NO) + Pyr.rot + 14% δip(Fe-N-O)
405	ip	407/406	Eu/w	ip	Pyr.trans + 32% ν(Fe-NPyr) (ν53/ν50)	420/410, Eu, ν50/ν53
		383	A1g/vw	oop	33% ν(Fe-NPyr)
372	ip	375	w	ip	Im.rot
338 (−2)	ip	337	Eu/vs	ip	24% ν(Fe-NPyr) + Pyr.rot + Pyr.tilt + 22% δoop(ON-Fe-NPyr) + 14% τ(NO) (ν50/ν49)	338/325, Eu, ν49/ν50/ν53
318	ip/oop = 3.4:1	320		ip/oop = 4.4:1	24% ν(Fe-NPyr) + Pyr.rot + Pyr.swiv + Pyr.tilt (ν50/ν49)
		319	/s	ip/oop = 7:1	Pyr.swiv + 20% ν(Fe-NPyr)
297	ip/oop = 5.3:1	309	Eu/s	ip/oop = 2:1	Pyr.tilt + 16% ν(Fe-NPyr) + Pyr.rot (ν49/ν50)	301
		294		ip/oop = 2.6:1	Pyr.tilt + 14% ν(Fe-NPyr) + Pyr.rot (ν49/ν50)
		298	B2u/m		Pyr.tilt
		289	/m		δoop(Im) + Pyr.tilt
248	ip	249	Eu/s	ip	γ(Ph) + δoop(Im) + Pyr.tilt + 4 % τ(NO)	255/244, Eu, ν42/ν5o
		245			γ(Ph) + Pyr.tilt + δip(N-Fe-N) + 6 % δip(Fe-N-O)
		234	/mw	ip	δoop(Im) + τ(Im)
209 (−6)	ip/oop = 1:1	206/202	/m	oop	Pyr.tilt + γCαCM + 5% ν(Fe-NIm)	226, ν(Fe-NIm), oop (different mode)
				ip	22 % τ(NO) + Pyr.tilt
180	ip/oop = 1:3	176	/w	ip/oop = 1:2	38% δip(Fe-N-CIm) + 24% ν(Fe-NIm)	172, δip(Im)
149	oop	151	A2u/s	oop	41% ν(Fe-NIm) + δoop(Fe-Im) + Pyr.tilt (γ9)	124, γ9/γ6, oop
		131	/w		Pyr.tilt + δoop(Fe-Im) + 4% ν(Fe-NIm)

^a(Δ) = ¹⁵N¹⁸O isotope shift.

^bBased on the BP86/TZVP calculation.

^cSymmetry (Sym) and calculated intensity (Int): vs = very strong, s = strong, m = medium, mw = medium weak, w = weak, vw = very weak.

^dFor nomenclature see ref. 48. Classification of porphyrin modes by Spiro and coworkers: ν₄₂: δ(C_M-X) (E_u); ν₄₉: Pyrrole (Pyr.) in-plane (ip) rotation (E_u); ν₅₀: ν(Fe-N_Pyr) (E_u); ν₅₃: Pyr.ip translation (E_u); γ₉: out-of-plane (oop) doming (A_2u); γ₆: oop Pyr.tilting (A_2u); see ref.s ^46a,c.

^eFrom ref. 31a.

Whereas the ¹⁵N¹⁸O isotope shifts are very insightful for the analysis of the vibrations of the FeN-O unit, more information is necessary in order to assign the porphyrin-based NRVS features of 1. One possibility to achieve this is to apply oriented single-crystal NRVS measurements,^{23,29,31b,53,41} which provide an opportunity to achieve such assignments efficiently. Figure 1 shows the z-polarized (red) and xy-polarized (blue) NRVS data for complex 1, where the z direction is orthogonal to the porphyrin plane along the (Im)N-Fe-N(O) axis (out-of-plane, oop; Im = imidazole), and the xy direction is located in the porphyrin plane (in-plane, ip). These polarized spectra are absolutely essential to obtain a reliable QCC-NCA fit of the NRVS data of 1 (vide infra).

The single-crystal data show that the δ_ip(Fe-N-O) mode at 563 cm⁻¹ has a stronger oop intensity component than predicted with the simple porphine model in ref. 7c, indicating stronger mixing with the Fe-NO stretching coordinate than previously determined. The Fe-NO stretch at 437 cm⁻¹ is strongly oop polarized as observed before.²³ The intense feature at 472 cm⁻¹ corresponds to a porphyrin-based vibration that is usually observed around 470 cm⁻¹ in TPP complexes,^27,31 but with much less intensity. The fact that this band shows strong oop intensity in the case of 1 indicates strong mixing with the nearby Fe-NO stretch at 437 cm⁻¹. In this way, the dramatic intensity increase of the 472 cm⁻¹ feature compared to other TPP complexes can be explained. This is also consistent with the observed isotope shift of this feature to 469 cm⁻¹ in the ¹⁵N¹⁸O complex. The intense bands in the 300 – 350 cm⁻¹ region belong to the E_u component (in ideal D_4h symmetry) of the Fe-N(porphyrin) stretching mode, ν(Fe-N_Pyr) (Pyr = pyrrole), mixed with other porphyrin-based vibrations of the same symmetry. The main components are observed at 338 and 318 cm⁻¹, and a smaller feature is located at 297 cm⁻¹. Due to the lower symmetry of 1, the E_u mode appears clearly split, but more importantly, the two main components also show distinct differences in their properties: whereas the feature at higher energy (338 cm⁻¹) has vanishing oop intensity, but shows an ¹⁵N¹⁸O isotope shift of 2 cm⁻¹, the lower energy feature (318 cm⁻¹) shows distinct oop intensity, but no isotope shift. Based on these properties, the two components can be distinguished and unambiguously assigned in our QCC-NCA simulation. As detailed below, the isotope sensitivity of the 338 cm⁻¹ feature is in fact due to a small admixture of the Fe-N(O) torsion.⁴² To lower energy, the mode at 248 cm⁻¹ is 100% ip polarized. The single-crystal data resolve the band at 209 cm⁻¹ into two different features, one of them ip and the other one oop polarized. Finally, the features at 180 and 149 cm⁻¹ are strongly oop polarized. In particular, the strong oop intensity of the 149 cm⁻¹ band indicates that this mode corresponds to the Fe-N_Im stretching vibration ν(Fe-N_Im). These assignments are further substantiated based on the QCC-NCA simulation described below.

Effects of low symmetry

Knowledge of the normalized ip and oop polarized NRVS data should also allow one to calculate the total NRVS intensity by the simple equation:

$$D(\stackrel{\sim }{\nu })=1/3D{(\stackrel{\sim }{\nu })}_{\text{oop}}+2/3D{(\stackrel{\sim }{\nu })}_{\text{ip}}$$ (4)

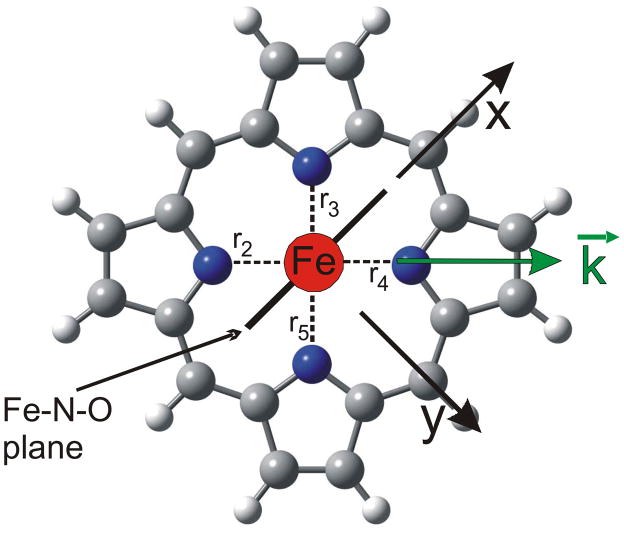
and the resulting total intensity should then correspond to the powder spectrum. Here, D(ν̃) is the total NRVS VDOS intensity, and D(ν̃)_oop and D(ν̃)_ip are the corresponding oop and ip intensities. However, the total NRVS data shown in green in Figure 1 calculated from the single-crystal data exhibit distinct deviations from the powder spectrum in black. How is this possible? The reason for this difference lies in the reduced symmetry of complex 1. In order to explain this effect, let us consider the E_u component of the Fe-N(porphyrin) stretching mode in D_4h symmetry first. Using the internal coordinate definitions shown in Scheme 1, the two components of the E_u mode could be expressed as:

$$\begin{array}{l}{\chi }_1^{Eu}=\sqrt{1/2}[r_2-r_4]\\ {\chi }_2^{Eu}=\sqrt{1/2}[r_3-r_5]\end{array}$$ (5)

Scheme 1.

However, any linear combination of these two coordinates is also a valid representation of the E_u mode, for example:

$$\begin{array}{l}{{\chi }^{\prime }}_1^{Eu}=1/2[r_2-r_3-r_4+r_5]\\ {{\chi }^{\prime }}_2^{Eu}=1/2[r_2+r_3-r_4-r_5]\end{array}$$ (6)

Therefore, measuring in just one direction in the xy plane is in fact sufficient to capture the total NRVS ip intensity, and eqn. (4) is valid. This picture changes when the symmetry of the complex is lowered, for example by adding non-linear axial ligand(s). This symmetry lowering will lead to an energy splitting between the two components of the E_u mode, but more importantly, the two components localize. In other words, whereas the direction of motion in D_4h symmetry in the xy plane is undefined, it becomes defined in lower symmetry. Most Fe-N(porphyrin) modes appear to localize with respect to the Fe-NO plane in the five-coordinate complex [Fe(OEP)(NO)].⁴³ In the case of the six-coordinate complex 1, however, the two components of any given E_u mode could localize either with respect to the Fe-NO or the Fe-Im plane (this probably depends on the nature and energy of the respective E_u mode). Considering the Fe-N(porphyrin) stretching mode of E_u symmetry, localization is observed with respect to the Fe-N-O plane such that one component (at 338 cm⁻¹) shows iron motion within and the other one (at 318 cm⁻¹) shows iron motion orthogonal to the Fe-N-O plane as indicated in Scheme 1 (direction x and y). The large energy splitting of the two components is due to the fact that they couple with different modes of the axial NO ligand; i.e. one component mixes with modes that correspond to Fe-N-O motions orthogonal to the Fe-N-O plane, and the other component interacts with in-plane modes of this axial ligand. Since these axial ligand vibrations are very different in energy, they influence the two E_u components differently. In this way, an anisotropy of the iron motion could also be introduced; i.e. the NRVS intensity of the two components could become different as observed for the 338 and 318 cm⁻¹ features in Figure 1. Because of this localization effect of ip porphyrin E_u-type vibrations, equation 4 is invalid. Scheme 1 illustrates this further: let’s assume that components I and II of the E_u mode show iron motion in x and y direction, respectively. If the ip polarized NRVS measurement is performed along the x axis, then component I shows full intensity, whereas component II vanishes! At an arbitrary measurement position k⃗ in the xy plane as indicated in Scheme 1, the intensities of components I and II scale with the scalar product of k⃗ and the iron displacement vector of each component, k⃗ · e⃗_Fe,α, as defined in equation 2. Hence, whereas the oop polarized NRVS intensity in Figure 1 (red) is well defined, the ip polarized intensity in Figure 1 (blue) is incomplete. This explains why the theoretical NRVS VDOS in green calculated from the single-crystal data (using equation 4) and the experimental powder spectrum deviate; it is in fact the green spectrum that is flawed. In the QCC-NCA fit, a stronger weight is therefore put on reproducing the oop intensity well, whereas the ip intensity is allowed to vary more strongly.

B. DFT calculations of the NRVS spectra of [Fe(TPP)(MI)(NO)] (1)

Calculated structures and vibrational energies

In order to investigate the assignments of the NRVS spectra of 1 systematically, we have performed DFT calculations on this complex without any simplifications applying both the BP86 and B3LYP functionals and the basis sets LanL2DZ* and TZVP (see Experimental Section). Table 3 lists calculated structural and vibrational data from these calculations. The best agreement between the optimized and experimental structures of 1 is obtained for BP86/TZVP. Figure 2, top shows the corresponding optimized structure. The obtained Fe-NO and N-O distances of 1.741 and 1.186 Å, respectively, show excellent agreement with the corresponding experimental bond lengths of 1.750 and 1.182 Å.⁹ The Fe-N_Im distance is predicted to be 2.204 Å, which is slightly overestimated compared to experiment (2.173 Å).⁹ This indicates that the Fe-N_Im bond strength is slightly underestimated by BP86/TZVP. Other computational methods yield somewhat larger deviations from the observed geometry. Using BP86/LanL2DZ*, a similar description of slightly lower quality is observed as shown in Table 3, but at a fraction of the computational cost. The LanL2DZ* basis set is therefore a good approximation for TZVP.

Table 3.

Geometric and vibrational properties of [Fe(Porphyrin)(L)(NO)] complexes where L is either vacant or 1-methylimidazole (MI) as axial ligand trans to NO.

Molecule a	Geometric Parameters [Å]						Vibrational Frequencies [cm−1]
	Fe-N	N-O	∠Fe-N-O	Fe-NP	Fe-NIm	Ref	ν(N-O)	ν(Fe-NO)	δip(Fe-N-O)	Ref	Condition
Five-Coordinate [Fe(Porphyrin(NO)] Complexes
[FeII(OEP)(NO)] Monoclinic (form I) Triclinic (form II)	1.722 1.731	1.167 1.168	144 143	2.004 2.010	- -	61	1671	522 d	388 d	28	KBr (N-O), solid
[FeII(OEP)(15N18O)]					-		1597	508 d	381 d
[FeII(TPP)(NO)] b	1.72	1.12	149	2.00	-	62	1697	532	371	7b	KBr
[FeII(TPP)(15N18O)]							1625	515	365
[FeII(TPP)(NO)]					-		1678	524		63	benzene
[FeII(TPP)(NO)]					-			538		27a	solid
[FeII(P)(NO)] Calc: BP86/TZVP	1.705	1.179	146	2.019	-	7b	1703	595	427	7b	-
[FeII(P)(NO)] Calc: BP86/LanL2DZ*	1.688	1.188	144	2.021	-	28	1726	619	428	28	-
[FeII(P)(NO)] Calc: B3LYP/TZVP	1.718	1.161	142	2.021	-	28	1790	585	444	28	-
[FeII(P)(NO)] Calc: B3LYP/LanL2DZ*	1.712	1.169	141	2.020	-	28	1826	538	435	28	-
	Fe-N	N-O	∠Fe-N-O	Fe-NP	Fe-NIm	Ref	ν(N-O)	δip(Fe-N-O)/ν(Fe-NO)	ν(Fe-NO)	Ref	Condition
Six-Coordinate [Fe(Porphyrin(MI)(NO)] Complexes
[FeII(TPP)(MI)(NO)] (1)	1.750	1.182	138	2.008	2.173	9	1630	563 d	437 d	7b, c	KBr (N-O), solid
[FeII(TPP)(MI)(15N18O)]							1556	551 d	429 d
[FeII(TPP)(MI)(NO)]	1.743	1.121	142	2.008	2.180	5	1625			5	KBr
[FeII(TPP)(MI)(NO)]	1.749	1.184	137	2.007	2.170	64	1631			64
[FeII(TPP)(MI)(NO)]	1.745	1.163	138	2.006	2.186	64	1629			64
[FeII(To-F2PP)(MI)(NO)]	1.752	1.202	138	2.012	2.188	7b	1624			7b	KBr
[FeII(TPP)(MI)(NO)] Calc: BP86/TZVP	1.741	1.186	140	2.018	2.204	c	1661	606/485 e		c	-
[FeII(TPP)(MI)(NO)] Calc: BP86/LanL2DZ*	1.717	1.194	140	2.023	2.195	c	1687	623/481 e		c	-
[FeII(P)(MI)(NO)] Calc: BP86/TZVP	1.734	1.186	140	2.022	2.179	7b	1662	609/482 e		7b	-
[FeII(TPP)(MI)(NO)] Calc: B3LYP/TZVP	1.790	1.165	140	2.024	2.156	c	1787	550/416 f		c	-
[FeII(TPP)(MI)(NO)] Calc: B3LYP/LanL2DZ*	1.776	1.173	140	2.030	2.127	c	1817	543/406 f		c	-
[FeII(P)(MI)(NO)] Calc: B3LYP/LanL2DZ*	1.780	1.172	140	2.032	2.138	c	1824	539/417 f		c	-

^aMI = 1-methylimidazole; P = Porphine ligand used for calculations; values for Fe-N_P (Fe-N(porphyrin) bond distances) are averaged.

^bHighly disordered structure.

^cThis work.

^dDetermined from NRVS using ⁵⁷Fe. Compared to natural abundance isotopes (n.a.i.) Fe, the modes ν(Fe-NO) and δ_ip(Fe-N-O) appear about 1 – 2 cm⁻¹ shifted to lower energy.

^eFrom the potential energy distribution (PED) matrix, the 606 cm⁻¹ mode has 58% Fe-NO stretching and 26% Fe-N-O bending contribution, whereas the 485 cm⁻¹ vibration has roughly equivalent Fe-NO stretching and Fe-N-O bending character (BP86/TZVP). The BP86/LanL2DZ* result is similar to this. The calculation based on the porphine approximation also delivers equivalent results.

^fFrom the PED, the mode around 400 – 420 cm⁻¹ has 30 – 40% Fe-NO stretching and ~2% Fe-N-O bending character, whereas the feature at around 550 cm⁻¹ has roughly 30 % Fe-N-O bending and 20 % Fe-NO stretching character in the B3LYP calculations.

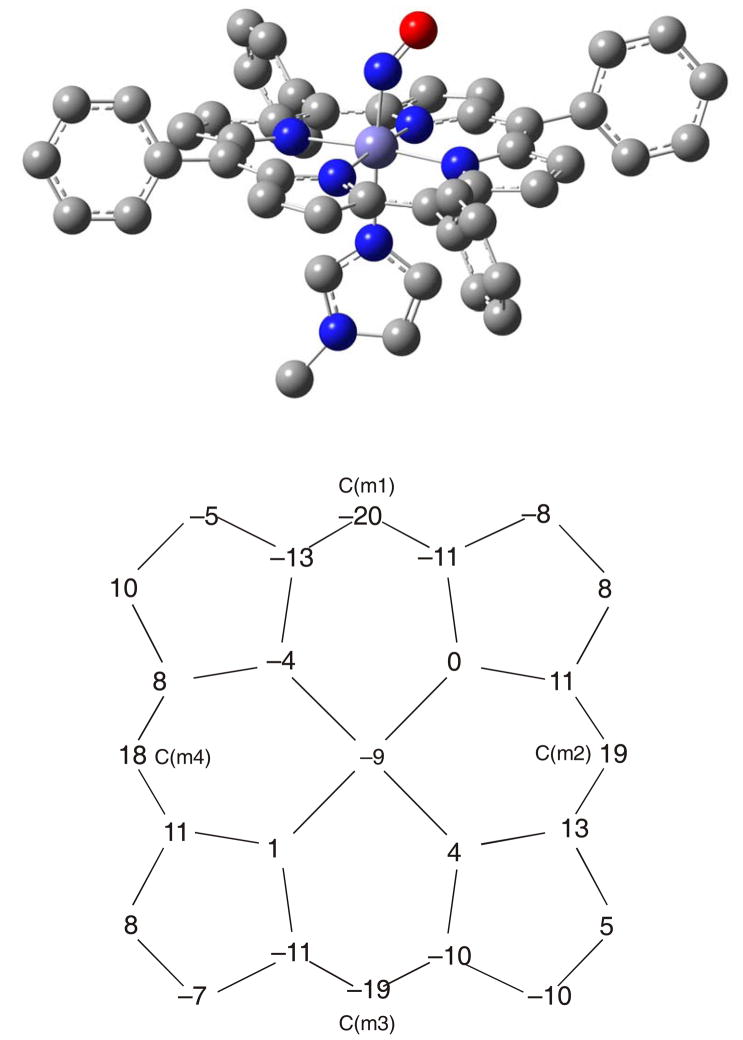
Figure 2.

Top: fully optimized structure of complex [Fe(TPP)(MI)(NO)] (1) using BP86/TZVP in side view. Bottom: porphyrin core diagram that indicates oop displacements of the atoms of the porphyrin ring, negative displacements are towards NO. The predicted distortion corresponds to ruffling. The angle between the Fe-N-O and the imidazole plane in the obtained structure is 26°, which is underestimated compared to experiment.

With BP86/TZVP, ν(N-O) is calculated at 1661 cm⁻¹, which is in good agreement with the experimental value of 1630 cm⁻¹ for 1. On the other hand, the frequencies that correspond to the Fe-NO stretching and Fe-N-O bending modes are predicted at 606 and 485 cm⁻¹. These are not pure vibrations and show a substantial degree of mode mixing as further discussed in Section C. In this case, the potential energy distribution matrix (ped) indicates that the feature at 606 cm⁻¹ has more dominant Fe-NO stretching than Fe-N-O bending character,⁴⁴ whereas the mode at lower energy shows comparable stretching and bending contributions (these characteristics vary somewhat as a function of the applied basis set). Moreover, these modes show quite large deviations of their vibrational frequencies from experimental NRVS data. The reasons for the observed deviations are twofold: (a) BP86 generally tends to overestimate metal-ligand covalencies, and hence, metal-ligand stretching frequencies are frequently observed at too high energy, especially for metal-NO bonds,^15,27b,45 and (b) more specifically for 1, the trans effect between the Fe-NO and Fe-N_Im bonds is not exactly reproduced in the calculations, where the Fe-NO bond is somewhat too strong (as evident from the shorter Fe-NO bond length and larger Fe-NO force constant) and the Fe-N_Im bond is somewhat too weak (as reflected by the longer FeN_Im bond length).

On the other hand, using B3LYP the covalency of the Fe-NO bond is generally reduced, ν(Fe-NO) is predicted around 400 – 420 cm⁻¹ as an almost pure Fe-NO stretching vibration, whereas the feature around 550 cm⁻¹ shows strong mixing of Fe-N-O bending and Fe-NO stretching contributions. Both modes also show substantial admixtures of porphyrin-based vibrations. The subtle interplay between the Fe-NO and Fe-N_Im bonds, which is related to a competition of the σ-donor orbitals of NO and imidazole for the d_z² orbital of iron(II) corresponding to a σ trans interaction (see Discussion), is still incorrectly predicted by B3LYP. In this case, the Fe-N_Im bond is too strong and correspondingly, the Fe-NO bond is now predicted too weak. This is evident from the Fe-NO and Fe-N_Im bond distances as shown in Table 3, which show clear deviations from experiment (although one has to be cautious here, because the Fe-N_Im distance is also sensitive to the environment; cf. Table 3). Correspondingly, ν(Fe-NO) is now underestimated at 416 cm⁻¹, and a second, strongly mixed feature as mentioned above is predicted at 550 cm⁻¹ (with B3LYP/TZVP). Compared to BP86, this corresponds to a somewhat better description of the Fe-NO bond strength and vibrational frequency, although the deviation from experiment is still significant. On the other hand, the B3LYP N-O stretching frequencies are predicted near 1800 cm⁻¹, which constitutes a very significant error. In conclusion, BP86 calculations show a somewhat better agreement in terms of structural and vibrational data compared to B3LYP, and serve as a reasonable starting point for the following QCC-NCA simulation (vide infra).

Interestingly, both functionals are inaccurate in determining the exact balance between the Fe-NO and Fe-N_Im trans interaction. As can be seen from a comparison of calculated and experimental Fe-NO bond lengths and force constants, the experimental reality is in fact between the BP86 and B3LYP results (values averaged from LanL2DZ* and TZVP calculations; cf. Table 3):

$$\begin{array}{l}{\text{r}}_{\text{Fe}-\text{NO}}:\text{BP}86(1.72-1.74)<\text{crystal}\text{structure}(1.750)<\text{B}3\text{LYP}(1.78-1.79)[\text{in}Å],\\ {\text{f}}_{\text{Fe}-\text{NO}}:\text{BP}86(3.24-3.43)>\text{QCC}-\text{NCA}(2.574)>\text{B}3\text{LYP}(2.05-2.18)[\text{in}\text{mdyn}/Å],\end{array}$$

where BP86 gives a too strong and B3LYP a too weak Fe-NO bond. In the case of the Fe-N_Im bond, the trend is roughly inverse:

$$\begin{array}{l}{\text{r}}_{\text{Fe}-\text{N}(Im)}:\text{B}3\text{LYP}(2.13-2.16)<\text{crystal}\text{structure}(2.17-2.18)<\text{BP}86(2.20)[\text{in}Å],\\ {\text{f}}_{\text{Fe}-\text{N}(Im)}:\text{B}3\text{LYP}(0.72-0.81)\ge \text{QCC}-\text{NCA}(0.783)>\text{BP}86(0.56-0.59)[\text{in}\text{mdyn}/Å].\end{array}$$

Because of these deviations, QCC-NCA simulations³³ are absolutely crucial to determine reliable force constants and vibrational assignments for the metal-N-O subunits in heme- and other transition metal nitrosyl complexes. Other structural features are similar for the BP86 and B3LYP calculations. In all cases, the Fe-N-O angle is 140°, which is in excellent agreement with experiment.⁹ Furthermore, the porphyrin ligand is predicted to be moderately ruffled as indicated in Figure 2, bottom, for BP86/TZVP (other porphyrin core displacement plots are given in the Supporting Information), which deviates from the saddled conformation observed experimentally. Finally, the dihedral angle between the Fe-NO and Fe-Im planes is similar in all calculations (~25°), which is somewhat underestimated compared to the experimental structure of 1.⁹ Altogether, good agreement with experiment is observed for the BP86/TZVP result, which is therefore used as the basis for the following QCC-NCA analysis.

Table 3 also shows structural and vibrational properties predicted for [Fe(P)(MI)(NO)] with BP86/TZVP, using the simple porphine (P²⁻; cf. Scheme 1) approximation. The calculated properties of the axial Fe-N-O subunit are very similar to the BP86/TZVP results obtained for the complete complex [Fe(TPP)(MI)(NO)], at a fraction of the computational effort. The porphine ligand is therefore a good approximation for OEP²⁻ and TPP²⁻ complexes, when the electronic properties of the axial Fe-N-O unit are considered.^7b,15,28 However, introduction of peripheral substituents induces substantial mixing between porphyrin-based and Fe-N-O vibrations (vide infra), which cannot be analyzed based on the porphine model.^7c

Calculated NRVS spectra for BP86/TZVP

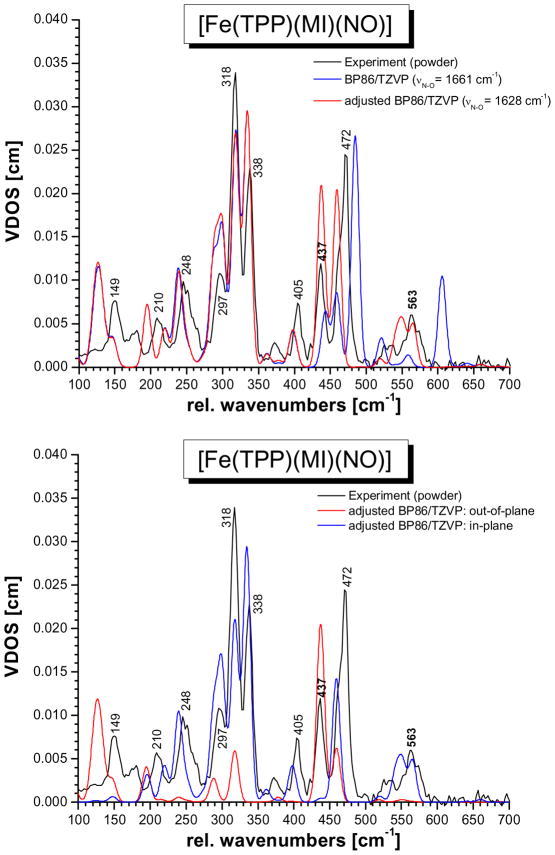
Figure S1 shows the DFT-calculated NRVS VDOS for the four functional/basis set combinations applied here. Apart from the findings regarding the vibrational energies of the Fe-N-O unit discussed above, the BP86/TZVP calculations also show the overall best agreement between the calculated and experimental frequencies and NRVS intensities of the porphyrin-based vibrations. Hence, for the following analysis, the BP86/TZVP result is used. In order to arrive at a preliminary assignment of the NRVS spectra of 1, we then used the BP86/TZVP calculated force field and substituted in the previously determined force constants of the Fe-N-O subunit obtained from a QCC-NCA fit of only the 437 and 563 cm⁻¹ features, using the porphine approximation.^7c This will be referred to as the ‘adjusted’ BP86/TZVP result. Figure 3, top shows a comparison of the original (blue) and adjusted (red) BP86/TZVP NRVS VDOS spectra. Surprisingly, the simple application of the previously determined force constants of the Fe-N-O unit yields vibrational frequencies for the Fe-NO stretch and the in-plane Fe-N-O bend that are in surprisingly good agreement with experiment, but, importantly, the experimental intensities of these modes are not reproduced well. Figure 3, bottom shows the oop and ip contributions to the total NRVS VDOS for the adjusted BP86/TZVP result. The overall agreement between the adjusted BP86/TZVP NRVS VDOS and experiment is quite impressive, considering how simple this approach is. Based on this, the experimentally observed NRVS features of complex 1 can be roughly assigned as listed in Table S2. The adjusted BP86/TZVP result is therefore an excellent starting point for the QCC-NCA fit of the NRVS data of 1 described in the next section. Based on the QCC-NCA fit, all features observed in the NRVS spectrum of 1 can be unambiguously assigned.

Figure 3.

Calculated NRVS VDOS spectra of [Fe(TPP)(MI)(NO)] (1). Top: BP86/TZVP (blue) and BP86/TZVP adjusted (red, using the calculated BP86/TZVP force field plus the QCC-NCA force constants for the Fe-N-O unit from ref. 7c). In the latter case, the vibrational energies of the Fe-NO stretch at 437 cm⁻¹ and the Fe-N-O bend at 563 cm⁻¹ are in surprisingly good agreement with experiment (black), but the experimental intensities of these modes are not reproduced well. Bottom: out-of-plane (z) and in-plane (xy) NRVS VDOS for the adjusted BP86/TZVP case.

C. Quantum Chemistry Centered Normal Coordinate Analysis (QCC-NCA)

In order to obtain proper simulations of the NRVS spectra of 1, a quantum chemistry centered normal coordinate analysis (QCC-NCA) was then performed to correct for the observed deviations in the adjusted BP86/TZVP result. Following the QCC-NCA philosophy, the force constants of the (Im)N-Fe-NO axial unit and the ‘FeN₆’ first coordination sphere of iron (the ‘core’) were varied in order to reproduce the vibrational energies, isotope shifts and polarized NRVS intensities of the spectral features associated with these internal coordinates. This includes Fe-N_Pyr stretching and N-Fe-N ip and oop octahedral bending modes. As evident from Figure 3, the porphyrin-based vibrations are already reproduced well in the BP86/TZVP calculation. Correspondingly, in the QCC-NCA fit, only diagonal force constants of internal coordinates of the porphyrin core and the imidazole ring (the ‘frame’) were adjusted, but the changes are generally small as shown in Table S1. All non-diagonal elements of these internal coordinates were left at the DFT-calculated values. Adjustments were also restricted to ip and oop porphyrin bending vibrations and torsions, and oop bending vibrations and torsions of the imidazole ring. This means that porphyrin- and imidazole-based vibrations were merely shifted in energy, but their nature was not changed significantly in this procedure. What has changed due to these shifts is the degree of mixing between ‘core’ and frame’ vibrations (vide infra). Finally, since spectral information about phenyl-based vibrations is scarce in the NRVS data, the force constants of the internal coordinates of the phenyl rings were not changed. Table S1 documents original (BP86/TZVP) and QCC-NCA force constants that were changed in the fitting procedure.

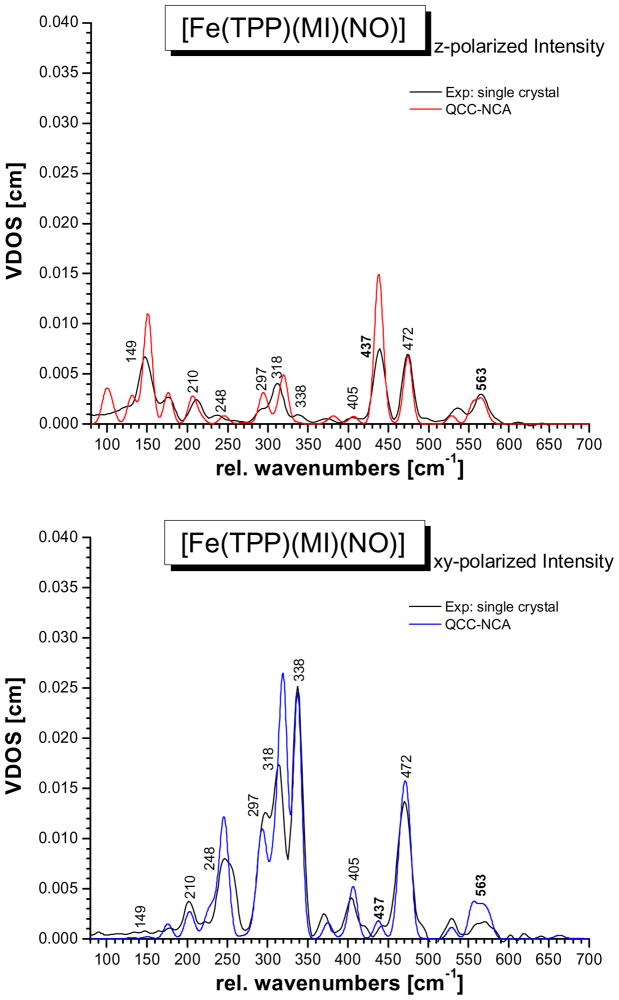
As shown in Figure 4, bottom, and Figure 5, excellent agreement between the QCC-NCA simulated NRVS spectra and the experimental data is obtained. In the following discussion of spectral assignments, the nomenclature of porphyrin-based vibrations largely follows the labeling scheme introduced by Spiro and coworkers (see footnote d in Table 2).⁴⁶ Note that in strict D_4h symmetry, the in-plane vibrations of the porphyrin ring have A_1g, A_2g, B_1g, B_2g and E_u symmetry,^47,48 and importantly, only the E_u-symmetric normal modes show an intrinsic iron displacement. Because of this, only E_u-type ip modes are NRVS active. Hence, the NRVS spectra of metalloporphyrins are generally dominated by originally E_u-symmetric modes, split to a larger or lesser extend in complexes of lower symmetry, like 1. This is also observed here.

Figure 4.

QCC-NCA fit of the NRVS VDOS data of complex [⁵⁷Fe(TPP)(MI)(NO)] (1) based on the BP86/TZVP result. Top: experimental powder data (black) and in-plane (blue) and out-of-plane (red) intensities form the QCC-NCA fit. Bottom: experimental powder data (black) and total NRVS VDOS intensity from the QCC-NCA fit (orange).

Figure 5.

QCC-NCA fit of the NRVS VDOS data of complex [⁵⁷Fe(TPP)(MI)(NO)] (1) based on the BP86/TZVP result. Top: single-crystal out-of-plane polarized data (black) and QCC-NCA calculated out-of-plane intensity (red). Bottom: single-crystal in-plane polarized data (black) and QCC-NCA calculated in-plane intensity (blue).

Assignment of the Fe-NO stretch and Fe-N-O bend

The Fe-NO stretching mode of 1 is assigned to the oop polarized feature at 437 cm⁻¹ in agreement with previous NCA simulations that were based on the porphine approximation.^7c The intense NRVS feature at 472 cm⁻¹ (BP86/TZVP (adjusted): 459 cm⁻¹) corresponds to the pyrrole rotation (Pyr.rot, labeled ν₄₉ by Spiro and coworkers) of E_u symmetry (in D_4h) with some admixture of the corresponding, E_u-symmetric ν(Fe-N_Pyr) stretching (ν₅₀) vibration. The resulting normal mode is ip polarized. The higher energy component of this E_u mode shows strong mixing with the Fe-NO stretch, which explains the strong oop intensity of this feature. The combined Fe-NO stretching contribution to the 437 and 471 cm⁻¹ features is about 60%. On the other hand, the admixture of Fe-N-O in-plane bending character is relatively small at about 15 %, which explains the lack of significant ip intensity for ν(Fe-NO) at 437 cm⁻¹. This assignment is also consistent with the observed isotope shifts of the 437 and 472 cm⁻¹ bands, which shift to 429 and 469 cm⁻¹ in the ¹⁵N¹⁸O labeled complex, respectively. The QCC-NCA calculated shifts of −9 and −3 cm⁻¹ for these modes are in excellent agreement with experiment.

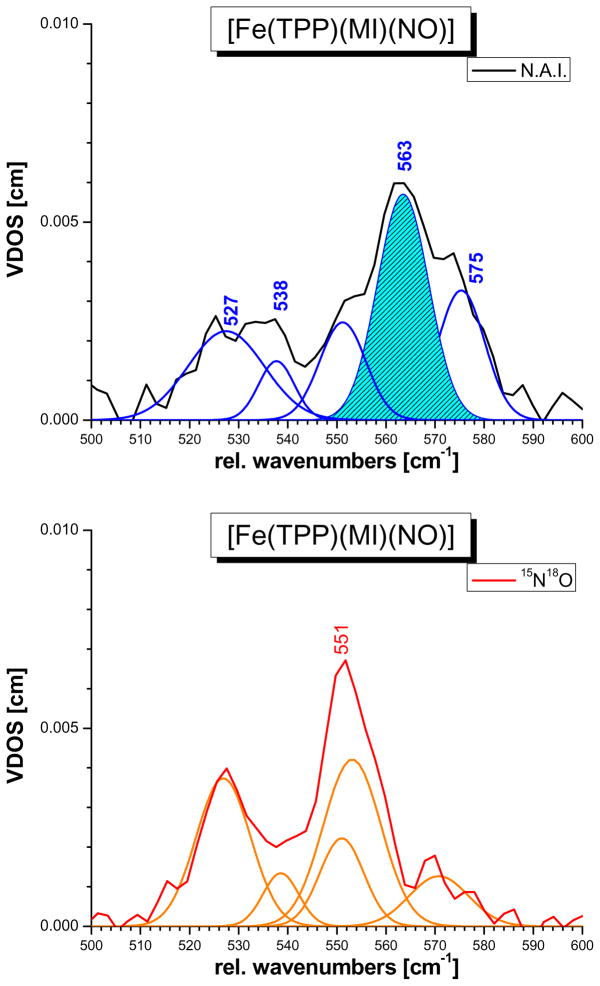
The DFT calculations show that the δ_ip(Fe-N-O) mode at 563 cm⁻¹ is mixed with a number of porphyrin-based vibrations in the 520 – 580 cm⁻¹ region of pyrrole folding (Pyr.fold) and rotation (Pyr.rot), meso-carbon oop bending (γC_αC_M), δ_ip(N-Fe-N) porphyrin-N (octahedral) bending, and phenyl oop bending type (cf. Table S2). A similar situation is encountered experimentally: a fit of the powder data of 1 from ref. 7c shown in Figure 6 reveals at least five normal modes in the 520 – 580 cm⁻¹ region that potentially have Fe-N-O bending contributions. The main feature is observed at 563 cm⁻¹, accompanied by a quite intense band (shoulder) at 575 cm⁻¹ and lower energy features at 538 and 528 cm⁻¹ as shown in Figure 6. Upon ¹⁵N¹⁸O isotope labeling, the FeN-O bending intensity is redistributed between these features, leading to a shift of the 563 cm⁻¹ band to 551 cm⁻¹, a dramatic intensity loss of the 575 cm⁻¹ band, and an intensity gain of the lower energy band at 527 cm⁻¹. This very particular behavior of the δ_ip(Fe-N-O) mode cannot be fully reproduced in the QCC-NCA simulation. In this case, a porphyrin-based vibration at ~575 cm⁻¹ with significant Fe-N-O bending character is also present as well as additional features at 568, 566, and 555 cm⁻¹ that show strong admixtures of the Fe-N-O bending internal coordinate as shown in Table 2. These features merge into one broad band centered around 562 cm⁻¹, leading to a similar intensity pattern as observed experimentally. However, the lower energy features around 530 cm⁻¹ in the QCC-NCA result do not show much mixing with the Fe-N-O bending mode, which becomes particularly evident in the ¹⁵N¹⁸O labeled case. This indicates that the porphyrin-based vibrations in this energy range are somewhat different experimentally compared to the QCC-NCA result, which might be due to small structural differences between the geometry optimized and the experimental structure of 1. Importantly, the oop polarized NRVS spectrum of 1 in Figure 5, top shows quite strong oop intensity in the 520 – 580 cm⁻¹ region, which is different from the adjusted BP86/TZVP result in Figure 3, bottom, and also the preliminary QCC-NCA fit of the NRVS powder data of this compound in ref. 7c (using the porphine approximation). Since all porphyrin-based vibrations in the 520 – 580 cm⁻¹ energy range observed in the NRVS data are almost exclusively ip polarized with respect to their iron motion, the experimentally observed NRVS oop intensity in this frequency range (cf. Figure 1) can therefore not stem from other porphyrin modes, but must be due to significant mixing with the oop polarized Fe-NO stretching motion. As mentioned in Section B, the oop NRVS intensity is well defined in the single-crystal measurements, whereas the ip intensity carries an uncertainty due to the low symmetry of 1. Our strategy to determine the mixing between the Fe-NO stretching and Fe-N-O bending internal coordinates was therefore to fit the diagonal force constants f_Fe-NO and f_Fe-N-O together with the corresponding non-diagonal element f_Fe-NO/Fe-N-O to reproduce (a) the energies and isotope shifts of the 437 and 563 cm⁻¹ features, (b) the strong oop polarization of the 437 cm⁻¹ band, and (c) the oop intensity in the 550 – 580 cm⁻¹ frequency region. As shown in Figure 5, excellent agreement with experiment has been obtained in the QCC-NCA fit of these modes. Altogether, all normal modes in the 550 – 580 cm⁻¹ energy region (main contributors are listed in Table 2) combined exhibit a total of about 60% Fe-N-O bending, some N-Fe-N octahedral bending, and ~50% Fe-NO stretching character. Compared to the initial QCC-NCA result obtained with the porphine approximation, a distinctively stronger mixing between the Fe-NO stretch and the Fe-N-O bend is therefore observed, and in addition, mixing of these features with porphyrin-based vibrations is drastically enhanced as discussed above. This is due to the fact that the porphyrin core vibrations of TPP²⁻ have much different energies compared to P²⁻, such that in the latter case, mixing of ν(Fe-NO) and δip(Fe-N-O) with porphyrin-based modes is quenched. The QCC-NCA simulation presented here provides a superior picture not only due to the fact that the porphyrin-based vibrations are now well described, but also because the fit of the Fe-NO stretching and Fe-N-O bending modes is now based on absolute ip and oop NRVS intensities, whereas in the case of our preliminary NCA using the porphine approximation, only the intensity ratio of the 437 and 563 cm⁻¹ features could have been used for the simulation.

Figure 6.

NRVS VDOS powder data of [⁵⁷Fe(TPP)(MI)(NO)] (1, black, top) and of the corresponding ¹⁵N¹⁸O labeled complex (red, bottom) in the energy region of the δ_ip(Fe-N-O) bending mode, together with fits of these data (blue: 1, orange: ¹⁵N¹⁸O-labeled complex).

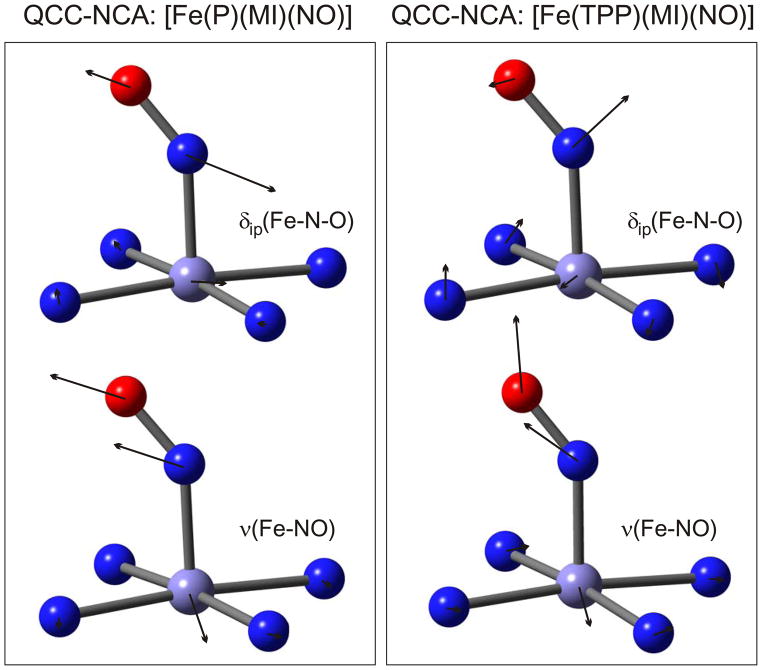
In summary, the Fe-NO stretching mode ν(Fe-NO) shows strong mixing with the porphyrin-based Pyr.rot E_u-type vibration, but its main component can be assigned to the strongly oop polarized band at 437 cm⁻¹. The lack of significant ip intensity of this feature is in agreement with only a small admixture of Fe-N-O bending character. The Fe-N-O bending mode is distributed over several porphyrin-based vibrations in the 520 – 580 cm⁻¹ region, with a main component at 563 cm⁻¹. Although admixture of Fe-NO stretching character is strong in this case, the Fe-N-O and octahedral bending contributions are more dominant. Hence, the assignment of this mode to δ_ip(Fe-N-O) is reasonable, but the admixture of Fe-NO stretching character is significant and has to be considered. The consequences of this finding are further analyzed in the Discussion. Note that the largest atomic displacements of this mode are found for the nitrogen atom of NO (cf. Figure 7 and Scheme 2),⁴⁴ and hence, the atomic motions and kinetic energies of this mode resemble more closely a Fe-N-O bending vibration, which is further in agreement with the designation of this mode as δ_ip(Fe-N-O).

Figure 7.

Atomic displacement (‘arrow’) plots for the QCC-NCA results for [Fe(TPP)(MI)(NO)] (1) based on the porphine approximation (left, from ref. 7c) and using the full TPP²⁻ ligand (right, this work) for the Fe-NO stretch at 437 cm⁻¹ (bottom) and the in-plane Fe-N-O bend at ~563 cm⁻¹ (top).

Scheme 2.

Effective internal coordinates for the Fe-NO stretch and the Fe-N-O bend in a [Fe(Porphyrin)] complex. These are taken from a BP86/TZVP calculation on [Fe(P)(NO)] where mixing of these internal coordinates is minimal. These effective internal coordinates are somewhat different from corresponding coordinates in a Fe-N-O trinuclear unit, because they account for intrinsic couplings of the isolated (pure) Fe-NO stretching and Fe-N-O bending coordinates of the triatomic with other internal coordinates in the actual complex. For example, in the bent Fe-N-O geometry, the Fe-N-O bending internal coordinate is always strongly mixed with (Pyr)N-Fe-N(O) octahedral bends (Pyr = pyrrole). Hence, the effective internal coordinates shown here are a better basis to understand the resulting Fe-NO stretching and Fe-N-O bending normal modes in complex 1. In comparison with Figure 7, one recognizes that the higher energy mode in 1 is always the ‘in-phase’ combination of these coordinates, whereas the lower energy mode is the corresponding out-of-phase combination, keeping in mind that (a) in the latter case, the contribution of the Fe-N-O bending internal coordinate is rather small, and (b) mixing with nearby porphyrin-based vibrations will influence the motions of the Fe-N-O unit.

Assignment of the remaining vibrations

The medium intense NRVS band at 405 cm⁻¹ is assigned to an E_u-type vibration, obtained at 406/407 cm⁻¹ in the QCC-NCA simulation (BP86/TZVP (adjusted): 399/400 cm⁻¹). This feature corresponds to a mixed pyrrole translation (Pyr.tans, ν₅₃) and ν(Fe-N_Pyr) stretching (ν₅₀, Pyr = pyrrole) vibration. As already discussed above, the 338 and 318 cm⁻¹ features are the two main components of the ν(Fe-N_Pyr) stretching vibration of E_u symmetry (ν₅₀), which are therefore the dominant NRVS features in the spectrum of 1 (cf. Figure 1). The QCC-NCA predicts these modes at 337 and 320 cm⁻¹ (BP86/TZVP (adjusted): 335 and 318 cm⁻¹). Note that ν₅₀ also contributes to the vibrations at 472, 405, and 297 cm⁻¹ as listed in Table 2. Other contributions to the 338 and 318 cm⁻¹ features are of Pyr.rot and pyrrole tilting (Pyr.tilt) character. Because of this, the bands at 338 and 318 cm⁻¹ should show exclusive ip iron motion. The large energy splitting between these two E_u components is due to the fact that the 338 cm⁻¹ feature shows strong mixing with the Fe-N(O) torsion τ(Fe-NO) and the ON-Fe-N_Pyr octahedral bending mode,⁴² which causes the distinct shift of this feature to higher energy relative to the 318 cm⁻¹ component. This result from the QCC-NCA fit therefore explains the experimental observation that the 338 cm⁻¹ band exhibits a 2 cm⁻¹ shift (predicted: ~3 cm⁻¹) upon ¹⁵N¹⁸O substitution, whereas the 318 cm⁻¹ vibration is invariant. The QCC-NCA simulation also shows that the 318 cm⁻¹ band actually corresponds to two features, due to mixing of the lower energy component of ν₅₀ with a pyrrole swiveling (Pyr.swiv) type vibration that is very close in energy. The two resulting features are predicted at 320 and 319 cm⁻¹ as shown in Table 2. The NRVS feature at 297 cm⁻¹ is assigned to the split E_u components of a mixed Pyr.tilt and ν(Fe-N_Pyr) stretching vibration, calculated at 294 and 309 cm⁻¹ from QCC-NCA. To lower energy, the NRVS feature at 248 cm⁻¹, identified with an out-of-plane phenyl bending mode of E_u symmetry (in D_4h), is obtained at 245 and 249 cm⁻¹ from QCC-NCA (BP86/TZVP (adjusted): 239 and 251 cm⁻¹). This feature is fully ip polarized. Again, strong anisotropy in mode mixing of the two components is observed, where the 249 cm⁻¹ vibration shows strong contributions from an imidazole oop bending mode δ^oop(Im) where the imidazole atoms move perpendicular to the imidazole plane, and τ(Fe-NO). The lower energy component at 245 cm⁻¹, on the other hand, has 6% δ_ip(Fe-N-O) character. The single-crystal NRVS data in Figure 1 resolve the medium intense NRVS feature at 209 cm⁻¹ into two bands that are ip (203 cm⁻¹) and oop (211 cm⁻¹) polarized. The QCC-NCA simulation places these features at 202 and 206 cm⁻¹, respectively, in very good agreement with experiment. Interestingly, the ip polarized band at lower energy shows a 22% τ(Fe-NO) contribution, which explains the ¹⁵N¹⁸O isotope sensitivity of this mode. Finally, strongly oop polarized NRVS features with Fe-N_Im stretching character are observed at 180 and in particular, 149 cm⁻¹. The latter mode has 41% Fe-N_Im stretching and porphyrin doming (γ₉) contributions, and is therefore assigned to ν(Fe-N_Im). The low energy of this mode reflects the strong σ trans effect of NO, which weakens the Fe-N_Im bond (vide supra and Discussion).⁷ Importantly, a comparison of Tables 2 and S2 shows (as indicated above) that the nature of the porphyrin-based modes from the BP86/TZVP calculation is almost fully preserved in the QCC-NCA simulation, whereas the frequencies are somewhat shifted in the fit.

Analysis of force constants

The obtained force constants for the Fe-NO stretching and Fe-N-O bending coordinates from the QCC-NCA fit are 2.57 mdyn/Å and 0.77 mdyn·Å, respectively, and the corresponding non-diagonal matrix element f_Fe-N/Fe-N-O, connecting these internal coordinates, is 0.399 mdyn (cf. Table 1). These force constants are very well defined from the fit: for example, a decrease in f_Fe-N/Fe-N-O increases the mixing of the Fe-NO stretching and Fe-N-O bending coordinates,⁴⁹ which leads to an unfavourable increase in the ip intensity of the 437 cm⁻¹ band and of the oop intensity in the 550 – 580 cm⁻¹ region. The force constants obtained here are therefore superior to the ones previously derived from a QCC-NCA fit using the porphine approximation, because in the latter case, only relative intensities of the 437 and 563 cm⁻¹ features could be used for the fit. Nevertheless, as shown in Table 3, the Fe-NO and Fe-N-O force constants of 2.380 mdyn/Å and 0.799 mdyn·Å, respectively, derived from the porphine model, are in good qualitative agreement with the results obtained here. The N-O force constants of 11.55 mdyn/Å are in fact identical. Finally, the small Fe-N_Im force constant of 0.783 mdyn/Å compared to >1.5 mdyn/Å for regular Fe(II)-Im bonds reflects the weak Fe-N_Im bond in 1 due to the σ trans effect of NO (see Discussion).⁷

Discussion

In this paper, oriented single-crystal Nuclear Resonance Vibrational Spectroscopy (NRVS) data of [⁵⁷Fe(TPP)(MI)(NO)] (1; TPP²⁻ = tetraphenylporphyrin; MI = 1-methylimidazole) are presented. Together with the powder NRVS data of this compound and of the corresponding ¹⁵N¹⁸O-labeled complex published before,^7c this is the only heme-nitrosyl species where such a complete set of experimental data is now available. This has allowed for the detailed simulation of the complete NRVS data of this compound, and the unambiguous assignment of both the porphyrin-based vibrations and the modes of the (Im)N-Fe-N-O subunit (Im = imidazole) of this complex for the first time. For this purpose, we have put our quantum chemistry centered normal coordinate analysis (QCC-NCA) to work,^7b where an initial force field for 1 is calculated using DFT, and then subsequently refined to reproduce the experimental NRVS spectra of this compound. In this way, the ambiguity of purely empirical normal coordinate analyses for large molecules is eliminated, which can lead to incorrect assignments and spectral interpretations.³³ In principle, one might argue that modern DFT methods have a high enough accuracy that should make empirical force field optimizations obsolete. However, whereas DFT is indeed very successful in describing the geometric and spectroscopic properties of organic molecules, the accuracy to which transition-metal ligand interactions can be determined is much more limited.³³ This is particularly true for six-coordinate ferrous heme-nitrosyls, where DFT methods have shown to fail in reproducing the exact properties of the axial (Im)N-Fe-NO unit,^7b,15 and similar results are obtained here. BP86/TZVP overestimates the Fe-NO bond strength, and correspondingly, the Fe-NO frequency and force constant, and slightly underestimates the Fe-N_Im interaction. In comparison, B3LYP calculations overestimate the Fe-N_Im bond strength, and N-O frequencies near 1800 cm⁻¹ are obtained (experimental for 1: 1630 cm⁻¹). Because of these problems, empirical improvement of the DFT results is essential for ferrous heme-nitrosyls in order to obtain good simulations of vibrational spectra, reliable assignments and force constants, and high-quality vibrational eigenfunctions for the Fe-N-O subunits in these complexes. Recently, DFT calculations (in particular with gradient-corrected functionals) have been used to predict how the vibrations of the Fe-N-O subunit respond to hydrogen bonding.⁵⁰ However, these gradient-corrected DFT calculations are primarily focused on the mode at about 600 cm⁻¹, which is dominated by the Fe-NO stretching contribution. This is incorrect both in terms of the vibrational energy, but equally importantly, also the actual nature of this mode. Hence, conclusions about changes in vibrational energies drawn from such calculations are problematic. Analyses of structural changes are more reliable in this case.⁵⁰

The QCC-NCA results obtained here show a very strong mixing between the vibrations of the axial (Im)N-Fe-NO unit and the porphyrin-based vibrations, which was absent in preliminary simulations using the porphine approximation.^7c It is therefore of critical importance to include porphyrin substituents in DFT and NCA calculations on heme complexes with axially bound diatomics, as these substituents greatly influence the energies of the porphyrin-based vibrations, and in this way, could strongly influence the vibrational properties of axial ligands. In particular, the Fe-NO stretch is split by interaction with a porphyrin-based vibration into two features observed at 437 and 472 cm⁻¹. The 437 cm⁻¹ feature involves Fe motion nearly perpendicular to the porphyrin plane and shows an ¹⁵N¹⁸O isotope shift of 8 cm⁻¹, and is therefore assigned to ν(Fe-NO). The 472 cm⁻¹ band corresponds to a porphyrin-based vibration of mostly Pyr.rot character with ~20% Fe-NO stretching contribution. The admixture of Fe-N-O bending character into ν(Fe-NO) is relatively small, as evidenced by the almost pure oop polarization of the 437 cm⁻¹ feature. Main contributions to the Fe-N-O bend are observed in the 520 – 580 cm⁻¹ region, distributed over a number of ip polarized porphyrin-based vibrations. The main component is identified with the feature at 563 cm⁻¹, which shifts to 551 cm⁻¹ upon ¹⁵N¹⁸O labeling, and is therefore assigned to δ_ip(Fe-N-O). Importantly, the Fe-N-O bend shows strong mixing with the Fe-NO stretching internal coordinate, as evidenced by the significant amount of oop NRVS intensity in the 520 – 580 cm⁻¹ region that does not originate from the porphyrin-based vibrations in this energy range. These spectral features are well reproduced in the QCC-NCA (cf. Table 2). From IR measurements, the NO stretch has been identified at 1630 cm⁻¹, which has also been included in the NCA simulation (cf. Table 4). In addition to the Fe-N-O unit, excellent agreement with experiment has also been obtained for the energies and NRVS intensities of the porphyrin-based vibrations. The corresponding assignments, listed in Table 2, are also in agreement with earlier work on [Fe(TPP)(MI)(CO)].³¹ Finally, based on the oop data, the Fe-N_Im stretch is assigned to the intense feature at 149 cm⁻¹, which is unusually low for a ferrous heme complex. As discussed below, this weak Fe-N_Im bond reflects the strong σ trans interaction between the Im and NO ligands. The identification of this vibration has not been possible before based on Raman and IR spectroscopy on 6C ferrous heme-nitrosyls. Analogous bands at 140 and 153 cm⁻¹ have been reported for the triclinic and monoclinic forms of [Fe(Tp-FPP)(MI)(NO)].²⁹ The Fe-N_Im stretch is Raman active in 5C deoxy states of heme proteins, but cannot be observed with this method when small ligands like NO or CO bind to the heme, pulling the iron(II) into the center of the porphyrin plane. NRVS is therefore a very useful method to identify ν(Fe-N_Im) stretching vibrations in heme proteins and model complexes independent of the coordination number of iron.

Table 4.

QCC-NCA results for [Fe(TPP)(MI)(NO)] and [Fe(P)(MI)(NO)] for comparison.

Method	Vibrational Frequency [cm−1]			Force Constant [mdyn/Å]
	ν(N-O)	ν(Fe-NO)	δip(Fe-N-O)/ν(Fe-NO)	fN-O	fFe-NO	fFe-N-Oa
[57Fe(TPP)(MI)(NO)]: EXP. b	1630 (1556)	437 (429)	563 (551)
[57Fe(TPP)(MI)(NO)]: BP86/TZVP	1668	606	485	12.219	3.241	0.694
QCC-NCA b	1630 (1558)	438 (429)	~562 (547)	11.55	2.574	0.773
[57Fe(P)(MI)(NO)]: QCC-NCA b (from ref. 7c)	1628 (1557)	439 (427)	560 (545)	11.55	2.380	0.799

^aThe force constant f_Fe-N-O is given in [mdyn·Å]

^bValues in brackets are calculated for the corresponding ¹⁵N¹⁸O labeled complex

In summary, the available powder and single-crystal NRVS data combined with the previously published ¹⁵N¹⁸O isotopically labeled data have allowed for a detailed simulation of the NRVS spectra of complex 1. The high accuracy of the fit obtained here was only possible because of the oriented single-crystal data, and the application of the QCC-NCA method as mentioned above. A good example for this is the degree of mixing between the Fe-NO stretching and Fe-N-O bending mode, which is well defined by the absolute ip and oop NRVS intensities of the 437 and 563 cm⁻¹ features as well as their ¹⁵N¹⁸O isotope shifts. Therefore, unambiguous spectral assignments, in particular for the vibrations of the (Im)N-Fe-N-O subunit, have been obtained in this study for a 6C ferrous heme-nitrosyl model complex, and reliable force constants for these bonds have been determined. The obtained eigenfunctions are depicted in Figure 7, right. Here, the bending mode, for example, can be understood as the in-phase combination of the ‘effective’ Fe-NO stretching and Fe-N-O bending internal coordinates sketched in Scheme 2.

One interesting observation in the QCC-NCA fit compared to experiment is that the oop intensity of the two strong oop bands at 437 and 149 cm⁻¹ is overestimated in the fit. This does not necessarily mean that the mode mixing of the corresponding Fe-NO and Fe-N_Im stretching internal coordinates with other porphyrin-based vibrations shows deviations, since the oop intensity of all other vibrations is reproduced very well (cf. Figure 5, top). We believe that this discrepancy in oop intensity is likely due to a solid state effect, where the magnitude of iron motion in these modes might be restricted. Alternatively, these modes could couple to low-energy lattice modes, and in this way, part of their oop intensity could be redistributed and dampened (see also discussion in ref. 28). One other important technical aspect with respect to single-crystal NRVS measurements on heme complexes is that in general, only two oriented single-crystal measurements on these systems are performed: one in z direction (orthogonal to the heme plane), and one for a chosen orientation in xy direction (parallel to the heme plane). However, due to the low symmetry of many heme sites, one in-plane measurement is not sufficient to capture all of the ip NRVS intensity. In fact, if the symmetry is less than four-fold, localization, splitting, and anisotropy of the dominant NRVS active ip porphyrin modes of E_u symmetry (in D_4h) is observed. This aspect has clearly not received the necessary attention in the literature. Additional experiments should therefore be performed, if possible, on low-symmetry heme model complexes to experimentally determine the directional dependency of the ip polarized NRVS intensity for the different E_u-type vibrations observed in the NRVS spectra.

Controversies about spectral assignments

Whereas the vibrational assignments for 5C ferrous heme-nitrosyls [Fe(Porphyrin)(NO)] are well established,^7b,27b,28 the assignment of the Fe-NO stretch and Fe-N-O bend in six-coordinate (6C) ferrous heme-nitrosyls has been controversial since the first reports of resonance Raman spectra for the NO adduct of Hb about 30 years ago.⁵¹ This is due to the fact that in resonance Raman, only the bending mode around 550 – 580 cm⁻¹ is usually observed, which was therefore assumed to be the Fe-NO stretching mode.²⁰ The feature at ~440 cm⁻¹ is usually too weak to be identified with resonance Raman spectroscopy. First doubts about this assignment were voiced by Benko and Yu, who reassigned the 550 – 580 cm⁻¹ feature to the Fe-N-O bending mode,²¹ based on selective NO isotope labeling, but this assignment was not adapted in the literature.²² Recently, however, NRVS has allowed for the identification of ν(Fe-NO) at 443 and δ(Fe-N-O) at 547 cm⁻¹ in Mb-NO, which is in close agreement with the assignments obtained for the 6C model complex 1 presented in this study (see also ref.s ^7b,c,23,29). Nevertheless, the assignment for 1 disagrees with recent resonance Raman results where it was claimed that ν(Fe-NO) in 1 is located at 582 cm⁻¹, and no feature around 440 cm⁻¹ was observed.²⁵ However, based on the level of analysis achieved for [Fe(TPP)(MI)(NO)] in this study and in agreement with the recent assignments for Mb-NO,²³ it must be concluded that this 582 cm⁻¹ Raman band cannot correspond to the Fe-NO stretch, because this mode is clearly located at ~440 cm⁻¹. More likely, the 582 cm⁻¹ Raman band from ref. 25 could belong to δ_ip(Fe-N-O), where the 19 cm⁻¹ difference in frequency compared to our NRVS data might be due to the different conditions applied for the measurements (solid state for NRVS vs. frozen solution state for Raman). The exact reasons for this discrepancy between NRVS and Raman data are unclear, especially since the N-O stretching frequency seems quite unresponsive to this change in conditions: ν(N-O) is observed at 1623 cm⁻¹ in solution, and at 1630 cm⁻¹ in a KBr disk and in pure solid.^7a−c In addition, the NRVS spectrum of 1 taken in THF solution, cf. Figure 8, does not show noticeable shifts in the 550 – 580 cm⁻¹ region, but interestingly, shows a shift of ν(Fe-NO) to 428 cm⁻¹. This point requires further study.⁵² Alternatively, the 582 cm⁻¹ Raman band observed in ref. 25 could also belong to an impurity of the corresponding ferric complex. It is striking that the vibrational energy of 582 cm⁻¹ is very similar to ν(Fe-NO) in the corresponding ferric complex, which was observed at 580 cm⁻¹ via NRVS in [Fe(TPP)(MI)(NO)](BF₄).³⁰ In summary, this discrepancy between NRVS and resonance Raman data for 6C ferrous heme-nitrosyls is puzzling, especially since both techniques deliver comparable results for 5C ferrous heme-nitrosyls and 6C ferrous heme-carbonyls, and requires further study.

Figure 8.

NRVS VDOS of [⁵⁷Fe(TPP)(MI)(NO)] (1) measured as a powder (black) and in frozen THF solution (red).

Biological Implications

The results obtained in this study have a number of important biological implications with respect to NO binding to five-coordinate (5C) ferrous heme active sites in globins, soluble guanylate cyclase (sGC), cytochrome c oxidase and bacterial NO reductase, and many other heme proteins. In particular, we can address the questions of (a) how strongly the vibrational dynamics of the heme change upon NO binding as a result of changes in the Fe-N_Im bond, the position of iron relative to the porphyrin ring, and the spin state, and (b) how strongly the presence of the distal His in globins influences the properties of the bound NO via hydrogen bonding, by comparison of the vibrational data of [Fe(TPP)(MI)(NO)] with those of Mb and corresponding active site mutants.

NO Binding to High-spin Ferrous Heme Active Sites

Comparison of the NRVS data and assignments of 1 with those of the 5C ferrous imidazole complex [Fe(TPP)(2-MeHIm)] (2; 2-MeHIm = 2-methylimidazole) from ref. 53 reveals how coordination of NO changes the vibrational dynamics of the 5C ferrous heme, which serves as a model for NO binding to 5C ferrous hemoglobin (Hb), myoglobin (Mb), and the biological NO sensor protein soluble guanylate cyclase (sGC). The most obvious effect of NO binding to a 5C deoxy heme site is caused by the change of the spin state of the iron(II) center from high-spin (hs) to low-spin (ls) upon axial ligand binding, which strengthens the Fe-N_Pyr (Pyr = pyrrole) bonds. This shifts the ν(Fe-N_Pyr) stretching mode of E_u symmetry (ν₅₀) to higher energy, and changes its mixing with pyrrole translation (ν₅₃) and rotation (ν₄₉) modes. This creates the intense NRVS features around 300 – 350 cm⁻¹ observed for 1 and also the corresponding CO complex [Fe(TPP)(MI)(CO)].³¹ In contrast, the most intense NRVS features of 2 are observed around 230 cm⁻¹. In previous studies, this distinct difference in heme dynamics had also been related to a change in the position of iron(II), which is pulled into the porphyrin plane upon coordination of a sixth ligand.^31a However, the fact that the NRVS spectrum of the low-spin complex [Fe(TPP)(NO)] shows similar features in the 300 – 350 cm⁻¹ region²⁷ as 1 indicates that the spin state change is the more important contribution. In addition, the strong energy splitting of ν₅₀ into two components at 318 and 338 cm⁻¹ in 1 is missing in 2. This large splitting originates from selective mode mixing of the higher energy component of this mode with the Fe-N(O) torsion⁴² and ON-Fe-N_Pyr octahedral bends. This selective mixing with axial ligand modes is further substantiated by a 2 cm⁻¹ shift to lower energy of the 338 cm⁻¹ band upon ¹⁵N¹⁸O isotope labeling, whereas the 318 cm⁻¹ band shows no shift. A similar situation is also encountered in the case of [Fe(TPP)(NO)], which also shows a strong splitting of the intense NRVS features in the 300 – 350 cm⁻¹ region,^27,43 likely associated with selective mode mixing of one of these vibrations with modes of the axially coordinated diatomic. On the other hand, a similar splitting observed for six-coordinate CO complexes, including the analogous [Fe(TPP)(MI)(CO)],^31b cannot result from mixing with vibrations of the linear Fe-C-O unit and must therefore reflect the influence of the imidazole ligand. Whether a similar situation is also encountered upon O₂ binding still waits to be determined.

A very important difference between the 6C CO and NO complexes is the strength of the Fe-N_Im bond, as reflected by the corresponding Fe-N_Im stretching frequency. In the deoxy heme complex 2 as well as deoxy Hb/Mb, this mode is observed at 210 – 220 cm⁻¹.⁵³ In comparison, multiple vibrations with Fe-N_Im stretching character contribute to the Fe VDOS of six-coordinate CO complexes, and in particular, modes at 172 and 225 cm⁻¹ are sensitive to the mass of the imidazole ligand.^31b This similar frequency range reflects the fact that CO serves almost exclusively as a π acceptor ligand, and therefore, does NOT give rise to a large trans effect.⁵⁴ On the other hand, it is known that NO exerts a strong σ trans effect on an axial N-donor ligand,^5,6,7a,15 as evident from small N-donor binding constants trans to NO,^7b,16,55 long Fe-N_Im bond distances in model complexes, ^5,9 and combined spectroscopic and DFT studies.^7,15 However, direct spectroscopic evidence for this weakening of the Fe-N_Im bond has been lacking. The obtained frequency of the Fe-N_Im stretching mode in complex 1 of only 149 cm⁻¹ underlines the strength of the σ trans interaction of Im with the bound NO ligand. Since the strength of the Fe-N_Im bond is of key importance for cooperative O₂ binding in Hb, one could speculate that the cooperativity of NO binding to Hb should be lower, since the weaker Fe-N_Im bond in this case will be less effective in communicating the binding event of the diatomic to the remaining subunits in the tetramer. On the other hand, the weakening of the Fe-N_Im bond in sGC serves as a means of activation of this protein, which critically depends on the σ trans effect of NO as discussed in the Introduction.

Direct Spectroscopic Quantification of the Trans Effect of NO

Based on the QCC-NCA performed here, reliable force constants for the (Im)N-Fe-N-O subunit have been determined, which further support the above conclusions. The obtained Fe-NO and N-O force constants are 2.57 and 11.55 mdyn/Å, respectively, which is in good agreement with a preliminary simulation based on the porphine approximation.^7c The small Fe-N_Im force constant of only 0.783 mdyn/Å is in agreement with the weak Fe-N_Im bond as analyzed above. The force constants and vibrational frequencies determined here provide a quantitative measure for the weakening of the Fe-N_Im bond upon binding of NO, and vice versa, the pronounced effect of Im coordination on the properties of the Fe-NO bond. The latter point is evident from a comparison of the electronic structures of five- and six-coordinate (5C and 6C) ferrous heme-nitrosyl complexes. These have recently been analyzed in detail using magnetic circular dichroism (MCD), NMR, and vibrational spectroscopies coupled to density functional calculations, and x-ray crystallography.^7,9,17,28 In the 5C case, a strong σ donor bond between the singly occupied π*_h orbital of NO and d_z² of iron is present, which leads to a complete delocalization of the unpaired electron of NO over the Fe-N-O unit. The strong σ donation from the π* orbital of NO leads to strong Fe-NO and N-O bonds as evidenced by the corresponding force constants of 2.98 and 12.53 mdyn/Å as determined for the analogous 5C complex [Fe(TPP)(NO)].7a,b Typical vibrational frequencies for these 5C compounds are 530 cm⁻¹ for ν(Fe-NO) and 1675 – 1700 cm⁻¹ for ν(N-O). Binding of Im (either free or in His) in axial position trans to NO weakens the Fe-NO σ bond, as reflected by the drop of the Fe-NO force constant to 2.57 mdyn/Å, and of the Fe-NO stretching frequency to ~440 cm⁻¹. This is due to a reduction of the mixing of the singly occupied π*_h orbital of NO with d_z² of iron. Due to the reduced donation from the antibonding π*_h orbital of NO, the N-O bond is also weakened as evident from π(N-O) observed around 1610 – 1630 cm⁻¹ and the N-O force constant of 11.55 mdyn/Å for these compounds.⁷ Importantly, this change in bonding in 6C complexes is reflected by a change in spin density: upon coordination of the axial N-donor ligand, the spin density is pushed back from the iron toward the NO ligand leading to spin populations of about +0.8 on NO and only +0.2 on iron in [Fe(TPP)(MI)(NO)] in agreement with EPR and MCD results.7a,b Similar trends have also been observed by Patchkovskii and Ziegler,⁵⁶ but the calculated spin densities are too iron-centered in this case due to the application of a gradient-corrected functional.¹⁵ This increase in radical character on NO, combined with the weakening of the Fe-NO bond, could be crucial for the activation of NO for catalysis by NorBC using a ferrous heme/non-heme active site.^7d,15

Effect of Hydrogen Bonding on the Fe-N-O Unit

Since the strong distal hydrogen bond of His to dioxygen is crucial for stable Fe-O₂ adduct formation in globins, the effect of the distal His on CO and NO binding to deoxy-Hb and -Mb has gained considerable attention. Crystallographic investigations on ferrous Mb-NO⁵⁷ in fact implicate the presence of a hydrogen bond between the distal His and NO, but the strength of this interaction, and correspondingly, its effect on the properties of the bound NO are not clear. Vibrational spectroscopy is a great method to gain further insight into this issue, since metal-NO stretching frequencies are very sensitive reporters of changes in the metal-NO bond as described above. If the distal His (His64) in wild-type (wt) Mb is mutated to leucine (H64L) or isoleucine (H64I) to remove the H-bond, a distinct increase of π(N-O) from 1613 to 1635 – 1640 cm⁻¹ is observed, accompanied by a moderate shift of δ_ip(Fe-N-O) from 547 to ~560 cm⁻¹,²² but unfortunately, the difference in ν(Fe-NO) is generally not known. Scheme 3 shows a plot of δ_ip(Fe-N-O) vs. ν(N-O) for human Mb and a series of mutants.

Scheme 3.

Correlation of δ_ip(Fe-N-O) and ν(N-O) in human myoglobin (Mb) wild-type (wt) and mutants. Importantly, in the His64 mutants the distal His that is able to form a hydrogen bond with a bound diatomic has been removed. The data are taken from ref. 22b. The data points in the upper right box correspond to mutants where the amino acid replacing His64 has only aliphatic side chains and no capability to form hydrogen bonds. The vibrational properties of these mutants, in particular H64L, correspond closely to the model complex [Fe(TPP)(MI)(NO)]. The dashed line is a linear fit of the data of wt and H64X mutants only, showing a direct correlation of δ_ip(Fe-N-O) and ν(N-O). However, note that a correlation diagram that includes a larger variety of heme proteins and mutants does not show any significant correlation as discussed in ref.15.

Interestingly, the vibrational properties of the His64 mutants, in particular H64L, are very similar to the model complex [Fe(TPP)(MI)(NO)], as indicated in Scheme 3. Hence, [Fe(TPP)(MI)(NO)] that lacks hydrogen bonding to the bound NO serves as an excellent model complex for the deoxy-Mb NO adduct in the absence of hydrogen bonding. The energy of the Fe-NO stretching frequency in the model complex and the His64 mutants are therefore likely similar, and in this way, the model system allows to estimate how the hydrogen bond of His64 influences the bound NO. The energy of ν(Fe-NO) at 443 cm⁻¹ in Mb-NO²³ and at ~439 cm⁻¹ (437 cm⁻¹ with ⁵⁷Fe) in the model complex is very similar, and hence, does not indicate significant changes in electronic structure due to the presence of the H-bond. Hence, the H-bond is likely weak in the NO case. DFT calculations are in agreement with this and estimate the H-bond to 2 – 3 kcal/mol.⁵⁸

In comparison, the lower ν(N-O) frequency in wt Mb-NO compared to the His64 mutants and [Fe(TPP)(MI)(NO)] might then be due to a simple polarization of the π/π* orbitals of NO by the weak H-bond with His64.⁵⁹ Importantly, the largest deviation in vibrational energies is actually observed for the Fe-N-O bend, obtained at 547 cm⁻¹ in Mb-NO²³ and at ~560 cm⁻¹ in the His mutants and the model complex. Based on our analysis of the single-crystal NRVS data of [Fe(TPP)(MI)(NO)] presented here, we conclude that this shift is either due to (a) the sensitivity of δ_ip(Fe-N-O) to changes in porphyrin vibrations (due to the strong mixing of this mode with porphyrin vibrations; see Section C), (b) the mechanical coupling of the Fe-NO unit with bending vibrations of the protein that include the His64-H atom, or (c) the fact that the polarization of the NO π/π* orbitals by the H-bond makes the Fe-N-O subunit less stiff and ‘easier’ to bend. The weak H-bond with His64 in Mb-NO is in agreement with the bonding description of ferrous heme-nitrosyls developed before,⁷ where NO binds as a neutral NO(radical) ligand. In contrast, coordination of O₂ leads to the formation of a complex with distinct Fe(III)-O₂⁻ character, where the negatively charged superoxide ligand then undergoes a much stronger H-bond with the distal His.⁶⁰

The energy of δ_ip(Fe-N-O) can be expected to be strongly influenced by porphyrin vibrations in the 520 – 580 cm⁻¹ range, due to the fact that the Fe-N-O bending internal coordinate is distributed over a number of porphyrin-based vibrations in this energy region (cf. Figure 6). Furthermore, these modes also show quite strong admixtures of the Fe-NO stretching internal coordinate as evidenced by their out-of-plane polarized intensity (vide supra). Due to this complexity, changes in the energies and natures of the porphyrin-based vibrations, for example by changes of porphyrin substituents or the planarity of the macrocycle, should then induce shifts in the energy and changes in the splitting pattern of δ_ip(Fe-N-O). Thus, the complex and strongly mixed nature of δ_ip(Fe-N-O) explains the observed, very limited correlation of δ_ip(Fe-N-O) with ν(N-O) when a large variety of heme proteins and corresponding mutants are compared. These data span a range of 540 – 580 cm⁻¹ in δ_ip(Fe-N-O) and 1600 – 1660 cm⁻¹ in ν(N-O).^15,22,25 This point is discussed in detail in ref. 15.