Simultaneous Truth and Performance Level Estimation with Incomplete, Over-complete, and Ancillary Data

Abstract

Image labeling and parcellation are critical tasks for the assessment of volumetric and morphometric features in medical imaging data. The process of image labeling is inherently error prone as images are corrupted by noise and artifact. Even expert interpretations are subject to subjectivity and the precision of the individual raters. Hence, all labels must be considered imperfect with some degree of inherent variability. One may seek multiple independent assessments to both reduce this variability as well as quantify the degree of uncertainty. Existing techniques exploit maximum a posteriori statistics to combine data from multiple raters. A current limitation with these approaches is that they require each rater to generate a complete dataset, which is often impossible given both human foibles and the typical turnover rate of raters in a research or clinical environment. Herein, we propose a robust set of extensions that allow for missing data, account for repeated label sets, and utilize training/catch trial data. With these extensions, numerous raters can label small, overlapping portions of a large dataset, and rater heterogeneity can be robustly controlled while simultaneously estimating a single, reliable label set and characterizing uncertainty. The proposed approach enables parallel processing of labeling tasks and reduces the otherwise detrimental impact of rater unavailability.

1. INTRODUCTION

Numerous clinically relevant conditions (e.g., degeneration, inflammation, vascular pathology, traumatic injury, cancer, etc.) correlate with volumetric/morphometric features as observed on MRI. Quantification and characterization of these correlations requires the labeling or delineation of structures of interest. The established gold standard for identifying class memberships is manual voxel-by-voxel labeling by a neuroanatomist, which can be exceptionally time and resource intensive. Furthermore, different human experts often have differing interpretations of ambiguous voxels (on the order of 5–10% of a typical brain structure). Therefore, pursuit of manual approaches is typically limited to either (1) validating automated or semi-automated methods or (2) the study of structures for which no automated method exists.

Statistical methods have been previously proposed to simultaneously estimate rater reliability and true labels from complete datasets created by several different raters or automated methods [1-4]. These maximum likelihood/maximum a posteriori methods (e.g., Simultaneous Truth and Performance Level Estimation, STAPLE [2]) increase the accuracy of a single labeling by combining information from multiple, potentially less accurate raters (as long as the raters are independent and collectively unbiased). However, the existing methods require that all raters delineate all voxels, which limits applicability in real research studies where different sets of raters may delineate arbitrary subsets of a population of scans due to the rater availability or the scale of the study.

Herein, we present and demonstrate Simultaneous Truth and Performance Level Estimation with Robust extensions (STAPLER) to enable use of data with:

1. Missing labels: partial labels sets in which raters do not delineate all voxels;

2. Repeated labels: labels sets in which raters may generate repeated labels for some (or all) voxels; and

3. Training trials: label sets in which some raters may have known reliabilities (or some voxels have known true labels). These may also be derived from catch trials. We consider this information ancillary as it does not specifically relate to the labels on structures of interest, but rather to the variability of individual raters.

STAPLER simultaneously incorporates all labels from all raters to estimate a maximum a posteriori estimate of both rater reliability and true labels. The impacts of missing and training data are studied with simulations based on two models of rater behavior. First, the performance is studied using traditional “random raters,” which are parameterized by confusion matrices (i.e., probabilities of indicating each label given a true label). Second, we develop a new, more realistic set of simulations in which raters make more mistakes along the boundaries between regions.

2. METHODS

STAPLE exploits expectation maximization to calculate rater reliabilities ${ϴ}_{jsT}^k$), i.e., the probability that a rater j) reports that a voxel i) has a particular label s) given a true label T). Rater reliabilities and observed data D_ijr) with repetition r can be used to calculate the conditional probability that a voxel belongs to a class $W_{si}^k$) at iteration k. First, we extend Eq. 20 in [2] to include all observed data:

$$W_{si}^k=p(T=s\mid {\mathit{D}}_{\mathit{i}},{ϴ}^{\mathit{k}})=\frac{p(T_i=s){\prod }_{j:D_{ijr}\ne \varnothing }{ϴ}_{jsT}^k}{{\Sigma }_{s^{\prime }}p(T_i=s^{\prime }){\prod }_{j:D_{ijr}\ne \varnothing }{ϴ}_{jsT}^k}$$ (1)

Second, we extend Eq. 24 in [2] to prevent update of rater reliabilities for raters with known reliabilities or without data:

$$\{\begin{array}{c}{ϴ}_{jsT}\text{fixed}\to \text{no update}\hfill \\ 0=\sum _{i:D_{ijr}=s}{W}_{Ti}^k\to {ϴ}_{jsT}^{k+1}=I\{s=T\}\hfill \\ \text{otherwise}\to {ϴ}_{jsT}^{k+1}=\frac{{\Sigma }_{i:D_{ijr}=s}{W}_{Ti}^k}{{\Sigma }_{i:D_{ijr}\ne \varnothing }{W}_{Ti}^k}\hfill \end{array}\phantom{\}}$$ (2)

where I is the indicator function. If a subset of truth labels is given, then an additional rater is introduced for these voxels with known perfect reliability. Alternatively, if label sets are available from a rater with known reliability, then the reliability of this rater may be treated as known. STAPLER was implemented in Matlab (Mathworks, Natick, MA). An adaptive mean label frequency is used to update the unconditional label probabilities p(T_i = s)).

DATA

Simulated label sets from simulated raters were derived from a high resolution labeling of 12 divisions of the cerebellar hemispheres (Figure 1A) (149×81×39 voxels, 0.82×0.82×1.5 mm resolution). Two distinct models of raters (described below) were evaluated within the following Monte Carlo framework: (1) Random raters were simulated; (2) Simulated label sets from the raters were generated according to the profiles; (3) Traditional STAPLE was evaluated by combining labels from 3 random raters; (4) STAPLER was evaluated by labels from 3*M raters where 3 raters were randomly chosen to delineate each slice, and each rater delineated approximately 1/M^th (i.e., each rater labels between 50% and 4% of slices with the total amount of data held constant); (5) The advantages of incorporating training data were studied by repeating step 4 with all raters fully labeling a second, independent test data set with known true labels.

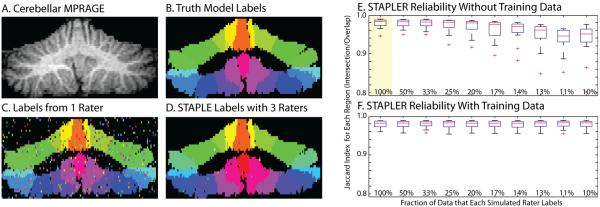
Figure 1.

Simulations with traditional random raters. Coronal sections of the three-dimensional volume show the high resolution MRI image (A), manually drawn truth model (B), an example delineation from one random traditional rater (C), and the results of a STAPLE recombination of three label sets (D). STAPLER enables fusion of label sets when raters provide only partial datasets, but performance suffers with decreasing overlap (E). With training data (F), STAPLER improved the performance even with each rater labeling only a small portion of the dataset. Box plots in E and F show mean, quartiles, range up to 1.5σ, and outliers. The highlighted plot in E indicates the simulation for which STAPLER was equivalent to STAPLE--i.e., all raters provide a complete set of labels.

3.1 Traditional Random Raters (errors distributed evenly within the volume)

In the first model, each rater was randomly assigned a confusion matrix such that the average true positive rate was 0.93. The i,jth element of this matrix indicates the probability that the rater would assign the jth label when the ith label is correct. Label errors are equally likely to occur throughout the image domain. This is the same model of rater performance as employed by the statistical framework. Ten Monte Carlo iterations were used for each simulation.

3.2 New, Boundary Random Raters (errors distributed along label boundaries)

In the second model, rater errors occurred at the boundaries of labels rather than uniformly throughout the image domain. Three parameters describe rater performance: r, l, and b. The scalar r is the rater’s global true positive fraction. The vector l encodes the probability, given an error occurred, that it was at the ith boundary. Finally the vector b describes the error bias at every boundary which denotes the probability of shifting a boundary toward either bounding label. For an unbiased rater, b_i = 0.5, ∀i . Twenty-five Monte Carlo iterations were used for each simulation. This random rater framework was implemented in the Java Image Science Toolkit (JIST, http://www.nitrc.org/projects/jist/).

4. RESULTS

4.1 Traditional Random Raters

The Jaccard index (i.e., intersection divided by union) for a single rater was 0.67±0.02 (one label set shown in Figure 1C). Using three raters in a traditional STAPLE approach increased the average Jaccard index to 0.98±0.012 (one label set shown in Figure 1D). Although STAPLER improved reliability for all simulations (Figure 1E), performance degraded with decreasing overlap. The decrease in reliability arises because not all raters have observed all labels with equal frequency, so the rater reliabilities for the unseen labels are under-determined, which leads to unstable estimates. Use of training trials greatly improves the accuracy of label estimation when many raters each label a small portion of the data set (Figure 1E).

4.2 New, Boundary Random Raters

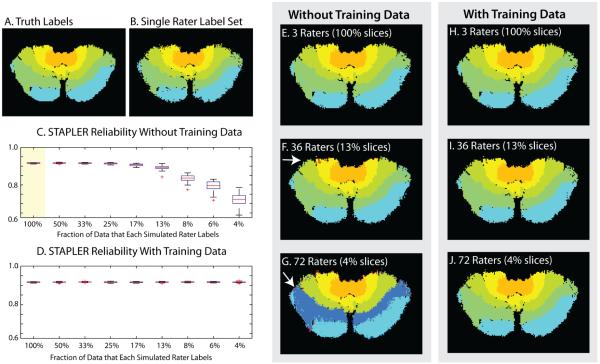
The Jaccard index for a single rater was 0.83±0.01 (one label set shown in Figure 2B). Using three raters in a traditional STAPLE approach increased the average Jaccard index to 0.91±0.01 (one label set shown in Figure 2E). With each rater performing very limited data sets (<10%), STAPLER was prone to “label inversion” an increased error over a single rater. In this case, off-diagonal elements of the estimated confusion matrix become large and lead to label switching (Figure 2C,E-G). Use of data from training trials alleviates this problem by ensuring that sufficient data on each label from each rater is available (Figure 2D,H-J).

Figure 2.

Simulations with boundary random raters. Axial sections of the three-dimensional volume show the manually drawn truth model (A) and sample labeling from a single simulated rater (B) alongside STAPLER fused results from 3, 36, and 72 raters producing a total of 3 complete labeled datasets without training data (E-G) and with training data (H-J). Note that boundary errors are generated in three-dimensions, so errors may appear distant from the boundaries in cross-sections. Boundary errors (e.g., arrow in F) increased with decreasing rater overlap. Label inversions (e.g., arrow in G) resulted in very high error with minimal overlap. As with the traditional model (Figure 1), STAPLER enables fusion of label sets when raters provide only partial datasets, but performance suffers with decreasing overlap (C). With the addition of training data (D), STAPLER results in sustained performance improvement even with each rater labeling only a small portion of the dataset.

5. CONCLUSIONS

STAPLER extends the applicability of the STAPLE technique to common research situations with missing, partial, and repeated data and facilitates use of training data to improve accuracy. These ancillary data are commonly available and may either have exact known labels or be labeled by a rater with known reliability. A typical scenario would involve a period of rater training followed by their carrying out a complete labeling on the training set. Only then would they carry out independent labeling of test data. STAPLE was successful both when simulated error matched modeled errors (i.e., the traditional model) and with more realistic, boundary errors, which is promising for future application to work involving efforts of large numbers of human raters. With the newly presented technique, numerous raters can label small, overlapping portions of a large dataset, which can then be recombined into a single, reliable label estimate, and the time commitment from any individual rater can be minimized. This enables parallel processing of manual labeling and reduces detrimental impacts should a rater become unavailable during a study. Evaluation of STAPLER with partially labeled datasets from human raters is an active area of research and will be reported in subsequent publications. As with the original STAPLE algorithms, STAPLER can readily be improved by introducing spatially adaptive unconditional label probabilities, such as with a Markov Random Field (MRF).