BIOFLUID MECHANICS OF SPECIAL ORGANS AND THE ISSUE OF SYSTEM CONTROL

Abstract

In the field of fluid flow within the human body, blood flow in the systemic circulation has been the main focus since the recognition by William Harvey that blood was in fact in continuous circulation and carried by a network of blood vessels. But beyond the systemic circulation, other fluids and other fluid flow phenomena pervade the body so totally that it would be hard to imagine a bodily function of any kind that does not involve fluids or fluid flow. In fact, the study of the systemic circulation is limited to not only the type of fluid involved but also to the type of service which the systemic circulation provides - the first being blood, of course, the second is transport - the principal function of the systemic circulation is to provide a means of transporting blood continuously from the heart to tissue cells and back again. Some of the most fascinating fluid flow phenomena within the human body involve fluids other than blood and a service other than transport- the lymphatic and pulmonary systems provide two striking examples. In this paper we outline the special fluid mechanics of these two systems. While transport is still involved in both cases, this is not the only service which they provide and blood is not the only fluid involved. In both systems, filtration, extraction, enrichment, and in general some “treatment” of the fluid itself is the primary function. In the pulmonary system, the liquid lining of the lungs plays a pivotal role, and the mechanical interaction between tissue and liquid is of key importance to lung viability. In disease states such as respiratory distress syndrome, the lining fluid can become dysfunctional, leading to reduced gas exchange and damage to sensitive pulmonary tissues. The study of the systemic circulation has also been conventionally limited to treating the system as if it were an open-loop system in which the main hemodynamic variables such as pressure and flow are governed by the laws of fluid mechanics independently from the physiological controls and regulations that govern these same variables. This implies that any failure of the system can be fully explained in terms of the laws of fluid mechanics, which of course is not the case. While a system failure due to a physical obstruction in a blood vessel can be readily explained in terms of the laws of fluid mechanics, a system failure due to arrhythmia cannot. In this paper we examine the clinical implications of these issues and of the special biofluid mechanics issues that arise in the lymphatic and pulmonary systems.

Biofluid Mechanics of The Lymphatic System

Introduction

The lymphatic system performs many crucial functions in health and is involved in diverse disease states. Lymphatics are responsible for fluid and protein balance, gathering approximately 4 liters/day of interstitial fluid and returning it to the venous system. As this fluid is filtered, undesirable elements such as tumor cells and foreign pathogens are normally destroyed in lymph nodes. This system is also part of the primary transport mechanism for the immune system. Lymphedema, a debilitating disease for which there is no known cure, affects a large number of cancer patients who have undergone lymph node dissection as well as trauma victims. The lymphatic system is also the major transport route for metastases of the most deadly cancers.

Understanding and modeling the transport of lymph remains a challenge. Tissue pressure is very low, and cannot account for even a small percentage of total lymph flow. Given its return to the venous system in the upper torso, much of the body’s lymph must be pumped “uphill.” There are extrinsic mechanisms such as muscle pumping that aid this task, but much of the work comes from the contraction of lymphatic vessel smooth muscle, with valves preventing backflow. Lymphatic vessels alter pumping characteristics in response to changes in diameter and flow, with the degree of response to these signals being regionally dependent. This implies that lymphatic endothelial cells respond to shear stress and circumferential stretch with substances that trigger lymphatic smooth muscle cell action. Unfortunately, little is known about lymphatic endothelial mechanotransduction, communication with smooth muscle, and how this integrates into a functioning system overall.

Importance of Lymphatic System in Health

The human lymphatic system plays several crucial roles in maintaining health, including fluid and protein balance, immune cell transport, and nutrient uptake. In approximate terms, out of 8000 liters of cardiac output per day, 20 liters of fluid flows out the capillaries, 16–18 liters of which is reabsorbed by the blood vessels. That leaves 2–4 liters to be returned via the lymphatic system. Returning interstitial proteins to the blood circulation is also of crucial importance, since we lose approximately 50% of circulating proteins through the capillaries every day. This movement of fluid, cells and solutes from the blood to the interstitial spaces, into the lymphatic compartment and back to the blood is essential to many crucial body functions.

The act of pumping this fluid back into the venous system at a point near the heart presents significant challenges. Interstitial tissue pressures hover around atmospheric. Thus, lymphatic system flow cannot rely on pressure-driven flow as in blood vessels. Furthermore, the location of the return point to the venous system in the upper torso means that the system must pump “uphill.”

The lymphatic system begins with terminal lymphatics that collect fluid and constituents from the interstitial space. There are approximately 40,000 terminal lymphatics per kg of tissue [1]. These rather porous structures consist of endothelial cells, intercellular primary valves, and a loosely organized substrate [2]. Their porosity is such that the concentration of proteins is practically identical in interstitial fluid and lymph, eliminating osmotic pressure gradients that might hinder fluid movement. The pressure gradient from the interstitium to the inside of terminal lymphatics is variable in magnitude and direction, but is typically less than 1 mmHg [3]. Terminal lymphatics outflow to small collecting vessels with the aid of valve structures in between endothelial cells that prevent backflow [4]. Valves are in fact ubiquitous in the lymphatic system. The vessels between valves are referred to as lymphangions. The lymphatic vessels eventually flow into lymph nodes. Lymph from afferent vessels flows in and is slowed within the subcapsular sinus. This facilitates interaction with the immune cells located in lymph node compartments, including the high-endothelial venous sinuses [5]. Filtered lymph then flows out through efferent vessels, eventually collecting in the thoracic duct that flow into the venous system. Movement of fluid through the lymphatic system facilitates immune response. The delivery of foreign bodies to the lymph nodes is enabled by lymph flow, as is the crucial trafficking of monocytes, dendritic cells and lymphocytes [6]. Finally, mesenteric lymphatic vessels play an important role in lipid uptake, which flow into the lymph and then into blood vessels.

Importance of Lymphatic System in Disease

Given the variety of challenges presented to the lymphatic system in health, it should not be surprising that there are numerous complexities in disease conditions. Local tissue swelling, or edema, occurs when the lymphatic system fails to remove fluid efficiently from the interstitium. There is no known cure for this critical condition, which can eventually lead to immune dysregulation and malnutrition. A functional definition of edema is a 50% increase in interstitital volume [7]. Some have suggested that presence of positive tissue pressure indicates edema, but some tissue pressures are positive in health. Edema affects 300 million people worldwide, including approximately 10 million patients who contracted the condition secondary to breast or pelvic cancer therapy, recurrent infections, trauma or vascular surgery [8]. Congenital lymphedema affects one of every 6000 newborns, but may not appear until puberty [9]. Acquired lymphedema caused by the filaria parasite (elephantiasis) affects 3–5 million people in Western countries, and is a common cause of disability in developing countries [10]. In the US, the majority of cases appear due to malignancy or its therapy. The onset of lymphedema in these cases can appear within days, or years later. It affects approximately half of breast cancer survivors undergoing axillary lymph node dissection; in some cases taking years to develop [11]. The risk following groin dissections is approximately the same [12]. Lymphedema is almost always accompanied by immune system disorders [10].

The lymphatic system plays a tremendously important role in the development and spread of cancer. The formation of new lymphatic vessels (lymphangiogenesis) in tumors is quite aggressive [13], and is an avenue for many cancers [14]. Furthermore, when cancerous tumors metastasize, offending cells travel through the lymphatic system. While it is a normal function of macrophages and lymphocytes to eliminate cancerous cells, this defense system can become overwhelmed or subverted. A large portion of cancer deaths are attributable to metastasis through the lymphatic system [13]. Pathologies may also develop in the presence of injuries due to lymphatic system dysfunction. In serious injuries involving open wounds, the lymphatic system is crucial in preventing infections through immune response. An important distinction between lymphatics and blood vessels is that the latter quickly shut down through vascular smooth muscle contraction, whereas lymph vessels remain open to aid in wound drainage.

Lymphatic System Pumping Characteristics

As discussed above, the lymphatic system is presented with the challenge of pumping several liters per day of fluid, proteins, cells, and foreign bodies from various interstitial spaces back to the venous system. It performs this function often against both an unfavorable pressure gradient and against gravity. While there are a few key mechanisms for overcoming this challenge, the degree to which each of these mechanisms functions varies tremendously around the body.

Lymphatic pumping in the neighborhood of skeletal muscle benefits from extrinsic pumping mechanisms, similar to those that aid venous return of blood from the lower limbs. External compression of lymphatic vessels due to muscle contraction or other means results in propulsion of lymph forward, with backward flow prevented by competent valves. Another possible extrinsic aid to pumping is positive tissue pressure. This pressure varies among different tissues. However, the estimated flow rate due to this pressure is a small percentage of overall lymph flow.

Much of the work associated with lymphatic pumping is performed via intrinsic mechanisms, i.e., those associated with direct action of the lymph vessels. The lymph vessels are exquisitely designed for this purpose. The intramural smooth muscle cells of lymphatic vessels possess far more mitochondria than smooth muscle of any other type [7]. Additionally, lymphatic vessels have proportionally large numbers of blood vessels feeding their walls, compared to the vasa vasora of comparably sized blood vessels [15]. Some of this extra vasculature may be due to lack of internal blood supply. Regardless, it is clear that lymphatic vessel walls contain significant contractile machinery.

There is tremendous regional variability in pumping capability. In general, peripheral vessels contract more, presumably to overcome the significant downstream resistance to flow [16]. It has been shown that mesenteric lymphatics pump rather strongly, compared to cervical and femoral lymphatics, as well as the thoracic duct [17,18]. There appear to be two primary intrinsic regulators of lymphatic smooth muscle. The first is a response to stretch, which has been shown to increase the frequency of the pacemaker activity [18]. Presumably, filling and thus stretching a lymphatic vessel is an indication to propel fluid forward to avoid edema. The second regulator is flow-related, and appears to be due to shear stress sensitivity of lymphatic endothelium. Increasing flow causes increases in both diastolic and systolic diameter (borrowing terminology from the heart), and decreases ejection fraction as well as contraction frequency [19]. Once again, it is important to note the regional variability in sensitivity to these regulating mechanisms. The thoracic duct is more sensitive to flow-induced smooth muscle relaxation than the mesenteric lymphatics [19]. If extrinsic mechanisms were successful at propelling flow, then smooth muscle cell contraction would actually increase flow resistance as well as being metabolically costly. One possible regional exception to this was noted in a study of rat iliac lymphatics [20], with an inhibition of the intrinsic pump at high inlet pressures. Removal of the endothelium blocked any response to changing inlet pressure. Similar endothelium-dependent contractile inhibition was noted by von der Weid et al. [21], who denuded the endothelium in guinea pig mesenteric lymphatic vessels, and inhibited the response to acetylcholine. Thus, lymphatic endothelium-expressed nitric oxide (NO) is likely a key factor in contractile control, as is endothelin-1 (ET-1) [22]. The production of both substances by blood vessel endothelium is known to be shear stress dependent.

Shear stress estimations, or indeed flow measurements of any kind, are difficult to perform in lymphatic vessels because the relatively low flow rates and delicate nature of these small vessels renders traditional blood flow measuring techniques useless. Based on high-speed (500 frames/s) in situ microscopic imaging of rat mesenteric lymphatic vessels, we have developed automated vessel and lymphocyte tracking algorithms to estimate lymph flow rate and wall shear stress, and then correlated those with the phasic pumping activity [23,24,25]. Average flow rates and wall shear stresses through individual vessels were 13.95 mliter/hour and 0.64 dyne/cm², respectively, with peak wall shear stresses ranging 4–12 dyne/cm². Diameter changes in these nominally 100 mm diameter vessels were typically 40% or greater over the contractile cycle. We have observed some vessels contracting down to nearly zero diameter in other experiments.

Lymphatic endothelial cells share some characteristics with blood vessel endothelial cells, such as alignment and elongation with the direction of flow. Crucial differences, however, include the expression of VEGFR-3 and Prox-1, both lymphangiogenic factors [26]. Prox-1 knockout mice do not develop lymphatic vessels [27]. Application of shear stress to cells resulted in inhibition of pan-cadherins only with lymphatic endothelial cells, and was noted at shear stresses as low as 2 dynes/cm² [26]. There are no reports of molecular-level changes in lymphatic endothelial behavior related to mechanical stimuli.

The lymphatic system is equipped with several extrinsic and intrinsic pumping mechanisms. When extrinsic mechanisms fail to produce sufficient flow, endothelial-based regulatory mechanisms kick in. However, the relative importance of the different pumping mechanisms varies throughout the body. Because of this regional variability, lymph pumping occurs in the absence of synchronized activity. While it appears that the intrinsic pumping is coordinated over short distances [28], there is no guarantee that the unsteady propulsion of lymph from one region occurs in phase with, or even at the same frequency as, that from adjacent tissue.

Reddy [29] developed a lymphatic flow network model that captured some of the essential flow characteristics (briefly published as Reddy et al., [30]). His network consisted of at most seven generations of branches; still far away from representing terminal lymphatics and the small lymphangions that perform the important pumping work. Vessel contraction was assumed to occur in response to wall strain at a single frequency and phase, regardless of tissue location. This model was constructed well before much of the basics of lymphatic function were revealed, however, such as the effects of flow on smooth muscle contraction inhibition.

Summary

Despite the importance of the lymphatic system in health and disease, comparatively little is known about its function, certainly relative to arterial and venous circuits [31]. The fact that the lymphatic system performs its pumping functions against pressure gradients and gravity makes it an interesting topic for engineering analysis. Clearly, the integration of the system components from the cellular to the systemic level is crucial in this function. Our future modeling efforts will focus on capturing physiologic features of clinically important disease states (edema, cancer, etc.), and predicting the likelihood of success of various interventions. Currently, there is no cure for edema, and prognoses of metastasized cancers remain grim. Further engineering analysis of the lymphatic system would serve a crucial role in expanding our understanding of, and ability to treat, these diseases.

Biofluid Mechanics of The Pulmonary System

Physiological significance

The delicate structure of the lung epithelium makes it susceptible to surface tension induced injury. In cases of sepsis leading to multi-organ failure, large regions of the lung can fill with fluid (become atelectic), eliminating gas-exchange to a significant fraction of the lung. In addition, liquid fills the lungs of all neonates at the time of birth. Those born prior to 25 weeks gestation are likely to have an immature surfactant system, resulting in elevated interfacial surface tension. As a result, large regions of the lung may remain atelectic or close due to interfacial instabilities. This disease is referred to as respiratory distress syndrome (RDS). Subsequent lung collapse after inflation can occur in surfactant deficient neonates as well as adults with “wet” lungs.

The deformation response of biological cells exposed to different flow conditions is a problem with important clinical implications. For example, patients suffering from acute lung injury (ALI) cannot breathe on their own due to the collapse and fluid occlusion of small pulmonary airways. These patients must be placed on a mechanical ventilator in order to survive. However, the microbubble flows generated during ventilation can exacerbate the existing lung injury and the mortality rate for ALI is very high (30–40%). Even for those patients who survive ALI, the tissues of the lung may be damaged due to the mechanical environment, which exposes the sensitive epithelium to abnormal physical forces that can initiate or exacerbate lung injury. This may occur with mechanical ventilation, leading to ventilator-induced lung injury (VILI).

Clearly the damage to the lung related to VILI and ALI is associated with liquid obstructions that accompany atelectasis. In order to understand this relationship, models of air-liquid interfacial flows and fluid-structure interactions in single airway and a network of airways that represent the bifurcating structure of the lung should be investigated. The liquid film consists of a mucus layer on top of a periciliary fluid layer [32]. Mucus is a non-Newtonian fluid possessing viscoelastic characteristics [33–37]. Surface tension on an air-liquid interface induces liquid flows, which may cause the lung’s airways to close due to the formation of a liquid plug as a result of drainage of the liquid lining coating the airways if the liquid film is sufficiently thick [36,37]. The stability of the liquid layer is also influenced by the air core flow [38] as well as the rheological properties of the liquid. Once occluded, either by a short plug or an extended collapsed region, the airway must be reopened to maintain ventilation to distal regions of the lung.

It is hypothesized that these events that may damage the lung – experimental and theoretical fluid mechanics models are essential to provide insight towards this hypothesis and may lead to clinical protocols that could reduce the morbidity and mortality of those suffering from ALI or RDS. In the sections that follow, we present predictions and observations related to interfacial flow-induced damage to the lung, and propose future studies that may enhance our understanding of these multi-scale problems.

Predictions of fluid mechanical events related to atlectrauma

Closure of airways can occur by a Rayleigh instability of the liquid lining, or an instability of the elastic support for the airway as the surface tension of the air – liquid interface pulls the tube shut, or both [39]. Airway closure may occur in normal lungs at low lung volumes resulting in liquid plugging [40]. The thickness of liquid film is 2–4% of the airway diameter under normal conditions [41,42], but may be as large as 20% in disease [43].

The effect of viscoelasticity of lung mucus on airway closure is still ongoing research. While to date most investigations use Newtonian models, the simplest viscoelastic model is that of a Maxwell fluid, where there are both viscous and elastic elements. When this viscoelastic system is oscillated, the dynamic response is frequency dependent and force vs displacement has both in-phase (elastic) and out-of-phase (viscous) components. Compared with a Newtonian fluid of the same base viscosity, the viscoelastic fluid layer grows faster and closure times are shorter because of a smaller effective viscosity. Due to the same mechanism as that shown by Halpern and Grotberg (2003)[38], oscillatory core flows can saturate the instability. Since the effective viscosity of the viscoelastic fluid depends on the frequency of the force applied, there may exist a series of optimum frequencies of the oscillatory flow [44], that would increase the longitudinal displacement of the liquid bulge and hence maintain airway patency.

Since the film flow is induced by the pressure gradient due to the surface tension forces, surfactant can retard the closure process. Several studies have investigated the effect of surfactant on airway closure [45–49].

The process of opening collapsed atelectic region involves complex fluid-structure interactions that depend on airway geometry, fluid properties and surfactant biophysical processes. Theoretical and computational models have been developed [50–55]. These models predict that a ‘two-branch’ response can exist with distinctly different low-velocity and high-velocity behavior. Recent studies show that the low-velocity branch is unstable [51] and this unstable solution is unfeasible under the transverse gravitational force [53]. These investigations also provide insight into mechanical stresses that can damage the lung. However, in general these are estimates based upon steady, fully-developed flow. Investigations of unsteady and transient flows in more complex geometries would improve our understanding of regions of the lung that might be highly sensitive to interfacial flows.

Predictions of micro-mechanical stresses that may damage the lung

Airway epithelial cells experience significant mechanical stresses during the reopening event. In extended regions of airway closure, computational analyses have predicted the existence of spatial/temporal gradients in shear and normal stress that may cause a local “pinching” effect on airway epithelial cells [50]. Alternatively, short regions of closure can occur wherein a liquid plug obstructs the airway. This liquid plug propagation results in a significant change in mechanical stress in the vicinity of the front meniscus surface [56–59]. In both situations, the behavior of these stresses and the system at macro-scale is modulated by surfactant behavior at the molecular scale, which demonstrates the importance of multi-scale interactions in this system [58,60,61].

Observations of damage due to fluid mechanical events

Previous computational studies indicate that microbubble or liquid plug flow imparts a complex combination of normal and shear stress to the epithelial cells on airway walls. Experiments in in vitro systems clearly demonstrate that these flows can impart injurious mechanical stresses on airway and alveolar epithelial cells [62–64]. It should be noted that the calculations of applied stresses are based upon simplifications of a flat cell monolayer, fully developed flow and a Newtonian lining fluid. In reality the surface geometry of the monolayer is complex and topological effects can greatly amplify the magnitudes of the hydrodynamic stresses [65]. These hydrodynamic stresses may result in cell deformation, membrane rupture and/or cell detachment. Recent study shows that sub-confluent cells experience more damages and cell detachment than confluent cells [66]. Hydrodynamic stresses may also be transduced into injurious biological responses including the up-regulation of inflammatory pathways and altered surfactant secretion [67–70].

Physico-chemical interactions

Pulmonary mucus possesses viscoelastic and shear thinning characteristics with a yield stress. It is still unclear which property of the mucus is most important in the context of atelectrauma. Experimental evidence [71] shows that the Maxwell fluid is inadequate to model the viscoelasticity of the mucus. In fact, the lining fluid properties vary substantially from region to region within the lung [34,35]. Therefore, a reliable rheological model of lung liquid is required to make progress in estimations of the importance of viscoelasticity in normal and pathophysiological conditions.

Surfactant physicochemical effects have been investigated under ideal conditions [58,60,61]. However, surfactant biophysical properties are extraordinarily complex [72,73]. For example, the surfactant on air-liquid interface is prone to buckle and collapse when its concentration exceeds the maximum dynamic concentration [72,74]. Multilayer models of pulmonary surfactant are essential for enhancing our understanding of surfactant physicochemical hydrodynamics. Finally, surfactant is released in the lung in lamellar bodies and can create multi-molecular micelles. Accurate models of micelle transport, rheological characteristics [75] and micelle dynamics at the air-liquid interface will substantially improve our understanding of these complex interactions. These models may be useful in developing strategies for pulmonary ventilation that could expand upon the “surfinacatant” work [76] that could lead to scenarios that could enhance surfactant uptake.

Cell models

Under hydrodynamic stresses applied, cellular deformation and its injury may be a function of various biophysical parameters including cytoskeletal structure, micro-mechanical properties, cell morphologies and cell-cell contact mechanics. Dynamic response of cells to a rapid change in surface force and the response of cells on a flexible membrane are necessary to study experimentally. New computational models of this system may be necessary to be developed in order to accurately evaluate experimental conditions. Pharmacological intervention may lead to protective strategies for VILI through modification of cell stiffness.

Airway interactions

While most models to date have relied on single or small networks of airways, in reality pulmonary airways are surrounded by parenchyma that consists of numerous alveoli, all of which are connected to distal airways. Therefore, the dynamics of each airway and alveolus is interdependent. As such, the behavior of one component may affect all others through parenchymal tethering. For this reason, the collapse and reopening process of an airway may affect other reopening processes. To understand these mechanical interactions, total lung lobe models need to be developed. Since the pressure in liquid-coated airways and alveoli are functions of their geometry and surface tension, this will naturally lead to multi-scale modeling. This modeling will allow us to identify differences in inflation/deflation mechanisms of atelectic regions of the lung, and may yield improved technologies for reducing the morbidity and mortality associated with RDS, ARDS and VILI.

Future work

Though simplified models of airway closure and reopening phenomena in single airways have led to advances in our understanding of atelectrauma, future investigations should explore the importance of physicochemical interactions, cell mechanics, and airway interactions.

SYSTEM DYNAMICS VERSUS HEMODYNAMICS IN THE CONTROL OF BLOOD FLOW

From a historical perspective, work on the systemic circulation has gone through a number of distinct eras: from the ancient era where blood was thought to be manufactured in the heart and then dispatched to the rest of the body, to the next era where it was recognized that blood is actually in continuous circulation through the body, then the era of steady Poiseuille flow where the focus was on the details of flow within the blood vessels, to the era of pulsatile flow, first in a rigid tube, then in an elastic tube, which led to the era of wave propagation and wave reflections and, finally, to the modern era where computer power coupled with the Navier-Stokes equations has made it possible to simulate blood flow in every possible configuration. It is interesting that every era was marked by an unwavering commitment to the subject of the day, all else being regarded as secondary, just as the pulsatile nature of blood flow was regarded as secondary in the era of Poiseuille flow, or as wave reflections were regarded as secondary in the early days of pulsatile flow. Secondary issues were actually seen as “aberrations” in the design of the cardiovascular system, even with some negative connotation. Indeed, to this day we continue to think of wave reflections in this negative way, as an added “cost” to the system, or an “afterthought” in the design of the system. Wave reflections have yet to be embraced in our minds as an intrinsic part of the system, not secondary or negative in any way, but simply an integral part of the system, essential as any other in the efficient working of the system, and as such they may actually be used by the system to some advantage [77].

In the modern era our commitment is to the Navier-Stokes equations and to our computer power to solve them under every conceivable condition, thereby making it possible to simulate most of the blood flow phenomena which we observe within the human body [78]. As in previous eras we feel that we have the subject essentially in hand, though, again, with the exception perhaps of some “secondary” issues. In what follows we consider one such issue, namely that of control and regulation of fluid flow within the human body, more specifically the control and regulation of blood flow [79,80].

While blood flow is certainly governed by the Navier-Stokes equations, it is at no time governed by the Navier-Stokes equations alone. Blood flow is part of a closed-loop control system, or more precisely it is under a hierarchy of local and global control loops in which the primary object is control of pressure and flow rate [81]. While the Navier-Stokes equations govern the relation between pressure and flow, it is an open-loop relation which they govern. In that relation, a change in pressure produces a change in flow and there the matter ends. There is no provision for any feedback from the change in flow back to the change in pressure, yet in the physiological system feedback loops are ever present [82].

Feedback loops in the cardiovascular system are mediated by a number of neural and humoral control mechanisms [79,83,84]. As in a man-made control system, each of these loops is associated with a controlled variable, a sensor, and a controller that is able to affect the value of the controlled variable. While a great deal has been learned about certain elements of these control systems, much is still unknown. Typically, a controlled variable such as blood pressure or heart rate is identified and some of the sensors associated with it are located, but the control system loop governing that variable can rarely be sketched out or isolated in complete form. This is not only because some of the sensors or pathways are unknown but because in most if not all cases the loops involved, rather than being distinct closed loops, may typically be interlaced with each other. The control systems for heart rate and stroke volume, for example, may have both local and central loops and these loops may interlace with each other as well as with others associated perhaps with the control of blood pressure and pCO₂ [79].

To deal with blood flow in its full breadth, therefore, it is necessary to integrate hemodynamics with the full dynamics of the system because the integrity of blood flow in any organ or system depends not only on hemodynamics within the blood vessels of that organ or system but also on the full dynamics of the system as a whole [85,86]. The first of these is governed by the Navier-Stokes equations, the second by the control loops and mechanisms associated with blood flow in that particular organ. Put another way, while satisfying the Navier-Stokes equations is a necessary condition for an accurate description of blood flow within the vascular bed of an organ, it is not a sufficient condition for a description of the overall dynamics of that flow in the context of control and regulation, or in the context of what is the ultimate objective of blood flow in that organ, namely cell perfusion.

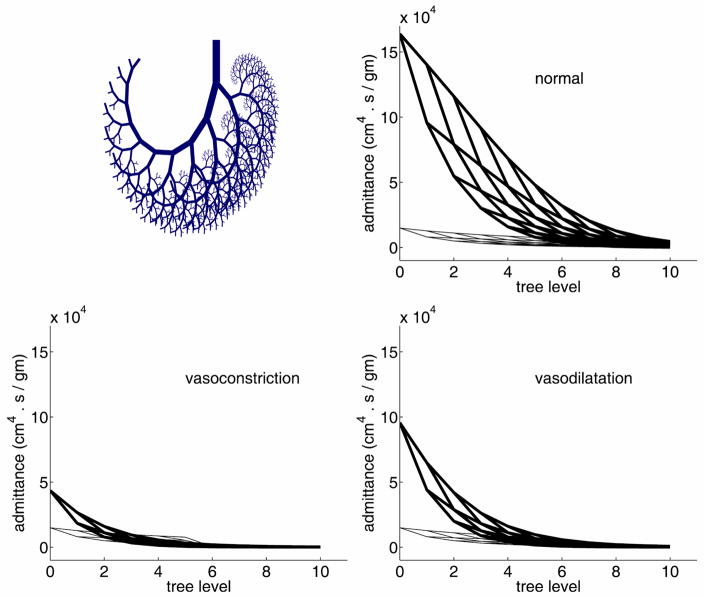
Arrhythmia, in all its forms, is a familiar example of this dichotomy [87,88]. It affects the harmony between the pumping rhythm of the heart and the compliance of the aorta, thereby affecting cardiac output and the dynamics of the systemic circulation. In the heart, similarly, a disruption in the harmony between the pulsatile rhythm of the input pressure driving the flow into the coronary circulation, the pulsatile rhythm of the contracting cardiac muscle and its effect on coronary vessels imbedded within it, and the combination of wave propagation and wave reflections within the coronary vascular tree, will lead to a failure of the dynamics of the coronary circulation while the flow within individual vessels is continuing to satisfy the Navier-Stokes equations. A much simplified version of this scenario is shown in Fig. 1 where the dynamics of the flow in a vascular tree is disturbed by vasodilatation or vasoconstriction at the peripheral levels of the tree. The result is a change in the distribution of admittance along the tree and therefore a change in the dynamics of blood flow through the tree. The flow in individual vessel segments remains orderly in the sense that it continues to satisfy the Navier-Stokes equations. Thus, while the overall dynamics of the flow have been affected, hemodynamics within the tree have not.

Figure 1.

Admittance distribution in an 11-level tree model (top) and how it is affected by vasodilatation or vasoconstriction in the peripheral vessels (bottom) [92].

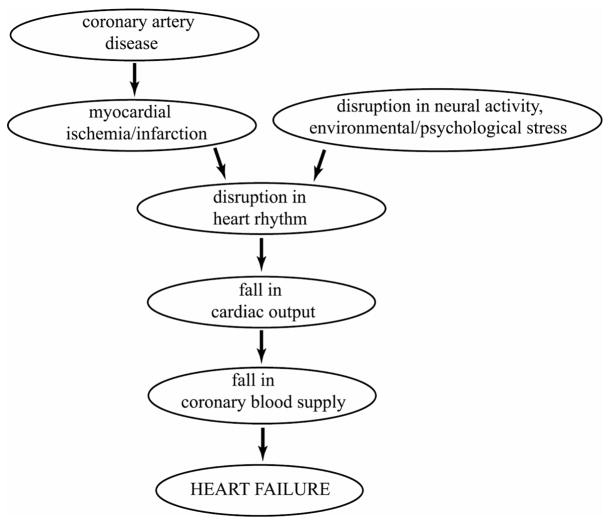
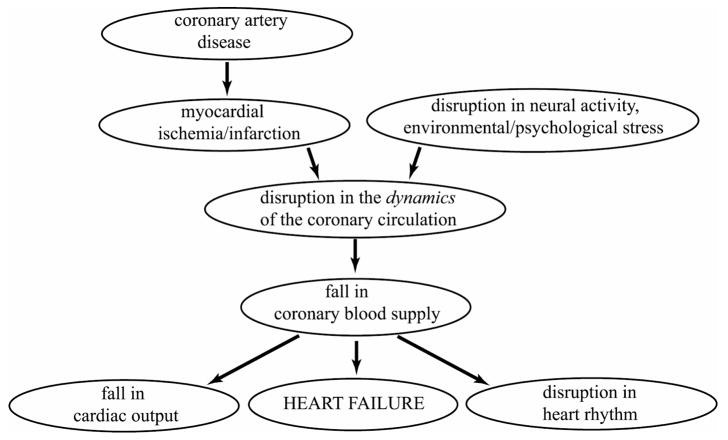
In sudden cardiac death there is a precipitous fall in cardiac output to levels that can no longer sustain cerebral or cardiac function [89]. By definition, the timing of this failure cannot be attributed to any prevailing coronary artery disease, so the disease if present is seen only as a participant in but not the immediate cause of the event. According to currently held view, coronary artery disease is seen as a precursor to conditions of myocardial ischemia and infarction, leading to a disruption in heart rhythm, fall in cardiac output, fall in coronary blood supply and finally heart failure, as illustrated in Fig. 2. A difficulty with this course of events is that it proposes that a fall in cardiac output is followed by a fall in coronary blood flow. The mechanism for this sequence is not clear if indeed possible, because if the fall in cardiac output leads to a drop in aortic pressure, it is well known that autoregulation of coronary blood flow ensures that this does not lead immediately to a fall in coronary blood flow [90,91]. Because of autoregulation, a fall in cardiac output is more likely to be the consequence rather than the cause of a fall in coronary blood flow, the latter being precipitated by a disruption in the dynamics of the coronary circulation produced by coronary artery disease, cardiac damage, or a disruption in neural activity. This alternative course of events is illustrated in Fig. 3.

Figure 2.

Current view of the course of events leading to sudden cardiac death in which a fall in cardiac output is followed by a fall in coronary blood supply [92].

Figure 3.

A more likely course of events leading to sudden cardiac death in which the fall in cardiac output is the consequence rather than the cause of a fall in coronary blood supply, and the primary trigger is a disruption in the dynamics of the coronary circulation [92].

Thus, the integrity of blood flow in its widest sense depends in the first place on hemodynamics within the vascular bed but ultimately on the dynamics of the system as a whole, and in the same way that the first of these may be disrupted by a vascular pathology, the second may be disrupted by what may be termed a “dynamic pathology” [92]. Arrhythmia is a clear example of a dynamic pathology while sudden cardiac death is, ultimately, the result of a dynamic pathology.

A dynamic pathology is not unlike a structural or functional pathology in a tissue or organ, but it deals specifically with dynamics. Furthermore, it deals with the dynamics of an integrated system as a whole, such as the dynamics of the systemic or of the coronary circulation, including all the feedback loops involved in the control and regulation of the system in each case. Thus, an atherosclerotic lesion in a coronary artery is a vascular pathology [93], but the ultimate significance of this lesion lies only in the dynamic pathology which it produces, more specifically in the way the lesion affects the dynamics of the coronary circulation as a whole, and in particular in the way it affects the ability of the coronary circulation to provide the heart with sufficient blood supply. If the occlusive progression of the lesion is sufficiently slow so that the occlusion is compensated for by vascular restructuring, for example, the dynamic pathology may be minimal or nonexistent. Thus, the presence of vascular pathology does not necessarily imply the presence of dynamic pathology, but the reverse is not necessarily true, namely the absence of vascular pathology does not necessarily imply the absence of dynamic pathology.

Perhaps the most celebrated example of a dynamic pathology is the phenomenon of a “broken heart” which has recently made the transition from the realm of folklore to that of medicine where it is now accepted as a legitimate clinical syndrome. Following a multi-patient clinical study, Wittstein et al [94] reported that “Emotional stress can precipitate severe, reversible left ventricular dysfunction in patients without coronary disease. Exaggerated sympathetic stimulation is probably central to the cause of this syndrome.” Because of the absence of coronary artery disease in these patient, the precipitating pathology in this case is again a dynamic pathology as in the case of sudden cardiac death, namely a disruption in the dynamics of the coronary circulation followed by a fall in coronary blood supply and a fall in cardiac output.

One of the most important aspects of dynamic pathologies is that unlike structural pathologies they do not leave a footprint after they have resolved or produced their damage. Following sudden cardiac death, indeed following any death attributed to heart disease, only structural pathologies can usually be found and they become the focus of attention. Any dynamic pathologies involved are not in evidence because they are no longer at play. This is the reason for which the broken heart syndrome has taken so long to be accepted by the medical community. The concept of a dynamic pathology, which is a failure in the overall dynamics of a dynamic system, is well familiar in science and engineering but is rather foreign in the clinical setting where the focus is on the more tangible hemodynamics. The broken heart syndrome, with the distinction of being transient and reversible, offers the opportunity to make the dynamic pathology more tangible, that is it makes it possible to detect the dynamic pathology while it is at play and in pure form, because the syndrome is not associated with coronary artery disease.