Robust processivity of myosin V under off-axis loads

Abstract

The dimeric motor myosin V transports organelles along actin filament tracks over long distances in cells. Myosin V is a smart ‘walker’ that is able to swiftly adjust to variable ‘road conditions’ to continue its processive movement across dense cellular environments. Coordination between the two heads via intramolecular load modulates biochemical kinetics and ensures highly efficient unidirectional motion. However, little is known about how load-induced regulation of the processive stepping occurs in vivo, where myosin V experiences significant off-axis loads applied in various directions. To reveal how myosin V remains processive in cells, we measured the effect of the off-axis loads, applied to individual actomyosin V bonds in a range of angles, on the coordination between the two heads and myosin V processive stepping. We found that myosin V remains highly processive under diagonal loads owing to asymmetrical ADP affinities and that the native 6IQ lever optimizes the subunit coordination, which indicates that myosin V is designed to be an intracellular transporter.

Myosin V transports cargos toward the barbed end of actin filaments in cells^1,2, taking multiple ~36-nm steps by alternately swinging forward two lever arms in a ‘hand-over-hand’ fashion^3–7. Single-molecule experiments reveal that one ATP molecule is consumed for each step, which confirms the tight coupling between mechanical and enzymatic events⁸. Combined with the unidirectionality of the processive movement, this mechanism implies that the ATPase cycles in two catalytic domains are precisely coordinated. Directional loads modulate ATPase kinetics in myosin V^9–11, which suggests that two subunits communicate via the intramolecular load, which is generated during binding to actin with both heads, to achieve the coordinated mechanical performance.

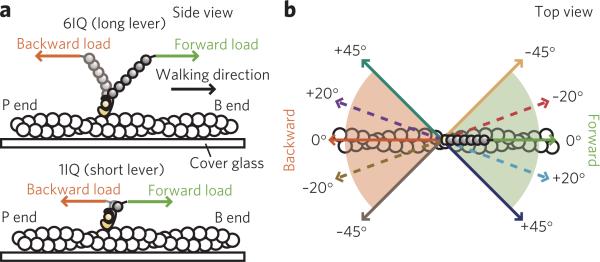
However, myosin V molecules processively traveling in vivo experience significant off-axis loads, both intramolecular and external, such as when switching actin tracks at the intersections¹² or following the left-handed helix around an actin filament¹³ (Supplementary Fig. 1), or when dragging cargo via a dense cellular network¹⁴. To investigate the mechanism enabling myosin V to remain processive in vivo, we measured the unbinding forces⁹ for the individual actin–myosin V 6IQ and 1IQ complexes (Fig. 1a) under loads applied diagonally to the filament's long axis in a range of precisely controlled angles, toward either the barbed or the pointed end, using optical tweezers (Fig. 1b and Supplementary Fig. 2).

Figure 1. Constructs and loading angles.

(a) Constructs used in this study (side view). (b) The tested loading angles (top view). Note that the 0° angle parallel to the filament's long axis is a negative angle considering the direction of the filament's right-handed helix.

The mechanochemical properties of many motor proteins, including myosin, kinesin and DNA motors, have been revealed by force spectroscopy under a microscope^15–18. These experiments demonstrate that the orientation of a motor relative to the ‘track’ is important for its activity. However, owing to experimental complications, not many loading directions can be tested, as it is either difficult to visualize the directionality of motors during the force measurements, or the transducer can be operated in only one direction, such as in the case of atomic force microscopy (AFM). Compared to previous studies, the experimental setup used here is advantageous because it enabled us to test five loading angles and (owing to the identified polarity of the actin filaments) twice as many loading directions. These measurements allowed us to characterize the loading direction–dependent modulation of actin and ADP binding affinities and the role of the native 6IQ lever, and the obtained results were tested by studying the effect of the off-axis loads applied to the processively traveling dimeric myosin V molecules.

RESULTS

Actin and ADP binding affinities under directional loads

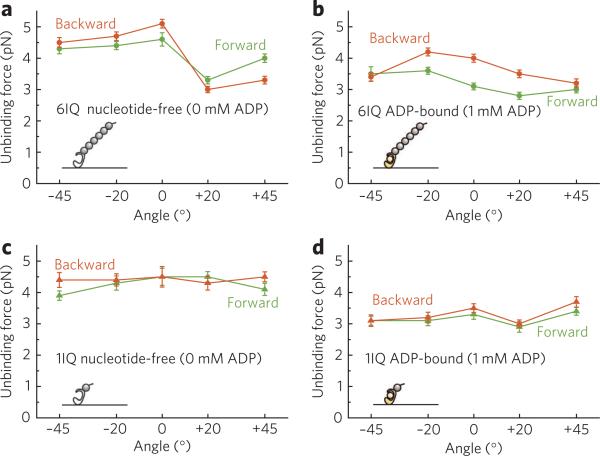
The unbinding forces for the long-lever (6IQ) construct in the nucleotide-free state and in the presence of 1 mM ADP (Fig. 2a,b) depended on both the loading angle and the loading direction relative to the filament's polarity. The unbinding forces in the presence of ADP were smaller than in the nucleotide-free state at all tested angles, with the exception of the backward +20° load, which indicates that ADP shortens the lifetime of the attached state. Compared with the long-lever construct, in the 1IQ construct the dependence on loading angle was weaker (Fig. 2c,d). In both nucleotide states, the long lever either weakened or strengthened the actin binding affinity, depending on the loading angle (Supplementary Fig. 3).

Figure 2. Dependence of the unbinding force on loading angle.

(a,b) The 6IQ construct in the nucleotide-free state (a) and the ADP-bound state (b). (c,d) The 1IQ construct in the nucleotide-free state (c) and the ADP-bound state (d). Hereafter, the green lines and symbols correspond to the forward loads, and the orange lines and symbols correspond to the backward loads. Error bars are the s.e.m. (n ≥ 22).

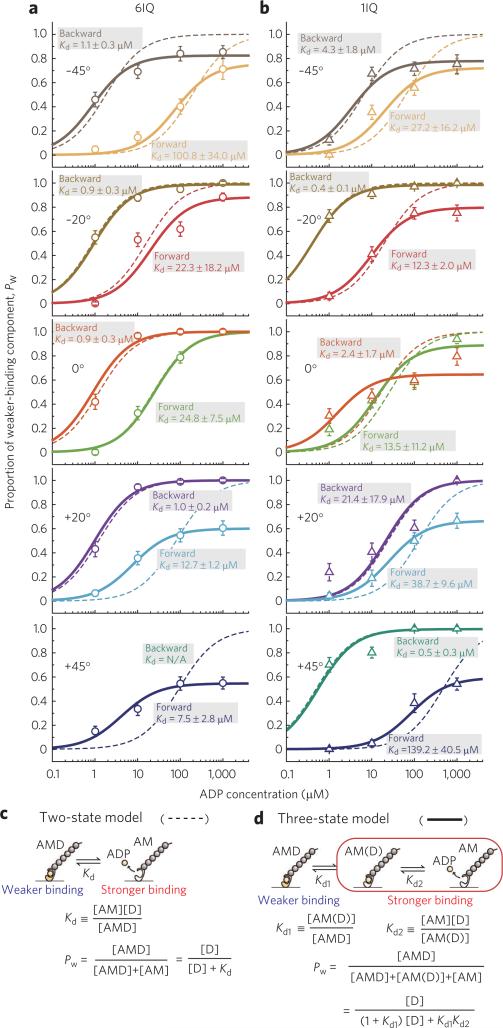
Next, we measured the unbinding forces for the 6IQ construct at each loading angle at various ADP concentrations (0–1 mM) (Supplementary Fig. 4). The unbinding force distributions were globally fitted with the sum of two Gaussians⁹, indicating the presence of two components corresponding to the weaker (left peak) and the stronger (right peak) binding. In all bimodal distributions the positions of the two peaks coincided with the peaks at 0 or 1 mM ADP, though this coincidence was not required by the fitting procedure. Therefore, the weaker and stronger peaks were attributed to the unbinding in the ADP-bound (AMD) and the nucleotide-free (AM) states, respectively, except for the backward +20° load, where the difference in the stability of the actomyosin bond ± ADP was the opposite (in this case, the weaker and stronger peaks were attributed to the unbinding in the AM and the AMD states, respectively) (Fig. 2a,b). The proportion of the weaker-binding component (or the stronger-binding component in the case of the backward +20° load), calculated as an area of the corresponding Gaussian divided by total area of each distribution, increased with [ADP] (Supplementary Fig. 4), which confirms that it corresponded to the AMD state. At all loading angles the proportion of the AMD state at each [ADP] was larger (indicating that ADP binds more tightly) under backward load than under forward load (Fig. 3a).

Figure 3. Dependence of the proportion of the weaker-binding state, P_w, on [ADP] at various angles under forward and backward loads.

(a) The 6IQ construct. (b) The 1IQ construct. Dashed and solid lines were obtained by the two-state and three-state models, respectively. Error bars represent the s.e.m., calculated as (p · (1 − p)/n)^1/2, where p is the existence probability of the weaker-binding state and n is the total number of data at each ADP concentration (n ≥ 28). P_w under the backward +45° load could not be estimated because of a small (only an ~0.1 pN) difference in the values of the unbinding forces ± ADP, which made fitting the unbinding force distributions with two Gaussians impossible (Supplementary Fig. 4). (c,d) Schematic representation of the two-state model (c) and the three-state model (d) of ADP dissociation. P_w is the proportion of the weaker-binding state.

The unbinding forces for the 1IQ construct were also measured at various [ADP] (0–1 mM ADP) (Supplementary Fig. 5). The unbinding force distributions also exhibited bimodality at each loading angle, which allowed us to estimate the proportion of the AMD state similarly to the 6IQ construct (Fig. 3b). For both 6IQ and 1IQ constructs, average unbinding forces plotted against [ADP] decreased with an increase in [ADP], with the exception of the backward +20° load for the 6IQ construct (Supplementary Fig. 6).

ADP dissociation is a two-step process

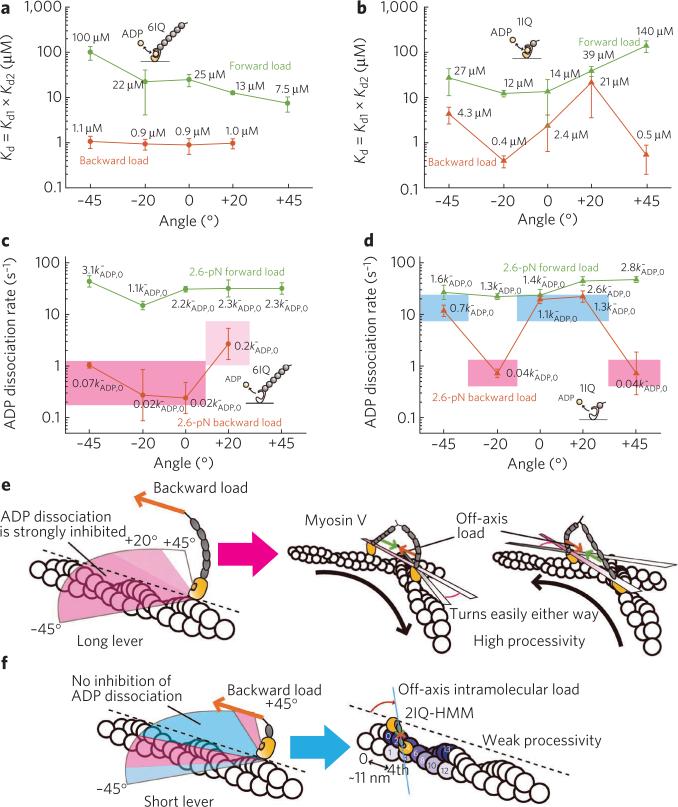
Analysis of the distributions based on a two-state model of ADP dissociation (Fig. 3c) did not fit the data well (dashed line in Fig. 3a,b), consistent with the existence of an intermediate state in the dissociation pathway, AM(D), that binds actin stronger than AMD¹⁹ (Fig. 3d). Indeed, the analysis based on a three-state model (solid line in Fig. 3a,b) fitted the data much better. The existence of the intermediate ADP-bound state indicates that ADP binds and dissociates via a two-step process, determined by K_d1 and K_d2 (K_d = K_d1 × K_d2), and the proportion of the AM(D) state depends on loading direction (Supplementary Fig. 7). The obtained dependence of ADP affinity, K_d, on loading angle under forward and backward loads is summarized in Figure 4a,b.

Figure 4. Asymmetry of ADP affinities depends on loading direction and lever length.

(a,b) Dependence of ADP affinity, K_d, on loading angle under forward and backward loads for the 6IQ construct (a) and the 1IQ construct (b) is shown. The values of ADP affinities are calculated based on the three-state model. Error bars represent the s.e.m. (n ≥ 28). (c,d) Angular dependence of the ADP dissociation rates for the 6IQ construct (c) and the 1IQ construct (d) under 2.6-pN forward and backward loads. 2.6 pN is the value of the intramolecular load as estimated in ref. 9. Areas colored pink, light pink and blue indicate, respectively, strong inhibition, weaker inhibition and no inhibition of ADP dissociation under backward loads. Values at each point are the coefficients of load-induced modulation of the ADP dissociation rate constant under no load ($k_{\mathrm{ADP},0}^{-}$)⁹,²². Error bars represent the parameter error. (e) The long lever efficiently inhibits ADP dissociation from the leading head irrespectively of the loading angle (left), which enables myosin V to switch an actin track in any direction (right). (f) Processive movement of the short-lever dimeric myosin V (for example, 2IQ-HMM²³,²⁴) would require translocation along the same protofilament due to a small step size, which would result in the intramolecular load acting in the 0° to +20° range (right); however, loads applied at these angles cannot sufficiently inhibit ADP dissociation from the leading head (left).

Modulation of ADP dissociation depends on loading angle

The load dependence of the ADP dissociation rate constants was determined by model-based analysis, as we reported previously⁹ (Fig. 4c,d). The unbinding force distributions were fitted with the modeled curves (Supplementary Figs. 8 and 9 for 6IQ and 1IQ constructs, respectively), and the obtained characteristic distances (Supplementary Table 1) indicate that in the 6IQ construct a large asymmetry between the ADP dissociation rates, modulated by forward and backward loads, exists at all angles (Fig. 4c,e and Supplementary Fig. 10a). Namely, backward loads at all angles greatly inhibit ADP dissociation (5- to 50-fold under 2.6 pN load), whereas forward loads weakly (at most 3-fold under 2.6 pN load) accelerate it. On the contrary, loads applied via a short lever are able to produce asymmetrical ADP affinities and dissociation rates only at several loading angles (Fig. 4b,d,f and Supplementary Fig. 10b). The rate constants of ADP binding are strongly inhibited by both forward and backward loads at all tested angles for both the 6IQ and 1IQ constructs (Supplementary Fig. 11).

Effect of the off-axis loads on myosin V stepping

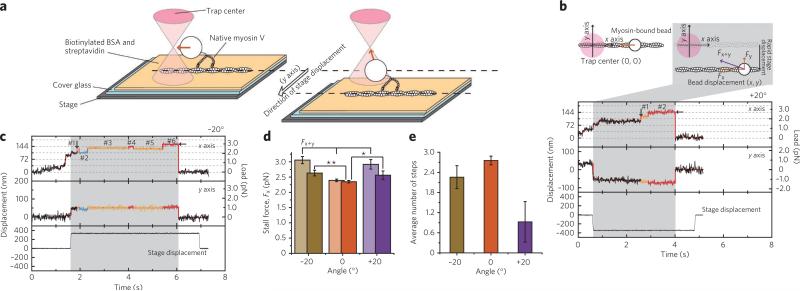
To directly test how the off-axis loads affect myosin V processivity, we applied off-axis loads of 1–2 pN at approximately −20° and +20° to the processively traveling dimeric myosin V molecules (Fig. 5 and Supplementary Fig. 12; see Supplementary Results for details). The application of the off-axis loads did not terminate the processive stepping (Fig. 5b,c). Moreover, the stall force, defined as an on-axis component of load at which myosin dissociates from actin, was similar at −20° and +20° and slightly larger than at 0° (Fig. 5d and Supplementary Table 2), despite an additional y-axis load of over 1 pN. However, whereas the −20° load did not significantly affect the back-and-forth stepping after entering the stall region (for definition of the stall region, see the legend of Fig. 5), the number of steps under the +20° load markedly decreased (Fig. 5e, Supplementary Fig. 13 and Supplementary Table 3), indicating that under high loads myosin V dissociates faster from actin at this loading angle.

Figure 5. Analysis of the stepping motion of myosin V under the off-axis external backward loads.

(a) To apply the off-axis load to myosin V during processive stepping, the stage was rapidly displaced perpendicularly to the long axis of the actin filament in either of the two directions, such that off-axis load was applied at either a positive or negative angle. (b,c) The typical traces of the back-and-forth stepping under loads applied at +20° (b) and −20° (c). The top and middle panels show traces of the bead displacement in the x and y directions, respectively. The bottom panels show the y displacement of the stage. The area in which the off-axis load is being applied is colored gray. The stall force is defined as the value of the on-axis component, F_x, of the external backward load at which myosin unbinds (marked by horizontal arrows). The vertical arrows indicate the beginning of the stall region, determined as one 36-nm step down the stall force. The steps within the stall region are indicated by the numbers 1–6. (d) Stall forces (F_x) and total load (F_x+y) under −20°, 0° and +20° directional loads. The obtained values of the on-axis (F_x, stall force) and the off-axis (F_y) components of the total load (F_x+y) and average angles are summarized in Supplementary Table 2. * and ** denote the one-tailed t-test's P values, 0.040 (<0.05) and 0.0028 (<0.01), respectively. (e) Dependence of the number of back-and-forth steps in the stall region on the loading angle. Error bars represent the s.e.m.

DISCUSSIoN

To characterize the effect of loads applied to the lever on the actin binding affinity, we measured the forces that rupture an actomyosin bond in the nucleotide-free and the ADP-bound states of myosin. In both 6IQ and 1IQ constructs, loads weaken the binding, decreasing the lifetime of an actomyosin bond compared to at no load, which indicates that the imposed load, irrespective of the lever length, reduces the potential barrier for breaking an actomyosin bond. However, the strength of the effects on the actin binding affinity produced by load is modulated by the lever length; in particular, the actin binding affinity of the long-lever construct strongly depends on loading angle (Fig. 2a,b and Supplementary Fig. 3).

The nucleotide binding to myosin induces changes in both the conformation of its actin-binding cleft and the orientation of the lever arm^20,21, which suggests that the conformational changes in the actin-binding cleft may lead to the lever rotation. Conversely, the lever rotation (or strain) may induce the conformational changes on the actin binding interface, thereby affecting the actin binding affinity of the motor domain. The post-power stroke conformation of the lever arm was reported to correlate with a closed actin- binding cleft²⁰, which is thought to strongly bind actin, whereas the lever-up conformation (pre-power stroke) is coupled with an open cleft that binds actin weakly. Previous studies have focused on the changes in the orientation of the lever induced by the conformational changes in the nucleotide binding pocket or on the actin binding interface. Here we tested the opposite relation: how load affects actin and ADP binding affinities; we also examined the role of the lever and the dependence of actin and ADP binding affinities on loading angle and direction.

We observed the loading angle–dependent differences of the unbinding force values, which were much larger in the long-lever construct compared to the 1IQ construct. It remains unclear, though, whether these variations in actin binding affinities correlate with the reported reorganization of the actin-binding cleft—specifically, transitions between the closed and open states. Moreover, in the long-lever construct, backward loads applied at negative (−45° to 0°) angles stabilize the actin binding more efficiently than forward loads. This result does not correlate with the reported coupling between the lever-up conformation and the weak actin binding state^20,21, because the lever-up conformation is more likely to exist under backward loads than under forward loads. Thus, we conclude that loads do not induce conformational changes in the actin-binding cleft, which would result in the transition from the closed to open state, at the angles where actin binding affinities under backward loads are stronger than under forward loads. However, at positive angles the backward loads destabilize the actin binding more strongly than forward loads (Fig. 2a), which is consistent with a previous report²¹. Thus, we suggest that the backward load at around +20° may be able to induce conformational changes in the actin-binding cleft corresponding to the transition from the closed state to the open state. If this prediction is correct, the orientation of the lever when the actin-binding cleft is in the open state may be similar to that under the backward +20° load.

We previously reported that at a 0° loading angle, the ADP affinity of the 6IQ construct under backward load is 20-fold higher than under forward load (1.2 ± 0.2 μM and 23.0 ± 3.7 μM, respectively)⁹. Here we estimated ADP affinities under the off-axis loads applied diagonally to the long axis of an actin filament at −45°, −20°, +20° and +45°. At these angles, ADP affinity under backward loads was 10- to 100-fold higher than under forward loads. Notably, the ADP affinities of the 6IQ construct under backward loads were ~1 μM, irrespective of the loading angle (Fig. 4a; the data at +45° could not be analyzed due to a small difference in the values of the unbinding forces between the stronger- and weaker-binding states), indicating that the backward off-axis loads do not affect ADP affinity (~1 μM at no load^9,22), whereas the forward off-axis loads strongly modulate it. To elucidate the role of the lever in modulating ADP affinity by directional loads, we also estimated ADP affinity for the short-lever (1IQ) construct (Fig. 4b). At all tested angles ADP affinity was weaker under forward loads than under backward loads; however, at +20° the difference was small compared to other angles. The ~6-fold difference in ADP affinities under forward and backward loads at 0° (13.5 ± 11.2 μM and 2.4 ± 1.7 μM, respectively) was smaller than in the 6IQ construct, where a 25-fold difference was observed (the small difference with the affinity values reported in ref. 9 is due to the application in this study of a three-state model–based analysis compared to a two-state model used in the previous report). Thus, we conclude that the long lever more efficiently produces the asymmetry in ADP affinities between forward and backward loads, and, importantly, does so irrespectively of the loading angle.

Previously the intermediate ADP-bound state, AM(D), was detected in a solution study¹⁹. Here we found that both K_d1 and K_d2, which determine the apparent ADP affinity, K_d (K_d = K_d1 × K_d2), depend on loading angle (Supplementary Fig. 7a–d). These results indicate that, even though the apparent ADP affinity remains constant at various loading angles, the proportion of AMD, AM(D) and AM states varies with loading angle. K_d1 characterizes the AMD ⇄ AM(D) equilibrium. In the 6IQ construct, forward loads at all angles except 0° facilitate the formation of the intermediate state. The [AM(D)]/[AMD] existence ratio becomes >10-fold larger than under no load, which was obtained by the solution study¹⁹; backward load at −45° increases the existence ratio observed at no load by ~10-fold (Supplementary Fig. 7a). At other angles and loading directions, K_d1 was very small, which indicates that the AM(D) state is not stable at these conditions. K_d2, which characterizes the accessibility of the nucleotide binding pocket for ADP, was 10–20 μM under forward +20° and +45° loads and 200–300 μM under forward −20° and −45° loads (Supplementary Fig. 7b). Under backward loads K_d2 was ~80 μM at −20° (same as at no load) and ~5 μM at −45° loads—that is, ~16-fold smaller than at no load.

In the 1IQ construct, K_d1 under forward loads was 10- to 50-fold larger than at no load, indicating that forward loads facilitate the formation of the AM(D) state from the AMD state. Backward loads applied at negative angles increased K_d1 as much as 40-fold compared to at no load, whereas K_d1 at +45° was threefold smaller than at no load and K_d1 at +20° was very small, indicating that the AM(D) state is not stable (Supplementary Fig. 7c). Forward loads had no significant effect on K_d2 in 1IQ (Supplementary Fig. 7d). Under backward loads K_d2 in 1IQ at negative angles (−45° to 0°) was threefold to tenfold smaller than at no load, whereas it was twofold larger at +45° than at no load. At +20°, K_d2 was very large, indicating that the intermediate state is short-lived.

In summary, the population of the intermediate state depends on loading angle and is also strongly affected by the lever length. In the 6IQ construct, the AM(D) state is generated under backward loads applied between −45° and −20° with a higher yield than at any other loading angle (Supplementary Fig. 7e); on the other hand, in the 1IQ construct backward loads tend to stabilize the AM(D) state in the −45° to +10° range (Supplementary Fig. 7f).

The large asymmetry in ADP affinities and dissociation rates between the two heads at all loading angles found in the long-lever construct (Fig. 4a,c) explains the ability of myosin V to maintain high processivity under loads directed not parallel to the long axis of an actin filament. As long as the unbound head is able to land on actin and strongly bind it, the external and/or intramolecular backward load exerted on the leading head strongly inhibits ADP dissociation regardless of the spatial orientation of the two lever arms (Fig. 4e). Therefore, irrespective of the direction of the applied load, the leading head remains bound to actin, which serves to maintain the high processivity of dimeric myosin V during its movement in vivo.

Note the large difference between the 6IQ and 1IQ constructs: in the 1IQ construct the difference between the ADP dissociation rates under forward and backward loads at 0° and +20° is small compared with 6IQ; the short lever, in contrast to the long lever, cannot inhibit ADP dissociation at these loading angles, which correlates with the previous report¹⁰. Therefore, while the loads applied to the 1IQ construct at several loading angles are also able to produce strongly asymmetrical ADP affinities and dissociation rates, the short lever would force the short-necked dimers to move along a single protofilament of a right-handed helix—that is, when the intramolecular load is applied at approximately +20°. However, at this angle ADP dissociation from the leading head is not sufficiently inhibited (Fig. 4d), which correlates with the reported weak processivity of the myosin V–2IQ dimer (Fig. 4f)^23,24.

Why is the native lever long? The complex dependence of the difference in the measured unbinding forces on loading angle between the 6IQ and 1IQ constructs (Fig. 2 and Supplementary Fig. 3) indicates that both long and short levers are capable of imposing sufficiently large net force on the actin binding interface. Therefore, rather than the length of the lever, it is the optimal orientation of the native 6IQ lever that is important for the precise modulation of ADP affinity by external loads. The 6IQ lever is therefore structurally optimized for efficient processive stepping and is thus more than simply an elon-gated short lever.

Backward loads applied at either −20° or +20° did not compromise the robust processivity of myosin V (Fig. 5b,c), which correlates with the large difference in ADP affinities between the two heads at all angles. However, when the off-axis load was applied to the stepp ing myosin V at +20°, the motor took fewer steps after entering the stall region and tended to dissociate faster than under the 0° or −20° loads. The unbinding force measurements provide two reasons for this. First, ADP dissociation under backward +20° load is the least inhibited (the light-pink region in Fig. 4c,e), which indicates that in a one-head-bound intermediate the bound head may release ADP and dissociate from actin after binding ATP. Second, the stability of an actomyosin bond in both the ADP-bound and especially the nucleotide-free states of the motor under the +20° load is the lowest among these three angles (Fig. 2a,b), which increases the possibility of the dissociation of a one-head-bound intermediate from actin even without the involvement of ATP. On the contrary, the average dwell time of all steps, both forward and backward, within the stall region was statistically identical at all three loading angles (Supplementary Figs. 14 and 15), which may imply that at stall myosin V always dwells with both heads bound to actin.

The same two reasons may also explain why the structurally favorable binding to the 15th actin monomer during the processive stepping of the dimeric myosin V²⁵, which would result in a right-handed rotation of the actin filament (Supplementary Fig. 1), was not observed in motility assays, and why the free head binds preferentially at the 11th or 13th monomer^13,26.

In molecular motors—both linear, such as myosin V or kinesin²⁷, and rotary, such as F₁-ATPase²⁸—coordination between the catalytic units is crucial for efficient unidirectional motion. Such coordination requires that strain in the linkages between subunits, which arises from conformational changes in each subunit, is coupled to the nucleotide state; however, it has remained unclear which structural elements of molecular motors are essential for subunit coordination. Here we have shown that the long lever in myosin V is the element that is essential for subunit coordination. We propose that the catalytic units of various molecular motors have the intrinsic ability to coordinate their ATPase cycles via strain within the catalytic units themselves, and some structural elements, such as the long lever in myosin V and possibly the neck linker in kinesin and the γ-subunit in F₁-ATPase, have developed during evolution to optimize subunit coordination so that the motor's efficiency is maximized.

METHoDS

Proteins

Actin was purified from rabbit skeletal muscle and biotinylated⁶. All experimental procedures conformed to the Guidelines for Proper Conduct of Animal Experiments approved by the Science Council of Japan and were performed according to the Regulations for Animal Experimentation at Waseda University. Recombinant myosin V (S1) was prepared as in ref. 9 (6IQ construct) and ref. 22 (1IQ). Native dimeric myosin V was purified from chick brain⁶.

Measurements of the unbinding force

The unbinding force was measured as in our previous study⁹. The average loading rate was 13.4 ± 0.07 pN s⁻¹ (mean ± s.e.m., n = 6,376). The experiments were performed in an assay buffer containing 20 mM HEPES-KOH (pH 7.8), 25 mM KCl, 5 mM MgCl₂, 1 mM EGTA and ADP (0–1 mM) (Roche). To apply the off-axis load, we chose the filaments that were in proper orientation relative to the direction of the stage movement.

Note that upon the application of external force, the bead moved within the x-y plane but not along the z axis; that is, the external force applied to the bead was almost parallel to the x-y plane, which indicates that the bead–myosin V–actin complex is stiff.

Observation of the stepping motion of myosin V under off-axis loads

The flow cell and the solution conditions were identical to those in the unbinding force measurements⁹, except that 1 mM ATP (Roche) was added instead of ADP. Native myosin V was attached to beads (diameter 1 μm, blue fluorescent, Molecular Probes) coated with rhodamine-labeled bovine serum albumin (BSA) by mixing them at a 3:1 motor-to-bead molar ratio. The off-axis external loads were applied to dimeric myosin V molecules during stepping by quickly displacing the piezo-driven substage perpendicularly to the long axis of the actin filament. For details, see Supplementary Results.

Global fit

The unbinding force distributions were globally fitted as in ref. 9. In the three-state model, the proportion of the weaker-binding component was calculated as shown in Figure 3d.