Machine-learning techniques for building a diagnostic model for very mild dementia

Abstract

Many researchers have sought to construct diagnostic models to differentiate individuals with very mild dementia (VMD) from healthy elderly people, based on structural magnetic-resonance (MR) images. These models have, for the most part, been based on discriminant analysis or logistic regression, with few reports of alternative approaches. To determine the relative strengths of different approaches to analyzing structural MR data to distinguish people with VMD from normal elderly control subjects, we evaluated seven different classification approaches, each of which we used to generate a diagnostic model from a training data set acquired from 83 subjects (33 VMD and 50 control). We then evaluated each diagnostic model using an independent data set acquired from 30 subjects (13 VMD and 17 control). We found that there were significant performance differences across these seven diagnostic models. Relative to the diagnostic models generated by discriminant analysis and logistic regression, the diagnostic models generated by other high-performance diagnostic-model–generation algorithms manifested increased generalizability when diagnostic models were generated from all atlas structures.

1 Introduction

Very mild dementia (VMD) is defined by a Clinical Dementia Rating (CDR) score 0.5; VMD may represent a preclinical form of dementia (Gauthier et al. (2006)). People with CDR = 0.5 may have mild cognitive impairment (MCI) or mild dementia (Gauthier et al. (2006)); they progress to dementia with an annual rate 6–16% (Daly et al. (2000); Devanand et al. (1997)). This progression rate is much higher than the incidence of Alzheimer disease in the general population (i.e., 1% – 2% per year). Therefore, the diagnosis of VMD is of great importance as a potential marker for early intervention to reduce the risk of Alzheimer disease.

Neuroimaging methods that are potentially sensitive to VMD include magnetic-resonance (MR) examination (Convit et al. (1997); Killiany et al. (2000)) and positron emission tomography (PET) (De Santi et al. (2001)).

There exists extensive research on using structural MR to differentiate people with MCI or VMD from normal elderly individuals. In many of these studies, data analysis included two components: the first step was feature extraction, in which researchers extract relevant features, such as regional brain volumes or regional gray-matter volumes, from MR images; the second step was the design of a diagnostic model that predicts whether or not a subject has MCI or VMD, based on the extracted features.

The design of an optimal diagnostic model for this purpose is an open problem. A computer scientist considers this problem to be a classifier-induction problem. Computer scientists have proposed many machine-learning (i.e., data-driven) algorithms to generate high-performance classifiers, or diagnostic models. Such approaches include decision trees, support vector machines, and artificial neural networks. A difficult diagnostic problem, such as the detection of VMD based on image data, provides an opportunity for clinicians to collaborate with computer scientists as they use these classifier-induction algorithms to generate novel diagnostic models.

Many studies have centered on the generation of a diagnostic model to differentiate individuals with VMD (as defined by CDR = 0.5) from normal elderly controls, based on MR volumetry (Killiany et al. (2000); Pennanen et al. (2004); Wolf et al. (2004); Jauhiainen et al. (2008)). Discrimination accuracy—that is, the accuracy resulting from applying the derived diagnostic model to the same data that were used to generate the model—has typically been in the range of 66–86%. Most of these studies used region-of-interest (ROI)-based approaches. For example, Pennanen et al. achieved discrimination accuracy of 65.9% when they used entorhinal cortex as the neuroanatomic marker, and discriminant analysis with an enter method as the classification approach (Pennanen et al. (2004)). More recently, Jauhiainen et al. reported discrimination accuracy of 85.7% between subjects with CDR = 0.5 and controls, also using entorhinal cortex and discriminant analysis (Jauhiainen et al. (2008)).

The two most widely used methods for generating a diagnostic model for VMD have been discriminant analysis (Pennanen et al. (2004); Jauhiainen et al. (2008)) and logistic regression (Wolf et al. (2004)), both of which are standard statistical methods. In contrast, machine-learning approaches to classification have not had much attention in this domain. However, in many applications, machine-learning algorithms achieve higher accuracy than discriminant analysis or logistic regression (Duda et al. (2001)). These machine-learning methods have the potential to complement existing statistical approaches.

To determine whether machine-learning algorithms could contribute to the effort to develop an accurate VMD classification model, we applied seven statistical and machine-learning algorithms to derive diagnostic models that differentiate VMD from normal elderly controls. The five machine-learning methods are: naïve Bayes, Bayesian-network classifier with inverse tree structure (BNCIT), decision tree, support vector machine (SVM), and multiple-layer perceptrons (MLP) (a form of neural network). We compared these approaches to two statistical methods: discriminant analysis and logistic regression.

In our evaluation, we focused on the generalizability, as well as the discrimination accuracy, of each diagnostic model. Generalizability, a model’s ability to correctly classify a future sample from the same population, is a crucial characteristic of a diagnostic model, in that it directly bears on the utility of applying a diagnostic model in the clinic. The discrimination accuracy reported in (Killiany et al. (2000); Pennanen et al. (2004); Wolf et al. (2004); Jauhiainen et al. (2008)) may not support model generalizability. Discrimination accuracy is an optimistic estimate of model generalizability, that is, it is biased. We can obtain an unbiased estimate of generalizability by applying the diagnostic model to an independent data set acquired from the same population. Toward this end, we employed a training data set consisting of 83 subjects, and an independent evaluation data set obtained from 30 additional subjects.

To summarize, our goal herein is to evaluate and compare comprehensively machine-learning and statistical methods for the diagnosis of VMD based on structural MR data. We hope that our findings will help clinicians, statisticians, and computer scientists design an optimal MR-based diagnostic model for very mild dementia.

2 Materials

We obtained data from two VMD studies to evaluate the seven approaches; we call these data sets VMD_train and VMD_test. We applied each classifier-generation algorithm to VMD_train, and obtained a diagnostic model; we then assessed that model’s performance based on VMD_test.

VMD_train included 83 elderly individuals recruited from the registry of the Washington University Alzheimer Disease Research Center (Head et al. (2005)). These individuals were right-handed and English-speaking. They had been screened for neurologic illness, current depression, head injury, and use of psychoactive medications that could cause cognitive impairment. These participants were assessed with the Washington University Clinical Dementia Rating (Morris (1993)). The Washington University CDR is a validated, interview-based measure that examines a participant’s abilities in memory, orientation, problem solving and judgment, community affairs and functions in the home, and hobbies and personal care. The presence of VMD was defined as CDR = 0.5; subjects with CDR = 0 were normal elderly individuals. Subjects with CDR = 0.5 manifested dementia of Alzheimer type (DAT); that is, these people suffered from changes in memory and cognitive ability. For subjects with CDR = 0.5, exclusion criteria included dementia other than DAT (e.g., cerebrovascular disease and Parkinson disease). The clinical distinction between subjects with CDR = 0 and those with CDR = 0.5 has been validated by neuropathological examination (Morris et al. (2001)).

VMD_train contained 33 VMD subjects and 50 controls. The T1-weighed structural MR scan of each subject was acquired using a Siemens 1.5-T Vision instrument (Erlangen, Germany), using a spoiled gradient-echo (MP-RAGE) sequence (repetition time 9.7 msec, echo time 4 msec, flip angle=10°, inversion time 20 msec, trigger delay 200 msec). The voxel size for these images was 1 × 1 mm, with slice thickness of 1.25 mm. The raw data are available from the National fMRI Data Center (http://www.fmridc.org), with access number 2-2004-1168x.

The second data set, VMD_test, consisted of 30 elderly individuals recruited from the registry of the Washington University Alzheimer Disease Research Center (Marcus et al. (2007)). Subjects were excluded if they had neurologic, psychiatric, or mental illness that may cause dementia. These individuals were right-handed and English-speaking. Exclusion criteria included dementia other than DAT. As with subjects in VMD_train, the presence of VMD in VMD_test subjects was determined using CDR: CDR = 0 identified normal controls, and CDR = 0.5 identified VMD subjects.

Of the 30 subjects in VMD_test, 17 were nondemented controls and 13 had VMD. These 30 subjects were a subset of the subjects described in (Marcus et al. (2007)). We constructed VMD_test based on three criteria: 1) VMD_train and VMD_test must be gender- and age-matched. 2) The proportions of subjects with VMD in VMD_train and VMD_test must be comparable. 3) The numbers of subjects in VMD_train and VMD_test are approximately 2:1, following the standard practice in the machine-learning community.

The VMD_test subjects were evaluated with a T1-weighed gradient-echo (MP-RAGE) structural-MR examination (repetition time 9.7 msec, echo time 4 msec, flip angle=10°, inversion time 20 msec, trigger delay 200 msec), using a Siemens 1.5-T Vision instrument (Erlangen, Germany).

3 Methods

3.1 Image Processing

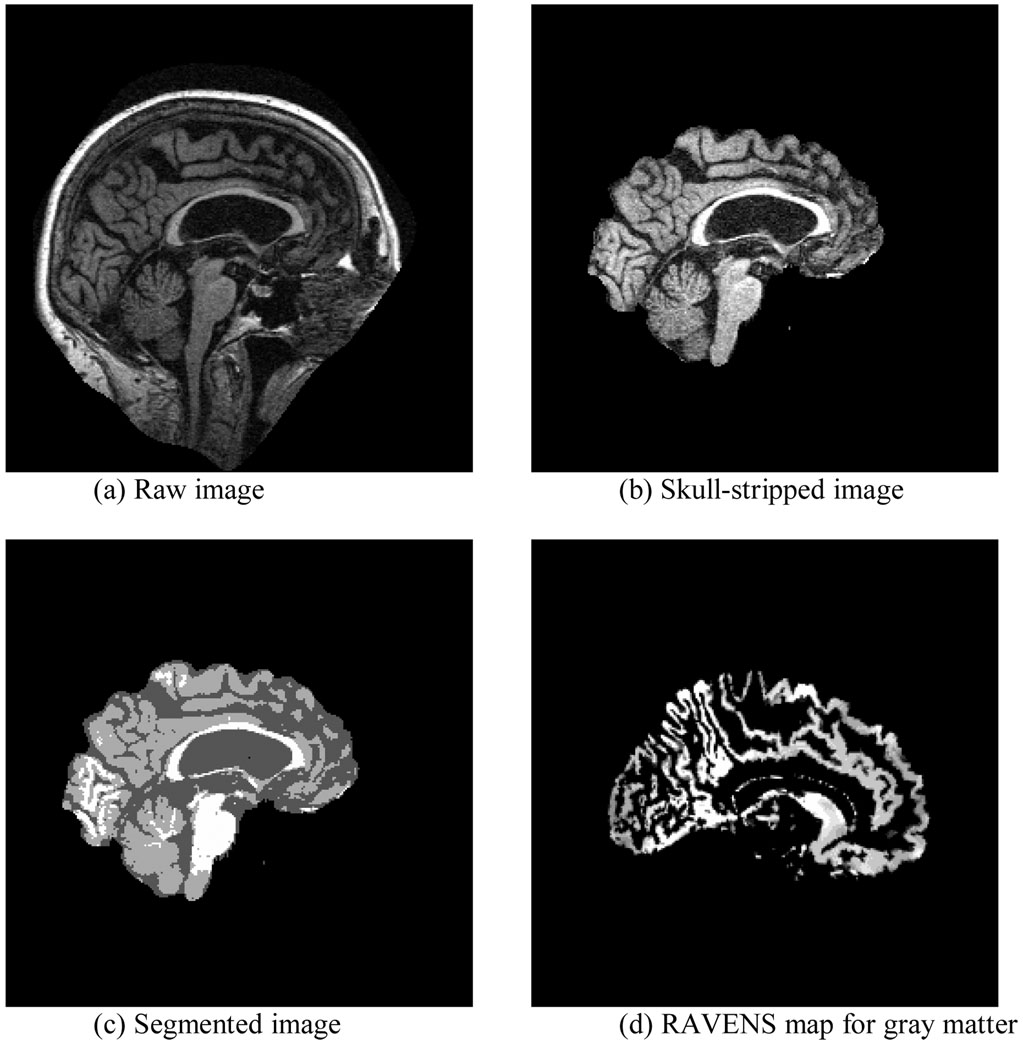
As shown in Figure 1, our image-processing pipeline consisted of four steps: skull stripping, segmentation, spatial normalization, and RAVENS (Regional Analysis of Volumes Embedded in Stereotaxic Space) analysis. In the skull-stripping step, we first used the brain extraction tool (Image Analysis Group, FMRIB, Oxford, UK) to remove the skull; we then manually edited the resulting image to remove residual non-brain tissue. We then used FMRIB’s automated segmentation tool (Image Analysis Group, FM-RIB, Oxford, UK) to segment the brain volume into gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF). After segmentation, we normalized each subject’s MR volume to a common stereotaxic space, namely, the MNI Jakob template (Kabani et al. (1998)); we used HAMMER (Hierarchical Attribute Matching Mechanism for Elastic Registration) (Shen and Davatzikos (2002)) for image registration. Finally, we performed RAVENS analysis (Goldszal et al. (1998)) of the deformation field generated by HAMMER to generate RAVENS maps. A subject’s RAVENS map is a density map whose voxel values represent tissue-specific volumetric measurements. The volume of an anatomic structure in a subject’s image is equal to the integral of voxel intensity within this structure in its RAVENS map. RAVENS maps are defined on the template space; therefore, they are spatially comparable across subjects. We used these RAVENS maps to compute the gray-matter volume of each Jakob atlas structure. To correct for head size, we normalized each atlas structure’s GM volume to total brain volume. This image-processing pipeline is identical to that used in our previous morphometric study of VMD (Chen and Herskovits (2006)).

Figure 1.

The image-processing pipeline.

3.2 Machine-Learning and Statistical Algorithms to Generate Diagnostic Models

A diagnostic model includes two components: the structural form of the model, and the corresponding model parameters. Any model-generation method must estimate both components. Let R_i denote the GM volume of brain region (atlas structure) i. For an atlas containing p atlas structures, we denote the p-dimensional feature vector as R: R = {R₁, …, R_p}. The goal of classification is to generate a funtion g that maps the p-dimensional feature vector onto the binary outcome variable C, thereby predicting its value for a given case. That is, g : ℝ^p→ {0,1} predicts C by means of g(R).

The most important performance metric in evaluating a diagnostic model is the classification error rate. For a model g generated using training data D, the error rate, ε[g], is the probability that subsequent classification will be incorrect. That is, ε[g] = Pr(g(R) ≠ C | D = d) = E[|C–g(R)| | d], where the expectation is taken of the distribution of (R, C), with fixed training set d.

In general, the distribution (R, C) is unknown, so we must estimate ε[g]; we can do so using any of several approaches. First, we can apply g to the training data D and tally correctly classified and mislabeled cases, from which we compute discrimination error ε_d[g]. However, ε_d[g] is a biased estimate of ε[g], in that it suffers from model-overfitting. In overfitting, a model is not only modeling the variation we observe in the population, but also the variation due to noise. Therefore, a model with poor ε[g] may achieve high ε_d[g]; that is, the model generalizes poorly.

A second approach estimating ε[g] is k-fold cross-validation: we partition D into k data sets. In each iteration, a group of subjects is left out as test data, and a model is generated based on the remaining subjects, and evaluated using the test data. The cross-validation error rate, ε_cv[g], is the average error rate across all iterations of this process. ε_cv[g] is an unbiased estimate of ε[g], and is therefore superior to ε_d[g]. The third approach, called external validation, is the most stringent approach; it is based on an independent test sample acquired from the same population used to generate the classifier. We denote this external-validation estimate of ε[g] as ε_ev[g].

There are three fundamental approaches to solving the classification problem, including the discriminative approach, the regression approach, and the generative approach. The discriminative approach centers on modeling directly the decision boundaries of a classification problem (i.e., the mapping from input R to output C). Discriminant analysis, decision trees, support vector machines (SVMs), and multiple-layer perceptrons (MLPs) are among the most widely used methods that are based on the discriminative approach. The regression approach explicitly models the class posterior probability Pr(C|R), and classifies based on maximum a posteriori calculations. For classification of VMD, logistic regression is the most common example of this approach. The generative approach centers on modeling the class conditional distribution Pr(R|C); Pr(R|C) describes how data are distributed for each class. Combining Pr(R|C) and an estimate of the prior distribution (i.e., prevalence) of C, π(C), we can compute the posterior distribution of C. The prediction of C is then based on maximum a posteriori calculations. Bayesian-network classifiers are a common example of the generative approach. We examine seven different approaches—Bayesian-network classifiers (naïve Bayes and BNCIT), discriminant analysis, decision tree, SVM, MLP, and logistic regression—for generating diagnostic models.

We provide brief descriptions of these approaches in the Appendix Section. We implemented these methods as follows:

Naïve Bayes

We implemented a naïve Bayes classifier based on the BN toolbox in Matlab (Kevin (2001)). Bayesian-network classifiers are based on categorical variables. We used the method described in (Fayyad and Irani (1993)) to discretize each continuous R_i into a binary variable.

BNCIT

We used the BN Toolbox in Matlab to implement BNCIT.

Discriminant analysis

We used discriminant analysis with the enter method (PROC stepdisc and PROC discrim), as implemented in SAS (SAS Institute, Raleigh, NC). In PROC stepdisc, we specified a significance level of 0.05.

Decision tree

We used the C4.5 algorithm (Quinlan (1993)), implemented in the machine-learning software package Weka (http://www.cs.waikato.ac.nz/ml/weka/), to generate a pruned decision tree.

SVM

We used the sequential minimal optimization (SMO) algorithm (Platt (1998)), implemented in Weka, to generate SVMs. We compared two kernels: polynomial and radial basis function (RBF). Weka tuned kernel parameters based on 10-fold cross validation in VMD _train. We found that the polynomial kernel resulted in better classification performance than the RBF kernel; cross validation also determined that the optimal degree of the polynomial kernel was 1 (i.e., a linear SVM). Therefore, we used a linear SVM to generate diagnostic models. Weka also optimized the complexity parameter in SVM based on 10-fold cross validation of VMD_train.

MLP

We used the multiple layer perceptron implemented in Weka. This MLP model had one hidden layer and logistic output. Parameters were optimized with weight decay. The number of nodes in the hidden layer, weight decay, and the number of training cycles were selected based on 10-fold cross-validation of VMD_train.

Logistic regression

We used PROC Logistic in SAS to generate a logistic-regression model, with forward selection and significance level of 0.05 to enter variables into the model.

Regardless of the particular approach to generating a diagnostic model for VMD, the set of candidate structures R may contain more variables than the number of subjects, leading to undersampling. In fact, the total number of structures available for model generation in the MNI Jakob template is 91, whereas the training data were acquired from 83 subjects. In this case, if the diagnostic-model–generation method does not incorporate feature selection or regularization (Hastie et al. (2009)), the resulting diagnostic model is prone to overfitting, and parameter estimation becomes difficult. One approach to preventing overfitting in the setting of undersampling is to select a subset of features (i.e., atlas structures) to train the classifier. Methods such as BNCIT have an embedded feature-selection mechanism (Chen and Herskovits (2005)). However, methods such as MLP require a separate, external feature-selection step. Based on Braak-and-Braak staging (Braak and Braak (1991)), we chose to analyze the following 12 structures in or near the medial temporal lobe (MTL): left/right hippocampus, left/right entorhinal cortex, left/right parahippocampal gyrus, left/right perirhinal cortex, left/right thalamus, and left/right amygdala.

To summarize, our goal is to evaluate seven diagnostic-model–generation algorithms by first applying each to a training data set, VMD_train, and then using an independent data set, VMD_test, to evaluate the classification accuracy of the resulting model. To evaluate each classifier, we compute discrimination accuracy (1 – ε_d[g]), ten-fold cross-validation accuracy (1 - ε_cv[g]), and predictive power (1 - ε_ev[g]). We performed these steps for two experiments. In the first experiment, the predictor variables included all 91 atlas structures in the MNI atlas; in the second experiment, we restricted the predictor variables to those 12 MNI atlas structures in or near the MTL. We designed the second experiment to ameliorate the overfitting problem for classifiers without an embedded feature-selection mechanism.

3.3 Performance Comparison

For each experiment, we compared diagnostic models using two metrics: predictive power difference and triangular discrimination (Topsoe (2000)). Let ε* denote the lowest error rate on the external test data across all seven approaches. We can estimate the standard error of the error rate, denoted by σ, by computing $\sqrt{{\epsilon }^{*}(1-{\epsilon }^{*})/n}$, where n is the number of subjects in the test data set. If an algorithm has an error rate within λσ, we consider this algorithm’s performance to be close to the best. λ controls the level at which we will label the error rate of an algorithm as different from the lowest error rate. For the purposes of this evaluation, we set λ = 0.5.

The principal limitation of using predictive power for evaluation is that it provides little information about false-positive and false-negative errors. To address this limitation, we computed the triangular discrimination metric to measure the similarity between classifiers. Using external validation, each classifier generates a confusion matrix that can be represented in a vector form as [TP FN FP TN], where TP is the number of subjects having VMD and also classified as having VMD, FN is the number of VMD subjects labeled as normal, FP is the number of normal subjects classified as having VMD, and TN is the number of normal subjects labeled as normal. If we divide the confusion matrix by the total number of subjects in a study, the resulting matrix is an estimate of the joint distribution of actual and predicted labels. We can then compute the triangular discrimination metric to measure the similarity between two probability distributions. Triangular discrimination is defined as

$$\mathrm{\Delta }(P,Q)={\displaystyle \sum \frac{|p_i-q_i{|}^2}{p_i+q_i},}$$ (1)

where P and Q are two probability distributions. The significance of the triangular discrimination measure lies in the strong connection with Kullback-Leibler divergence (Topsoe (2000)). Kullback-Leibler divergence is one of the most widely used metrics to measure the similarity between two probability distributions; however, Kullback-Leibler divergence is non-symmetric, and is not a distance, whereas triangular discrimination is a symmetric distance function.

4 Results

4.1 Demographic Variables

Among the subjects in VMD_train, 60.1% (n = 50) were normal elderly adults, and 39.9% (n = 33) carried the VMD diagnosis. Subjects in the VMD group had a mean age of 77.2 years (SD = 5.8), and those in the control group had a mean age of 76.8 years (SD = 6.9). The two-sample t-test revealed no significant age difference between the two groups (p-value = 0.8). In the VMD group, 21 subjects were female and 12 were male, and in the control group, 36 subjects were female and 14 were male. There were no significant group differences in sex distributions (χ² p-value = 0.7).

For the VMD_test data set, 56.7% (n = 17) of subjects were normal elderly adults, and 43.3% (n = 13) had VMD. Subjects in the VMD group had a mean age of 75.7 years (SD = 8.3), and those in the control group had a mean age of 74.4 years (SD = 11.4). The two-sample t-test indicated that there was no significant difference in age between the two groups (p-value = 0.7). In the VMD group, 6 subjects were female and 7 were male. In the control group, 10 subjects were female and 7 were male. The χ² test indicated no significant difference in sex distributions (p-value = 0.5).

4.2 Diagnostic Models Generated from All Atlas Structures

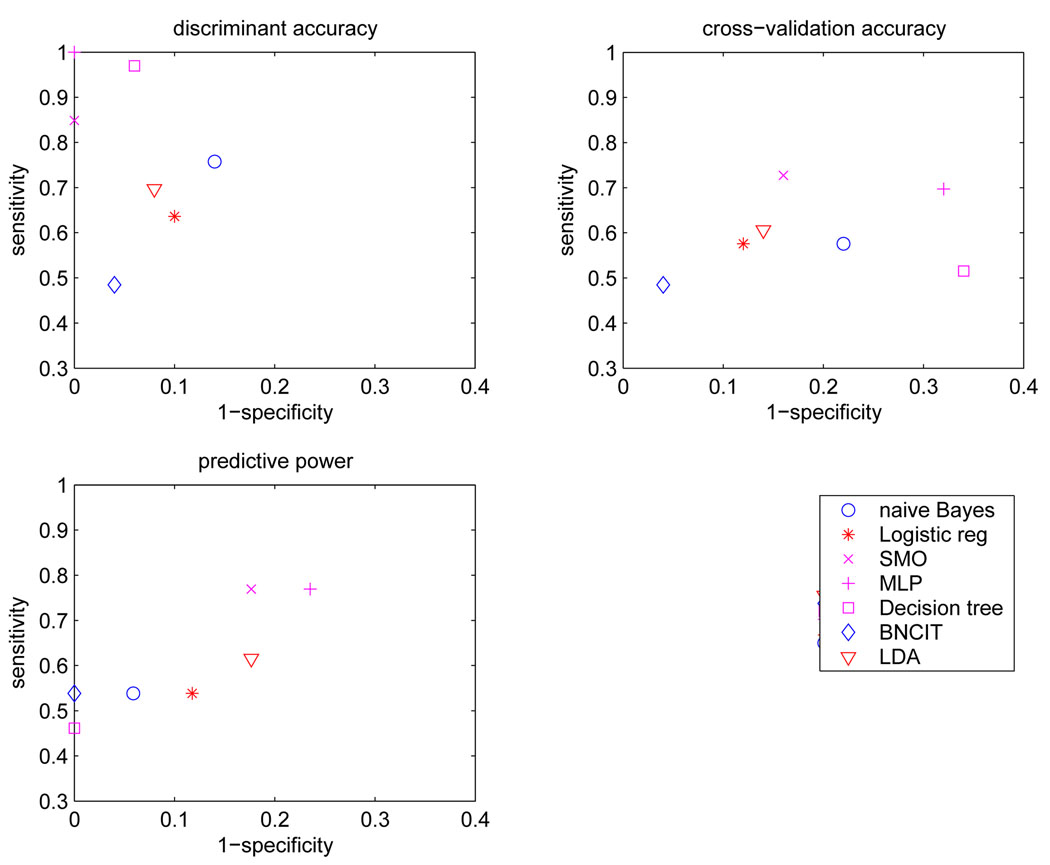
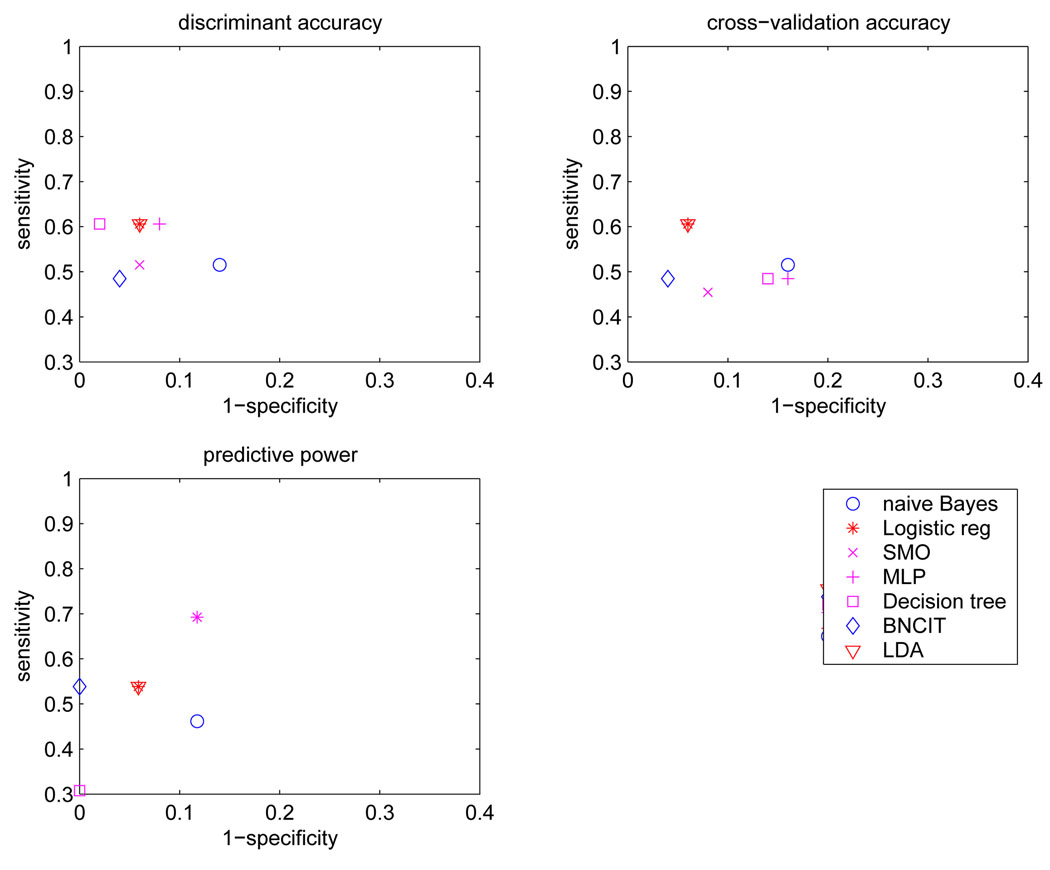
Table 1 lists discrimination accuracy, cross-validation accuracy, and predictive power for diagnostic models generated from all 91 atlas-structure variables. Figure 2 shows the corresponding sensitivity and specificity values.

Table 1.

Discrimination accuracy, cross-validation accuracy, and predictive power of different diagnostic models, based on all 91 atlas structures.

Method	discrimination accuracy	cross-validation accuracy	predictive power	structures included
BNCIT	77.1	77.1	80.0	RH
Naïve Bayes	81.9	69.9	76.7	All
Decision tree	95.1	57.8	76.7	RH, LPG, RSN, RNA, LC, LPG, RC
SVM	94.0	79.5	80.0	All
MLP	100	68.7	76.7	All
discriminant analysis	83.1	75.9	73.3	RH, LITG, RAG, RNA
Logistic regression	79.5	75.9	73.3	RH, LITG, RAG

RH - right hippocampus; LPG - left parahippocampal gyrus; RSN - right subthalamic nucleus; RNA - right nucleus accumbens; LC - left cuneus; LPG -left precentral gyrus; RC - right cuneus; LITG - left inferior temporal gyrus; RAG - right angular gyrus.

Figure 2.

Sensitivity and specificity for each diagnostic model based on all 91 atlas structures.

BNCIT, decision tree, discriminant analysis, and logistic regression generated descriptive diagnostic models. These methods selected a subset of structures, and the resulting models describe the relationships among the predictors and the outcome variable. In contrast, MLP, SVM, and naïve Bayes used all features. One cannot characterize the relationships among structures and C by examining the resulting models.

For BNCIT, the diagnostic model contained one predictor variable: the right hippocampus (RH). The conditional probabilities Pr(C|RH) are Pr(C = VMD|RH = atrophy) = 0.73, Pr(C = NC|RH = atrophy) = 0.27, Pr(C = VMD|RH = normal) = 0.15, and Pr(C = VMD|RH = normal) = 0.85.

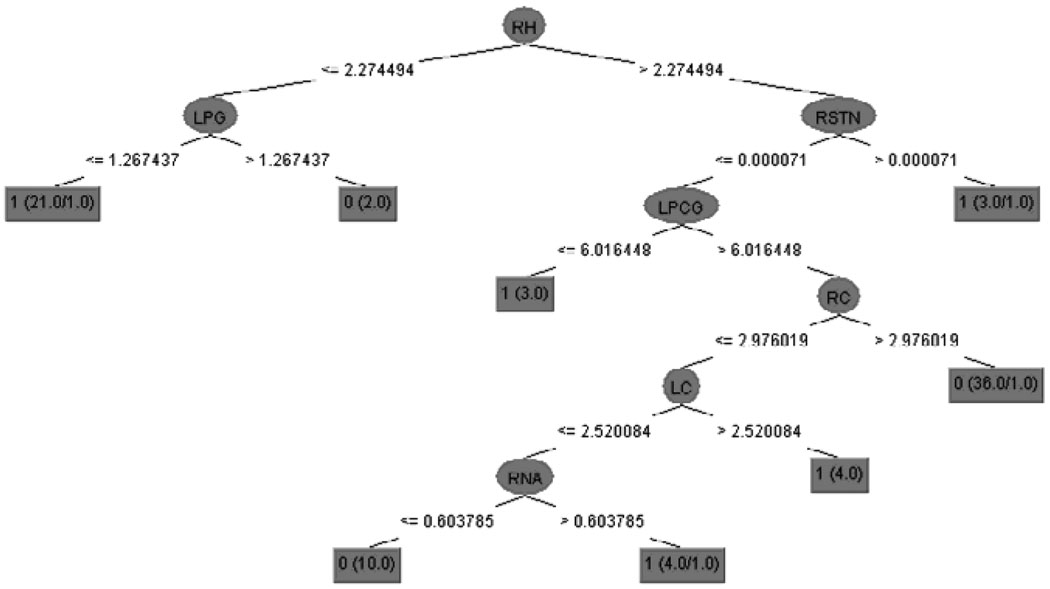
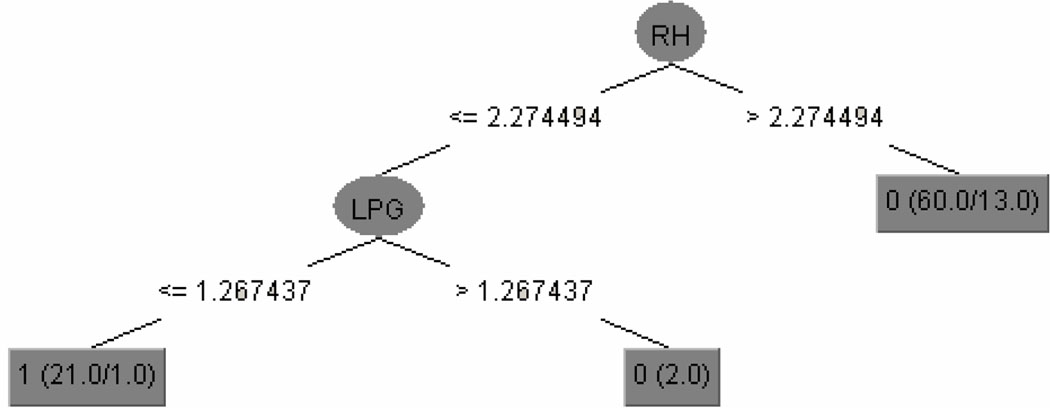
The decision-tree model is depicted in Figure 4. This tree has seven predictor variables: the right hippocampus, left parahippocampal gyrus, right subthalamic nucleus, right nucleus accumbens, left cuneus, left precentral gyrus, and right cuneus.

Figure 4.

The decision tree generated from all 91 atlas structures. RH - right hippocampus; LPG - left parahippocampal gyrus; RSTN - right subthalamic nucleus; RNA - right nucleus accumbens; LC - left cuneus; LPCG - left precentral gyrus; RC - right cuneus. Class label: 0 - normal control, 1 - VMD.

The models generated by discriminant analysis contain four predictor variables: the right hippocampus, left inferior temporal gyrus (LITG), right angular gyrus (RAG), and right nucleus accumbens (RNA). For normal controls, the discriminant function is

$$-172.8+24.2RH+11.9LITG+24.1RAG+36.1RNA;$$ (2)

for subjects with very mild dementia, the discriminant function is

$$-147.4+19.6RH+10.8LITG+22.5RAG+44.0RNA.$$ (3)

For logistic regression, three structures entered into the model: right hippocampus, left inferior temporal gyrus, and right angular gyrus. The estimated function was

$$\text{log}\frac{1-Pr(C=VMD|\mathbf{r})}{Pr(C=VMD|\mathbf{r})}=-26.77+1.43RAG+4.49RH+0.86LITG.$$ (4)

The Hosmer and Lemeshow goodness-of-fit test demonstrated that there was no lack of fit (p-value= 0.28).

Model sensitivities and specificities obtained using external validation are depicted in the lower left portion of Figure 2. The sensitivities of these diagnostic models were in the range [0.46 0.77], and the specificities were in [0.76 1.00]. BNCIT (sensitivity = 0.54, specificity = 1.00) and na¨ıve Bayes (sensitivity = 0.54, specificity = 0.94) were superior to logistic regression (sensitivity = 0.54, specificity = 0.88). SVM (sensitivity = 0.77, specificity = 0.82) was superior to discriminant analysis (sensitivity = 0.66, specificity = 0.82).

The smallest error rate ε* was 0.2, achieved by BNCIT and SVM. The standard error of the error rate was 0.08. The error rates for discriminant analysis and logistic regression were significantly higher than the smallest error rate (above half of the standard error of ε*).

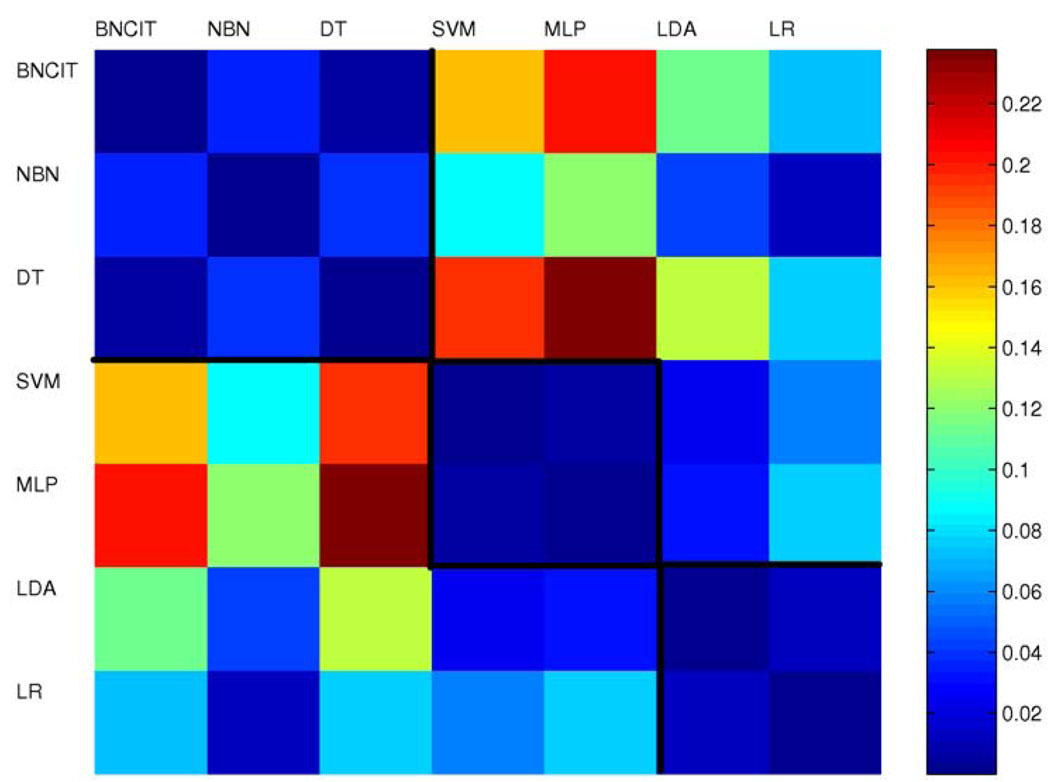
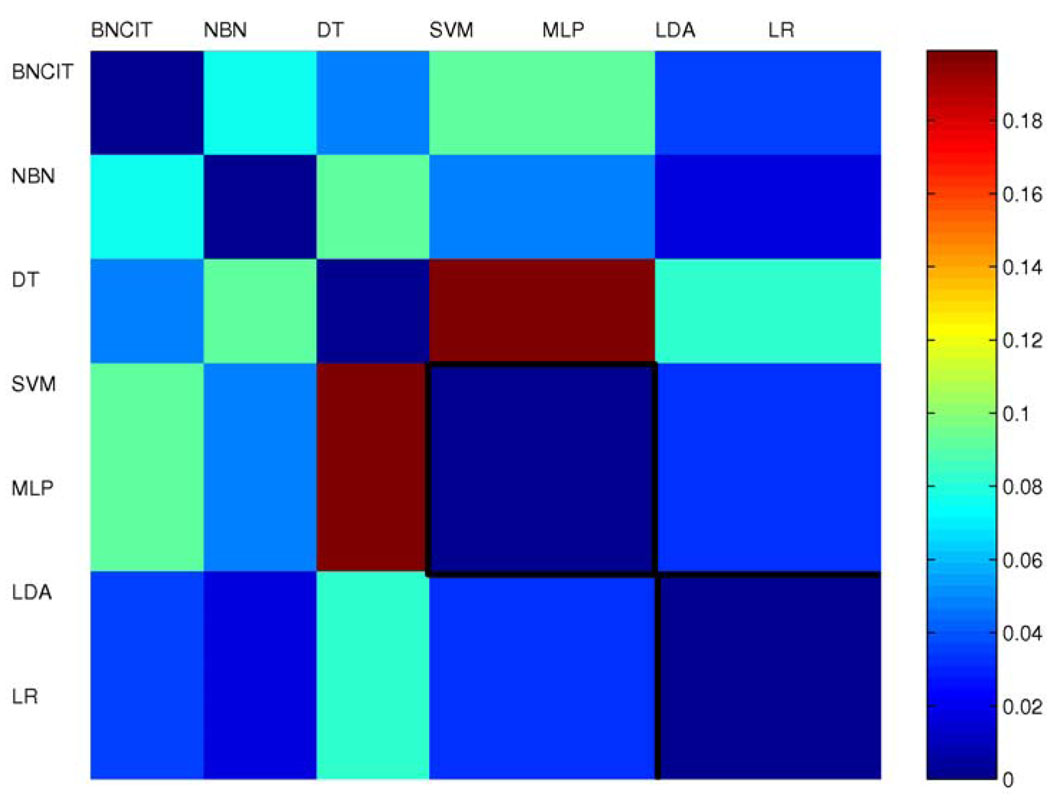
Figure 3 shows the triangular discrimination matrix for the seven diagnostic models. In the triangular discrimination matrix, each element represents the discrimination between two models. This matrix is symmetric (with diagonal terms equal to zero). The mean triangular discrimination value was 0.07.

Figure 3.

Triangular discrimination metrics for models generated from all 91 atlas structures.

4.3 Diagnostic Models Based on Structures Near or in the Medial Aspects of the Temporal Lobes

For each diagnostic model based on the 12 atlas-structure variables that are centered on or near the MTL, that model’s discrimination accuracy, cross-validation accuracy, and predictive power are listed in Table 2. The corresponding sensitivities and specificities are shown in Figure 5.

Table 2.

Discrimination accuracy, cross-validation accuracy, and predictive power of different diagnostic models that are based on structures primarily in the medial temporal lobe.

Method	discrimination accuracy	Cross-validation accuracy	predictive power	structure included
BNCIT	77.1	77.1	80.0	RH
Naïve Bayes	72.3	71.1	70.0	All
Decision tree	83.1	71.1	70.0	RH, LPG
SVM	77.1	73.5	80.0	All
MLP	79.5	69.9	80.0	All
discriminant analysis	80.7	80.7	76.7	RH
Logistic regression	80.7	80.7	76.7	RH

RH: right hippocampus; LPG: left parahip-pocampal gyrus.

Figure 5.

Sensitivity and specificity of each diagnostic model computed from structures primarily in the medial aspect of the temporal lobe.

The diagnostic model generated by BNCIT is identical to that generated from all 91 structures. There is one predictor variable: the right hippocampus.

The decision-tree approach generated the model shown in Figure 7. This model has two predictor variables: the right hippocampus and the left parahippocampal gyrus.

Figure 7.

The decision tree generated from structures primarily in the medial aspect of the temporal lobe. RH - right hippocampus; LPG - left parahippocampal gyrus. Class label: 0 - normal controls, 1 - VMD.

Discriminant analysis generated a model involving one predictor variable: the right hippocampus. For normal controls, the discriminant function is

$$-29.68+23.05RH;$$ (5)

for subjects with VMD, the discriminant function is

$$-20.66+19.23RH.$$ (6)

For logistic regression, one structure—the right hippocampus—entered into the diagnostic model. The estimated function is

$$\text{log}\frac{1-Pr(C=VMD|\mathbf{r})}{Pr(C=VMD|\mathbf{r})}=-11.19+4.78RH.$$ (7)

Hosmer and Lemeshow goodness-of-fit test shows that there was no lack of fit (p-value = 0.66).

Model sensitivities and specificities obtained using external validation are shown in the lower left portion of Figure 5. The sensitivities of these diagnostic models were in the range [0.30 0.70], and the specificities were in [0.88 1.00]. BNCIT (sensitivity = 0.54, specificity = 1.00) was superior to both discriminant analysis and logistic regression (sensitivity = 0.54, specificity = 0.94).

The smallest error rate ε* was 0.2, achieved by BNCIT, SVM, and MLP. The standard error of the error rate was 0.08. The error rates of discriminant analysis and logistic regression were not significantly different from ε *, while those of Naïve Bayes and decision tree were significantly greater than ε* (greater than half of the standard error of ε*).

Figure 6 shows the triangular discrimination matrix for all seven diagnostic models based on the 12 structure variables that are centered on or near the medial aspects of the temporal lobes. The mean triangular discrimination value was 0.05.

Figure 6.

Triangular discrimination metrics for models generated from structures primarily in the medial aspect of the temporal lobe.

5 Conclusion and Discussions

We have presented a comprehensive evaluation and comparison of machine-learning and statistical methods for the diagnosis of VMD based on structural MR data, as well as investigations into model generalizability. We quantified classification-performance differences among diagnostic models as error rates and triangular-discrimination metrics, based on an independent test-data set.

5.1 Model-Performance Comparison

We evaluated seven diagnostic-model–generation algorithms, using them to construct diagnostic models for distinguishing VMD from normal control subjects, based on structural MR images. We found that, relative to the diagnostic models generated by discriminant analysis and logistic regression, the diagnostic models generated by BNCIT and SVM achieved greater predictive power. Based on Table 1, when we supply these algorithms with all 91 MNI atlas structures, the predictive power of BNCIT and SVM are approximately 7 percentage points higher than those of discriminant analysis and logistic regression. The error rates of discriminant analysis and logistic regression are significantly higher than the error rates of BNCIT and SVM (above half of the standard error of error rate of BNCIT and SVM). When the structures are restricted to the 12 structures near or in MTL(Table 2), predictive power for discriminant analysis and logistic regression improve. The accuracies of SVM and BNCIT are 3 percentage points higher than those of discriminant analysis and logistic regression. The error rate differences between discriminant analysis and logistic regression, and BNCIT and SVM are not significant.

For the purpose of comparing diagnostic-model performance, the triangular discrimination metric, which differentiates two types of errors, provides more information than accuracy. In particular, two diagnostic models can have the same error rate, yet have triangular discrimination far from zero. For example, for models based on all 91 structures, BNCIT and SVM have the same error rate; however, the triangular discrimination metric between these two approaches is 0.16, which is significantly different from zero, because SVM has fewer type II errors, while BNCIT has fewer type I errors.

For models based on all 91 structures (Figure 3), intuitively, the diagnostic models can be organized into three groups. Group 1 includes BNCIT, na¨ıve Bayes, and decision tree; group 2 includes SVM and MLP; and group 3 includes discriminant analysis and logistic regression. Within each group, triangular discrimination differences are small. That is, diagnostic models within the same group tend to have similar behavior. For models based on structure near or in MTL (Figure 6), SVM and MLP remain in the same group, as do discriminant analysis and logistic regression. However, BNCIT, Na¨ıve Bayes, and decision tree no longer form a group. It is clear that, for models generated either from all 91 structures or from structures near or in the MTL, the triangular discrimination metric demonstrates significant performance differences across models (non-zero triangular discrimination).

We found that SVM and MLP had similar classification performances, which is expected. Both SVM and MLP are margin-based classifiers, and can model non-linear decision boundaries (Hastie et al. (2009)). We also found that discriminant analysis and logistic regression had similar classification performances, which has long been recognized by statisticians (Hastie et al. (2009)).

5.2 Model generalizability

We found that there was a mismatch between predictive power and discrimination accuracy. We found that a diagnostic model’s discrimination accuracy tended to exceed its predictive power. The discrepancy between discrimination accuracy and predictive power is particularly apparent in MLP and SVM, which have been designed to model complex nonlinear decision boundaries. When using all structures, the discrimination accuracies of MLP and SVM were 100% and 94%, respectively. However, the predictive power of these models were 76.7% and 80.0%, respectively. These findings suggest that we should be cautious in interpreting discrimination accuracy.

In many applications, an independent test set is not available; in this case, we must estimate the model error rate using the training data. To do so, we can use cross-validation to estimate model error rate. Let d_dis–preddenote the absolute difference between discrimination accuracy and predictive power, and let d_cv–pred denote the absolute difference between cross-validation accuracy and predictive power. For diagnostic models generated from all structures, the mean d_dis–pred was 11.4 (SD = 7.5), while the mean d_cv–pred was 5.7 (SD = 5.4). The Mann-Whitney test indicates that d_dis–pred is greater than d_cv–pred (p-value = 0.05). Based on these results, researchers should consider reporting cross-validation accuracy in studies of diagnostic models, instead of classification accuracy. Although this finding has been known by computer scientists, it has not received much attention in studies of diagnostic models for VMD. Most of the studies in (Killiany et al. (2000); Pennanen et al. (2004); Wolf et al. (2004); Jauhiainen et al. (2008)) reported discrimination accuracy only. In other neuroimaging studies using machine-learning methods (Kawasaki et al. (2007); Kloppel et al. (2008); Davatzikos et al. (41)), investigators recognized the limitations of classification accuracy, and reported cross-validation accuracy.

5.3 Model Interpretability

We found that parsimonious models have comparable predictive power to more-complicated models. In particular, BNCIT generated a simple model with one structure-variable predictor, from both the 91- and 12-structure training-data sets. This diagnostic model achieved 80.0% predictive power in both Table 1 and Table 2. This predictive power is the best among models from all structures and the best among models generated from structures primarily in MTL. Logistic regression generated a model involving 3 predictors when the training data contained all structures, but the number of predictors was reduced to 1 when the training data contained structures primarily in MTL. The model with 1 predictor had better predictive power than that with 3 predictors, suggesting that some predictor variables in the complex model may not contribute substantially to predictive power.

Data-analysis methods that incorporate feature selection can automatically identify neuroanatomic markers for very mild dementia. This is not a new finding, having already been reported in studies such as Davatzikos et al. (2008). Of the approaches considered in this study, BNCIT, decision tree, discriminant analysis, and logistic regression have this feature. We found that the neuroanatomic markers identified by different approaches were consistent. The most stable neuroanatomic marker is the right hippocampus, which is always the first structure entered into the model. When we restrict structures to be primarily in MTL, the right hippocampus is the only predictor in models generated by BNCIT, discriminant analysis, and logistic regression. Other studies also have shown consistently that hippocampal volume reduction is a sensitive marker for VMD (Convit et al. (1997); Killiany et al. (2000); Wolf et al. (2001); Du et al. (2001); Chen and Herskovits (2006)).

5.4 Recommendations for Selecting Diagnostic Model Generation Methods

We provide recommendations for studies that focus on building diagnostic models for VMD, based on model performance and interpretability.

Model performance

1) If we focus on the classification error rate, SVM and BNCIT would appear to be superior approaches. However, error rates for discriminant analysis and logistic regression are close to those of SVM and BNCIT, if we can pre-select a subset of structures. 2) If the goal is to minimize a specific type of error (i.e., type I or II), BNCIT and decision tree tend to have low type I error rates, and SVM and MLP tend to have low type II errors. Naïve Bayes, discriminant analysis and logistic regression are intermediate.

Model interpretability

If model interpretability is an important factor, logistic regression, discriminant analysis, BNCIT, and decision tree are declarative, and have embedded feature-selection mechanisms. The models generated by these methods are straightforward to interpret.

One recommendation for studies focusing on building diagnostic models for VMD is to use different model-generation approaches. If VMD can be consistently differentiated from normal controls across diagnostic models, this suggests that the predictors (i.e., structure volumes) are informative about group membership, regardless of what kind of functional form the diagnostic model takes. This stability is a desired characteristic.

Note that in this paper, we have not focused on computational cost, because studies focusing on building diagnostic models for VMD often involve a limited number of samples. For small sample-size data, all seven model-generation methods generate models in a reasonable time period. Usually Na¨ıve Bayes, BNCIT, decision tree, discriminant analysis, and logistic regression take less than 1 minute to generate a diagnostic model, using a workstation with a 2.6 GHz CPU and 1 Gb memory. Using the same machine, SVM with parameter tuning and kernel selection requires approximately half an hour, and MLP with parameter tuning requires several hours, to generate a model.

5.5 Limitations and future works

We have focused on building diagnostic models for VMD based on neuroimaging data, extending the results presented by (Killiany et al. (2000); Pennanen et al. (2004); Wolf et al. (2004); Jauhiainen et al. (2008)). The importance of such studies is twofold. First, these diagnostic models can help clinicians identify subjects at high risk for VMD. If an elderly person does not have dementia (as determined based on neuropsychological tests), but does manifest the morphometric pattern for VMD, it might be advisable to closely monitor that patient’s neurocognitive status. Second, diagnostic models can identify neuroanatomic markers for VMD. Future clinical trials can use these neuroanatomic markers as a component of outcome measurement, or to target therapy. These neuroanatomic markers can also be used to generate new hypotheses for dementia research.

Although cross-sectional studies for VMD are important, such studies do have major limitations. The principal limitation of cross-sectional studies is that they do not address the temporal course of VMD. Ideally, we should study a normal aging population, and generate predictive models for the development of amnestic VMD, with the goal being to predict outcome. Toward this end, we plan to generate models to predict subsequent cognitive decline in subjects with VMD, based on their baseline neuroimaging data.

One limitation of our analysis is that we did not include white matter lesions (WML) in our analysis. In both VMD_train and VMD_test, subjects with CDR = 0.5 may manifest white-matter lesions, including deep WML, periventricular WML, and infarct-like lesions (Burns et al. (2005)). Usually, the volume of WML is very small relative to total WM volume. However, these WML may affect the tissue-segmentation step and introduce additional variability into regional-volume calculations, which could, in turn, compromise classification.

In this study, we generated diagnostic models from small sample-size data, to ensure that our analyses were based on sample sizes comparable to those reported in recent studies of structural-MR–based diagnostic models for VMD (Killiany et al. (2000); Pennanen et al. (2004); Wolf et al. (2004); Jauhiainen et al. (2008)). However, there are a few relatively large-scale studies, such as the Alzheimer Disease Neuroimaging Initiative (ADNI) (Mueller et al. (2006)), in which 200 healthy elderly subjects and 400 subjects who have MCI were recruited between June 2005 and June 2006. Such large sample sizes ameliorate the overfitting problem. The diagnostic models generated from large samples by machine-learning and statistical algorithms behave differently from those generated from small samples. We plan to extend our current work to evaluate the performance of these diagnostic-model–generation algorithms for large sample-size data.

Having access to data from studies with a range of sample sizes will allow us to evaluate classifiers’ performances as a function sample size, different feature-selection methods, and classifier stability.

Appendix

Statistical and machine-learning algorithms

Bayesian-network classifiers (Friedman et al. (1997)) are based on a probabilistic graphical model called a Bayesian network (BN). A BN model’s structure is a directed acyclic graph, and its parameters are conditional probabilities. A BN can model a joint probability distribution compactly; that is, a BN can represent a full joint probability distribution with fewer parameters than listing all joint probabilities in the full joint distribution.

The structure of a BN encodes a set of conditional-independence statements. BNs support efficient inference for classification of new samples. In a BN classifier, we first model the joint distribution of (R, C). For a new case, consisting of observations of R, we can infer C (i.e., compute P(C|R)) using readily available BN-inference algorithms (Cowell (1998)).

To reduce the computational complexity of data mining, researchers have evaluated BNs that are restricted in terms of model structure. The naïve Bayes classifier is a widely used BN classifier; this architecture is based on the assumption that all features are conditionally independent given the value of C; that is, Pr(R|C = c) = Π_i Pr(R_i|C = c). Surprisingly, researchers have found this class of models may classify accurately even when this conditional-independence assumption is not met. We use Bayes’ theorem to obtain the prediction for C:

$$Pr(C=c|\mathbf{R})=Pr(C=c){\displaystyle \prod _{i}Pr(R_i|C=c).}$$ (8)

Another category of BN classifier is the Bayesian-network classifier with inverse-tree structure (BNCIT) (Chen and Herskovits (2005)). A key concept of Bayesian networks is that of the Markov blanket. Let I(X;Y|Z) represent the statement that X is conditionally independent of Y given Z. The Markov blanket of node X, mb(X), is defined as the smallest set such that I(X;Y | mb(X)) for all Y ϵ V|{Y, mb(X)} (Pearl (1988)), where V is the set of all variables. If we assume that the training data were generated by a BN, and if we let mb*(C) denote the Markov blanket of C in this BN, then knowing the states of variables outside mb*(C) will not improve the predictive accuracy of X (Friedman et al. (1997)). However, it is computationally intensive to determine mb*(C); in general, detecting this model would require an exhaustive search of a vast number of candidate BN models. To reduce the computational burden of computing mb*(C), BNCIT was designed to identify a subset of mb* (C). Let A denote this subset: subsequent prediction of C for new cases is based on computing Pr(C|A), which can be inferred from the generated BN.

Discriminant analysis (Duda et al. (2001)) assumes that each group is multivariate normal with respect to the structure variables; in the context of our evaluation, the distribution of volumes for the atlas variables follows a multivariate-normal distribution. If we encode C as {1, 2}, the discriminant functions are as follows:

$$g_i(\mathbf{r})=-\frac{1}{2}{(\mathbf{r}-{\mu }_i)}^T{\displaystyle {\sum }_i^{-1}(\mathbf{r}-{\mu }_i)-\frac{p}{2}\text{log}|{\displaystyle {\sum }_i{|}^{1/2}-\text{log}{\pi }_i,}}$$ (9)

where i = {1, 2}, µ_i is the mean vector, Σ_i is the covariance matrix, and π_i is the prior probability of C = i. We estimate µ_i and Σ_i from training data, and we compute π_i from the context. The decision boundary between classes 1 and 2 is defined by solving g₁(r) − g₂(r) = 0.

A decision tree is a tree-structured prediction method (Quinlan (1986)) in which each node in the tree has either zero or two outgoing edges. If a node has no edge, it is assigned a class-membership label; otherwise that node is associated with a predictor R_i, called a splitting attribute. Decision trees are based on the assumption that g(R) is a piecewise-constant function, in which splits on the individual feature axes define the individual components.

A support vector machine (SVM) is a classifier that directly maximizes the margin, that is, the space between the decision boundary and the closest points from each of the classes (Vapnik (1995)). If we code C as {−1, +1}, the SVM optimization problem in Wolfe dual form is

$$\underset{\alpha }{\text{max}}W(\alpha )=\underset{\alpha }{\text{max}}({\displaystyle \sum _{i=1}^m{\alpha }_i-\frac{1}{2}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^m{\alpha }_i{\alpha }_j{c}_i{c}_j{\mathbf{R}}_i^{\prime }{\mathbf{R}}_j),}}}$$ (10)

with constraints

$${\alpha }_i\ge 0;{\displaystyle \sum _{i=1}^m{\alpha }_i{c}_i=0,}$$

where α_i is a parameter associated with case i. Usually, most of the {α_i} parameters will be zero. The cases with non-zero α are called support vectors (SV). The prediction of C is based only on support vectors. The linear SVM described in Equation (10) can be extended to model a nonlinear decision boundary using kernel methods. A widely used approach is to replace ${\mathbf{R}}_i^{\prime }{\mathbf{R}}_j$ by polynomials $K({\mathbf{R}}_i,{\mathbf{R}}_j)={(1+{\mathbf{R}}_i^{\prime }{\mathbf{R}}_j)}^c$. The prediction of C is based on

$$g(\mathbf{R})=sgn({\displaystyle \sum _{i\in SV}{\alpha }_{i}K({\mathbf{R}}_i,{\mathbf{R}}_j))}$$ (11)

where sgn is the sign operator.

A multi-layer perceptron (MLP) is a neural-network model (Duda et al. (2001)). The input layer of a MLP consists of the predictor variables {R_i}, the output layer is C, and there are several hidden layers. The most widely used MLP architecture has one hidden layer. The prediction of C is based on the following computation:

$$Pr(C=+|\mathbf{x})=\frac{\text{exp}h(\mathbf{x})}{{\displaystyle \sum \text{exp}h(\mathbf{x})}},$$ (12)

and h(x) = Bφ(AR + a) + b, where A is the matrix of weights of the first layer, a is the bias vector of the first layer, B and b are the weight matrix and the bias vector of the hidden layer, respectively, and φ(x) is the logistic transformation that takes the form $\frac{1}{1+e^{-x}}$. Model parameters {A, B, a, b} can be estimated using the back-propagation method.

Logistic regression is based on the assumption that the log-odds can be computed from a linear function of R. That is,

$$\text{log}\frac{Pr(C=+|\mathbf{r})}{1-Pr(C=+|\mathbf{r})}={\beta }_0+{\beta }_1{R}_1\cdots +{\beta }_p{R}_p.$$ (13)

Parameters {β_i} can be estimated using maximum likelihood methods.

Area under the receiver operating characteristic (ROC) curve

In this paper, we evaluated classifiers’ performances based on accuracy, sensitivity, and specificity. These metrics are well established and widely used for comparing classifiers’ performances. Recently, some researchers have argued that computing the area under the ROC curve (AUC) is better than accuracy for evaluating classification algorithms (Huang and Ling (2005)). We used the Mann Whitney statistic (Huang and Ling (2005)) to calculate the AUCs of different classification algorithms; the AUCs are listed in Table 3. We found that the AUCs of BNCIT, SVM, logistic regression, and MLP were similar. Comparing Table 3 to Table 1 and Table 2, we found a mismatch between AUCs and accuracies. For example, for data including all 91 structures, the accuracy of naïve Bayes’ was 76.7, which was lower than those of SVM and BNCIT. However, the AUC of naïve Bayes was 0.89, which was much higher than those of SVM and BNCIT. The mismatch between AUCs and accuracies was also reported in Huang and Ling (2005).

Table 3.

AUCs of different diagnostic models that are based on structures primarily in the medial temporal lobe.

Method	All 91 structures	Structures near MTL
BNCIT	0.82	0.82
Naïve Bayes	0.89	0.81
Decision tree	0.67	0.56
SVM	0.80	0.79
MLP	0.84	0.80
discriminant analysis	0.85	0.73
Logistic regression	0.80	0.73

91 structures defined in the MNI Jakob template

The 91 structures defined in the MNI Jakob template are listed as follows (‘G’ denotes gyrus, ‘R’ is right, and ‘L’ is left) : medial-front-orbital-G-R, middle-frontal-G-R, insula-R, precentral-G-R, lateral-front-orbital-G-R, cingulate-region-R, medial-frontal-G-L, superior-frontal-G-R, globus-palladus-R, globus-palladus-L, putamen-L, inferior-frontal-G-L, putamen-R, frontal-lobe-WM-R, parahippocampal-G-L, angular-G-R, temporal-pole-R, subthalamic-nucleus-R, nucleus-accumbens-R, uncus-R, cingulate-region-L, fornix-L, frontal-lobe-WM-L, precuneus-R, subthalamic-nucleus-L, posterior-limb-of-internal-capsule-inc-cerebral-peduncle-L, posterior-limb-of-internal-capsule-inc-cerebral-peduncle-R, hippocampal-formation-R inferior-occipital-G-L, superior-occipital-G-R, caudate-nucleus-L, supramarginal-G-L, anterior-limb-of-internal-capsule-L, occipital-lobe-WM-R, middle-frontal-G-L, superior-parietal-lobule-L, caudate-nucleus-R, cuneus-L, precuneus-L, parietal-lobe-WM-L, temporal-lobe-WM-R, supramarginal-G-R, superior-temporal-G-L, uncus-L, middle-occipital-G-R, middle-temporal-G-L, lingual-G-L, superior-frontal-G-L, nucleus-accumbens-L, occipital-lobe-WM-L, postcentral-G-L, inferior-frontal-G-R, precentral-G-L, temporal-lobe-WM-L, medial-front-orbital-G-L, perirhinal-cortex-R, superior-parietal-lobule-R, lateral-front-orbital-G-L, perirhinal-cortex-L, inferior-temporal-G-L, temporal-pole-L, entorhinal-cortex-L, inferior-occipital-G-R, superior-occipital-G-L, lateral-occipitotemporal-G-R, entorhinal-cortex-R, hippocampal-formation-L, thalamus-L, parietal-lobe-WM-R, insula-L, postcentral-G-R, lingual-G-R, medial-frontal-G-R, amygdala-L, medial-occipitotemporal-G-L, parahippocampal-G-R, anterior-limb-of-internal-capsule-R, middle-temporal-G-R, occipital-pole-R, corpus-callosum, amygdala-R, inferior-temporal-G-R, superior-temporal-G-R, middle-occipital-G-L, angular-G-L, medial-occipitotemporal-G-R, cuneus-R, lateral-occipitotemporal-G-L, thalamus-R, occipital-pole-L, fornix-R.