How cofilin severs an actin filament

Abstract

The actin regulatory protein, cofilin, promotes actin assembly dynamics by severing filaments and increasing the number of ends from which subunits add and dissociate. Recent studies provide biophysical descriptions of cooperative filament interactions in energetic, mechanical and structural terms. A one-dimensional Ising model with nearest-neighbor interactions permits thermodynamic analysis of cooperative binding and indicates that one or a few cofilin molecules can sever a filament. Binding and cooperative interactions are entropically driven. A significant fraction of the binding free energy results from the linked dissociation of filament-associated ions (polyelectrolyte effect), which modulate filament structure, stability and mechanics. The remaining binding free energy and essentially all of the cooperative free energy arise from the enhanced conformational dynamics of the cofilactin complex. Filament mechanics are modulated by cofilin such that cofilin-saturated filaments are approximately 10- to 20-fold more compliant in bending and twisting than bare filaments. Cofilin activity is well described by models in which discontinuities in topology, mechanics and conformational dynamics generate stress concentration and promote fracture at junctions of bare and decorated segments, analogous to the grain boundary fracture of crystalline materials and the thermally driven formation of shear transformation zones in colloidal glass.

Introduction

Actin is an abundant approximately 43-kDa protein that self-assembles into helical, non-covalent filament polymers which grow and shrink from their ends in an adenine nucleotide-dependent manner (Pollard et al. 2000). Filaments provide cells with mechanical strength (Bathe et al. 2008), and their assembly generates piconewton forces (Kovar and Pollard 2004) capable of displacing physical boundaries, such as membrane vesicles (Heuvingh et al. 2007), bacteria (Marcy et al. 2004) or the leading edge of a migrating cells (Pollard 2007) when large filament numbers are organized as bundles or networks. Sustained motility requires the constant reorganization (i.e. assembly and disassembly) of actin filaments. Rapid filament disassembly is necessary to replenish the monomer pool needed for continuous filament elongation. Because filaments grow and shrink from their ends, the filament assembly and disassembly rates depend linearly on the filament end concentration.

Cofilin is an essential actin regulatory protein that severs filaments and accelerates actin assembly dynamics by increasing the number of filament ends from which subunits add and dissociate (Michelot et al. 2007; Roland et al. 2008). Cofilin binding alone is sufficient to promote filament fragmentation, in marked contrast to the severing of microtubules by severing proteins, which is ATP dependent. A biophysical description of filament severing requires knowledge of the binding affinities and energetics, structure and material properties of filaments. Recent biochemical and biophysical in vitro studies of cofilin and actin filaments have provided the parameters needed for such a quantitative description and provide a foundation from which to evaluate the effects of regulatory proteins, such as tropomyosin (Kuhn and Bamburg 2008) and AIP1 (Ono 2003), which play critical functional roles in vivo by influencing the filament binding and severing activities of cofilin.

Cooperative actin filament binding

Biochemical studies with purified proteins have established that cofilin binds actin filament subunits stoichiometrically (one cofilin per actin subunit) with positive cooperativity (Hawkins et al. 1993; Hayden et al. 1993; McGough et al. 1997; Ressad et al. 1998, 1999; De La Cruz 2005). Bound cofilin molecules do not directly interact (McGough et al. 1997), so cooperative cofilin–actin filament interactions must arise from allosteric changes in filament structure and/or dynamics. Cofilin-decorated filaments have a shorter average crossover length and mean twist than native actin filaments (McGough et al. 1997). The filament subunit tilt also shifts with cofilin binding (Galkin et al. 2001). The changes in subunit tilt and filament twist provide a rational structural basis for actin filament allostery. These observations generally favored a severing mechanism in which twisted and tilted filaments saturated with cofilin are fragile and more susceptible to thermal fragmentation than bare, native filaments.

Cooperative cofilin binding to the actin filament is typically analyzed using the Hill equation, and assays yield Hill coefficients in the range of approximately 4–10 (Hawkins et al. 1993; Hayden et al. 1993; McGough et al. 1997; De La Cruz 2005). The Hill treatment is informative, but relating the binding constants to thermodynamic binding and cooperative free energies is difficult (the apparent binding affinity obtained from the fit to the Hill equation represents the nth root of the product of all individual n binding constants). Binding models firmly grounded in thermodynamics are needed to evaluate the energetics of cooperative cofilin binding to actin filaments.

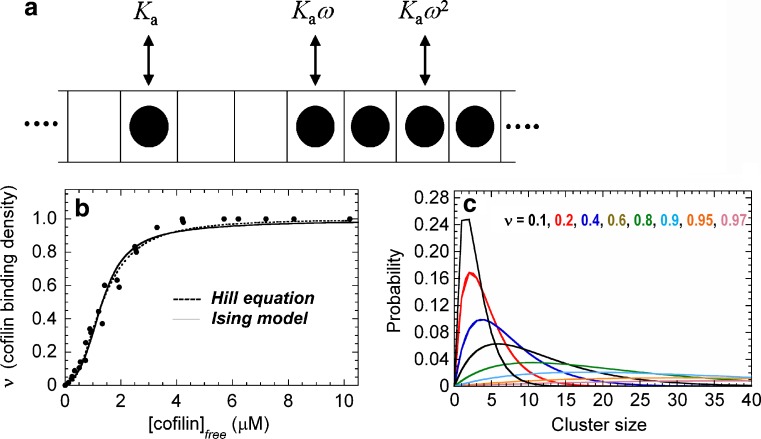
Treating a filament as a one-dimensional lattice of binding sites (i.e. actin subunits), each of which exists as vacant or occupied by cofilin (Fig. 1a), makes it possible to express cooperative cofilin binding to actin filaments in terms of intrinsic and cooperative binding energies and affinities (McGhee and von Hippel 1974; De La Cruz 2005). Three types of binding modes exist on an infinite, linear one-dimensional lattice (Fig. 1a): isolated (no nearest neighbors), singly contiguous (one nearest neighbor) and doubly contiguous (two nearest neighbors). When cooperative binding interactions among neighboring sites exist, the cooperativity parameter (ω) defines how much easier (or harder) it is to bind with a neighboring cofilin molecule. The cooperativity parameter is directly related to the cooperative free energy according to [ΔG°_coop= −RTln (ω)]. An ω > 1 is observed when positive cooperativity exists (ΔG°_coop < 0); negative cooperativity generates ω < 1 (ΔG°_coop > 0), and ω = 1 (ΔG°_coop = 0) when no cooperative interactions are present. The overall binding affinity of a singly contiguous cofilin is given by K _a ω, and that of a double contiguous cofilin is given by K _a ω ². When sites are independent and non-interacting, ω = 1, and a single constant (K _a) defines the cofilin binding affinity and corresponding binding free energy [ΔG°_bind = −RTln (K _a)].

Fig. 1.

a Schematic of one-dimensional Ising model of cofilin binding to an actin filament. Individual filament subunits are depicted as squares of an infinite, one-dimensional (1-D) lattice. A subunit with bound cofilin is indicated with a filled circle. K_a is the association equilibrium binding constant, and ω is the unitless cooperativity factor. The overall binding constants are given by K_a (isolated, non-contiguous bound cofilin), K_aω (singly-contiguous bound cofilin) and K_aω² (doubly contiguous bound cofilin). b Cooperative cofilin binding to actin filaments. The lines represent the best fit of the data for human cofilin-1 binding to rabbit muscle actin (filled circles) to the Hill equation (dotted line) or binding to a 1-D lattice with nearest neighbor interactions as depicted in a. The figure is adapted from De La Cruz (2005). c Cofilin cluster size distribution. The probability of bound cofilin being in a given cluster size. Each line represents the distribution at the color-specified binding density

An isolated cofilin molecule that binds is an actin filament subunit with an affinity (1/K _a) of approximately10 μM. Singly contiguous cofilin binds with an affinity of approximately 0.5 μM (ω ~ 20) and doubly contiguous with an approximately 25 nM affinity (De La Cruz 2005; Cao et al. 2006). Isolated (non-cooperative) cofilin binding is slow (approx. 10⁴  M ^-1 s^-1; Andrianantoandro and Pollard 2006; Cao et al. 2006; ), and ω is dominated by contributions to the association rate constant (i.e. cooperativity arises from more rapid association).

This model describes well the observed equilibrium (Fig. 1b; De La Cruz 2005) and kinetic (Cao et al. 2006) behavior of cooperative cofilin binding, despite being an oversimplification of the actin filament structure (Oda et al. 2009). The model assumes that cooperative interactions arise from each bound neighbor. Long-range, non-nearest neighbor interactions are not considered. The observation that nearest-neighbor interactions describe the behavior well, suggests that non-nearest neighbor interactions, such as changes in filament twisting dynamics (Prochniewicz et al. 2005) and thermal stability (Dedova et al. 2004; Bobkov et al. 2006) are not determinants of cooperative binding. This does not mean that non-nearest neighbor interactions do not exist (Galkin et al. 2001; Dedova et al. 2004; Prochniewicz et al. 2005; Bobkov et al. 2006), but that they do not favor cofilin binding.

One or a few bound cofilin molecules efficiently sever filaments

When binding to a linear polymer displays positive cooperativity, as with cofilin and actin filaments, clusters of bound ligand will form along the polymer lattice. Quantitative knowledge of the affinities for binding to an isolated site and with neighbors allows for the distribution of cofilin cluster sizes to be readily predicted and linked to filament severing activity (Fig. 1c; De La Cruz 2005). Efficient filament severing is readily observed at <1 μM cofilin (Moriyama and Yahara 1999, 2002). The predicted cofilin cluster sizes are very small (approx. one to two molecules) at this concentration and indicate that one or a few bound cofilin molecules are sufficient to destabilize the filament lattice and promote fragmentation (De La Cruz 2005). Mathematical models that incorporate filament severing by two adjacently bound cofilin molecules reliably account for actin filament assembly dynamics in the presence of cofilin (Roland et al. 2008), consistent with severing by one or a few bound cofilin molecules (De La Cruz 2005; see also Andrianantoandro and Pollard 2006; Pavlov et al. 2007).

Energetics of cooperative actin filament interactions

The values of K _a and ω depend weakly on temperature, indicating that the overall enthalpic contributions are small and that binding and cooperative interactions are driven by large, positive entropy changes (ΔS°_bind and ΔS°_coop > 0; Cao et al. 2006). Binding measurements are made in dilute solution with purified protein components, so the entropy changes must originate from solvent, ions (salts and buffer) and/or protein (actin and cofilin) components. The solvent and ion contributions are evaluated from the dependence of the binding parameters (K _a and ω) on water and ion activity (Cao et al. 2006; Frederick et al. 2008). Binding parameters are weakly affected by the manipulation of water activity with inert crowding agents, suggesting that cofilin binding is not thermodynamically coupled to large net changes in solvent interactions and organization.

Isolated, non-cooperative cofilin binding (K _a) is weakened by salt, but cooperative interactions (ω) are not (Cao et al. 2006). The inhibitory salt effect arises because cofilin competes with cations for binding to charge sites on the actin filaments. As a result, ions weaken the observed binding affinity and vice-versa (i.e. ion and cofilin binding represent a case of identical heterotropic linkage). The contributions of ionic interactions to cofilin binding energetics can be evaluated from the ion concentration-dependence of the observed binding constants (see Cao et al. 2006).

Actin filaments are polyelectrolytes with a linear charge density of approximately 4 e/nm (Tang and Janmey 1996). Negatively charged linear polymers sequester cations in their surrounding electric field. These associated ions have long been known to stabilize actin filaments; monomers are typically polymerized by the addition of salt, which means that filaments bind ions and are stabilized by the interaction (i.e. a case of polysteric linkage). A significant fraction of the non-contiguous cofilin binding free energy arises from the linked dissociation of approximately two protein-associated K⁺ ions (or one Mg²⁺). Cooperative interactions are not linked to ion release, indicating that electrostatic contributions to cooperative interactions are small. The sum of electrostatic and solvent components, however, do not account for the total binding and cooperative free energies. Therefore, the energy difference must be balanced by favorable entropy changes of the protein components, presumably originating from increased conformational dynamics of the cofilin–actin filament complex, at either the subunit or filament level.

Actin filament conformational dynamics and mechanics

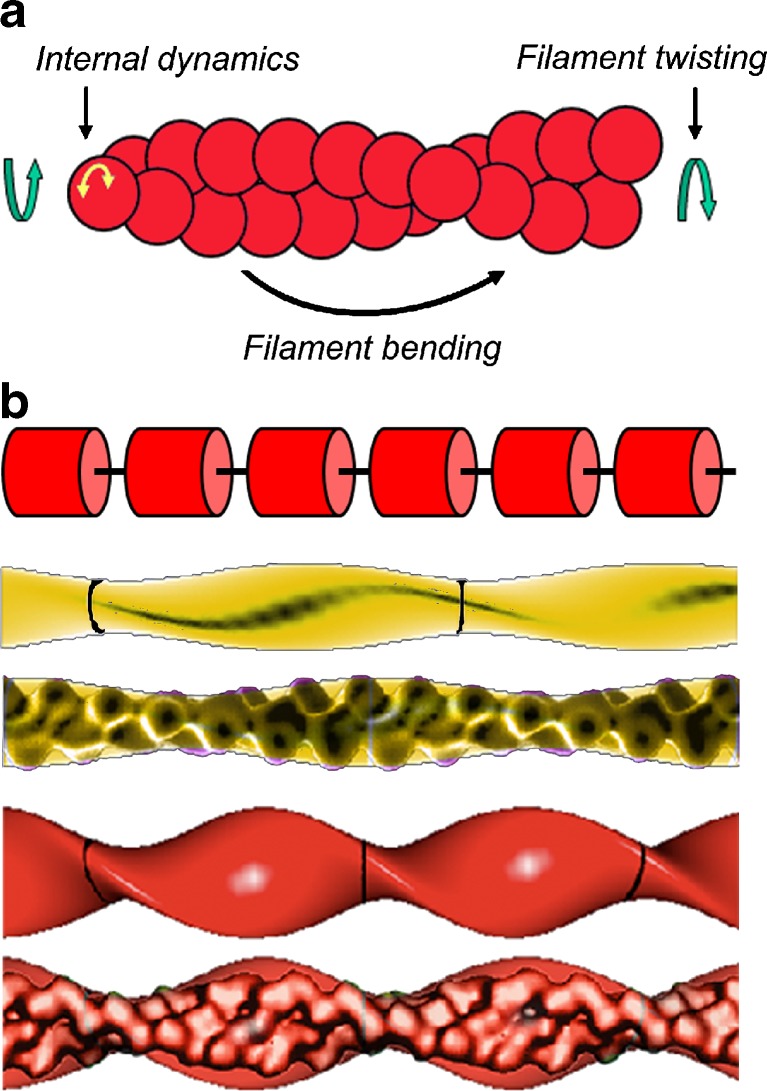
Actin filaments are semi-flexible polymers on cellular length scales that display four characteristic modes of large-scale conformational motion (Fig. 2a): twisting, bending, tumbling (i.e. rigid-body translational diffusion) and internal subunit dynamics. These motions occur over a broad range of timescales: internal subunit motions occur rapidly on the sub-microsecond timescale; twisting occurs on the microsecond timescale; bending occurs in milliseconds to seconds; tumbling occurs on very long second timescales that are much slower than severing. Cofilin binding affects actin motions on all of these timescales.

Fig. 2.

Conformational dynamics of actin filaments. a Schematic representation of actin filament thermal motions. Figure is adapted from Prochniewicz et al. (2005). b Models used to analyze material properties of filaments. Top to bottom Schematic of a linear array of cylindrical subunits connected by a flexible elastic linker that is used when modeling filament torsional dynamics. An actin filament (yellow) modeled with an elliptical cross-section of a 2.7-nm minor radius, a 4.5-nm major radius and 37-nm crossover lengths, and a cofilactin filament (red) modeled with an elliptical cross-section of a 2.7-nm minor radius, a 6.7-nm major radius and 27-nm crossover lengths. These geometric models were used to calculate the second moment of inertia (I) and apparent elastic modulus (E) from the filament flexural rigidity. An actin filament modeled as a homogenous isotropic elliptical cylinder has a second moment of inertia (I) of 120 nm⁴. Cofilin binding increases the filament radius and has a value of 240 nm⁴ for I. Models are presented with and without overlays of the corresponding reconstructions based on cryoelectron microscopy (McGough et al. 1997). Parts of the figure are adapted from McCullough et al. (2008)

Subunit dynamics are enhanced with cofilin binding, as indicated from an increased mobility of the actin C-terminus (Prochniewicz et al. 2005) and subdomain 2 (Bobkov et al. 2002; Galkin et al. 2003; Muhlrad et al. 2004). The distribution of inter-probe distance between the actin C-terminus and the DNAse binding loop of subdomain 2 favors the existence of multiple conformations in dynamic equilibrium (Scoville et al. 2009). These changes occur as a consequence of cofilin binding between subdomains 1 and 3 of a filament subunit (Paavilainen et al. 2008), which shifts the position and orientation of the DNAase I binding loop of a long-pitch neighbor.

Determining the effects of cofilin on actin filament bending and twisting requires measurements of the filament mechanical properties, namely, the filament rotational and bending stiffness. Torsional dynamics can be measured from the time-resolved phosphorescence anisotropy (TPA) decays of filaments labeled with erythrosine, a phosphorescent probe with a microsecond excited state lifetime (Prochniewicz et al. 2005). Cofilin binding lowers the anisotropy and rotational correlation time of erythrosine-labeled actin filaments. These spectroscopic changes indicate that the filament microsecond motions are more rapid and have greater amplitude when cofilin is bound.

Filament motions contributing to TPA cannot be accounted for by rigid body rotations or tumbling, rather they reflect primarily filament torsional motions that are well described in terms of an elastic linker model (Allison and Schurr 1979; Barkley and Zimm 1979; Schurr 1984; Prochniewicz et al. 2005). In this model, the actin filament is treated as an array of cylindrical elementary rods (i.e. subunits) linked in series by elastic elements (Fig. 2b). Filament stiffness in torsion (and bending) may then be ‘tuned’ by varying the compliance of the intervening elastic linkers, which mediates both inter-subunit bending and twist. A filament behaves as a rigid rod when the elastic linker is stiff. Subunit angular disorder exists when the linker is elastic. The degree of disorder depends on the thermal energy and on the linker stiffness, which is proportional to the filament torsional stiffness.

Cofilin-decorated filaments are more compliant in twist than native actin filaments, with an approximately 20-fold lower torsional stiffness (C) (Prochniewicz et al. 2005). That is, the elastic element linking filament subunits (Fig. 2b) is more compliant when cofilin is bound. As a result, the thermally driven root-mean square torsional angle between adjacent filament subunits increases from approximately 4° to approximately 17° at 298 K with cofilin binding (Table 1).

Table 1.

Elastic bending and twisting parameters for native actin and cofilactin filaments^a

Filament	Lp (pN nm)b	κ (pN μm2)b	I (nm4)b	Eapp (pN nm-2)b	C (pN μm2 rad-1)c
Actin	9.8 (± 0.14)	40 (± 0.49) × 10-3	120	330	2.30 (± 1.00) × 10-6
Cofilactin	2.2 (± 0.026)	9.1 (± 0.11) × 10-3	240	38	0.13 (± 0.06) × 10-6

^aConditions: 20 mM imidazole (pH 6.6), 25°C, 50 mM KCl, 0.2 mM ATP, 2 mM MgCl₂, 2 mM DTT, 1 mM NaN₃

^b The values of the filament persistence length (L_p) flexural stiffness (κ), shape-dependent geometric moment of inertia (I) and apparent elastic Young’s modulus (E_app) are taken from McCullough et al. (2008)

^c The values of the filament torsional stiffness (C) are taken from Prochniewicz et al. (2005)

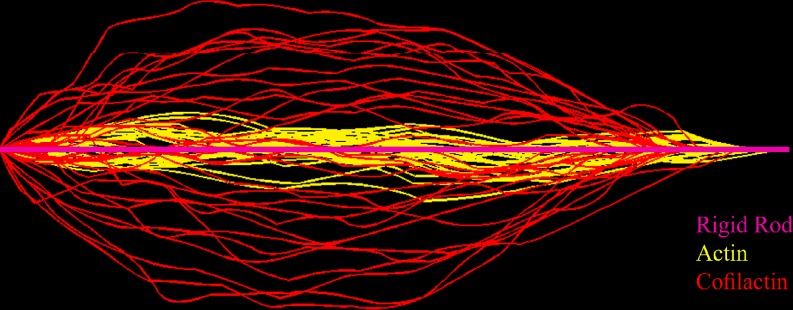
Direct visualization of filaments undergoing thermally driven fluctuations (Fig. 3) permits the measurement of an apparent filament bending stiffness (Gittes et al. 1993; Isambert et al. 1995; Le Goff et al. 2002; McCullough et al. 2008). Filaments decorated with cofilin appear to bend with a higher variance (amplitude) than bare actin filaments (Fig. 3). Analysis of the equilibrium tangent–tangent correlation function reveals that the apparent filament flexural rigidity (κ) and the corresponding persistence length (L _p) are approximately fivefold lower when cofilin is bound (Table 1). Naturally, the corresponding Euler buckling load of cofilin-decorated filaments is also reduced fivefold with respect to native filaments, which may have consequences for force generation, motility and filament turnover under load. The depletion of filaments from non-binding surfaces (Fisher and Kuo 2009) will also be affected.

Fig. 3.

Overlay of actin and cofilactin filament shape configurations. Digital images of actin (yellow) and cofilactin filament (red) segments of identical length undergoing thermal fluctuations were overlaid and oriented with one end starting from the same point of origin and the other end on the same axis. The straight pink rod represents a rigid filament. Image is adapted from McCullough et al. (2008)

The flexural stiffness (κ) of a homogenous and isotropic elastic rod is equal to the product of the shape-independent elastic (Young’s) modulus (E) and the geometric moment of inertia (I). Increasing the radius of a rod without changing its elastic modulus thereby increases the geometric moment I and increases filament bending stiffness. For example, the bending stiffness of a tropomyosin-decorated actin filament is well accounted for by the contribution of increased filament radius and mass to the geometric moment. Accounting for the geometric contribution of bound cofilin to the filament (Fig. 2b) reveals that the apparent elastic modulus of cofilin-decorated actin filaments is approximately 20-fold lower than that of bare filaments (Table 1). The elastic modulus is referred to as an apparent quantity because filaments are not necessarily isotropic in cross-section or along their length and because significant changes in the radial distribution of material and, consequently, the geometric moment can also contribute to enhancing filament flexibility.

The elasticity of non-covalent polymers, such as actin filaments, is influenced by the properties of intersubunit bonds and contacts. Cofilin makes filaments bend and twist more easily, so binding could affect subunit interactions in the filament. Biochemical (Grintsevich et al. 2008) and structural (Galkin et al. 2001, 2003) evidence favors a mechanism in which cofilin binding between subdomains 1 and 3 of an actin monomer disrupts contacts made with subdomain 2, specifically the DNase I binding loop, of the adjacent subunit, thereby weakening intersubunit contacts along the filament long-pitch helix. In addition, subdomain 2 of actin makes the highest radius contact in the filament, so breaking this longitudinal contact narrows the radial mass distribution of the filament, which lowers the filament bending stiffness by affecting the geometric moment (McCullough et al. 2008).

Fragmentation due to mechanical asymmetry

Knowledge of the cofilin binding energetics and filament mechanics permits the development of models of filament fragmentation based on the distribution of bound cofilin (Fig. 4a, b). Of particular importance is identifying the site(s) of preferential filament fragmentation and whether it occurs at junctions of bare and decorated regions, or internally within homogenous (bare or cofilin-decorated) segments. It was previously suggested that severing by small clusters of bound cofilin occurred at junctions of bare and decorated regions and that this was a consequence of an asymmetry in filament dynamics and mechanics (De La Cruz 2005; Prochniewicz et al. 2005; McCullough et al. 2008). This hypothesis relied on three important observations: (1) severing occurs at low cofilin binding densities and small cluster sizes (De La Cruz 2005); (2) cofilin-decorated filaments display significantly different mechanical properties than bare filaments (Prochniewicz et al. 2005; McCullough et al. 2008); (3) partially cofilin-decorated filaments are considerably less stable than bare or cofilin-saturated filaments (Dedova et al. 2004; see also Bobkov et al. 2006).

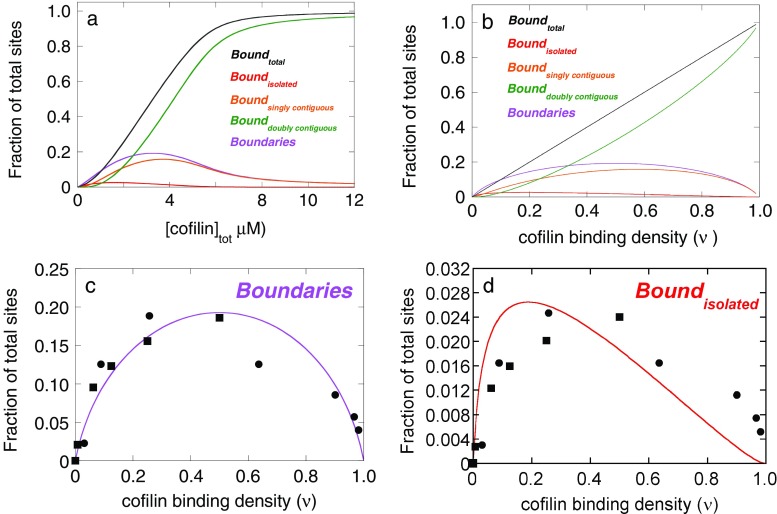
Fig. 4.

Correlation of filament assembly dynamics activity with cofilin binding modes. a Cofilin concentration-dependence of the populated bound state equilibrium distributions. The lines represent the fractional distribution of actin filament sites as predicted from the equilibrium binding constants obtained from the nearest-neighbor cooperative binding model (De La Cruz, 2005; Cao et al. 2006). Note that the sites are plotted as a function of the total cofilin concentration, and not of free cofilin concentration; the actin concentration used in the calculations is approximately 1/K _a ω. b Same as a, except plotted as a function of the filament binding density. c Correlation of cofilin activity with the existence of bare and cofilin-decorated boundaries (i.e. junctions) on a filament. Boundaries were calculated as the sum of singly contiguous sites plus twice the sum of non-contiguous bound cofilin. The filled squares represent the change in phase transition temperature as measured by differential scanning calorimetry (Bobkov et al. 2006). The filled circles represent the cofilin-dependence of net subunit dissociation from filament pointed ends presented by Yeoh et al. (2002). Both sets of data have been normalized to scale the y-axes for presentation. These measurements were made under buffer conditions similar to those used to measure cooperative binding parameters and with the identical cofilin and actin isoforms. d Overlay of cofilin activity with formation of non-contiguous (isolated) bound cofilin

A mechanism in which severing occurs preferentially at boundaries, such as junctions of bare and cofilin-decorated segments, predicts that severing activity should first increase and then decrease with increasing cofilin binding density (Fig. 4a, b) since heterogeneity and asymmetry are absent from bare and saturated filaments (Fig. 4a, b). The observation that actin filament severing and depolymerization occurs efficiently at low cofilin binding densities (De La Cruz 2005) but is inhibited at high binding densities (Fig. 4c, d; Yeoh et al. 2002; Andrianantoandro and Pollard 2006; Pavlov et al. 2007) is consistent with such a boundary-fracture mechanism. More convincing is that cofilin activity, as assayed from filament subunit turnover (Yeoh et al. 2002) or change in calorimetric transition temperature (Bobkov et al. 2006), correlates well with the existence of boundaries of bare and decorated segments (Fig. 4c). It should be noted that the fraction of isolated bound cofilin sites also varies non-monotonically with cofilin concentration and binding density (Figs. 1c, 4a, b), but reaches a maximum at a binding density of approximately 0.2 so that the correlation with cofilin activity, which reaches a maximum at a binding density of approximately 0.5, is not very strong (Fig. 4d). This behavior suggests that cofilin activity (severing, depolymerization and destabilization) scales with heterogeneity and asymmetry in filament topology and mechanics in a manner that parallels the formation of decorated and undecorated boundaries. Note that the fraction of total sites that exists as isolated, noncontiguous bound cofilin never exceeds 3% of the total number of sites. The boundaries maximally occupy 20% of the total site number when the filament is half saturated (Fig. 4).

Satisfactory models of actin filament mechanics (Chu and Voth 2005; see also Mitra and Sept 2009 for an example with microtubules) and fracture should include detailed structures of actin filaments and alterations of subunit contacts at atomic resolution. However, the functional motions of numerous proteins have been successfully described by homogeneous elastic models that lack detailed and specific atomic interactions (e.g. electrostatics, van der Waals, bonded terms, etc.), accounting only for molecular-level protein shape (see Bathe 2007 and references therein). In fact, the mechanical properties of actin filaments are well-described by geometric models that treat filaments as a solid elastic continuum (Gittes et al. 1993; Isambert et al. 1995; Howard 2001; Le Goff et al. 2002; Bathe 2007; McCullough et al. 2008).

While continuum models describe well the macroscopic deformation and mechanical properties of actin filaments, it is less clear how well they can account for actin filament fragmentation and cofilin-mediated severing. The incorporation of fracture and material failure concepts from brittle, inorganic material science and engineering is complicated by the fact that protein “fracture” might differ considerably from that of crystalline or colloidal materials due to their distinct atomic packing and interactions. This translation of concepts is further complicated by the uncertainty in the elasticity or reversibility of filament deformations under thermally induced or other loading. Despite these differences, however, some conceptual parallels can be drawn (Ackbarow and Buehler 2007).

Preferential severing at topological boundaries, such as the junctions of bare and cofilin-decorated filament segments, displays analogous behavior with the fracture of some non-protein materials. This observation may provide a foundation from which one may apply, at least as a first approximation, engineering principles of fracture and failure. For example, experimental data accumulated thus far suggest that filaments fragment because stress generated from thermal induced fluctuations accumulates locally at bare and decorated boundaries (Fig. 4). This behavior resembles the grain boundary fracture of crystals (Anderson 2005) and the thermally driven formation of shear transformation zones in colloidal glass (Schall et al. 2007). Proteins behave more like glasses in physiological solution than they do like crystals (Vitkup et al. 2000), so thermally activated shear transformation zones may be more relevant when considering thermally driven severing of actin filaments. Although shear transformation zones are activated by thermal fluctuations, external strain promotes their formation (Schall et al. 2007), suggesting that intracellular forces, such as those generated by contractile proteins, could influence the severing activity of cofilin.