Review Article—Dielectrophoresis: Status of the theory, technology, and applications

Abstract

A review is presented of the present status of the theory, the developed technology and the current applications of dielectrophoresis (DEP). Over the past 10 years around 2000 publications have addressed these three aspects, and current trends suggest that the theory and technology have matured sufficiently for most effort to now be directed towards applying DEP to unmet needs in such areas as biosensors, cell therapeutics, drug discovery, medical diagnostics, microfluidics, nanoassembly, and particle filtration. The dipole approximation to describe the DEP force acting on a particle subjected to a nonuniform electric field has evolved to include multipole contributions, the perturbing effects arising from interactions with other cells and boundary surfaces, and the influence of electrical double-layer polarizations that must be considered for nanoparticles. Theoretical modelling of the electric field gradients generated by different electrode designs has also reached an advanced state. Advances in the technology include the development of sophisticated electrode designs, along with the introduction of new materials (e.g., silicone polymers, dry film resist) and methods for fabricating the electrodes and microfluidics of DEP devices (photo and electron beam lithography, laser ablation, thin film techniques, CMOS technology). Around three-quarters of the 300 or so scientific publications now being published each year on DEP are directed towards practical applications, and this is matched with an increasing number of patent applications. A summary of the US patents granted since January 2005 is given, along with an outline of the small number of perceived industrial applications (e.g., mineral separation, micropolishing, manipulation and dispensing of fluid droplets, manipulation and assembly of micro components). The technology has also advanced sufficiently for DEP to be used as a tool to manipulate nanoparticles (e.g., carbon nanotubes, nano wires, gold and metal oxide nanoparticles) for the fabrication of devices and sensors. Most efforts are now being directed towards biomedical applications, such as the spatial manipulation and selective separation∕enrichment of target cells or bacteria, high-throughput molecular screening, biosensors, immunoassays, and the artificial engineering of three-dimensional cell constructs. DEP is able to manipulate and sort cells without the need for biochemical labels or other bioengineered tags, and without contact to any surfaces. This opens up potentially important applications of DEP as a tool to address an unmet need in stem cell research and therapy.

INTRODUCTION

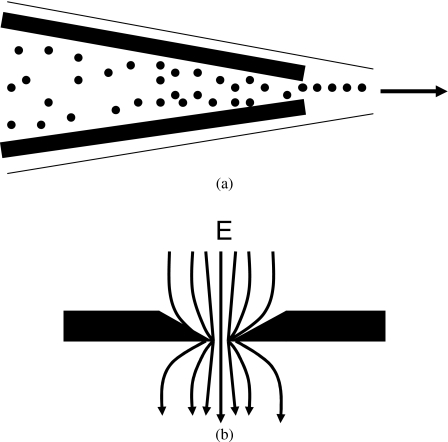
The term dielectrophoresis (DEP), first adopted by Pohl,¹ implies from the Greek word phorein an effect where a particle is carried as a result of its dielectric properties. Pohl defined this effect as “the motion of suspensoid particles relative to that of the solvent resulting from polarization forces produced by an inhomogeneous electric field.” The effect was in fact known to the ancient Greeks and Romans. According to Mottelay (Ref. ², p. 7), Thales of Miletus described it approximately 600 B.C. in observations that vigorously rubbed pieces of amber can attract straws, dried leaves, and other light bodies in the same way that a magnet attracts iron. The first theoretical treatment of the ponderomotive forces acting on dielectric spheres in an inhomogeneous electric field followed Maxwell’s theories (e.g., Ref. 3, pp. 90–91), and Hatfield⁴ appears to be the first to exploit the effect for the treatment of tin ores, where the valuable mineral cassiterite has to be separated from a large excess of quartz material. Hatfield recognized that a key experimental problem was the generation of intense nonuniform electric fields, having strengths even remotely approaching that of the weakest magnetic fields used in magnetic separation, without problems associated with dielectric breakdown. Pohl’s initial interest in this subject was also directed toward an industrial application and in particular to the problem of removing carbon-black filler from polyvinyl chloride samples. He later directed his efforts to the development of methods and theories for the dielectrophoretic characterization and separation of biological cells and bacteria, as described in his seminal book on the subject.⁵ It took time for the term to gain universal recognition. The title of a paper⁶ was changed to include the words “measurements using nonuniform electric field effects” because a referee insisted there was no such word as “dielectrophoresis”!

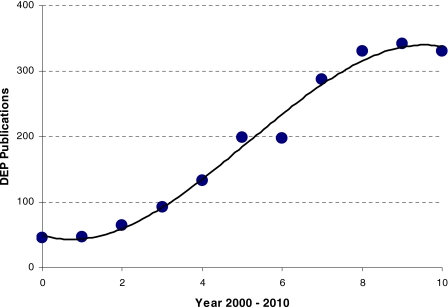
As shown in Fig. 1, there has been a significant increase in the number of DEP publications over the past decade (leveling off if the estimate for 2010 is roughly correct). A search of databases (MEDLINE, ScienceDirect, Web of Science) generates details of nearly 2000 publications (excluding conference reports and patents) in this field of study over the past 10 years. The total number in the decade leading up to 2000 was less than 300. The papers cover various aspects of the theory and technology. Published applications of DEP are directed toward areas such as biosensors, cell therapeutics, drug discovery, medical diagnostics, microfluidics, nanoassembly, and particle filtration. Characterizing the content of a paper in terms of whether it can be categorized as addressing the theory, technology or application of DEP is sometimes not straightforward (many key papers address all three aspects). However, an attempt to do this is shown in Fig. 2. Current trends suggest that the theory and technology have matured sufficiently for most effort to now be directed toward applying DEP to solve unmet practical needs.

Figure 1.

Number of publications on DEP for the period 2000–2010. (The estimate for 2010 is based on the 110 papers published up to 1 May 2010.)

Figure 2.

Classification of DEP publications since 1995, in terms of whether their content mainly addresses theory, technology (Tech), or applications (Appl), expressed as a percentage of the total number of papers published. The trend for 2010 suggests that the theory (5%) and technology (18%) have matured sufficiently for efforts to be directed mainly toward publication of applications (77%).

In this review, an attempt is made to describe the present status of the theory, technology, and applications of DEP. It is not intended to be a comprehensive review of all the papers published, but takes the form of an expanded version of introductory notes supplied to Masters and Doctoral students about to engage in various aspects of DEP research. It is hoped that established researchers in the field, together with those requiring a detailed introduction (e.g., lecturers, patent examiners, venture capitalists!) will also find it of use and interest. References are given to key papers, some of them published many years ago. This reflects strong empathy with the sentiment, expressed by James Clerk Maxwell, that “It is of great advantage to the student of any subject to read in the original memoirs on that subject, for science is always most completely assimilated when it is found in its nascent state. Every student should, in fact, be an antiquary in his subject” (Ref. ²: frontispiece).

THEORY

Most publications on DEP quote an expression for the time-average DEP force (acting on a spherical particle) of the form

$$F_{\text{DEP}}=2\pi {\epsilon }_m{R}^3\text{CM}\left(\nabla E^2\right),$$ (1)

where ε_m is the absolute permittivity (ε_rε_o) of the surrounding medium, R is the particle radius, CM is the Clausius–Mossotti factor related to the effective polarizability of the particle, E is the amplitude (rms) of the electric field, and ∇ represents the gradient operator. Although Clausius⁷ and Mossotti⁸ did not derive this factor in this context, the factor is named after them in recognition of their early studies of the relationships between the dielectric constant and refractive indices of different materials. This led to the recognition that the factor (ε−1)∕(ε+2) should be proportional to the density of a material.

In reviewing the status of DEP theory it is instructive to examine how Eq. 1 is derived. The first step involves evaluating the polarization of the particle in terms of an equivalent induced dipole moment p. We conduct the imaginary exercise of inserting a lossless dielectric sphere, of radius R and absolute permittivity ε_p, into a fluid dielectric medium of permittivity ε_m that occupies the whole of the rest of space. We suppose that a uniform field E (directed along the positive x-axis) existed in this dielectric before insertion of the sphere. Our task is to deduce the form of particle polarization whose field, when superposed onto E, produces a resultant potential ϕ that satisfies the following standard conditions in the formulation of electrostatic problems (Ref. ⁹, p. 195):

• (i)On either side of the sphere’s surface the normal component of the gradient of ϕ changes such that ε(∂ϕ∕∂n) remains constant.
• (ii)ϕ is continuous across this boundary defined by the sphere’s surface.
• (iii)In all of the space ϕ satisfies Laplace’s equation (∇²ϕ=0).

  We also make the condition:

• (iv)At distances far beyond the sphere ϕ=−Ex.

If the sphere consists of an isotropic and homogeneous dielectric, it will be homogeneously polarized by the external field E to create an internal field E_i symmetric about the x-axis,

$${\varphi }_i=-E_{i}x=E_{i}r\text{\hspace{0.17em}cos}\theta \left(\text{polar}\text{coordinates},x=r\text{\hspace{0.17em}cos}\theta \right).$$ (2)

We represent this polarization as an induced dipole of effective moment p=kE located at the sphere’s center (Fig. 3). As a result of the spherical geometry and the lossless nature of the dielectric, this induced dipole moment will be aligned with the original external field E. Thus, for all space outside the sphere, the field created by this dipole is superposed onto the field E to give

$${\varphi }_o=-Ex+E\frac{k}{4\pi {\epsilon }_m{r}^2}\cdot \frac{x}{r}=-E\text{\hspace{0.17em}cos}\theta \left(r-\frac{k}{4\pi {\epsilon }_m{r}^2}\right).$$ (3)

The forms given for ϕ in Eqs. 2, 3 satisfy condition (iii), while boundary conditions (i) and (ii) require

$${\varphi }_i={\varphi }_o\text{and}{\epsilon }_p\frac{\partial {\varphi }_i}{\partial r}={\epsilon }_m\frac{\partial {\varphi }_o}{\partial r},\text{when}r=R.$$ (4)

Thus,

$$E_i=E\left(1-\frac{k}{4\pi {\epsilon }_m{R}^3}\right)$$

and

$${\epsilon }_p{E}_i={\epsilon }_{m}E\left(1+\frac{2k}{4\pi {\epsilon }_m{R}^3}\right).$$

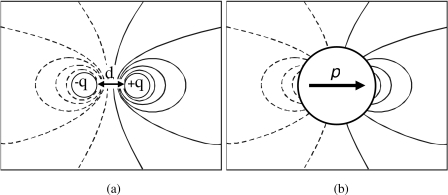
Figure 3.

(a) The lines of electric potential associated with a dipole of moment qd. (b) The potential generated outside an uncharged dielectric sphere, polarized by an imposed field E, is identical to that produced by an induced dipole moment p. The resultant potential, when this dipole potential is superposed onto that of the original field E, must satisfy standard electrostatic boundary conditions at the surface of the sphere.

On solving for k we obtain the sphere’s induced dipole moment as

$$p=kE=4\pi {\epsilon }_m{R}^3\left(\frac{{\epsilon }_p-{\epsilon }_m}{{\epsilon }_p+2{\epsilon }_m}\right)E.$$ (5)

The DEP force acting on the polarized sphere, when it is now subjected to a nonuniform field, is the algebraic sum of the forces acting on the positive and negative elements of the induced dipole moment:

On performing a Taylor series expansion of E(x+d) about x, and taking the effective length of the dipole shown in Fig. 2 as d=2R (i.e., p=q2R) then

$$E_{\text{DEP}}=q\left[E\left(x\right)+2R\cdot \frac{\partial E}{\partial x}+\cdots \cdot +\frac{{\left(2R\right)}^n}{n!}\cdot \frac{{\partial }^{n}E}{\partial x^2}+\cdots \right]-qE\left(x\right).$$

If the particle’s diameter is much smaller than the scale of the field nonuniformity, we can ignore the higher-order terms (n>1) to give to a good approximation,

$$E_{\text{DEP}}=q2R\cdot \frac{\partial E}{\partial x}=p\cdot \nabla E.$$ (6)

On substitution of p from Eq. 5 into Eq. 6 we obtain

$$F_{\text{DEP}}=4\pi {\epsilon }_m{R}^3\left(\frac{{\epsilon }_p-{\epsilon }_m}{{\epsilon }_p+2{\epsilon }_m}\right)\left(E\cdot \nabla \right)E=2\pi {\epsilon }_m{R}^3\left(\frac{{\epsilon }_p-{\epsilon }_m}{{\epsilon }_p+2{\epsilon }_m}\right)\left(\nabla E^2\right).$$ (7)

This result is equivalent to Eq. 1 with the CM factor

$$\text{CM}=\left(\frac{{\epsilon }_p-{\epsilon }_m}{{\epsilon }_p+2{\epsilon }_m}\right).$$ (8)

Equation 7 is presented in classical texts on electrostatics (e.g., Ref. 3, pp. 90–91) well before the term DEP was introduced.¹ We can interpret this result in terms of electrostatic energy, with the factor ε_mR³(CM)E² being proportional to the energy required to withdraw a sphere of radius R from a field E into a region where there is no field (assuming that the medium is isotropic and linear, such that ε_m may be a function of position but not of the field E). A positive value for CM indicates that work will be required to withdraw the particle from the highest field region, whereas for a negative CM value work is required to push the particle from a low to a high field region. The dependence on R³ indicates that DEP is a ponderomotive (particle volume-dependent) effect.

We now note that the formulation of Eq. 7 involves the following simplifications:

• (i)The particle is composed of a homogeneous dielectric that exhibits no conductive losses and carries no net charge.
• (ii)The nonuniform nature of the applied field E is not taken into account in the derivation of the particle’s induced polarization, which is assumed to take the form of a simple dipole moment.
• (iii)The particle exists in a dielectric medium of infinite extent, implying that the field in the vicinity of the particle is not perturbed by the presence of a boundary, such as a metal or dielectric surface, or another polarizable particle, for example.

Before reviewing the consequences of these approximations, and how the derivation of DEP forces can be improved, we note that Eq. 7 accurately informs us the following:

• The DEP force is zero if the field is uniform (i.e., for ∇E=0).

• The DEP force is ponderomotive—with all other factors remaining constant the larger the particle volume the greater will be the DEP force acting on it.

• The induced dipole moment is either aligned with or directed against the applied field, depending on whether the particle’s permittivity is greater or less than that of the surrounding medium, respectively. This corresponds to positive or negative DEP, where a particle is attracted to or repelled from a region of high electric field strength, respectively.

• The DEP force depends on the square of the applied field magnitude, indicating that DEP can be observed using either dc or ac field.

• Electrode geometry is an important experimental factor in the control of the factor (E⋅∇E), which has dimensions of V²∕m³. A value for this factor of 10¹² V²∕m³ can induce a significant DEP force on biological cells, for example, using suitably scaled microelectrodes and applied voltages of the order 1 V.

Particle inhomogeneity, conductive losses, and net charge

Particles such as bacteria and cells exhibit a conductivity associated with mobile ions in their structures, and their suspending medium is usually a conducting electrolyte. When ac fields are applied, these conduction losses are accommodated in the form of either a complex permittivity ${\epsilon }_p^{*}$,

$${\epsilon }_p^{*}={\epsilon }_o{\epsilon }_p-\frac{j{\sigma }_p}{\omega },$$

or a complex conductivity ${\sigma }_p^{*}$,

$${\sigma }_p^{*}={\sigma }_p+j\omega {\epsilon }_o{\epsilon }_p,$$

where j is the imaginary vector $\left(j=\sqrt{-1}\right)$ and ω is the angular frequency (ω=2πf) of the applied ac field. The CM factor given by Eq. 8 can thus be expressed as a complex function using either of the two equivalent forms,

$${\text{CM}}^{\ast }=\left(\frac{{\epsilon }_p^{\ast }-{\epsilon }_m^{\ast }}{{\epsilon }_p^{\ast }+2{\epsilon }_m^{\ast }}\right)\text{or}{\text{CM}}^{\ast }=\left(\frac{{\sigma }_p^{\ast }-{\sigma }_m^{\ast }}{{\sigma }_p^{\ast }+{\sigma }_m^{\ast }}\right).$$ (9)

The total current in the particle can be considered to comprise two elements—one associated with field-induced movement of free charges and the other arising from the field-induced perturbation of bound charges. At low frequencies (ω→0) the current is dominated by the conduction of free charges and there is essentially no phase difference between the field and the current. At high frequencies (ω→∞) the dielectric displacement current dominates and the particle acts like a capacitor with the current leading the applied field by a phase angle close to π∕2 radians.

The instantaneous value of the applied field at location r and time t is given by

$$E\left(r,t\right)=\text{Re}\left[E\left(r\right)e^{j\omega t}\right],$$ (10)

where “Re” signifies that the real part of the expression is to be used [E⋅e^jωt=E(cos ωt+j sin ωt) so that Re[E]=E cos ωt; Im[E]=E sin ωt, where Im is the imaginary part]. From Eqs. 5, 10 the instantaneous effective dipole moment value at time t becomes

$$p\left(t\right)=\text{Re}\left[4\pi {\epsilon }_m{R}^3{\text{CM}}^{\ast }E\left(r\right)e^{j\omega t}\right].$$ (11)

From Eq. 6 the time-dependent expression for the DEP force is thus

$$F_{\text{DEP}}\left(t\right)=\text{Re}\left[p{e}^{jwt}\right]\cdot \nabla \text{\hspace{0.17em}Re}\left[E{e}^{jwt}\right].$$

Substituting for the effective dipole moment from Eq. 11 we obtain the time-average DEP force, acting on a lossy homogeneous spherical particle of radius R, as

$$⟨F_{\text{DEP}}⟩=2\pi {\epsilon }_o{\epsilon }_m{R}^3\text{\hspace{0.17em}Re}\left[{\text{CM}}^{\ast }\right]\nabla {\left|E\right|}^2.$$ (12)

At frequencies below ≈50 kHz,

$$\text{Re}\left[{\text{CM}}^{\ast }\right]\approx {\epsilon }_m\left(\frac{{\sigma }_p-{\sigma }_m}{{\sigma }_p+2{\sigma }_m}\right),$$ (13)

and for frequencies above ≈50 MHz,

$$\text{Re}\left[{\text{CM}}^{\ast }\right]\approx {\epsilon }_m\left(\frac{{\epsilon }_p-{\epsilon }_m}{{\epsilon }_p+2{\epsilon }_m}\right).$$ (14)

At low frequencies the DEP force thus depends on the conductive properties of the particle and suspending medium, while at high frequencies the permittivity values are important. At intermediate frequencies both the conductive and dielectric properties of the medium and particle dictate the magnitude and polarity of the DEP force. Continuity of the displacement flux density across the interface between the particle and the fluid medium [Eq. 4] controls the initial temporal response (equivalent to the high-frequency response) to an applied electric field and, because this involves perturbations of bound charges at the atomic and molecular scale, is independent of particle size. With increasing time after application of the field (equivalent to a lower frequency response) as conduction effects appear, a continuity of current density (J=σ_mE_m=σ_pE_i) must now be maintained across the particle-medium interface. Charges will build up at the particle-medium interface—a process referred to as Maxwell–Wagner interfacial polarization, named after Maxwell’s original “mixture theory”¹⁰and Wagner’s modification to include ac fields.¹¹ This polarization involves the macroscopic movement of free charges (mainly ions) around and through the particle, and so does depend on particle size and the effective surface area over which the particle’s conductive and capacitive properties are expressed. We can estimate the frequency where the displacement (dielectric polarization) current takes over from the conduction current regime (and charges begin to accumulate at particle surfaces) from the relaxation time τ=ε∕σ (Ref. ⁹, p. 15). For an aqueous medium of conductivity of ∼50 mS∕m (a value typical for DEP experiments on cells) the value for τ is ∼1.4×10⁻⁸ s, corresponding to a frequency of ∼10 MHz. If the medium is a physiological strength buffer (∼1.5 S∕m), this transition frequency rises to ∼300 MHz. The relaxation time for the Maxwell–Wagner interfacial polarization is (Ref. ¹², p. 19)

$${\tau }_{\text{MW}}=\frac{{\epsilon }_p+2{\epsilon }_m}{{\sigma }_p+2{\sigma }_m}.$$

So far, we have considered the case of DEP arising from either dc or stationary ac fields. The time-averaged DEP force acting on a particle arises from the interaction of the induced dipole moment with the applied field phasor—in other words both the magnitude and phase of the various field components should be taken into account. This is summarized by the following equation:¹³

$$⟨F_{\text{DEP}}⟩=2\pi {\epsilon }_m{R}^3\left\{\text{Re}\left({\text{CM}}^{\ast }\right)\nabla E^2+\text{Im}\left({\text{CM}}^{\ast }\right)\Sigma E^2\nabla \varphi \right\},$$

where ΣE²∇ϕ represents a summation involving the magnitude and phase ϕ of each field component in a Cartesian coordinate frame. This is the DEP force that acts in traveling-wave DEP experiments (e.g., Ref. 14).

Most particles, especially biological ones, are not homogeneous. Bacteria and cells can be modeled to take account of their heterogeneous structures using the so-called multishell model.¹⁵ Erythrocytes are usually discoid in shape, but when suspended in an electrolyte they often take the form of a spherical particle (about 7 μm in diameter) and can be represented as a thin spherical membrane (i.e., a single shell) surrounding the cytoplasm. To represent cells such as leukocytes, which possess a nucleus, we require a three-shell model (first shell the plasma membrane; second shell the cytoplasm; and third shell the membrane envelope surrounding the nucleoplasm). The multishell model has been extended to describe nonspherical shells¹⁶ and to account for the dielectric anisotropy of the plasma membrane.¹⁷ Maxwell–Wagner polarizations will take place at the interfaces between the various shells, and the magnitudes and temporal dynamics of these various polarizations will depend on the dielectric properties of the materials that make up these shells.

The CM function for a multishell particle can be obtained by evaluating effective values for the relative complex permittivity ${\epsilon }_p^{*}$ or conductivity ${\sigma }_p^{*}$ of the particle. The term effective is used to signify that a heterogeneous (multishell) particle may be replaced conceptually with one having homogeneous smeared-out bulk properties, such that substitution of one particle with the other would not alter the electric field in the surrounding medium. The progressive simplification of a nucleated cell to a simple, homogeneous sphere is depicted in Fig. 4, and a method for achieving this that employs equations readily adaptable to computer modeling has been formulated by Huang et al.¹⁸ Thus, for a human erythrocyte we can use the single-shell model, and its effective complex permittivity is given by

$${\epsilon }_p^{\ast }={\epsilon }_{\text{mem}}^{\ast }\left[\frac{{\left(R∕\left[R-d\right]\right)}^3+2\left(\frac{{\epsilon }_{\text{cyt}}^{\ast }-{\epsilon }_{\text{mem}}^{\ast }}{{\epsilon }_{\text{cyt}}^{\ast }+2{\epsilon }_{\text{mem}}^{\ast }}\right)}{{\left(R∕\left[R-d\right]\right)}^3-\left(\frac{{\epsilon }_{\text{cyt}}^{\ast }-{\epsilon }_{\text{mem}}^{\ast }}{{\epsilon }_{\text{cyt}}^{\ast }+2{\epsilon }_{\text{mem}}^{\ast }}\right)}\right],$$ (15)

in which ${\epsilon }_{\mathrm{mem}}^{*}$ is the complex permittivity of the plasma membrane, ${\epsilon }_{\mathrm{cyt}}^{*}$ is the effective complex permittivity of the cell interior (i.e., the cytoplasm for an erythrocyte), R is the outer radius of the cell, and d is the plasma membrane thickness. The modeling replaces d with the membrane capacitance C_m=ε_mem∕d. This will be discussed in more detail in Sec. 5 to follow. The corresponding CM function is then obtained by substituting this effective value for ${\epsilon }_p^{*}$ into Eq. 9.

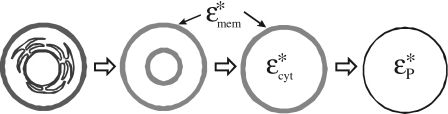
Figure 4.

Schematic representation of how a nucleated cell can progressively be simplified to a homogeneous sphere of effective permittivity ${\epsilon }_p^{*}$, given by Eq. 15, that mimics the dielectric properties of the nucleated cell. The first step in simplification shown here is to represent the endoplasmic reticulum as a topographical feature that increases the effective capacitance of the nuclear envelope. The penultimate step represents the cell as a smeared-out cytoplasm surrounded by a membrane of complex permittivities ${\epsilon }_{\mathrm{cyt}}^{*}$ and ${\epsilon }_{\mathrm{mem}}^{*}$, respectively.

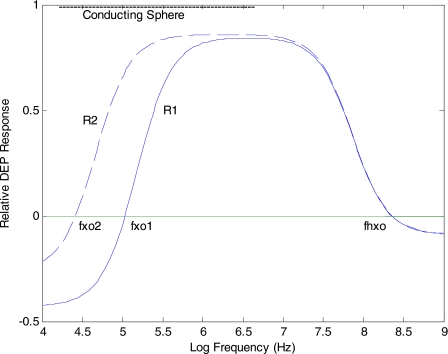
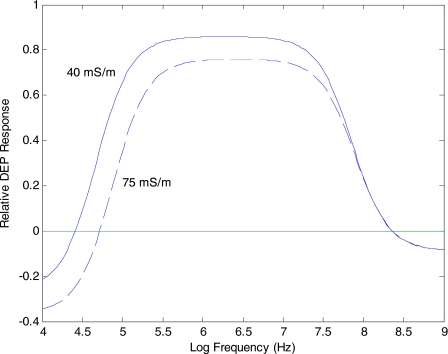
Equation 15 and versions of it to accommodate cells having a nucleus (or bacteria and plant cells possessing a cell wall and∕or vacuole) can be used with Eqs. 9, 12 to model the expected DEP behavior of cells over a wide frequency range.¹⁸ Examples of DEP responses modeled for a viable cell are given in Fig. 5, and show clearly the effect first observed by Höber¹⁹ that with increasing frequency the dielectric properties of a cell with an intact nonconducting membrane approaches that of a conducting sphere. The DEP force, shown for two values of the cell radius, makes the transition from a negative to positive value at a “cross-over” frequency f_xo. Although f_xo is sensitive to the size of the cell, we can see from Fig. 5 that the frequency f_hxo, where the DEP force can reverse polarity again at a higher frequency, does not change with cell size. This agrees with the discussion above that establishing continuity of current density is a low-frequency macroscopic process involving ionic conduction within and around the particle (and therefore depends on particle size), while at higher frequencies microscopic dielectric polarizations are dominant. This fundamental difference in the physicochemical properties that govern the two cross-over frequencies f_xo and f_hxo is also illustrated in Fig. 6, which demonstrates that f_xo is sensitive to changes of the surrounding medium conductivity, whereas f_hxo does not respond to such changes. At the high frequencies, the membrane capacitance effectively shorts out the high resistance of the cell membrane, and the DEP response depends on the relative differences between the permittivities of the cell interior and the surrounding medium.

Figure 5.

Solid line: DEP response modeled for a viable cell normalized against the DEP response for a sphere composed of the same electrolyte as the cell cytoplasm. With increasing frequency the cell’s DEP behavior approaches that of the conducting sphere, making the transition from negative to positive DEP at the “cross-over” frequency f_xo. Dashed line: DEP response for a larger cell (radius R2>R1). The cross-over frequency f_xo is sensitive to cell size, but the cross-over at the higher frequency f_hxo is not sensitive to cell size (with all other dielectric factors remaining constant).

Figure 6.

DEP response modeled for a viable cell for two values of the conductivity of the suspending medium. The DEP cross-over frequency f_xo increases with increasing medium conductivity, but the high-frequency cross-over f_hxo is not sensitive to the medium conductivity.

In principle, the different materials that make up the various shells in the dielectric model should each exhibit a dielectric dispersion given approximately by the well-known Debye single relaxation expression,

$${\epsilon }^{\ast }\left(\omega \right)={\epsilon }^{\prime }\left(\omega \right)-j{\epsilon }^{″}\left(\omega \right)={\epsilon }_{\infty }+\frac{{\epsilon }_s-{\epsilon }_{\infty }}{1+j\omega \tau },$$ (16)

where ε_s and ε_∞ are the low-frequency and high-frequency limits of the permittivity, respectively, and τ is the mean relaxation time (Ref. ²⁰, p. 83). However, over the frequency range from around 1 kHz to 100 MHz, the cell plasma membrane and the suspending medium (if it consists essentially of a weak electrolyte) should not exhibit dielectric dispersions of any significance. The cytoplasm will exhibit dispersions related to the presence of small bodies (e.g., mitochondria, protein structures) and solvated proteins, amino acids, and other biopolymers.^{21, 22} Such dielectric dispersions, when incorporated into the multishell model, introduce relatively small modifications to the overall DEP spectrum and can slightly influence the high-frequency DEP cross-over frequency f_hxo.²³

Particles generally carry a net charge associated with the presence of charged polymers and∕or ionizable acidic and basic groups on their surfaces. Early studies^{24, 25} demonstrated that the low-frequency DEP response for erythrocytes and erythroleukemia cells was affected following neuraminidase-treatment to reduce their cell membrane charge by 50%–60%. The fixed charge on the surface of a particle can influence its DEP behavior through electrophoresis and counterion relaxations and conduction in the double layer that forms around all charged particles when they are suspended in aqueous media. Evidence for an electrophoretic contribution to the low-frequency (<10 Hz) DEP response of a suspension of bacteria was observed by Burt et al.,²⁶ but inertial constraints will render such contributions to be insignificant at higher frequencies, even for very small particles. Counterion relaxation processes, involving both ionic diffusion and ionic conduction around particle surfaces, will however contribute to the total polarizability and influence the DEP response for frequencies up to ∼1 MHz. A comprehensive treatment of electrical double layer polarizations is given by Lyklema.²⁷ In summary, the electrical double layer can be considered to consist of two classes of counterions—those strongly attracted to the fixed charges on the particle surface (termed the Stern layer) and those more loosely associated in the diffuse outer layer where the electrical potential of the charged particle approaches that of the surrounding bulk medium with increasing distance from the particle surface. The “physical” boundary between these two populations of counterions can be considered to be the so-called “slip-plane” at the zeta-potential, where a charged particle plus its Stern layer separates from the outer diffuse population of counterions during electrophoresis.

The influence of the electrical double layer on DEP behavior is particularly important for nanoparticles, where the thickness of the electrical double layer can approach, or even exceed, the particle’s physical diameter (2R). Field-induced mobility of counterions in the double layer gives rise to a surface conductance K_s (typically ∼1 nS) whose influence on the overall polarizability can exceed that of the bulk conductivity, σ_bulk. The total conductivity of a particle can be described as the sum of its bulk and surface conductivity,

$${\sigma }_p={\sigma }_{\text{bulk}}+\frac{2K_s}{R}.$$

This relationship demonstrates that the influence of K_s can dominate over the bulk conductivity for very small particles. Counterions are more mobile in the diffuse layer than in the Stern layer, and contribute separately to the overall magnitude of K_s and thus to the DEP behavior of nanoparticles.^{28, 29, 30, 31} A comprehensive study of the ac and dc electrokinetic properties of latex nanoparticles, as a function of suspending medium conductivity and viscosity, has been reported by Ermolina and Morgan,³² and a theoretical modeling of the DEP force that takes into account the influence of the electrical double layer has been presented by Zhou et al.³³ Analysis of the normal and tangential ionic currents that occur around and at the surface of a particle, when its diameter approaches and becomes smaller than the width of its own electrical double layer, indicates that a capacitance effect contributes to the total polarizability of the particle, and exceeds the influence of the surface conductance K_s.^{34, 35} Basuray and Chang³⁴ also showed that the DEP cross-over frequency for nanocolloids is inversely proportional to the RC time constant of the diffuse layer component of the electrical double layer. This is considered to offer a sensitive method for detecting the hybridization of target molecules onto functionalized nanocolloid probes, based on the change of the surface conductance of these probes and the corresponding change of their DEP cross-over frequency.³⁵ Hoffman and Zhu³⁶ and Hoffman et al.³⁷ demonstrated that electrical double layer effects influence the way nanoparticles aggregate under the influence of a DEP force.

Refining the induced dipole approximation

Equation 1 is referred to as the dipole approximation for the DEP force, because it is based on the assumption that the field nonuniformity is large enough to create a significant DEP force on the particle, but that the field does not vary so strongly throughout the particle as to induce within it a polarization not properly described by Eq. 5. A uniform polarization of the particle is assumed, and represented as an induced dipole moment located at the particle center (e.g., Ref. 3, p. 91; Ref. 5, p. 35). In reality the response of a dielectric to an imposed electric field involves the polarization of its constituent atoms∕molecules, distributed as a continuous function of position, whose polarizations will be sensitive to the value of the local electric field. An inhomogeneous field will result in an inhomogeneous polarization of a dielectric.

The treatment of the polarization of a particle in a nonuniform field can be refined by incorporating an important theorem in electrostatics, which states that the potential generated outside an uncharged sphere, by an arbitrary distribution of charges within it, is identical with the potential of a system of multipoles p_n (n=0 is a point charge, n=1 is the dipole, and so on) located at its center (Ref. ⁹, pp. 176–183). Jones¹² in his book “Electromechanics of Particles” gives an excellent treatment of how the forces and torques experienced by particles subjected to electric and∕or magnetic fields can be understood in terms of multipole theory.

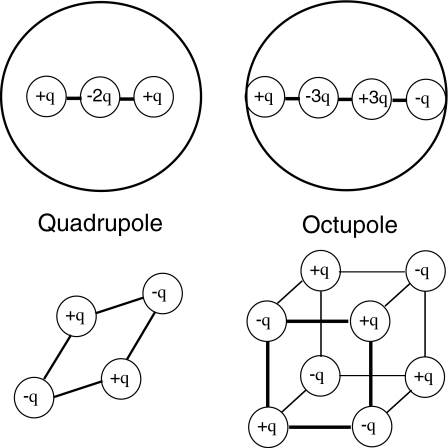
Multipoles can be distributed along an axis of symmetry in a particle, or take a more general form, as shown in Fig. 7. For the linear quadrupole (n=2) shown in Fig. 7, located on and aligned with the field E along the x-axis, it is straightforward to derive the x-directed DEP force as

$$F_{{\text{DEP}}_{n=2}}=q\left[E\left(x+d\right)-2E\left(x\right)+E\left(x-d\right)\right]=q{d}^2\cdot \frac{{\partial }^{2}E}{\partial x^2}.$$

For the octupole (n=3) shown in Fig. 4 we have

$$F_{{\text{DEP}}_{n=3}}=q\left[E\left(x+\frac{3d}{2}\right)-3E\left(x+\frac{d}{2}\right)+3E\left(x-\frac{d}{2}\right)-E\left(x-\frac{3d}{2}\right)\right]=q{d}^3\cdot \frac{{\partial }^{3}E}{\partial x^3}.$$

Only nth-order Taylor series terms survive these calculations, and so for the general nth-order linear multipole we have

$$F_{{\text{DEP}}_n}=q{d}^n\cdot \frac{{\partial }^{n}E}{\partial x^n}.$$

The more general multipoles are treated by Washizu and Jones.³⁸ Green and Jones³⁹ provide a method for determining the linear multipoles (up to the ninth-order) for a range of particle shapes other than spheres (ellipsoids, truncated cylinders, and an approximation of an erythrocyte).

Figure 7.

Examples of axial and nonaxial multipoles constructed from evenly spaced point charges (Ref. ⁹, pp. 176–183). The axial quadrupole is constructed by adding a moment +qd to an original negative moment −qd, a distance d from an initial negative moment −qd located at the origin. The axial octupole is created by repeating this exercise with two quadrupoles.

For the situation where the particle is subjected to an arbitrary nonuniform field we are required to derive a resultant potential ϕ that satisfies the standard boundary conditions as well as Laplace’s equation (∇²ϕ=0). Equation 3 is thus replaced to give a more general expression for the potential ϕ_o generated outside the sphere by a system of multipoles located within it,

$${\varphi }_o=-Ex+\sum _{n=0}^{\infty }{\varphi }_n.$$

The partial potential ϕ_n of the general multipole p_n of nth-order is given by

$${\varphi }_n=\frac{1}{4\pi {\epsilon }_m}{p}_n\frac{Y_n}{r^{n+1}},$$

in which p_n=n!qdⁿ and Y_n involves a Legendre polynomial function determined by the spherical coordinates defining the multipole geometry (Ref. ⁹, pp. 180–181). Thus, the potentials of higher-order moments fall off more rapidly with distance than for a dipole (r⁻⁴ versus r⁻² for a quadrupole, for example) and so their relative importance increases with increasing field nonuniformity.

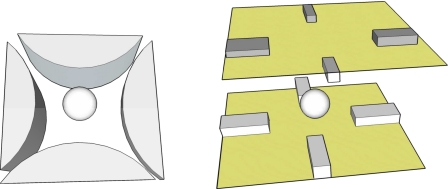
The first report of a DEP force calculation to include the higher-order components of an arbitrary field and the induced multipole moments is that of Washizu,⁴⁰ who illustrated the importance of this for the quadrupole “polynomial” electrode design shown in Fig. 8. Particles can be directed into the central location, and slightly levitated above the plane, of these electrodes by a negative DEP force.⁴¹ At this central location the factor ∇E² is zero, and so no DEP force can be exerted. Washizu⁴⁰ demonstrated that in this situation, and especially for distances less than the particle radius from the center, the induced quadrupole moment should be included in the DEP force calculation. However, for distances far from the center the dipole approximation gives accurate results. This condition is readily satisfied by taking DEP measurements on cells located nearer to the quadrupole electrode edges than to the central location.^{42, 43} The importance of higher-order moments was also found to apply to azimuthally periodic electrode structures used to achieve passive DEP levitation of particles, where a pronounced size-dependent effect not anticipated by the conventional dipole-based theory was observed.^{44, 45} Higher-order moments are responsible for the levitation force achieved by such electrode structures because the electric field is zero along the central axis and so the induced dipole moment is zero. Schnelle et al.⁴⁶ investigated the situation for DEP field cages formed by a sandwich structure of two planar quadrupole electrode structures (Fig. 8), and concluded that quadrupole moment forces contribute ∼5% of the total DEP force for particles larger than about a quarter of the electrode spacing. For particles smaller in diameter than about a tenth of the electrode spacing, the error arising from a DEP force calculation that ignores the quadrupole contribution is typically smaller than 1%.

Figure 8.

A spherical particle trapped (left) by quadrupole polynomial electrodes (Ref. ⁴¹) and (right) in a 3Dl eight electrode field cage (Ref. ⁴⁶). The field acting along the axis of symmetry in these two electrode assemblies is zero, and so no dipole moment can be induced in the particles. Higher-order moments are induced and account for the DEP forces.

For a spherical dielectric particle of radius R with complex permittivity ${\epsilon }_p^{\ast }$, suspended in a medium of permittivity ${\epsilon }_m^{\ast }$, and subjected to a sinusoidal steady-state electric field vector E, the effective nth-order multipolar moment is a tensor phasor of the form^{45, 47}

$$p_n=\frac{4\pi {\epsilon }_m{R}^{2n+1}}{\left(2n-1\right)!!}{\text{CM}}_{\left(n\right)}{(\nabla )}^{n-1}E.$$

CM_(n) is the general multipole form of the CM factor given by

$${\text{CM}}_{\left(n\right)}=\frac{{\epsilon }_p^{\ast }-{\epsilon }_m^{\ast }}{n{\epsilon }_p^{\ast }+\left(n+1\right){\epsilon }_m^{\ast }}.$$

The general, time-average expression for the DEP force acting on the nth-order multipole is thus

$$⟨F_{{\text{DEP}}_n}⟩=\text{Re}\left[\frac{p_n{[\cdot ]}^n{(\nabla )}^{n}E}{n!}\right],$$

where [⋅]ⁿ represents n dot products performed on the dyadic tensors and (∇)ⁿ represents n vector ∇ operations.⁴⁷ This multipolar analysis was also applied by Jones and Washizu⁴⁷ to traveling-wave DEP. The important conclusion was also reached that the various multipolar DEP forces show similar frequency dependencies, and so will not influence the interpretation of DEP cross-over measurements or cell separation protocols that are based on such measurements [e.g., Ref. 48, 49, 50]. Washizu⁵¹ extended the multipole moment analysis of the DEP force to the case of spherical particles being manipulated by focused laser beams (i.e., optical tweezers).

The overall, time-average DEP force is a summation of the multipole contributions,

$$⟨F_{\text{DEP}}⟩=\frac{1}{2}\sum _{n=1}^{\infty }\text{Re}\left[\frac{p_n{[\cdot ]}^n{(\nabla )}^{n}E}{n!}\right].$$

For the case of an axially symmetric nonuniform field acting on a sphere, and including only the dipole and quadrupole contributions, we have

$$⟨F_{\text{DEP}}⟩=2\pi {\epsilon }_m{R}^3\text{\hspace{0.17em}Re}\left[\frac{{\epsilon }_p^{\ast }-{\epsilon }_m^{\ast }}{{\epsilon }_p^{\ast }+2{\epsilon }_m^{\ast }}\right]\nabla E^2+\frac{2}{3}\pi {\epsilon }_m{R}^5\text{\hspace{0.17em}Re}\left[\frac{{\epsilon }_p^{\ast }-{\epsilon }_m^{\ast }}{2{\epsilon }_p^{\ast }+3{\epsilon }_m^{\ast }}\right]\nabla \cdot \nabla E^2.$$

For small particles the first (dipole force) term dominates the overall DEP force, while for larger particles the quadrupole term becomes important.

Presence of perturbing boundaries or particles

It is usually the case that during DEP experiments many of the particles are close to an electrode or channel surface, or interact to form “pearl chains” oriented along field lines. The DEP behavior of isolated cells can be different from those that form doublets, triplets, or higher-order aggregates, and those that are close to metal or dielectric boundaries.

The influence of a neighboring particle can be appreciated from the following simple example, based on a model described by Stoy.⁵² Instead of considering a single sphere inserted into an infinite medium and imposed uniform field E, we consider the case of two identical spheres, placed distance D apart along the x-axis and collinear with the field E. We place the center of sphere 1 at the origin of the spherical coordinate system employed for Eq. 3. Sphere 2 now experiences a net field E₂ given by

$$E_2=E\left(1+\frac{2\left(\text{CM}\right)}{D^3}\right).$$

Sphere 1 now sees this added field from sphere 2 and produces an induced dipole moment,

$$p_1=4\pi {\epsilon }_m\left(\text{CM}\right)E\left[1+\frac{2\left(\text{CM}\right)}{D^3}\left(1+\frac{2\left(\text{CM}\right)}{D^3}\right)\right].$$

Sphere 2 will now see this field created by the induced dipole of sphere 1. If this procedure is repeated ad infinitum we obtain the interactive dipole moments p₁ and p₂ in closed form,⁵²

$$p_1=p_2=4\pi {\epsilon }_m\left(\text{CM}\right)E\left(\frac{1}{1–2\left(\text{CM}\right)∕D^3}\right).$$

Each sphere distorts the local field of the other, and the mutual attractive DEP force acting on them is⁵²

$$F_{\text{DEP}2}=-F_{\text{DEP}1}=-\frac{6p_1\cdot p_2}{4\pi {\epsilon }_m{D}^4}.$$

Only when the spheres are more than a radius apart will the major contribution to this mutual DEP force come from the dipole-dipole interaction. As the spheres approach more closely and then touch, the DEP force between them will depend upon the interaction of all the multipoles in sphere 1 with all the multipoles in sphere 2. Stoy⁵³ extended his model to compute the DEP force between identical touching spheres in a parallel field, to include up to 2800 interactive linear multipoles. The DEP force between two lossy particles in a lossy medium, incorporating multipoles polarized by an external field, has been treated by Sancho et al.⁵⁴ A multiple image approximation has been employed to study the polarization spectra of a pair of touching cells and colloidal particles.⁵⁵ These studies were restricted to plain spherical particles, aligned with the direction of the electric field. The practical calculation of the interaction requires truncation of expansions at some finite number of terms and is affected by convergence problems when particles have high permittivity or they are closely spaced. Giner et al.⁵⁶ employed the dipole approximation for heterogeneous (shelled) particles to model the formation of longitudinal and transverse pearl chains observed in DEP experiments of mixtures of yeast cells and latex particles. The effect of mutual interactions in governing the coupled electrorotation of two dielectric microspheres has been investigated both theoretically and experimentally by Simpson et al.⁵⁷ The effect that pearl chaining of cells has on the DEP cross-over frequency, and how dipole-dipole interactions influence electrorotation (including the observation of a new precession effect), has been studied both theoretically and experimentally.⁵⁸

The effect of the perturbing influence of boundaries has not received as much attention as that given to particle-particle interactions. A polarized particle located near a metal or dielectric wall will induce image charges in the wall material to create an attractive force. Lo and Lei⁵⁹ employed the theory of images (Ref. ⁹, pp. 193–194; Ref. 12, pp. 196–207) to derive DEP force and torque expressions for a sphere of radius R located a distance h from a wall. The ratio of the wall perturbing force to the DEP force was found to be of the order (L∕h)(R∕2h)³. L is the length scale of the electric field, taken to be the distance between opposing electrodes for DEP and electrorotation experiments. For L=100 μm, and a particle radius of 5 μm, the particle center would need to be more than 12 μm from a boundary for the wall effect to be negligible (i.e., less than 5% of the primary DEP force or electrorotation torque). This condition can readily be satisfied for electrorotation experiments, but this is not the case when particles are being attracted to an electrode by positive DEP. For traveling-wave DEP, L is the distance between every second electrode, corresponding to a one-half wavelength when quadrature phase voltages are used, and thus equal to the distance of maximum phase difference on the electrode track.¹⁴ A typical value for L is 20 μm. A 5 μm radius particle would need to be levitated more than 8 μm above the electrode plane for the wall effect to be negligible. Levitation heights above 25 μm are common, and so this condition is readily met in traveling-wave DEP.

THEORETICAL MODELING

A detailed analysis of the factor (E⋅∇)E is often required for the design of the electrodes in a DEP device. A common problem when attempting this arises from the nature of the boundary conditions. The applied electric potential is chosen for the surface of metal electrodes (the Dirichet condition) and in the rest of the space to be analyzed the Neumann condition is used to specify that the normal derivative of electric potential at a boundary surface is zero. This can limit the number of simple geometries able to be analyzed accurately. Numerical methods have been adopted to derive approximate solutions, based on Green’s theorem⁶⁰ and Fourier series.⁶¹ However, as discussed by Green et al.,⁶² these methods can lead to inaccurate results. A closed-form solution with the exact boundary conditions for conventional DEP electrodes has been presented by Chang et al.,⁶³ but is difficult to apply to traveling-wave DEP, for example. Analytical solutions of the electric potential for planar electrodes that are relevant to both normal DEP and traveling-wave DEP applications have been presented by Sun et al.⁶⁴ Song et al.⁶⁵ recently described a new semianalytical approach to the modeling of the DEP force generated by planar parallel electrodes as well as those forming three-dimensional (3D) arrays of the form developed by Chen et al.⁶⁶ The unknown coefficients of the Fourier series derived for the electric potential equation were determined by training a linear neural network, using appropriate data that satisfy both the Dirichet and Neumann conditions.

Voldman et al.^{67, 68} developed simulation tools to model the performance of quadrupole DEP particle traps. This simulation takes as inputs the electric-field data and other experimental parameters and computes the total force acting on a particle everywhere in space. From this it can be determined if the total force on the particle in the trap stably goes to zero at some location. Such locations are called holding points, and represent where the particle will be held in a trap. By varying the applied flow rate for a given experimental condition, this modeling environment can determine when the holding points cease to exist and therefore the strength of the DEP particle trap. Schnelle et al.⁶⁹ conducted a comprehensive analysis and experimental investigation of the forces acting on dielectric particles and living cells exposed to alternating and rotating fields generated by 3D multielectrode microsystems. This analysis included a description of numerical procedures for calculating the electric field distribution and negative DEP forces for electrodes of any shape, and dielectric particles of complex structure, produced by high-frequency ac or rotating electric fields up to 400 MHz. Various multielectrode systems were tested for their ability to move and assemble microparticles or living cells without contact with the electrodes. Park and Beskok⁷⁰ provided a simple, but valuable, theoretical model that considers the relative magnitudes of DEP, electrophoresis, ac-electro-osmosis, and Brownian motion forces acting on microparticles. This theoretical model provides quantitative descriptions of ac electrokinetic transport, for a given target species and suspending medium conductivity, over a wide spectrum of electric field amplitude and frequency. Experimental validations of the model were conducted by Park and Beskok⁷⁰ using interdigitated microelectrodes for polystyrene and gold particles, as well as Clostridium sporogenes bacterial spores.

TECHNOLOGY

The techniques used for the study and exploitation of DEP have advanced considerably since the overview presented by Pohl in his seminal text of 1978. Apart from the term DEP now being universally accepted there have been significant advances in electrode design, the construction of DEP test chambers, and with methods to monitor the DEP collection of particles at electrodes.

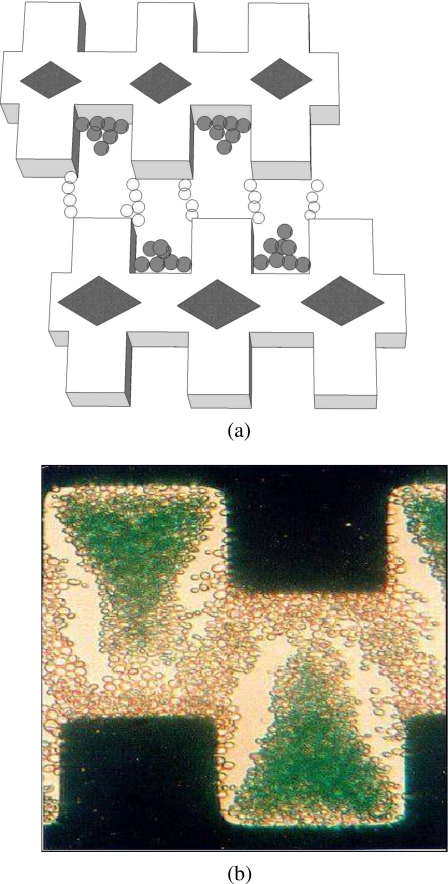
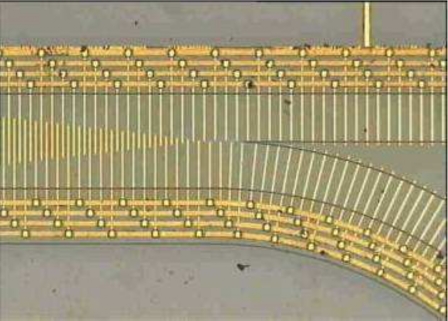
Pohl describes the use of wire electrodes (diameter 0.258–1.59 mm), energized with applied voltages up to 11 kV, in DEP experiments to separate various types of particles in mixtures (Ref. ⁵, pp. 122–367). To quantify DEP collection of particles, the electrodes were observed through a microscope and particle collection (often in the form of pearl chain growth) was photographed over several minutes (Ref. ⁵, pp. 361–380). The use of high voltages often resulted in fluid motion, arising from thermal effects, that perturbed the DEP-induced motions of the particles. This problem has been reduced in a DEP microfluidic device in which 100 μm diameter platinum wires, in a pin-plate configuration, span the entire depth of the DEP chamber and are energized with 15 Vpp voltages.⁷¹ The fact that the parameter (E⋅∇)E in Eq. 7 has units of V² m⁻³ provided the clue that, by miniaturizing the electrodes, DEP measurements could be improved, in terms of speed and the avoidance of thermal and electrolysis effects, using much smaller applied voltages. For example, by reducing the pertinent scale of the electrode geometry 1000-fold, the same DEP force on a particle can be achieved with a 100-fold reduction of applied voltage. The technology for fabricating microelectrodes already existed in the form of photolithography and metallic vapor deposition (e.g., Ref. 72). The interdigitated, castellated geometry shown in Fig. 9a was chosen because it provides a large value for (E⋅∇)E using modest values of applied voltage.⁷³ The electrode thickness is ∼70 nm, and the characteristic dimension defining the planar geometry typically ranges from 10 to 120 μm, chosen to be 5–10 times the diameter of the particles to be manipulated by DEP. As depicted in Fig. 9b, this electrode geometry can be used to simultaneously observe both positive and negative DEP of cells across an array of microelectrodes.⁷⁴ Cells experiencing negative DEP are elevated above the electrode plane into the fluid medium, and this has been exploited in flow-through devices for the DEP separation and isolation of different cell types in mixtures (e.g., Ref. 75). By aligning the castellations, as shown in Fig. 10a, particles elevated into a flowing fluid are directed into well defined flow paths.⁷⁶ This effect has been exploited by Yasukawa et al.⁷⁷ in a modified design, shown in Fig. 10b, to separate particles according to their size. By coupling acoustic waves into an interdigitated microelectrode system, particles can first be preconcentrated before focusing them into flow channels and to precise locations using DEP forces.⁷⁸ Rajaraman et al.⁷⁹ describe rapid and low cost microfabrication methods to produce electrode arrays of the interdigitated, castellated geometry.

Figure 9.

(a) The interdigitated, castelled, electrode design for observing both positive and negative DEP collection of particles (Ref. ⁷⁴). Particles collecting in the diamond-shaped areas on the electrodes are driven there by hydrodynamic fluid flow (Ref. ⁸⁰). (b) Viable yeast cells collecting by positive DEP into pearl chains, and (stained) nonviable cells collecting by negative DEP into triangular aggregations levitated above the electrode plane (e.g., Ref. 49, 50).

Figure 10.

(a) Particles focused into narrow bands of flow in an interdigitated, castellated, electrode system (e.g., Ref. 76). (b) A modified interdigitated, castellated design for separating particles according to their size into separate fluid flow streams (Ref. ⁷⁷).

In the original investigations⁷⁴ of the castellated design, cells were observed to collect as diamond-shaped aggregations on the upper surface of the planar electrodes at frequencies below 500 Hz [Fig. 9a]. With increasing conductivity of the suspending medium, the frequency up to which this effect was observed increased to an upper limit of around 100 kHz. This type of particle aggregation was concluded to not arise from positive DEP, but possibly to be influenced by electrophoretic effects. However, Green and Morgan⁸⁰ and Ramos et al.⁸¹ correctly interpreted this effect in terms of a hydrodynamic fluid flow induced by electro-osmotic stress arising from the interaction of the electric field and the electrical double layer on an electrode surface. Anomalous frequency effects, not explainable by DEP forces alone, were also observed by Voldman et al.⁶⁷ for particles held in traps, and this was also attributed to electrohydrodynamic flow. Hoettges et al.⁸² later designed a DEP particle trap to exploit such fluid flow effects in a so-called “zipper” electrode design. A DEP device architecture that offers interesting possibilities for particle transport without the use of fluid flow is the ratchet geometry described by Gonzalez and Remcho.⁸³

Another electrode design, the quadrupole polynomial electrode system shown in Fig. 8, was chosen to provide defined analytical expressions for the spatial variation of the factor ∇E².⁴¹ The design of polynomial electrodes is based on the assumption that the electrical potential at any point created by an electrode system of interest is defined by a polynomial that obeys Laplace’s equation. By substituting this polynomial into Laplace’s equation the corresponding equipotentials can therefore be determined, and these in turn can be used to define the electrode boundaries. The general design comprises 2n electrodes, but the most common one employs n=2, namely, the quadrupole. Electrode separations from 5 to 500 μm (as measured between opposing electrodes across the center) have been extensively used for both DEP and electrorotation experiments. The quadrupole design has found wide application. For example, a quadrupole electrode array has been used in a device to monitor the DEP cross-over frequencies (Fig. 5) of oligonucleotide-functionalized silica nanoparticles as they participate in DNA-DNA hybridization reactions,⁸⁴ and Kuo and Hsieh⁸⁵ describe a method for performing single-bead-based biochemical assays on a quadrupole DEP microfluidic chip. Voldman et al.^{67, 68} designed extruded quadrupole electrodes, with an asymmetric trapezoidal geometry, that are electrically switchable and can be scaled up to form a dynamic array cytometer. The ability of quadrupole electrodes to form negative DEP traps is useful when operating at high values of the fluid medium conductivity. For example, they have been developed as single-cell trapping devices for fluids having conductivities (1.25 S∕m) typical of physiological fluids and culture growth conditions.⁸⁶ A zipper electrode design has been described by Hoettges et al.⁸² in the form of an array of interlocking, approximately circular electrode pads. As already mentioned, this design exploits field-induced electrohydrodynamic fluid flow to direct particles toward the electrode pads, and then DEP forces to trap them. This increases the effective capture volume for particles, and there is also the advantage that the particles are deposited at the centers of relatively large electrodes and can potentially be detected by surface plasmon resonance or evanescent light scattering. A general overview of electrodes commonly used for DEP studies of cells is given by Hoettges.⁸⁷

Methods other than photographic recording through a microscope have been developed to measure the DEP collection of particles at electrodes. This can be achieved by monitoring changes in the optical scattering of light beams through particle suspensions,⁸⁸ by computerized image analysis of particle motion,^{42, 89} and by measuring changes of the impedance of the electrodes.^{90, 91} More recently, fluorescence spectroscopy has been used to measure the DEP collection of submicron particles.⁹² An array of zipper DEP electrodes has been fabricated onto a quartz crystal to provide an extra force to drive particles toward the crystal surface.⁹³ Particles loading onto the crystal can be detected very sensitively as a shift in resonant frequency of the crystal, and this DEP-aided device was found to perform up to five times faster than other quartz crystal microbalance surface loading techniques described in the literature. Surface enhanced Raman scattering has been used as an on-chip detection method in an integrated DEP device for the continuous filtering, trapping, and sorting of bacteria.⁹⁴

A significant development has also been the introduction of new materials and methods for fabricating DEP devices. Early devices (e.g., Ref. 73) consisted of two glass slides held apart by a thin gasket, with microelectrodes deposited on one or both inner faces, sealed together with inlet and outlet fluid ports using epoxy resin. The microelectrode fabrication required access to photolithography and metallic vapor deposition facilities in a clean room. The introduction of the silicone polymer poly(dimethylsiloxane) (PDMS) has enabled fast and inexpensive fabrication of microfluidic devices by “soft lithography” under normal benchtop conditions.^{94, 95} Apart from being robust, flexible, biocompatible, and of low thermal conductivity, PDMS is also ideal for producing devices that require more than one material in fabrication, since it can seal to a variety of materials. 3D devices are easily fabricated by aligning and sealing different layers of PDMS containing channels, reservoirs, valves, and electrode-bearing substrates. Valuable protocols for using PDMS in the fabrication of microfluidic devices has been provided by Friend and Yeo.⁹⁶ A reconfigurable microfluidic chip system has been developed by Dalton and Kaler.⁹⁷ PDMS microchannels are reversibly bonded onto the chip, and are readily removed for cleaning, changing analytes, or to allow different microfluidic channel or electrode geometries to be used. Using this technique, rapid prototyping of both microelectrode designs and microfluidic systems can be performed by most research groups (PDMS is commercially available as a two-part self-curing material supplied as liquids). Using photopatternable silicones, two levels of metal deposited electrodes can be sandwiched into a microchannel layer, without an extra etching step being required to make electrical contact between the fluid in the channel and electrodes on the upper and lower layers.⁹⁸ There is also now the ability to pattern microfluidic networks using dry film resist in either clean room conditions or in a basic laboratory environment. The resist can be double-bonded at relatively low temperatures without the use of extra adhesives, and so complex devices can be fabricated with active elements on two substrate layers.⁹⁹ Aspect ratios of more than two can be achieved for free standing structures such as channels and pillars. The dry resist is inexpensive, fluid sealable, biocompatible, and can be processed on almost any substrate with any dimension, ranging from a single chip to complete silicon wafer.

Electron beam lithography and thin film techniques have been used to fabricate vertical microelectrodes, with electrode gaps down to 0.2 μm, made by the superposition of niobium, titanium, and gold layers.¹⁰⁰ The niobium layer improves the mechanical strength and ensures a good resistance of the structure to galvanic corrosion. Excimer laser ablation, capable of high-resolution patterning over large areas, has also been used to fabricate DEP devices. Examples of this are glass-based chips, combining traveling-wave DEP and electrorotation, to concentrate and assay the viability of microorganisms,¹⁰¹ and structures incorporating DEP, traveling-wave DEP, and electrorotation for characterizing and selectively trapping cells, microorganisms, and other particles.¹⁰² Figure 11 shows a traveling-wave DEP junction, fabricated by excimer laser ablation and designed to bring together or separate different particle types.¹⁰² Combining the complementary techniques of DEP, traveling-wave DEP, and electrorotation is a continuing trend. For example, DEP and traveling-wave DEP have been combined onto a single, personal computer (PC)-controlled, printed circuit board and tested by manipulating tumor cells.¹⁰³ All three ac electrokinetic techniques have been incorporated onto a single, integrated, silicon chip (3×6 mm²) using conventional microfabrication, and tested using human malignant cells to demonstrate the ability to perform as a programmable microsystem.¹⁰⁴ Electrode arrays have also been produced by the excimer laser ablation of indium tin oxide (ITO) electrodes.^{105, 106, 107} Although the optical transparency of an ITO film is high, making this electrode material particularly suitable for observing DEP particle manipulation with transmission microscopy, UV radiation such as that used in an excimer laser beam is efficiently absorbed by the ITO for it to be micromachined.

Figure 11.

A traveling-wave DEP junction, fabricated by laser ablation, for the separation or bringing together of different particles types (Ref. ¹⁰²).

The development of DEP technology has always been driven by both curiosity and the search for potential practical applications. The separation of target cells from cell mixtures or biofluids for diagnosis, drug screening assays, therapeutic applications, or for further analysis are obvious applications. Examples of how DEP technology has evolved to address such opportunities include the “funnel” design shown in Fig. 12 and developed by Fiedler et al.¹⁰⁸ Particles are guided by the angled electrodes to a small exit gap, at which point particle concentration can be considerably enhanced over the starting concentration introduced into the device. Angled electrodes are employed in an integrated DEP chip design for the continuous filtering and sorting of bioparticles,¹⁰⁹ and also used to great effect in a continuous DEP size-based particle sorter¹¹⁰ and a multitarget DEP activated cell sorter described by Kim et al.¹¹¹ A simple arrangement for aligning cells in fluidic channels, consisting of two face-to-face strip electrodes mounted on the top and bottom of a microchannel, has been described by Schnelle et al.¹¹² In this device, particles exhibiting negative DEP are brought by fluid flow to an energized electrode pair, and as a result of experiencing repulsion forces from both electrodes are lifted into the central stream of the fluid flow. This basic concept has been refined by Demierre et al.¹¹³ who fabricated a microfluidic device based on an arrangement of lateral metal electrodes and a patterned insulator. This device combines the concept of insulator-based “electrodeless” DEP with multiple frequencies to achieve focusing and continuous separation of dielectric particles flowing through a channel. The opposition of two DEP-force fields, operating at different frequencies, defines a position of equilibrium for the dielectric particles placed in these fields. The use of curved microchannels for focusing particles into defined flow streams has also been investigated.¹¹⁴ As well as being able to direct particles into specific fluidic streams or ports, the selective trapping of them is also important. A simple method for producing microwell DEP traps has been described by Fatoyinbo et al.¹¹⁵ and involves drilling holes through a laminate consisting of 20 aluminum layers and 19 epoxy layers. Bocchi et al.¹¹⁶ describe a similar method that involves drilling holes through a polyimide substrate containing copper-gold or aluminum metal layers that form three annular electrodes within the well. A channel under the device provides the means for fluid flow into the microwells by capillary action. An array of traps designed for single-particle patterning, and capable of holding cells in position against the force produced by practical fluid flow rates, has been described by Rosenthal and Voldman.¹¹⁷ Thomas et al.¹¹⁸ describe a particle trap, consisting of a metal ring electrode and a surrounding ground plane, to create a closed electric field cage for particles experiencing negative DEP. The simplification that each trap requires just one electrical connection allows for the fabrication of a large array of single particle trapping centers, capable of holding the particles in a flowing fluid. The operation of the device was demonstrated by trapping single latex spheres and HeLa cells against a moving fluid. Cells can be maintained on the chip for further culture, or released from the chip by fluid flow. Kang et al.¹¹⁹ describe a microfluidic device for separating particles based on a hybrid design of a PDMS insulating hurdle and a pair of embedded metal electrodes to generate DEP forces. DEP forces can be used to increase the rate at which particles drift toward a sensing element. An example of this is described by Pham et al.,¹²⁰ who theoretically modeled and fabricated electrodes, in the form of pyramidal shaped trenches, to enhance the transport of bioparticles such as cells, proteins, and DNA toward reactive surfaces. Particles experiencing either positive or negative DEP can be attracted toward separate collection regions in this pyramidal design. Iliescu et al.¹²¹ describe a bidirectional field-flow DEP separation system, comprising a glass∕silicon∕glass sandwich structure. The silicon layer defines the walls of the microfluidic channels and also provides the electrodes in the form of rows of 3D square-shaped pillars.

Figure 12.

(a) The DEP funnel electrode design for focusing and concentrating particles in a flowing aqueous suspension (based on Ref. 108). This design has been exploited in a particle sorting device described by Kralj et al. (Ref. ¹¹⁰) and an on-chip molecular library screening device (Ref. ²⁰²). (b) An electrodeless DEP particle trap formed by a dielectric constriction, etched into a quartz plate, for creating local and large field gradients for DEP (Ref. ¹²²). This design has been used to concentrate and pattern DNA (Refs. ¹²², ¹²³) and to design assays based on DNA hybridization (Refs. ¹²⁴, ¹²⁵).

DEP trapping of particles is typically carried out using metal electrodes to provide high field gradients. Measurements below ∼1 kHz are often limited because of water electrolysis (hydrogen and oxygen gas bubbles can appear at the electrode edges and destroy the integrity of the electrodes!). Chou et al.^{122, 123} avoided this limitation by using constrictions or channels in an insulating material to squeeze the electric field in a conducting solution, thereby creating a high field gradient with a local maximum. The advantages of this electrodeless form of DEP are that no metal evaporation is required during the fabrication process, it is mechanically robust and chemically inert, and very high fields can be applied without gas evolution due to electrolysis at metal electrodes. Chou et al.^{122, 123} demonstrated that this electrodeless form of DEP can be used to concentrate and pattern both single-strand and double-strand DNA, at far lower frequencies than are feasible with metallic trapping structures. This technology brings DEP down to the molecular level, an exciting development that is already being directed toward rapid DNA hybridization assays.^{124, 125} The ultimate in an electrodeless approach must surely be the use of cusp-shaped silica nanocolloids to create a localized high-field gradient to attract single-stranded DNA in a DNA hybridization assay.¹²⁵ An alternative “conventional” electrode approach, in which some electrodes are energized but others are left electrostatically floating, has been presented by Golan et al.¹²⁶ They demonstrate that floating electrodes can produce effective DEP forces, with the advantage that they do not require a connection to an external signal. This greatly simplifies the situation where nanoelectrodes are to be used, and is envisaged as a potential bottom-up DEP fabrication tool where nanoparticles need to be manipulated with nanometer spatial resolution. Cummings¹²⁷ developed a particle filter∕concentrator that operates without any metal electrodes. A relatively large, low-frequency, or dc voltage is applied across an array of insulating studs. Particles flowing through these studs are directed into flow paths according to the relative influences of the electrokinetic and negative DEP forces acting on them. Positive DEP has been demonstrated for DNA in an optical manipulator using micron-sized localized electrodes created by laser illumination of hydrogenated amorphous silicon.¹²⁸ The concept of four-dimensional manipulation using DEP forces has been introduced by Honegger et al.¹²⁹ using Janus particles. Janus particles are dissymmetric systems with two faces that could present two different physical∕chemical properties, offering new possibilities in microfluidic research fields. In their microfluidic experiment, Honegger et al.¹²⁹ demonstrated that not only precise 3D localization of these particles is possible, but also that their rotation can be controlled by the gradient of the applied electrical field.

An impressive achievement was the first demonstration of in vitro DEP force microscopy (DEPFM) on immobilized cells.¹³⁰ DEP force spectra were obtained in situ in the very short time of ∼125 ms for red blood cells, and acquired over a region comparable in dimension to the effective diameter of a scanning probe microscopy tip. Good agreement was observed between the measured DEP spectra and predictions using a single-shell model for the cells. In addition to allowing for highly localized DEP characterization, DEPFM should be able to provide the means for monitoring localized changes in cell membrane capacitance of cells under aqueous conditions. Another impressive development has been the integration on a disposable silicon chip of DEP actuators and optical sensors using complementary metal-oxide-semiconductor (CMOS) technology. Manaresi et al.¹³¹ describe an 8×8 mm² chip containing 102 400 actuation electrodes, arranged in an array of 320×320, 20×20 μm² microsites each comprising addressing logic, an embedded memory for electrode programming, and an optical sensor. This design can enable software-controlled displacement of more than 10 000 individual living cells in enclosed fluidic channels. By changing, under software control, the pattern of voltages applied to the electrodes, DEP field cages can be independently moved around the electrode array. Any cell or particle trapped in these field cages is detected by the photodiodes located in each microsite. A cell-based biosensor comprising integrated DEP electrodes for cell positioning, ion-sensitive field-effect-transistors (ISFETs), and pseudoreference electrodes has been fabricated using n-channel metal-oxide-semiconductor (nMOS) silicon technology.¹³² The ISFETs act as pH sensors, and were used to monitor the metabolism of bacteria that had been positioned on the active area of the ISFET using DEP forces. A general purpose DEP system has also been described by Liu et al.,¹³³ consisting of a series of planar microelectrode arrays of different shapes and interelectrode spacings, that is suitable for mass production. This “test bed” can be used to investigate the DEP properties of a wide range of particles, as well as being able to assemble devices (e.g., ZnO nanorods as a humidity sensor) using DEP forces at the micro- and nanoscale.

APPLICATIONS

It is evident from Fig. 2 that the major efforts in DEP are now directed toward applications. To cover the range of applications in detail would merit a review of its own, and so only a broad overview is presented here—mostly in the form of tabulated information.

Patents

A good way to appreciate the state of applications of a technology is to review the relevant intellectual property. This can reveal more details of the technology than appears in the scientific literature, as well as the types of companies concerned with its commercial exploitation. The first U.S. patent in the field of DEP appears to be that granted to Hatfield¹³⁴ for separating powder mixtures (to include liquids as well as solids) suspended in a liquid, whose “dielectric capacity” lies between that of the constituents of the powder. It is understood in this patent that those suspended particles of greater dielectric constant than the liquid will move to the strongest part of an applied electrostatic field, while those particles of less dielectric capacity than the liquid will move out of the electrostatic field between the electrodes. “The rule is that the particles tend to move so as to increase the dielectric capacity of the system.” This, basically, is the guiding principle of “energetics” followed in all subsequent technologies developed to separate or manipulate particles using DEP (factor ε_mR³(CM)E² being proportional to the work required to move a particle of radius R between field E and a zero field region).

Table 1 provides a list of U.S. patents granted in the field of DEP from January 2005 to May 2010, and gives an insight into the range of perceived applications.

Table 1.

Patent number, date of grant, inventors, and title of U.S. patents granted in the field of DEP for the period January 2005–May 2010.

6,875,329 (5 April 2005): Washizu and Kawabat, Method for separating substances using a dielectrophoretic apparatus
6,881,314 (19 Apr 2005): Wang, Cheng, Wu and Xu, Apparatuses and methods for field flow fractionation of particles using acoustic and other forces
6,887,362 (3 May 2005): Huang, Ewalt, Haigis, Forster and Krihak, Dielectrophoretic separation and immunoassay methods on active electronic matrix devices
6,916,656 (12 July 2005): Walters, Walters and King, Nonlinear amplitude dielectrophoresis waveform for cell fusion
6,936,151 (30 August 2005): Lock, Pethig and Markx, Manipulation of particles in liquid media
6,942,776 (13 September 2005): Medoro, Method and apparatus for the manipulation of particles by means of dielectrophoresis
6.942.776 (24 January 2006): Cheng, Sheldon, Wu and O’Connell, Channel-less separation of bioparticles on a bioelectronic chip by dielectrophoresis
7,014,747 (21 March 2006): Cummings and Singh, Dielectrophoretic systems without embedded electrodes
7,029,564 (18 April 2006): Lock and Pethig, Dielectrophoretic apparatus and method
7,056,746 (6 June 2006): Seul and Li, Array cytometry
7,060,224 (13 June 2006): Edman, Heller, Formosa and Gurtner, Methods for the electronic, homogeneous assembly and fabrication of devices
7.063.777 (20 June 2006): Lee, Pethig and Talary, Dielectrophoretic particle profiling system and method
7,081,192 (25 July 2006): Wang, Wu, Cheng, Yang and Xu, Methods for manipulating moieties in microfluidic systems
7,135,144 (14 November 2006): Christel, Gregory, McMillan, Northrup, Petersen and Pourahmadi, Method for the manipulation of a fluid sample
7,153,648 (26 December 2006): Jing, Zhang and Cheng, Dielectrophoretic separation of stained cells
7,161,107 (9 January 2007): Krupke and Hennrich, Method, arrangement, and use of an arrangement for separating metallic carbon nanotubes from semiconducting carbon nanotubes
7,169,282 (30 January 2007): Talary, Pethig and Lee, Dielectrophoresis apparatus
7,198,702 (3 April 2007): Washizu and Kawabata, Method for separating substances using dielectrophoretic forces
7,204,923 (17 April 2007): Cummings, Continuous flow dielectrophoretic particle concentrator
7,259,744 (21 August 2007): Arango and Jacobson, Dielectrophoretic displays
7,267,752 (11 September 2007): King, Lomakin, Jones and Ahmed, Rapid flow fractionation of particles combining liquid and particulate dielectrophoresis
7,338,636 (4 March 2008): Tupper, Cima and Chopinaud, Manipulating micron scale items
7,347,923 (25 March 2008): Cummings and Fiechtner, Dielectrophoresis device and method having insulating ridges for manipulating particles
7,381,316 (3 June 2008): Lee and Chung, Methods and related systems for carbon nanotube deposition
7,384,791 (10 June 2008): Tyvol, Childers, Norton and Johnson, Method of analyzing blood
7,390,387 (24 June 2008): Childers, Tyvol and Norton, Method of sorting cells in series
7.390.388 (24 June 2008): Childers and Tyvol, Method of sorting cells on a biodevice
7,419,574 (2 September 2008): Cummings, Fintschenko and Simmmons, Dielectrophoresis device and method having nonuniform arrays for manipulating particles
7,425,253 (16 September 2008): Voldman and Taff, Microscale sorting cytometer
7,455,757 (25 November 2008): Oh and Zhou, Deposition method for nanostructure materials
7,519,420 (14 April 2009): Palti, Apparatus for selectively destroying dividing cells
7,534,334(19 May 2009): Fiechtner, Cummings and Singh, Apparatus and method for concentrating and filtering particles suspended in a fluid
7,534,336 (19 May 2009): Volkel, Lean, Hsieh and Daniel, Continuous flow particle concentrator
7,583,251 (1 September 2009): Arango, Jacobson, Amundson, Dielectrophoretic displays
7,615,762 (10 November 2009): Satyanarayana and Dwarakanath, Method and apparatus for low quantity detection of bioparticles in small sample volumes
7,626,483 (1 December 2009): Ohtsuka and Hikita, Self-recovering current limiting fuse using dielectrophoretic force
7,635,420 (22 December 2009): Li, Cassall and Arumagum, Dielectrophoresis-based particle sensor using nanoelectrode arrays
7,658,829 (9 February 2010): Kanagasabapathi, Kaler and Jones, Integrated microfluidic transport and sorting system
7,666,289 (23 February 2010): Simmons, Cummings, Fiechtner, Fintschenko, McGraw and Salmi, Methods and devices for high-throughput dielectrophoretic concentration
7,678,256 (16 March 2010): Davalos, Simmons, Crocker and Cummings, Insulator-based DEP with impedance measurements for analyte detection
7,682,827 (23 March 2010): Yu, Microelectronic positioning for bioparticles
7,686,934 (30 March 2010): Hodko, Huang and Smolko, Three dimensional dielectrophoretic separator and methods of use
7,704,362 (27 April 2010): Hamers and Beck, Apparatus for transport and analysis of particles using dielectrophoresis
7,704, 363(27 April 2010): Bryning and Taylor, Methods and apparatus for the location and concentration of polar analytes using an alternating electric field
7,709,195 (4 May 2010): Segawa and Kishi, Hybridization detecting unit relying on dielectrophoresis and sensor chip provided with the detecting unit
7,713,395 (11 May 2010): James, Galamos and Derzon, Dielectrophoretic columnar focusing device

Industrial

Hatfield’s efforts¹³⁴ (as embodied in U.S. patent 1,498,911, granted June 1924) were directed toward separating minerals, and it is interesting to find that this objective is again being pursued—as for example in the works of Lungu,¹³⁵ Batton et al.,¹³⁶ Wang et al.,¹³⁷ and Ballantyne and Holtham.¹³⁸ Apart from mineral separation, other “industrial” applications of DEP have been examined. Ohtsuka and Hikita (U.S. patent 7,626,483, Table 1) describe a self-recovering current-limiting fuse. The current-limiting operation is achieved by switching repeatedly between a conducting state, brought about by DEP collection of conductive particles between two electrodes, and an evaporation∕spreading state of the conductive particles. Oh and Zhou (U.S. patent 7,455,757, Table 1) describe a method for depositing a patterned coating of a nanostructure material onto a substrate, that includes applying a direct and∕or alternating current electrical field between two electrodes for a certain period of time, thereby causing the nanostructure materials in the solution to migrate toward and attach themselves to the electrodes. Edman et al. (U.S. patent 7,060,224, Table 1) claim a method and apparatus for the fabrication of micron-scale and nanoscale devices, composed of movable component devices brought together in a fluidic medium by forces that include DEP. Along the same lines, Tupper et al. (U.S. patent 7,338,636, Table 1) claim a method for the DEP collection of micron-scale particles (granular, threadlike, sheets, or microelectronic parts) toward high field regions generated by planar counterelectrode, or by dual electrodes such as parallel pins, loops, or plates. All the other patents listed in Table 1 are primarily directed toward applications in the biomedical sciences.

Other nonbiological applications include that described by Kim et al.¹³⁹ for polishing local areas of 3D surfaces using abrasive powders, such as Al₂O₃, diamond, or SiC, dispersed in silicone oil and agitated by DEP forces. The performance of this method was evaluated using a borosilicate glass specimen, with atomic force microscopy being used to determine material removal rate and surface quality. Tests by Luo et al.¹⁴⁰ on bench-scale samples of sandy loam, spiked with phenol as a model organic pollutant, have demonstrated that nonuniform ac electrokinetic processes accelerate the movement and in situ biodegradation of organic pollutants in soil. Airborne particles significantly contribute to the toxicity of environmental pollution. To address this, Chen and Shen¹⁴¹ present a theoretical model to aid the design of DEP systems, consisting of vertical microchannels to capture airborne particles. The ability to dispense and manipulate small fluid droplets, ranging from picoliters to nanoliters, has many potential applications in lab-on-chip devices, and significant efforts have been directed toward this (e.g., Refs. ^{142, 143, 144}). Advances in the technology to enable the DEP manipulation of nanoparticles is also opening up new applications, including the fabrication of a new generation of electronic devices and sensors. Publications describing the DEP manipulation of a range of nanoparticles, including those addressing the development of new nanoparticle-based sensors, are listed in Table 2.

Table 2.

DEP manipulation of nanoparticles.

Nanoparticle	Publications
Carbon nanotubes (manipulation)	Seo et al. (Refs. 145, 146); Lutz et al. (Ref. 147); Liu et al. (Ref. 148); Zhang et al. (Refs. 149, 150) ; Kim et al. (Ref. 151); Shim et al. (Ref. 152); Wei et al. (Refs. 153, 154)
(Devices∕Sensors)	Li et al. (Ref. 155); Lucci et al. (Ref. 156); Suehiro et al. (Refs. 157, 158, 159); Wei et al. (Ref. 160)
Wires and rods	Evoy et al. (Ref. 161); Kumar et al. (Ref. 162); Leeet al. (Refs. 163, 164, 165, 166); Seo et al. (Ref. 167); Wang & Gates (Ref. 168); Mahmoodi et al. (Ref. 169); Nocke et al. (Ref. 170)
Gold, metal oxides	Jiang et al. (Ref. 171); Liu et al. (Ref. 172); Lee et al. (Ref. 173); Kumar et al. (Ref. 174); Seo et al. (Ref.145)
Latex and silica (Janus particles)	Lumsdon et al. (Ref. 175); Hoffman et al. (Ref. 36); Zhang & Zhu (Ref. 176); Honegger et al. (Ref. 129)

Biomedical

By far the most effort in exploring applications of DEP has been directed toward addressing unmet needs in the biomedical and biotechnological sciences. The range of bioparticles that have been investigated in DEP studies is listed in Table 3. The earliest studies listed were largely directed toward understanding how cells respond to DEP forces, and to what extent this could lead to a better understanding of their physicochemical properties. There is now, though, considerable effort being directed toward applying DEP for biomedical and biotechnological applications, such as cell sorting, tissue engineering, and biosensors. Of importance to the development of point-of-need devices for detecting and identifying pathogenic microorganisms is the ability to manipulate DNA. As already noted, the electrodeless DEP trap shown in Fig. 12b is capable of trapping DNA, and this has been used to enhance the preconcentration of single-stranded target DNA in the vicinity of sensors, on which capture probe DNA molecules are immobilized, within the relatively high ionic strength buffers required for DNA hybridization.¹²⁴ This provides a tenfold enhancement of the DNA hybridization kinetics at target concentration values down to the sensitivity limit of 10 pM for the sensor platform. Another approach to developing a simple, rapid, and portable genetic detection method for point-of-need or field use is the detection of the amplitude and direction of the DEP mobility of oligonucleotide-functionalized silica nanoparticles as a function of DNA-DNA hybridization.⁸⁴ The sensitivity is at nanomolar concentrations of the target single-stranded DNA, and permits visual detection of the hybridization event without fluorescent labeling and confocal microscopy. Cheng et al.¹²⁵ describe a novel and potentially important technique they term molecular DEP in which a cusp-shaped silica nanocolloid, functionalized with a DNA probe, is used to create a localized large field gradient to attract target single-stranded DNA by a DEP force, and provide picomolar detection and identification within 1 min.

Table 3.

DEP characterization and manipulation of biological particles.

Bioparticle	Publications
Blood cells	Pohl (Ref. 5); Burt et al. (Ref. 24); Gascoyne et al. (Refs. 25, 178); Becker et al. (Refs. 76, 177); Huang et al. (Ref. 179); Chan et al. (Ref. 180); Yang et al. (Ref. 181); Minerick et al. (Ref. 71); Menachery & Pethig (Ref. 182); Nascimento et al. (Ref. 183); Hashimoto et al. (Ref. 184); Cheng et al. (Ref. 185)
Stem cells	Talary et al. (Ref. 186); Stephens et al. (Ref. 187); Vykoukal et al. (Ref. 188); Flanagan et al. (Ref. 189); Markx et al. (Ref. 190)
Neurons	Heida et al. (Ref. 191); Prasad et al. (Ref. 192); Jaber et al. (Ref. 193); Flanagan et al. (Ref. 189)
Pancreatic β-cells	Pethig et al. (Refs. 107, 194)
Bacteria and yeast	Pohl (Ref. 5); Price et al. (Ref. 73); Inoue et al. (Ref. 195); Asencor et al. (Ref. 196); Urano et al. (Ref. 197); Markx et al. (Refs. 49, 198); Kiljlstra and Wal (Ref. 199); Li and Bashir (Ref. 200); Suehiro et al. (Ref. 201); Bessette et al. (Ref. 202); Lapizco-Encinas et al. (Ref. 203); Castellarnau et al. (Ref. 204); Cheng et al. (Refs. 109, 185); Park and Beskok (Ref. 70)
Cell viability	Markx et al. (Ref. 49); Markx and Pethig (Ref. 75); Patel and Markx (Ref. 205); Mernier et al. (Ref. 206)
Apoptosis	Wang et al. (Ref. 207); Labeed et al. (Ref. 208); Pethig and Talary (Ref. 209)
Viruses	Schnelle et al. (Ref. 210); Müller et al. (Ref. 211); Gimsa (Ref. 212); Morgan and Green (Ref. 213); Hughes et al. (Refs. 214, 215); Morgan et al. (Ref. 216); Kentsch et al. (Ref. 217); Akin et al. (Ref. 218); Lapizco-Encinas et al. (Ref. 203); Grom et al. (Ref. 219)
DNA	Asbury and Engh (Ref. 220); Washizu and Kurosawa (Ref. 221); Yamamoto et al. (Ref. 222); Kawabata and Washizu (Ref. 223); Asbury et al. (Ref. 224); Chou et al. (Ref. 122); Hölzel et al. (Ref. 225); Ying et al. (Ref. 226); Zheng et al.227; Bakewell and Morgan (Ref. 228); Sung and Burns (Ref. 229); Hoeb et al. (Ref. 128); Kurosawa and Washizu (Ref. 230); Gagnon et al. (Ref. 84); Dalir et al. (Ref. 231); Swami et al. (Ref. 124); Lei et al. (Ref. 232); Cheng et al. (Ref. 125)
Chromosome	Prinz et al. (Ref. 233)
Proteins	Washizu et al. (Ref. 234); Zheng et al. (Ref. 227); Clarke et al. (Ref. 235)

An integrated DEP microfluidic device using planar electrodes that form 3D DEP gates has been developed and tested by Cheng et al.¹⁰⁹ This device, which has the potential to perform as multitarget pathogen detection platform, can continuously perform the tasks of filtration, sorting, and trapping of cellular debris and bioparticles with a throughput of 3 μl∕min. In another device a common set of inert planar electrodes has been used to position monocytes prior to their electroporation for gene delivery.²³⁶ The extent to which electric pulses increased the permeability of the cell membranes to florescent molecules and to DNA plasmids was found to depend on prior positioning. For a given set of electric pulse parameters, electroporation was either irreversible (resulting in cytolysis), reversible (leading to gene delivery), or not detectable, depending on where cells were positioned. The results of MacQueen et al.²³⁶ clearly demonstrated that position-dependent electroporation of cells can be controlled by DEP. A procedure that yields a rapid, sensitive, and separation-free immunoassay in a simple DEP device has been described by Lee et al.²³⁷ An interdigitated microelectrode array is fabricated onto a PDMS substrate. Fluorescent microbeads bearing antimouse immunoglobulin (IgG) are suspended in an analyte (mouse IgG) solution, where the beads trap the analyte to form immunocomplexes on the beads. Negative DEP is then used to attract the beads to designated areas of the PDMS surface precoated with antimouse IgG, where they are captured via an antibody-antigen-antibody (sandwich) reaction. These captured beads are detected selectively by fluorescence measurements, regardless of the presence of uncaptured beads suspended in the solution, for an analyte concentration range of 0.01–10 ng∕ml. Thus, the separation and washing-out steps usually required for conventional immunoassay are eliminated in this procedure, and the use of DEP accelerates this immunoassay to time periods down to 30 s. Kuo and Hsieh⁸⁵ describe a method for performing single-bead-based, consecutive biochemical assays on a quadrupole DEP microfluidic chip using the interaction of fluorescein isothiocyanate (FITC)-labeled streptavidin with biotin-coated 2 μm polystyrene beads as a model system. Scanning electrochemical microscopy has been used for the analysis of gene-expression signals for single cells, seeded by positive DEP at a concentration of 1 cell per well, located in a 4×4 array fabricated on an ITO electrode.²³⁸

Applying DEP in a simple tool for isolating and accurately positioning single cells during cell culture has been investigated. Optical tweezers have already been developed to achieve such manipulation, but DEP “tweezers” could offer advantages in terms of their low cost and simple construction. Applications would include the ability to pick fewer or rare cells (such as primary cells, stem cells, or fungi and protists) from native environments, and to pick or position particular and fragile cells for experimental purposes. The first reported design of a twin-electrode DEP tweezer for manipulating cells took the form of a microring-ring electrode assembly formed by the vacuum deposition of platinum and gold films onto the outer and inner surfaces, respectively, of a 6–10 μm diameter capillary tip.²³⁹ Single myeloma cells could be trapped by positive DEP, but this was found to result in cell damage arising from electroporation of the cell membrane. With a later design, in the form of a dual-microdisk comprising two platinum-rhodium electrodes of diameter ∼2 μm, single chlorella cells were captured by positive DEP and released by negative DEP at a new location, without harming the cell.²⁴⁰ Hunt and Westervelt²⁴¹ demonstrated that a DEP tweezer, fabricated by vacuum evaporating electrically isolated Ti–Au films onto two sides of a sharpened glass rod, can trap yeast cells for several hours without harming them (the trapped cells were observed to bud and form daughter cells). A DEP tweezer design reported by Menachery et al.²⁴² offers advantages in terms of its relatively simple fabrication, being capable of construction using facilities available in most electrophysiology laboratories. The tweezer was tested using transfected HEI 193 human schwannoma cells, with visual identification of the target cells being aided by labeling the incorporated gene product with a green fluorescent protein.

As shown in Fig. 9, cells can be collected into aggregations by both positive and negative DEP. Sebastian et al.²⁴³ investigated the shapes that aggregations of mammalian cells form at interdigitated, oppositely castellated electrodes under positive DEP as a function of fluid flow and the value of E². The ability to engineer artificial 3D cell aggregations offers a new investigative tool for cell biologists, taking them away from two-dimensional cell cultures. Suspensions of insulinoma (beta) cells have been directed into 3D aggregates in an array of 10×10 field cages, using micromachined ITO electrodes and negative DEP.¹⁰⁷ Some of these beta-cell constructs, measuring approximately 150 μm in diameter and 120 μm in height and containing ∼1000 cells, were of the same size and cell density as a typical islet of Langerhans. With the DEP force maintained, the cell constructs were able to withstand mechanical shock and fluid flow forces. The hematon is a 3D aggregate of cells which is able to produce all blood types. To be able to do this, it must be able to create within the cell aggregate a microenvironment which enables hematopoietic stem cell maintenance, renewal, and differentiation. A first step has been taken by Markx et al.¹⁹⁰ toward the creation of artificial hematopoietic stem cell microniches in vitro by the creation with DEP of hemispherical cell aggregates. These aggregates were of a height of 50–100 μm, having an internal structure similar to that of a putative hematon, and with the cells in direct contact with each other to potentially allow for direct cell-cell communication. It was also shown by Markx et al.¹⁹⁰ that, after their DEP manipulation, the cells remained viable and active. Yusvana et al.²⁴⁴ demonstrated that DEP can be used to create engineered skin with artificial placodes of different sizes and shapes in different spatial patterns. The cells in the aggregates remain viable, and reorganization and compaction of the cells in the aggregates occur when the artificial skin is subsequently cultured. This technique could be of considerable use for the in vitro study of developmental processes where local variations in cell density and direct cell-cell contacts are important.

Current techniques in high-speed cell sorting are limited by the inherent coupling among three competing parameters of performance: throughput, purity, and rare cell recovery. Hu et al.²⁴⁵ described a DEP device that provides an alternate strategy to decouple these parameters through the use of arrayed devices that operate in parallel. The DEP amplitude response of rare target cells was modulated by labeling cells with particles that differ in polarization response. Cell mixtures were interrogated in this DEP-activated cell sorter in a continuous-flow manner using a field frequency to achieve efficient separation between the DEP labeled and unlabeled cells. To demonstrate the efficiency of this marker-specific cell separation, Hu et al.²⁴⁵ applied this technique to the affinity-based enrichment of rare bacteria expressing a specific surface marker from an excess of nontarget bacteria that do not express this marker. Rare target cells were enriched by more than 200-fold in a single round of sorting at a single-channel throughput of 10 000 cells∕s. Bessette et al.²⁰² extended this methodology to develop the capability to screen molecular libraries using a disposable microfluidic device. This provides the potential to simplify and automate reagent generation and to develop integrated bioanalytical systems for clinical diagnostics. Antibody epitopes were mapped by Bessette et al.²⁰² using a disposable microfluidic DEP device to screen a combinatorial peptide library composed of 5×10⁸ members displayed on bacterial cells. On-chip library screening was achieved in a two-stage, continuous-flow microfluidic sorter that separates antibody-binding target cells captured on microspheres through DEP “funneling” electrodes of the form described by Schnelle et al.⁶⁹ and Fiedler et al.¹⁰⁸ and depicted in Fig. 12a. The antibody fingerprints identified by Bessette et al.²⁰² were comparable to those obtained using state-of-the-art commercial cell sorting instrumentation. This method has been extended even further¹¹¹ with the demonstration of the capability to simultaneously enrich multiple, distinct target cells into independent fractions. This multitarget DEP activated cell sorter operates a two-input, multiple-output device in a continuous flow manner. The input consists of a running buffer and a sample mixture containing multiple types of target cells, each labeled with a distinct DEP tag. After a single pass through the device, the target and nontarget cells are separated and eluted through multiple, independent, spatially segregated outlets. A continuous high throughput bioparticle sorter based on 3D traveling-wave DEP has been designed and tested on various heterogeneous samples (red blood cells plus cell debris or bacteria, polydispersed liposomes) by Cheng et al.¹⁸⁵ Table 4 summarizes the performance reported for various DEP cell sorters. An important parameter is not included, namely, the purity or enrichment achieved for the recovered cell fractions. This is sometimes reported, but not always, and generally it can be taken that a compromise exists between the sorting rate and the purity or enrichment achieved. All of the DEP devices listed in Table 4, apart from the immuno-DEP device of Kim et al.,¹¹¹ did not involve the labeling or engineered tagging of the cells. Kim et al.¹¹¹ employed synthetic particles as tags that were larger than the cells, a method also adopted in the immunomagnetic method.²⁴⁸

Table 4.

Performance, in terms of maximum sample flow rate and particle sorting rate, for various DEP particle sorting devices reported in the literature. Magnetic activated cell sorting and FACS are included for comparison.

Method	Authors (Year)	Max flow (μl∕min)	Sorting rate (particles∕s)
DEP	Markx et al. (Ref. 49)	500	1.2×105 (yeast)
	Markx and Pethig (Ref. 75)	2.5	4.2×103 (yeast)
	Becker et al. (Refs. 76, 177)	5	4.2×103 (blood cells)
	Markx et al. (Ref. 198)	0.44	4×105 (bacteria)
	Cheng et al. (Ref. 109)	3	0.3 (bacteria)
	Kim et al. (Ref. 111)	2.5	4.2×103 (tagged cells)
	Cheng et al. (Ref. 185)	6	100 (blood cells)
DEP-FFFa	Markx et al. (Ref. 246)	50	8.3×103 (yeast)
	Huang et al. (Ref. 247)	160	3×103 (cancer cells)
	Vykoukal et al. (Ref. 188)	1.5	5×103 (stem cells)
Magnetic	Adams et al. (Ref. 248)	80	2.8×105 (tagged cells)
FACS (LSR II cell analyzer)	BD Biosciences, San Jose, California	60	5×103 (labeled cells)

^aFFF: Field flow fractionation.

The work of Markx et al.¹⁹⁰ in creating artificial stem cell microniches is an example of how DEP can be used as a tool to address an unmet need in stem cell research and therapy. Stem cells are immature cells characterized by a varying capacity for growth and the ability to differentiate into one or more different derivatives with specialized function. These capacities can vary depending on the in vivo origin of the stem cell populations, the in vitro environment, and the manipulation(s) to which they are subjected. Methods to monitor, characterize, and manipulate stem cells should ideally be relatable to individual cells (which might be sampled to represent larger populations), and non- or minimally invasive so as not to alter the behavior of the cells. Currently, the most common methods used to quantitatively characterize or positively∕negatively select or purify cell populations for research or translational applications include flow cytometry [fluorescence activated cell sorting (FACS)] or magnetic bead-coupled cell separation. These methods are dependent on the existence of specific cell-surface antigens and the formulation∕availability of high-affinity probes to these antigens. Irreversible attachment of these probes to target cells also has the potential to influence cell behavior. In the absence of a specific or unique marker or to avoid potentially confounding interactions of probes with cells, alternative methods are required to identify and manipulate target stem cells in heterogeneous cell populations. DEP operates on the intrinsic dielectric properties of cells, and so is potentially capable of sorting cells without the need for engineered labels or tags.

The number of reported DEP experiments on stem cells is small. The first studies^{186, 187} demonstrated that DEP could be used to enrich hematopoietic stem cells (defined as those expressing the CD34 antigen) from a mixed cell population in bone marrow and peripheral blood, without the requirement for any cell manipulation such as antibody binding. The different cell fractions exhibited a spread of DEP characteristics, suggesting some form of heterogeneity within the CD34⁺ cell population. The separated cells were viable and data from colony forming assays correlated well with the percentage of CD34⁺ cells in each collected cell fraction. In more recent work, DEP has been used to obtain populations enriched for putative adult stem cells, as defined by expression of the stromal marker NG2 from enzyme-digested adipose tissue.¹⁸⁸ Of particular interest is the work of Flanagan et al.,¹⁸⁹ whose objective was to determine whether stem cells and their more differentiated progeny can be identified by means other than flow cytometry. Mouse neural stem∕precursor cells (NSPCs) and their differentiated derivatives (neurons and glia) were found to have distinct differences in their positive DEP behavior. Moreover, the DEP signatures were found to distinguish NSPCs from different developmental ages in a fashion that predicted their respective fate biases. This suggests that the developmental progression of progenitor cell populations can be revealed by the cells’ dielectric properties. These results also highlight the fact that stem cell differentiation is a gradual process and that cells may begin to develop some characteristics of their more differentiated progeny before known cell surface markers can be detected and well before the cells become fully differentiated. Values for the DEP cross-over frequency f_xo1 (see Fig. 5) can be extrapolated from the data shown by Flanagan et al.¹⁸⁹ However, cell size was not determined (or at least reported), and so we are unable to relate the observed DEP differences for the various differentiated states of the neural stem cells in terms of cell membrane capacitance. This would have provided an insight into possible differences in the intrinsic surface properties of the cells.

A cell’s cytoplasmic membrane acts as a capacitor because it is constructed like one—namely, a thin dielectric situated between two conductors (the outer and inner electrolytes). For a cell of radius R suspended in an electrolyte of conductivity σ_m, the membrane capacitance C_cm can be determined from a measurement of the DEP cross-over frequency f_xo1 using the following relationship:

$$C_{cm}=\frac{\sqrt{2}}{2\pi R{f}_{x01}}{\sigma }_m.$$

This equation assumes that the high resistance value of the cell membrane has not been impaired due to damage or the onset of cell death, for example.²⁰⁹ For a fixed cell radius, the effective membrane capacitance of a smooth cell will be less than that for a cell having a complex cell surface topography associated with the presence of microvilli, blebs, membrane folds, or ruffles, for example. This will influence the value observed for f_xo1, which has important implications for applying DEP to characterize and selectively isolate target cells from other cells.^{249, 250, 251, 252}

CONCLUDING COMMENTS

The basic theory describing the DEP behavior of particles is now well established, and has brought the “user-friendly” effective dipole moment method¹² to the stage where it leads to results that match those produced using the more rigorous (but not so user-friendly) Maxwell stress tensor method (e.g., Ref. 59). Areas that could benefit from more attention include perturbing effects associated with particles interacting with physical boundaries (e.g., chamber walls) and other particles. Understanding the influence that the electrical double-layer surrounding a nanoparticle has on its DEP behavior is an ongoing pursuit (e.g., Refs. ^{32, 34, 35, 36}). The technology has reached an exciting stage, as for example the use of CMOS,^{131, 132} the development of scanning force DEP,¹³⁰ and the assembly of nanoparticles composed of two or more physicochemically differing surfaces (i.e., Janus particles) as described by Lumsdon et al.¹⁷⁵ Large steps have been made toward translating the theoretical treatment of both biological and nonbiological nanoparticles to practical applications (e.g., biosensors, bioassays). Also, DEP, initially used to characterize the dielectric properties of cells and other bioparticles, is now at the stage of developing into a tool to address very important unmet needs in stem cell research and therapy.

It may be fitting to conclude by quoting the final paragraph written by an unknown author on the dust cover of Pohl’s book of 1978: “A far wider range of potential applications exists than Professor Pohl has been able to include. The book should thus provide stimulating reading for imaginative research workers in the physical, medical, and biological sciences”.