Effects of Measured Susceptibility Genes on Cancer Risk in Family Studies

Abstract

Numerous family studies have been performed to assess the associations between cancer incidence and genetic and non-genetic risk factors and to quantitatively evaluate the cancer risk attributable to these factors. However, mathematical models that account for a measured hereditary susceptibility gene have not been fully explored in family studies. In this report, we proposed statistical approaches to precisely model a measured susceptibility gene fitted to family data and simultaneously determine the combined effects of individual risk factors and their interactions. Our approaches are structured for age-specific risk models based on Cox proportional hazards regression methods. They are useful for analyses of families and extended pedigrees in which measured risk genotypes are segregated within the family and are robust even when the genotypes are available only in some members of a family. We exemplified these methods by analyzing 6 extended pedigrees ascertained through soft-tissue sarcoma patients with p53 germ-line mutations. Our analyses showed that germ-line p53 mutations and sex had significant interaction effects on cancer risk. Our proposed methods in family studies are accurate and robust for assessing age-specific cancer risk attributable to a measured hereditary susceptibility gene, providing valuable inferences for genetic counseling and clinical management.

Introduction

Family history is an important risk factor for various cancers, suggesting that genetic components play a causal role in cancer incidence. Familial aggregations of cancers, particularly among young people, have been shown to result from hereditary mutations that predispose individuals to diseases (Knudson, Jr. and Strong, 1972;Malkin et al., 1990). In epidemiology, family studies to determine the genetic basis, disease-susceptibility genes, and possible risk factors of various cancers have been performed extensively over the past few decades. However, many of these studies fail to provide robust or reliable estimates of high-risk genotypes’ effects on cancer risk. Most importantly, when increasing susceptibility genes and risk alleles are detected or identified and could make a major impact on cancer risk estimation, current methods for family studies do not account for the effects of known susceptibility genes or incorporate them into mathematical models (Antoniou and Easton, 2006).

Segregation analysis methods are frequently performed to characterize the underlying inheritance modes and predict the genetic relative risks in family studies. Most segregation analysis programs assume that a putative major gene is segregated within a family and allow the covariates adjusted for epidemiological and environmental risk factors to be tested for significance in models. Risk analyses in family studies have been performed to assess the associations between cancer incidence and genetic and non-genetic risk factors and to quantitatively evaluate the cancer risk attributable to these factors prior to the identification of susceptibility genes (Lustbader et al., 1992;Sellers et al., 1990;Xu et al., 2005). More recently, several family studies have considered mutation status in probands and incorporated this information into analyses. Notably, breast cancer family studies in Australia stratified the analyses by BRCA1/2 mutation status in probands and other studies have analyzed multiple-affected families with BRCA1/2 mutations in probands (Antoniou et al., 2003;Antoniou et al., 2002;Cui et al., 2001).

As more mutated genes or risk alleles associated with increased cancer risk are discovered, such as p53 mutations for various cancers, BRCA1/2 mutations for breast and ovarian cancer, and hMSH2/hMLH1 mutations for colorectal cancer, it becomes important to incorporate information on known susceptibility genotypes for both probands and relatives into risk analyses. However, mathematical models that account for measured hereditary susceptibility genes have not been fully explored in family studies. Thus, development of statistical genetic methods is needed that not only model these measured high-risk genotypes by fitting them to family data as precisely as possible but also simultaneously determine the combined effects of individual risk factors and their interactions (Antoniou and Easton, 2006). Such approaches are challenging but are likely to provide accurate and robust estimates of measured susceptibility genotypes’ effects on cancer risk.

Gauderman et al. developed the complex joint segregation and linkage analysis model by maximum likelihood for censored age-of-onset traits based on Cox proportional hazards regression (Gauderman and Faucett, 1997). In this study, we proposed statistical approaches that extend the usual complex joint segregation and linkage analysis models developed by Gauderman et al. These methods are proposed to account for measured susceptibility genotypes of the proband and each relative in a family. Our proposed methods are structured for age-specific risk models and use an existing program package based on Cox proportional hazards regression (Cox, 1972). They are designed to jointly assess the associations between cancer incidence and genetic and non-genetic risk factors, evaluate the cancer risk attributable to a measured susceptibility genotype, allow for interaction effects between the measured gene and other risk factors to be tested for significance and accounted for in the models, and provide the 95% confidence intervals (95% CIs) for the risk estimates.

We illustrated our proposed approaches by analyzing the cancer incidence in 6 extended pedigrees with germ-line p53 mutations ascertained through childhood soft-tissue sarcoma patients. These kindreds have been followed systematically for > 20 years; p53 mutation testing has been performed in probands and extended family members (Hwang et al., 2003b;Hwang et al., 2003a;Law et al., 1991;Malkin et al., 1990).

Our proposed methods are useful for analyses of families and extended pedigrees in which risk alleles or mutant genes are observed and are robust even when the genotypes are available only in some members of a family. They allow us to robustly and reliably assess and predict the cancer risk associated with the measured hereditary risk genotype in family studies, providing valuable inferences for genetic counseling and clinical management in advance of cancer prevention and control.

Methods

Joint segregation and linkage analysis models

Segregation analysis is a statistical method that is frequently performed to evaluate and compare various modes of inheritance for a trait and test for evidence of age modification of genetic relative risks in association with epidemiological and environmental factors. It is often performed in statistical analyses of family studies ascertained through affected individuals. Linkage analysis is traditionally performed to estimate the recombination fraction between the trait locus and 1 or more marker loci by fixing the trait model parameters (such as allele frequencies and penetrance values) to their maximum likelihood estimates based on the segregation analysis outcomes. Joint segregation and linkage analyses were originally proposed as improvements over separate analyses (that is, performing segregation analyses first followed by linkage analyses). Various complex joint segregation and linkage analysis models have been developed, including the parametric approaches based on logistic regression models (Bonney, 1986;Bonney et al., 1988), Markov-Chain Monte Carlo methods (Guo and Thompson, 1992), and semi-parametric survival analysis methods based on Cox proportional hazards regression models (Gauderman et al., 1997a;Gauderman and Faucett, 1997).

In this study, we used a model that is based on Cox proportional hazards regression methods and that is implemented by the program package of Genetic Analysis Package (G.A.P.) (1997). To account for variability in age of onset for right-censored traits, Cox proportional hazards models express the age-specific incidence rate as a function of a vector of measured covariates (z), a covariate (G) for a putative major gene, and their interactions (G×z):

$$\lambda (t|z,g,\mathrm{\Omega })={\lambda }_0(t)\text{exp}({\beta }^{T}z+\gamma G+{\eta }^{T}G\times z).$$ (1)

Let g denote the diallelic genotype at the putative major gene that has high-risk allele A with frequency q_A and normal allele a; G is a covariate that depends on this genotype and assumed inheritance mode. Under the assumption of dominant inheritance, G is coded as 1 for genotype g = AA or Aa and 0 for g = aa. The letter d is a disease status indicator, and t represents the age of onset for diseased subjects (d = 1) or the last known disease-free age for unaffected subjects (d = 0). β, γ and η are regression coefficients to be estimated; η measures the degree of departure from a purely multiplicative hazards model. The function λ₀(t) describes the age-specific incidence rate for the baseline group; it is often expressed as a step function on a pre-determined set (e.g. 5 equal age intervals of 0–75: λ₀(t) = λ_k for t_k-1 < t ≤ t_k, k = 1,…, 5, with t₀ = 0 and t_k = 15 × k). The set of hazard model parameters is denoted by Ω = {β, γ, η, λ_k}.

Suppressing subscripts, the penetrance function for a given individual is expressed as f(d, t | z, g, Ω) = λ(t | z, g, Ω)^dS(t | z, g, Ω), where $S(t|z,g,\mathrm{\Omega })=\text{exp}\left(-{\displaystyle {\int }_0^t\lambda (s|z,g,\mathrm{\Omega })\mathit{\text{ds}}}\right)$ is the survival function (the probability of remaining disease-free up to time t). In segregation analyses, the family-specific likelihood, which is formed by the summation over all possible combinations of joint genotypes and the product of the individual-specific penetrance functions in a family, is expressed as

$$L_I(\mathrm{\Omega },q_A)={\displaystyle \sum _{g}P(g|q_A){\displaystyle \prod _{i\in I}f(d_i,t_i|z,g,\mathrm{\Omega }).}}$$ (2)

We let M_i denote a marker phenotype for a given individual (i) that is determined by a fully-penetrant gene (m_i) with an arbitrary number of alleles and corresponding allele frequency (q_B). P(M_i|m_i) is the marker-penetrance function that is assumed to be 1 for all m_i, consistent with M_i, and to be 0 otherwise. In joint segregation and linkage analyses, the family-specific likelihood is expressed as

$$L_I(\mathrm{\Omega },q_A,q_B,\theta )={\displaystyle \sum _{g,m}P(g,m|q_A,q_B,\theta ){\displaystyle \prod _{i\in I}f(d_i,t_i|z,g,\mathrm{\Omega })P(M_i|m_i).}}$$ (3)

The first factor depends on q_A, the marker allele frequency q_B for founders, and the recombination fraction θ for non-founders (Bonney et al., 1988).

The total likelihood for all pedigrees is the product of the family-specific likelihoods that are expressed in [2] and [3] for complex segregation analysis models and complex joint segregation and linkage analysis models, respectively. Numerical procedures for computing and maximizing likelihood functions are performed using peeling algorithms (Elston and Stewart, 1971;Lange and Elston, 1975). Details of the methods and applications of these models have been described elsewhere (Gauderman et al., 1997b;Gauderman et al., 1997a;Gauderman and Faucett, 1997).

Model measured susceptibility genes as linked markers

Joint segregation and linkage analyses may have greater power for detecting linkage than the usual linkage studies (Gauderman et al., 1997a) and more power for detecting gene-environment interactions than the usual segregation analyses (Gauderman and Faucett, 1997). Segregation analysis programs typically assume that a putative major gene is segregated within a family and allow the measured covariates, adjusted for epidemiological and environmental risk factors, to be tested for significance. Adding a linked marker in joint analyses could provide additional information on characterizing the putative major gene, resulting in increased power compared with segregation analyses alone.

Gauderman et al. developed the complex joint segregation and linkage analysis model based on Cox proportional hazards regression and the program package of G.A.P. for the model (Gauderman and Faucett, 1997). In this study, we proposed to use the measured susceptibility genotype (instead of the ordinary genetic allele marker) as the linked marker to the putative major gene in joint segregation and linkage analyses to estimate the cancer risk attributable to a measured susceptibility gene in family studies. We further proposed to test the significance of linkage disequilibrium (LD) between the putative gene and measured susceptibility gene and to account for LD in the model. Such proposed novel applications have not been discussed or used in the literature. We proposed to use the measured high-risk genotypes as the linked marker to the putative major gene in joint segregation and linkage analyses to evaluate the cancer risk attributable to a measured susceptibility gene in family studies. This approach would allow us to assess the effect of a measured susceptibility gene on cancer risk through the regression coefficient γ of the putative major gene in equation [1]. To what extent the putative major gene represents the measured susceptibility gene on cancer risk estimation depends on several factors, including the degree of genetic heterogeneity and complexity and the values of penetrance and prevalence of the disease.

Testing for significance of linkage disequilibrium

Using the measured susceptibility gene as a linked marker to the putative major gene in joint segregation and linkage analyses, we will obtain a small estimated recombination fraction θ̂ when the study families have been ascertained through affected individuals with a measured susceptibility gene that is segregated within the families. We suggest testing for significance of the LD between the measured susceptibility gene and the putative major gene. LD has been widely used to associate the disease phenotype with genetic markers that are tightly linked to disease-susceptibility loci (Balding, 2006). The stronger the LD magnitude, the more the markers represent the true susceptibility genes in associations with cancer risk. In this application, LD magnitude can be used as a measure to indicate how well or to what extent the putative major gene serves as a proxy of the measured susceptibility gene in cancer risk estimation. Our proposed methods should be particularly effective when there is strong LD between the measured susceptibility gene and the putative major gene.

Gene-environment and gene-gene interactions play important roles in disease risk. However, current statistical approaches have limited power for detecting such interactions (Altshuler et al., 2008). When the measured susceptibility gene and the putative major gene have strong LD, the effect of the interaction between the measured susceptibility gene and the environmental or epidemiological factor on cancer risk is closely approximated by the interaction effect between the putative major gene and the corresponding factor, which can be estimated through the regression coefficient η of the interaction covariate G×z in equation [1]. This approach is more efficient than existing approaches that do not precisely account for measured high-risk genotypes in estimating the effect of gene-environment interactions in mathematical modeling.

Missing genotypes of measured high-risk alleles

Removing individuals with missing genotypes or data from likelihood calculations may result in substantial power loss and distort the estimates of risk factors’ effects on cancer incidence. This problem could become particularly complex and serious in studies of extended pedigrees in which genotypes are only available for some individuals in a family. When the measured high-risk genotypes used as linked markers are incorporated into joint segregation and linkage analysis models, the individuals with missing genotypes at the respective susceptibility locus are assigned all possible genotypes conditional on the observed genotypes of relatives with corresponding probabilities. Therefore, not only relatives with known genotypes but also those with missing genotypes at the respective susceptibility locus contribute to the likelihood calculations shown in equation [3], making our methods more powerful for estimating the cancer risk attributable to the measured hereditary susceptibility gene.

Furthermore, unlike existing studies that only use information on probands’ mutation carrier status or stratify family data by this status (Antoniou et al., 2003;Antoniou et al., 2002;Cui et al., 2001), our methods precisely model the measured susceptibility genotypes for the proband and each relative in a family and incorporate this information into the mathematical models, resulting in more robust estimation.

Hypothesis testing

The logarithm ln(L) of the maximum likelihood of the data was computed for each model. The likelihood ratio test (LRT) was used to test a specific model against the baseline model — usually the general model — in which the transmission probability τ_µof allele A for genotype µ is arbitrary (instead of Mendelian transmission modes) to identify the best fit to the data for the general model. The specific model serves as the null model, and the baseline model as the alternative model. The LRT is computed as follows:

$$\text{LRT}=-2\{\text{In}({\mathrm{L}}_{\text{specific}})-\text{In}({\mathrm{L}}_{\text{baseline}})\},$$

where LRT approximately follows a χ² distribution with degrees of freedom equal to the difference in the numbers of independent parameters estimated in the two models. The LRT is frequently used to compare the general model with several nested alternatives, such as Mendelian dominant, additive, and recessive models, and sporadic (no major gene) and environmental (no parent-to-offspring transmission) models. We also used Akaike’s Information Criteria (AIC) (AIC = −2 ln(L) + 2 [number of independent parameters estimated]) to compare non-nested models. The model with the lowest AIC value and fewer estimated parameters is generally considered the most parsimonious. The LRT is also used to test the significance of covariates when the model that includes additional covariates is used as the baseline model. The analyses presented in this report were performed using the program package of G.A.P. (1997).

Study Population

The study population that we used to illustrate our approaches consisted of 6 patients with childhood soft-tissue sarcoma and germ-line p53 mutations who had been diagnosed before age 16 years, had survived > 3 years after diagnosis, and had been treated at The University of Texas M. D. Anderson Cancer Center (Houston, Texas, U.S.A.) from 1944 to 1975; we also included their extended relatives (grandparents, aunts and uncles, parents, siblings, and offspring) at risk for carrying a p53 mutation. These kindreds belong to a unique cohort study of Li-Fraumeni syndrome (LFS) that has been followed up prospectively for > 20 years at M D Anderson. LFS is a rare familial cancer syndrome characterized by a high frequency of early-onset and diverse tumor types and a high frequency of multiple primary tumors.

We included all invasive cancers, excluding non-melanoma skin cancers and in situ carcinoma, as a single combined phenotype. These disease criteria are broader than the classic LFS component tumors, but are based on observations of diverse cancer types occurring in excess in p53 germ-line mutation carriers. Medical records or death certificates were used to confirm all cancers included in the analysis. Individuals were considered at risk from their date of birth to their date of cancer diagnosis, death, loss to follow-up, study termination (December 31, 2001, was the study termination date for medical record and death certificate documentation), or age 75 years, whichever came first. The evaluation of cancer incidence was truncated at age 75 years because of the limited reliability of cancer rates at older ages. Genotyping included probands and adult relatives at risk of carrying a p53 mutation, without regard to affection status. Because extension through mutation status was not performed with respect to the phenotype, this approach to extending the family should not introduce an ascertainment bias during the segregation analysis.

The final dataset for these 6 extended kindreds with multiple germ-line p53 mutations consisted of 262 individuals with 42 men and 38 women affected with cancers. Sixty-two were carriers, 133 were wild-type, and 67 were at risk for being a mutation carrier but had unknown genotypes. The family-specific frequencies of the size and mutation carrier are shown in Table 1. The data collection methods, overall cancer incidence, germ-line p53 mutation identification, and frequencies of site-specific cancers have been described elsewhere (Hwang et al., 2003b;Hwang et al., 2003a;Lustbader et al., 1992;Strong et al., 1987;Strong et al., 1992).

Table 1.

Family-Specific Frequency Distribution of Germ-Line p53 Mutation Carriers

Pedigree No.	Family Size No. of p53	Mutation Carriers
STS-005	115	32
STS-032	13	4
STS-045	20	4
STS-170	84	17
STS-174	13	2
STS-204	17	3
Total	262	62

Results

Using the germ-line p53 gene as a linked marker to the putative major gene in the mathematical model of joint segregation and linkage analyses, we estimated the trait model parameters and recombination fraction θ̂_p53 between the p53 gene and putative major gene. Because the measured germ-line p53 gene is a dominant gene, the underlying mode of inheritance for the putative major gene is assumed to be dominant, indicating that the effect of genotype AA is the same as that for genotype Aa, as reflected by γ_AA = γ_Aa.

Model without Linkage Disequilibrium

Under the assumption of proportional hazards, we used a 5-step baseline hazard model λ₀(t) for the age-specific incidence rate, in which t₀ = 0, t_k = 15 × k, and λ₀(t) = λ_k for t_k-1 < t ≤ t_k and k = 1,…, 5. The highest LOD-score was 17.74 at θ̂_P53=0.0 and γ_AA = γ_Aa = 4.06 indicating that the p53 and putative major genes were very close and the relative risk (RR) for being affected was e^4.06 (= 57.97) for individuals with a p53 mutant allele.

Model with Linkage Disequilibrium

We tested the significance of LD between the p53 and putative major genes and accounted for LD in the model. We obtained the highest LOD-score of 21.21 at θ̂_p53 = 0.0, γ_AA = γ_Aa = 3.69, and the LD measure of D' ≈ 1, suggesting nearly perfect LD between the p53 and putative major genes (Devlin and Risch, 1995). We also obtained q_AB ≈ q_B, where q_B denotes the frequency of high-risk allele B for the linked marker (germ-line p53 mutant allele in this case) and q_AB denotes the frequency of haplotype A and B. The values of θ̂_p53 =0.0, q_AB ≈ q_B and D' ≈ 1 suggest that not only were the p53 genotypes directly associated with cancer phenotype but also that the haplotype of high-risk allele A and p53 mutant allele was transmitted intact through generations within the families. The roles of the p53 gene and putative major gene were identical in this application. The analyses with and without LD are summarized in Table 2. The parameter λ represents the estimates of the baseline annual age-specific cancer incidence rate per 100,000 persons for age groups of 0–15, 15–30, 30–45, 45–60, and 60–75 years, respectively.

Table 2.

Testing for Significance of Linkage Disequilibrium between the Putative Major Gene and the p53 Gene

		Maximum-Likelihood Estimate (Standard Error)
	Parameter	Male without LD	Model with LD
Baseline Risk λk (10−5):
Age Group	0 – 15	6.60	9.70
	15 – 30	25.88	37.96
	30 – 45	64.80	94.58
	45 – 60	152.17	213.51
	60 –75	596.74	704.22
p53 Major Gene: γ(g=Aa, AA)		4.06 (0.41)	3.69 (0.40)
Relative Risk (=exp(γ))		57.97	40.04
	qA	2.84×10−2(1.55×10−2)	4.66×10−3(3.20×10−4)
	qB	6.25×10−14(0.00)	1.22×10−10(3.20×10−4)
	qAB	N. A.	1.22×10−10(3.20×10−4)
Lindage Analysis
	Highest LOD-scpre	17.74	21.21
	θ̂p53	0.00	0.00
−2 Log-Likelihood:		878.67	865.46
Likelihood Ratio Test (LRT):
Degree of freedom			1
	χ2 value		13.21
	P-value		2.78×10−4

The parameter λ_k represents the estimates of the baseline annual age-specific cancer incidence rate per 100,000 persons for age groups of 0–15, 15–30, 30–45, 45–60, and 60–75 years, respectively.

Using the LRT to compare the 2 models shown in Table 2, the χ² value was 13.21 that gives a p-value of 2.78 × 10⁻⁴ with 1 degree of freedom, suggesting that the model without LD is rejected at a 0.001 nominal significance level. This was further evidenced by the difference in LOD-scores. An LOD-score difference of 1.5 is considered evidence of a better model (Greenberg, 1989); we found a LOD-score difference of 3.47 (= 21.21 – 17.74), which indicates the model accounted for LD was a far better fit to the data. Because the germ-line p53 gene played a nearly identical causal role to that of the putative major gene in associations with the disease phenotype, as reflected by D' ≈ 1, the coefficient γ_AA = γ_Aa = 3.69 provided a robust estimate of the effects of germ-line p53 mutations on cancer risk: the RR was e^3.69 (= 40.04) for individuals with a germ-line p53 mutant allele to be affected.

Interaction between sex and germ-line p53 mutation

Because of the recent observations that female p53 mutation carriers have an increased cancer risk (Chompret et al., 2000;Hwang et al., 2003b;Wu et al., 2006), we investigated the effects of sex on cancer risk in p53 germ-line mutation carriers. Because the mathematical model that accounted for LD is significantly better than the one without LD (shown in Table 2), we used it as the base model to further test the significance of sex in cancer risk assessment.

Letting the model that includes the covariate Male serve as the baseline model and the model with no covariates serve as the null model, the χ² value for the LRT with 1 degree of freedom was 4.36, which gives a p-value of 3.68 × 10⁻² and rejects the null hypothesis at a 0.05 nominal significance level. The null and baseline models for the LRT testing are presented in the 2^nd and 3^rd columns of Table 3, respectively. Note that Male is coded as 0 for females and 1 for males.

Table 3.

Outcomes of Complex Joint Segregation and Linkage Analyses

		Covariates Included in the Models
	Parameter	No Covariate	Male	Male×p53	Male + Male×p53
Baseline Risk λk (10−5):
Age Group	0 – 15	9.70	13.41	9.63	8.81
	15 – 30	37.96	52.87	38.07	34.85
	30 – 45	94.58	143.85	107.48	98.30
	45 – 60	213.51	337.00	260.58	238.58
	60 –75	704.22	863.72	649.62	598.16
p53 Major Gene: γ(g=Aa, AA)		3.69 (0.40)	3.67 (0.37)	4.09 (0.41)	4.18 (0.52)
Relative Risk (=exp(γ))		40.04	39.25	59.74	65.37
		4.66 × 10−3	1.76 × 10−4	1.09 × 10−3	1.85 × 10−3
	qA	( 3.20 × 10−4 )	(2.62 × 10−5 )	(2.16 × 10−4 )	(1.66 × 10−5 )
		1.22 × 10−10	2.13 × 10−11	1.75 × 10−10	1.15 × 10−11
	qB	(3.20 × 10−4 )	(5.01 × 10−5 )	(3.29 × 10−4 )	(1.91 × 10−5 )
		1.22 × 10−10	2.13 × 10−11	1.75 × 10−10	1.15 × 10−11
	qAB	(3.20 × 10−4 )	(5.01 × 10−5 )	(3.29 × 10−4 )	(1.91 × 10−5 )
Covariate z
	Male		−0.65 (0.31)		0.15 (0.59)
	Male×p53			−0.88 (0.32)	−1.02 (0.66)
−2 Log-Likelihood:		865.46	861.10	858.99	858.96
AIC:		887.46	885.10	882.99	884.96
Likelihood Ratio Test (LRT):
Degree of freedom			1	1	1
	χ2		4.36	6.47	0.03
	P-value		3.68 × 10−2	1.01 × 10−2	0.86

Male is coded as 0 for females and 1 for males. The values of θ̂_p53 = 0.0 and D' ≈ 1 are across the models of Table 3.

Because the p53 gene and putative major gene had nearly perfect LD with D' ≈ 1, we further tested the significance of the interaction between the p53 mutation and sex by letting the covariate Male depend on the putative gene. Male×p53 ≈ Male×G because of LD in the model, the covariate Male×p53 was used to estimate the excess of cancer risk in male carriers over female carriers. Using the LRT to compare the model with Male×p53 (baseline model) and the model with no covariates (null model), the χ² value with 1 degree of freedom was 6.47, giving a p-value of 1.01 × 10⁻² and indicating that the model with p53 and Male×p53 effects is significantly better than the model with p53 effect alone. The model with interaction covariate Male×p53 is presented in the 4^th column of Table 3. We used the AIC criterion to compare the model with Male and the model with Male×p53; the latter model was better because of a substantially lower AIC value.

We also analyzed the data by including both Male and Male×p53 in the model and present the result in the 5^th column of Table 3. This model did not result in an improvement over the model with Male×p53 alone. In conclusion, the model that included the interaction covariate Male×p53 and accounted for LD between the p53 and putative major genes was most plausible. The AIC criterion confirmed this result, as shown in Table 3.

Our plausible model revealed that both p53 and Male×p53 were strongly associated with familial cancer incidence, as shown in the 4^th column of Table 3. The estimated coefficient γ_AA = γ_Aa was 4.09, indicating that the RR for being affected was e ^4.09 (= 59.74) for women with germ-line p53 mutations. The covariate coefficient of Male×p53 was −0.88, indicating that the RR for being affected was e ^4.09-0.88 (= 24.78) for men with p53 mutations. Women with p53 mutations had ane ^0.88 (= 2.41) -fold higher RR for cancer incidence than did men with mutations. We calculated the associated 95% CIs by inverting the Fisher Information Matrix, which was obtained as a part of the maximum likelihood estimation of independent variables. The 95% CIs of the RR for developing cancer in individuals with p53 mutations were (26.84, 132.95) and (11.36, 54.05) for women and men, respectively. The 95% CI of the RR for the difference in women over men with p53 mutations was (1.28, 4.53).

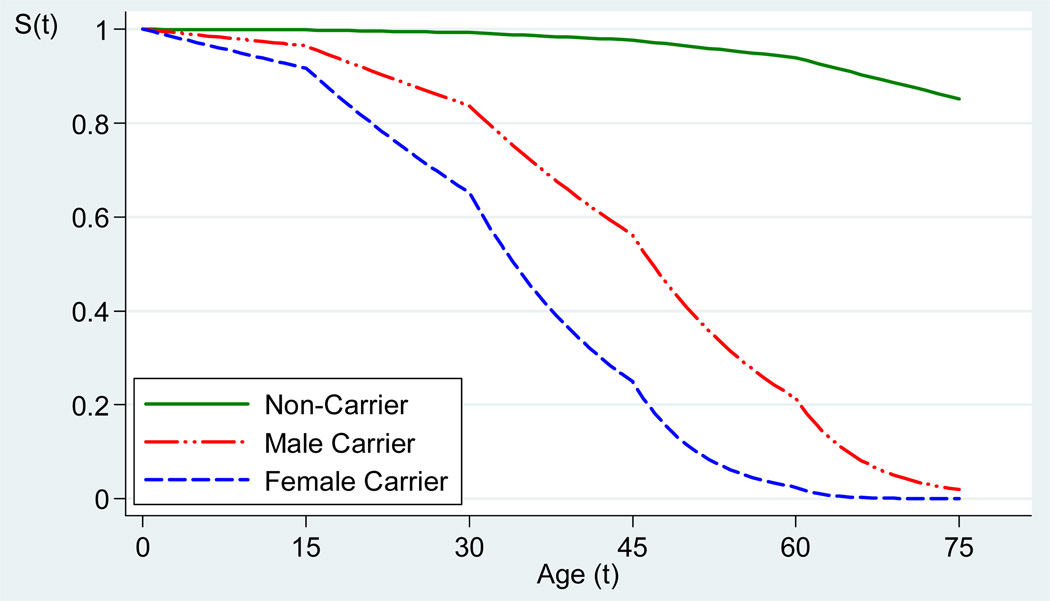
The significance of sex difference on cancer incidence indicated that women with germ-line p53 mutations were substantially younger at developing first cancer incidence than were men with mutations. According to the parameter estimates in our plausible model, we calculated the cancer-free survival curves by p53 mutation status, sex, and age on the basis of the assumption of Cox proportional hazards models with the survival function of $S(t|z,g,\mathrm{\Omega })=\text{exp}\left(-{\displaystyle {\int }_0^t\lambda (s|z,g,\mathrm{\Omega })\mathit{\text{ds}}}\right)$.

These age-specific survival plots are shown in Figure 1. The estimated cancer-free survival probabilities for the highest risk group, female mutation carriers, were 65.2%, 24.9%, and 2.4% at age 30, 45, and 60 years, respectively. The corresponding survival rates for male carriers were 83.8%, 56.2%, and 21.3%. In contrast, the estimated cancer-free survival rates for non-carriers were 99.3%, 97.7%, and 94.0%.

Figure 1.

Cancer-Free Survival Curves by p53 Mutation Carrier Status, Sex, and Age

Discussion

As more risk alleles and mutant genes associated with increased cancer risk are discovered, the paucity of mathematical models that accurately estimate the cancer risk attributable to the measured susceptibility gene in family study becomes particularly pronounced (Antoniou and Easton, 2006). Here, we developed statistical approaches for age-specific risk models based on Cox proportional hazards regression. Our proposed methods extend the usual complex joint segregation and linkage analysis models for censored age-of-onset traits. Using the measured susceptibility genotypes as the linked marker to the putative major gene, we used LD magnitude as a measure to indicate to what extent the putative major gene serves as a proxy of the measured susceptibility gene in associations with cancer phenotype in the models. We obtained;θ̂_p53 = 0.0 and D' ≈ 1 in the application of our proposed approaches to 6 extended pedigrees with p53 germ-line mutations. These values suggest that the p53 genotype was directly associated with cancer phenotype and that the haplotype of allele A and p53 mutant allele was transmitted intact through generations within the families, which indicates that the roles of the p53 gene and putative major gene are nearly identical in this application.

Our approaches are designed to simultaneously assess the associations between cancer incidence and genetic and non-genetic risk factors and quantitatively evaluate the cancer risk attributable to a measured susceptibility gene; in addition, the interactions between these risk factors were tested for significance and accounted for in the model. When strong LD exists between the putative major gene and measured susceptibility gene, our approaches are not only particularly efficient at estimating the effect of the measured gene but also the interaction effects between the gene and other factors. This was important in our study, especially because gene-environment and gene-gene interactions play important roles in disease risk (Altshuler et al., 2008) and because compared with the detection of main component effects, existing statistical methods have relatively limited power for detecting interaction effects (Breslow and Day, 1987;Gauderman and Faucett, 1997).

Inappropriate management of missing genotypes in relatives could lead to substantial power loss and distorted estimates of risk factors’ effects. Modeling the measured susceptibility gene as the linked marker enables all possible genotypes to be assigned to individuals with missing genotypes at the susceptibility locus with corresponding probabilities conditional on the known genotypes of others in the family, leading to robust estimates of main and interaction effects of the measured susceptibility genes. In contrast with existing approaches that only used the information on probands’ mutation carrier status (Antoniou et al., 2003;Antoniou et al., 2002;Cui et al., 2001), our methods precisely accounted for the genotypes at the susceptibility locus for the proband and each relative. Compared with the method that used an independent genetic covariate adjusted for probands’ and relatives’ mutation carrier status in segregation analysis models (Wu et al., 2006), our approaches accounted for intra-familial correlations in hereditary mutation distributions by using the measured susceptibility genotypes as the linked marker in the joint segregation and linkage analyses. The use of independent genetic covariates for hereditary mutation carrier status does not fully account for intra-familial correlations in the distributions of hereditary mutations among relatives in a family (e.g., the offspring of a mutation carrier generally has 50% chances to become a carrier).

Our proposed methods are useful for analyzing families and extended pedigrees ascertained through affected individuals in which the measured risk genotypes are observed within a family. We illustrated and exemplified these methods by an analysis of 6 extended pedigrees ascertained through soft-tissue sarcoma patients with p53 germ-line mutations. Information on p53 genotypes was missing for 26% of the 256 relatives in these pedigrees. Our analyses showed nearly perfect LD between the p53 gene and putative major gene with D' ≈ 1. We also revealed the significance of sex difference on cancer risk in mutation carriers: women with germ-line p53 mutations developed first cancer at a substantially younger age than did men with mutations. Statistical methods are fundamental to accurately and robustly estimate the effects of various risk factors on cancer incidence. We proposed efficient statistical models for quantitatively evaluating the effect of the measured hereditary susceptibility gene on cancer risk in family studies. An accurate assessment and prediction of age-specific cancer risk attributable to a measured susceptibility gene in family studies would provide valuable inferences for genetic and clinical counseling, personalized risk management, and ultimately gain in cancer prevention and control.