Empty Sets as Part of the Numerical Continuum: Conceptual Precursors to the Zero Concept in Rhesus Monkeys

Abstract

The goal of the current research was to explore whether monkeys possess conceptual precursors necessary for understanding zero. We trained rhesus monkeys on a nonsymbolic numerical matching-to-sample task, and on a numerical ordering task. We then introduced nondifferentially reinforced trials that contained empty sets to determine whether monkeys would treat empty sets as numerical values. All monkeys successfully matched and ordered the empty sets without any training. Accuracy showed distance effects, indicating that they treated empty sets as values on a numerical continuum.

A large corpus of data suggests that humans and nonverbal animals share a nonverbal mechanism for representing number without language. Recent experiments have shown that nonhuman animals can represent the number of objects in a stimulus array (numerosity), independent of alternative stimulus dimensions such as size, density, and surface area (e.g., Brannon & Terrace, 1998; Cantlon & Brannon, 2005, 2006; Nieder & Miller, 2003). One hallmark feature of this representation is that it follows Weber's law, whereby the ratio between two numerosities determines the ease of discrimination (e.g., Beran, 2007; Feigenson, Dehaene, & Spelke, 2004; Gelman & Gallistel, 2004). Weber's Law can be seen in numerical comparison tasks by the combination of distance and magnitude effects. As the disparity (distance) increases between two numerical sets, the discrimination accuracy increases, and reaction time (RT) decreases. Likewise, when the distance between two numerical sets is held constant, but the magnitude of those sets increases (e.g., 2 and 4 vs. 8 and 10), the discrimination accuracy decreases and RT increases. Furthermore, monkeys, like adult humans and even children, are able to perform nonverbal approximate addition on their numerosity representations (Barth, Kanwisher, & Spelke, 2003; Cantlon & Brannon, 2007). Finally, nonverbal number representations can be abstract in that they are not always tied to the sensory modality in which a numerical set is experienced (e.g., Barth et al., 2003; Jordan, Brannon, Logothetis, & Ghazanfar, 2005; Jordan, MacLean, & Brannon, 2008).

Beyond numerosity discrimination, some nonhuman animals have been trained to match symbols to specific numerosities (Biro & Matsuzawa, 2001; Boysen & Berntson, 1989; Olthof, Iden, & Roberts, 1997; Pepperberg & Gordon, 2005), perform simple mathematical operations with those symbols (Boysen & Berntson, 1989; Olthof et al., 1997), and symbolically label subsets of items embedded within heterogeneous arrays (Pepperberg & Gordon, 2005).

Given the sophisticated numerical abilities shown by nonhuman animals, and the similarity in numerical psychophysics shown by human and nonhuman animals implicating a common mechanism, it is of interest to see whether nonhuman animals share conceptual precursors of a zero concept. Nonzero natural numbers are counting numbers that are considered abstract representations because they are not bound to the concrete physical properties of stimuli. For example, the symbol for three can represent three triangles, three trees, three tinker toys, or three people. In contrast, zero is special amongst numbers because it is not a counting number and also because it represents the absence rather than the presence of a specific quantity (Wellman & Miller, 1986). Thus, an understanding of zero may be fundamentally different from that of other numbers and may follow a different developmental trajectory.

Historically, zero was introduced into symbolic notational systems much later than the integer list. It is thought that the earliest use of the symbol for zero was by the Babylonians as placeholders to indicate the absence of a particular numerical value (e.g., zero in the number 101 represents the absence of a value in the “tens” column). Later, the Greeks used zero symbolically to represent the “absence” of a quantity, but it took several additional centuries before zero was used in India as a number that could be mathematically manipulated in the same way as other numbers (Bialystok & Codd, 2000; Menninger, 1992).

Paralleling the history of zero in numerical notational systems, children master the use of the symbol zero later than the use of other numerals. Wellman and Miller (1986) found that when items were removed from an array, children were much better at verbally identifying the number of remaining items when those items were greater than zero. Similarly, young children's judgments of relative numerical magnitude with number symbols were more accurate when nonzero numbers were used. Wellman and Miller argue that young children develop zero-like concepts in a series of stages. They first learn to verbally identify the symbol for zero without an understanding of what the symbol means. Later, children learn to recognize that zero represents “none” or “nothing,” but they still fail to recognize the relationship between zero and the other numbers on the continuum. For example, when given the choice between zero and one, young children will insist that “one” is the smaller number. Finally, children learn the relationship between the symbol zero and the other number symbols and appreciate that zero is a smaller number than one. In addition, Wellman and Miller also showed that grasping the meaning of the symbol zero aids children in the acquisition of early algebraic rules.

Studies with infants in the first year of life suggest that babies may find it easier to track magical disappearances compared with magical appearances when the events require representing zero objects behind an occluder. Wynn and Chiang (1998) modified the well-known paradigm developed by Wynn (1992) and showed that 8-month-old infants detected a magical disappearance of a single object (leaving an empty set) but failed to notice a magical appearance of an object surreptitiously added to an empty set. Wynn and Chiang argued that infants did not notice the magical appearance because they were unable to represent the initial empty set and, therefore, did not have the expectation that there should be no objects behind the occluder. Wynn and Chiang argued that if infants rely on a nonverbal counting-like system to represent number, this system may not have the capacity to represent empty sets (i.e., accumulator system or mode-control model; Meck & Church, 1983; Wynn, 1995).

Together, research with babies and children suggests that both in symbolic and in nonsymbolic form, children's concept of empty sets lags behind that of nonzero whole numbers. In addition, children's understanding of zero does not happen all at once, but rather, children gradually acquire the important elemental properties of zero before those elements are fully integrated (Bialystok & Codd, 2000; Wellman & Miller, 1986). Given that nonverbal animals show remarkable similarity to humans in other types of numerical tasks, it is of interest to see whether they also possess conceptual precursors to a zero concept.

A few studies have directly addressed this question by training animals to use a symbol to represent empty sets. Pepperberg (1988) showed that an African Grey parrot (Alex) was able to respond by saying “none” when asked about a relationship that did not exist in a same/different task. For example, when two identical stimuli were presented, and Alex was asked “What's different?” he correctly responded by saying “none.”

In a later study, Pepperberg and Gordon (2005) presented Alex with a series of blue, red, and green blocks scattered on a tray. The number of blocks for each color ranged from one to six. Alex was then asked which color corresponded to a particular number. For example, if shown one blue, four red, and six green blocks, and Alex was asked “what color four?” the correct response would be “red.” However, when Alex was asked to name the color for a numerosity that was not present, he spontaneously said “none.” This finding was particularly impressive in that Alex had not been previously trained to use “none” as a response in the context of numerical judgment tasks, but rather, he transferred his use of “none” from previous non-numerical tasks.

Pepperberg and Gordon (2005) suggested that Alex's spontaneous transfer of “none” to numerical judgment tasks indicated that he may have a concept for “absence” or “nonexistence.” If so, this would suggest that Alex's understanding of zero is similar to that of young children (Wellman & Miller, 1986). However, in a follow-up study (Pepperberg, 2006), Alex failed to say “none” when asked how many items were located under two empty cups. Pepperberg (2006) explained that Alex may have used “none” to describe the absence of a particular attribute associated with a collection of items, but that he was unable to use “none” to describe the absence of the items themselves. Another possibility is that Alex may have used “none” as a response when he simply could not find the specific alternative he was trying to locate. For example, if a four-item array was not present and he was asked “What color 4?” his response “none” may have indicated a failed search or failure to find the alternative. If so, it might explain why he did not say “none” when asked to indicate the number of items under empty cups. It was a different type of question, in which he was directly asked “how many?” as opposed to being asked to locate a specific alternative (e.g., color or shape). Of the eight test trials he was given, he failed to provide a response for five of the trials, but for three of the trials, Pepperberg noted that Alex labeled the empty sets as “one.” This suggests that he may have understood that an empty set occupied a place on the small end of the numerical continuum.

In another study, Boysen and Berntson (1989) demonstrated that a chimpanzee was able to match the Arabic numeral zero with an empty tray and, further, was able to correctly perform addition with numbers zero through four. Similarly, Olthof et al. (1997) trained squirrel monkeys to choose between two Arabic numbers containing corresponding quantities of food (e.g., 0, 1, 3, 5, 7, 9). The monkeys quickly learned to choose the larger Arabic numeral. Next, the monkeys were given tests in which they had to choose between two sets of Arabic numerals (e.g., 1 + 3 vs. 0 + 5). They found that the monkeys consistently chose the larger sum. Although the monkeys may have summed numerically, an alternative possibility is that they summed the associated hedonic value of the stimuli.

Although the experiments reviewed above suggest that animals may be able to learn that a symbol represents an empty set, another important developmental milestone necessary for a full understanding of zero is the ability to determine its ordinal relationship to other numbers. Biro and Matsuzawa (2001) tested a chimpanzee (named Ai) to see whether she could spontaneously acquire the ordinal properties of zero once she understood its cardinal meaning (e.g., that the symbolic form of zero represents “absence” or “nothing”). Ai was trained to match a set of dots with its corresponding Arabic numeral. For trials involving zero, the correct match for the Arabic numeral zero was a blank square that did not contain any dots. Once this task was learned, Ai was tested with an ordinal task in which she was required to select the Arabic numbers in order from smallest to largest. Although Ai had previously been trained to order Arabic numbers in other experiments (Tomonaga & Matsuzawa, 2000), she had not received any prior training with zero. Ai performed quite well on both tasks with training, but she showed no transfer for zero from the matching task to the ordinal task.

Ai's failure to spontaneously demonstrate knowledge of zero's ordinal properties is consistent with the finding that children's ordinal understanding of the symbol for zero lags behind their mapping of the symbol to empty sets. However, it is possible that both children and animals may recognize that “nothing” or “absence” bears a relationship to the other numerosities on the continuum, but that they may be unable to demonstrate this knowledge when required to do so by using symbols. Perhaps, nonhuman animals understand the ordinal relationship between empty sets and other numerosities, and this understanding could be revealed if the symbolic component of the task were removed.

Our goal in the present experiments was to see whether numerically experienced monkeys possess conceptual precursors to the concept zero. An educated adult human's conceptual understanding of zero encompasses its cardinal and ordinal meaning. That is, zero is understood to represent the absence or nonexistence of something specific, and zero has a value on the number continuum that can be compared with other numbers. Consequently, we ask whether monkeys understand that empty sets are numerically equivalent to each other and whether they understand that empty sets are smaller in numerical magnitude than nonempty sets.

To test whether rhesus monkeys appreciate the numerical equivalence between empty sets, we used a matching-to-sample (MTS) task where monkeys were required to choose which of two arrays numerically matched a sample array. To test whether monkeys appreciate that empty sets can be ordered on a numerical continuum, we used a comparison task that required them to choose the numerically smaller of two arrays. In both paradigms, we inserted empty-set stimuli in unreinforced probe trials to determine if monkeys would spontaneously treat empty sets as a value along a numerical continuum. We were specifically interested in whether empty sets would show confusion matrices that indicated that their numerical magnitude was perceived as being less than one. If so, it would suggest that monkeys were representing empty sets as a value along the numerical continuum, as opposed to a qualitatively different “picture-like” stimulus. Although success on both tasks would not suggest a zero concept, it would suggest that monkeys possess two important features of a zero concept: that empty sets have a numerical value and that empty sets can be compared with and ordered relative to other numerosities.

Experiment 1

The goal of Experiment 1 was to determine whether monkeys could match empty sets in a numerical matching task. The novel question addressed by this study was whether empty sets would be spontaneously treated as a numerical value, as evidenced by distance effects.

Method

Subjects

The subjects were 2 adult female rhesus macaques (Mikulski and Schroeder). Both monkeys had previous training in numerical tasks, including numerical match-to-sample and numerical ordering tasks with arrays that ranged between 1 and 12 in value (see Jordan & Brannon, 2006).

Apparatus

Subjects were tested in sound-attenuated booths while seated in Plexiglas primate chairs fitted with a juice-delivery system. Stimuli were presented on a 17-in. touch-screen computer monitor fixed to the inside wall of the soundproof booth. A custom-built program written in RealBasic presented the stimuli and registered responses. Stimuli were presented on a 3 × 3 touch-screen matrix such that the spatial positions of the stimuli on the screen were randomly selected from nine possible locations.

Procedure

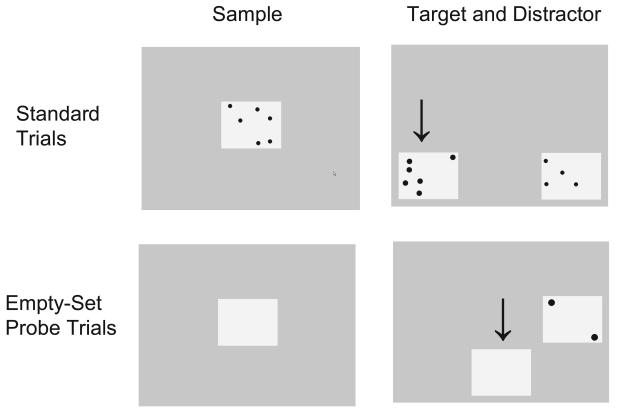
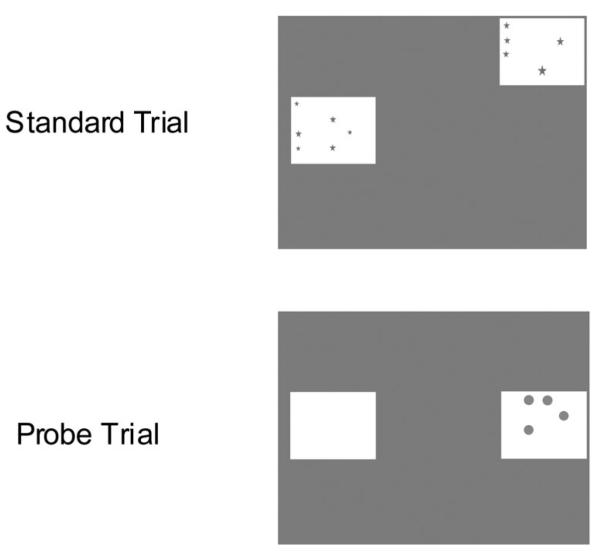
Monkeys were required to match, on the basis of number, a numerical target with a previously shown sample that had the same numerical value (see Figure 1). At the beginning of each trial, a start stimulus (a red square against a green background) appeared in the lower left corner of the screen. Pressing the start stimulus caused it to disappear, after which, the sample stimulus appeared in the center of the screen. When the sample was pressed, it disappeared, and both the target and distractor stimuli appeared in random locations on the screen. Correct selection of the target stimulus was rewarded with 0.3 ml of Kool-Aid. Additional feedback was given in the form of a 1-s auditory chime, and, a 1-s pink screen. An incorrect selection (the distractor) produced a timeout during which the screen turned black for 3 s, and an auditory warning tone was presented for 1 s.

Figure 1.

An example training and probe trial in the numerical matching-to-sample task. The task was to select the target that contained the same number of elements as the sample. The background color of the screen was green. The size and color of the elements was determined randomly for each stimulus, and all elements were presented against a 9 × 7.5-cm yellow background.

Training and testing

Monkeys were given several refresher sessions on the numerical matching task on which they had been previously trained. Stimuli were trial-unique exemplars of the numerosities (1, 2, 3, 4, 6, 8, and 12). The elements consisted of circles presented within a 9 × 7.5-cm yellow background. Both circle size and color were determined randomly for each stimulus so that matching could not be done on the basis of surface area, perimeter, or color.

During testing, monkeys were presented with the same numerical trials they received during training, but empty sets were also presented. The empty-set stimuli were the same 9 × 7.5-cm yellow squares that served as the background for the other numerosity exemplars (see Figure 1). For any trial that contained an empty set, selection of either the distractor or the target produced juice reinforcement. This was done so that no information about the empty set was conveyed during the experiment and extinction was prevented. All possible pairs were presented in a random order. The monkeys were given a total of twelve 200-trial test sessions.

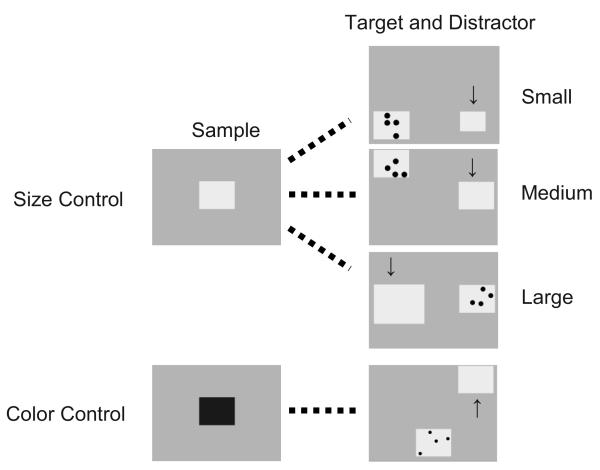
Following testing, we conducted five color and five surface-area control sessions to eliminate the possibility that monkeys were matching empty sets on the basis of relative amount of background surface area or color. In color-control sessions, the color of the empty-set sample was selected randomly from an array of six colors. The color of the target and the distractor backgrounds remained yellow (see Figure 2). Thus, correct empty-set matching required matching two 9 × 7.5-cm squares that differed in color. Because no differential reinforcement was given on empty-set trials, paired associate learning could not take place (e.g., empty blue goes with empty yellow). In surface-area control sessions, we tested whether the monkeys were matching on the basis of the amount of background visible in each stimulus. For empty-set probe trials, the empty-set target was the same size as the empty-set sample on one third of trials but was half or twice as large as the sample on the remaining two thirds of trials. The distractor was always the same size as the sample. Thus, although the sample and distractor stimuli were always 9 × 7.5 cm, the target stimulus was 9 × 7.5 cm, 6.36 × 5.32 cm, or 12.73 × 10.6 cm on a third of trials each (see Figure 2). Accordingly, if the monkeys were basing their decisions on the amount of visible background area, they should have had difficulty when the empty-set targets differed in size from the empty-set samples.

Figure 2.

For the size-control condition, the empty-set target was the same size as the empty-set sample on one third of trials but was half or twice as large as the sample on the remaining two thirds of trials. The distractor was always the same size as the sample. In color-control sessions, the color of the empty-set sample was selected randomly from an array of six colors. The color of the target and the distractor backgrounds remained yellow.

Results and Discussion

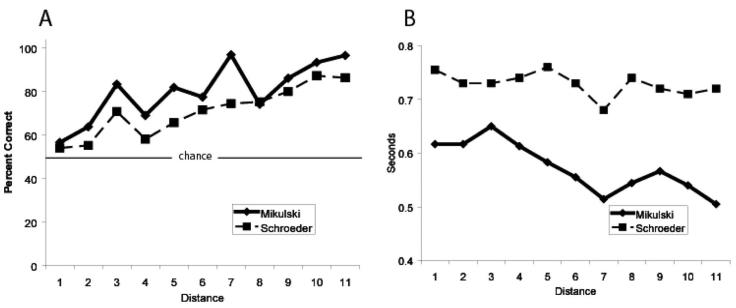
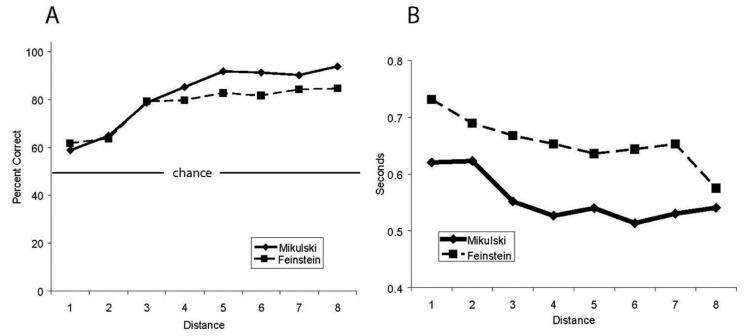
An analysis of session means for overall accuracy (not including empty sets) showed that both monkeys were able to match numerosities at an accuracy that exceeded chance expectations: 75% for Mikulski, one-sample t(11) = 17.0, p < .05, and 63% for Schroeder, one-sample t(11) = 8.7, p < .05. To examine the effects of numerical distance¹ between pairs on accuracy and RT, we obtained mean values for each session and then conducted linear regressions on those values as a function of distance. These analyses revealed that there was an overall accuracy distance effect for both monkeys. As shown in Figure 3, there was an increase in accuracy as the numerical distance between the pairs increased: Mikulski, F(1, 250) = 63.38, p < .05; Schroeder, F(1, 250) = 93.83, p < .05. An overall RT distance effect was found for Mikulski, F(1, 248) = 11.93, p < .05, but not Schroeder, F(1, 244) = 0.24, p = .63.

Figure 3.

Accuracy (A) and reaction time (B) for all pairs as a function of the numerical distance between the target and the distractor for Mikulski and Schroeder in Experiment 1.

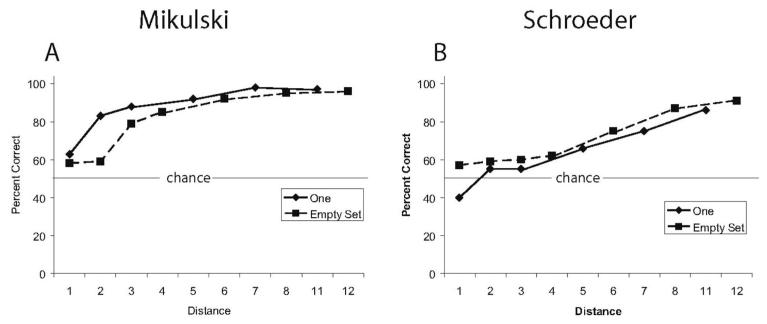
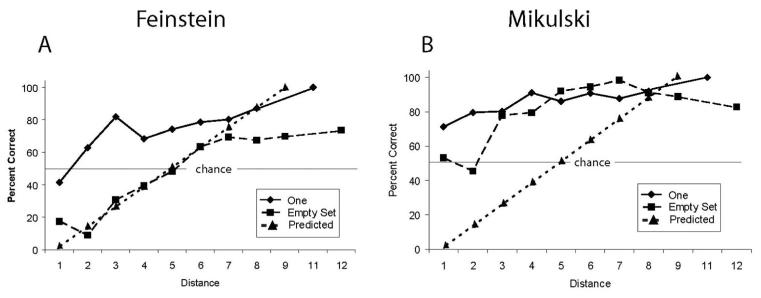
Overall, both monkeys performed well on empty-set matching, with 79% correct for Mikulski, one-sample t(11) = 12.9, p < .05, and 72% correct for Schroeder, one-sample t(11) = 9.1, p < .05. An important question during empty-set testing was whether the empty set was represented as a value on a numerical continuum, or whether it was considered to be a qualitatively different “picture-like” stimulus. If the comparisons were based on numerosity, then we would expect distance effects for empty sets where numerical discriminations become easier as the numerical difference between the empty-set target and distractor increased. As shown in Figure 4, both monkeys showed distance effects for empty sets that were similar to the corresponding distance effects for the numerosity one. Linear regressions on session means for both Mikulski (see Figure 4A) and Schroeder (see Figure 4B) showed significant increases in accuracy as a function of distance for both empty sets—Schroeder, F(1, 82) = 43.63, p < .05; Mikulski, F(1, 82) = 42.86, p < .05—and the numerosity one, Schroeder, F(1, 70) = 37.33, p < .05; Mikulski, F(1, 70) = 30.55, p < .05. Mikulski also showed significant decreases in RT as a function of distance for both empty sets, F(1, 82) = 6.00, p < .05, and one, F(1, 70) = 9.75, p < .05, but Schroeder did not show RT differences for either empty sets, F(1, 80) = 2.93, p = .09, or one, F(1, 69) = 0.98, p = .33.² The finding that monkeys showed similar accuracy distance effects for empty sets and the numerosity one supports the idea that the empty set was treated as a numerical stimulus.

Figure 4.

Accuracy on trials containing an empty set or one element as a function of the numerical distance between the target and the distractor for Mikulski (A), and Schroeder (B) in Experiment 1.

Although both monkeys showed distance effects for the empty-set comparisons, it is possible that they were not comparing on the basis of number but were relying, instead, on other continuous variables, such as background surface area. Larger numerosities, on average, occlude more of the stimulus background and therefore provide an additional cue that can be used to accurately order the stimuli. To test for this possibility, we varied the background size of the empty set throughout the study. The purpose of this manipulation was to assess whether background surface area modulated responses to the empty set. The overall accuracies for the large, medium, and small stimulus sizes were 92%, 83%, and 86% for Mikulski and 67%, 89%, and 75% for Schroeder, respectively. A one-way analysis of variance ANOVA on session means revealed that there were no significant differences between the three different size conditions for either monkey—Mikulski, F(2, 12) = 0.94, p = .42; Schroeder, F(2, 12) = 2.37, p = .14 —thus, responses were not modulated by background size. As a test of generalization, we also included trials in which the sample background color differed from the choice stimuli. A paired-samples t test revealed that there were no significant differences in accuracy on empty-set trials when the color of the empty sets (i.e., sample and target) matched versus when they did not match for either Mikulski, t(4) = −0.66, p = .55, or Schroeder, t(4) = −0.74, p = .50.

Experiment 2a

In Experiment 2a, we inserted empty-set probe trials into a numerical ordering task. Monkeys were already proficient at ordering arrays on the basis of numerosity. The novel question addressed by this study was whether empty sets would be spontaneously treated as a numerical value that can be ordered on a numerical continuum. We were also interested in whether the monkeys would show distance effects that were qualitatively similar to those shown by other (nonempty) sets of numerical stimuli. Successful ordering of empty-set probes would suggest that the monkeys were treating the empty sets as points on a numerical continuum that were comparable to the other numerosities and that they were not simply viewing the empty sets as qualitatively different “picture-like” stimuli.

Method

Subjects

The subjects were 2 adult female rhesus macaques. One monkey (Mikulski) had participated in Experiment 1 and the other monkey (Feinstein) had not yet experienced empty sets. Both monkeys had previous training in numerical ordering tasks.

Apparatus

The apparatus was the same as that for Experiment 1.

Procedure

Monkeys were required to select the numerically smaller of two numerosities (see Figure 5). At the beginning of each trial, a start stimulus (a black square on a red background) appeared in the lower right corner of the screen. Pressing the start stimulus caused it to disappear, after which, the two numerical stimuli appeared in random locations on the screen. If the monkey correctly selected the smaller numerosity, a black border would appear around the stimulus, and the item would remain on the screen until the second item was selected. A correct trial produced visual feedback (the screen turned white for 1 s), auditory feedback (a 1-s auditory chime), and 0.3 ml of Kool-Aid as reinforcement. If the monkey made an incorrect response by selecting the larger numerosity first, the screen immediately turned black for 3 s, and a 1-s warning tone was presented.

Figure 5.

An example training and probe trial in the numerical-ordering task. The task was to select the smaller numerosity first and the larger numerosity second. The background color of the screen was red. The size and color of the elements were determined randomly for each stimulus, and all elements were presented against a yellow background.

Each stimulus was a 9 × 7.5-cm yellow square with a given number of elements randomly placed within. Stimuli were trialunique exemplars of numerosities that varied (both within and between stimuli) in size, shape, and color so that none of these dimensions could be used as ordering cues.

Training and testing

Monkeys were given 10 refresher sessions in which they were required to order the values one through nine. Subsequently in test, empty-set stimuli and exemplars of the numerosity 12 were introduced. On trials that contained empty sets or the numerosity 12, juice reinforcement was given regardless of the order in which the stimuli were selected to prevent learning during testing. The numerosity 12, which was not included during training, was introduced to test the remote possibility that monkeys would show a bias toward pressing an unfamiliar value first. All possible pairings of the values 0–9 and 12 were presented in random order with equal probability of occurrence. The monkeys were given a total of twelve 200-trial test sessions. Because pairs were selected at random, the frequency of presentation for each pair was not matched within a particular session, but rather, frequency was approximately equal over the course of all 12 sessions.

Controls

To eliminate the possibility that the monkeys were using background surface area as a cue on empty-set trials, we implemented the same background-size controls used in Experiment 1. Following testing, both monkeys received five additional sessions of testing, in which the size of the empty set was half normal size on one third of all trials, normal size on one third of all trials, and twice normal size on one third of all trials.

An additional control was implemented to more directly assess whether any distance effects obtained for empty sets could be attributed to perceptual similarity on the basis of the relative foreground-to-background area within each stimulus instead of numerical similarity. The empty set was paired with numerosities 1, 2, 3, and 12, and the numerosity 1 was paired with 2, 3, and 12. The total surface area was made inversely related to numerosity such that the cumulative surface area for the numerosity 1 was two, three, and four times as large as that for numerosities 2, 3, and 12, respectively. If distance effects were driven by the relative amount of foreground to background or total cumulative area, then we should have seen an inverse effect of numerical distance on empty sets.

Results and Discussion

Both monkeys showed a high level of overall accuracy ordering numerosities that did not include empty sets (81% for Mikulski and 80.5% for Feinstein). Linear regressions on session means for each pair revealed an overall distance effect for both monkeys (see Figure 6), with accuracy increasing as a function of distance—Mikulski, F(1, 142) = 58.09, p < .05; Feinstein F(1, 142) = 26.93, p < .05—and RT decreasing as a function of distance for Mikulski, F(1, 137) = 12.97, p < .05, and for Feinstein, F(1, 141) = 10.39, p < .05.

Figure 6.

Accuracy (A) and reaction time (B) for all pairs as a function of numerical distance between the two numerosities for Mikulski and Feinstein in Experiment 2a.

In test, Mikulski spontaneously placed the empty sets in the correct order at above-chance levels, one-sample t(11) = 27.17, p < .05. Because we included more distance comparisons relative to Experiment 1 (without increasing the number of trials per session), we had few observations for each distance in each session. Thus, for analyses purposes, we combined the 12 sessions of data into four three-session blocks. We then obtained mean accuracy and RTs for each pair in each of the four blocks and conducted linear regressions on those means. As illustrated in Figure 7B, Mikulski showed an increase in accuracy as numerical distance increased for both empty sets, F(1, 38) = 16.42, p < .05, and one, F(1, 34) = 16.21, p < .05, but did not show significant decreases in RT for either empty sets, F(1, 38) = 3.33, p = .08, or one, F(1, 34) = 0.74, p = .40. As shown in Figure 7A, Feinstein showed distance effects in accuracy for both empty sets, F(1, 38) = 69.26, p < .05, and one, F(1, 34) = 23.68, p < .05, but showed no RT distance effect for one, F(1, 33) = 0.08, p = .78, and actually showed the opposite trend for empty sets, F(1, 35) = 5.63, p < .05, with RT increasing as distance increased. Further, although Feinstein showed distance effects with regard to accuracy, she demonstrated a strong bias against responding to the empty set, which was only overcome at the larger distances. As a result, her overall accuracy was at chance, one-sample t(11) = −0.61, p = .55.

Figure 7.

Accuracy on trials containing an empty set or one item as a function of the numerical distance between the two numerosities for Feinstein (A) and Mikulski (B) in Experiment 2a. The dotted line indicates the expected level of accuracy on empty-set trials if responding was based on the reinforcement contingencies of the nonempty set.

Although both monkeys showed distance effects with respect to accuracy, an important question is whether these effects resulted from numerical comparisons or whether they resulted from the relative frequency with which each numerosity was previously reinforced in a particular ordinal position during training. For example, during training with all possible pairs using the values one through nine, a first touch to “one” was reinforced in every pair, whereas a first touch to “nine” was never reinforced. Therefore, if the monkeys ignored the numerical value of the empty set and responded on the basis of reinforcement contingencies, we would expect that empty sets would rarely be selected first when paired with small numbers (which would result in an “incorrect” response) and frequently be selected first when paired with larger numbers (which would result in a “correct” response). This would result in accuracy increasing with distance, but accuracy should be considerably below chance when empty sets are paired with small values. Thus, if the effects of reinforcement contingencies were masquerading as distance effects, performance should be significantly below chance when empty sets were paired with small numerosities (e.g., one or two) and only reach chance levels when paired with values greater than or equal to five. In contrast, if empty sets are treated as a value on the ordinal numerical continuum and accuracy reflects the degree to which empty sets are confused with each numerical value, then performance should be expected to range between chance expectations when discrimination is difficult and ceiling performance when discrimination is easy. Examination of Figure 7B indicates that Mikulski's accuracy showed a true numerical distance effect, whereas Feinstein's performance was significantly below chance for empty sets versus small values and, thus, likely reflects prior reinforcement contingencies.

First trial data also support the conclusion that Mikulski treated empty sets as values on the ordinal continuum, whereas Feinstein ignored the empty sets and based her decisions on the prior reward history of the other value in the pair. Of the 10 possible pairings of empty sets with numerosities (1–9, and 12), Mikulski chose the empty set first on 8 of the 10 trials. She made incorrect responses to Items 1 and 3 when they were paired with the empty set. In contrast, Feinstein responded first to the empty set on 4 of the 10 first trial pairings. She avoided empty sets when they were paired with the numerosities one through five and eight.

Given that Feinstein appeared to be basing her decisions on prior reward history of the non-empty-set value, we conducted the control manipulations only with Mikulski at this point. For the background-size control, a one-way ANOVA conducted on session means revealed that Mikulski's responses to the empty sets were not modulated by background surface area, F(2, 12) = 0.032, p = .97. Her overall accuracy on large, medium, and small background sizes for the empty set was 74.4%, 77.5%, and 75.1%, respectively. In addition, Mikulski's responses were not modulated by familiarity. Her accuracy for the numerosity 12 was 98.2%, indicating that she did not have a bias for selecting unfamiliar values first.

In the final control condition, surface area was made to be inversely related to numerosity (see Methods). If distance effects for empty sets reflected perceptual similarity gradients of relative foreground to background, then accuracy should have been inversely related to distance for these sessions. However, a linear regression conducted on session means for each distance revealed that Mikulski showed an accuracy distance effect that was positively related to numerical distance, F(1, 18) = 7.84, p < .05.

Finally, to assess the contribution of other perceptual cues above and beyond numerical representations, we performed a multiple logistic regression on accuracy using the variables cumulative surface area (of the elements), individual element size, and numerical distance as predictors. The analysis was conducted on individual empty-set trials for Mikulski, and we used the Wald chisquare to assess the unique contribution of each predictor. The analysis revealed that numerical distance was a significant predictor of accuracy, χ²(1, N = 467) = 18.45, p < .05, but surface area χ²(1, N = 467) = 1.27, p = .26, and element size χ²(1, N = 467) = 2.65, p = .10, were not.

Experiment 2b

In the previous experiment, Feinstein showed a strong avoidance of the empty set during comparison with small numerosities. The steep accuracy function shown in Figure 7A suggests that her behavior was governed by the relative frequency with which each numerosity was previously reinforced in a particular ordinal position (i.e., first or second). Experiment 2b tests this hypothesis by altering the probability structure that governed when a numerosity was reinforced in the first or second ordinal position. Specifically, pairs were selected, and the frequency of pair presentation was altered such that each numerosity (with the exception of 1 and 12) occurred as the correct first and the correct second response in a pair with equal frequency.

Method

Subject

The subject in this experiment was Feinstein from Experiment 2a.

Procedure

The procedure was the same as that of Experiment 2a, with a few exceptions noted below.

Training and testing

Feinstein was given ten 244-trial retraining sessions using the same general procedures that were used in Experiment 2a. The difference, however, was that instead of drawing from all possible numerosities at random for each trial, only a subset of numerosities were included, and they were drawn at predetermined frequencies. Table 1 shows the relative frequencies for each pair. We did this to ensure that each numerosity was the smaller and the larger value in each pair equally often. After the retraining sessions were completed, Feinstein was given ten 370-trial testing sessions. Because the numerosity 12 was differentially reinforced in the retraining sessions of Experiment 2b, we introduced the novel numerosity 16 in test. Each session contained 244 training pairs and 126 probe trials with either the empty set or the numerosity 16. Probe trials containing the empty set and the numerosity 16 were reinforced regardless of which item was selected. Following testing, the control manipulations used with Mikulski in Experiment 2a were used with Feinstein.

Table 1.

Frequencies per Session at Which Training Pairs Were Presented

	Larger no.
Smaller no.	2	3	4	5	6	7	8	9	12
1	24	14	8	6
2		10	8	6
3			8	6	10
4				6	8	10
5					6	8	10
6						6	8	10
7							6	8	10
8								6	18
9									24

Note. Values in the side column represent the smaller number in a particular pair, and the numbers in the top row represent the larger number in a particular pair.

Results and Discussion

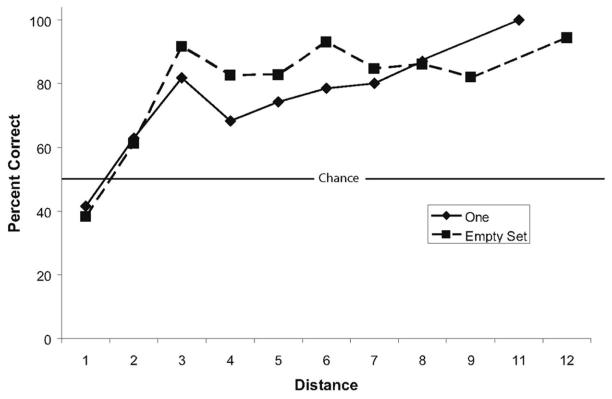
Unlike in the previous experiment, Feinstein's overall performance on probe trials containing an empty set was above chance, with 77.9% correct, one-sample t(11) = 34.7, p < .05. It is important to note that her performance could no longer be accounted for by numerical reinforcement probabilities given that each numerical value was reinforced equally often as the smaller and larger number. As in Experiment 2a, we combined Feinstein's data into three-session blocks and conducted linear regressions using the means from each block. The analysis revealed that as the distance between the empty set and the distractor increased, Feinstein's accuracy increased, F(1, 42) = 13.05, p < .05; (see Figure 8). These patterns are qualitatively similar to those shown by Feinstein in Experiment 2a for the numerosity one (see Figures 7A and 8) and were also very similar to those shown by Mikulski for both empty sets and one (see Figure 7B). Although these findings suggest that Feinstein understood empty sets numerically, it is important to address whether Feinstein attended to the numerical properties of the empty set, or whether her new reinforcement probabilities simply tempered her previous reinforcement structure. If her new reinforcement probabilities reduced, but did not eliminate, the effects of her previous reinforcement structure, then her performance on empty sets should have increased for smaller numbers and decreased for larger numbers when compared with her performance in Experiment 2a. In addition, overall performance on empty sets should have remained at chance.

Figure 8.

Accuracy on empty sets as a function of the numerical distance between the two numerosities for Feinstein after controlling for reinforcement probabilities during training in Experiment 2b. For comparison purposes, Feinstein's accuracy distance function for “one” from Experiment 2a is included.

Feinstein's performance did not fit with these predictions. In fact, although Feinstein's accuracy on small number/empty-set pairs increased, her accuracy on large number/empty-set pairs did not decrease as predicted (see Figures 7A and 8), and as mentioned earlier, her overall performance on empty sets was above chance. Thus, she did not seem to be using reinforcement contingencies, but rather, it appears that removal of the probabilistic cues during training prompted Feinstein to rely on numerical representations during empty-set trials.

Again, we examined first-trial data for each of the empty-set pairings to determine whether nondifferential reinforcement created response biases. Feinstein was correct on 9 of the 11 possible pairings; her two incorrect trials occurred when empty sets were paired with one and two. Overall, Feinstein's data looked very similar to that of Mikulski when reinforcement probabilities were controlled, and both monkeys appeared to treat the empty set as a numerical value that could be evaluated in relation to other numerosities.

We next assessed performance on the control conditions on which Mikulski was tested in Experiment 2a. Feinstein's performance was unaffected by the size-control manipulation. A oneway ANOVA conducted on session means revealed that accuracy on empty-set trials did not vary as a function of background size, F(2, 12) = 2.08, p = .17). When surface area was made inversely related to numerosity, Feinstein, like Mikulski, still showed a numerical distance effect, F(1, 18) = 16.19, p < .05. In addition, we performed a multiple logistic regression on accuracy using the variables cumulative surface area (of the elements), individual element size, and numerical distance as predictors to assess the role of non-numerical perceptual cues. The analysis was conducted on individual empty-set trials, and we used the Wald chi-square to assess the unique contribution of each predictor. The analysis revealed that numerical distance was a significant predictor of accuracy, χ²(1, N = 771) = 7.45, p < .05, but surface area, χ²(1, N = 771) = 0.18, p = .67, and element size, χ²(1, N = 771) = 1.16, p = .28, did not significantly predict accuracy. Finally, Feinstein's accuracy was 99% for all probe trials containing the numerosity 16; thus, it does not appear that she had a bias for selecting novel values first.

Experiment 2c

Both monkeys in Experiment 2a had been previously trained on a conditional discrimination that allowed them to flexibly order numerosities in ascending or descending order on the basis of the background color of the screen. If the monkeys view empty sets numerically, then they should be able to spontaneously order empty sets in the ascending or descending direction on cue without any training. Indeed, if the monkeys treat empty sets numerically, then they should show distance effects for both ascending and descending trials separately. In addition, this experiment should provide further evidence that the monkeys' responses in Experiments 2a and 2b were not the result of a bias toward selecting the empty set first.

Method

Subject

The monkeys Mikulski and Feinstein from Experiment 2a were tested.

Procedure

Monkeys were required to select the numerically smaller of two numerosities when the stimulus background was red and the larger of the two numerosities when the stimulus background was blue. All other aspects of the procedure were as described for Experiment 2a.

Training and testing

Both monkeys were previously trained on a conditional discrimination that required them to select the numerically smaller of two numerosities when the stimulus background was red and the larger of the two numerosities when the stimulus background was blue (Cantlon & Brannon, 2005). Monkeys were given one refresher session with the values one through nine, where 50% of trials used the blue background and, thus, required descending responses (e.g., two and then one) and the other 50% of trials used the red background which required ascending responses (e.g., one and then two). Subsequently in test, on 75% of trials, exemplars of the numerosity one were paired with the values two through nine and were differentially reinforced. On the remaining 25% of trials, empty sets were paired with the values one through nine and were nondifferentially reinforced. Half of all trials in test used the blue background, and half used the red background. The monkeys were tested on a total of five 250-trial test sessions.

Results and Discussion

Performance on ascending (red) and descending (blue) trials was high for both monkeys during the test phase. Feinstein correctly ordered 87.4%, one-sample t(4) = 16.1, p < .05, of ascending trials and 64.3 %, one-sample t(4) = 3.51, p < .05, of descending trials. Similarly, Mikulski correctly ordered 75.1%, one-sample t(4) = 8.4, p < .05, of ascending trials and 77.8%, one-sample t(4) = 14.6, p < .05, of descending trials. The main finding was that both monkeys showed distance effects for empty sets in both ascending and descending directions. Linear regressions showed significant increases in accuracy as a function of distance for empty sets under the red ascending cue—Mikulski, F(1, 43) = 4.4, p < .05; Feinstein, F(1, 43) = 22.3, p < .05—and also under the blue descending cue, Mikulski, F(1, 43) = 7.8, p < .05; Feinstein, F(1, 43) = 14.5, p < .05.

Collectively, the results of Experiments 2a, 2b, and 2c indicate that both monkeys have the capacity to treat empty sets as values along the numerical continuum. Mikulski did so spontaneously, whereas Feinstein attempted an alternative strategy first and only treated empty sets as numerical values after this alternative strategy was prevented. One speculative possibility for why Mikulski and Feinstein performed differently is that Mikulski's prior experience in Experiment 1 may have primed her to treat empty sets as numerical values. In contrast, Feinstein had no prior experience with the empty sets.

General Discussion

An educated adult human's concept of three is quite elaborate. We grasp that the symbol “3” represents the class of all sets that have exactly three tokens. We further comprehend that “3” is less than “4” and more than “2.” We know that three is an odd number, a prime number, and that it is the square root of nine. Nonhuman animals cannot be said to have a full-blown conceptual understanding of the numeral three. However, an animal can learn to classify novel sets of three objects together. Animals also appear to appreciate the ordinal relationships between numerosities, even when faced with numerical values with which they have not been trained. It is in this sense that an animal can be said to have a concept of “threeness” (Gallistel & Gelman, 1992).

The studies reported here demonstrate the same type of conceptual understanding of zero. The rhesus monkey apparently treats the class of all empty sets as equivalent and appreciates that empty sets are smaller in numerical magnitude than nonempty sets. Most important, the current studies show that the monkey clearly appreciates empty sets as occupying a place on a numerical continuum. In the first experiment, two monkeys spontaneously matched empty-set stimuli and showed distance effects, whereby accuracy increased on empty-set trials as the numerosity of the distractor increased. In the second experiment, monkeys were tested on their ability to order numerosities with probe trials that included empty sets. One monkey spontaneously treated the empty sets as a numerical value, showing above-chance accuracy on empty-set trials. She also showed distance effects, with accuracy increasing on empty-set trials as the numerical value of the alternative stimulus increased. A second monkey initially appeared to use an alternative strategy, whereby she ignored the empty set stimuli, and instead, her responses were governed by the prior probability that the alternative numerosity stimulus was rewarded as a first or second response. Once we initiated a new probability structure, such that all numerosities were rewarded as a first and second response equally often, she switched strategies and ordered empty-set trials on the basis of relative numerosity.

These results share similarities with those obtained by Biro and Matsuzawa (2001). Their chimpanzee (Ai) learned to match the symbol “0” with empty sets and showed distance effects as a function of the numerical disparity between the choices. Ai also showed distance effects on a symbolic numerical ordering task, with zero and one being highly confusable. Thus, in a symbolic task, Ai showed patterns that were similar to those shown by our monkeys. However, in both the matching and ordinal task, Ai needed to be trained to learn the discriminations, and she showed no ability to transfer use of the symbol from the matching task to the ordinal task. As noted earlier, an African Gray Parrot was able to transfer the use of “none” from a same/different task to a numerical task, but transfer failed when the parrot was asked to identify the number of items under an empty cup (Pepperberg, 2006; Pepperberg & Gordon, 2005). This notably differs from our results in that our monkeys received no training with empty sets, yet they were able to spontaneously match and order empty sets.

One question that arises from these studies is why animals trained on a symbol for “none” or “zero” were not able transfer the use of that symbol across ordinal and matching tasks the same way that our monkeys were able to do so with nonsymbolic empty sets? One possibility is that the animals did not recognize that the symbol represented something numerical. In Pepperberg's (2006) study, Alex may have used “none” to indicate a failed search when the requested option could not be found, which would explain why he was unable to use “none” to describe the number of items under an empty cup. In Biro and Matsuzawa's (2001) study, the chimpanzee may have learned that the symbol for zero represented “absence of information pertaining to number,” rather than “absence of particular stimuli.” If so, it would make sense that Ai was able to match zero proficiently, yet was unable to spontaneously place zero in the proper order relative to nonzero symbolic numbers.

Beyond understanding that empty sets form an equivalence class and that empty sets are values along a numerical continuum, educated adults have a much richer understanding of the implications that zero is a number. We understand that any number plus zero is itself, that any number minus itself is zero and that multiplying any number by zero results in zero. We have also mastered zero as a place holder in the grammatical system of representing numbers with Arabic numerals. We posit here that such an advanced understanding of zero would not be possible without the conceptual building blocks observed in nonhuman primates.

Given that monkeys treat empty sets as numerical stimuli, it seems likely that humans had the cognitive tools necessary to understand some of the basic features of zero long before the introduction of the symbolic number system. Why then did it take so long, historically, for the numeral zero to emerge? One reason may have been the way numbers were viewed and the path by which symbolic zero entered into the numerical system. As mentioned previously, the earliest uses of zero were as placeholders to skip a position so that the digits before and after the zero refer to the appropriate units. In addition, numerical systems predating the place system made it difficult to accommodate a zero value (Menninger, 1992). For example, consider the system of Roman numerals, which appears to have been derived from tallying. Each number has its own unique symbol or combination of symbols, with each symbol contributing its additive (or subtractive) value to the number (i.e., X represents 10, XX represents 20, and IX represents 9). A symbolic representation for zero would not fit very well into such a system. How does adding up a series of nothings add up to anything but nothing? Not only was zero not needed in such a system, but the system itself made it difficult to accept that a symbol for nothing could represent a valid number (Menninger, 1992).

Given the above, it is understandable how existing numerical systems may have produced resistance to zero, but why didn't zero develop alongside the other numbers in the first place? The fact that numbers are most often used in the context of counting may have presented a major obstacle toward accepting zero as a number. Whereas other natural numbers represent tangible things that can be enumerated, zero represents things that are absent or nonexistent, which may limit its practical usefulness in everyday activities. Although it might be useful to add five units of length to something, or to compare the value of two items with three items, it is rarely useful to add zero units of length to something, or explicitly compare the value of zero items with three items. Certainly, the Roman system allowed these kinds of simple measurements and comparisons without the use of a zero. Thus, acceptance of zero might not have been necessary or useful until the adoption of the more advanced place system.

The developmental lag seen for zero compared with other numerals may reflect the child's early counting experience. Children are initially taught that the counting sequence begins at one (rather than zero), and parents rarely make remarks such as “look, zero ducks!” Thus, it may be that children's delay in learning the cardinal and ordinal aspects of the word or symbol zero are due to early experiences with number, rather than to fundamental difficulties in understanding that empty sets are values on a numerical continuum. We are currently exploring this question by testing young children in the same nonsymbolic tasks we used here with monkeys.

Given that our monkeys were able to understand and reason about the numerical properties of empty sets, it seems unlikely that delays shown by humans historically and developmentally are caused by fundamental difficulties in appreciating empty sets as values on the numerical continuum. At this point, however, it is not clear how the symbolic representation of empty sets and zero develop from processes governing the nonsymbolic understanding of empty sets. Additional research examining the development of such processes in young children, as well as presymbolic processing of empty sets, may shed light on the developmental precursors to the understanding of zero concepts in humans.