Abstract
The medical and personal circumstances of older persons present challenges for designing and analyzing clinical research studies in which they participate. These challenges presented by elderly study samples are not unique but they are sufficiently distinctive to warrant deliberate and systematic attention. Their distinctiveness originates in the multifactorial etiologies of geriatric health syndromes and the multiple morbidities accruing with aging at the end of life. The objective of this article is to identify a set of statistical challenges arising in research with older persons that should be considered conjointly in the practice of clinical research and that should be addressed systematically in the training of biostatisticians intending to work with gerontologists, geriatricians, and older study participants. The statistical challenges include design and analytical strategies for multicomponent interventions, multiple outcomes, state transition models, floor and ceiling effects, missing data, and mixed methods. The methodological and pedagogical themes of this article will be integrated by a description of a proposed subdiscipline of “gerontologic biostatistics” and supported by the introduction of new set of statistical resources for researchers working in this area. These conceptual and methodological resources have been developed in the context of several collaborating Claude D. Pepper Older Americans Independence Centers.
Keywords: clinical research, statistics, aging, study design
INTRODUCTION
The major objective of this article is to summarize some, though, not all, of the distinctive challenges of applied statistics that arise in clinical research with older study participants. To give coherence to the diverse topics we discuss, we propose gerontologic biostatistics as a new subdiscipline characterized by the methodological issues that arise when working with study samples whose health conditions feature multifactorial etiologies and multiple morbidities occurring at the end of life. In making this proposal we emphasize methodological and practical factors more than theoretical ones. (We also emphasize clinical applications in this presentation; basic aging research with animal or in vitro samples has a separate but related set of statistical challenges that we will not review here.) Statistical theory is valuable precisely for its numerous useful applications, yet as biometry and biostatistics did previously, gerontologic biostatistics specifies its subject matter as a means for making applications more informative and productive1. Furthermore, this proposed subdiscipline seeks to advance interdisciplinary thinking and practice by incorporating contributions from gerontology and geriatrics, as well as biology, into a statistical discipline.
As researchers become conscious of distinctive aspects of their field they seek resources that are valuable for addressing them. Resources, including online libraries of measurement instruments and statistical programs, have recently been assembled by collaboration among researchers at three Claude D. Pepper Older American Independence Centers. A second objective of this article is to introduce readers to these online resources. Our overall goals—in developing these resources and proposing a new subdiscipline—are to clarify the tasks of current researchers and facilitate the training of future researchers by expediting the development of analytical methods and teaching materials for biostatisticians collaborating with colleagues dedicated to the study of health conditions of older persons.
DISTINCTIVE CHALLENGES
Design Characteristics: Multicomponent Interventions
The design of multicomponent interventions to be conducted with older persons is complicated by both clinical and statistical issues2, 3. In full factorial randomized clinical trials (RCT)4, 5, all participants are eligible for all levels of intervention components (e.g., diet composition, drug regime, physical therapy), meaning they can be assigned to any treatment arm. As there are a total of 2k possible treatment arms for k binary (present or absent) intervention components, this may result in an unwieldy number of treatment arms. By contrast, in intervention trials addressing multifactorial geriatric health syndromes or multiple morbidities, participants rarely have all risk factors. Consequently, participants are not randomly assigned to all levels of intervention components. Rather, a common practice for those randomized to the intervention arms is to receive only those intervention components corresponding to the modifiable risk factors present at the time of enrollment. This type of intervention component assignment is called “standardly-tailored”6, 7. Other designs for multicomponent interventions have been reviewed in detail elsewhere3.
When analyzing data that arise from a full factorial multicomponent intervention, several methods can implement the estimation of both overall and component level effects. However, when a standardly-tailored design is applied, one must determine the appropriate comparison group to estimate each component. For example, when an individual component effect is estimated in a standardly-tailored design, the appropriate comparison group should only include those participants in the control arm having the risk factors making them eligible for that particular intervention component. With judicious construction of these subgroups, individual intervention components can be estimated, but such analyses should be pre-planned to ensure adequate power. The comparison group of an individual intervention component often differs from one consisting of all participants who did not receive the component. This is because participants in the control group who did not have the risk factor would not be candidates for the component. When carefully considered randomization strategies are not applied to balance the risk factors between the control and intervention arms, the standardly tailored design is limited to estimation of only the overall treatment effect. In studies of aging participants with geriatric syndromes, it is often the overall effect of intervention that is of greatest clinical interest. However, when sampling strategies ensure both a balance of risk factors between the treatment arms and appropriate numbers of participants for each component of intervention, the effects of individual intervention components can be estimated.
Outcome Characteristics: Multiple Outcomes
Biological aging is a complex process involving a progressive failure of the body's various homeostatic adaptive responses at numerous levels—cellular, organic and systemic. Thus, such failures are multifactorial in nature. The probability of acquiring chronic diseases increases as people age. To understand aging itself, all aspects of it need to be considered and researchers often investigate multiple morbidities simultaneously, such as physical performance and cognitive functions. This comprehensive approach to study design leads to multiple outcomes in data analysis.
When multiple outcomes are obtained, for instance, from a randomized clinical trial, the most common approach in the medical literature is to analyze each outcome separately, presenting multiple p-values. It is well known, however, that the excessive use of multiple significance tests can substantially increase the chance of false positive findings (Type I error). This practice also ignores the fact that some outcomes are correlated; hence, inferences made for a particular variable may be due to the difference between comparison groups on some other related measures. These multiple outcomes problems are covered under the umbrella of multiple testing, i.e., the testing of more than one hypothesis at a time.
General procedures in randomized clinical trials for multiple test adjustments include multivariate global test statistics such as Hotelling's T2, p-value based procedures such as Bonferroni adjustment or its modified versions, and resampling-based procedures8–10]. Global test statistics provide an overall assessment of effects of treatment, but offer no estimate of the magnitude of effects and no information about the effects of individual outcomes. By contrast, p-value based methods evaluate treatment effects on individual outcomes. For study design purposes, p-value based methods also provide a basis for sample size and power considerations.
Among p-value based methods, one possible solution is to control a predefined error rate such as family error rate (FER) in the strong sense, i.e., the probability of rejecting falsely at least one true individual null hypothesis, irrespective of which and how many of the individual null hypotheses are in fact true. The Bonferroni method controls FER in the strong sense and is easy to apply. When outcomes are correlated, however, the Bonferroni method is too conservative, or overcorrects. However, it is difficult to evaluate how this overcorrection affects the power of a trial to detect the true treatment effect. Pocock et al. considered a special case of k normally distributed outcomes, each with known variance, for which all possible pairs have the same known correlation ρ within each of two treatment groups11. They suggested that, if most correlations are no more than 0.5, the Bonferroni method does not overcorrect seriously. If any two variables are highly correlated (e.g., ρ = 0.9) it would be wise to select one of them or to predefine some combination of them. Recently, Xiong et al. proposed an intersection-union test (IUT), in which correlation between two primary endpoints was also considered12. It was successfully applied to a double-blinded, placebo-controlled 24-week Alzheimer's treatment clinical trial of the safety and efficacy of a novel treatment.
Resampling-based methods (such as bootstrap and permutation methods) are computationally intensive but appealing in that information regarding the dependencies and distributional characteristics of the test statistics are incorporated into the adjustments and therefore are considerably more powerful than p-value based methods when tests are highly correlated and no simple formula is available. The multiple outcomes of aging research studies are often correlated and so recent research in p-value based methods incorporating correlations and resampling-based methods are especially pertinent to gerontologic biostatistics.
Another class of methods worth mentioning is based on the false discovery rate (FDR), first introduced by Benjamini et al.13, where the FDR is the expected value of the ratio of the number of falsely significant tests to the total number of significant tests. This error rate is less conservative than the FER and has been applied frequently in genomic14, microarray15, neuroimaging16, molecular epidemiology studies17, and many other areas in which large numbers of correlated simultaneous measurements are taken.
Outcome Characteristics: State Transitions
Transition models for longitudinal data are important tools for understanding the disablement process in older persons. Disablement is often defined in terms of multiple geriatric outcomes that include measurements in mobility and other activities of daily living (ADL). Thus, statistical methods analyzing disablement data first and foremost must be able to handle multiple outcomes in a longitudinal context. Another methodological challenge in studying age-related disablement is the nonlinearity of the process and the possible oscillations between disability states. Until recently, disability was conceptualized much like other chronic health problems, as a progressive disorder that was irreversible18. Gill and his colleagues, however, have shown that older persons actually move in and out of disability, suggesting that it is best conceptualized as a state, rather than a trait19, 20.
State-based transition models can be used to delineate risk factors associated with older persons' possible cycling back and forth between disability states. In a recent study, Gill et al. used a marginal multivariate Cox model to analyze transitions between disability subtypes21. Rejeski et al.22 have used an alternative approach to transition modeling; they fitted multivariate hidden Markov models to study the change in physical functions in a sample of older persons (aged 65 or above) with knee pain over a period of three years. These authors examined the transition probabilities between the several disability states based on individuals' obesity statuses (Body Mass Index (BMI) < 30, BMI between 30 and 35, and BMI > 35). The authors concluded that obese older persons tend to stay in the worst disabled state with higher probabilities and that they are also more likely to enter into less favorable functional states than non-obese older persons.
Physical functional status may worsen along several different pathways. For example, within the domain of basic Activities of Daily Living (ADL) disability, function may be gradually compromised in tasks that require changing one's body position, e.g., getting into and out of a chair, car, or bed. On the other hand, disability onset may occur because of a single traumatic event like a fall. Also, disability pathways are not necessarily linearly ordered; so new methodological challenges arise for designing parsimonious models for capturing the effects of risk factors and treatment options for older persons on outcomes involving complex transitions between states.
Data Characteristics: Floor and Ceiling Effects
Due to the multifactorial etiology of aging and the multiple morbidities that older persons' experience, aging research emphasizes functional status—physical, mental, and emotional—as well as the presence or absence of a disease. Questionnaires and functional tests with continuous or count outcomes are often used to describe a range of function. When assessments cannot be completed or are inappropriate, spikes might occur at one end of a distribution. These are referred to as floor or ceiling effects, or as data with “excess zeroes”, “clumping at zero,” or semicontinuous data. In psychometrics it is often implicit in the definition of these effects that they are artificial, arising from the instrument rather than an actual floor or ceiling for the construct23. In gerontologic research, such spikes may result from using an instrument developed for another population; however, they may also reflect a true floor that occurs in a geriatric population. For example, the SF-36 is a well-validated health instrument for general adult populations. Its use in older persons with comorbidities may lead to floor effects, due to inadequate discrimination in the lower range of function. When measures are chosen judiciously, floor and ceiling effects can often be avoided. For example, the use of the Stroke Impact Scale rather than the Barthel Index avoids ceiling effects in assessing the impact of stroke24. Increasing the size of the item pool used to measure the construct of interest may also lessen the chance that floor and ceiling effects may occur, although this may increase participant response burden. Contemporary psychometric methods including item response theory and computerized adaptive test (CAT) can be used to circumvent this problem. An example of large-scale application of item banking and CAT to the measurement of health is the National Institutes of Health (NIH)-sponsored network Patient- Reported Outcomes Measurement Information System (PROMIS)25. Existing PROMIS item banks that are relevant to aging studies include physical function (Instrumental Activities of Daily Living (IADL), lower and upper extremities, central neck and back), cognitive function, and depression.
Floor effects may also arise from the inability of a participant to complete a task; a zero in this case arises from the participant's status rather than from an inadequacy of the measure. An example of this might occur upon administering the 400-meter walk to study participants: some may not be able to complete the walk at all, resulting in a distribution of walking speed with a large spike at zero. Due to large variability in status domains and between individuals, the selection of measures for gerontologic research is particularly difficult and prone to floor and ceiling effects.
There have been several general statistical approaches to modeling data with floor or ceiling effects. Because floor effects with many zeroes are most common, we will discuss these, but the methods are applicable to other types of effects. One approach is to treat zeroes as occurring from a truncated distribution, i.e., a smaller value would have been observed if the assessment tool was more sensitive, rather than a zero. In this approach Tobit model for left censored data is commonly used26. Another approach is to model the distribution with many zeroes in a generalized linear model whose mixture distribution accommodates them, e.g., zero-inflated Poisson27 or negative binomial regression models28. For example, Byers et al. used a negative binomial model to evaluate the effectiveness of a prehabilitation program on the onset of disability, in which 40% of subjects had no disability at follow-up28. A third approach is also appropriate for true zeroes. A two-part model is used, separating the probability of occurrence from the intensity when the activity is completed29.
Aging researchers often seek to capture the trajectory of aging, modeling outcomes such as decline in functional status over time. Statistical methods are needed to model these trajectories, in which a floor effect may be reached gradually or precipitously, or may occur at one time point, but not the next (e.g., from an acute illness). A two-part mixed effects model with correlated random effects for repeated measures data with excess zeroes and a continuous, non-zero response for intensity has been developed30, 31. One advantage of this model is that it models the correlation that often arises between an activity's probability and its intensity.
Data Characteristics: Missing Data
One of the most common analytical issues in longitudinal studies of gerontologic outcomes is how to handle missing values that occur because study participants die or become so ill that they cannot provide requisite information32. Missing values of this sort have implications for both the design and analysis of gerontologic studies. For example, triggered sampling designs can mitigate the impact of losses to follow-up by collecting additional data when study participants experience a decrement in health such as a hospitalization33; also, the use of multiple imputation to handle missing values should be integrated logically into a regression model fitting process34.
While techniques such as survival analysis and generalized linear mixed models account for censoring, they typically assume that the mechanism generating the missingness is either completely independent of the observed values, i.e., missing completely at random (MCAR), or dependent only on the observed values, i.e., missing at random (MAR)35. The assumption of MCAR or MAR is clearly of dubious value when evaluating the associations between important variables and longitudinal outcomes where death has resulted in termination of measurement. Gerontologic research therefore calls for a thorough examination of missing data, and will be greatly strengthened by use of statistical techniques that rigorously account for the informativeness of measurement cessation caused by death or informative dropout. Recent work in joint modeling of survival and longitudinal outcomes shows promise in allowing for a differential evaluation of the associations between specific covariates and the intertwined processes of aging and dying36, 37.
Data Interpretation: Mixed Methods
Older persons often suffer from multiple morbidities from which they will never fully recover and to which their deaths might eventually be attributed. Decisions that they, their families, and doctors make regarding medical treatments characteristically consider not only whether such treatments will increase longevity but whether, on balance, they will enhance quality of life. Judgments regarding quality of life at the end of life have ethical dimensions that often reflect religious and spiritual concerns. Addressing these ethical and spiritual issues in clinical research involving older persons is aided by collecting qualitative, as well as quantitative data. For example, it is often desirable to ask study participants open-ended questions that they answer in their own words. Recent methodological38 and software advances39, 40 in qualitative data analysis have made this research approach more rigorous and have made the integration of quantitative and qualitative information (often called “mixed methods”) a challenge especially germane for gerontologic biostatisticians.
There are at least three areas in which qualitative and quantitative techniques—or mixed methods—can be productively employed in gerontologic research. They are instrument development, association interpretation, and presupposition evaluation. Qualitative studies by Fried et al.41 provided new insights into key ideas like treatment burden and treatment outcome that figured prominently in subsequent quantitative studies of medical decision-making at the end of life42. This type of mixed method can also be used in health services research impacting older persons. Bradley et al. used qualitative methods to identify strategies for reducing “door-to-balloon time” for patients who have had a myocardial infarction accompanied by ST-segment elevation43, 44. The effectiveness of the identified strategies was then tested in a quantitative study45.
Qualitative studies can be useful in interpreting statistical associations46. Schoenberg et al. report an association between taking over-the-counter medications for cardiac symptoms and longer time to treatment, and conducted a complementary qualitative study of such cardiac self-care strategies to take a “closer look at who was likely to pursue such strategies and their reasons behind so doing”47. Another example of mixed methods research of this type examined with qualitative methods the meanings of different “self-ratings of health” and conducted concomitant quantitative analyses in order to provide insight into whether self-rated health should be measured the same way in older study samples as in younger samples48. Finally, more recently, qualitative methods for eliciting expert probability judgments have been used to specify subjective prior probabilities for Bayesian statistical analyses, thereby allowing inquiry into the extent to which expert opinion achieves clinical equipoise or conforms to results from a particular study sample49. Tan et al. used a questionnaire developed with qualitative methods to elicit prior distributions from experts regarding “2-year recurrence free survival” for an analysis comparing surgery alone to surgery with an adjuvant treatment for hepatocellular carcinoma50.
CONCLUSION
A principal task of biostatisticians is to ensure that statistical inferences are sound and informative. Good designs foster good inference. Standardly-tailored study designs help researchers draw informative inferences about multi-component interventions. Chance, bias, ambiguity, and unaccounted for data dependencies are potential threats to good inference. Adjustment methods for multiple outcomes minimize the threat of chance; missing data methods combat bias from losses to follow-up; mixed methods can clarify the meanings of key ideas in clinical research. In all of these areas biostatisticians working with older study participants are making valuable methodological contributions.
Data dependencies can lead to artificially small estimates of variability and uncontrolled associations between study variables can cause confounding. To identify and correctly account for such dependencies requires subject matter knowledge—gerontologic and geriatric expertise—as well as statistical skill. This interdisciplinary combination is actively promoted by the proposed subdiscipline of gerontologic biostatistics and is practically empowered by the resources we have begun to assemble. We hope that these conceptual and practical resources will enhance the training of a new generation of clinical researchers working with older study participants.
Table 1.
Defining Features of Gerontologic Biostatistics
| Definition: Gerontologic Biostatistics is the biostatistical subdiscipline that grapples with the applied statistical challenges that emerge when conducting research on aging or with older study participants. | ||
|---|---|---|
| Subdivisions | Key Sample Characteristics | Contributions to Aging Research |
| Basic | Animal or In Vitro Samples | Promotes more efficient designs, thus often reducing the number of experimental animals required |
| Adjusts for correlations among repeated measures on the same animals or samples | ||
| Introduces advanced methodologies to address heterogeneity, multiple testing, and other issues | ||
|
| ||
| Clinical | Primarily Human Aging at the End of Life | Promotes interdisciplinary collaboration |
| Multifactorial Etiologies Of Health Conditions | Clarifies conceptual thinking | |
| Multiple Morbidities | Facilitates training of new biostatisticians for aging research | |
| Death as Informative Censoring | ||
Table 2.
Statistical Challenges and Methodologies for Gerontologic Research
| Statistical Challenge | Methodology | Techniques (with citations of applications) | Utility |
|---|---|---|---|
| Multi-component Interventions | Clinical Trial Design | Full Factorial Design4,5 |
|
| (2k treatment arms where k is number of components) | |||
| Standardly-tailored Designs6,7 | |||
| (2 treatment arms, but within each intervention arm 2k − 1 possible combinations of intervention components where k is number of components) | |||
|
| |||
| Multiple Outcomes | Multiple Testing Procedures | Global Statistics |
|
| P-value Methods12 | |||
| Resampling Methods | |||
| False Discovery Rate Methods14–17 | |||
|
| |||
| State Transitions | Longitudinal Transition Models | Extended Cox Models21 |
|
| Hidden Markov Models22 | |||
|
| |||
| Floor and Ceiling Effects | Item Response Theory Methods and Regression Modeling | Item banking and computerized adaptive test (CAT) techniques24,25 |
|
| Tobit Models and Negative Binomial Models28 | |||
| 2-part Mixed Effects Model30 | |||
|
| |||
| Missing Data | Missing Data Methods | Triggered Sampling Designs42 |
|
| Multiple Imputation34 | |||
| Joint Modeling of Survival and Longitudinal Outcomes36 | |||
|
| |||
| Qualitative and Quantitative Data | Mixed Methods | Instrument Development41–42,43–35 |
|
| Association Interpretation46–48 | |||
| Presupposition Evaluation50 | |||
ACKNOWLEDGMENTS
Drs. Van Ness, Murphy, Allore, and Mr. Charpentier were supported in part by grants from the Claude D. Pepper Older Americans Independence Center at Yale University School of Medicine (P30 AG021342-06) and by an NIA Supplement grant for the GRASP project (P30 AG021342-0651). Drs. Leng and Ip were supported in part by the Claude D. Pepper Older Americans Independence Center at Wake Forest University School of Medicine (P30 AG21332). Dr. Ip was supported by NIH grant number R01AGO31827A of which he is the Principal Investigator and Dr. Geert Molenberghs is a Co-Principal Investigator.
Other Contributions: The authors thank and acknowledge the contributions of Gail McAvay in the development of the GRIL web resource and of Geraldine Hawthorne in the development of the GRASP web resource and in the design of Figure 1.
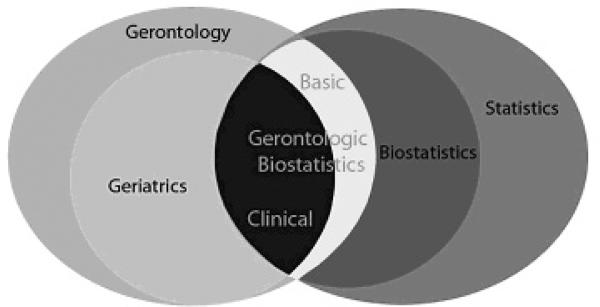
Figure 1.
Gerontologic Biostatistics and its Relationships with Kindred Disciplines
APPENDIX: PRACTICAL RESOURCES
The Geriatrics Research Instrument Library (GRIL) is an online collection (www.gril.yale.edu) of information about data collection instruments commonly used in gerontologic research. A minimal description includes a summary of purpose, a bibliography, and contact information and links to relevant web sites. Copyright permitting, complete descriptions including section and question scripts, response value sets, and interviewer instructions are provided. GRIL content navigation is managed by an expandable and searchable tree that arranges the instruments into thematic categories. While content selection is ongoing, GRIL currently includes 66 data collection instruments.
Gerontologic Research Algorithms and Statistical Programs (GRASP) is a web resource (www.grasp.yale.edu) for biostatisticians, epidemiologists, and clinical researchers that includes an online repository of biostatistical programs, data structures, and algorithms developed to address design and analytical issues characteristic of gerontologic research. (Several relevant contributions from co-authors of this article are available there.) It also includes a forum for communication and collaboration among biostatisticians and investigators in the field. The two foci of GRASP are content and community. The GRASP content manager is the “GRASP Explorer,” which, like GRIL, uses a tree structure as the main navigation tool. The GRASP Explorer tree may be organized by topic, author or institution, and all textual content is indexed for searching. All GRASP content is downloadable, and most content may be viewed directly from the GRASP Explorer. Users who register with GRASP may upload new content which, upon review, may be added to the repository. The GRASP Explorer is integrated with two community resources: the GRASP Wiki and a discussion forum. Each GRASP submission is represented in the Wiki, and locatable by a table of contents, a keyword index, or by a search function. The GRASP Wiki allows users to add new articles or expand existing ones. The GRASP Discussion Forum is a traditional bulletin-board style website.
Footnotes
Conflict of Interest: The authors have no financial or any other kind of personal conflicts regarding the composition of his manuscript.
Sponsor's Role: The organizations funding this essay had no role in the preparation, review, or approval of this manuscript.
REFERENCES
- 1.Molenberghs G. Biometry, biometrics, biostatistics, bioinformatics, bio-x. Biometrics. 2005;61:1–9. doi: 10.1111/j.0006-341X.2005.040831.x. [DOI] [PubMed] [Google Scholar]
- 2.Allore HG, Peduzzi PN, Tinetti ME. Experimental designs for multicomponent interventions among persons with multifactorial geriatric syndromes. Clin Trials. 2005;2:13–21. doi: 10.1191/1740774505cn067oa. [DOI] [PubMed] [Google Scholar]
- 3.Allore HG, Murphy TE. An examination of effect estimation in factorial and standardly-tailored designs. Clin Trials. 2008;5:121–130. doi: 10.1177/1740774508089278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sullivan DH, Roberson PK, Smith ES, et al. Effects of muscle strength training and megestrol acetate on strength, muscle mass, and function in frail older people. J Am Geriatr Soc. 2007;55:20–28. doi: 10.1111/j.1532-5415.2006.01010.x. [DOI] [PubMed] [Google Scholar]
- 5.Friedman L, Zeitzer JM, Kushida C, et al. Scheduled bright light for treatment of insomnia in older adults. J Am Geriatr Soc Mar. 2009;57:441–452. doi: 10.1111/j.1532-5415.2008.02164.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Eliott AF, Burgio LD, DeCoster J. Enhancing caregiver health: findings for the resources for enhancing Alzheiner's caregiver health II intervention. J Am Geriatr Soc. 2010;58:30–37. doi: 10.1111/j.1532-5415.2009.02631.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wenger NS, Roth CP, Shekelle PG, et al. A practice-based intervention to improve primary care for falls, urinary incontinence, and dementia. J Am Geriatr Soc. 2009;57:547–555. doi: 10.1111/j.1532-5415.2008.02128.x. [DOI] [PubMed] [Google Scholar]
- 8.Bauer P. Multiple testing in clinical trials. Stat Med. 1991;10:871–890. doi: 10.1002/sim.4780100609. [DOI] [PubMed] [Google Scholar]
- 9.Shaffer JP. Multiple hypothesis testing. Annu Rev Psychol. 1995;46:561–584. [Google Scholar]
- 10.Westfall PH, Young SS, Wright SP. On adjusting p-values for multiplicity. Biometrics. 1993;49:941–945. [Google Scholar]
- 11.Pocock SJ, Geller NL, Tsiatis AA. The analysis of multiple endpoints in clinical trials. Biometrics. 1987;43:487–498. [PubMed] [Google Scholar]
- 12.Xiong C, Yu K, Gao F, et al. Power and sample size for clinical trials when efficacy is required in multiple endpoints: Application to an Alzheimer's treatment trial. Clin Trials. 2005;2:387–393. doi: 10.1191/1740774505cn112oa. [DOI] [PubMed] [Google Scholar]
- 13.Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J R Stat Soc Series B Stat Methodol. 1995;57:289–300. [Google Scholar]
- 14.Forner K, Lamarine M, Guedj M, et al. Universal false discovery rate estimation methodology for genome-wide association studies. Human Heredity. 2008;65:183–194. doi: 10.1159/000112365. [DOI] [PubMed] [Google Scholar]
- 15.Reiner A, Yekutieli D, Benjamini Y. Identifying differentially expressed genes using false discovery rate controlling procedures. Bioinformatics. 2003;19:368–375. doi: 10.1093/bioinformatics/btf877. [DOI] [PubMed] [Google Scholar]
- 16.Genovese CR, Lazar NA, Nichols T. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage. 2002;15:870–878. doi: 10.1006/nimg.2001.1037. [DOI] [PubMed] [Google Scholar]
- 17.Wacholder S, Chanock S, Garcia-Closas M, et al. Assessing the probability that a positive report is false: An approach for molecular epidemiology studies. J Nat Cancer Institute. 2004;96:434–442. doi: 10.1093/jnci/djh075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Verbrugge LM, Reoma JM, Gruber-Baldini AL. Short-term dynamics of disability and well-being. J Health Soc Behav. 1994;35:97–117. [PubMed] [Google Scholar]
- 19.Gill TM, Gahbauer EA, Allore HG, et al. Transitions between frailty states among community-living older persons. Arch Intern Med. 2006;166:418–423. doi: 10.1001/archinte.166.4.418. [DOI] [PubMed] [Google Scholar]
- 20.Gill TM, Kurland BF. Prognostic effect of prior disability episodes among nondisabled community-living older persons. Am J Epidemiol. 2003;158:1090–1096. doi: 10.1093/aje/kwg237. [DOI] [PubMed] [Google Scholar]
- 21.Gill TM, Murphy TE, Barry LC, et al. Risk factors for disability subtypes in older persons. J Am Geriatr Soc. 2009;57:1850–1855. doi: 10.1111/j.1532-5415.2009.02443.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rejeski WJ, Ip EH, Marsh AP, et al. Obesity influences transitional states of disability in older adults with knee pain. Arch Phys Med Rehabil. 2008;89:2102–2107. doi: 10.1016/j.apmr.2008.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nunnally J, Bernstein I. Psychometric Theory. 3rd ed. McGraw Hill; New York: 1994. p. 570. [Google Scholar]
- 24.Lai S-M, Studenski S, Duncan PW, et al. Persisting consequences of stroke measured by the Stroke Impact Scale. Stroke. 2002;33:1840–1844. doi: 10.1161/01.str.0000019289.15440.f2. [DOI] [PubMed] [Google Scholar]
- 25.Cella D, Yount S, Rothrock N, et al. The Patient-Reported Outcomes Measurement Information System (PROMIS): progress of an NIH Roadmap cooperative group during its first two years. Medical Care. 2007;45:S3–S11. doi: 10.1097/01.mlr.0000258615.42478.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tobin J. Estimation for relationships with limited dependent variables. Econometrica. 1958;26:24–36. [Google Scholar]
- 27.Lambert D. Zero-inflated Poisson regression, with an application to defects in manufacturing. Technometrics. 1992;34:1–14. [Google Scholar]
- 28.Byers AL, Allore H, Gill TM, et al. Application of negative binomial modeling for discrete outcomes: A case study in aging research. J Clin Epidemiol. 2003;56:559–564. doi: 10.1016/s0895-4356(03)00028-3. [DOI] [PubMed] [Google Scholar]
- 29.Duan N, Manning WG, Morris CN, et al. A comparison of alternative models for the demand of medical care. RAND Corporation; Santa Monica, CA: 1982. R-2754-HHS. [Google Scholar]
- 30.Tooze JA, Grunwald GK, Jones RH. Analysis of repeated measure data with clumping at zero. Stat Methods Med Res. 2002;11:341–355. doi: 10.1191/0962280202sm291ra. [DOI] [PubMed] [Google Scholar]
- 31.Olsen MK, Schafer JL. A two-part random-effects model for semicontinuous longitudinal data. J Am Stat Assoc. 2001;96:730–745. [Google Scholar]
- 32.Hardy SE, Allore HG, Studenski SA. Missing data: A special challenge in aging research. J Am Geriatr Soc. 2009;57:722–729. doi: 10.1111/j.1532-5415.2008.02168.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Van Ness, Allore HG, Fried TR, et al. Inverse intensity weighting in generalized linear models as an option for analyzing longitudinal data with triggered observations. Am J Epidemiol. 2010;171:105–112. doi: 10.1093/aje/kwp333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Van Ness, Murphy TE, Araujo KLB, et al. The use of missingness screens in clinical epidemiologic research has implications for regression modeling. J Clin Epidemiol. 2007;60:1239–1245. doi: 10.1016/j.jclinepi.2007.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Little RJA, Rubin DB. Statistical Analysis with Missing Data. 2nd ed. John Wiley & Sons; Hoboken, NJ: 2002. [Google Scholar]
- 36.Gao S. A shared random effect parameter approach for longitudinal dementia data with non-ignorable missing data. Stat Med. 2004;24:211–219. doi: 10.1002/sim.1710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lin H, McCulloch C, Mayne S. Maximum likelihood estimation in the joint analysis of time-to-event and multiple longitudinal variables. Stat Med. 2002;21:2369–2382. doi: 10.1002/sim.1179. [DOI] [PubMed] [Google Scholar]
- 38.Rihoux B, Ragin CC, editors. Configurational Comparative Methods: Qualitative Comparative Analysis (QCA) and Related Techniques. Sage; Los Angeles: 2009. Applied Social Research Methods Series. [Google Scholar]
- 39.NVivo 8 [computer program] QSR International Pty Ltd; Doncaster, Victoria 3108, Australia: 2008. [Google Scholar]
- 40.ATLAS.ti 6.0 [computer program] ATLAS.ti GmbH; Berlin, Germany: 2009. [Google Scholar]
- 41.Fried TR, Bradley EH. What matters to seriously ill older person making end-of-life decisions?: A qualitative study. J Palliat Med. 2003;6:237–244. doi: 10.1089/109662103764978489. [DOI] [PubMed] [Google Scholar]
- 42.Fried TR, Van Ness PH, Byers AL, et al. Changes in preferences for life-sustaining treatment among older persons with advanced illness. J Gen Intern Med. 2007;22:495–501. doi: 10.1007/s11606-007-0104-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bradley EH, Curry LA, Webster TR, et al. Achieving rapid door-to-balloon times: how top hospitals improve complex clinical systems. Circulation. 2006;113:1079–1085. doi: 10.1161/CIRCULATIONAHA.105.590133. [DOI] [PubMed] [Google Scholar]
- 44.Bradley EH, Roumanis SA, Radford MJ, et al. Achieving door-to-balloon times that meet quality guidelines: How do successful hospitals do it? J Am College Cardiol. 2005;46:1236–1241. doi: 10.1016/j.jacc.2005.07.009. [DOI] [PubMed] [Google Scholar]
- 45.Bradley EH, Herrin J, Wang Y, et al. Strategies for reducing the door-to-balloon time in acute myocardial infarction. N Engl J Med. 2006;355:2308–2320. doi: 10.1056/NEJMsa063117. [DOI] [PubMed] [Google Scholar]
- 46.Fried TR, van Doorn C, O'Leary JR, et al. Older persons' preferences for site of terminal care. Ann Intern Med. 1999;131:109–112. doi: 10.7326/0003-4819-131-2-199907200-00006. Erratum appears in Ann Intern Med 2000;132:419. [DOI] [PubMed] [Google Scholar]
- 47.Schoenberg NE, Amey CH, Stoller EP, et al. The pivotal role of cardiac self-care in treatment timing. Soc Sci Med. 2005;60:1047–1060. doi: 10.1016/j.socscimed.2004.06.045. [DOI] [PubMed] [Google Scholar]
- 48.Idler EL. The meanings of self-ratings of health. Res Aging. 1999;21:458–476. [Google Scholar]
- 49.O'Hagan A, Buck CE, Daneshkhah A, et al. Uncertain Judgements: Eliciting Experts' Probabilities. John Wiley & Sons; Hoboken, NJ: 2006. [Google Scholar]
- 50.Tan S-B, Chung YFA, Tai B-C, et al. Elicitation of prior distributions for a phase III randomized controlled trial of adjuvant therapy with surgery for hepatocellular carcinoma. Con Clin Trials. 2003;24:110–121. doi: 10.1016/s0197-2456(02)00318-5. [DOI] [PubMed] [Google Scholar]