Gene structure prediction in syntenic DNA segments

Abstract

The accurate prediction of higher eukaryotic gene structures and regulatory elements directly from genomic sequences is an important early step in the understanding of newly assembled contigs and finished genomes. As more new genomes are sequenced, comparative approaches are becoming increasingly practical and valuable for predicting genes and regulatory elements. We demonstrate the effectiveness of a comparative method called pattern filtering; it utilizes synteny between two or more genomic segments for the annotation of genomic sequences. Pattern filtering optimally detects the signatures of conserved functional elements despite the stochastic noise inherent in evolutionary processes, allowing more accurate annotation of gene models. We anticipate that pattern filtering will facilitate sequence annotation and the discovery of new functional elements by the genetics and genomics communities.

INTRODUCTION

The increasing diversity of metazoan and other eukaryotic genomes is a major opportunity for the comparative genomics community. Two principle approaches are used to predict protein-coding regions in genomic sequences (1–5). Ab initio methods analyze codon usage, potential splice site sequences, exon length and other features to distinguish coding regions from non-coding regions and thereby construct gene models (6–8). Extrinsic methods compare genomic sequences with those of known proteins at either the amino acid or nucleotide level (9–11). Ab initio methods can detect proteins for which there is no known homolog, while extrinsic methods cannot. However, ab initio methods are trained on limited data sets, making them apt to predict genes structurally resembling those in their training sets while missing others (12).

As more genomes of closely related organisms are sequenced (13–15), another approach is becoming increasingly valuable (16,17). In this approach, long homologous sequences, also called syntenic sequences, are compared, and less diverged regions are assumed to be functional elements since these elements are generally subject to significant selection. This approach identifies not only potential coding regions, but also non-coding regions which can regulate the expression of genes or which serve as templates for non-coding RNAs. In addition to the manual use of such an approach (18–24), in the last few years several gene prediction programs have been created to exploit these comparative approaches (25–28).

Here, we describe the implementation of a method called pattern filtering for comparative gene finding and demonstrate its capacity to identify gene structures and putative regulatory elements (29). It is based on a fundamental evolutionary model which has two parts and has been used previously for gene finding by others (30). First, coding exons are generally more conserved than neighboring sequences. Secondly, the first and second codon positions are more conserved than the third, or wobble, position. Thirdly, regulatory elements are also more conserved than neighboring sequences but, unlike coding exons, they do not show the same distinctive triplet pattern found in coding sequences.

The core of pattern filtering is a Wiener filter, or optimal linear filter (31). This technique optimally separates the signals desired from the noise which obscures them. In our case, the signals correspond to the spatial distributions of sequence variation, while the noise comes primarily from the stochastic nature of a mutation corresponding to discrete change at an alignment position. By eliminating this noise, we generate estimates of the evolutionary distance at each site, thereby making regions containing coding regions readily apparent.

MATERIALS AND METHODS

Our process for annotating genetic structures and identifying putative regulatory elements has two steps. First, from an alignment of syntenic sequences, we compute quantities we call the filtered distances and the filtered coding bias. Next, gene models are constructed from the interpretation of the filtered distances, filtered coding bias, possible splice sites and possible peptide sequences. Here we primarily illustrate these methods for two sequences, though they are extended to more than two.

Distance maps

In order to compute the filtered distances, which are measures of sequence divergence, one first needs to convert an alignment of symbols (A, C, G, T, –) to a series of numbers suitable for filtering. The two alternative maps that we use to create this numeric function are called the 1-D (one-dimensional) and 5-D (five-dimensional) maps.

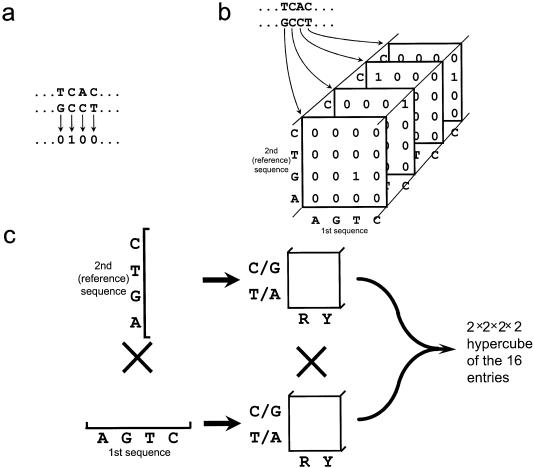
The 1-D map is a simple distance function. Each alignment position is given the value 0 or 1, depending on whether homologous sites share the same or different nucleotide states, respectively (Fig. 1a) (29). All alignment positions gapped in the sequence we wish to annotate, which we call the reference sequence, are omitted from the function, making the function the same length as the reference sequence. If more than two sequences are analyzed, then the function is typically the sum of all pairwise distances between sequences. This function is then floated and padded with zeroes to increase the number of points to twice the next greater power of 2 for the subsequent fast Fourier transforms (32).

Figure 1.

(a) The simple distance function of the 1-D map. Each alignment position is given a value of 0 or 1 depending on whether the nucleotides are matched or mismatched, respectively. (b) The first step in construction of the 5-D map. For each position of the alignment, a joint probability matrix is constructed. These matrices are ordered by corresponding alignment position. Alignment positions gapped in the reference sequence are omitted from the analysis. Positions gapped in the first sequence are omitted only in multiples of three in order to conserve the potential coding frames; the joint probability matrices of any remaining gapped positions are filled with 0s. (c) To construct the 5-D map, each of the dimensions that are four long are rearranged to create two dimensions that are two long.

To construct the 5-D map, one first produces a sequence of joint probability matrices, one for each pair of homologous sites, resulting in a three-dimensional array (Fig. 1b). Each of the dimensions that are four long are then rearranged, creating two dimensions that are two long, one corresponding to purines versus pyrimidines and the other corresponding to G/C versus A/T; this produces a 2 × 2 × 2 × 2 hypercube in place of the joint probability matrix (Fig. 1c). These rearranged joint probability matrices maintain information which we will later use to construct distances at each site based on general evolutionary models. Each of the 16-long sections of the function are floated individually, and the whole is padded as in the 1-D map.

The 5-D map is superior for gene finding in gene-dense regions, while the 1-D map is better in regions that are gene poor. This is because the 1-D map concentrates all the signal from the codons into one peak, making the signal easy to identify and describe even when there is very little signal; however, the 5-D map spreads this signal among 16 potential peaks, making this identification and description difficult in gene-poor regions.

For three sequences, the 1-D map is logically extended by taking the average of the three pair-wise distances, yielding values of 0, 2/3 or 1. Likewise, the 5-D function is extended to seven dimensions (7-D). Generalizations to four or more sequences are also implemented though not demonstrated.

The Wiener filter and pattern filtered distances

The resulting numeric function is filtered by an optimal linear filter, also known as a Wiener filter (31). In brief, spatially varying signals will have well-defined frequency bands, while stochastic noise will not; the Wiener filter optimally eliminates most of the noise in frequency space where it is easily recognizable, and then the result is transformed back to real space to see the filtered signals. Details of the filter are given below; see Lake (29) and Press et al. (32) for additional descriptions of the Wiener filter.

Fourier transforms of the numeric function are performed using a real fast Fourier transform (32,33). Power spectra are calculated by windowing the sequence alignment positions using a Parzen window in order to improve the estimate of the variance and minimize leakage (32). The resulting one-sided power spectra are between 32 and 512 long, increasing as the length of the reference sequence increases; e.g. the ∼200 kb sequence of our test set created a power spectrum 128 long.

The noise component, |N|², of the power spectrum is approximated by a constant plus a sum of cosine curves fit through the points away from the (possible) signal peaks. The possible signal peaks are at or near frequencies of 1/(3 bp), 1/(2 bp) and 0/(bp). To estimate the signal component, |S|², an extrapolation of the noise is subtracted from the power spectra. For each peak which is present, the estimated |S|² is fitted around 0/(bp) and 1/(3 bp) with a sum of either one or two Gaussians. The sometimes present signal peak at 1/(2 bp) is not included because it does not correlate with coding and non-coding regions.

The formula for the Wiener filter is

|S|² / (|S²| + |N|²).

The Fourier transform of the numeric function created above is multiplied by the Wiener filter to separate the signal from the noise; this product is inverse Fourier transformed, yielding the optimal estimate of the signal. In the case of the 1-D map, the end result is a filtered distance at each site. Yet in the case of the 5-D map, this estimate is a sequence of joint probability matrices. To more easily interpret these, paralinear, also called LogDet, distances are then calculated from the joint probability matrices, yielding generally additive distances which more accurately reflect the extent of evolution (34,35).

The 7-D map for three sequences is also a sequence of three-dimensional joint probabilty matrices. Columns of these joint probability matrices are summed three times to create three two-dimensional joint probability matrices at each position. These are then used to calculate paralinear/LogDet distances, and the three distances at each position are averaged. As before, this is easily generalized to four or more sequences.

Coding bias

In addition to filtered distance, we also use a filtered single-sequence content measure which we call the coding bias to additionally aid in the identification of coding regions. In order to calculate the coding bias, we first classify hexamers from the May 19, 2000 Sanger Center human chromosome 22 sequence into coding and non-coding according to the annotation at the time [(36) http://www.sanger.ac.uk/HGP/Chr22a]; from the analysis, we omitted hexamers overlying coding–non-coding boundaries, lying in partial genes or ambiguously annotated segments, or containing ambiguous nucleotides.

Next we constructed a set of 2 × 2080 = 4160 hexamer bins. The 2 comes from the two possible states, coding and non-coding, and 2080 is the number of possible unique hexamers when the reverse complement is considered [2080 = (4⁶ – 4³ palindromes)/2 + 4³ palindromes]. We next sort each of the 406 041 coding hexamers and 32 877 917 non-coding hexamers into these bins according to their sequences and coding status. We calculate the coding bias by the formula:

[NonCodingBin_n / (80 × CodingBin_n + NonCodingBin_n)]

Values appreciably less than 0.5 represent hexanucleotides that are systematically favored for coding, while those above are unfavored.

The distribution of values for the hexanucleotide bias is wide, robust and statistically meaningful. The minimum and maximum values are 0.0585 and 0.9711. No bin has too few counts, since the minimum number of counts in any bin is 8. The standard deviation of the coding bias of the bins is 0.1895. To test whether this is statistically different from random, we performed 1000 simulations with the same hexanucleotide distribution, but now randomly distributed into exon and intron bins. The standard deviations of these simulations were approximately normally distributed, with a mean of 0.0291 and standard deviation of σ = 0.0011. Since the standard deviation of the coding bias of the bins is 141σ from the mean standard deviation, it is clearly statistically different from random.

To calculate the coding bias function of an alignment, we first take the coding bias of each hexanucleotide of both sequences and average the results; if gaps are present, only one hexanucleotide bias is used. The resulting function is subjected to a Wiener filter analysis as in the 1-D map above but with any peak at the frequency 1/(3 bp) ignored.

Annotation

The annotation is done by the user with the GeneGrabber program, a viewer which displays the filtered distances, filtered coding bias, possible splice sites and potential peptide sequences. New exons are included by a combination of seven criteria: (i) the overall conservation of a segment; (ii) the presence of a pattern where every third position is appreciably less well conserved than the others; (iii) a filtered coding bias favoring coding; (iv) no stop codons in the favored reading frames; (v) the presence of strong flanking splice sites or in-frame start or stop codons; (vi) the agreement of the frames of adjacent exons; and (vii) previously described length distributions of introns, exons and genes. By clicking near putative exon ends and choosing a gene model, one inserts an exon into that gene model. The sequences and structures of gene models as well as the sequence of interesting conserved regions can be saved to files.

Regulatory regions are identified as highly conserved regions where all three possible codon positions are approximately equally conserved; for our purposes, ‘highly conserved’ is defined as a segment of 30 or more nucleotides with filtered distances below 0.20. Their positions and sequences can also be saved to files.

Potential 3′ splice sites are scored by a weight matrix based on the results of Senapathy et al. (37). 5′ Splice sites are predicted either by a similar metric or by the maximal dependence decomposition method (6).

The black traces in GeneGrabber plots are the filtered distances averaged over a 3 bp window, which are calculated by the formula D_n = (d_{n – i} + d_n + d_{n + i})/3, where d_i is filtered distance at position i. The multicolored trace shows the relative differences between the filtered distances and these averages, which are calculated by the formula (d_n – D_n)/D_n. Positions 0 modulo 3 are red, positions 1 modulo 3 are green, and positions 2 modulo 3 are colored blue to show frameshifts.

RESULTS

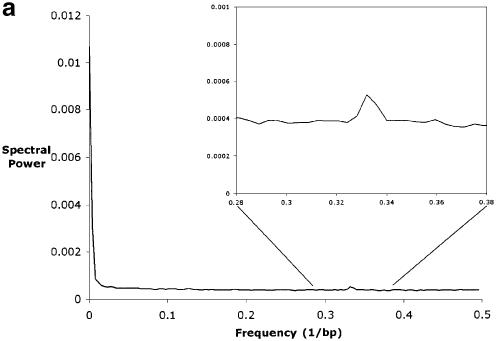
We aligned the syntenic sequences of the CD4 region of mouse and human (NCBI accession numbers AC002397 and U46924) (19,38) with the set of programs PickAl and COMGAP (unpublished); other genomic length alignment algorithms could also be used (39,40). We then calculated the filtered coding bias, and the filtered evolutionary distances from both the 1-D and 5-D maps. The intermediate power spectra are shown in Figure 2.

Figure 2.

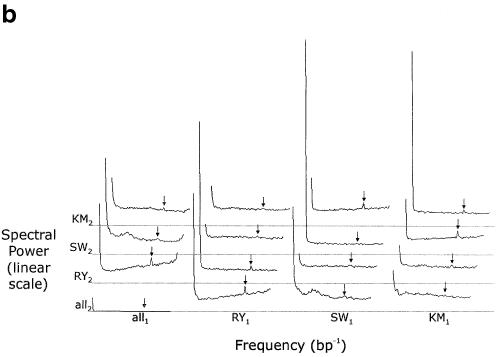
(a) The one-sided power spectrum resulting from the 1-D map of the alignment between the human and mouse CD4 regions. Note the non-zero floor of the trace stemming from the noise in the data, and the two signal peaks near frequencies of 0/(bp) and 1/(3 bp) corresponding to alternating long conserved and unconserved elements and to the codon triplets of coding regions, respectively. The peak at 1/(3 bp) and the region around it are magnified in the inset. (b) The power spectrum from the 5-D map of the same alignment. The left and right ends of each of the 16 1-D segments correspond to frequencies of 0/(bp) and 1/(2 bp), respectively. The arrows show the frequency 1/(3 bp). Each gray line indicates a spectral density of 0 for the four traces immediately above it. The abbreviations are as follows: R = (A or G), Y = (C or T), S = (G or C), W = (A or T), K = (A or C), M = (G or T). Subscripts indicate the first (human) or second (mouse) sequence. The plot can be divided into four conceptual regions: the trace in the bottom left corner, the remaining traces in the left column, the remaining traces in the bottom row, and the other nine traces. The bottom left corner trace tells us only about the distribution of gaps in the alignment and nothing about the sequences’ compositions or comparative relationship. Unsurprisingly, there is little high-frequency information in this trace, indicating that most gaps are relatively long. The remaining traces in the left column tell us only about the composition of the mouse sequence, and nothing about the human sequence or their comparative relationship; if the mouse sequence were aligned to any sequence, these three traces would be the same. The all₁·RY₂ trace describes how the mouse purines and pyrimidines are distributed relative to random. The large low-frequency peak indicates there are long relatively purine-rich regions and long relatively pyrimidine-rich regions. The peak at 1/(2 bp) shows the tendency of a purine to be followed by a pyrimidine, and vice versa. Purine–pyrimidine patterns of length three generate the triplet peak. Finally, note the general upward slope of the remainder, showing that once large-scale purine–pyrimidine composition effects are taken into account, a DNA segment tends to be more mixed than one would expect at random. The all₁·SW₂ trace describes how Gs and Cs are distributed relative to As and Ts. Note that this trace has the same peaks as the all₁·RY₂ trace, but now the remainder slopes downward, indicating that once the effects from the peaks are accounted for, Gs and Cs tend to be more clustered than one would expect at random. The all₁·KM₂ trace describes how the remaining pair of pairs, AC and GT, are distributed. The remaining traces in the bottom row are identical to those in the left column except that these describe the composition of the human sequence. The other nine traces tell us how the sequences relate to one another. For example, the RY₁·RY₂ trace tells us about the distribution of purine–pyrimidine conservation. It has a low-frequency peak indicating that there are long regions where purines and pyrimidines are more conserved and long regions where they are less conserved. Purine–pyrimidine conservation patterns of length three, which come largely from the coding regions, create the triplet peak. Finally, the very flat remainder indicates that all other perceived purine–pyrimidine conservation patterns stem from randomness or are a very small effect. One can interpret the other eight traces in a similar fashion.

Though not utilized in subsequent analyses because of the superior quality of the 5-D results, the power spectra of the 1-D map best illustrate the stochastic noise and the two signal peaks (Fig. 2A). The relatively flat portion extending across most of the plot comes from stochastic noise. The peak at very low frequency corresponds to long alternating conserved and non-conserved structures, such as entire exons and introns as well as genic and intergenic regions. The peak at the 1/(3 bp), henceforth called the triplet peak, comes from the codons of the coding regions. The first and second positions of codons tend to be conserved, since changing them will usually change the amino acids which are coded, and the third positions tend to be more divergent, since changing them usually will not change the amino acids coded or will minimally impact function. This alternating conserved–conserved–divergent pattern creates waves of period three nucleotides, resulting in the triplet peak. The small size of this peak is due to the small fraction of overall sequence which is coding; very gene-sparse data sets, such as the piebald region (24), have very small triplet peaks, while those of very gene-dense regions, such as mitochondrial genomes, rival the low frequency peak in size. Most of the 16 one-dimensional segments of the 5-D map’s power spectrum show the same structure (Fig. 2B).

Using only GeneGrabber with the 5-D filtered distances, we annotated the mouse sequence. Mouse was chosen because Ansari-Lari et al. (19) originally annotated it with the assistance of the human sequence and cDNAs, while the human sequence’s original annotation did not have the benefit of the mouse. To serve as a comparison, both sequences were separately analyzed using the GENSCAN web server at http://genes.mit.edu/GENSCAN.html (6). [We attempted comparisons with other programs, but technical errors or limitations of the length of the sequence allowed to be analyzed prohibited these attempts; note that our methods analyze the sequences of Peterson et al. (24), which exceed 4 Mb.]

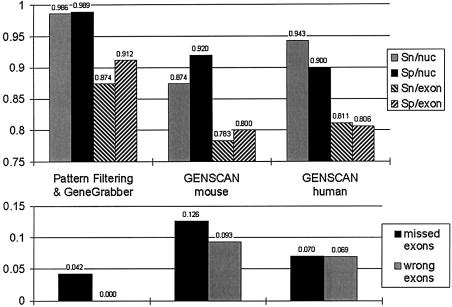
As one can see from Figure 3 and Table 1, our methods perform well in all measures of prediction accuracy, and appreciably surpass the predictions of GENSCAN. Two statistics are particularly noteworthy. Note how close the sensitivities and specificities are to 1.0 for pattern filtering and GeneGrabber. Secondly, there are no wrong exons, i.e. exons predicted that do not overlap part of an existing exon.

Figure 3.

Accuracy measures comparing pattern filtering with GENSCAN for each of the sequences. Sn/nuc, sensitivity per nucleotide; Sp/nuc, specificity per nucleotide; Sn/exon, sensitivity per exon; Sp/exon, specificity per exon. For explanations of these measures, see Table 1. Note the better performance in all statistics for pattern filtering, in particular that the sensitivities and specificities per nucleotide are very close to 1.0 and also that the fraction of wrong exons is 0.

Table 1. Accuracy statistics for pattern filtering and for GENSCAN (6) analyzing the mouse and human sequences of Ansari-Lari et al. (19,38).

Method, sequence	Sensitivity/nucleotide	Specificity/nucleotide	Correlation coefficient	Sensitivity/exon	Specificity/exon	Missing exons	Wrong exons
Pattern filtering	0.986	0.989	0.986	0.874	0.912	0.042	0.000
GENSCAN, mouse	0.874	0.920	0.885	0.783	0.800	0.126	0.093
GENSCAN, human	0.943	0.900	0.910	0.811	0.806	0.070	0.069
GENSCAN, or’d	0.954	0.850	0.885	0.832	0.753	0.056	0.139
GENSCAN, and’d	0.863	0.986	0.914	0.762	0.865	0.140	0.008

The total number of nucleotides analyzed is ∼200 000, the number of actual coding regions is 143, and the number of genes is 16. GENSCAN or’d is an analysis designed to utilize GENSCAN predictions from both sequences, maximize the sensitivities and minimize the missing exons; GENSCAN and’d is the same, but designed to maximize specificity and minimize wrong exons. Note that pattern filtering predicts exons better than even these measures. All accuracy statistics are calculated as in Burset and Guigó (12). Specificity per nucleotide is the fraction of actual coding nucleotides which are predicted to be coding; sensitivity per nucleotide is the fraction of nucleotides predicted to be coding which are actually coding. The correlation coefficient simultaneously measures both sensitivity and specificity per nucleotide. Sensitivity per exon is the fraction of coding regions for which both ends are correctly predicted. Specificity per exon is the portion of true exons correctly predicted at both ends, while sensitivity per exon is the portion of predicted exons which correctly match a true exon at both ends. The fraction of true exons without overlap to predicted exons is called missing exons and, conversely, the fraction of predicted exons without overlap to true exons is called wrong exons.

One could imagine attributing the success of pattern filtering to simply the inclusion of two sequences in the analysis. In order to test this possibility, we performed two combination analyses using GENSCAN. In the first, called GENSCAN or’d, a mouse nucleotide is considered coding if either it or the human nucleotide to which it is aligned is predicted to be coding. In GENSCAN and’d, a mouse nucleotide is considered coding if both it and the human nucleotide to which it is aligned are predicted to be coding; if a mouse nucleotide is aligned with a gap, the decision is based only on the designation of the mouse nucleotide.

GENSCAN or’d should have a greater sensitivity relative to the single-sequence analyses, since it now has two opportunities to predict a nucleotide or exon as coding. Likewise, GENSCAN and’d should have a greater specificity, since it requires a predicted coding sequence in both cases. Both of these hold true, but pattern filtering still outperforms each method in both statistics (Table 1). Therefore, the success of pattern filtering comes not just from the use of multiple sequences, but also from the noise-filtered comparison of these sequences.

These statistics also surpass the published accuracies of ROSETTA, TWINSCAN and DOUBLESCAN, other programs that also exploit homology between two genomes. Direct comparisons between these are not possible since the sequences analyzed are different (25,27,28); however, note that only Korf et al. (27) also analyzed sequences containing more than one gene.

We also documented 41 conserved regions that did not fit the coding region model. We learned from the cDNA annotations that 11 of these largely overlap either the 3′- or 5′-untranslated regions, leaving 30 putative regulatory elements. Eighteen of these lie between 2.5 kb upstream and 0.5 kb downstream of a gene’s transcription start site, seven others lie within introns, and five lie outside of these regions altogether. (Four of these five lie clustered within a single 2 kb region.) The distribution of these 30 putative regulatory elements suggests that most of them are indeed transcriptional or splicing regulatory elements.

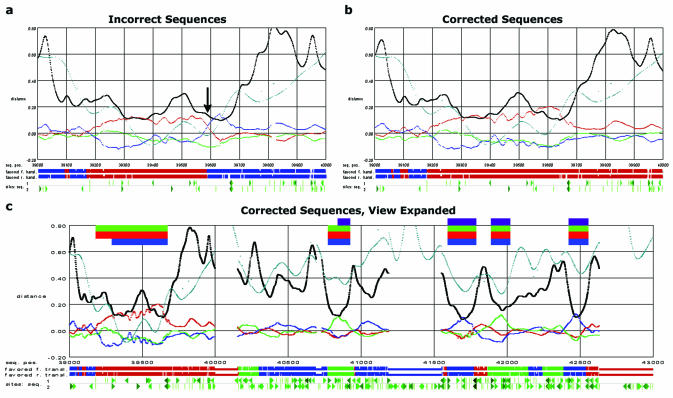
The filtered distances can also reveal some sequencing errors, and the discovery of a particular error allowed us to substantially correct the previously published biological annotation. In Figure 4a, the long region between positions 39 200 and 39 660 of the mouse CD4 region strongly resembles a coding region, except that around 39 590, two codon positions cross in the conservation plot. Observing that this apparent frameshift could result from a sequencing error and that 45 out of the 50 nearest positions are G or C, making such an error very possible, we submitted the region to various NCBI databases and the Celera human database looking for near matches. We found five matches spanning the whole region without gaps, three of which are from the original papers supplying the genomic sequence and its annotation (19,38). Yet, we also found 15 mammalian matches spanning the whole region with only one gap from a G inserted at position 39 593 (Table 2). The P-value for this distribution is 0.021 calculated by the binomial distribution, implying that it is significantly more likely that the sequence with the inserted G is correct.

Figure 4.

(a) A 1 kb region with a confirmed sequencing error, as it would be seen in the GeneGrabber viewer. The horizontal axis represents the position in the mouse sequence (19). The vertical axis of the graph represents the relative filtered distance averaged across a three-nucleotide window (black trace), the relative difference between the filtered distances and these averages (the trace that alternates red, green and blue), and the filtered hexanucleotide bias (teal trace). Note that the black trace results primarily from the low-frequency peaks, while the multicolored trace stems primarily from the triplet peaks. Below the plot is a symbolic diagram of the two preferred peptide translations, where stop codons are indicated by breaks in the continuity; the preferred frames are determined by assuming that the fastest evolving position of a putative codon is the third. Below this diagram is another indicating potential slice sites (triangles), and start and stop codons (Ts) with the ones above the gray line in the human sequence and the ones below in the mouse. The left–right mirror symmetry of the symbols is designed so that sites that could delimit a coding region will point toward one another, e.g. the putative 3′ splice sites in the forward direction point right, and their putative 5′ counterparts point left. In order to simplify the plot, sites in the reverse direction are not shown. (b) A view of the same 1 kb region, with the sequencing error corrected. Note how the crossing that originally occurred at approximately sequence postion 39 590 has now disappeared, making that region resemble a typical, though long, exon. (c) The same 1 kb region plus an adjacent 3 kb. The additional 3 kb is shown to provide examples of what typical exons look like. The bars at the top of the plot indicate the coding regions as annotated by the following techniques: purple, cDNA by Ansari-Lari et al. (19); green, pattern filtering and GeneGrabber; red, GENSCAN using the human sequence; and blue, GENSCAN using the mouse sequence. All annotations of this gene continue to the right; only the GENSCAN annotation using the mouse sequence continues to the left, including a segment not in the cDNA used for annotation by Ansari-Lari et al. (19).

Table 2. The sequences obtained from database searches which aligned 20 bases on either side of the sequencing error without any gaps.

Source	Database	CGC sequence (error)	CGGC sequence (correct)
NCBI	Non-redundant	3a	4
	Human EST	1	6
	Mouse EST	0	2
	High-throughput genome sequence	1b	2c
Celera	Human genome	0	1
Totals		5	15

The database searched and its source are listed along with the number of mammalian matches containing each subsequence. All sequences are either human or mouse, unless otherwise indicated.

^aAll three from Ansari-Lari et al. (19,38).

^bFrom Pan troglodytes.

^cBoth from Rattus norvegicus.

Assuming that the missing G was a sequencing error, we inserted the G into Ansari-Lari et al.'s human and mouse sequences (19,38) and input this new alignment into pattern filtering, which leads to Figure 4b. The troublesome event around 39 590 has now gone away, and we annotate the gene as indicated by the green row of bars at the top of Figure 4c. This is the same annotation that GENSCAN produces from the human sequence (the red row of bars in the figure).

The original annotation of the sequence by Ansari-Lari et al. (19) is indicated by the purple row of bars. Their original cDNA data showed a spliced intron between nucleotides 39 671 and 40 771, the same as we predicted. We presume that the sequencing error at position 39 593 led them to conclude its segment was part of a 5′-untranslated region, since predicting the translation start site at 39 181 would have resulted in a stop codon shortly after the 39 593 sequencing error. This same crossing of codon traces should also be observed when comparing sequences that undergo translational frameshift (41).

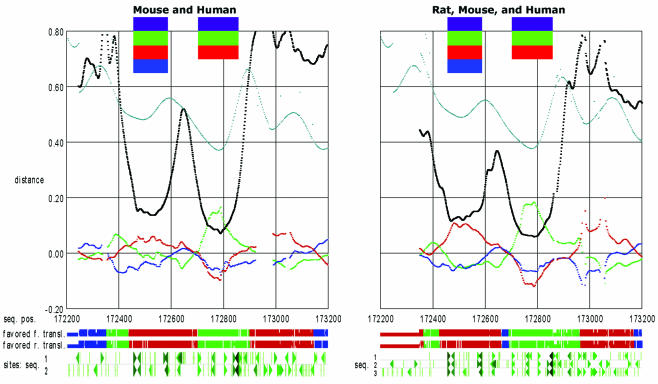
Additional power in such analyses can be gained by using more than two syntenic sequences. In order to demonstrate this, we aligned the human, rat (contig NW_043769.1) and mouse CD4 segments. From this alignment, we calculated the filtered coding bias, and the filtered evolutionary distances from the 7-D map. Since mouse and rat are such evolutionarily close relatives, we did not expect an enormous change in the resulting GeneGrabber plots. However, somewhat difficult segments of the plots became significantly easier to interpret (Figure 5). We anticipate that the inclusion of a sequence from a different mammalian order would greatly enhance this approach.

Figure 5.

Views of a 1 kb region containing exons 9 and 10 of the gene PTPN6. The axes and plots are as in Figure 4. The left plot shows the filtered distances resulting from the human and mouse sequences using the 5-D map; the right plot shows the same distances but from the human, rat and mouse sequences using the 7-D map. Note how the characteristic splitting pattern is substandard for the first exon in the left plot. As shown in the right plot, the addition of the third sequence rectifies this situation.

DISCUSSION

Our analysis demonstrates that pattern filtering is an effective and accurate comparative method for the annotation and prediction of coding genes in syntenic DNA segments. In addition, pattern filtering identifies conserved non-coding sequence elements. The results are straightforward for a user to interpret, and our approach allows valuable flexibility when faced with more challenging aspects of annotation such as the detection of sequencing errors like the example above, alternative splice models, overlapping genes and difficult to detect exons which can precipitate a cascade of errors as a gene finder attempts to construct a full gene model (8).

The mathematics behind pattern filtering is well grounded in its proof, and decades of empirical experience have demonstrated the mathematics’ power; to our knowledge, it is only the second gene finding approach to use spectral analysis, and the first of these to utilize filtering or to use comparative information (42). Pattern filtering’s utilization of the three-nucleotide conserved pattern within codons is nearly unique among gene finders (30). Additionally, pattern filtering effectively uses the comparative information from two or more sequences. These are the three greatest strengths of pattern filtering.

Many closely related eukaryotic genomes are presently being sequenced, or their sequencing is being planned. These include human, mouse, cow, rat, dog, cat and other upcoming vertebrate genomes, as well as multiple angiosperm and insect genomes (43). Not only will this provide a greater quantity of sequence for comparative analyses, but it should also lead to a higher quality of comparisons, since the optimal evolutionary distance differs depending on the task at hand (44). Because of this, methods such as the one described here for the analysis of syntenic segments will become increasingly important and more powerful in the annotation of genomes and the discovery of new genes and regulatory elements.

Availability

To aid in its distribution and widespread use, we are making applications, manuals and examples available at http://genomics.ucla.edu/patfilt/.