Abstract
A method to detect DNA-binding sites on the surface of a protein structure is important for functional annotation. This work describes the analysis of residue patches on the surface of DNA-binding proteins and the development of a method of predicting DNA-binding sites using a single feature of these surface patches. Surface patches and the DNA-binding sites were initially analysed for accessibility, electrostatic potential, residue propensity, hydrophobicity and residue conservation. From this, it was observed that the DNA-binding sites were, in general, amongst the top 10% of patches with the largest positive electrostatic scores. This knowledge led to the development of a prediction method in which patches of surface residues were selected such that they excluded residues with negative electrostatic scores. This method was used to make predictions for a data set of 56 non-homologous DNA-binding proteins. Correct predictions made for 68% of the data set.
INTRODUCTION
A method to detect DNA-binding sites on the surface of a protein structure is important for functional annotation. In addition, if a protein is known to bind DNA, but the site of interaction is unknown, random mutagenesis studies are commonly used to identify binding site residues experimentally. A reliable computational method to help identify DNA-binding sites on the protein surface would facilitate directed mutagenesis experiments, in which specific residues could be mutated and their effect on DNA binding analysed. Previously, methods have been developed for the prediction of protein–protein interaction sites on the surface of proteins using patches of surface residues (1–5). In the current work, this approach has been extended to the prediction of DNA-binding sites on the 3D structure of proteins. A number of physical and chemical parameters of surface residue patches have been analysed to find which one(s) are the best predictors of DNA-binding sites. This information was then used to develop a new method for the prediction of DNA-binding patches on the surface of a protein. These patches are selected on the basis of electrostatic potential. The patch with the most positive potential is predicted as a site for DNA binding.
MATERIALS AND METHODS
Data set definition
427 protein–DNA complexes with a resolution better than 3.0 Å were extracted from the Nucleic Acid Database (NDB) (on-line version on 19 March 2003) (6). This list was then clustered into homologous families (by protein chain) based on structural similarity using the CATH Protein Families Database (7). Multi-domain proteins were grouped together in the same homologous family if the DNA-binding domains were homologous (i.e. had the same CATH code). A representative protein with the best resolution was taken from each family to create a data set of 56 non-homologous proteins bound to double-stranded DNA (dsDNA) (see columns 1–3 of Table 1).
Table 1. DNA-binding site prediction results for the data set of 56 protein–dsDNA complexes.
| PDB code | Protein name | Resolution | Residue overlap patch ranked 1 | Random prediction value | Number of residues in DNA-binding interface |
|---|---|---|---|---|---|
| 1qnaA | Transcription initiator factor TFIID-1 | 1.80 | 10 | 0.04 | 42 |
| 1mjoB | Methionine repressor | 2.10 | 10 | 0.09 | 17 |
| 1d02A | Restriction endonuclease MUNI | 1.70 | 10 | 0.10 | 27 |
| 1bg1A | STAT3β | 2.25 | 10 | 0.03 | 23 |
| 1gdtA | Gamma-delta resolvase | 3.00 | 10 | 0.15 | 33 |
| 1hcrA | HIN recombinase | 1.80 | 10 | 0.40 | 26 |
| 1ewnA | AAG DNA repair glycosylase | 2.10 | 9 | 0.06 | 25 |
| 1qpzA | Purine repressor | 2.50 | 9 | 0.06 | 29 |
| 1fokA | Restriction endonuclease FOKI | 2.80 | 9 | 0.09 | 67 |
| 1am9A | Sterol regulatory element binding protein 1A | 2.30 | 9 | 0.11 | 17 |
| 1azpA | SAC7D | 1.60 | 9 | 0.14 | 20 |
| 1dp7P | RFX-DBD | 1.50 | 9 | 0.14 | 21 |
| 1a73A | Endonuclease I | 1.80 | 9 | 0.15 | 36 |
| 1dctA | DNA (cytosine-5) methylase | 2.80 | 9 | 0.15 | 46 |
| 1dmuA | Restriction endonuclease BGLI | 2.20 | 9 | 0.15 | 50 |
| 1vasA | Endonuclease V | 2.75 | 9 | 0.16 | 43 |
| 1bp7A | Endonuclease I-CREI | 3.00 | 9 | 0.21 | 47 |
| 1tupB | Tumour supressor P53 | 2.20 | 8 | 0.06 | 18 |
| 2bop | E2 DNA-binding domain | 1.70 | 8 | 0.08 | 23 |
| 1crxA | Cre recombinase | 2.40 | 8 | 0.10 | 65 |
| 1dfmA | Restriction endonuclease BGII | 1.50 | 8 | 0.14 | 45 |
| 3htsB | Heat shock transcription factor | 1.75 | 8 | 0.14 | 21 |
| 1gd2E | BZIP transcription factor RAPI | 2.00 | 8 | 0.15 | 15 |
| 1qpiA | Tetracycline repressor | 2.50 | 7 | 0.02 | 23 |
| 1eqzA | Histone H2A | 2.50 | 7 | 0.03 | 27 |
| 1emhA | Uracil-DNA glycosylase | 1.80 | 7 | 0.06 | 20 |
| 1qrvA | Endonulcease V | 2.20 | 7 | 0.06 | 27 |
| 2irfJ | Interferon regulatory factor-2 | 2.20 | 7 | 0.10 | 24 |
| 6mhtA | HHAI methyltransferase | 2.05 | 7 | 0.10 | 40 |
| 3pviA | Endonulcease PVUII | 1.59 | 7 | 0.12 | 33 |
| 1bdtA | Arc transcription regulator | 2.50 | 7 | 0.14 | 15 |
| 1ecrA | Replication terminator protein (TUS) | 2.70 | 7 | 0.15 | 69 |
| 1pdnC | PRD paired domain | 2.50 | 7 | 0.15 | 36 |
| 1b3tA | EBNA-1 nuclear protein | 2.20 | 7 | 0.19 | 34 |
| 1ignA | RAP1 | 2.25 | 7 | 0.19 | 56 |
| 1au7A | PIT-1 POU domain | 2.30 | 7 | 0.22 | 44 |
| 1sknP | SKN-1 transcription factor | 2.50 | 7 | 0.25 | 21 |
| 1a1hA | QGSR zinc finger | 1.60 | 7 | 0.30 | 36 |
| 1hwtC | HAP1 | 2.50 | 6 | 0.00 | 13 |
| 1dizA | 3-Methladenine DNA glycosylase | 2.50 | 6 | 0.03 | 27 |
| 1a36A | DNA topisomerase | 2.80 | 5 | 0.01 | 71 |
| 1qumA | Endonuclease IV | 1.55 | 5 | 0.02 | 31 |
| 2cgpA | Catabolic gene activator protein | 2.20 | 5 | 0.02 | 17 |
| 2hmi | HIV-1 reverse transcriptase | 2.80 | 5 | 0.02 | 59 |
| 1xbrA | Transcription factor T domain | 2.50 | 5 | 0.03 | 30 |
| 1eonA | Type II restriction enzyme ECORV | 1.60 | 5 | 0.07 | 37 |
| 1a3qA | NF-KAPPA-B | 2.10 | 4 | 0.00 | 21 |
| 1c9bA | Transcription factor IIB | 2.65 | 4 | 0.02 | 22 |
| 1mhdA | SMAD MH1 domain | 2.80 | 4 | 0.02 | 17 |
| 2bdpA | DNA polymerase I | 1.80 | 4 | 0.04 | 65 |
| 1ihfA | Integration host factor | 2.50 | 4 | 0.07 | 30 |
| 6croA | Lambda CRO | 3.00 | 4 | 0.35 | 20 |
| 1lmb3 | Lambda repressor | 1.80 | 1 | 0.07 | 23 |
| 1tauA | DNA polymerase | 3.00 | 0 | 0.02 | 46 |
| 1zqfA | DNA polymerase β | 2.90 | 0 | 0.02 | 28 |
| 2dnjA | Deoxyribonuclease 1 | 2.00 | 0 | 0.02 | 22 |
The protein name as it appears annotated in the PDB file is shown column 2 and the resolution of the structure is in column 3. The number of residues in the top ranked patch that overlap with the known DNA-binding interface is shown in column 4. The proteins in the table have been ordered by this value. The maximum value is 10 as this is the maximum size of the patches used. The random prediction value (RPV) is the probability of selecting a patch with >70% overlap with the known DNA-binding site by chance. The number of residues in the known DNA-binding interface is shown in column 6 (see Materials and Methods).
Surface accessible residue definition
The relative accessible surface area (ASA) of each residue in a protein in the data set was calculated using NACCESS (8) without the DNA molecule present (non-complexed). Hence, non-complexed in this context refers to the protein structure extracted alone from the PDB file for the protein solved with DNA bound. Surface accessible residues were defined as those residues that had a relative ASA of >5%.
DNA-binding interface definition
The ASA of each residue in a protein with DNA present (complexed state) and the same protein without DNA present (non-complexed state: the protein structure extracted alone from the PDB file for the protein solved with DNA bound) was calculated using NACCESS (8). If a residue lost more than 1 Å2 ASA when going from the non-complexed to the complexed state it was defined as a DNA-binding residue, and included in a set of residues referred to as the known DNA-binding interface. The number of residues in the known DNA-binding interface is shown in column 6 of Table 1.
Patch definition for analysis
Each surface accessible residue (see above for definition) was taken as the starting point for the definition of a patch. A patch was defined as the N nearest neighbouring residues (in terms of distances between Cα atoms), where N was taken as the number of residues in the known DNA-binding interface set for each specific protein. If any identical patches were defined from different residue start points only one was used for the subsequent analysis. Five parameters were then calculated for each patch on a protein and the known DNA-binding interface.
Definition of patch parameters
Accessible surface area. The absolute ASA value assigned to each residue was summed for all residues in the patch. All subsequent patch parameter values were normalized for the ASA of the patch. This insured that although the generated patches and the known DNA-binding interface might not have comparable shapes, the patch parameter calculated for each were comparable in terms of ASA.
Electrostatic potential. The electrostatic potential is computed using the software package Delphi (9). The potential is computed for individual protein chains, with the DNA removed. The potential is computed on a discrete cubic grid, with 101 points in the x, y and z directions, defined such that the protein fills 30% of the total volume of the cubic grid. Debye-Huckel boundary conditions were employed (the default for this package) and a simplified charge set defined from the molecular dynamics package CHARMM (10) was used (Table 2).
Table 2. The simplified relative charge set defined from CHARMM (10) used in the calculation of the electrostatic potential of atoms in the DNA-binding proteins.
| Atom type (PDB entry) | Residue | Relative charge |
|---|---|---|
| NZ | Lys | 1.00 |
| NH1 | Arg | 0.50 |
| NH2 | Arg | 0.50 |
| OE1 | Glu | –0.50 |
| OE2 | Glu | –0.50 |
| OD1 | Asp | –0.50 |
| OD2 | Asp | –0.50 |
| OXT | All residues | –1.00 |
| N | All residues | –0.10 |
| CA | All residues | 0.10 |
| C | All residues | 0.55 |
| O | All residues | –0.55 |
The radius for each atom is defined using the default values from the visualization package GRASP (11). The dielectric constant is taken to be 4 within the protein and 80 outside. The ion concentration was taken to be 0.5 M with an exclusion layer radius of 2 Å. The maximum change in the ion concentration was 100 µM and the calculation was carried out with 200 non-linear iterations. The potential at all points in the neighborhood of the protein is derived from those values calculated on the grid points using linear interpolation.
An electrostatic score ΔQi for the ith surface atom is defined using the following equation:
where Φ(r) is the potential at a point r. The area ΔSi is defined by placing spheres of radius 7 Å around each surface accessible atom, with ΔSi being the area of the sphere around the ith atom which does not intersect with any other equivalent sphere centered around each atom. The integration and average in the above equation is computed by randomly sampling the potential on ΔSi 1000 times and averaging the result. There is a statistical error associated with this random sampling procedure. In order to estimate this, the electrostatic score for a single protein from the data set was calculated using 100 and 1000 samples. From these two calculations, the sum of the electrostatic scores varied by <3% and the average difference was ∼4%, indicating there was little difference between the two sampling multiples. Hence, sampling was conducted 1000 times.
In this way, an electrostatic score is assigned to each atom on the protein surface. If ΔSi is too small (i.e. random sampling cannot locate the region satisfying the above criteria) then the electrostatic score is set to zero. A single electrostatic score was then assigned to each residue (residue electrostatic score) by summing the score of all atoms in the residue and dividing by the number of atoms in that residue.
Residue interface propensity. The relative frequencies of amino acids in known DNA-binding interfaces were used to derive residue interface propensities. Propensities were calculated for each of the 20 amino acids from the data set of 56 protein–dsDNA complexes. Propensities were calculated for each amino acid (AAj) as the fraction of ASA that AAj contributed to the known DNA-binding interface compared with the fraction of ASA that AAj contributed to the protein surface as a whole, as described previously (12,13). The propensities and their natural logarithms (ln) are shown in Table 3. A positive logarithmic propensity indicates that a residue occurs more frequently in a DNA-binding interface than on the protein surface. The propensities show similar trends to those calculated previously for a smaller data set (13). The positively charged arginine, and polar serine and tyrosine show the most affinity for DNA-binding interfaces. This is expected as a protein interface has to complement the negative charge on the surface of the DNA molecule bound.
Table 3. The natural logarithms (ln) of the residue interface propensities for the 20 standard amino acids derived from the complete data set of 56 protein–dsDNA complexes.
| Amino acid | ln residue interface propensity | SD of propensities for 56 ‘jack-knifed’ data sets |
|---|---|---|
| Arg | 0.53 | 0.01 |
| Ser | 0.44 | 0.01 |
| Tyr | 0.41 | 0.02 |
| Thr | 0.33 | 0.02 |
| Asn | 0.26 | 0.02 |
| Met | 0.19 | 0.05 |
| Lys | 0.19 | 0.01 |
| Phe | 0.06 | 0.03 |
| Gly | 0.03 | 0.02 |
| Cys | 0.02 | 0.04 |
| Ala | 0.02 | 0.02 |
| Gln | –0.08 | 0.02 |
| Ile | –0.20 | 0.03 |
| His | –0.23 | 0.02 |
| Leu | –0.29 | 0.04 |
| Val | –0.38 | 0.03 |
| Trp | –0.39 | 0.03 |
| Pro | –0.62 | 0.03 |
| Asp | –1.38 | 0.03 |
| Glu | –1.54 | 0.02 |
The amino acids are shown in descending order by propensity. A positive propensity indicates that a residue occurs more frequently in the interface than on the protein surface. The standard deviations (SD) for each propensity over the 56 ‘jack knifed’ data sets are shown in the last column of the table.
Table 3 shows the propensities calculated over the complete data set of 56 proteins. A jack-knifed (14) set of propensities was also created for use with each protein. Hence, 56 sets of propensities were created, each calculated with one protein removed from the data set. When propensities were used in the analysis of surface patches for one protein, the set created with that one protein removed was used for the calculation to avoid bias. The standard deviations of the propensities for each of the 56 ‘jack-knifed’ data sets are shown for each residue type in Table 3.
Hydrophobicity. The experimentally derived amino acid hydrophobicity scale of Fauchere and Pliska (15) was used to assign a hydrophobicity value to each surface patch. The value assigned to each residue in the scale was summed for all residues in the patch.
Conservation. A conservation score for each patch was calculated using Scorecons, a tool for scoring residue conservation in multiple alignments (16). The protein sequence for each member of the data set was extracted from its PDB file. BLAST was then used to find close sequence homologs in a non-redundant set of GenBank (17) sequences, using an E-value threshold of 0.001. The multiple alignments from the BLAST searches were used as input to Scorecons (16). This tool calculates a score for each residue in a protein sequence that measures the degree to which it is conserved in evolution as inferred from the multiple alignment. Thus, each residue in a protein is assigned a single conservation score. The conservation score for a patch is the sum of the constituent residue conservation scores. For one protein (1dmuA), the lack of sufficiently diverse sequence homologs meant a valid conservation score could not be calculated and this protein was excluded from the analysis of parameter ranks for conservation.
Calculating parameter and rank distributions
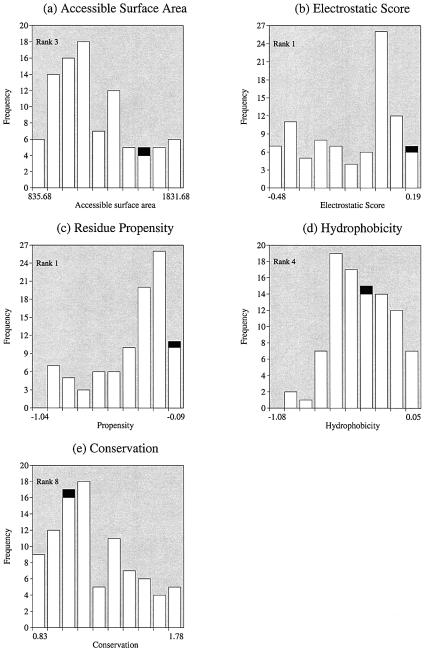
A frequency distribution for all surface patches for each parameter was then calculated. Each parameter was divided into 10 equal-sized bins and the position of the parameter value of the known DNA-binding interface calculated within each protein’s distribution. An example of all five parameter distributions for the structure of methionine repressor (PDB code 1mjoB) is shown in Figure 1.
Figure 1.
Distribution of parameters for all patches in methionine holorepressor (PDB code 1mjo). Distributions shown are for (a) accessible surface area (ASA), (b) electrostatic score, (c) residue interface propensity, (d) hydrophobicity and (e) residue conservation. On each graph all the surface patches are represented in white and the known DNA-binding sites in black. Relative rankings (on a scale of 1–10) were calculated from each distribution and are shown on each graph.
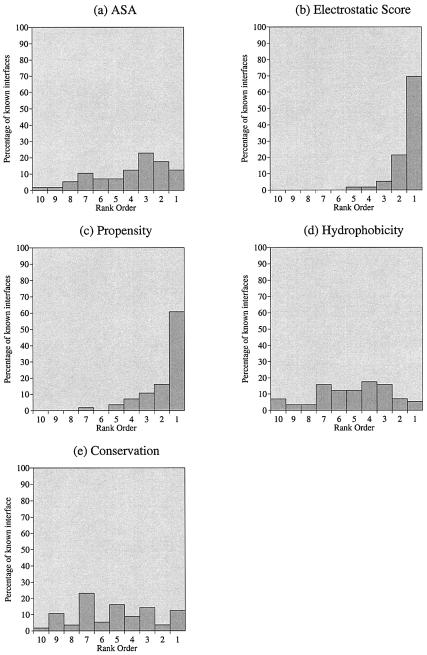
The position of the parameter value for the known DNA-binding interface within each distribution was recorded as a rank between 1 and 10, dependent upon its position in the distribution. For the example shown in Figure 1b, the DNA-binding interface has an electrostatic score that is assigned to bin 1 of this protein’s electrostatic score distribution. In this protein, the known DNA-binding interface has the highest electrostatic score of all surface patches and is hence given a rank of 1. In Figure 1d, the known interface is assigned to bin 4 of the hydrophobicity distribution, and hence for this protein the known interface is ranked as 4 for this parameter. The distribution of these rank values for each parameter over the complete data set of 56 proteins is shown in Figure 2.
Figure 2.
Patch analysis distributions for 56 proteins bound to dsDNA, showing the rank ordering (on a scale of 1–10) of known DNA-binding sites relative to other patches on the surface of the protein. The 56 observations were combined for each parameter separately: (a) ASA, (b) electrostatic score, (c) residue interface propensity, (d) hydrophobicity and (e) residue conservation.
Patch definition for prediction
The above analysis showed that the electrostatic score of the surface patches was the best predictor of a DNA-binding site (see Results). This knowledge led to a new surface patch definition for the prediction phase of the work.
As described above, each surface accessible residue of a protein is assigned an electrostatic score. If a residue has a positive electrostatic score it is used as a starting point (residue A) for the definition of a patch for prediction. The closest neighboring residue (in terms of distance between Cα atoms) to residue A is calculated (residue B). If residue B has an electrostatic score that is either positive or zero it is included as the next residue in the patch. [If residue B has a negative score then it is discarded and the next nearest positive or neutral neighbour residue (residue C) is selected.] The nearest neighbour to residue B is then selected, and the same process of electrostatic score evaluation was conducted. Any residues that had a negative electrostatic score, were always discarded, and the next nearest neighbour selected and tested.
In this way a surface patch was selected like an amoeba, with the patch only ‘extending’ in the direction of residues with positive or zero electrostatic scores. The maximum number of residues selected was defined as 10. Patches were defined with each surface accessible residue taken as a starting point. If residue selection from different start points resulted in the same patch being defined (i.e. two patches with exactly the same residues included) then only one was used for the subsequent ranking procedure.
Ranking of patches for prediction
In this way multiple surface patches with positive electrostatic scores were defined on each protein. The patches were then ranked according to their electrostatic score. The patch with the largest positive score was given a rank of 1, the patch with the next largest positive score a rank of 2, etc. The patch with the lowest score had a rank equal to the total number of different patches defined on the protein.
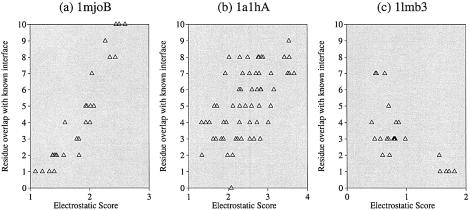
The overlap between a patch and the known DNA-binding interface was calculated. The relationship between the electrostatic score of a patch and the number of residues that overlapped with the known interface was analysed (Fig. 3). The number of residues, out of a maximum of 10, that overlapped with the known DNA-binding interface for the top ranked patch (rank 1) for each protein are shown in Table 1. Examples of top ranking patches are shown with the known DNA-binding interface residues for four proteins [1mjo, 1d02 (18), 1qna (19) and 1lmb (20)] in Figure 4. A correct prediction was defined as one where a protein had a predicted patch ranked 1 that had at least 70% of residues overlapping with the known DNA-binding interface.
Figure 3.
The relationship between the electrostatic score of a surface patch and the overlap (in terms of the number of residues) of a patch with the known DNA-binding sites. Each patch is 10 residues and hence the maximum overlap is 10. Data is shown for three proteins: (a) methionine holorepressor (PDB code 1mjo), (b) zinc-finger ZIF268 (PDB code 1a1h) and (c) lambda repressor (PDB code 1lmb).
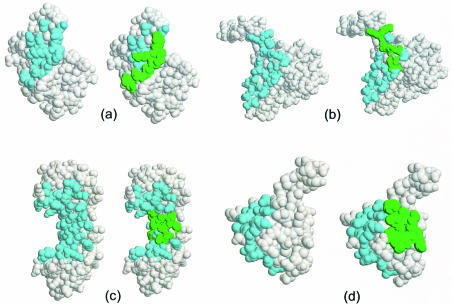
Figure 4.
DNA-binding site predictions for four proteins in the data set. In each diagram the protein is shown in CPK format with the residues in the known DNA-binding interface shown in pale blue on the left and the 10 residues in the top ranking patch shown in green on the right. The diagrams are images from Rasmol (32): (a) methionine repressor (PDB code 1mjo), (b) restriction endonuclease MUNI (PDB code 1d02) (18), (c) transcription initiator factor TFIID-1 (PDB code 1qna) (19) and (d) lambda repressor (PDB code 1lmb) (20). The proteins shown in (a), (b) and (c) have a top ranking patch in which all 10 residues occur in the known DNA-binding interface and are classified as correct predictions. In (d), only one residue in the top ranking patch overlaps with the known interface and this is an incorrect prediction.
Calculating a random prediction value for comparison
The total number of patches that had ≥70% of residues overlapping with the known DNA-binding interface was also calculated for patches defined without using the criteria of positive or neutral electrostatic score selection. Hence, each surface residue was used as a start point as before, but every residue selected as a nearest neighbor was included in the patch regardless of its electrostatic score. These are referred to as random patches. The ‘number of random patches that had ≥70% of residues overlapping with the known DNA-binding divided by the total number of patches’ was defined as the ‘random prediction value’ (RPV). This value gave a reference point by which to assess the predictions. A large RPV would indicate a high probability of selecting a patch containing ≥70% DNA-binding interface residues just by chance. The RPV for each protein is shown in Table 1.
RESULTS
Analysis of surface patch parameters
Our analysis has showed that DNA-binding sites on proteins are amongst the patches with the most positive electrostatic score. From the rank distributions in Figure 2b it is seen that for ∼70% of the data set the known DNA-binding sites are amongst the surface patches with the most positive electrostatic scores. This confirms the results obtained by Stawiski et al. (21), and the observation that the positively charged residues lysine and arginine occur more frequently in DNA-binding interfaces than on the protein surface as a whole (13,22).
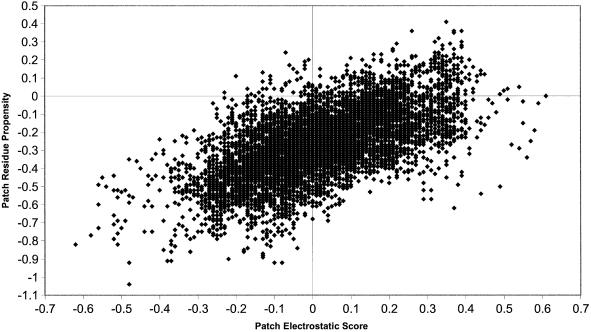
The known DNA-binding sites are also amongst the patches with the highest interface residue propensities. In Figure 2c, 61% of proteins are observed to have known DNA-binding sites amongst the 10% of surface patches with the highest propensity scores. From Table 3, it appears that the residue propensities are approximately correlated with residue charge. For example, the negatively charged residues aspartic acid and glutamic acid have the most negative propensities, whilst the positively charged arginine residue has the highest positive propensity. To test if the propensity values for a patch were correlated to the electrostatic score of a patch, values for each parameter were plotted for the 9778 patches generated for the 56 proteins (Fig. 5). The correlation coefficient (r) of a trend line fitted to this data is 0.61 showing that the two parameters are correlated to some degree.
Figure 5.
The relationship between the electrostatic score and the residue interface propensity for 9778 surface patches defined over the 56 proteins in the data set. A best-fit straight line is shown that has a correlation coefficient (r) of 0.61.
The other three parameters (ASA, hydrophobicity and conservation) showed no discriminatory power, with the known DNA-binding interfaces lying anywhere within the parameter distributions for all surface patches (Fig. 2a, d and e).
Amino acid conservation in DNA-binding sites presents a complex picture. In a recent analysis of 21 protein families (23), it was found that, in general, residues that make contacts to the DNA backbone are conserved, but conservation of residues that make contacts to DNA bases varies depending on the binding specificity of the complex in question. The current data set of 56 complexes contains proteins in all three of the specificity classes defined by Luscombe and Thornton (23), namely non-specific, highly specific and multi-specific. It was expected that for the highly specific proteins (that have conserved backbone and base contacting residues) the DNA-binding sites would be more conserved than other patches on the surface. This was observed for some proteins (e.g. 1qnaA has a DNA-binding site ranked as 1, i.e. amongst the most conserved) but the trend was not apparent for other proteins in the data set classified as highly specific. However, these proteins belong to families that include many paralogs that have evolved to recognize different target DNA sequences. For proteins not in this class it was not expected that the binding sites would be more conserved as the surface patches defined potentially comprise residues that make both backbone and base contacts. In addition, it is possible that the results are further confused by the presence of other binding sites on the protein surface that might also show residue conservation.
From this analysis, the electrostatic score (which showed the best discriminatory power and was correlated with interface residue propensity) was chosen as the parameter on which to base the DNA-binding site predictions.
DNA-binding site predictions
A correct prediction was evaluated in a similar way to our previous patch prediction method for protein–protein interaction sites (2). If a protein had a predicted patch ranked 1 that had ≥70% of residues overlapping with the known DNA-binding interface the prediction for that protein was defined as correct. Using this assessment criteria, 68% (38/56) of the predictions are correct.
In Table 1 the 56 proteins in the data set have been ordered by the number of residues in the patch that overlap with the known DNA-binding interface and are shown with their RPVs. For example, methionine repressor structure (1mjoB) has all 10 residues in the top ranked patch overlapping with the known DNA-binding interface. The RPV for this prediction is 0.09 indicating that there is only a 9% chance of selecting such a patch by chance.
For two of the incorrect predictions (1hwt, 1a3q) the RPV was zero, indicating that a 10 residue patch defined on these structures never overlapped the known interface by ≥7 residues. HAP1 (1hwt) has a known interface site that comprised 13 residues and is an irregular shape, and hence selecting 10 of these 13 in one circular patch proved impossible. NF-KB P65 is a two-domain structure in which the 22 DNA-binding residues span both domains and the loop structure that joins the two. This site is an elongated shape and the circular shape of the 10 residue patches defined on the surface was not adequate to overlap ≥7 interface residues in this structure.
Another three structures (2dnj, 1lmb, 1qum), for which incorrect predictions were made, had known DNA-binding sites that have negative electrostatic potentials. One of these proteins, endonuclease IV (1qum), includes three Zn2+ ions at the DNA-binding site that are critical for the enyzme’s activity (24). Hosfield et al. (24) calculated that the grooved DNA-binding site has an overall net positive electrostatic potential when these metal ions are included. The electrostatic score for the proteins in the current work was calculated without metal ions present and hence this could explain why the known binding site for this structure is negative and why the prediction was unsuccessful. It has been observed in other complexes that the binding of metal ions affects the binding of DNA (25–27) and the inclusion of such ions should be considered in further developments of the current method.
Predictions for another three proteins (1tau, 1zqf, 2dnjA) had the residue overlap of the patch ranked top as zero (Table 1). Both 1tau and 1zqf are polymerase structures that comprise ‘thumb’, ‘fingers’ and ‘palm’ domains (28) complexed with a short DNA double helix comprising just 8 bp. On further analysis, it proved that for both polymerase I (1tau) (29) and polymerase β (1zqf) (30) the top ranked patches were located in the fingers domain and could potentially interact with the DNA if the DNA molecule bound was not a short fragment. Polymerase I (1tau) also had a top ranking patch that mapped to the exonuclease domain of the structure. A mechanism has been proposed that explains the editing of DNA by the polymerase structure in which the exonuclease domain binds single-stranded DNA (28). It is possible that the positive electrostatic patch identified may constitute part of this binding site. In the DNase I (2dnj) (31) structure, the top ranked patch occurs on a surface of the protein that is far from the DNA-binding site, and there is no evidence that suggests a function for a positive electrostatic patch in this region.
DISCUSSION
In this work, we have used a fast and simple method to make predictions of DNA-binding sites on the surface of 3D protein structures. We have obtained a 68% correct prediction rate for a large data set of 56 non-homologous proteins known to bind DNA. The prediction method is based on the observation that DNA-binding sites are, in general, amongst the most positive electrostatic patches on the surface of a protein.
A recent paper has addressed the wider issue of predicting whether a protein structure binds DNA (21). This method employs a total of 12 sequence and structural features of positively charged surface patches to make predictions using a neural network. The properties used include secondary structure content, ASA, hydrogen bonding potential, surface concavity, amino acid frequency and sequence conservation. Each property alone is insufficient to determine DNA binding, but in combination a neural network was successfully trained for prediction. With such methods, where training occurs using a large number of features, it is impossible to deconvolute which properties contribute most to the predictions. In the current method, we have achieved successful predictions using scores based on electrostatic potentials without the addition of other parameters.
In the current work, it has been assumed that the protein solved with DNA bound has the same structure and surface properties as the protein solved without DNA bound. However, it is known that many proteins undergo conformational changes on binding DNA. There are examples of protein structures that have been solved with and without DNA bound, and the changes that occur in such structures range from disorder-to-order transitions to changes in tertiary, quaternary and domain structure (22). However, restricting the current analysis and predictions to the small number of structures that have been solved in both states would reduce the data set considerably and not allow general conclusions to be drawn. A much larger number of proteins solved in both states would be required to quantitatively analyse how such changes affect the surface properties of the protein. However, Stawiski and co-workers have showed that their analysis of positively charged electrostatic patches for binding site prediction was still valid when used on a small subset of protein structures solved without DNA bound (21).
We have previously published a method for the prediction of DNA-binding sites in proteins using 3D motif templates (5). This method involves the scanning of 3D templates of helix–turn–helix (HTH) motifs across the PDB and the evaluation of a root-mean-squared deviation threshold below which a protein is predicted as including a DNA-binding motif. In this method, a number of false positive matches still remained even when an additional ASA threshold was applied to the data (false positives are proteins predicted to contain HTH motifs but for which there is no evidence that they bind DNA). In the current work, it has been shown that DNA-binding sites are amongst the surface patches with the most positive electrostatic potential. An obvious next step is to combine the structural template method with electrostatic potential data to make the template scanning method more specific to DNA-binding motifs.
It is intended that the current prediction method based on electrostatic potentials will be made available as a Web server. The server will enable the user to upload protein structure coordinates, calculate electrostatic scores for surface atoms and then get a prediction of the surface patches included within the DNA-binding site. This new server will be organized concurrently with the motif server which implements the method of using 3D motif templates to identify DNA-binding proteins (http://www.ebi.ac.uk/thornton-srv/databases/DNA-motif) (5).
Acknowledgments
ACKNOWLEDGEMENTS
S.J. was supported by a US Department of Energy grant (DE-FG02-96ER62166) and H.S was supported by a MRC/PPARC fellowship.
REFERENCES
- 1.Lijnzaad P. and Argos,P. (1997) Hydrophobic patches on protein subunit interfaces: Characteristics and prediction. Proteins Struct. Funct. Genet., 28, 333–343. [PubMed] [Google Scholar]
- 2.Jones S. and Thornton,J.M. (1997) Prediction of protein-protein interaction sites using patch analysis. J. Mol. Biol., 272, 133–143. [DOI] [PubMed] [Google Scholar]
- 3.Landgraf R., Xenarios,I. and Eisenberg,D. (2001) Three-dimensional cluster analysis identifies interfaces and functional residue clusters in proteins. J. Mol. Biol., 307, 1487–1502. [DOI] [PubMed] [Google Scholar]
- 4.Ma B.Y., Elkayam,T., Wolfson,H. and Nussinov,R. (2003) Protein–protein interactions: structurally conserved residues distinguish between binding sites and exposed protein surfaces. Proc. Natl Acad. Sci. USA, 100, 5772–5777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jones S., Barker,J.A., Nobeli,I. and Thornton,J.M. (2003) Using structural motif templates to identify proteins with DNA binding function. Nucleic Acids Res., 31, 2811–2823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Berman H.M., Olson,W.K., Beveridge,D.L., Westbrook,J., Gelbin,A., Demeny,T., Hsieh,S.H., Srinivasan,A.R. and Schneider,B. (1992) The Nucleic Acid Database. A comprehensive relational database of 3-dimensional structures of nucleic-acids. Biophys. J., 63, 751–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shepherd A.J., Martin,N.J., Johnson,R.G., Kellam,P. and Orengo,C.A. (2002) PFDB: a generic protein family database integrating the CATH domain structure database with sequence based protein family resources. Bioinformatics, 18, 1666–1672. [DOI] [PubMed] [Google Scholar]
- 8.Hubbard S.J. (1993) NACCESS. Department of Biochemistry and Molecular Biology, University College, London. [Google Scholar]
- 9.Rocchia W., Alexov,E. and Honig,B. (2001) Extending the applicability of the nonlinear Poisson–Boltzmann equation: multiple dielectric constants and multivalent ions. J. Phys. Chem. B, 105, 6507–6514. [Google Scholar]
- 10.Brooks B.R., Bruccoleri,R.E., Olafson,B.D., States,D.J., Swaminathan,S. and Karplus,M. (1983) CHARMM—a program for macromolecular energy, minimization and dynamics calculations. J. Comput. Chem., 4, 187–217. [Google Scholar]
- 11.Nicholls A., Sharp,K.A. and Honig,B. (1991) Protein folding and association—insights from the interfacial and thermodynamic properties of hydrocarbons. Proteins Struct. Funct. Genet., 11, 281–296. [DOI] [PubMed] [Google Scholar]
- 12.Jones S. and Thornton,J.M. (1996) Principles of protein-protein interactions. Proc. Natl Acad. Sci. USA, 93, 13–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jones S., van Heyningen,P., Berman,H.M. and Thornton,J.M. (1999) Protein–DNA interactions: a structural analysis. J. Mol. Biol., 287, 877–896. [DOI] [PubMed] [Google Scholar]
- 14.Efron B. (1979) Computers and the theory of statistics: thinking the unthinkable. SIAM Rev., 4, 460–480. [Google Scholar]
- 15.Faucher J. and Pliska,V. (1983) Hydrophobic parameters pi of amino acid side chains from the partitioning of N-acetyl-amino-acid amides. Eur. J. Med. Chem., 18, 369–375. [Google Scholar]
- 16.Valdar W.S.J. and Thornton,J.M. (2001) Protein–protein interfaces: analysis of amino acid conservation in homodimers. Proteins Struct. Funct. Genet., 42, 108–124. [PubMed] [Google Scholar]
- 17.Benson D.A., Karsch-Mizrachi,I., Lipman,D.J., Ostell,J. and Wheeler,D.L. (2003) GenBank. Nucleic Acids Res., 31, 23–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Deibert M., Grazulis,S., Janulaitis,A., Siksnys,V. and Huber,R. (1999) Crystal structure of MunI restriction endonuclease in complex with cognate DNA at 1.7 angstrom resolution. EMBO J., 18, 5805–5816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Patikoglou G.A., Kim,J.L., Sun,L.P., Yang,S.H., Kodadek,T. and Burley,S.K. (1999) TATA element recognition by the TATA box-binding protein has been conserved throughout evolution. Genes Dev., 13, 3217–3230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Beamer L.J. and Pabo,C.O. (1992) Refined 1.8 Å crystal-structure of the lambda-repressor operator complex. J. Mol. Biol., 227, 177–196. [DOI] [PubMed] [Google Scholar]
- 21.Stawiski E.W., Gregoret,L.M. and Mandel-Gutfreund,Y. (2003) Annotating nucleic acid-binding function based on protein structure. J. Mol. Biol., 326, 1065–1079. [DOI] [PubMed] [Google Scholar]
- 22.Nadassy K., Wodak,S.J. and Janin,J. (1999) Structural features of protein–nucleic acid recognition sites. Biochemistry, 38, 1999–2017. [DOI] [PubMed] [Google Scholar]
- 23.Luscombe N.M. and Thornton,J.M. (2002) Protein–DNA interactions: amino acid conservation and the effects of mutations on binding specificity. J. Mol. Biol., 320, 991–1009. [DOI] [PubMed] [Google Scholar]
- 24.Hosfield D.J., Guan,Y., Haas,B.J., Cunningham,R.P. and Tainer,J.A. (1999) Structure of the DNA repair enzyme endonuclease IV and its DNA complex: double-nucleotide flipping at abasic sites and three-metal-ion catalysis. Cell, 98, 397–408. [DOI] [PubMed] [Google Scholar]
- 25.Jayaram B., Dicapua,F.M. and Beveridge,D.L. (1991) A theoretical-study of polyelectrolyte effects in protein DNA interactions—Monte-Carlo free-energy simulations on the ion atmosphere contribution to the thermodynamics of lambda repressor operator complex-formation. J. Am. Chem. Soc., 113, 5211–5215. [Google Scholar]
- 26.Jeltsch A., Maschke,H., Selent,U., Wenz,C., Kohler,E., Connolly,B.A., Thorogood,H. and Pingoud,A. (1995) DNA-binding specificity of the Ecorv restriction-endonuclease is increased by Mg2+ binding to a metal-ion binding-site distinct from the catalytic center of the enzyme. Biochemistry, 34, 6239–6246. [DOI] [PubMed] [Google Scholar]
- 27.Conlan L.H. and Dupureur,C.M. (2002) Dissecting the metal ion dependence of DNA binding by PvuII endonuclease. Biochemistry, 41, 1335–1342. [DOI] [PubMed] [Google Scholar]
- 28.Steitz T.A. (1999) DNA polymerases: structural diversity and common mechanisms. J. Biol. Chem., 274, 17395–17398. [DOI] [PubMed] [Google Scholar]
- 29.Eom S.H., Wang,J.M. and Steitz,T.A. (1996) Structure of Taq polymerase with DNA at the polymerase active site. Nature, 382, 278–281. [DOI] [PubMed] [Google Scholar]
- 30.Pelletier H. and Sawaya,M.R. (1996) Characterization of the metal ion binding helix-hairpin-helix motifs in human DNA polymerase beta by X-ray structural analysis. Biochemistry, 35, 12778–12787. [DOI] [PubMed] [Google Scholar]
- 31.Lahm A. and Suck,D. (1991) Dnase I-induced DNA conformation 2A structure of a Dnase I–octamer complex. J. Mol. Biol., 222, 645–667. [DOI] [PubMed] [Google Scholar]
- 32.Sayle R.A. and Milnerwhite,E.J. (1995) Rasmol: biomolecular graphics for all. Trend Biochem. Sci., 20, 374–376. [DOI] [PubMed] [Google Scholar]