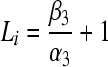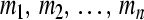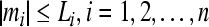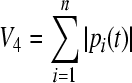Unconditional global exponential stability in Lagrange sense of genetic regulatory networks with SUM regulatory logic

Abstract

In this paper, the global exponential stability in Lagrange sense for genetic regulatory networks (GRNs) with SUM regulatory logic is firstly studied. By constructing appropriate Lyapunov-like functions, several criteria are presented for the boundedness, ultimate boundedness and global exponential attractivity of GRNs. It can be obtained that GRNs with SUM regulatory logic are unconditionally globally exponentially stable in Lagrange sense. These results can be applied to analyze monostable as well as multistable networks. Furthermore, to analyze the stability for GRNs more comprehensively, the existence of equilibrium point of GRNs is proved, and some sufficient conditions of the global exponential stability in Lyapunov sense for GRNs are derived. Finally two numerical examples are given to illustrate the application of the obtained results.

Introduction

With the appearance and development of DNA microarray technology (Pease et al. 1994), it has become possible to measure gene expression levels on a genomic scale and furthermore analyze the genetic regulatory networks (GRNs). Considerable attention has been contributed to theoretical analysis and experimental investigation on GRNs (Becskei and Serrano 2000; Gardner et al. 2000; Li et al. 2006a, b; Ren and Cao 2008; Chen and Aihara 2002). And the GRN is the key to understand how genes and proteins interact to form a network that performs complicated biological functions. In living organisms, the process in which the information encoded in DNA is converted into proteins through transcription and translation is called gene expression. So gene expression is a process consisting of transcription and translation. During transcription process, mRNAs are synthesized from genes by the regulations of transcription factors, which are proteins. During translation process, the sequence of nucleotides in the mRNA is used in the synthesis of a protein. A genetic regulatory network is a dynamic system to describe highly complex interactions among two main species of gene product: mRNAs and proteins, in the interactive transcription and translation processes. Several computational models have been applied to investigate the behaviors of genetic regulatory networks: Bayesian network models (Friedman et al. 2000; Hartemink et al. 2002), Petri net models (Chaouiya et al. 2008; Hardy and Robillard 2004), the Boolean models (Somogyi and Sniegoski 1996; Weaver et al. 1999), and the differential equation models (Bolouri and Davidson 2002; Chen and Aihara 2002; Jong 2002; Smolen et al. 2000), etc. In the differential model, the variables describe the concentrations of gene product, such as mRNA and proteins, as continuous value of the genetic regulatory systems. Meanwhile the differential model has been more widely used to investigate the GRNs, and certain quantitative results have been presented (Chen and Aihara 2002; Jong 2002; Goodwin 1963; Chen et al. 1999; Tian et al. 2007).

As a dynamic system, it is natural of great importance to investigate the stability of GRNs. Li et al. (2006), Ren and Cao (2008), Chen and Aihara (2002), Wang and Cao (2009), Wang et al. (2009) have derived some results. Li et al. (2006), presented a nonlinear model for GRNs with SUM logic and gave some criteria for the stability. Ren and Cao (2008), studied the stability for a class of GRNs with time delays and the robust stability for GRNs with norm bounded uncertainties. Wang and Cao (2009) presented some sufficient conditions for the robust stability for stochastic GRNs with parameters uncertainty. And GRNs with distributed delays were addressed in Wang et al. (2009). From a dynamical system point of view, globally stable networks in Lyapunov sense are monostable systems, which have a unique equilibrium point attracting all trajectories asymptotically. But in many real applications, biological systems are no longer globally stable, thus more appropriate notions of stability are needed to deal with multistable networks. Yi and Tan (2004) investigated three important properties: boundedness, attractivity and complete convergence of a multistable networks. Liao and Wang (2003) addressed the global dissipativity of a general class of continuous-time recurrent neural networks.

The main difference between Lagrange stability and Lyapunov stability is that Lagrange stability refers to the stability of total systems, not the stability of equilibrium points. When studying the stability in Lagrange sense, we don’t make any assumption on the numbers of the equilibrium points. Especially as to the asymptotical stability in Lagrange sense, only if all the solutions of a system ultimately enter into an attractive compact set, we call the system to be asymptotically stable in Lagrange sense or ultimately bounded. Lagrange stability can be used in analyzing both monostable systems and multistable systems and it is less conservative. And in the special case where the attractive compact set is a single point, the system is globally stable in Lyapunov sense and the attractive compact set is the unique equilibrium point.

We have noted that Lagrange stability has long been studied in the theory and applications of dynamical systems. LaSalle (1960) and Yoshizawa (1966), apply Lyapunov functions to study Lagrange stability. In Thornton and Mulholland (1974), Rekasius considers asymptotic stability in Lagrange sense for nonlinear feedback control systems. In Rekasius (1963), Lagrange stability is discussed by Thornton and Mulholland as a useful concept for determining the stability of ecological systems. More recently, Passino and Burgess (1995) adapt the concept of Lagrange stability to investigate discrete event systems, and Hassibi et al. (1999) study the Lagrange stability of hybrid dynamical systems. Wang et al. (2006) and Yang and Huang (2006), investigates Lagrange stability for pendulum-like systems. See also (Liao et al. 2008a, b; Chen and Luo 2009) for recent results on global exponential stability in Lagrange sense for neural networks with time delay.

To the best of our knowledge, the current results of stability analysis for GRNs is all based on the Lyapunov global stability. The Lagrange stability for GRNs has not been touched. Hence, from the perspective of theory and application, it is of significance to study the Lagrange stability for GRNs. In this paper, we first study the globally exponentially stability in Lagrange sense for GRNs with time delay and presents some criteria for global exponential attractive set of GRNs. In order to give a comprehensive study of the stability for GRNs, we also investigate the stability in Lyapunov sense for GRNs. We first prove the existence of the equilibrium point of the GRNs, and then study the global exponential stability in Lyapunov sense for GRNs and derive two theorems. It is believed that our results are useful for comprehensive analysis of GRNs and have certain applicable value.

The rest of this paper is organized as follows. In the section following the introduction section, a description of problem formulation and preliminaries are given. We then present the main results of global exponential stability in Lagrange sense for GRNs. The existence of the equilibrium point of GRNs is proved in the following section. The next section considers the global exponential stability in Lyapunov sense of GRNs. In the final section, two numerical examples are given to illustrate the application of our results.

Problem formulation and preliminaries

In this paper, we consider the GRN described by the following differential equations (Wang and Zhang 2007; Li et al. 2006; Chen and Aihara 2002):

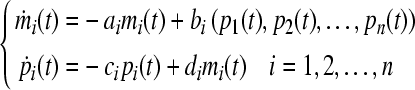1

where m_i(t), p_i(t) are the concentrations of mRNA and protein of the ith node, respectively. In this network, there is only one output but multiple inputs for a single node or gene. If the transcriptional factor or protein j regulates the gene i, a direct edge will be linked from node j to i (Chen and Aihara 2002). In (1), the parameters a_i and c_i are the decay rates of mRNA and protein, respectively, d_i is a constant, which is the translational rate. b_i is the regulation function of the ith gene, and it is generally a nonlinear function of the variables (p₁(t), p₂(t), …, p_n(t)) but has a form of monotone with each variable (Jong 2002; Smolen et al. 2000).

The gene activities are tightly controlled in cellular, and the gene regulation function b_i plays an essential role in the dynamics. Generally the form of b_i may be very complicated, depending on all biochemical reactions involved in this regulation. In this paper, we investigate the model of GRN where each transcriptional factor acts additively to regulate the ith gene. That is the regulation function has a form of 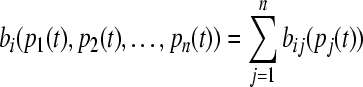, which is also called SUM logic (Yuh et al. 1998; Kalir et al. 2005). The function b_ij(p_j(t)) is a monotonic function of Hill form, which can be expressed as follows:

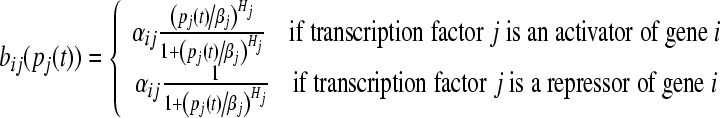where H_j is the Hill coefficient, β_j is a positive constant, α_ij is the dimensionless transcriptional rate of transcriptional factor j to gene i, which is a bounded constant.

Note that,

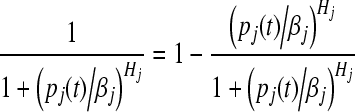Hence, we can rewrite Eq. (1) as follows,

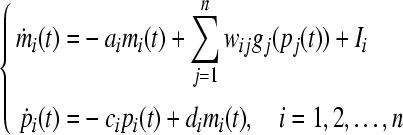2

where 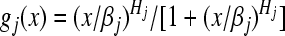is a monotonically increasing function. I_i is defined as a basal rate, , in which V_i1 is the set of repressors of gene i. And w_ij is defined as follows: if there is no link from node j to node i, w_ij = 0; if transcription factor j is an activator of gene i, w_ij = α_ij; if transcription factors j is a repressor of gene i, w_ij = −α_ij.

In the real genetic regulatory networks, time delays usually exist due to the slow process of diffusion, transcription and translation of modular. Taking the time delays into account, (2) can be transformed to

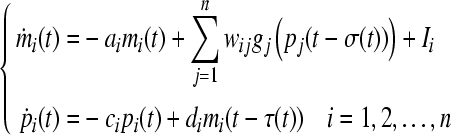3

where τ = max {τ(t), σ(t)}.

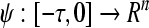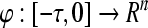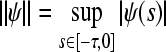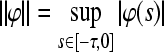Let C_[−τ,0] be the Banach space of continuous functions , with the norm and , respectively. Define two subsets on space C_[−τ,0],

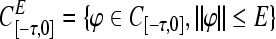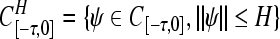where E > 0, H > 0 are positive constants. Let BBF⁺ be the set of all non-negative continuous functional 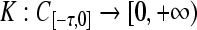, mapping bounded sets in C_[−τ,0] into bounded sets in [0, +∞).For any initial function φ ∈ C_[−τ,0], ψ ∈ C_[−τ,0], the solution of (2) with initial conditions (φ, ψ)will be denoted by m(t, φ), p(t, ψ), respectively.

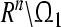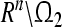Let Ω₁, Ω₂ ∈ Rⁿ be compact sets in Rⁿ. Denote the complement by and , respectively. For any 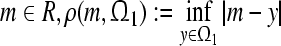is the distance between m and 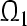, and for any 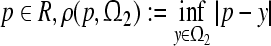is the distance between p and 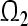. We call the compact set 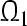a global attractive set with respect to partial variables (m₁, m₂, …, m_n) of system (3) if for every solution such that 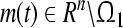, one has 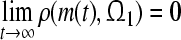. Similarly, We call the compact set Ω₂ a global attractive set with respect to partial variables 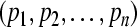of system (3) if for every solution such that 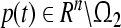, one has 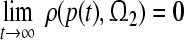. The compact set 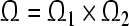is the global attractive set of system (3).Obviously, if the system (3) has a global attractive set, then the solutions of (3) are ultimately bounded.

Now we introduce some necessary definitions (Kalir et al. 2005).

Definition 1 The GRN(3) is said to be uniformly stable in Lagrange sense (or uniformly bounded), if for any E > 0, H > 0, there exist constants K₁ = K(E) > 0, K₂ = K(H) > 0 such that m(t, φ) < K₁, p(t, ψ) < K₂, t ≥ 0 for all 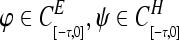.The GRN(3) is said to be uniformly asymptotically stable in Lagrange sense (or ultimately uniformly bounded), if for any E > 0, H > 0, there exist constants K₁ = K(E) > 0, K₂ = K(H) > 0 and T > 0 such that m(t, φ) < K₁, p(t, ψ) < K₂, t ≥ T for all .

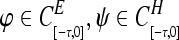Definition 2 If there exist a positive constant α₁ > 0 (α₂ > 0) and a continuous function 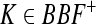, such that for 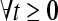, every solution of system (3) with respect to partial variables (m₁, m₂, …, m_n) ((p₁, p₂, …, p_n)) 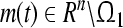(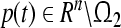) satisfies, 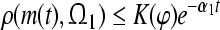(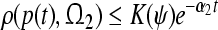). So the compact set 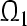(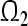) is said to be a globally exponentially attractive (GEA) set with respect to partial variables 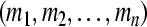(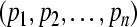) of system (3). The compact set 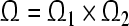is the globally exponentially attractive set of GRN(3).The above definition for a GEA set is often difficult to use. The main difficulty is that the distance function seems hard to be direct linked to the exponential decay function. So we now cite following definitions, which involve positive definite function and hence typically suitable in employing Lyapunov-like function to analyze the global exponential attractivity of GRN(3).

Definition 3 If there exist positive constants l₁ > 0, α₁ > 0 (l₂ > 0, α₂ > 0) and a radially unbounded Lyapunov function V₁(m) (V₂(p)), and a continuous functional 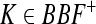such that for every solution with respect to partial variables (m₁, m₂, …, m_n) ((p₁, p₂, …, p_n)) of system (3) m(t) = m(t, φ)(p(t) = p(t, ψ)), V₁(m(t)) > l₁, t ≥ 0, (V₂(p(t)) > l₂, t ≥ 0) implies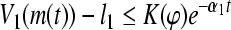 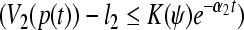.Then the GRN(3) is said to be globally exponentially attractive with respect to partial variables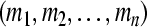 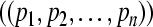, the GRN(3) is globally exponentially attractive with respect to 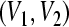. The compact set 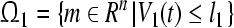(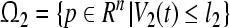) is called a GEA set with respect to partial variables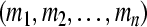 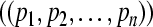of system (3). The compact set 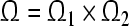is the GEA set of GRN(3).

Definition 4 The GRN(3) is called globally exponentially stable (GES) in Lagrange sense, if it is both uniformly stable in Lagrange sense and globally exponentially attractive. If there is a need to emphasize the Lyapunov-like functions, the network (3) will be called globally exponentially stable in Lagrange sense with respect to (V₁, V₂).

We now give a lemma that will be used in the proof of main results.

Lemma 1 (Liao 2000) Let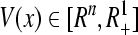be a positive definite and radially unbounded function, and there exist two constants α > 0, β > 0 such that

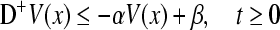4

Then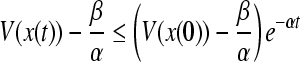.Particularly if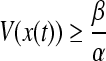, for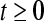, V(x) exponentially approaches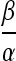as t increases.

Proof We consider the comparison equation of (4)

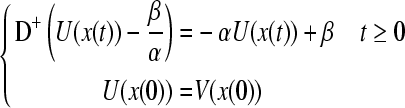5

The solutions of the comparison equation of (5) as

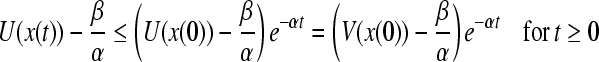By the comparison theory, we have

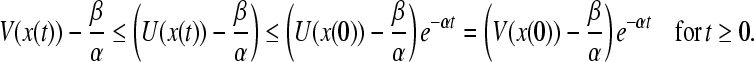Unconditional global exponential stability in Lagrange sense for GRNs

We should point out that the unconditional stability in Lagrange sense indicates that the system is stable in Lagrange sense without any additional conditions. We also don’t make any assumption about the model or the parameters of the model, either. The results derived are all constructive and not dependent on any existence conditions. In the following, we will consider the unconditional global exponential stability in Lagrange sense for GRN(3).

From the above discussion, we can derive 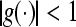, in the following, we will take full advantage of this property. Choose 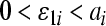, 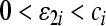. And denote , , , .

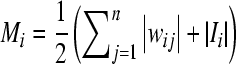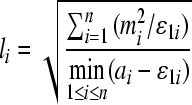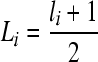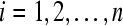Theorem 1 GRN(3) is unconditionally globally exponentially stable in Lagrange sense. The compact set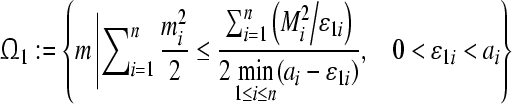is a GEA set with respect to partial variables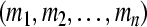; The compact set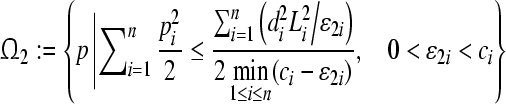is a GEA set with respect to partial variables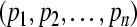. And the compact set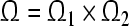is a GEA set of GRN(3).

Proof

1. Construct a radially unbounded and positive definite Lyapunov function with respect to partial variables 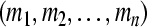for the first equation of (3).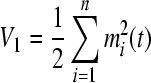

   

Choose 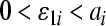, and compute the derivative of V₁ along (3)

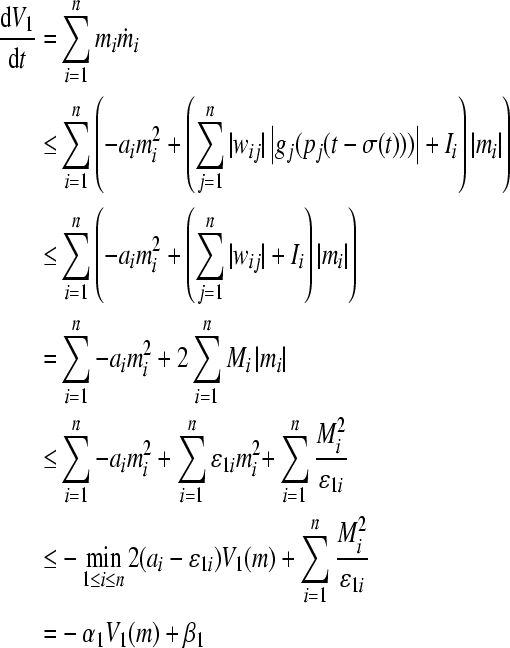where 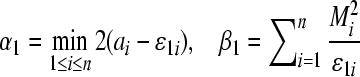. By Lemma 1, we have 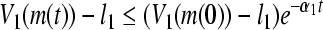, where 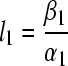. That implies the uniform boundedness and ultimate uniform boundedness of the solution with respect to partial variables 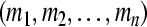of system (3), which means the GRN(3) is uniformly stable in Lagrange sense with respect to partial variables 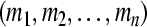. Note that,

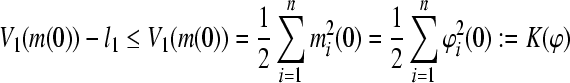where 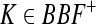,and this implies that for t ≥ 0

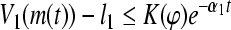by Definition (3), GRN(3) is globally exponentially attractive and 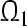is a GEA set with respect to partial variables .

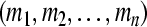1. From step 1), we can see that m_i(t) is uniformly bounded, and the ultimate bound is 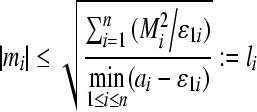. Let 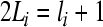. For the partial variables 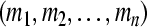of the second equation of (3), we may let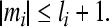

We now construct a radially unbounded and positive definite Lyapunov function with respect to partial variables 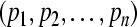for the second equation of (3) as

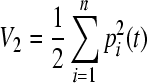Choose 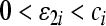and compute the derivative of V₂ along (3)

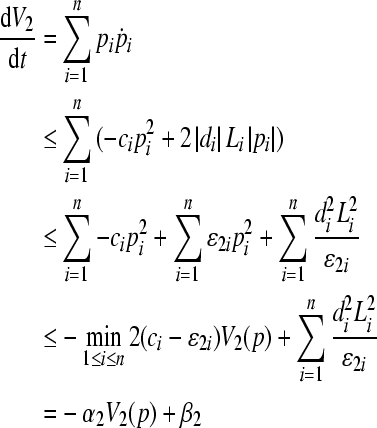where 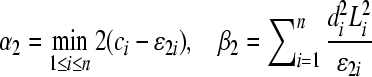. By Lemma 1, we have 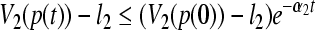, where 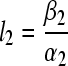. That implies the uniform boundedness and ultimate uniform boundedness of the solution with respect to partial variables 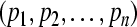of system (3), which means the GRN(3) is uniformly stable in Lagrange sense with respect to partial variables 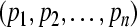. Note that,

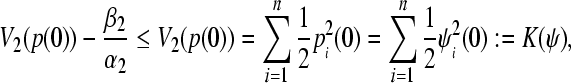where 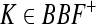, and this implies that for t ≥ 0

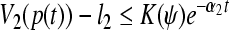By Definition (3), GRN(3) is globally exponentially attractive and 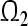is a GEA set with respect to partial variables 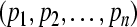.According to 1) and 2), we can conclude that the GRN(3) is uniformly stable and the compact set 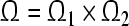is GEA set of GRN(3). Hence by Definition 4, GRN(3) is globally exponentially stable in Lagrange sense.Proof is completed.

Denoting , , .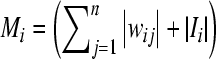

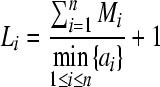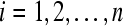Theorem 2 GRN(3) is unconditionally globally exponentially stable in Lagrange sense. And the compact set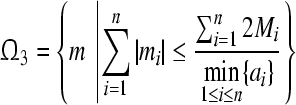is a GEA set with respect to partial variables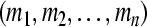; The compact set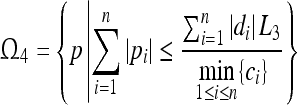is a GEA set with respect to partial variables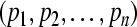. Thus the compact set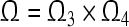is a GEA set of GRN(3).

Proof

1. Employ a radially unbounded and positive definite Lyapunov function for the first equation of (3)

   

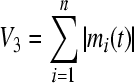
Take the right upper Dini derivative along (3),

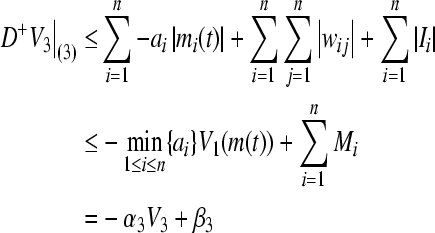where 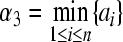, 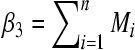. By Lemma 1, we can obtain 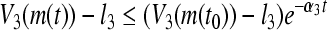, where 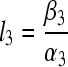. This implies the uniform boundedness and ultimate uniform boundedness of the solution with respect to partial variables 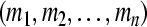of system (3), which means the GRN(3) is uniformly stable and uniformly asymptotically stable in Lagrange sense with respect to partial variables 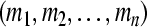. Note that,

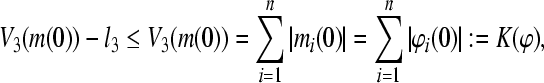where 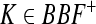. Thus, 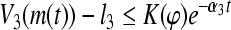. By Definition 3, 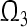is a GEA set with respect to partial variables of GRN(3).

1. Let . From the Proof in 1), we may assume the variables in the second equation of (3) satisfy . We employ another radially unbounded and positive definite Lyapunov function for the second equation of (3),

   

Take the right upper Dini derivative along (3),

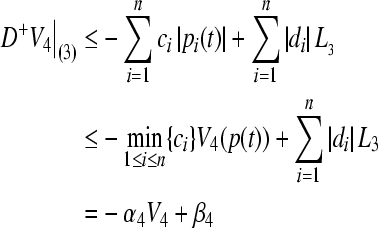where 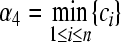, 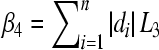. By Lemma 1, we can obtain 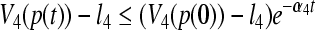, where 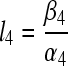. This implies the uniform boundedness and ultimate uniform boundedness of the solution with respect to partial variables 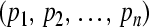of system (3), which means the GRN(3) is uniformly stable and uniformly asymptotically stable in Lagrange sense with respect to partial variable 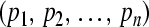. Observe that 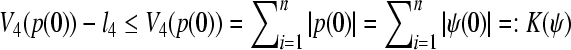, where 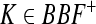. Then 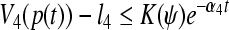. By Definition 3, GRN(3) is globally exponentially attractive and 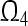is a GEA set with respect to partial variables 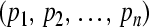.According to 1) and 2), we can conclude that the GRN(3) is uniformly stable and the compact set 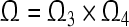is GEA set of GRN(3). Hence by Definition 4, GRN(3) is globally exponentially stable in Lagrange sense.Proof is completed.

Denoting , .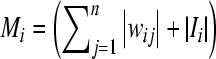

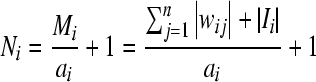Theorem 3 GRN(3) is unconditionally globally exponentially stable in Lagrange sense. The compact set 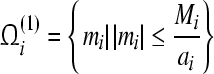is a GEA set with respect to partial variable m_i, the compact set 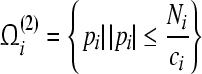is a GEA set with respect to partial variable p_i. Hence, the compact set 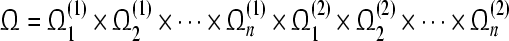is a GEA set of GRN(3).

Proof

1. Employ a radially unboundedness and positive definite Lyapunov function

   

   

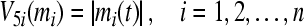
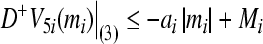
By Lemma 1, we can obtain

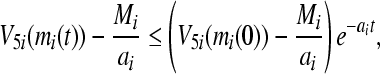which deduces the uniform boundedness and ultimate uniform boundedness(i.e. uniformly stable and uniformly asymptotically stable in Lagrange sense)of the solution of partial variable m_i of system (3). Observe that

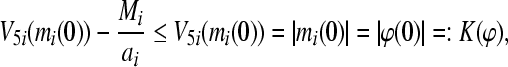where 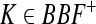. Then 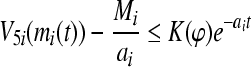. By Definition 3, we have 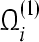is a GEA set of partial variable m_i of (3).

1. Employ another radially unbounded and positive definite Lyapunov function

   

   

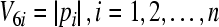
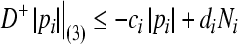
By Lemma 1, we obtain

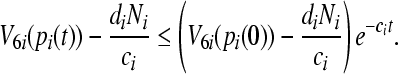This deduces the uniform boundedness and ultimate uniform boundedness (i.e. uniformly stable and uniformly asymptotically in Lagrange sense)of the solution of partial variable p_i of system (3). Observe that

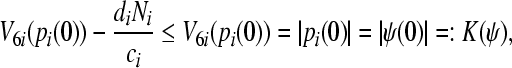where 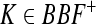. Then 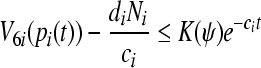. By Definition 3, 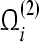is a GEA set of partial variable p_i of (3).According to 1) and 2), we can deduce that the GRN(3) is uniformly stable and the compact set 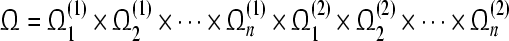is GEA set of GRN(3). Hence by Definition 4, GRN(3) is globally exponentially stable in Lagrange sense.Proof is completed.

Theorem 4 GRN(3) is unconditionally globally exponentially stable in Lagrange sense, and the GEA set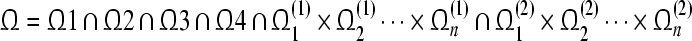is a better GEA set of GRN(3).

Proof According to the properties of intersection sets, the result is obvious.

Proof of existence of the equilibrium point of GRNs

In the following, we will investigate the stability in Lyapunov sense of the genetic regulatory network with SUM logic. So, we need to prove the existence of equilibrium point of the GRNs. As to the uniqueness of the equilibrium point, it will be settled during the proof of the globally asymptotic stability, because the uniqueness of the equilibrium point is the necessary condition of the globally asymptotic stability of GRNs.

Theorem 5 Under the above assumption, the equilibrium point always exists of GRN(2).

Proof Consider the following mapping operator,

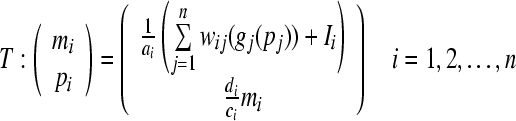6

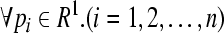, for the first group mapping component operator

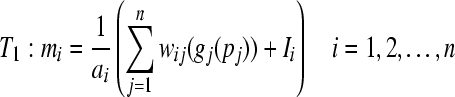One has

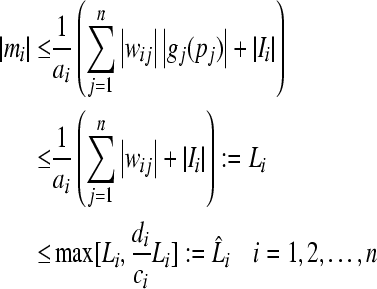7

Hence 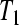maps the 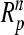space into the compact set 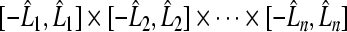in space 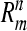. Specially, it maps the compact set 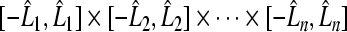in space 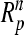into the compact set 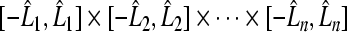in space 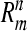.Consider the second group mapping component operator

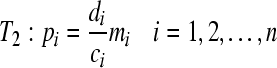For 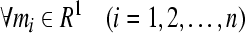, due to the first group operator, we can let

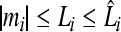Then, we have

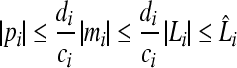Thus the second group mapping operator 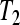maps the compact set in space 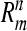into the compact set 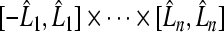in space 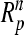.So the combined operator 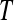maps 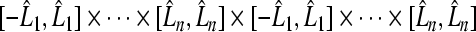in space 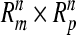into 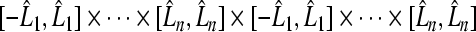in space 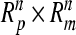. Let 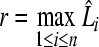, in space 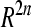. Construct a 2n-dimension hypersphere with radius r and take origin as its circle center

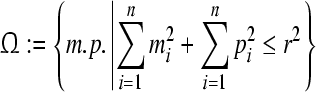Thus 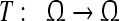.According to the Brown fixed point theorem, the combined operator has a fixed point i.e. there exists at least one equilibrium point of equation (3).

Stability analysis in Lyapunov sense of GRNs

Based on the existence of the equilibrium point of GRNs, we will analyze the stability in Lyapunov sense of GRN(3) with time delay.

Let 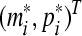be an equilibrium point of (3), i.e. it is the solution of equation

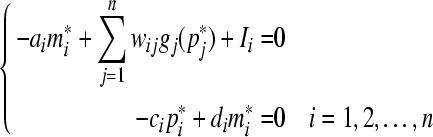For convenience, in the following, we will always shift an intended equilibrium point to origin. Using 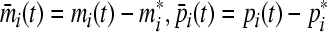, (3) can be transformed to

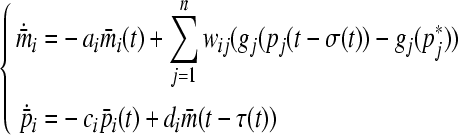8

Hence the Lyapunov stability of the trivial solution of (8) is equivalent to the Lyapunov stability of the equilibrium point 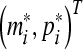of (3).

Let 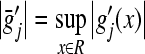and .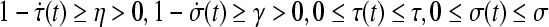

Theorem 6 Assume that there exist positive constants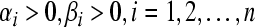satisfying

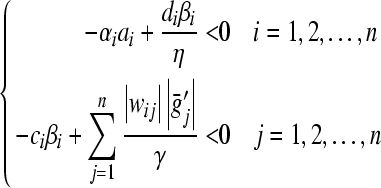9

Then the trivial solution of (8) is globally exponentially stable in Lyapunov sense, and thereby the equilibrium point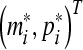of (3) is globally exponentially stable in Lyapunov sense.

Proof The condition (9) implies that there exists 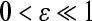, such that

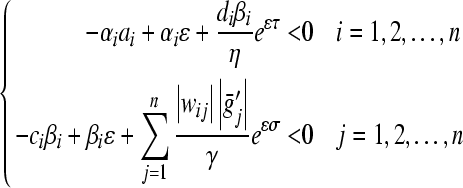10

Employing a radially unbounded and positive definite Lyapunov functional

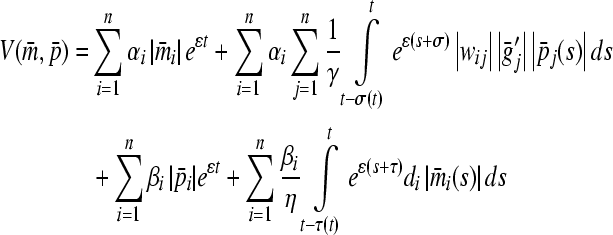Taking the right upper Dini derivative along the solution of (8),

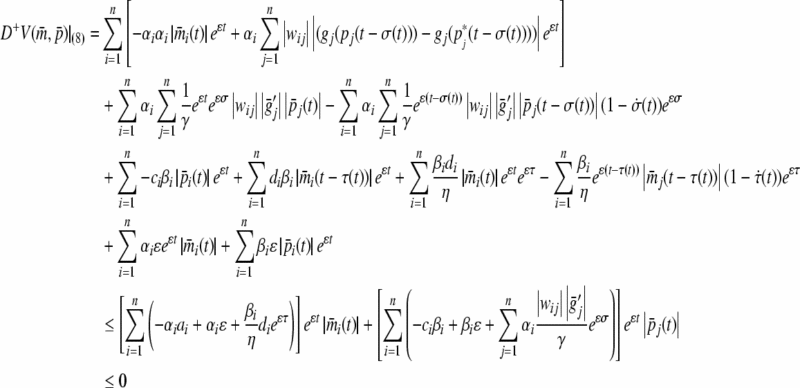We can obtain 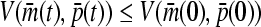, then

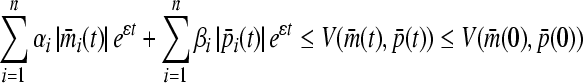11

Thus

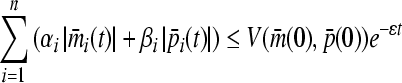12

(12) implies the trivial solution of (8) is globally exponentially stable in Lyapunov sense. Hence the equilibrium point 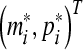of (3) is globally exponentially stable in Lyapunov sense.Proof is completed.

Corollary 1 If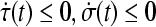(specially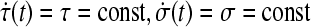), then the condition

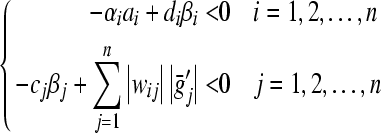implies the trivial solution of (8) is globally exponentially stable in Lyapunov sense. Thus the equilibrium point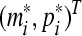of (3) is globally exponentially stable in Lyapunov sense.

Proof The condition (12) implies there exists 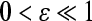, such that

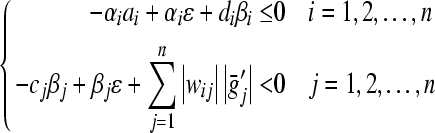13

We can let 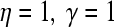. By Theorem 6, the result is derived.Proof is completed.

In the following, we let .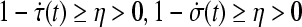

For convenience, we define some necessary vectors and matrices. Let

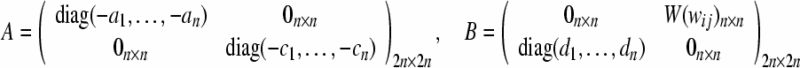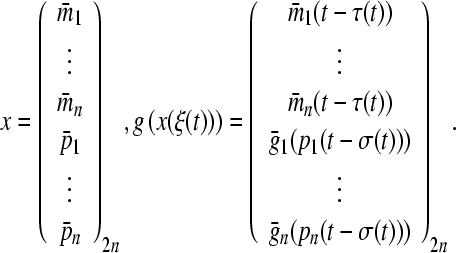where 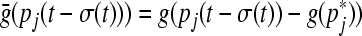, then (8) can be transformed to vector form as follows

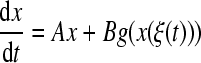14

Theorem 7 If there exists a positive definite diagonal matrix satisfying

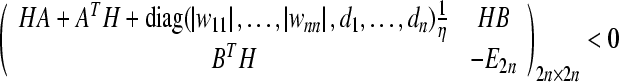15

Then the trivial solution of (8) is globally exponentially stable in Lyapunov sense, thus the equilibrium point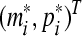is globally exponentially stable in Lyapunov sense.

Proof By the dependence of matrices to the coefficient, (15) implies there exists 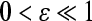such that

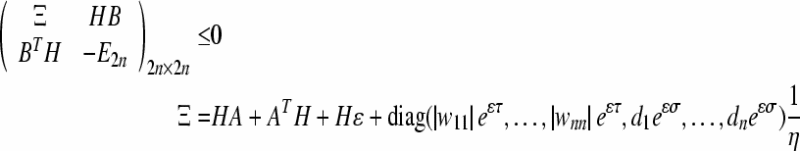Construct a radially unbounded and positive definite Lyapunov functional

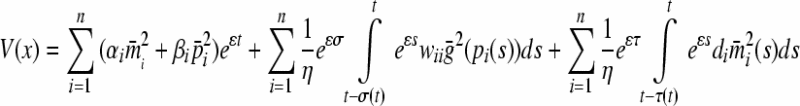Compute the derivative along the solution of (8)

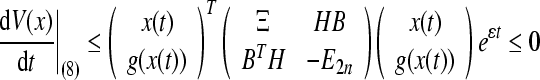Then

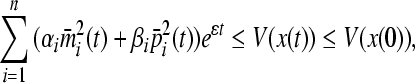Thus

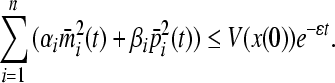This implies the result.Proof is completed.

Corollary 2 If

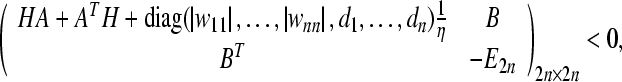then the trivial solution of (8) is globally exponentially stable, thus the equilibrium point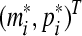is globally exponentially stable.

Proof Let and apply Theorem 8, conclusion is derived.

Numerical examples

Example 1 In this example, we consider repressilator which has been experimentally investigated in Escherichia coli (Elowitz and Leibler 2000).The repressilator is a cyclic negative feedback loop comprising three repressor genes (lacl,tetR,and cl) and their promoters. The kinetics of the system is described as follows:

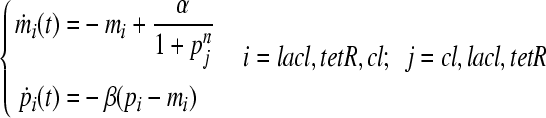where 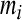and 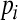are the concentrations of the three mRNAs and repressor-proteins, and 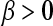denotes the ratio of the protein decay rate to the mRNA decay rate. Taking the transcriptional delays into account and selecting a set of biologically plausible parameters, we rewrite the above equlities in the vector form,

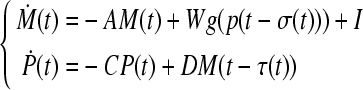16

where , , , ,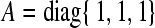

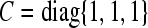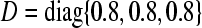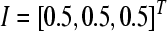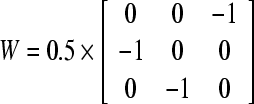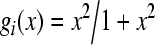, Assuming the time delays 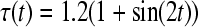, 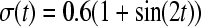According to Theorem 1, we may choose 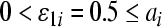, 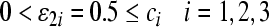. Then we can obtain the compact set 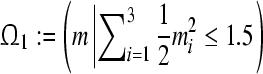is a GEA set with respect to partial variables 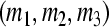of (16). The compact set 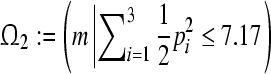is a GEA set with respect to partial variables 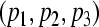of (16). Thus the compact set 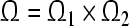is a GEA set of (16).According to Theorem 2, we can obtain 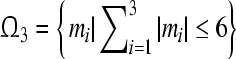is a GEA set with respect to partial variables 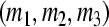of (16). The compact set 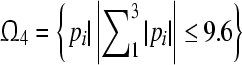is a GEA set with respect to partial variables 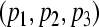of (16). Thus the compact set 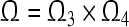is GEA set of (16). According to Theorem 3, we obtain 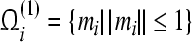is a GEA set with respect to partial variable 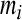, 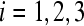. The compact set 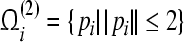is a GEA set with respect to partial variable 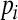, , 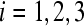the compact set 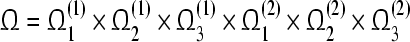is a compact set of (16). The compact set 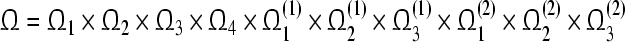is a better GRA set of (16) by Theorem 4.

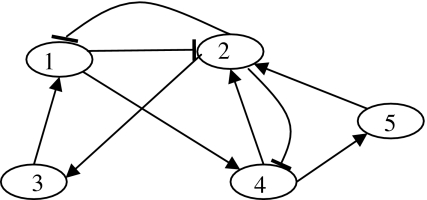
Example 2 Now we consider another GRN with five nodes (Fig. 1) presented in Li et al. (2006). Let

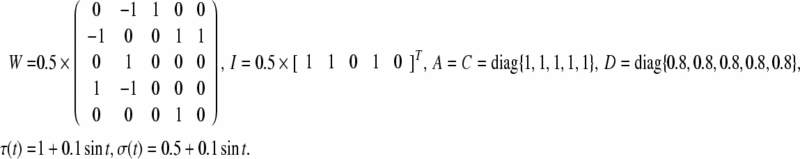We can choose the appropriate parameters that satisfy the condition of Theorem 6 as follows, 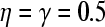, 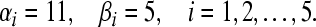Then according to Theorem 6, we can conclude the GRN is globally exponentially stable.

Fig. 1.

Genetic network model (↑: activation, ⊥: repression)

Conclusion

In this paper, we investigated the global exponential stability in Lagrange sense for a class of genetic regulatory networks with SUM regulatory networks. From the results obtained, we can see this class of GRNs is unconditionally globally exponentially stable in Lagrange sense, which in some degree meets the natural facts and shows the rationality of the model presented. Several criteria are also derived for the boundedness and global exponential attractivity. Besides, to study the stability of GRNs more comprehensively, we then firstly prove the existence of the equilibrium point of GRNs, and we give some sufficient condition for GRNs to be globally exponentially stable in Lyapunov sense. Finally two numerical examples are given to illustrate the application of our results.