Analyzing inner and outer synchronization between two coupled discrete-time networks with time delays

Abstract

This paper studies two kinds of synchronization between two discrete-time networks with time delays, including inner synchronization within each network and outer synchronization between two networks. Based on Lyapunov stability theory and linear matrix inequality (LMI), sufficient conditions for two discrete-time networks to be asymptotic stability are derived in terms of LMI. Finally numerical examples are given to illustrate the effectiveness of our derived results. The theoretical understanding provides insights into the dynamics of two or more neural networks with appropriate couplings.

Introduction

The human brain has been described as a large, sparse, complex network consisting of a hierarchy of interacting elements on different levels, of different functions and different interconnections. There are at least three basic levels in the hierarchical structure: the microscopic level of interacting neurons, mesoscopic level of mini-columns and local neural circuits, and macroscopic level of large-scale organization of the brain areas (Zhou et al. 2007). While details at the first two levels are still largely missing, extensive information has been collected about the latter level in the brain of animals, such as cats and macaque monkeys (Stam and Reijneveld 2007). Based on the cortical connectivity of mammalian brains, the authors investigated the synchronization dynamics on the corticocortical network of the cat by modeling each node (cortical area) of the network with a sub-network of interacting excitable neurons, and understanding the relationship between structural and functional connectivity is of crucial importance in neuroscience (Zhou et al. 2007).

Over the years, the researchers in physics, biology, mathematics and computer science dedicate to the study of complex networks (Albert and Barabási 2002). The complexity of networks lies in two aspects: topological structures and node dynamics, which are closely linked to each other. Recently, using the approach of complex network analysis, the studies in neuroscience have received a great deal of research attention (Bullmore and Sporns 2009). For example, the cerebral cortex network exhibits small-world (Watts and Strogatz 1998) attributes, characterized by the presence of abundant clustering of connections combined with short average distances between neuronal elements (Sporns and Zwi 2004). Functional brain networks (connecting correlated human brain sites) extracted by the functional magnetic resonance imaging are of scale-free (Barabási and Albert 1999) and small-world characteristics (Eguíluz et al. 2005). In the literature (Liu et al. 2008), the authors found that the brain functional networks had efficient small-world properties in the healthy subjects; whereas these properties were disrupted in the patients with schizophrenia.

During the studies on complex networks, our concern is to know the impact of topological structures on the dynamics of the networks. For example, synchronization of coupled oscillators is one of the crucial dynamical behaviors on complex networks, for its relevance in neural systems. The observations of synchronous neural activity (Melloni et al. 2007; Gray 1944; Kanamaru 2006; Börgers and Kopell 2003; Mancilla et al. 2007; Wang and Jiao 2006) in the central nervous system have encouraged a great deal of theoretical work on synchronization in coupled neural networks, which is beneficial to explore the activities of the brain.

Low-dimensional dynamics in high-dimensional networks is a ubiquitous phenomenon observed in various physical, chemical, and biological problems. Node dynamics in a network can be various depending on the context of discussion, often taken as the neuron models or chaos dynamics etc. While studying the synchronized motion in networks, synchronizing all the nodes is an interesting thing (Liang et al. 2008; Torikai and Saito 2004). Synchronization inside a coupled network, or called “inner synchronization” for convenience, has been intensively and extensively. Besides this kind of network synchronization, outer synchronization, i.e., synchronization between two coupled networks has been studied in the literature (Li et al. 2007), aiming at the study of dynamics between coupled networks.

Time delays commonly exist in biological systems since the finite speed of signal transmission over a distance gives rise to finite time delay, which plays an importance role in the stability of synchronization (He and Cao 2008; Jirsa 2008; Masoller et al. 2009; Ramirez et al. 2009). For instance, time delay enhancing neuron synchrony, and cortical neurons synchronized by time delay feedback, for details, see (Dhamala et al. 2004; Landsman and Schwartz 2007). For two coupled networks, the signals from one network to another often exist delays due to the distance. Therefore, motivated by the synchronization in neural systems which is very relevant to cognition, and the impact of topological structures and the delays on the dynamics of the networks. This paper mainly investigates the synchronization between two coupled networks with time delays by using Lyapunov functional and LMI technique which is used frequently for its easily being verified. A criterion is derived to guarantee the asymptotic stability within each network. Two numerical examples are also given to verify the effectiveness of our obtained results.

Notation: Throughout this paper, the following notations always work. A^T denotes the transpose of a matrix A. ||A|| denotes certain matrix norm. Rⁿ denotes the n dimensional Euclidean space. R^n×m is the set of all n × m real matrices. I denotes the identity matrix with appropriate dimensions. The notation A > 0 (respectively, A < 0) means that the matrix A is positive (negative) definite, that is the eigenvalues of A are positive (respectively, negative).

Methods

Model presentation and preliminaries

Based on the dynamical models inside a network, the coupled equations of two networks can be expressed as follows:

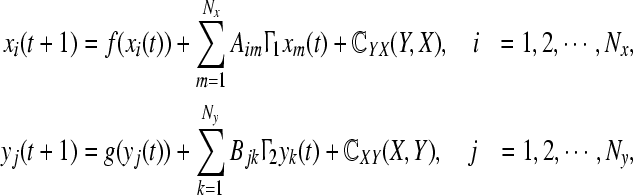1

where the node dynamical equation is x_i(t + 1) = f(x_i(t)), i = 1, ..., N_x and y_j(t + 1) = g(y_j(t)), j = 1, ..., N_y, respectively, and 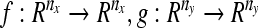are continuously differential functions, x_i(y_j) is an n_x-dimensional (n_y-dimensional) state vector. A = (A_im)_Nx×Nx and B = (B_jk)_Ny×Ny represent the coupling configurations of both networks, whose entries A_im(B_jk) are defined as follows: if there is a connection between node i and node m (m ≠ i), then set A_im(B_jk) > 0, otherwise A_im(B_jk) = 0, (m ≠ i); the matrices A and B can be symmetric or asymmetric, but satisfying the sum of every row being zero. 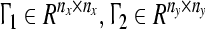are inner-coupling matrices.

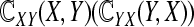represents the interaction from network X(Y) to network Y(X). There are lots of active forms between two networks, for instance, communicated by signals, special nodes or bidirectional actions. In Li et al. (2009), the authors choose 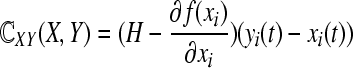and 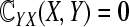to realize outer synchronization, where 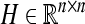is a constant Hurwitz matrix.

Here we focus on bidirectional actions and the delay effect, and we choose 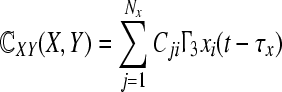and 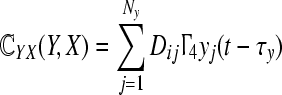, then the dynamical equations of the network systems are as follows:

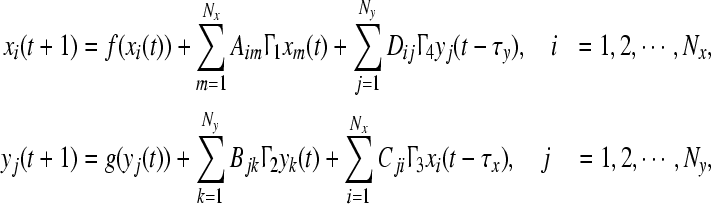2

where C is an N_y × N_x dimensional coupling matrix, whose entries (C_ji) represent the intensity of the direct interaction from j in network Y to i in network X, analogously the entries of (D_ij) are same defined as (C_ji). Matrix 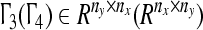is the inner-coupling matrix. τ_x,τ_y (positive integers) are time delays between networks. The action sketch between two networks with time delays is shown in Fig. 1.

Fig. 1.

A simple action sketch between networks X and Y with time delays

For simplicity, we first discuss the effect of interactions and delays on synchronization under the absence of individual connections within each network, i.e., consider

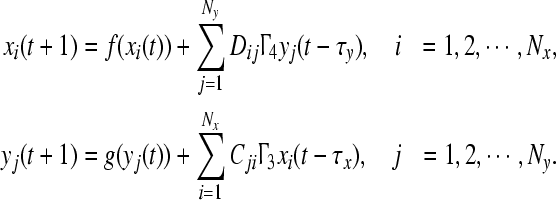3

Analysis

Let’s now consider the possibility whether the individual network achieve synchronization, i.e., x₁(t) = ... = x_Nx(t) = x_s(t) and y₁(t) = ... = y_Ny(t) = y_s(t). If there exist such synchronous states, satisfying

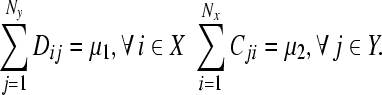without loss of generality, we set μ₁ = μ₂ = 1.

Thus the synchronized state equations are

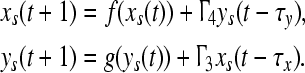4

Linearizing the synchronous state around x_s and y_s, we get

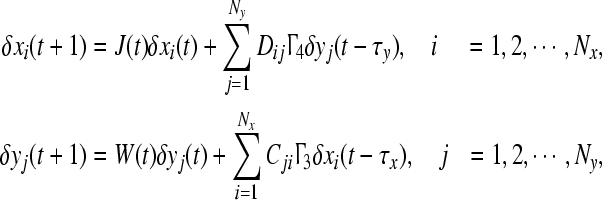5

where J(t) = Df(x_s(t)), W(t) = Dg(y_s(t)) are the Jacobians of f(x(t)), g(y(t)) at x_s and y_s, respectively.

We assume that the (N_x + N_y)-independent solutions of Eq. 5 can be expressed in the form 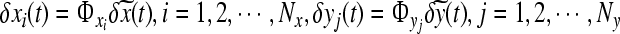, where 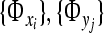are appropriate time-independent scalars. If the dimension of the space vectors given by the values of 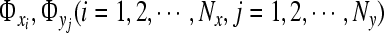is N_x + N_y, we can see this assumed form include all possible linear solutions of Eq. 5. Substituting this assumption into Eq. 5, yields

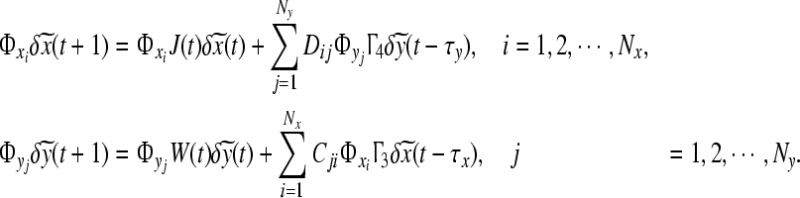6

In order to make Eq. 6 satisfy all i(j), we require that 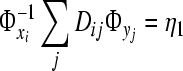, where η₁ is independent of i, and 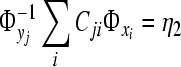, where η₂ is independent of j. Set 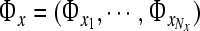and 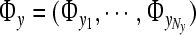. From this, we get 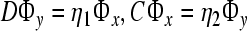, that is

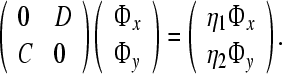7

Substitution Eq. 7 in Eq. 6 we obtain

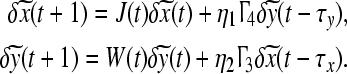8

One particular solution of Eq. 8 is derived when η₁ = η₂ = λ, then

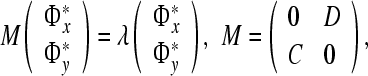9

where λ is the (possibly complex) eigenvalues of the matrix M.

Set 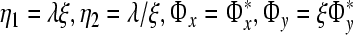, where ξ is a free parameter. Eq. 7 becomes

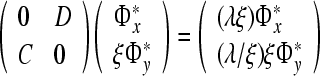10

which shows the solutions of Eq. 10 contains all the possible solutions of Eq. 7. We rewrite Eq. 8 as

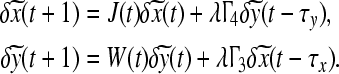11

where λ = λ₁, λ₂, ..., λ_Nx+Ny.

The authors in Sorrentino and Ott (2007) gave the explicit analysis on the spectrum of M, and two forms of constructed matrix M were shown. In the sequel, we utilize the LMI method to obtain a synchronous theorem on inner synchronization within each network.

Results

Theorem 1 Consider network model (3). If there exist two positive matricesP,Q > 0, satisfying

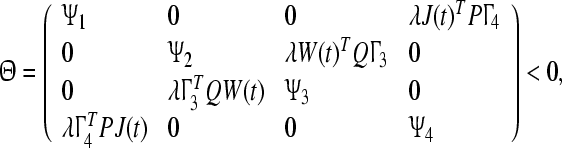12

where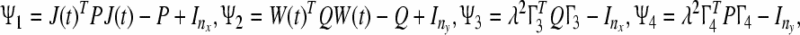then the network (3) asymptotically synchronizes tox_s,y_sdefined by the Eq. 4for the fixed delays τ_x,τ_y, respectively.

Proof Consider the Eq. 11. Choose the Lyapunov function as

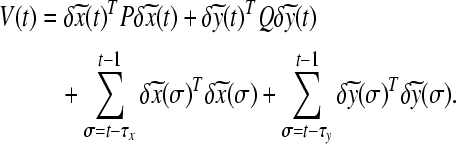13

Therefore,

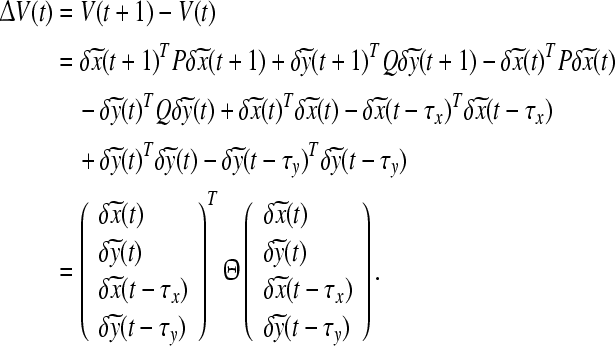14

From the above condition, we know the zero solutions of Eq. 11 is asymptotically stable, which shows that the networks achieve individual inner synchronization.

Remark The linear matrix equality method is inadequate for assessing the stability of the synchronous solution when both intragroup and extra-group connections are allowed in the network (2).

Numerical examples

In this section, we will give two examples to illustrate our obtained results, which includes two cases: n_x ≠ n_y and n_x = n_y. For the case n_x ≠ n_y, we only consider the inner synchronization within each network. On the other hand, owing to n_x = n_y, we not only discuss the inner synchronization within each network, but also investigate the outer synchronization between two networks.

Example 1. We consider the following coupled discrete-time networks, which are in the form (3),

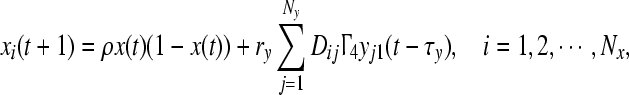15

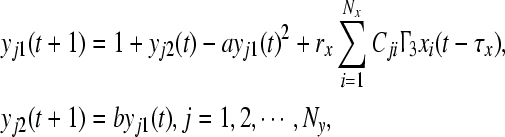16

In the absence of coupling r_x = r_y = 0, the node dynamics in Eqs. 15 and 16 is Logistic map and Henön map respectively, which have colorful dynamical properties, for instance, ρ = 3.1, a = 0.5, b = 0.3, they both have periodic solutions. In the following numerical simulation, we always take ρ = 3.1, a = 0.5, b = 0.3 and τ_x = τ_y = τ, N_x = N_y = N, and 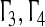are identity matrices in the Figs. 2, 3 and 4. For simplicity, D_ij = C_ji = 1/N for i, j = 1, ..., N. To measure the extent to which inner synchronization is achieved, we introduce the following quantities, E_x = ||x_i − x_s||, i = 1, ..., N, and E_y = ||y_j − y_s||, j = 1, ..., N. When ρ = 3.1, a = 0.5, b = 0.3, by using the Matlab LMI Toolbox, we solve the LMI (12) for P > 0, Q > 0, and obtain

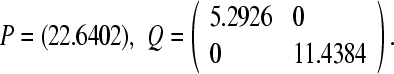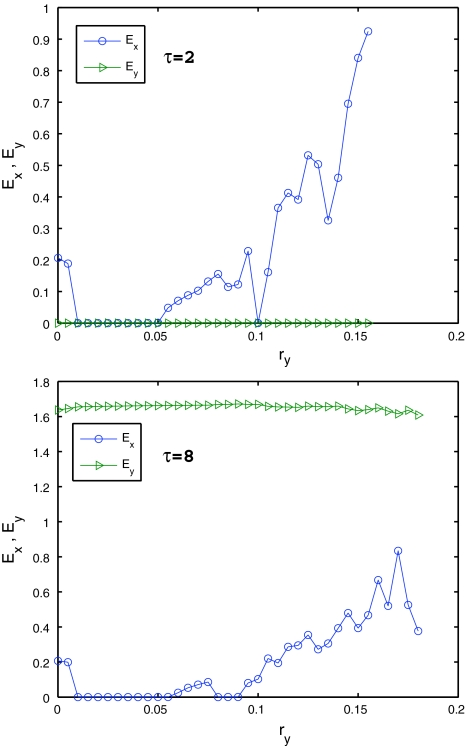
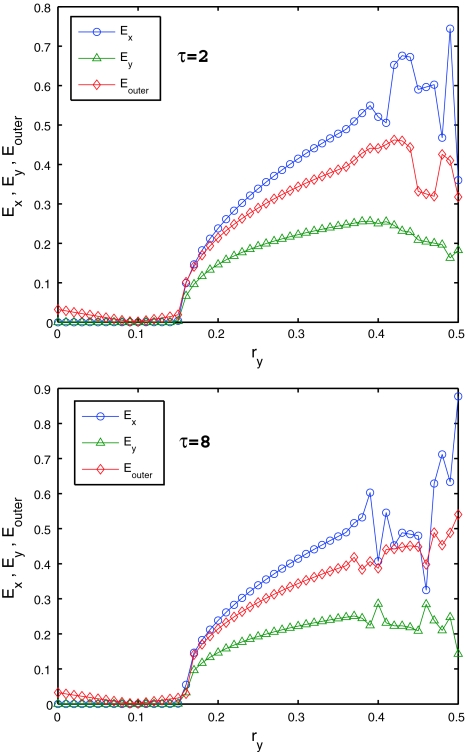
Therefore, it follows from Theorem 1 that the inner synchronization within each network is achieved for some values of coupling strength r_y. Figure 2 plots the curves of E_x, E_y concerning r_y with τ = 2 and τ = 8, respectively.

Fig. 2.

The panels exhibit E_x, E_y at t = 400 concerning r_y for N = 10, r_x = 0.1 with τ = 2 and τ = 8. The upper one shows that inner synchronization within network Y can be easily achieved than network X. While for the value of τ = 8, network Y becomes unsynchronized, which illuminates that the delays have more influence on network Y than network X

Fig. 3.

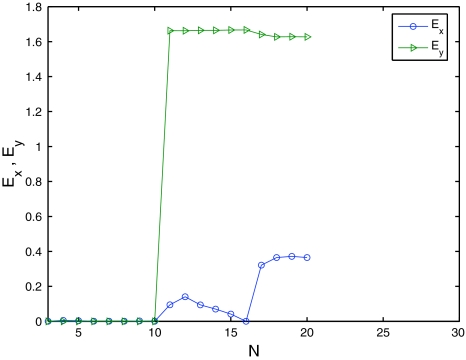
The curves of E_x, E_y at t = 400 regarding N with τ = 2, r_x = r_y = 0.1

Fig. 4.

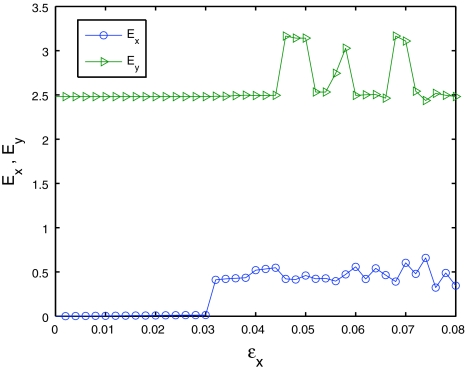
The trajectories of E_x, E_y at t = 400 for (17) with τ = 2, r_x = r_y = 0.1, ɛ_y = 0.05

Next we discuss the effect of network size N on inner synchronization, and take D_ij = C_ji = 1/N, the detailed numerical results are shown in Fig. 3. We find that inner synchronization within each network both appear when the size of network is less than 10. With the increasing value of τ ∈ [2, 12], network Y always remains synchronized, while network X becomes unsynchronized little and little. Now we add the individual connections in network X and network Y, i.e., consider the general model (2),

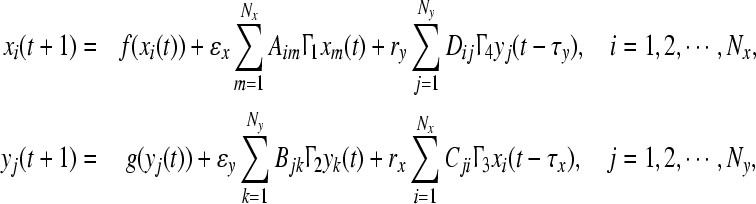17

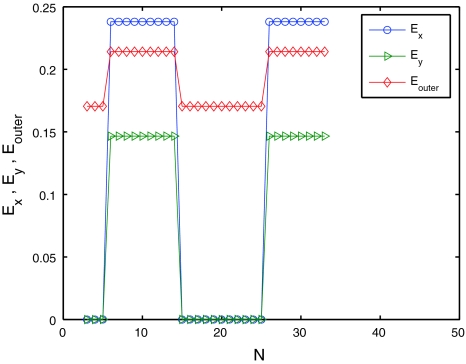
We now choose the same parameters as those in Fig. 3, and ɛ_y = 0.05, N = 10, the coupling matrices A,B are chosen as two random matrices. With this coupling configuration (17), we find that only network X achieve the inner synchronization for ɛ_x ≤ 0.03, while network Y is all through unsynchronized, the delay τ ∈ [2, 8]. Figure 4 depicts the evolution of E_x, E_y on ɛ_x.

Example 2. For this case n_x = n_y, we not only discuss inner synchronization inside network X or Y, but also study outer synchronization (Li et al. 2007) between network X and network Y. Therefore, we introduce the quantity E_outer = ∥x_i − y_i∥ for i = 1, ..., N to demonstrate whether outer synchronization happens. Consider the Logistic map as the dynamical nodes of the complex networks which is described by

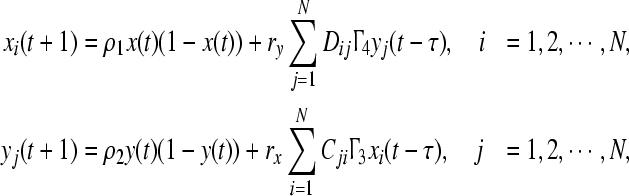18

The parameters 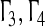and C_ji,D_ij are taken as same as in Example 1, and we choose ρ₁ = 2.6, ρ₂ = 2.3 for simulation, by solving the LMI (12) for P > 0, Q > 0, we obtain P = (4.2082), Q = (3.8691), which indicates that inner synchronization of network (18) is realized. The numerical details are summarized in Figs. 5, 6 and 7.

Fig. 5.

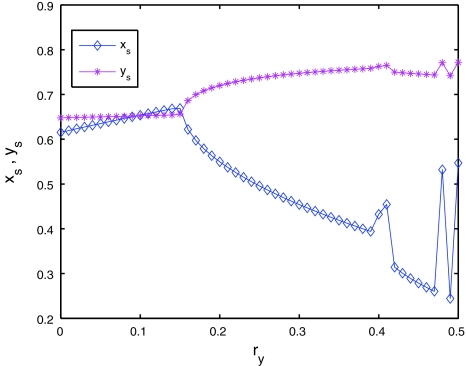
The evolution curves of synchronized state x_s, y_s at t = 400 with regard to r_y for r_x = 0.2, τ = 2

Fig. 6.

The plot shows E_x, E_y, E_outer at t = 400 on r_y for r_x = 0.2 with τ = 2 and τ = 8. Inner synchronization happens for r_y being in [0, 0.15], yet outer synchronization only appears when r_y approaches 0.1, and the delays influence the synchronization less

Fig. 7.

The curves of E_x, E_y, E_outer at t = 400 regarding N with τ = 2,r_x = r_y = 0.2. When the delay τ ≥ 10, inner synchronization also disappears

When ρ₁, ρ₂ > 3, the map evolves periodically and even behaves chaotically, but this condition does not satisfy the stability condition, so inner synchronization within each network doesn’t appear, and numerical simulation shows that outer synchronization between them also doesn’t happen. Next we consider the model (17), and also take the coupling matrices A,B as two random matrices, the numerics show that two kinds of synchronization don’t happen whatever the coupling strength is adjusted.

Conclusions and discussions

This paper discussed inner synchronization within each network and outer synchronization between two networks with time delays. We studied the stability of the synchronization manifold within each network by means of LMI method. Through the numerical examples, we found that the delays affect the inner synchronization more in Example 1 and less in Example 2. How to derive a theoretical domain of time-delay will be the scope of our future work, and we reported numerical evidence that the added connections within each network can’t enhance the network synchronizability. It is noted that outer synchronization in Example 2 is very difficultly achieved than inner synchronization, which shows that outer synchronization between two networks needs strong coupling form. Owing to the diversity of 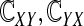, deriving the criteria on inner and outer synchronization simultaneously is an technical challenge, besides the control skills can be used to realize outer (inner) synchronization.

Our results of this study can be applied to analyze some biological systems, such as two coupled neuronal populations (Wang and Jiao 2006) with (without) time delays. The theoretical understanding is helpful to study the synchronization between two or more neural networks (He and Cao 2008; Liang et al. 2008) with appropriate couplings. We hope that such reports will appear elsewhere.