Abstract
Parameter setting plays an important role for improving the performance of a brain computer interface (BCI). Currently, parameters (e.g. channels and frequency band) are often manually selected. It is time-consuming and not easy to obtain an optimal combination of parameters for a BCI. In this paper, motor imagery-based BCIs are considered, in which channels and frequency band are key parameters. First, a semi-supervised support vector machine algorithm is proposed for automatically selecting a set of channels with given frequency band. Next, this algorithm is extended for joint channel-frequency selection. In this approach, both training data with labels and test data without labels are used for training a classifier. Hence it can be used in small training data case. Finally, our algorithms are applied to a BCI competition data set. Our data analysis results show that these algorithms are effective for selection of frequency band and channels when the training data set is small.
Keywords: Electroencephalogram (EEG), Motor imagery, Brain computer interface (BCI), Channel, Frequency band, Semi-supervised learning
Introduction
Brain computer interface (BCI) is a system that allows a brain to control a computer directly through a non-muscular communication channel, particularly for the paralyzed people who suffer severe neuromuscular disorders (Wolpaw et al. 2002; Dornhege 2007; Freeman 2007). BCIs can be invasive or non-invasive. Brain signals for non-invasive BCIs include electroencephalogram (EEG), magnetoencephalogram (MEG) and functional magnetic resonance imaging (fMRI), while brain signals for invasive BCIs include electrocorticogram (ECoG) and neuron spikes. A class of EEG-based BCIs which rely on the motor imagery of users are of particular interest to the BCI community since this type of BCIs have relative robust communication performance and can help to understand the underlying mechanism of motor imagery (Pfurtscheller et al. 2006).
Because of many facts such as low topographical resolution and high noise level, it has been a big challenge to extract effective features from EEG signals and perform classification. Until now, a lot of methods have been proposed for EEG signal analysis (see e.g. Muller et al. 2004; Blankertz et al. 2008) as well as its feature extraction and classification of EEG signals (Shenoy et al. 2006; Vidaurre et al. 2007). For a BCI system, there usually exist several parameters. For instance, channels and frequency band are two important parameters in motor-imagery based BCI systems. Parameter setting plays an important role for improving the performance of a BCI system.
This paper discusses channel and frequency band selection for motor-imagery based BCI systems. Generally, channels and frequency band are set separately. For instance, frequency band selection was discussed in Pregenzer and Pfurtscheller (1999), Garrett et al. (2003) and Blankertz et al. (2008), while channel selection was discussed in Schroder et al. (2003), Al-Ani and Al-Sukker (2006), Lal et al. (2004) and Wang et al. (2005). Blankertz et al. (2008) presented a heuristic procedure to automatically select the discriminant frequency band with a small number of channels. In Lal et al. (2004), channel selection was carried out by ranking all channels according to their relevance to experimental tasks and selecting a subset of channels. The state-of-the-art approaches for rating the relevance of channels include zero-norm optimization based-support vector machine (SVM), recursive feature elimination (RFE) and Fisher ratio (Lal et al. 2004). After ranking all channels, the number of selected channels was generally determined by the average classification accuracy obtained in cross-validation of training data set (Al-Ani and Al-Sukker 2006; Lal et al. 2004; Wang et al. 2005). In Schroder et al. (2003), genetic algorithm was used to directly select a subset of channels without channel ranking. However, heavy computational burden is a disadvantage of genetic algorithm.
In addition, the discriminant frequency band depends on individual subject and electrodes’ position (Pregenzer and Pfurtscheller 1999). Hence, a BCI system benefits from joint channel-frequency selection (Pregenzer and Pfurtscheller 1999; Garrett et al. 2003; Lemm et al. 2005; Dornhege et al. 2006; Wu et al. 2008). In Pregenzer and Pfurtscheller (1999), several channel-frequency pairs were selected by distinction sensitive learning vector quantization (DSLVQ) method. However, only two channels (’C3’ and ’C4’) were considered. Genetic algorithm was used to select several channel-frequency pairs, in which only six channels were considered (Garrett et al. 2003). In Lemm et al. (2005), Dornhege et al. (2006), Wu et al. (2008), common spatial pattern (CSP) was modified to exploit temporal structure in EEG for determining the subject-specific ’optimal’ temporal filters. In Wu et al. (2008), an iterative spatio-spectral patterns learning (ISSPL) method was proposed for improving the classification performance by optimizing the spatial and spectral filter, in which channels and frequency band were jointly selected through the weights of the spatial and spectral filter. However, these modified CSP methods need sufficient training dataset that plays an important role to obtain a reliable transformation matrix. Thus these algorithms are supervised ones. Considering that it is either time consuming or even intractable to collect sufficient training data (Wolpaw et al. 2000), it is worthy to discuss parameter setting for a BCI system when the training data set is insufficient.
Generally, if the number of trials in a training set is insufficient for training a reliable classifier through a supervised learning method, then we regard it as a small training set. In (Li and Guan 2008), an iterative semi-supervised SVM algorithm was proposed for joint feature extraction and classification for small training data set. In this paper, we extend this algorithm for joint channel-frequency band selection in the case when the training data set is small. In our proposed algorithms, both training data with labels and testing data without labels are used to jointly select the channels and frequency band. Fisher ratio is applied to rank channels, while Rayleigh coefficient distance is applied to determine the number of selected channels and frequency band. The computation of Fisher ratio and Rayleigh coefficient is based on both training data and test data.
To validate the proposed algorithm, we apply it to the data set IVa of BCI competition III in 2005 (Dornhege et al. 2004). Furthermore, we compare our algorithm with an existing method (Fisher ratio based cross-validation) for channel selection. Data analysis results show that our algorithm can effectively perform channel and frequency-band selection with small training data set and provide satisfactory classification accuracy.
The remaining part of this paper is organized as follows. In Section "A semi-supervised SVM algorithm for channel selection", an iterative semi-supervised SVM algorithm is proposed for channel selection with given frequency band. In Section "Frequency selection", the algorithm in Section "A semi-supervised SVM algorithm for channel selection" is first modified for frequency band selection, which is presented in Algorithm 2. In Section "Joint channel-frequency selection", an iterative algorithm is obtained through combining the previous two algorithms for joint channel-frequency selection. Data analysis results including the comparison with an existing method (Fisher ratio based cross-validation) are presented in Section "Data analysis". Finally, conclusions in Section "Conclusions" review the approach of this paper.
A semi-supervised SVM algorithm for channel selection
In this section, we first briefly describe Fisher ratio and Rayleigh coefficient, which are used for rating the relevance of each channel and determining the number of selected channels, respectively. Then we present the steps of a semi-supervised SVM algorithm for channel selection in the case of small training data set.
Fisher ratio
Fisher ratio is defined as the ratio of the interclass difference to the intraclass spread (Bishop 1995). Denote Pl,i(f) (l = 1, ..., N, i = 1, ..., d) as the discrete power spectral density function of a segment of EEG signal which is extracted from the lth channel and ith trial. N denotes the number of channels and d represents the number of trials. Then the power feature of each channel is calculated as,
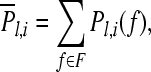 |
1 |
where F is the selected set of frequency band indices.
The Fisher ratio score of the lth channel is defined as
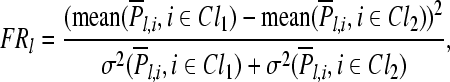 |
2 |
where Cl1 and Cl2 denote two classes of trials with labels being +1 and −1, respectively. Mean and σ represent mean and standard deviation, respectively.
The relevance of the lth channel is quantified by the Fisher ratio score FRl, and {FRl|l = 1, ..., N} are used for ranking all channels.
Rayleigh coefficient
After the channels are ranked through Fisher ratio, we then determine the number of selected channels. This is performed by Rayleigh coefficient.
Define n −1 subsets of channels Qj (j = 2, ..., n) which contain j channels with the highest Fisher ratio scores, where n ≤ N. Here j ≥ 2 means that we select at least two channels. We now define Rayleigh coefficient of Qj.
Using a band-pass filter with frequency band F, we first filter a segment of EEG signal from the lth channel and ith trial, where l ∈ Qj. The filtered EEG signal is denoted as a row vector xl,i. Furthermore, denote Xi = [xT1,i, ..., xTj,i]T, where (·)T represents the transposition operators.
We can define the discriminant activity Γd and common activity Γc between two conditions, respectively, as follows
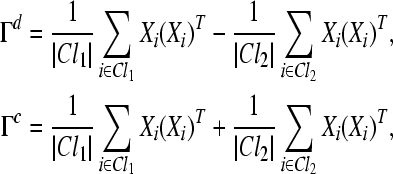 |
3 |
where |Cl1| and |Cl2| denote the sizes of the sets Cl1 and Cl2, respectively.
The definition of Rayleigh coefficient is
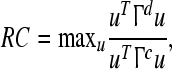 |
4 |
where u is designed to maximize the discriminative activity Γd simultaneously to minimize the common activity Γc (Blanchard and Blankertz 2004; Ramoser et al. 2000). u can be obtained by jointly diagonalizing the matrices Γd and Γc.
Suppose that U is a matrix which jointly diagonalizes the matrices Γd and Γc. Note that U can be obtained through a standard procedure for joint diagonalization of two matrices (Blankertz et al. 2008). The first column u1 and the last column uj are two generalized eigenvectors of Γd and Γc corresponding to the largest and the smallest generalized eigenvalue, respectively. Using u1 and uj, the Rayleigh coefficient of the subset of channels Qj is calculated as follows (Li and Guan 2008):
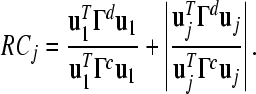 |
5 |
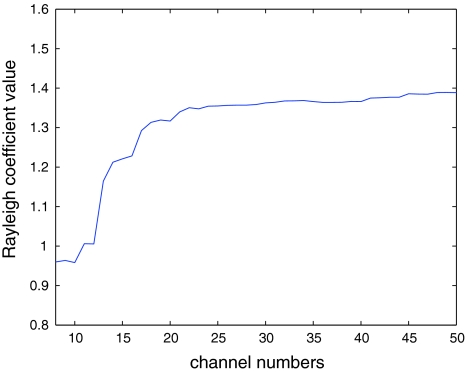
From our experience of data analysis, the Rayleigh coefficient value would increase when the number j of channels increases. For instance, Fig. 1 shows the curve of Rayleigh coefficient value with respect to the number j of selected channels.
Fig. 1.
An illustrative example: The curve of Rayleigh coefficients with respect to the number of channels
Hence, we cannot simply compare the Rayleigh coefficient values of the subsets of channels to determine the number j of selected channels (or the subset Qj of channels). We first calculate difference,
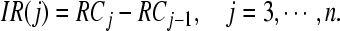 |
6 |
Then the number of channels j0 corresponding to the maximal difference in (7) is determined as follows
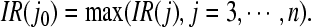 |
7 |
Hence, the subset of selected channels is Qj−0.
Channel selection for the case of small training data set
When the training data set is small, the subset of channels selected by Fisher ratio and Rayleigh coefficient are not reliable. This is because reliable Fisher ratio and Rayleigh coefficient rely on sufficient training data with labels. In this case, we propose to use semi-supervised SVM technique for channel selection in which both labeled training data and unlabeled test data are used.
Our approach relies on a standard SVM classifier, which is commonly used in BCIs (Thulasidas et al. 2006; Meinicke et al. 2003; Kaper et al. 2004). More details about SVM can be found in (Vapnik 1998; Burges 1998). A standard SVM classifier for two-class problem can be described as
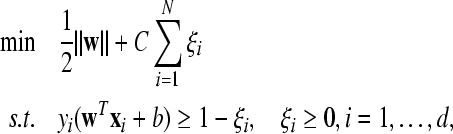 |
8 |
where 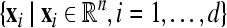 are feature vectors extracted from a training data set,
are feature vectors extracted from a training data set, 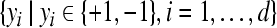 are the corresponding labels of
are the corresponding labels of 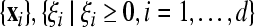 are slack variables, C > 0 is a regularization constant, w is a weight vector, b is a bias value.
are slack variables, C > 0 is a regularization constant, w is a weight vector, b is a bias value.
Given two raw EEG data sets, including a small training data set Dc containing Nc trials of EEG signals with labels yi ∈ { +1, −1}, (i = 1, ..., Nc) and a test data set Dt containing Nt trials of EEG signals without labels, in the following, we present the outline of an iterative semi-supervised SVM algorithm for channel selection and motor imagery classification.
| Algorithm 1 Summary of channel selection algorithm |
|---|
| Define: [1] Data vector construction function: FV(X(j), Qi) consisting the operations of constructing new data set by removing the EEG signals of those channels not in Qi. |
| [2] Iteration stopping criterion: the normalized difference between labels predicted in two successive iterations being less than a predefined threshold δ0. |
Input: the training set 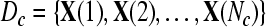 and their corresponding labels and their corresponding labels 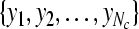 the test set the test set 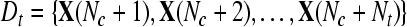 threshold δ0 for stopping the iterations threshold δ0 for stopping the iterations |
| iter = 0 |
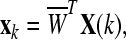 where where 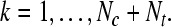 and and 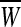 is a transformation matrix, which is composed by the first and last three columns of CSP spatial transformation matrix. is a transformation matrix, which is composed by the first and last three columns of CSP spatial transformation matrix. |
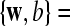 SVMtrain SVMtrain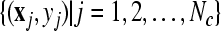 by solving Eq. 8 by solving Eq. 8 |
| Forj = Nc + 1 to Nc + Nt |
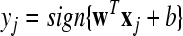
|
| end |
| Repeat |
| iter = iter + 1 |
| Forl = 1 to N |
with 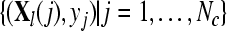 and and 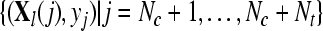 , obtain FR(l) by Eq. 2 , obtain FR(l) by Eq. 2 |
| End |
rank 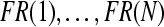 in a descending order, and the corresponding channel sequence is denoted as a vector Q in a descending order, and the corresponding channel sequence is denoted as a vector Q
|
| Fori = 2 to N |
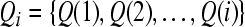 , which defines an i-channel subset , which defines an i-channel subset |
Obtain the Rayleigh coefficient 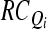 according to Eq. 5. according to Eq. 5. |
| end |
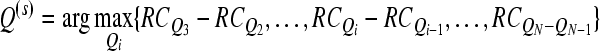
|
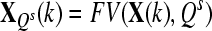 , for k = 1 to Nc + Nt , for k = 1 to Nc + Nt
|
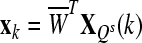 , where , where 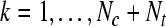 and and 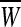 is a transformation matrix, which is composed by the first and last three columns of CSP spatial transformation matrix based on is a transformation matrix, which is composed by the first and last three columns of CSP spatial transformation matrix based on |
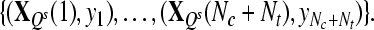
|
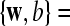 SVMtrain SVMtrain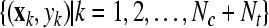 by solving Eq. 8, where yj, by solving Eq. 8, where yj, |
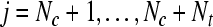 are the labels predicted in the previous iteration. are the labels predicted in the previous iteration. |
| Forj = Nc + 1 to Nc + Nt |
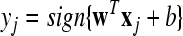
|
| end |
| Until stopping criterion satisfied |
Output: the subset of channels Q(s) and the corresponding labels 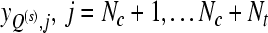
|
Remarks 1 (1) Another way for termination of the algorithm is to compare the set of channels Q(k−1) with Q(k). Suppose that the number of different channels between Q(k−1) and Q(k) is nch(k), and calculate the ratio:
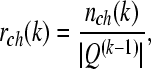 |
9 |
where |Q(k−1)| is the number of channels in Q(k−1). Obviously, rch(k) = 0 implies Q(k−1) and Q(k) are equal. From our data analysis, we found that this case often happens. If rch(k) is less than a given constant saying δ1, the algorithm is terminated. Otherwise, perform the (k +1)th iteration. (2) In Algorithm 1, the frequency band F0 is generally set by experience. In this paper, F0 is 8–14 Hz for mu rhythm extraction.
Frequency selection
As mentioned above, there are two key parameters related to the performance of motor imagery-based BCIs: frequency band and channel. In the previous section, an iterative semi-supervised SVM algorithm is presented to select channels. In the following, we present an algorithm for frequency selection with a given subset of channels which is similar to Algorithm 1.
| Algorithm 2 Summary of frequency band selection algorithm |
|---|
| Define: [1] Data vector construction function: FV(X(j), Qi) consisting the operations of constructing new data set by removing the EEG signals of those channels not in Qi. |
| [2] Iteration stopping criterion: the normalized difference between labels predicted in two successive iterations being less than a predefined threshold δ2. |
Input: the training set 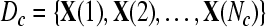 and their corresponding labels and their corresponding labels 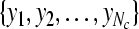 the test set the test set 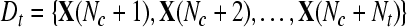 frequency sub-bands frequency sub-bands 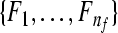 threshold δ1 for stopping the iterations threshold δ1 for stopping the iterations |
| iter = 0 |
| Fori = 1 to nf |
Xi(k) = BF(X(k)), Fi, where 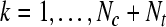 . . |
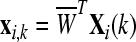 , where , where 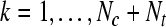 and and 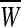 is a transformation matrix, which is composed by the first and last three columns of CSP spatial transformation matrix. is a transformation matrix, which is composed by the first and last three columns of CSP spatial transformation matrix. |
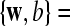 SVMtrain SVMtrain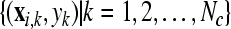 by solving Eq. 8 by solving Eq. 8 |
| Fork = Nc + 1 to Nc + Nt |
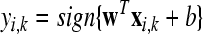
|
| end |
| end |
| Repeat |
| iter = iter + 1 |
| Fori = 1 to nf |
| Ifi = = 1 |
with 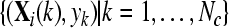 and and 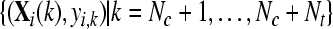 , , |
obtain 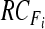 by Eq. 5 by Eq. 5 |
| Else |
with 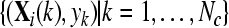 and and 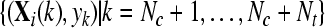 , , |
obtain 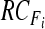 by Eq. 5 by Eq. 5 |
| End |
| End |
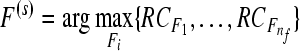
|
corresponding predicted labels 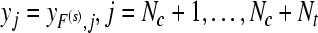
|
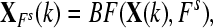 for k = 1 to Nc + Nt for k = 1 to Nc + Nt
|
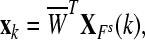 where where 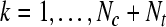 and and 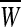 is a transformation matrix, which is composed by the first and last three columns of CSP spatial transformation matrix based on is a transformation matrix, which is composed by the first and last three columns of CSP spatial transformation matrix based on 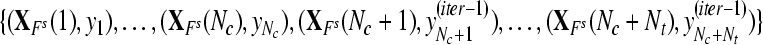
|
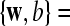 SVMtrain SVMtrain 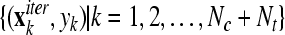 by solving Eq. 8, where yk, by solving Eq. 8, where yk, 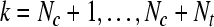 are the labels predicted in the previous iteration. are the labels predicted in the previous iteration. |
| Fork = Nc + 1~to~Nc + Nt |
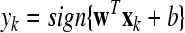
|
| end |
| Until stopping criterion satisfied |
Output: the frequency sub-band F(s) and the corresponding labels 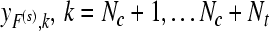
|
Remark 2 The time interval is also an important parameter for motor imagery BCI system. Similar to frequency band selection, Algorithm 2 can be extended for determining the time interval in the current motor imagery BCI system. If the training data set is insufficient, semi-supervised learning can be used.
Joint channel-frequency selection
Until now, channels and frequency band selection have been presented separately. In this section, we combine Algorithms 1 and 2 to perform joint channel-frequency selection in an alternative manner. Initially given a frequency band F0, we apply Algorithm 1 to determine a subset of channels. This subset is denoted as Q(1)s here. Based on Rayleigh coefficient, we use Algorithm 2 to select a frequency sub-band denoted as F(1)s. Repeating this process for several times, the final subset of channels and frequency band are obtained. The following is the outline of our algorithm.
| Algorithm 3 Summary of joint channel-frequency selection algorithm |
|---|
| Define: [1] Iteration stopping criterion: the normalized difference between labels predicted in two successive iterations being less than a predefined threshold δ3. |
| [2] Algorithm1{F0} represents performing Algorithm 1 with a frequency band F0; similarly, Algorithm2{Q0} means performing Algorithm 2 with a given subset of channels Q0. |
| Input: a frequency band F0 |
| iter = 1 |
| Repeat |
| Qs = Algorithm1{F0}, |
Fs = Algorithm2{Qs}, corresponding predicted labels 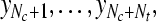
|
| iter = iter + 1 |
| Until stopping criterion satisfied |
Output: the frequency band Fs, the subset of channels Qs and the corresponding labels 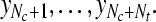
|
Remarks 3 (1) In Algorithm 3, channel selection and frequency band selection are alternatively carried out. We also can define a Fisher ratio for a subset of channels and a frequency band, which is used as an objective function. We then perform joint channel-frequency selection using genetic method to maximize the objective function. However, the computational burden will increase significantly. For reducing the computational complexity, we apply the iterative strategy to alternatively select the channels and frequency band. (2) To avoid selecting the termination parameters δ0 and δ2 in Algorithms 1 and 2, respectively, we fix the number of iterations of these two algorithms to be 5 in this paper. Data analysis results show the effectiveness of this setting (see Example 2 in Section "Data analysis"). (3) Furthermore, we can extend Algorithm 3 for joint channel-frequency-time interval selection by selecting these three parameters alternatively.
Note that if the subset of selected channels do not change between the kth and (k −1)th iteration, the selected frequency band will not change. According to our data analysis, Algorithm 3 often converges in several iterations (e.g. 6 iterations) even if we set δ3 = 0.
Data analysis
In this section, we apply Algorithm 1 and 3 to data set IVa provided by the BCI competition III (Dornhege et al. 2004) to demonstrate the effectiveness of our algorithms. Two examples are presented, in which the first example illustrates channel selection by Algorithm 1 and the second example illustrates joint selection of channels and frequency band by Algorithm 3 for small training data case. All SVM classifications in the iterations of Algorithm 1 and Algorithm 3 are performed by the LibSVM toolbox (Chang and Lin 2001).
Data description: The aim of data set IVa in BCI competition III was to discriminate different motor imagery tasks with small training data set. This data set contains EEG signals from five subjects (aa, al, av, aw, ay). During every trial of the experiment, the subjects were prompted by visual cues to imagine for 3.5 s one of the following three motor imageries: (L) left hand, (R) right hand and (F) foot. 280 trials of EEG data (118 channels, down-sampled to 100 Hz) of two tasks i.e. imageries of right hand and foot were provided for competition. The details of this data set can be referred to the website: http://www.ida.first.fraunhofer.de/projects/bci/competition-ii.
Data partition: In the following two examples, the data set for each subject is partitioned into two subsets: the first one containing the first 200 trials is used for eightfold cross-validation and the other one containing the last 80 trials is used as an independent test set which is not involved in the training process. In each fold of cross-validation, 25 trials of EEG signals are used as the training data set, while the other 175 trials of EEG signals are used as the test data set.
Example 1 In this example, we apply Algorithm 1 to the above data set to demonstrate its effectiveness in channel selection for small training data set. We also compare Algorithm 1 with an existing method (Fisher ratio based cross-validation) mentioned in Lal et al. (2004).
Data preprocessing steps include spatial filtering (Common Average Reference, CAR), band-pass filtering in the range of 8–14 Hz corresponding to mu rhythm. During motor imagery tasks, event-related desynchronization (ERD) occurs in mu and beta frequency band which can be used as the discriminative frequency bands (Wolpaw et al. 2002). Since ERD generally happens in sensorimotor cortex, we only use 60 EEG channels located in the central area of scalp.
Now we apply Algorithm 1 for eightfold cross-validation. In each fold of cross-validation, a subject-specific subset of channels is selected. At the same time, we obtain the predicted labels for the test dataset. Table 1 shows the average number of selected channels for all subjects (averaged across eightfolds).
Table 1.
The average numbers of selected channels for all subjects over the eightfold cross-validation
| Subject | aa | al | av | aw | ay |
|---|---|---|---|---|---|
| Number of channels | 17 | 16 | 21 | 25 | 15 |
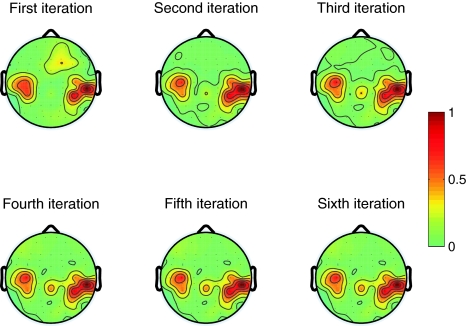
In each iteration of Algorithm 1, we perform channel selection based on Fisher ratios and Rayleigh coefficients. We also perform prediction of labels for the test data set and the independent test set. Figure 2 displays the topographies of Fisher ratios for all channels obtained in the first six iterations of the first fold of cross-validation for Subject al. We can find out from this figure that, in the last three iterations, large Fisher ratio appear more concentrative in sensorimotor cortex than that in the previous iterations. Furthermore, the topographies of Fisher ratios do not vary in the last three iterations. This implies that the selected subset of channels in the last three iterations keeps unchanged and the convergence of Algorithm 1 is demonstrated. For the other folds of cross-validation of this subject and for the other subjects, similar phenomena can be observed.
Fig. 2.
Topographies of Fisher ratios for all channels obtained in the first fold of cross-validation for subject al
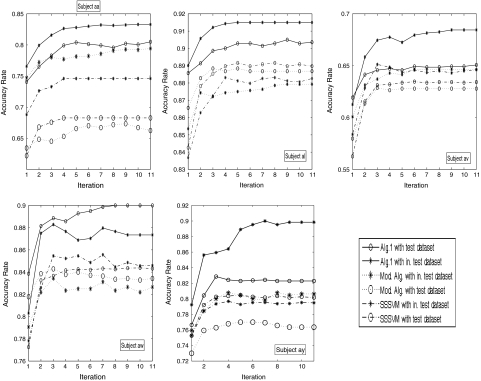
In each fold of cross-validation of one subject, we obtain two iterative curves of prediction accuracies for the test data set and the independent test set, respectively. We average these prediction accuracies across eightfolds. Five subplots of Fig. 3 show the iteration curves of the averaged classification accuracies obtained by Algorithm 1 (solid lines) for the five subjects, respectively. In each subplot, the curve depicted by solid line with “*” corresponds to the independent test set, while the curve depicted by solid line with “o” corresponds to the test data sets which are involved in semi-supervised learning. From these subplots, we can see: (1) satisfactory prediction accuracies can be obtained by Algorithm 1; (2) most of these curves of prediction accuracies obtained by Algorithm 1 (solid lines) show an increasing tendency; (3) Algorithm 1 converges generally in about 10 iterations. Thus the effectiveness of Algorithm 1 is demonstrated here.
Fig. 3.
Curves of averaged prediction accuracies for five subjects. The solid lines are the results of Algorithm 1, while the dashed lines are for the modified algorithm in which the channel selection is performed by a leave-one-out cross-validation method. And the dot-dashed lines are the results of standard semi-supervised SVM (SSSVM) algorithm without channel selection. The curves with “o” correspond to test data sets used in eightfold cross-validation, while the curves with “*” correspond to independent test sets
For comparison, firstly, we now modify Algorithm 1 as follows. (1) Channel selection: Fisher ratio is used to rank the channels. The number of selected channels is determined by a leave one (trial) out cross-validation approach on the small training data set, where the classifier is a standard SVM. (2) Once the subset of channels is determined, an iterative semi-supervised SVM algorithm is used for joint feature extraction and classification. This algorithm is obtained by removing all steps related to channel selection in Algorithm 1. Thus it can be seen as a simplified version of Algorithm 1. Now we apply this approach to the data set and perform similar data analysis as above. In each fold of the eightfold cross-validation of one subject, we also obtain two average iteration curves of prediction accuracies for the test data set and the independent test set, respectively. Five subplots of Fig. 3 show the iterative curves of the averaged classification accuracies (dashed lines) for five subjects, respectively. In each subplot, the curve depicted by dashed line with “*” corresponds to the independent test set, while the curve depicted by dashed line with “o” corresponds to test data sets which are involved in semi-supervised learning. Secondly, we further apply a standard semi-supervised SVM (SSSVM) algorithm without channel selection to the data set and perform similar data analysis as above, where the initial frequency band and initial channels in Algorithm 1 are used. The obtained classification results are shown in Fig. 3.
From the above data analysis, we have the following comparison results: (1) In fact, the results of the first iteration of Algorithm 1 in Fig. 3 can be seen as ones obtained by a supervised SVM (without using the test dataset). The increasing tendency of the curves in Fig. 3 show that the performance of our algorithm is better than that of the standard SVM. (2) Through Fig. 3, we can see that the performance of Algorithm 1 for channel selection is better than that of the modified algorithm and the standard semi-supervised SVM algorithm. The main reason is that channel selection of the modified algorithm is based on the small training data set, while the channel selection of Algorithm 1 is performed by a semi-supervised approach in which both the small training data set and the test data set are involved.
Example 2 In this example, we evaluate Algorithm 3 for joint channel-frequency selection using the same data set as above. In the first iteration of Algorithm 3, we set the initial frequency band F0 to be 8–14 Hz as in Example 1. Using the frequency band 8–21 Hz, we generate the sub-bands as follows: Fsub = [f, f + Δf], where f ∈ {8, 9, ..., 16}, Δf ∈ {2, 3, 4, 5}. Thus totally 36 sub-bands denoted as F1, ..., F36 are obtained for frequency band selection.
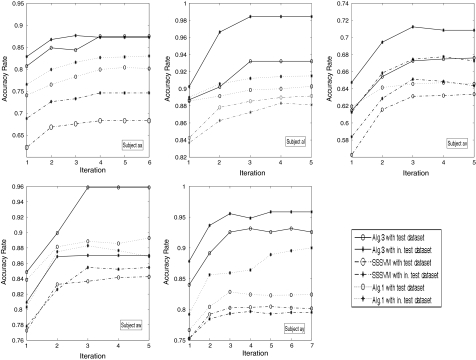
Using the first 200 trials of EEG data of each subject, Algorithm 3 is applied to perform eightfold cross-validation. At the same time, the last 80 trials of EEG data are used as an independent test set. In each fold of cross-validation, we obtain two iterative curves of prediction accuracy for the test set and the independent test set, respectively. For each subject, we average the prediction accuracies for these test sets across eightfolds and obtain an average iteration curve of prediction accuracy. Similarly, we obtain an average iteration curve of prediction accuracy for independent test sets. The two average iteration curves of prediction accuracy are shown in each subplot of Fig. 4, in which five subplots correspond to five subjects, respectively.
Fig. 4.
Iteration curves of average prediction accuracy rates (%) obtained by Algorithm 3 with solid lines, while the dashed lines are the results of Algorithm 1 and the dot-dashed lines are the results of SSSVM. The five subplots correspond to the five subjects, respectively. In each subplot, the curve with “o” is for test data sets, while the curve with “*” is for the independent test set
According to Fig. 4, satisfactory accuracy rates have been achieved for all subjects. Meanwhile in most of the cases, we see an increasing tendency in the curves of prediction accuracy as the numbers of iterations increase. Furthermore, these curves show that Algorithm 3 converges fast (generally in about 6 iterations).
After Algorithm 3 converges, the selected subset of channels and frequency band does not vary in the following iterations. The effectiveness of Algorithm 3 for joint channel-frequency selection is demonstrated in this example.
From our data analysis, we found that the selected subset of channels and a frequency band depend on the training dataset and subject. However, most of selected channels and frequency bands are consistent for different folds. For example, 75% of selected channels on average are consistent for two different folds and the frequency band 12–13 Hz is always included in the selected frequency bands in all eightfolds for subject al.
For comparison, firstly, we plot the average iteration curves of prediction accuracy of Algorithm 1 with dashed lines and standard semi-supervised SVM algorithm with dot-dashed lines in Fig. 4. The accuracy of the first iteration of these curves is obtained with standard supervised algorithm without using test dataset. Through Fig. 4, we can see that most of the curves show an increasing tendency. Thus the performance of our algorithm is better than that of the standard supervised SVM. Moreover, we can see that the performance of Algorithm 3 is better than that Algorithm 1 and standard semi-supervised SVM algorithm without channel selection. The main reason is that both channel selection and frequency band selection are performed in Algorithm 3, and a semi-supervised approach based on both training data and test data is used to select these two parameters.
Secondly, we also use a genetic algorithm to jointly select channels and frequency band under the same data partition as above. We perform channel and frequency band searching over all the combinations of the sixty channels and 36 frequency bands as described above. Hence, there are totally 2,160 (60 × 36) choices. The average accuracy of fivefold cross-validation was used as the individual’s fitness measure for optimization. More details about this algorithm can be found in Garrett et al. (2003). Using the data of Subject al as an example, we performed channel and frequency band selection. Then the labels were predicted for the test dataset and the independent test dataset through a semi-supervised learning procedure. The final accuracy rates are 60.2 and 65.3% for the test data set and the independent test data set, respectively, which are much lower than the results of our proposed Algorithm 3 (93.2 and 98.4%) presented in the second subplot in Fig. 4. Such results unleash that parameter selection based on small training dataset is unreliable even if genetic algorithm is adopted. Strategically involving unlabeled test dataset may improve the effectiveness of parameter setting, which ultimately results in significantly better accuracy. On the other hand, regarding computational efficiency, our semi-supervised approach for parameter setting is also much superior to the genetic algorithm.
Note that data set IVa in BCI competition III includes five data sets corresponding to five subjects. Each data set including a training data set and a test data set contains 280 trials totally. The numbers of trials in training data sets are 168, 224, 84, 56 and 28 for subjects aa, al, av, aw and ay, respectively. In this paper, we use the same data partition for all subjects. The number of trials of the training data is always set to 25 for all subjects, which is much smaller than that in BCI competition III except subject ay. Furthermore, an independent data set containing 80 trials of EEG data is used here for each subject. This independent data set is not involved in semi-supervised learning. Therefore, our data partition is much different from that in BCI competition III and the accuracy rates obtained in this paper are not comparable to those obtained by the winners of this data set (Wang et al.). Additionally, Y. Li (one of authors of this paper) and his colleagues attended BCI competition III. They analyzed this data set using an extended EM algorithm and obtained the second. At that time, they selected channels and frequency band manually (Li and Guan 2006).
Conclusions
In this paper, we first presented a semi-supervised SVM algorithm for channel selection. This algorithm is designed for motor-imagery based BCI. Next, a modified version of this algorithm is obtained for frequency band selection. Combining these two algorithms, an iterative algorithm is obtained for joint selection of channels and frequency band. Based on semi-supervised learning strategy, these algorithms are tailored for the case of small training data set. The effectiveness of our algorithms were demonstrated through analyzing the data set IVa in BCI competition III.
Acknowledgments
The authors would like to thank the Berlin BCI group for providing the data set IVa in BCI competition III.
Footnotes
This work was supported by National Natural Science Foundation of China under Grants 60825306 and 60802068; Natural Science Foundation of Guangdong Province, China under grant 9251064101000012 and supported by the Fundamental Research Funds for the Central Universities, SCUT under grant 2009ZZ0055.
Contributor Information
Jinyi Long, Email: long.jinyi@mail.scut.edu.cn.
Yuanqing Li, Email: auyqli@scut.edu.cn.
Zhuliang Yu, Email: zlyu@scut.edu.cn.
References
- Al-Ani A, Al-Sukker A (2006) Effect of feature and channel selection on EEG classification. In: Proceedings of international conference on IEEE EMBS, pp 2171–2174 [DOI] [PubMed]
- Bishop C. Neural networks for pattern recognition. Plus. USA: Oxford University Press; 1995. [Google Scholar]
- Blanchard G, Blankertz B. BCI competition 2003-data set IIa: spatial patterns of self-controlled brain rhythm modulations. IEEE Trans Biomed Eng. 2004;51(6):1062–1066. doi: 10.1109/TBME.2004.826691. [DOI] [PubMed] [Google Scholar]
- Blankertz B, Tomioka R, Lemm S, Kawanabe M, Muller K. Optimizing spatial filters for robust EEG single-trial analysis. IEEE Signal Process Magazine. 2008;25(1):41. doi: 10.1109/MSP.2008.4408441. [DOI] [Google Scholar]
- Burges C. A tutorial on support vector machines for pattern recognition. Data Mining Knowledge Discovery. 1998;2(2):121–167. doi: 10.1023/A:1009715923555. [DOI] [Google Scholar]
- Chang C, Lin C (2001) LIBSVM: a library for support vector machines [online]. Software available at http://www.csie.ntu.edu.tw/cjlin/libsvm
- Dornhege G (2007) Toward brain-computer interfacing. MIT Press
- Dornhege G, Blankertz B, Curio G, Muller K. Boosting bit rates in noninvasive EEG single-trial classifications by feature combination and multiclass paradigms. IEEE Trans Biomed Eng. 2004;51(6):993–1002. doi: 10.1109/TBME.2004.827088. [DOI] [PubMed] [Google Scholar]
- Dornhege G, Blankertz B, Krauledat M, Losch F, Curio G, Muller K. Combined optimization of spatial and temporal filters for improving brain-computer interfacing. IEEE Trans Biomed Eng. 2006;53(11):2274–2281. doi: 10.1109/TBME.2006.883649. [DOI] [PubMed] [Google Scholar]
- Freeman W. Definitions of state variables and state space for brain-computer interface. Cogn Neurodyn. 2007;1(1):3–14. doi: 10.1007/s11571-006-9001-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrett D, Peterson D, Anderson C, Thaut M. Comparison of linear, nonlinear, and feature selection methods for EEG signal classification. IEEE Trans Neural Syst Rehabil Eng. 2003;11(2):141–144. doi: 10.1109/TNSRE.2003.814441. [DOI] [PubMed] [Google Scholar]
- Kaper M, Meinicke P, Grossekathoefer U, Lingner T, Ritter H. BCI competition 2003-data set IIb: support vector machines for the P300 speller paradigm. IEEE Trans Biomed Eng. 2004;51(6):1073–1076. doi: 10.1109/TBME.2004.826698. [DOI] [PubMed] [Google Scholar]
- Lal T, Schroder M, Hinterberger T, Weston J, Bogdan M, Birbaumer N, Scholkopf B. Support vector channel selection in BCI. IEEE Trans Biomed Eng. 2004;51(6):1003–1010. doi: 10.1109/TBME.2004.827827. [DOI] [PubMed] [Google Scholar]
- Lemm S, Blankertz B, Curio G, Muller K. Spatio-spectral filters for improving the classification of single trial EEG. IEEE Trans Biomed Eng. 2005;52(9):1541–1548. doi: 10.1109/TBME.2005.851521. [DOI] [PubMed] [Google Scholar]
- Li Y, Guan C. An extended EM algorithm for joint feature extraction and classification in brain-computer interfaces. Neural Comput. 2006;18(11):2730–2761. doi: 10.1162/neco.2006.18.11.2730. [DOI] [PubMed] [Google Scholar]
- Li Y, Guan C. Joint feature re-extraction and classification using an iterative semi-supervised support vector machine algorithm. Mach Learn. 2008;71(1):33–53. doi: 10.1007/s10994-007-5039-1. [DOI] [Google Scholar]
- Meinicke P, Kaper M, Hoppe F, Heumann M, Ritter H (2003) Improving transfer rates in brain computer interfacing: a case study. In: Proceedings of advanced neural information processing system, pp 1131–1138
- Muller K, Krauledat M, Dornhege G, Curio G, Blankertz B. Machine learning techniques for brain-computer interfaces. Biomed Tech. 2004;49(1):11–22. doi: 10.1515/BMT.2004.058. [DOI] [Google Scholar]
- Pfurtscheller G, Brunner C, Schlögl A, Lopesda Silva F. Mu rhythm (de) synchronization and EEG single-trial classification of different motor imagery tasks. Neuroimage. 2006;31(1):153–159. doi: 10.1016/j.neuroimage.2005.12.003. [DOI] [PubMed] [Google Scholar]
- Pregenzer M, Pfurtscheller G. Frequency component selection for an EEG-based brain to computerinterface. IEEE Trans Neural Syst Rehabil Eng. 1999;7(4):413–419. doi: 10.1109/86.808944. [DOI] [PubMed] [Google Scholar]
- Ramoser H, Muller-Gerking J, Pfurtscheller G. Optimal spatial filtering of single trial EEG during imagined handmovement. IEEE Trans Rehabil Eng. 2000;8(4):441–446. doi: 10.1109/86.895946. [DOI] [PubMed] [Google Scholar]
- Schroder M, Bogdan M, Hinterberger T, Birbaumer N (2003) Automated EEG feature selection for brain computer interfaces. In: Proceedings of 1st International IEEE EMBS Conference on Neural Engineering, pp 626–629
- Shenoy P, Krauledat M, Blankertz B, Rao R, Müller K. Towards adaptive classification for BCI. J Neural Eng. 2006;3(R13–R23):1–1. doi: 10.1088/1741-2560/3/1/R02. [DOI] [PubMed] [Google Scholar]
- Thulasidas M, Guan C, Wu J. Robust classification of EEG signal for brain-computer interface. IEEE Trans Neural Syst Rehabil Eng. 2006;14(1):24–29. doi: 10.1109/TNSRE.2005.862695. [DOI] [PubMed] [Google Scholar]
- Vapnik V (1998) Statistical learning theory. New York, Wiley
- Vidaurre C, Schlogl A, Cabeza R, Scherer R, Pfurtscheller G. Study of on-line adaptive discriminant analysis for EEG-based brain computer interfaces. IEEE Trans Biomed Eng. 2007;54(3):550–556. doi: 10.1109/TBME.2006.888836. [DOI] [PubMed] [Google Scholar]
- Wang Y, Gao S, Gao X (2005) Common spatial pattern method for channel selelction in motor imagery based brain-computer interface. In: Proceedings of international conference on IEEE EMBS, pp 5392–5395 [DOI] [PubMed]
- Wang Y, Gao X, Zhang Z, Hong B, Gao S. BCI competition IIIdata set IVa: classifying single-trial EEG during motor imagery with a small training set. IEEE Trans Neural Syst Rehab Eng, to be published
- Wolpaw J, McFarland D, Vaughan T. Brain-computer interface research at the Wadsworth Center. IEEE Trans Rehabil Eng. 2000;8(2):222–226. doi: 10.1109/86.847823. [DOI] [PubMed] [Google Scholar]
- Wolpaw J, Birbaumer N, McFarland D, Pfurtscheller G, Vaughan T. Brain–computer interfaces for communication and control. Clin Neurophysiol. 2002;113(6):767–791. doi: 10.1016/S1388-2457(02)00057-3. [DOI] [PubMed] [Google Scholar]
- Wu W, Gao X, Hong B, Gao S. Classifying single-trial EEG during motor imagery by iterative spatio-spectral patterns learning (ISSPL) IEEE Trans Biomed Eng. 2008;55(6):1733–1743. doi: 10.1109/TBME.2008.919125. [DOI] [PubMed] [Google Scholar]