Abstract
Clinical trials often include binary endpoints. In some cases, no successes are observed and the usual large-sample estimates of relative risk are undefined. This paper proposes an estimator for relative risk based on the median unbiased estimator. The proposed relative risk estimator is well defined and performs satisfactorily for a wide range of data configurations. To facilitate the use of the estimator, a deterministic bootstrap confidence interval is also proposed, and a SAS MACRO is available to perform the necessary calculations. An ongoing randomized clinical trial motivated the development of the estimator and is used to illustrate the approach.
1 Introduction
Modern clinical trials often include at least one categorical outcome variable. These categorical outcomes are used to describe an intervention’s efficacy or safety profile. For example, binary outcomes could be used to describe the occurrence of a serious adverse event, a treatment ‘response’ (e.g., tumor remission), or an observation of a desired result (e.g., a urine drug screen negative for illicit substances). The analysis of the data generated by such studies usually presents no difficulties, but there are situations in which the large sample estimators generally break down.
Typically, the sample size of a pilot study or early phase clinical trial is small. Nonetheless, decisions to further examine a treatment are based on these small, initial investigations. Similarly, interim monitoring of safety in clinical trials, of any size, may yield few observed events even in instances when the adverse events of interests are not rare (Carter & Woolson 2007). In these cases, large-sample estimators of proportions and relative measures of association may perform poorly. This poor performance is magnified when the sample size is small and/or when the success probabilities are at or near 0 or 1 (Agresti 2003).
In this paper, we derive a point estimate for the relative risk based on the median unbiased estimator. In addition, a confidence interval based on the precisely enumerated discrete distribution of the estimate (i.e., a ‘deterministic’ bootstrap) is proposed. This approach is designed particularly for use when the number of subjects in each group is small, or the proportions are at or close to the boundary values of 0 and 1. The proposed estimator is compared to the standard large-sample (‘Wald’) estimator and to the class of estimators that rely on the addition of a small constant to the cells of the contingency table. The method is illustrated by an interim safety analysis of an ongoing clinical trial.
1.1 Motivating Example
For patients with type 1 diabetes mellitus, intensive glycemic therapy, which may more closely resemble the body’s own glycemic control achieved through a functioning endocrine system, has been commonly regarded as the optimal therapy, but recently, the safety and efficacy of intensive therapy in patients with type 2 diabetes has been called into question (Weir 2007). Regardless of the type of diabetes, complications due to severe hypoglycemic events (blood glucose levels less than 40 mg/dL), are of critical concern(Finfer et al. 2009). For clinical trials evaluating intensive diabetes therapy relative to conventional diabetes therapy, one must carefully evaluate whether there is an increased risk of severe hypoglycemia in the intensively-treated participants to ensure adequate protections of human subjects. However, close monitoring during inpatient hospital stays with corrective actions taken if low blood glucose are observed may help minimize the risk for severe hypoglycemia (Hermayer et al. 2007). Statistically speaking, these clinical procedures may create situations in which the risk for severe hypoglycemia is small and few, if any, occurrences of severe hypoglycemia are observed over the course of the clinical trial. As will be shown later when the motivating example is revisited, ordinary calculations involving the ratio of the risks become poorly defined when few, if any, events are observed.
2 Methods
2.1 Median Unbiased Estimators
Consider a binomial random variable, Y ~ Bin(n, p), where n and p are the usual binomial parameters. The maximum likelihood estimate (MLE) for p is , where y is the observed number of successes in n independent Bernoulli trials. This estimate and its asymptotic confidence interval have poor statistical performance when n is small or when y is, or in some cases approaches, 0 or n (Newcombe 1998, Agresti 2002). While asymptotically the MLE is an efficient estimator for p, there has been significant research on the finite sample properties, see Brown et al. (2001) for an excellent review. A general estimation approach not covered by Brown et al is the use of the median unbiased estimator (MUE) (Read 1985, Hirji et al. 1989). The MUE, , is an estimator that satisfies the following property:
In the context of the binomial distribution with probability mass
the MUE is defined as the value that satisfies
For discrete data, there is no unique (Hirji et al. 1989), so we obtain lower and upper values, and , by solving
| (1) |
and
| (2) |
for and . The midpoint is usually chosen as the MUE (Hirji et al. 1989). Thus, let denote the MUE of p.
Iterative procedures can be used to solve equations 1 and 2, but in practice, iterative solutions are not needed since one may rely on the relationship between the cumulative beta distribution and the binomial distribution. In particular,
| (3) |
and
| (4) |
where F−1(Q|α, β) is the Qth quantile of the cumulative beta distribution, a value that is readily available in most common statistical packages.
2.2 Special case of zero or all successes
Special considerations are needed when y is either 0 or n. If y = 0,
Thus, any value of in the interval [0, 1] satisfies the definition of MUE, so is taken as 0, the lowest possible value (Parzen et al. 2002). Additionally when must satisfy
This expression is easily solved in terms of . Therefore, when no successes are observed, the MUE is
The MUE is also well defined in instances when all of the Bernoulli trials are successes. If y = n, it can be shown that and . Thus,
when y = n.
It should be noted that the assignment of when y = 0 and when y = n is arbitrary. These values, which represent the extreme cases, are useful to yield a conservative estimate of , but other choices for and could be considered. Their use in the present context is consistent with previous use for the odds ratio (Parzen et al. 2002) and the risk difference (Lin et al. 2009).
2.3 Estimator for the relative risk
Theorem: The ratio of two median unbiased estimators for independent proportions is always defined
The proof of this theorem is straight forward. Consider two independent binomial random variables, Yg ~ Bin(ng, pg), where ng and pg are the usual binomial parameters for group g, g = 1, 2. From inspection of equations 3 and 4, it is inferred that when yg is not 0 or 1, . Likewise, when provided ng > 0. Similarly, when provided ng > 0. Thus, the ratio of two median unbiased estimates is always defined. That is, the estimator for relative risk (RR) based on the ratio of two MUEs is always defined. Therefore, let be defined as
It is worth noting that while are MUE, is not necessarily an MUE.
2.4 Deterministic bootstrap confidence interval
A confidence interval for can be obtained by using the exact enumeration of the full bootstrap distribution for (Y1, Y2). This ‘deterministic’ bootstrap differs from the usual non-parametric boot-strap in that no Monte Carlo simulations are needed. To establish the bootstrap sample space, a parametric bootstrap sample can be obtained by drawing random binomial samples of size ng from the binomial distribution defined by , which is represented as follows:
This parametric bootstrap sample, denoted as , is defined as one random binomial sample of size ng from this distribution. When the two groups are considered together, the sample space consists of (n1 + 1)(n2 + 1) elements denoted as . Since the two groups are usually independent, the probability mass for each element in the sample space is
For each element in the sample space, an estimate of RR is obtained. It is important to note that not all of the estimates, denoted as , are unique. This stems from the fact that under certain conditions such as when with n1 = n2, i.e., k = 1. Thus, the individual joint probabilities, P*, need to be summed over identical estimates of to yield the , the probability mass, and , the cumulative bootstrap probability distribution. To obtain the lower end point of a two-sided 100(1 – α)% confidence interval, one identifies the value such that . Likewise, to obtain the upper limit, the value is chosen such that .
Since the bootstrap distribution is discrete, there are special considerations that need to be addressed. First, if the cumulative distribution is such that or , then the value for the end point of the confidence interval is poorly defined. To account for this, the lower and/or upper confidence limits are set at either 0 and/or ∞, respectively. Furthermore, it is unlikely that and will be observed directly, so linear interpolation may be used to estimate the lower and upper confidence limits. For example,
where and πl are the closest quantile cutting off a tail area less than α/2; and and πu are the closest quantile cutting off a tail area above α/2.
3 Evaluation study
The small to moderate sample properties of the proposed estimator for the relative risk were examined through an evaluation study. In essence, for sample sizes of n1 and n2, the sample space consisted of (n1 + 1)(n2 + 1) elements. For each element, estimates of RR and confidence intervals were obtained using the methods described below. To allow for a variety of scenarios to estimate the performance of the proposed statistical method in terms of coverage probability, power, type I error rate, and mean squared error, the underlying binomial parameters (p1 and p2) were allowed to range from 0.02 to 0.98 in two percentage point increments thereby yielding 2401 different combinations of binomial parameters and a wide range of relative risks. Sample sizes of 10, 25, 50 and 100 for each group were also considered. However, for brevity of publication, a subset of all possible results have been presented. The online appendix to this article contains the full results of the statistical performance study.
3.1 Alternative estimation methods
For comparative purposes, the proposed relative risk estimator was compared to the large-sample (i.e., ‘Wald’) approximation and the general class of add a small constant (ψ) to each cell of the contingency table. The large sample estimate of the binomial parameter, is
where yg is the observed number of successes out of ng trials for group g, g = 1, 2. The large sample estimates of the relative risk and associated standard error are
and
Two values of ψ were considered. The first let ψ = 0.5 if any cell in the 2 × 2 equaled zero. With this approach
The regular large-sample estimate of the standard error was used with ng = ng + 1.0 if there was at least one zero cell.
The second value of ψ mirrors the method of Agresti and Caffo(Agresti & Caffo 2000). This method was presented in the context of the risk difference in their paper and was originally based on a realization that the addition of two success and two failures to a single binomial readily approximated a 95% score confidence interval for a binomial proportion (Agresti & Coull 1998). For this examination, the Agresti-Caffo method is extended to include the relative risk. The Agresti-Caffo method adds one success and one failure (ψ = 1) to each treatment group regardless of whether or not a zero cell is obtained. Thus, pg,ψ=1.0 = (yg + 1)/(ng + 2) for g = 1, 2. Therefore, the relative risk and associated standard error for this approach are
and
3.2 Special considerations for statistical performance comparisons
The combination of small sample sizes and success probabilities close to the boundaries necessitated special handling of zero cells in addition to the previously defined estimators. The large-sample based point estimate for RR and its confidence interval are poorly defined when at least one group fails to observe a success. For the calculation of the statistical properties of the Wald estimator, any element of the sample space that did not contain at least one success in each group was determined to have failed to have rejected the null hypothesis. The point estimate was set at 1.0 and the confidence interval at (0, ∞) to represent completely uninformative information, but at the expense of inflating the coverage probability since the confidence interval would always contain the true population parameter. As Figure 1 illustrates, the probability of having to utilize this non-estimated interval is non-trivial and is in fact the motivation for this paper.
Figure 1.
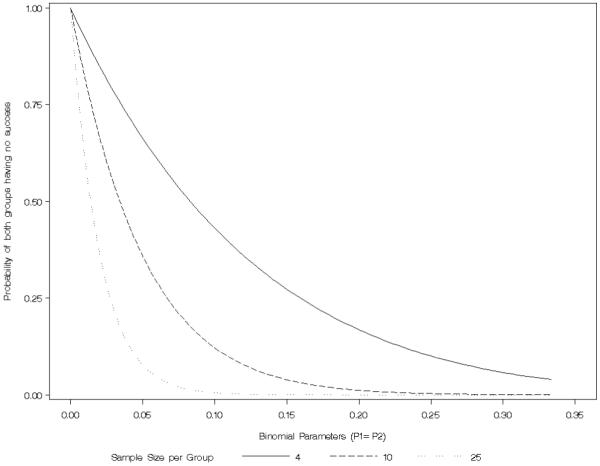
Probability of observing no successes for small to moderate sample sizes and a variety of binomial proportions
3.3 Statistical performance results
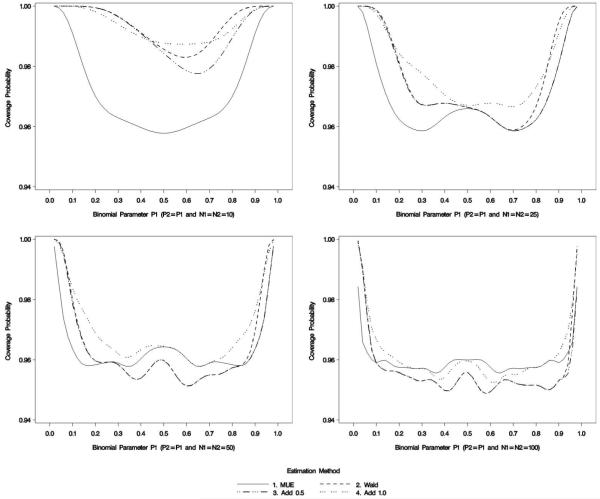
Figure 2 portrays the coverage probabilities under the null (p1 = p2) for all binomial parameters considered. With small sample sizes, the proposed MUE-based methods performs close to the desired 95% target for most values of p, but all methods are conservative in that they have higher than the nominal coverage probability when the binomial parameter is close to the boundaries. Some of the conservativeness is due to the decision rules used to create a confidence interval described above; however, as the sample size increases, these decision rules do not affect as profoundly. It is worth noting that while Figure 2 shows that the MUE has coverage probability strictly greater than 95% (under the null RR = 1), this is not the general result.
Figure 2.
Coverage probability
Since the MUE always produces a finite estimate, the MUE estimate will be biased as RR → ∞. To examine this issue further, the mean coverage probabilities for various relative risk groupings was computed (Table 1; see online appendix for raw data). From this illustration, sample sizes of 10 with large relative risks have, on average, less than the nominal coverage probability. The lowest coverage probability was 0.14, a value corresponding to true underlying probabilities of 0.02 and 0.58 (RR ∈ {29−1, 29}. It is worth noting that coverage probability improves as p2 increases beyond 0.58 with p1 = 0.02. The reason for this is associated with the discreteness of the bootstrap sample space. As the RR → ∞, the probability of observing the largest MUE-based estimate of RR (denoted as above) increases. At some point, this probability will exceed α/2 and the upper limit of the confidence interval is administratively set at ∞.
Table 1.
Average coverage probabilities for relative risk groupings by statistical method and sample size
| Sample Size | Relative Risk Grouping | MUE | Wald | Add 0.5 | Add 1.0 |
|---|---|---|---|---|---|
| 10 | [1.5, 2.0) | 0.947 | 0.970 | 0.963 | 0.962 |
| [2.0, 5.0) | 0.954 | 0.966 | 0.958 | 0.933 | |
| [5.0, 25.0) | 0.963 | 0.961 | 0.950 | 0.843 | |
| [25.0, 49.0] | 0.561 | 0.975 | 0.945 | 0.805 | |
|
| |||||
| 25 | [1.5, 2.0) | 0.946 | 0.960 | 0.957 | 0.957 |
| [2.0, 5.0) | 0.946 | 0.963 | 0.960 | 0.944 | |
| [5.0, 25.0) | 0.964 | 0.960 | 0.956 | 0.894 | |
| [25.0, 49.0] | 0.998 | 0.940 | 0.935 | 0.784 | |
|
| |||||
| 50 | [1.5, 2.0) | 0.947 | 0.955 | 0.954 | 0.954 |
| [2.0, 5.0) | 0.947 | 0.958 | 0.956 | 0.948 | |
| [5.0, 25.0) | 0.950 | 0.962 | 0.961 | 0.918 | |
| [25.0, 49.0] | 0.984 | 0.956 | 0.954 | 0.869 | |
|
| |||||
| 100 | [1.5, 2.0) | 0.949 | 0.952 | 0.952 | 0.952 |
| [2.0, 5.0) | 0.948 | 0.953 | 0.953 | 0.949 | |
| [5.0, 25.0) | 0.944 | 0.960 | 0.960 | 0.934 | |
| [25.0, 49.0] | 0.977 | 0.955 | 0.955 | 0.879 | |
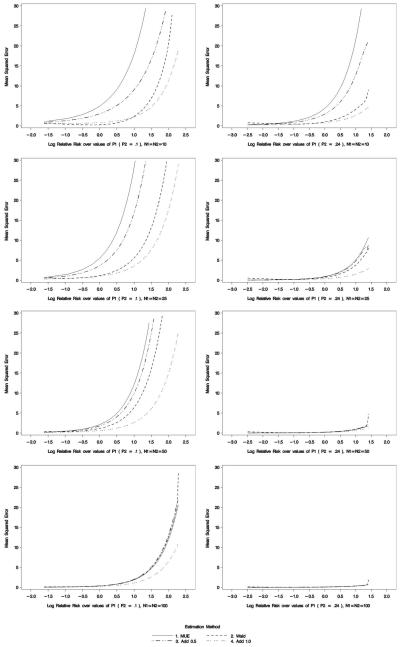
The mean squared error (MSE) is illustrated in Figure 3. The MSE for the MUE-based the largest of the four methods considered, however, as the sample size increases, the differences become negligible. The increase in MSE is most apparent for large relative risks, which as just stated, is a limitation of the finite nature of the MUE-based approach.
Figure 3.
Mean Squared Error. Mean squared error is calculated on the relative risk scale but for illustrative purposes, the x-axis has been natural log transformed to aid in presentation.
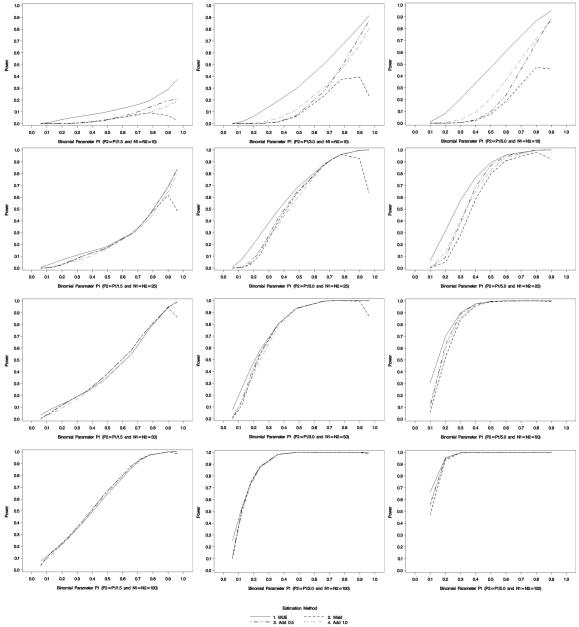
For small sample sizes (Figure 4, row 1), the MUE had the highest power to reject the null hypothesis for relative risks of 1.5, 3.0 and 5.0, values that represent a modest association up to a very strong association. The MUE-based estimator consistently had higher power than the Agresti-Caffo (ψ 1.0) estimator. This is likely do to the fact that the Agresti-Caffo estimator provides greater ‘shrinkage’ towards p = 0.5 than the MUE-based estimator (Figure 5). As the sample size increased, the power to detect these relative risks converged. Figure 4 illustrates a drop in power for the Wald estimator as p1 approaches 1.0. This is due to the decision rule of if there was a zero cell, the confidence interval was set to the full range of relative risk. Furthermore, the power curves show an important consideration–power to detect a fixed RR varies as a function of the magnitude of the underlying success probabilities. That is, there is more power to detect RR = 2.0 when (p1, p2) = (.8, .4) than when they equal (.02, .01).
Figure 4.
Power
Figure 5.
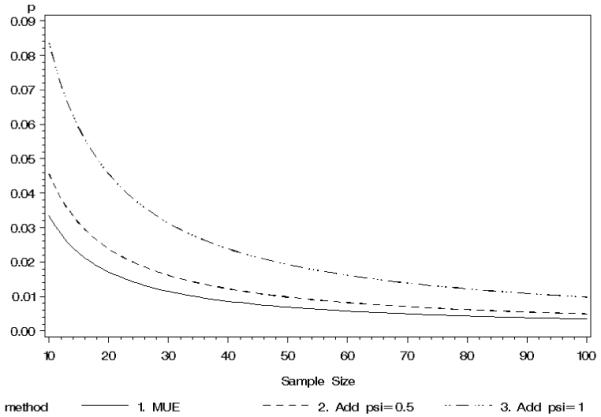
Comparison of MUE with estimators that add constants to each cell when zero successes are observed
4 Motivating example revisited
Patients undergoing renal transplantation are subjected to high doses of steroids and immunosuppressants to help improve graft survival (i.e., to decrease the risk of the recipient rejecting the foreign kidney). A complication of these therapies is that they render the patient with significant glucose intolerance afterward due to stress hyperglycemia, steroid use, immunosuppressive agents such as calcineurin inhibitors, and other contributing factors(Hosseini et al. 2007, Pham et al. 2007, Mazali et al. 2008). The incidence of post-transplant diabetes occurs in 4% to 25% of those patients undergoing renal transplantation (Pham et al. 2007). Therefore, interventions are required to manage the recipient’s blood glucose levels such as insulin or oral hypoglycemic agents (Hermayer et al. 2006). An ongoing clinical trial (Clinicaltrials.gov ID: NCT00609986) is evaluating the safety and efficacy of intensive glycemic control in the peri-operative, immediate post-operative, and outpatient time periods at the time of renal transplantation. The primary hypothesis is that the intensive glycemic therapy administered during the peri-operative, immediate post-operative, and outpatient time periods will lead to improvement in graft survival when compared to standard glycemic therapy. Intensive therapy, however, may increase the likelihood of a severe hypoglycemic event (a blood glucose less than 40mg/dL). This risk is one of the primary concerns of the study’s data and safety monitoring board (DSMB). Another parameter being followed by the DSMB in hyperglycemia defined as a blood glucose reading in excess of 350 mg/dL. In particular, the DSMB requires quarterly reports of the occurrence of severe hypoglycemia and hyperglycemia. The DSMB charter stipulates that the relative risk and associated 95% confidence interval will be computed for each interim safety report. Should this confidence interval yield a conclusion that the intensive therapy has greater than three times the risk of a severe hypoglycemic event, the trial would require reevaluation of the risk-to-benefit ratio.
Three interim reports have been completed to date. The large sample estimates of the probability of experiencing a severe hypoglycemic event, denoted as for groups g =1 and 2, and t = 1, 2, 3 for interim safety report at time t were as follows: p11 = 0/3, p21 = 0/4; p12 = 1/9, p22 = 0/11; and p13 = 1/12, p23 = 1/15. Note that for the first two interim safety reports, the MLE estimate of the relative risk is undefined or infinite. A ‘Wald’ confidence interval for the third report period is estimable, but the validity of such an estimate is questionable given the small sample size at this point in the trial. Table 2 provides a detailed summary of the point estimates, and associated confidence intervals, for the relative risk of developing a severe hypoglycemic event for group 1 relative to group 2 (i.e., a partially-blinded comparison).
Table 2.
Comparison of relative risk estimates for the occurrence of severe hypoglycemia (BG < 40mg/dL) at three time points
| Interim Analysis |
Estimated Probabilities | Estimated Relative Risk |
|||
|---|---|---|---|---|---|
| Estimator | Group 1 | Group 2 | 95% CI | ||
| 1 | Observed data (Successes/Trials) | 0/3 | 0/4 | ||
|
| |||||
| Wald | 0.0000 | 0.0000 | Undefined | N/A | |
| Add psi=0.5 | 0.1250 | 0.1000 | 1.25 | [0.03, 50.2] | |
| Add psi=1.0 | 0.2000 | 0.1667 | 1.20 | [0.1, 14.69] | |
| Agresti-Min Uncond. Exact | - | - | - | - | |
| Approx. Uncond. Exact | - | - | - | - | |
| MUE-based | 0.1032 | 0.0796 | 1.30 | [0.21, 8.06] | |
|
| |||||
| 2 | Observed data (Successes/Trials) | 1/9 | 0/11 | ||
|
| |||||
| Wald | 0.1111 | 0.0000 | ∞ | [0,∞) | |
| Add psi=0.5 | 0.1500 | 0.0417 | 3.6 | [0.16, 79.01] | |
| Add psi=1.0 | 0.1818 | 0.0769 | 2.36 | [0.25, 22.7] | |
| Agresti-Min Uncond. Exact | 0.1111 | 0.0000 | ∞ | [0.173, ∞) | |
| Approx. Uncond. Exact | 0.1111 | 0.0000 | ∞ | [0.325, ∞) | |
| MUE-based | 0.1269 | 0.0305 | 4.16 | [0.35, 13.89] | |
|
| |||||
| 3 | Observed data (Successes/Trials) | 1/12 | 1/15 | ||
|
| |||||
| Wald | 0.0833 | 0.0667 | 1.25 | [0.09, 17.98] | |
| Add psi=0.5 | 0.0833 | 0.0667 | 1.25 | [0.09, 17.98] | |
| Add psi=1.0 | 0.1429 | 0.1177 | 1.21 | [0.2, 7.55] | |
| Agresti-Min Uncond. Exact | 0.0833 | 0.0667 | 1.25 | [0.08, 20.38] | |
| Approx. Uncond. Exact | 0.0833 | 0.0667 | 1.25 | [0.13, 11.57] | |
| MUE-based | 0.0961 | 0.0773 | 1.24 | [0.13, 11.46] | |
Both the Agresti-Min unconditional exact and the asymptotic unconditional method were computed in StatXact v6.2 using the two-sided test inversion method. StatXact was unable to compute the unconditional exact confidence intervals for Interim Analysis 1 on account of the 2×1 table structure.
The MUE-based and general class of ψ estimators yield similar results when either both treatment groups fail to yield a success or when both groups have at least one success. In the event of only one group containing a success, there are some notable differences in the point estimates. The point estimates for the relative risk are remarkably different for the second interim analysis ( vs. RRψ=1.0 = 2.36). This difference is the result of greatest shrinkage of the Agresti-Caffo (ψ = 1.0) estimates for the two proportions, particularly for Group 2 which had zero instances of severe hypoglycemia in 11 participants (See Figure 5). In fact, the Agresti-Caffo estimate of p22 is 2.5 times higher than that estimated by MUE. Since this proportion is in the denominator, it leads to attenuation (shrinkage towards the null) in the estimated relative risk. The point estimates for Agresti-Min’s unconditional exact test have been added for completeness, but these estimates are equal to the MLE in this instance. The confidence intervals, however, for this method are unique to the unconditional approach proposed by Agresti and Min (Agresti & Min 2001).
Overall, the confidence intervals are wide and reflect the uncertainty in the estimated relative risk with small sample sizes. The implementation of Agresti-Min’s confidence interval in StatXact (Cytel Software Corporation 2003) fails to run for interim analysis 1; the software produces an error that the table is not a 2 × 2 table and terminates. The MUE-based confidence interval provides for a finite confidence interval that is the most narrow of all methods considered except for the case of the Agresti-Caffo for the interim analysis 3. While there is some evidence of a difference in the proportion of participants experiencing severe hypoglycemia, the data do not suggest that the study needs to be reevaluated at the present time.
5 Discussion
The proposed estimator for relative risk based on the ratio of two median unbiased estimates of a proportion works well in a variety of settings. It particularly is well suited for small sample sizes with rare events such as was illustrated by the motivating example. The use of Agresti and Caffo’s ‘add one success and one failure’ (ψ = 1.0) approach can be recommended with little reservation in this setting too, especially considering the ease at which it can be computed. As would be expected, the large sample estimator is not recommended for small samples involving rare events.
Beyond the obvious limitation of using large-sample asymptotics for small samples, the relative risk defined as the ratio of two MLEs is not well defined when no successes are observed. One could reason evidence for the null hypothesis when no successes are observed in either group and the sample size is large, but instances in which the sample sizes are not equal, this conclusion is more difficult to support. Furthermore, no formal test for the tenability of the null hypothesis can be performed if the point estimate of the relative risk is undefined. Likewise, if the outcome is considerable more prevalent in one group (e.g., adverse events occurring on the active treatment and not on placebo), the relative risk based on MLEs may still be undefined, yet the data suggest a difference in the proportions. Both the MUE-based and Agresti-Caffo estimators for the relative risk are properly defined in this case. While not an estimator of relative risk, Fisher’s exact test could be used in this situation to test the general null hypothesis of no association.
The estimation of the confidence interval for the MUE-based approach is straightforward, but for large sample sizes, the computations become time consuming. For an individual dataset, this is only a minor consideration, but for the evaluation study, sample sizes of 500 proved too time consuming to be included in this manuscript. While the exact enumeration of the bootstrap sample space is viewed as a limitation with large sample sizes, in the context of smaller studies it is actually a strength of the method as it avoids Monte Carlo error.
The evaluation study focused on equal sample size allocations, yet slight imbalances in the group sample sizes were observed in the transplant example. We believe that for such slight differences in allocation, no direct impact will be observed on the point estimate or confidence interval for the MUE-based relative risk estimate. However, should significant imbalance be observed (e.g., 4:1 or higher), further evaluation of the confidence interval may be warranted since the deterministic bootstrap sample space will be more defined by the larger group’s sample size. Since the context of this method is that of a randomized clinical trial, the scenario of greatly imbalanced sample sizes is not anticipated. An additional limitation of the evaluation study is that it did not include the Agresti-Min unconditional exact estimator (Agresti & Min 2001). There were two primary reasons for this omission. First, the computation requirements of evaluation study were significant without the addition of the unconditional exact method and this addition, while scientifically interesting, would have hindered the timeliness of this manuscript. Second, the unconditional exact implementation in StatXact has the limitation that the method will not run if at least one success is not observed. Future research, with increased computational capabilities, will be needed to fully compare the proposed estimator to the unconditional exact estimator.
The determination of the MUEs for the two groups can present some logistical problems and could hinder the application of the MUE-based relative risk estimator in practice. In addition, the exact enumeration of the bootstrap sample space requires specialized programming. To facilitate the use of the proposed methodology, a SAS MACRO has been written to perform all necessary calculations. This program is available upon request from the first author.
In summary, the difficulties in estimating relative risk when zero cells are observed are encountered in practice and warrant novel analytical advances. The proposed relative risk estimator based on the ratio of two median unbiased estimators for the group proportions can be recommended for these situations.
6 Acknowledgements
The renal transplant study is supported by a grant from the American Diabetes Association (HR 17383, Hermayer (PI)). Methodological aspects of this research were partially supported by Grant 1 UL1 RR024150 from the National Center for Research Resources (NCRR), a component of the National Institutes of Health (NIH).
Contributor Information
Rickey E. Carter, Department of Health Sciences Research, Mayo Clinic
Yan Lin, Division of Quantitative Sciences, MD Anderson Cancer Center, University of Texas
Stuart R. Lipsitz, Division of General Internal Medicine, Brigham & Women’s Hospital
Robert G. Newcombe, Department of Primary Care and Public Health, Centre for Health Sciences Research, Cardiff University
Kathie L. Hermayer, Department of Medicine, Division of Endocrinology, Diabetes & Medical Genetics, Medical University of South Carolina
References
- Agresti A. Categorical Data Analysis. Wiley; 2002. [Google Scholar]
- Agresti A. Dealing with discreteness: making ‘exact’ confidence intervals for proportions, differences of proportions, and odds ratios more exact. Stat Methods Med Res. 2003;12(1):3–21. doi: 10.1191/0962280203sm311ra. [DOI] [PubMed] [Google Scholar]
- Agresti A, Caffo B. Simple and effective confidence intervals for proportions and differences of proportions result from adding two successes and two failures. The American Statistician. 2000;54:280–288. [Google Scholar]
- Agresti A, Coull B. Approximate is better than ‘exact’ for interval estimation of binomial proportions. The American Statistician. 1998;52(2):119–126. [Google Scholar]
- Agresti A, Min Y. On small-sample confidence intervals for parameters in discrete distributions. Biometrics. 2001;57(3):963–971. doi: 10.1111/j.0006-341x.2001.00963.x. [DOI] [PubMed] [Google Scholar]
- Brown LD, Cai TT, DasGupta A. Confidence intervals for a binomial proportion. Statistical Science. 2001;16(1):101–133. [Google Scholar]
- Carter RE, Woolson RF. Advances in Statistical Methods for the Health Sciences. Brickhauser; 2007. pp. 349–358. chapter Safety Assessment in Pilot Studies When Zero Events Are Observed. [Google Scholar]
- Cytel Software Corporation . StatXact with Cytel Studio. 6.2 edn. 2003. [Google Scholar]
- Finfer S, Chittock DR, Su SY-S, Blair D, Foster D, Dhingra V, Bellomo R, Cook D, Dodek P, Henderson WR, Hbert PC, Heritier S, Heyland DK, McArthur C, McDonald E, Mitchell I, Myburgh JA, Norton R, Potter J, Robinson BG, Ronco JJ. Intensive versus conventional glucose control in critically ill patients. N Engl J Med. 2009;360(13):1283–1297. doi: 10.1056/NEJMoa0810625. [DOI] [PubMed] [Google Scholar]
- Hermayer K, Baliga P, Luttrell L, Arnold P, Turrisi K, Mensching K, Cox C, Janulyte B, Cumbie B, Sutton A, Carter R. American Diabetes Association 66th Scientific Sessions. American Diabetes Association; 2006. Outcomes of tight glycemic control utilizing a diabetes management service team in the renal transplant patient. [Google Scholar]
- Hermayer KL, Neal DE, Hushion TV, Irving MG, Arnold PC, Kozlowski L, Stroud MR, Kerr FB, Kratz JM. Outcomes of a cardiothoracic intensive care web-based online intravenous insulin infusion calculator study at a medical university hospital. Diabetes Technol Ther. 2007;9(6):523–534. doi: 10.1089/dia.2007.0225. [DOI] [PubMed] [Google Scholar]
- Hirji K, Tsiatis A, Mehta C. Median unbiased estimation for binary data. The American Statistician. 1989;43:7–11. [Google Scholar]
- Hosseini MS, Nemati E, Pourfarziani V, Taheri S, Nourbala MH, Einollahi B. Early hyperglycemia after allogenic kidney transplantation: does it induce infections. Ann Transplant. 2007;12(4):23–26. [PubMed] [Google Scholar]
- Lin Y, Newcombe R, Lipsitz S, Carter R. Fully-specified bootstrap confidence intervals for the difference of two independent binomial proportions based on the median unbiased estimator. Stat Med. 2009;28:2876–90. doi: 10.1002/sim.3670. [DOI] [PubMed] [Google Scholar]
- Mazali FC, Lalli CA, Alves-Filho G, Mazzali M. Posttransplant diabetes mellitus: incidence and risk factors. Transplant Proc. 2008;40(3):764–766. doi: 10.1016/j.transproceed.2008.03.018. [DOI] [PubMed] [Google Scholar]
- Newcombe RG. Two-sided confidence intervals for the single proportion: comparison of seven methods. Stat Med. 1998;17(8):857–872. doi: 10.1002/(sici)1097-0258(19980430)17:8<857::aid-sim777>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- Parzen M, Lipsitz S, Ibrahim J, Klar N. An estimate of the odds ratio that always exists. Journal of Computational and Graphical Statistics. 2002;11(2):420–436. [Google Scholar]
- Pham P-TT, Pham P-CT, Lipshutz GS, Wilkinson AH. New onset diabetes mellitus after solid organ transplantation. Endocrinol Metab Clin North Am. 2007;36(4):873–90. vii. doi: 10.1016/j.ecl.2007.07.007. [DOI] [PubMed] [Google Scholar]
- Read CB. Encyclopedia of Statistical Sciences. John Wiley; 1985. pp. 424–426. chapter Median Unbiased Estimator. [Google Scholar]
- Weir MR. Microalbuminuria and cardiovascular disease. Clin J Am Soc Nephrol. 2007;2(3):581–590. doi: 10.2215/CJN.03190906. [DOI] [PubMed] [Google Scholar]