Abstract
Objective. To develop an additive numerical scoring scheme for the BILAG-2004 index.
Methods. SLE patients were recruited into this multi-centre cross-sectional study. At every assessment, data were collected on disease activity and therapy. Logistic regression was used to model an increase in therapy, as an indicator of active disease, by the BILAG-2004 index score in the nine systems. As both indicate inactivity, scores of D and E were set to 0 and used as the baseline in the fitted model. The models were used to determine the numerical values for Grades A–C. Different scoring schemes were compared.
Results. There were 1510 assessments from 369 SLE patients. The coding schemes suggested for the Classic BILAG index (A = 12, B = 5, C = 1, D/E = 0 and A = 9, B = 3, C = 1, D/E = 0) did not fit the data well. A coding scheme (A = 12, B = 8, C = 1 and D/E = 0) was recommended, based on analysis results and consistency with the numerical coding scheme of the Classic BILAG index.
Conclusion. A reasonable additive numerical scoring scheme based on treatment decision for the BILAG-2004 index is A = 12, B = 8, C = 1, D = 0 and E = 0.
Keywords: SLE, Outcome measures, Disease activity, BILAG-2004, Statistics, Global score, Regression model, Treatment decision
Introduction
The BILAG-2004 index is a comprehensive composite clinical index that has been recently validated for the assessment of SLE disease activity [1–4]. This index is based on the Classic BILAG index and has many similarities with its predecessor: it is based on the principle of the physician’s intention to treat, has transitional property that captures changing severity of clinical manifestations and has a similar ordinal scale scoring system. However, it has nine systems and many of the changes (from the Classic BILAG index) are in the items, glossary and scoring scheme. As with the Classic BILAG index, the individual system scores were not intended to be summated into a global score.
However, the accommodation of ordinal data and the multiplicity of systems do limit statistical analyses. In situations where a single summary (numerical) measure for the BILAG-2004 index is desirable, there is currently no coding scheme available. We recently performed a formal analysis to derive a numerical coding scheme for the Classic BILAG index based on data from clinical practice [5]. The numerical coding scheme for the Classic BILAG index is not expected to be applicable to the BILAG-2004 index due to the changes made during development.
We have performed a similar analysis to develop an additive numerical scoring scheme for the BILAG-2004 index based on treatment decision. This analysis used the same data set from which the numerical scoring of the Classic BILAG index was derived, as data on the BILAG-2004 index were available.
Patients and methods
The data for this cross-sectional analysis came from a multi-centre study in the UK to validate the BILAG-2004 index that has been reported [3]. Details of the study have been described previously [6]. In summary, patients with SLE who satisfied the revised ACR criteria for classification of SLE were recruited [7, 8]. At every assessment, data on disease activity using the BILAG-2004 index and treatment were collected. This study received multi-centre research ethical approval from Hull and East Riding Research Ethics Committee as well as approval from the local research ethics committees of all participating centres. Written consent was obtained from all patients. This study was carried out in accordance with the Declaration of Helsinki.
BILAG-2004 index
This is an ordinal scale index that has nine systems (Constitutional, Mucocutaneous, Neuropsychiatric, Musculoskeletal, Cardiorespiratory, Gastrointestinal, Ophthalmic, Renal and Haematological). Disease activity is categorized into five levels, Grades A–E [4].
Following completion of the study, some issues with the scoring scheme for the Haematological system were noted. Through consensus of the BILAG, changes were made to this scoring scheme, that were based on data (data not shown), to improve the scoring system. These changes only affected the Haematological system score calculation and had no impact on data collection. The modified Haematological scoring system was used in this analysis. The revised index (BILAG-2004 index form, glossary and scoring scheme—revision 1 September 2009) incorporating this change is available as supplementary data at Rheumatology Online.
Change in therapy
Change in therapy has been chosen as the reference standard for disease activity and used as the response (outcome) variable. This is based on the well-defined benchmark for active disease, which is the decision to treat and is in line with the previous study that derived the scoring for the Classic BILAG index [6].
A robust definition for change in therapy was used, similar to the definition used in our previous study [6]. Change in therapy was the change in treatment following the assessment. The medications of interest included immunosuppressives, anti-malarials, glucocorticoids, biological therapy, topical glucocorticoids, topical immunosuppressives, intravenous immunoglobulins, plasmapheresis, anti-coagulation, prasterone, thalidomide and retinoids. NSAIDs were not included as they are commonly used to treat non-lupus indications (especially for pain relief) and some could be obtained as non-prescription medication. For this analysis, change in therapy was categorized into ‘increase in therapy’ and ‘no increase in therapy’.
Statistical analysis
All analyses were performed using R software (Vienna, Austria) [9]. Logistic regression was used to relate the probability of an increase in therapy (outcome variable) to the counts of the BILAG-2004 index scores obtained in each system (explanatory variables) at each assessment. Grades D and E were combined for this analysis, both indicating inactivity. Thus, four categorical scores were possible (A–D).
What we term a total counts model is defined as
where P is the probability of an increase in therapy, α is the intercept term and xA, xB, xC and xD are explanatory variables representing the number of Grades A, B, C and D/E scores, respectively, at each assessment. βA, βB, βC and βD are the coefficients for the corresponding explanatory variables xA, xB, xC and xD.
Grade D/E, indicating inactivity, was used as the reference category in the model. As such, both Grades D and E were implicitly assigned the numerical value of 0 (coefficient βD for Grade D/E had a value of 0). The coefficients for the other explanatory variables (βA, βB and βC) can be estimated and used to derive the numerical values for Grades A, B and C. Estimation was based on generalized estimating equations with an independent working correlation matrix to account for the correlation between multiple assessments from the same patient. This generated a robust estimate for the variance matrix of the maximum likelihood estimates. The ratios of the estimates of these coefficients (denoted by 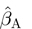 ,
, 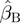 and
and 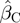 ), and their distributions, provided a relative weighting of Grades A, B and C, which was used in the formulation of possible numerical values for Grades A, B and C.
), and their distributions, provided a relative weighting of Grades A, B and C, which was used in the formulation of possible numerical values for Grades A, B and C.
A numerical global score would be the summation of the numerical value for the nine-system scores, as given by the following formula:
where xA, xB and xC represent the number of Grades A, B and C, respectively, at each assessment. NA, NB and NC represent the numerical scores associated with Grades A, B and C, respectively.
Various coding schemes were considered, including the recommended (A = 12, B = 5, C = 1 and D/E = 0) and original (A = 9, B = 3, C = 1 and D/E = 0) numerical scoring for the Classic BILAG index [6]. Further logistic regression models were used to determine how well these coding schemes are compared with the total counts model. These single-variable models were of the form:
where P is the probability of an increase in therapy, α is the intercept term, xS is the numerical global score obtained using a particular coding scheme and βS is the coefficient for the numerical global score xS.
Wald tests on 2 degrees of freedom were used to examine whether there was a demonstrable difference in fit between a single-variable model and the total counts model. Comparable fits between the models indicate that the weightings suggested in the coding scheme for Grades A, B, C and D/E are consistent with the data.
Results
There were 369 SLE patients with 1510 assessments available for analysis. Eighty-eight per cent of these patients had more than one assessment during the study period. An increase in therapy occurred in 22.6% of the assessments. Patient demographics are summarized in Table 1. Summaries of the individual assessment BILAG-2004 index scores, for patients with and without an increase in therapy, are given in Table 2.
Table 1.
Demographics of patients recruited into the study (n = 369)
| Patient characteristics | Value |
|---|---|
| Female sex, % | 92.7 |
| Age, mean (s.d.), years | 41.6 (13.2) |
| Race, % | |
| Caucasian | 59.9 |
| Afro-Caribbean | 18.4 |
| South Asian | 18.4 |
| Oriental | 1.4 |
| Others | 1.9 |
| Disease duration, mean (s.d.), years | 8.8 (7.7) |
| Number of assessments, % | |
| 1 | 11.4 |
| 2 | 12.5 |
| 3 | 19.8 |
| 4 | 18.7 |
| 5 | 15.2 |
| 6 | 10.0 |
| ⩾7 | 8.1 |
Table 2.
Summary of the BILAG-2004 index scores at each assessment, by change in therapy (n = 1510)
| Scoring characteristics of visits | Increase in therapy | No increase in therapy |
|---|---|---|
| No. of visits with ⩾1 Grade A (%) | 69 (76.7) | 21 (23.3) |
| No. of visits with ⩾1 Grade B and 0 Grade A (%) | 207 (52.9) | 184 (47.1) |
| No. of visits with ⩾1 Grade C, 0 Grade B and 0 Grade A (%) | 62 (8.5) | 666 (91.5) |
| No. of visits with just Grades D or E recorded (%) | 4 (1.3) | 297 (98.7) |
| Total | 342 | 1168 |
The recommended (A = 12, B = 5, C = 1 and D/E = 0) and original (A = 9, B = 3, C = 1 and D/E = 0) numerical scoring scheme for the Classic BILAG index were assessed to determine if they were applicable to the BILAG-2004 index. Using Wald tests, there was significant evidence that both the recommended and original coding schemes for the Classic BILAG index were not appropriate as they did not fit the data as well as the total counts model (P < 0.001 for both). More specifically, for the analysis of the recommended Classic BILAG index scoring scheme, modification of the A score through the addition of the variable xA was not significant (P = 0.457), whereas the addition of the B scores through xB was (P = 0.022). Thus, the numerical coding of 5 for Grade B may be inappropriate.
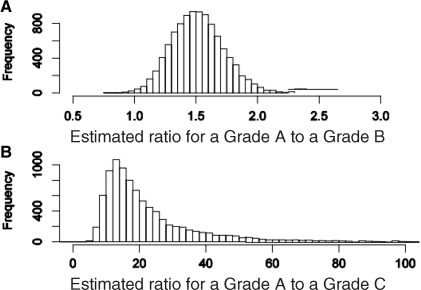
Figure 1 presents simulated distributions of the maximum likelihood estimates of the Grade A to B (A/B) and Grade A to C (A/C) scoring ratios from the total counts model. The estimated A/B ratio is ∼1.5 and the ratio from the recommended Classic BILAG index scoring, 12/5 = 2.4, is in the extreme upper tail of the distribution and not supported by the data. In contrast, the estimated A/C ratio is 19.7 but the Classic BILAG index value of 12 lies well within the lower tail at the 23rd percentile of the distribution, consistent with the data.
Fig. 1.
Histograms showing the distribution of the estimated ratio for (A) a Grade A to a Grade B, (B) a Grade A to a Grade C for the BILAG-2004 index.
Therefore, a suggested modification of the Classic BILAG index scoring for use with the BILAG-2004 index is A = 12, B = 8, C = 1 and D/E = 0, with the A/B ratio now 1.5 and the A/C ratio unchanged at 12. The single-variable model based on this scoring demonstrates no lack of fit when compared with the total counts model (P = 0.74).
Maximum likelihood estimation of the total counts model gave the coefficient estimates 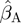 = 2.96,
= 2.96, 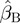 = 1.97 and
= 1.97 and 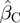 = 0.15. With a baseline score of 1 assigned to Grade C, these values suggest that the numerical value for Grade A could be ∼2.96/0.15 = 19.7, and the numerical value for Grade B could be ∼1.97/0.15 = 13.1. Therefore, an alternative scoring scheme of A = 20, B = 13, C = 1 and D/E = 0 would also fit the data well but to retain maximum consistency with the Classic BILAG index scoring, while retaining a good fit to the data, the A = 12, B = 8, C = 1 and D/E = 0 coding is recommended.
= 0.15. With a baseline score of 1 assigned to Grade C, these values suggest that the numerical value for Grade A could be ∼2.96/0.15 = 19.7, and the numerical value for Grade B could be ∼1.97/0.15 = 13.1. Therefore, an alternative scoring scheme of A = 20, B = 13, C = 1 and D/E = 0 would also fit the data well but to retain maximum consistency with the Classic BILAG index scoring, while retaining a good fit to the data, the A = 12, B = 8, C = 1 and D/E = 0 coding is recommended.
Discussion
This study has determined empirically an additive numerical coding scheme for the BILAG-2004 index using data from clinical practice. A simple modification of the recommended Classic BILAG index coding [5] (A = 12, B = 8, C = 1 and D/E = 0) was found to be acceptable.
The results indicate that numerical coding schemes suggested for the Classic BILAG index (A = 12, B = 5, C = 1, D/E = 0 and A = 9, B = 3, C = 1, D/E = 0) should not be used with the BILAG-2004 index. Apart from the difference in the number of systems (nine in BILAG-2004 and eight in Classic BILAG), the changes to the items, glossary and scoring scheme during the development of the BILAG-2004 index have made it operationally different from the Classic BILAG index. These changes have made Grades A and B much more difficult to achieve and, simultaneously, resulted in Grade C being much less likely to be treated.
Before this analysis, the Haematological scoring scheme was changed as it was noted during initial analysis that Haematological Grades A and B did not independently predict an increase in therapy. It was subsequently found that Grades A and B cut-off values for leucopenia and neutropenia and anaemia were too high as many of these manifestations of lupus were rarely treated. As a result, the cut-off values for leucopenia/neutropenia and anaemia for Grades A and B were revised downwards and greater emphasis was put on haemolytic anaemia in determining Grades A and B. These changes are in line with clinical practice.
One limitation of this study is the cross-sectional design, whereby only the disease activity at the time of assessment is considered, although patients did contribute multiple observations over time. No allowance was made for other factors linked to treatment decisions, such as prior disease activity, current therapy, previous therapy (and its response), presence of comorbidities and patient’s opinion (in particular, refusal to change therapy as advised). Furthermore, the data used did not encompass a full range of possible scores. Nevertheless, the data are representative of routine clinical practice. Other limitations to this analysis are as described for the derivation of the numerical scoring for the Classic BILAG index [5], and hence will not be repeated here.
The BILAG-2004 index provides system-specific information and there will be loss of information if nine ordinal system scores are combined into a single numerical value. Therefore, there are many circumstances in which the use of a single score will be inappropriate and the ordinal system scores are preferable. However, where a single summary numerical measure is required, such as assessing laboratory data, comparison with global score indices and for area under the curve analysis, the coding scheme of A = 12, B = 8, C = 1 and D/E = 0 achieves this reasonably.

Supplementary data
Supplementary data are available at Rheumatology Online.
Supplementary Material
Acknowledgements
We would like to thank the Arthritis Research Campaign, Medical Research Council, Lupus (UK), the nurse specialists of all participating centres and the Wellcome Trust Clinical Research Facility (Birmingham), and Sandwell and West Birmingham Hospital NHS Trust for their support. Lupus (UK) funded a research associate who helped with recruitment at Royal Blackburn Hospital.
Funding: This study was supported by grants from Arthritis Research Campaign (Grant No. 16081), Medical Research Council (U.1052.00.009) and Aspreva Pharmaceuticals (unrestricted educational grant). Funding to pay the Open Access publication charges for this article was provided by the Arthritis Research Campaign.
Disclosure statement: C.-S.Y. has received consultancy payments and honoraria from Roche Pharmaceuticals, Merck Serono and Genentech. C.-S.Y. is currently funded by an unrestricted educational grant from Vifor Pharma/Aspreva Pharmaceuticals. C.G. has received consultancy payments and honoraria from Roche Pharmaceuticals, Genentech, Merck Serono, UCB, BMS and Amgen. All other authors have declared no conflicts of interest.
Footnotes
See page 1616 for the editorial comment on this article (doi:10.1093/rheumatology/keq231)
References
- 1.Isenberg DA, Rahman A, Allen E, et al. BILAG 2004. Development and initial validation of an updated version of the British Isles Lupus Assessment Group’s disease activity index for patients with systemic lupuserythematosus. Rheumatology. 2005;44:902–6. doi: 10.1093/rheumatology/keh624. [DOI] [PubMed] [Google Scholar]
- 2.Yee CS, Farewell V, Isenberg DA, et al. Revised British Isles Lupus Assessment Group 2004 index: a reliable tool for assessment of systemic lupus erythematosus activity. Arthritis Rheum. 2006;54:3300–5. doi: 10.1002/art.22162. [DOI] [PubMed] [Google Scholar]
- 3.Yee CS, Farewell V, Isenberg DA, et al. British Isles Lupus Assessment Group 2004 index is valid for assessment of disease activity in systemic lupus erythematosus. Arthritis Rheum. 2007;56:4113–9. doi: 10.1002/art.23130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yee CS, Farewell V, Isenberg DA, et al. The BILAG-2004 index is sensitive to change for assessment of SLE disease activity. Rheumatology. 2009;48:691–5. doi: 10.1093/rheumatology/kep064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cresswell L, Yee CS, Farewell V, et al. Numerical scoring for the Classic BILAG index. Rheumatology. 2009;48:1548–52. doi: 10.1093/rheumatology/kep183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cresswell L, Yee CS, Farewell V, et al. Numerical scoring for the Classic BILAG index. Rheumatology. 2009;48:1548–52. doi: 10.1093/rheumatology/kep183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tan EM, Cohen AS, Fries JF, et al. The 1982 revised criteria for the classification of systemic lupus erythematosus. Arthritis Rheum. 1982;25:1271–7. doi: 10.1002/art.1780251101. [DOI] [PubMed] [Google Scholar]
- 8.Hochberg MC. Updating the American College of Rheumatology revised criteria for the classification of systemic lupus erythematosus. Arthritis Rheum. 1997;40:1725. doi: 10.1002/art.1780400928. [DOI] [PubMed] [Google Scholar]
- 9.Hornik K. The R FAQ. Comprehensive R Archive Network. 2009 http://CRAN.R-project.org/doc/FAQ/R-FAQ.html. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.