Computational Alanine Scanning with Linear Scaling Semi-Empirical Quantum Mechanical Methods

Abstract

Alanine scanning is a powerful experimental tool for understanding the key interactions in protein-protein interfaces. Linear scaling semi-empirical quantum mechanical calculations are now sufficiently fast and robust to allow meaningful calculations on large systems such as proteins, RNA and DNA. In particular, they have proven useful in understanding protein-ligand interactions. Here we ask the question: can these linear scaling quantum mechanical methods developed for protein-ligand scoring be useful for computational alanine scanning? To answer this question, we assembled 15 protein-protein complexes with available crystal structures and sufficient alanine scanning data. In all, the data set contains ΔΔGs for 400 single point alanine mutations of these 15 complexes. We show that with only one adjusted parameter the quantum mechanics based methods out perform both buried accessible surface area and a potential of mean force and compare favorably to a variety of published empirical methods. Finally, we closely examined the outliers in the data set and discuss some of the challenges that arise from this examination.

Introduction

Protein-Protein interactions are critical in most biological systems. They comprise an important and exceptionally challenging family of drug targets^1–5. A first step to targeting a protein-protein interaction is to understand the atomic interactions on an individual residue basis. Alanine scanning has proven to be a powerful experimental tool for dissecting and understanding protein-protein interactions at the atomic level^6–7. The key consistent finding is that contributions to ΔG are not distributed evenly throughout residues in the interface^8–11. Rather contributions to ΔG tend to be localized to a small number of key interactions, now referred to as hot spots. Further these hot spots tend to cluster as well. Identifying hot spots is particularly important because tenable small molecule binding sites that directly disrupt protein-protein interactions are typically found around hot spots^12–14.

Because of the importance of alanine scanning, a number of computational alanine scanning methods have been developed to predict the likely hot spots in protein-protein interactions. The majority of these approaches are empirically derived scoring functions or classifiers. The commonality between this set of methods is that they parameterize their scoring functions or classifiers on a large data set of ΔΔGs. These methods include pattern recognition methods such as support vector machines¹⁵, decision trees^16–17, and others^18–20 and incorporate empirical descriptors of the interaction such as sequence conservation, relative and absolute buried surface area, various atom or residue contact indices, shape specificity. Also included in the empirical methods are those that are parameterized starting from forcefield based terms^21–22 such as Leonard-Jones potentials, electrostatics, hydrogen bonding potentials, and solvation models.

A second approach to computational alanine scanning is the statistical or database-derived potentials. These approaches differ from the empirical methods in that they are not explicitly fit to binding data of any sort rather they are built on the frequency of occurrence of interactions of different types over a large data set of protein-protein complexes. These are most often potentials of mean force (PMF)^23–24.

A third approach to computational alanine scanning includes methods based on simulations^25–28. These include a direct estimate of ΔΔG using techniques such as molecular mechanics/Poisson-Boltzmann/surface area or molecular mechanics/generalized Born/surface area methods typically from a trajectory derived from a simulation of the wild type complex^25–27. In an alternate simulations based approach, Chong and co-workers²⁸ used high temperature dynamic simulations of the p53 dimer and correlated changes in unfolding kinetics with experimental ΔΔGs.

Linear scaling semi-empirical methods are now fast and robust enough to be used on large systems such as proteins, RNA, and DNA. In particular, they have been used extensively on protein-ligand complexes^29–40. Merz and colleagues have developed a protein-ligand scoring function based on these quantum mechanical calculations⁴¹. Our question is simply: to what extent can these methods developed for protein-ligand complexes be extended to protein-protein interactions in the form of predicting ΔΔG from alanine scanning experiments.

To answer this question, we assembled a case of 15 protein-protein interactions from the AESDB^42–43 and the Binding Interface Database Wiki^44–46. Complexes were chosen if they had sufficient alanine scanning data and a co-crystal structure of sufficient resolution. The full list of protein-protein complexes used is given in Table I. Only mutations to alanine were considered, and those in which the residue mutated was either glycine or proline were not considered as these mutations might lead to significant conformational changes. In all, 400 mutations with experimental ΔΔGs were used in this studied.

Table I.

The Data Set Summary

PDB Code	Number of Mutations	ΔΔG std dev kcal/mo	Resolution Å	Protein1	Protein2
1a4y61	28	0.96	2.0	Ribonuclease Inhibitor	Angiognenin
1brs62	14	2.46	2.0	Barnase	Barstar
1cbw63	8	0.61	2.6	Chymotrypsin	BPTI
1dfj57	14	1.40	2.5	Ribonuclease Inhibitor	Ribonuclease A
1dqj64	21	1.86	2.0	Lysozyme	HYHEL-63
1dvf65	24	1.22	1.9	D1.3	E5.2
1emv55	38	1.41	1.7	Im9	Colcin E9
1fak66	19	0.85	2.1	Factor VIIa	Tissue Factor
1gc167	49	0.39	2.5	CD4	gp120
1hwg68	67	1.10	2.5	Growth Hormone	Growth Hormone Receptor
1jrh69	31	1.38	2.8	Antibody A6	Interferon γ-receptor
1jtg70	23	1.8	1.7	TEM-1 β-lactamase	β-lactamase inhibitor protein II
1ktz71	19	0.70	2.2	TGF-β3	TGF-β3r
1vfb72	29	0.98	1.8	Lysozyme	D1.3
3d9a56	16	2.13	1.2	Lysozyme	HYHEL-10

Materials and Methods

All proteins were prepared using the protein preparation work flow in Maestro⁴⁷ largely following the defaults. In particular, only hydrogens were minimized. All mutants were created using the OEChem SDK⁴⁸ by simply deleting the atoms beyond the Cβ and adding the one or two necessary hydrogens to the Cβ with ideal bond length. All calculations were preformed using divcon version 4.6.2^49–50 with defaults: in particular the PM3 basis set was used. All calculations reported here, unless otherwise noted, were performed with no explicit waters.

Divcon uses a number of terms in its protein-ligand scoring function: gas phase heat of formation, desolvation of the QM charges using the Poisson-Boltzmann equation, a vibrational entropy term, and the attractive portion of the Leonard-Jones potential using AMBER. For the protein-ligand calculations, to calculate the vibrational entropy term the ligand is minimized in the absence of the protein and all vibrational motion is assumed lost upon binding. A comparable term for a computational alanine scanning scoring function would be to minimize just the side chain of the residue to be mutated in its monomer and then calculate the vibrational entropy loss of the side chain by assuming again that all vibrational motion is lost. Because, at this point, this calculation is not practical for this many mutations, the vibrational entropy term was omitted. The assumption that all vibration is lost upon binding would, however, clearly not be valid in the case of protein-protein interactions. We would expect that a residue far from the interface would exhibit very little change in vibration upon binding whereas one completely buried in the interface would lose most vibrational motion. Thus without significant additional investigation the vibrational entropy term would likely add little to this study.

The form of the scoring function is:

$$\text{QM}-\mathrm{\Delta }\mathrm{\Delta }\text{G}={\alpha }^{\ast }(\mathrm{\Delta }\text{Gas}\text{phase}\text{HOF}+\mathrm{\Delta }\text{PB}\text{Desolvation})+\mathrm{\Delta }\text{Attractive}\text{LJ}$$ (1)

where α is the lone parameter to be determined and the Δs in the right portion of the equation indicate the difference between each term in the mutated and wild type complexes. α was chosen so as to maximize the correlation between QM-ΔΔG and the experimental ΔΔG. We found α=0.26 to be optimal. Here the “Gas Phase HOF” term is the gas phase heat of formation of the complex minus that of the two domains in isolation and thus “ΔGas Phase HOF” is the difference in the “Gas Phase HOF” for the wild type complex and the mutant complex. The “PB desolvation” term is the desolvation of the CM2 atomic charges obtained from the PM3 calculation. Similarly, “ΔPB Desolvation” indicates the difference between the “PB desolvation” terms of the wild type and mutant complexes. Taken together these two terms represent the electrostatic portion of ΔG and are the only parts of the function that rely on quantum mechanics. The “Attractive LJ” term is the attractive component of the Leonard-Jones potential calculated using the AMBER forcefield.

A Potential of Mean Force

Given their success with protein-ligand scoring^51–52 and their simplicity, a potential of mean force was built for comparison purposes. To do so first, atoms were typed according to residue and atom type (i.e. atomic number and remoteness). Similar atoms, for example Oδ of Asp and Oε of Glu, were grouped together into a single atom type. In all, 19 different atom types were used. For two atoms of type i and j a distance r from one another, the energy of interaction is determined by:

$$E_{ij}(r)=-\mathit{RT}log\left(\frac{C_{ij}(r)}{C_{ij}}\frac{C}{C(r)}\right)$$ (2)

where C_ij(r) is the number of interactions between atoms of type i and j whose distance is between r and r+dr, C_ij is the total number of interactions between atoms of type i and j, C(r) is the total number of interactions between atoms of any type whose distance is between r and r+dr, and C is the total number of interactions between any two atoms. Here we use dr=0.25 Å.

A non-redundant data set was downloaded from the PDB with a resolution cutoff of 2.5 Å. Homologues were removed at 90% sequence identity. This gave a set of 8298 crystal structures. Interactions were counted in two different ways. These counting methods, described below, gave surprisingly different results.

The first PMF, (PMF1), was created by counting interactions between different but interacting monomers. Within a PDB file, two monomers were considered to be interacting if the buried surface area between the two was >600 Ų, and the pair of monomers had the greatest buried surface area of any two monomers in the PDB file. The second PMF, (PMF2), was created by counting interactions between atoms in the same monomer. Here all interactions between pairs of atoms in the same monomer were counted unless the two atoms were in the same or sequential residues.

When we applied these two PMFs to the data set described in Table I, we found that PMF1 showed significant agreement with the alanine scanning data whereas PMF2 showed no agreement whatsoever. This result is consistent with the observations of Tsai and coworkers⁴⁶ regarding differences between packing in monomers and that in protein-protein interfaces. In particular, they find the architecture in monomers to be similar to that at an interface if the two domains fold cooperatively whereas when the domains fold independently prior to binding, they exhibit significant architectural differences.

We expect that the monomers of the complexes listed in Table I largely fold independently prior to binding whereas the set of complexes used to create PMF1 contains complexes that cooperatively fold and complexes with monomers that fold independently. This led to the conclusion that PMF1 is a combination of PMF2 and the ideal PMF for assessing protein-protein interactions (PMF-PPI), i.e.,

$$\text{PMF}1=\alpha \text{PMF}-\text{PPI}+(1-\alpha )\text{PMF}2,$$ (3)

or

$$\text{PMF}-\text{PPI}=[\text{PMF}1-(1-\alpha )\text{PMF}2]/\alpha .$$ (4)

PMF-PPI was then determined by optimizing its correlation within the data set over values of α between 0 and 1. A value of α=0.655 was found to be optimal. PMF-ΔΔG for a particular mutant is then the PMF-PPI score for the mutant complex minus that for the wild type complex.

Buried Accessible Surface Area

As a second comparison, buried accessible surface area was used. Here each residue was simply ranked by the change in its solvent accessible surface area upon formation of the complex. Surface areas were calculated using only non-hydrogen atoms excluding solvent molecules. Radii were set to Van der Waals radii plus 1.4 Å.

Results and Discussion

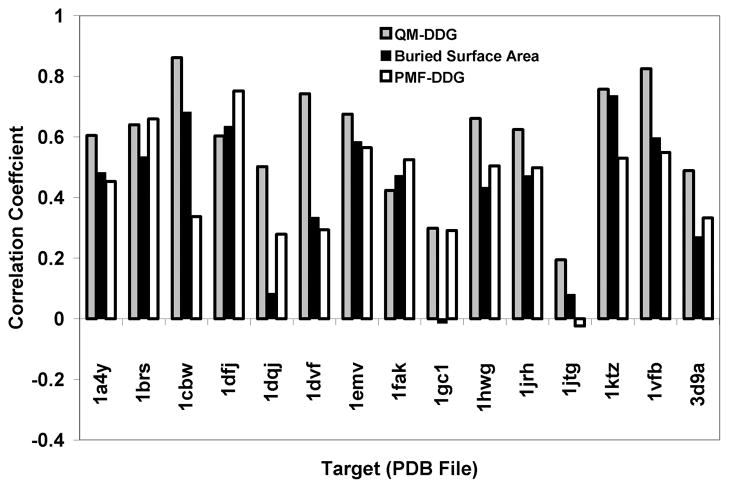
The overall results, expressed as correlation coefficients, on a case by case basis are shown in Fig. 1, for QM-ΔΔG, PMF-ΔΔG, and buried surface area. Of the three different methods for ranking the contributions of individual amino acids to binding, QM-ΔΔG is the best in 11 of the 15 cases and is nearly so in the other 4 cases.

Figure 1.

The correlation coefficients for the three methods: QM-ΔΔG (gray), buried surface area (black) and PMF-ΔΔG (white)

Table II contains a variety of additional statistics on the entire data set to compare the three methods as well as to allow comparisons to other methods. For this table the overall correlation coefficients and two correct classification rates with different cutoffs are reported. The cutoff schemes are described below. In addition, these three statistics are reported for all 400 residues or for the 309 contact residues, i.e., those that bury at least 1 Ų of surface area in their complex. All the statistics indicate that QM-ΔΔG outperforms PMF-ΔΔG and buried surface area. In particular, QM-ΔΔG has a correlation coefficient between 0.55 and 0.60 over the entire data set. We believe this to be a good degree of correlation given the fact that the data was gathered under many different conditions, with different assay methodologies and in different laboratories.

Table II.

The classification statistics for QM-ΔΔG, PMF-ΔΔG and Buried Surface Area.

Data Set	Statistic	QM-ΔΔG	PMF-ΔΔG	Buried Surface Area
All Residues	Correlation Coefficient	0.60	0.10	0.43
	Correct Classification Rate: 1.5/0.5 Cutoffs	81%	74%	71%
	Correct Classification Rate: 2.0/1.0 Cutoffs	83%	76%	76%
Contact Residues	Correlation Coefficient	0.55	0.01	0.33
	Correct Classification Rate: 1.5/0.5 Cutoffs	75%	68%	64%
	Correct Classification Rate: 2.0/1.0 Cutoffs	80%	67%	64%

The first cutoff scheme was chosen in order to compare with the published computational alanine scanning results of Li and co-workers¹⁹. In this scheme, residues are classified as experimental hot spots if ΔΔG>1.5, as warm spots if 0.5<ΔΔG≤1.5, and as unimportant if ΔΔG≤0.5 with all units in kcal/mol. Further, only contact residues were included in the study. In our data set this left, 114 hot spots, 92 warm spots, and 103 unimportant residues. Finally, for the purposes of the classification assessment, Li and co-workers considered only the hot spots and unimportant residues. Cutoffs of 5.0, 66.0, and 37.0 were used for QM-ΔΔG, PMF-ΔΔG and buried surface area respectively to computationally classify an interface residue as either a hot spot or unimportant. These cutoffs were determined as those that gave the best correct classification rate. As can be seen in Table II, in the second to last row, the results with QM-ΔΔG were significantly better than with either PMF-ΔΔG or buried surface area. The overall correct classification rate for QM-ΔΔG is 75% compared to 68% for the PMF-ΔΔG and 64% for buried surface area. Further, the 75% success rate compares favorably to the four methods that Li and co-workers¹⁹ tested. These methods include their own¹⁹, PP_SITE⁵³, the alanine scanning method of Kortemme and Baker²², and FOLDEF²¹. In this study the success rates for the four methods range from 66–72%. It should be noted that while there is significant overlap between the data set Li and co-workers used and the one used here, they are not identical.

The second cutoff scheme we use for Table II is similar to the first except that we classify a residue as a hot spot if ΔΔG>2.0, as a warm spot if 1.0<ΔΔG≤2.0, and as unimportant ifΔΔG≤1.0 kcal/mol. Again the correct classification rate given uses only the hot spots and the unimportant residues. For the contact residues this left 82 hotspots and 148 unimportant residues. Again, QM-ΔΔG performed significantly better than either PMF-ΔΔG or buried surface area: on the data set of interface residues QM-ΔΔG had a 80% correct classification rate compared to 67% and 64% for the PMF-ΔΔG and buried surface area methods.

Individual cases

1dvf - D1.3 and E5.2

Metals in the interface - This case is noteworthy in that this is the only case where there is a critical metal involved in the interface. QM-ΔΔG is able to perform well (correlation coefficient of 0.78) without additional parameterization. In contrast, both buried surface area and the PMF (correlation coefficient < 0.4) performed significantly worse. In principle, the PMF could be further parameterized given sufficient data with metal containing complexes. It is, however, not clear that this would be straightforward as the presence of the metal greatly perturbs the neighboring residues and may very well impact the subsequent interactions these residues make. This effect may be difficult to describe with simple pairwise potentials without significant additional parameterization.

1gc1 - CD4 and gp120

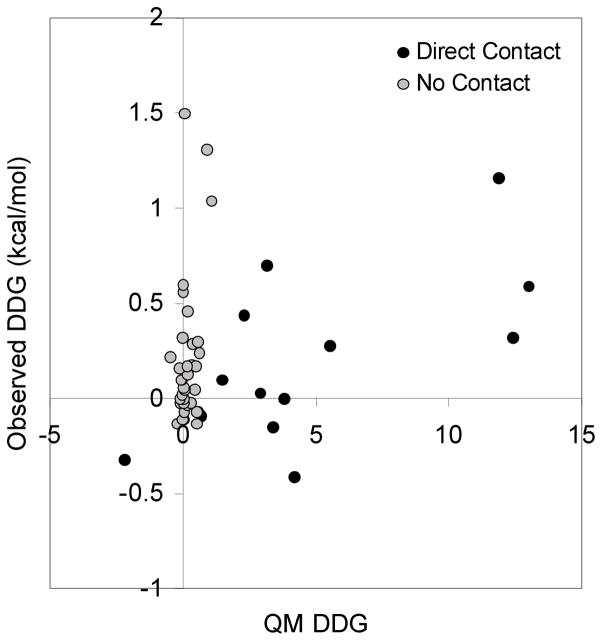
In this case, none of the methods perform particularly well. QM-ΔΔG works the best with a modest correlation coefficient of 0.30. A visual inspection reveals that many of the residues make no direct contact with gp120. In fact of all the mutated residues, the greatest ΔΔG occurs with Thr81 (1.5 kcal/mol) which is at least 20Å from gp120. As can be seen in Fig. 2, excluding those amino acids that have no buried surface area in the complex leads to a significantly better correlation coefficient of 0.64.

Figure 2.

The results for the 1gc1 case (CD4/gp120) with the QM-ΔΔG scoring function. All mutations are mutations of CD4. The gray are those for which the wild type residue has no contact with gp120 as measured by having no buried surface area upon complex formation. The black are those that make direct contact with gp120.

1jtg - TEM-1 β-lactamase (TEM) and β-lactamase inhibitor protein II (BLIP)

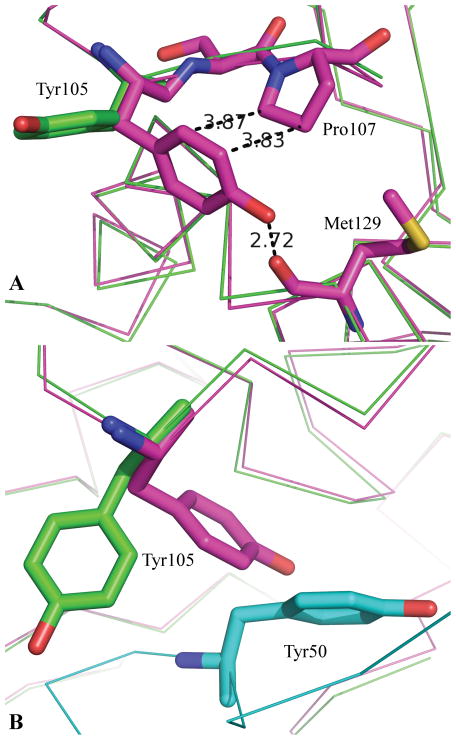
Breaking interactions upon complex formation - In this case, all three methods perform seemingly poorly with QM-ΔΔG having the best correlation coefficient of 0.21. Two of these mutations (Tyr105 of TEM and Tyr50 of BLIP) are significant outliers. Without these two mutations the correlation coefficient between QM-ΔΔG and the experimental ΔΔG increases to a more respectable 0.52. The reason for these residues being such significant outliers is quite telling of the limitations of using a static structure for these calculations.

In the complex, TEM Tyr105 makes a number of seemingly good interactions with BLIP including stacking against BLIP Phe142, hydrophobic contact with the aliphatic portion of BLIP Lys74 and a hydrogen bond with BLIP Gly141. Overall, TEM Tyr105 buries over 141 Ų of surface area in the complex yet its mutation to alanine has essentially no effect on the stability of the complex. A comparison of a TEM apo structure (1zg4⁵⁴) to that in the complex reveals a potential explanation as to why these interactions of Tyr105 observed in the complex do not lead to a significant contribution to the binding affinity. As shown in Fig. 3a, the backbone structure of TEM changes very little between the bound and apo structures. In fact, side chain conformations change very little with the exception of TEM Tyr105. In the apo structure, it stacks against TEM Pro107 and forms a hydrogen bond with the backbone carbonyl of TEM Met127. Thus while TEM Tyr105 makes significant interactions in the BLIP/TEM complex, it must break significant interactions in order to form these interactions. The net effect being that it contributes nothing to the binding affinity.

Figure 3.

A comparison of the Apo and bound structures of TEM. 3a: The green structure is that of TEM as bound to the BLIP from 1jtg⁷⁰. The purple structure is that of apo TEM from the structure 1zg4⁵⁴. 3b: The green and purple structures are those of 3a. The cyan structure is that of BLIP from the complex with TEM. From 3b it is evident that Tyr105 of TEM-1 cannot adopt the same conformation in the bound (green) as observed in the apo (purple) due largely to the presence of Tyr50 of BLIP.

Mutation of BLIP Tyr50 to alanine increased the stability of the complex by 2.2 kcal/mol. This is by far the largest stability gain with any of the mutations considered in this study. The comparison of the TEM apo structure to the TEM-BLIP complex structure again suggests a potential reason for this. As is apparent from Fig. 3b, the reason TEM Tyr105 cannot adopt the same conformation in the complex as it does in the apo structure is because of a steric clash with BLIP Tyr50. Based on the complex structure it seems likely that not only would TEM Tyr105 be able to maintain its apo conformation in a Y50A BLIP mutant it might also be able to interact with the Cβ of the resulting alanine thereby leading to the gain in stability with the Y50A BLIP mutant.

Other examples of interactions in a complex that simply replace those in one of the monomers leading to significant over estimation of a residue’s importance in binding affinity include Im9 Glu41 of 1emv⁵⁵. In this case, Im9 Glu41 makes a salt bridge with E9DNase Arg54. In the apo structure of E9DNase, E9DNase Arg54 is observed to be making a salt bridge with E9DNase Asp51 along with a pair of hydrogen bonds. Thus while the Im9 Glu41-E9DNase Arg54 interaction appears to be energetically significant, it simply replaces energetically comparable interactions in the E9DNase apo structure, and as a result, does not lead to a significant contribution to the binding affinity. It is difficult to assess how frequently this phenomenon occurs as in most cases suitable apo structures are not available.

1brs – Barnase/Barstar

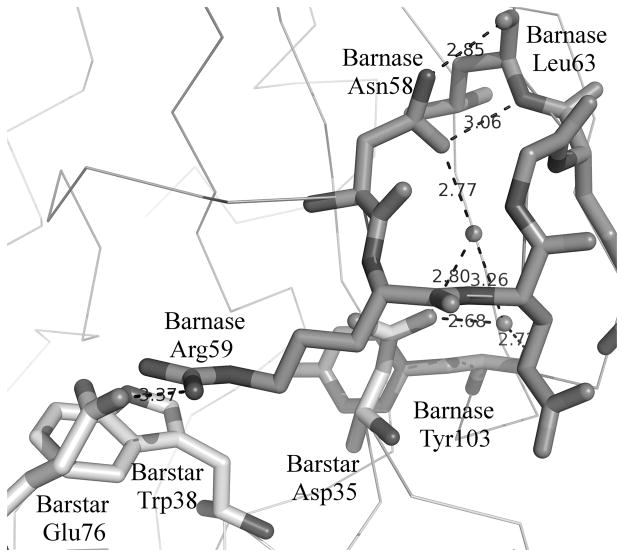
The role of water and stabilization of secondary structure - In this case, the correlation coefficients are all reasonable with the QM-ΔΔG having a correlation coefficient of 0.64. Of the 14 mutations studied in this case, 8 have a measuredΔΔG>3.0 kcal/mol whereas for the full dataset only 53 of 409 mutations have a measured ΔΔG>3.0 kcal/mol. Thus there are an unusual number of significant hotspots in the barnase/barstar interface. The calculated change in binding of most of the mutations is significantly smaller than expected relative to the magnitude of the experimental ΔΔGs. This potentially arises because of the number of water mediated hydrogen bonds in the interface. There are at least 10 observed water molecules that interact with one of these hot spots and also with a residue from the other member of the complex. Fig. 4 shows the interaction of two of these water molecules which help mitigate the interaction between the two domains.

Figure 4.

Barnase/Barstar. Barnase is dark. Barstar is light. Here we highlight two aspects of the role of barnase Asn 58. First, barnase Asn 58 interacts with barstar only through water mediated interactions with barstar Asp35. Second, the hydrogen bonds between barnase Asn 58 and barnase Leu63 may stabilize the β-turn and thereby affect the ability of barnase Arg59 to interact with barstar.

Barnase Asn58 is particularly telling from two aspects. First, its experimental ΔΔG is 3.1 kcal/mol whereas it buries essentially no surface area in the complex and is calculated to have almost no impact on binding. As can be seen in Fig. 4, it forms water mediated interactions with barnase Asp35 (ΔΔG=4.5 kcal/mol) which may lead to a contribution to the binding affinity. Second, barnase Asn58 forms a pair of hydrogen bonds with the backbone of barnase Leu63 across a β-turn. The loss of these hydrogen bonds might destabilize the β-turn thereby affecting the interactions of barnase Arg59 (ΔΔG=5.2 kcal/mol) with barstar Glu76 and Trp78. Thus the large ΔΔG with the mutation of Barnase Asn58 could in part be due to its impact on the stability of the β-turn.

A similar stabilization of a secondary structural element is seen with the case 3d9a⁵⁶ in which the HYHEL Asp401Ala mutant leads to a 3.75 kcal/mol loss in affinity despite Asp401 being no closer than 6.5 Å to HEL. Given its distance from the interface, it is calculated to have no effect on the binding. In this case, Asp401 hydrogen bonds via its side chain across a β-turn to HYHEL Asn397. Though its effect on binding has not been studied via mutagenesis, HYHEL Trp398 appears to be a likely candidate for a binding hotspot in this interface. As HYHEL Trp398 is in the turn between HYHEL Asn397 and Asp401, the loss of the hydrogen bonding between the two may lead to a destabilization of this loop and disruption of the interaction between HYHEL Trp398 and HEL.

Many examples of water mediated interactions can be found throughout this dataset. Examples include the 1emv⁵⁵ case with Im9 Asp51 and the case 1dfj⁵⁷ with RNase Inhibitor Asp431. In both of these cases, there is a water molecule that is entirely bound mediating significant interactions between these residues and their respective partners. The calculated importance of mutation of either of these two residues to alanine is significantly underestimated likely because the water molecules are omitted from the calculation. When we redo the calculations with the assumption that the water molecule is displaced as a result of the mutation of the corresponding residue then the calculations are much more consistent with the experimental ΔΔG. It should be noted, however, that isolated bound waters are less common than networks of bound waters such as that in the barnase-barstar interface. Thus simply removing individual waters when they are involved with the mutated residue will not fully address the role of water in determining ΔΔG.

Interleukin 2 (IL2) and its α receptor (IL2rα) - An example identification of a small molecule binding site

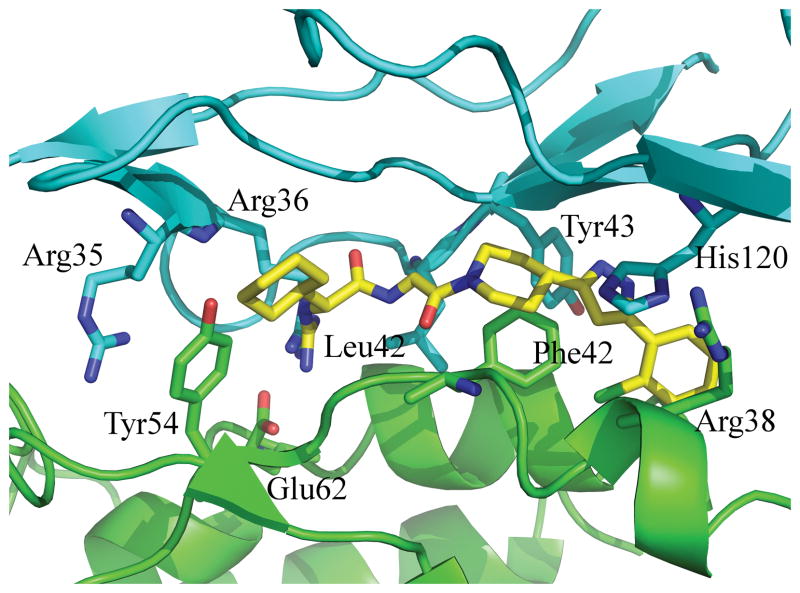
A potential use for alanine-scanning is the identification of a small molecule binding site in a protein-protein interaction. Here we present an example of a prototypical use for computational alanine scanning and ligand binding site identification within a protein-protein interface. In this case, we use IL2 and IL2rα because there is an available co-crystal structure of the two (1z92⁵⁸) and a co-crystal structure of IL2 bound to a small molecule disruptor of the complex(1pw6⁵⁹). Here we calculated the QM-ΔΔG for any residue that has more than 10 Ų of buried surface area in the 1z92 complex. This included 15 residues from IL2 and 20 residues from IL2rα. The top ranked residues are shown in Fig. 5. Though these residues represent just over a third of the interface in terms of buried surface area, they localize in one hot spot thereby suggesting this region as a small molecule binding site. Indeed, as is evident in Fig. 5 the small molecule binding site on IL2 is completely engulfed in the calculated hot spots.

Figure 5.

Computational hot spots for the IL2/IL2rα complex. IL2 is shown in green. IL2rα is shown in cyan. The complex is taken from the structure 1z92⁵⁸. The displayed residues are those that have the greatest QM-ΔΔG. Shown in yellow is a disruptor of this interaction. It is extracted from its co-crystal structure, 1pw6⁵⁹, with IL2 and aligned via aligning the IL2 domains from the two structures. The key point is that the calculated hot spots essentially engulf the ligand binding site.

Conclusion

The overall results with the QM-ΔΔG computational alanine scanning are encouraging. It is particularly so because with only a single adjustable parameter a scoring function developed for protein-ligand interactions performed for protein-protein interactions as well as empirical methods with tens of adjustable parameters. Furthermore, it is encouraging that electrostatics play a significant role in producing reasonable agreement with experiment. This is likely only possible with the more rigorous approach which explicitly includes effects such as polarization and charge transfer. The importance of electrostatics would likely increase with more accurate basis sets.

The individual cases discussed above highlight several challenges with computational alanine scanning particularly as it relates to applying quantum mechanics. The first difficulty is in considering how side chains reorient upon complex formation. In many cases, it appears to be a reasonable assumption that the conformations adopted by side chains in the complex are not significantly higher in energy than those adopted in the apo structure. There are, however, going to be examples where this assumption is not valid. The only way in which this effect can be accurately captured is through side chain sampling in both the complex and apo structures. This challenge is well demonstrated with the 1jtg example. It is worth noting that identifying those residues that seemingly make strong interactions across the interface but result in no gain in binding affinity due to the loss of similar interactions in one of the apo forms could be very important. These sites are areas where small molecules may be able to improve upon the protein-protein interactions. In this regard, computational alanine scanning is complementary to experimental alanine scanning

A second challenge is to properly handle the rearrangement of discrete water molecules at the interface. This is likely a straightforward exercise when there is a single tightly bound water affected by a mutation. In a situation such as barnase/barstar where the interface is highly solvated and the effects of a single mutation might propagate further along the interface, properly handling the waters may prove to be quite challenging. Indeed, Jiang and co-workers have shown improvement with their computational alanine scanning by explicitly handling discrete waters through a solvated rotamer approach.⁶⁰

The biggest challenge in general with applying quantum mechanics to computational alanine scanning and ultimately protein design is speed. Even with the linear scaling algorithms, quantum mechanical calculations require on the order of hours of CPU time for a single point energy calculation compared to milliseconds for traditional force field based or empirical methods. This is further exasperated when addressing side chain and water sampling issues discussed in the previous paragraph. Given the resources needed, quantum mechanics is best suited as a final filter in the selection of mutants or design of new proteins. The results we present here suggest that current quantum mechanical tools could be a valuable asset as a final filter and offer more evidence that improvements in rigor will lead to improved calculations.