Motor strategies used by rats spinalized at birth to maintain stance in response to imposed perturbations

Abstract

Some rats spinalized P1/P2 achieve autonomous weight supported locomotion and quiet stance as adults. We used force platforms and robot applied perturbations to test such spinalized rats (n=6) which exhibited both weight supporting locomotion and stance, and also normal rats (n=8). Ground reaction forces in individual limbs, and the animals’ center of pressure were examined. In normal rats, both forelimbs and hindlimbs participated actively to control horizontal components of ground reaction forces. Rostral perturbations increased forelimb ground reaction forces, and caudal perturbations increased hindlimb ground reaction forces. Operate rats carried 60% body weight on the forelimbs and had a more rostral center of pressure placement. Normal rats pattern was to carry significantly more weight on the hindlimbs in quiet stance (~60%). Operate rats strategy of compensation for perturbations was entirely in forelimbs; as a result, the hind-limbs were largely isolated from the perturbation. Stiffness magnitude of the whole body was measured: its magnitude was hourglass shaped, with the principal axis oriented rostrocaudally. Operate rats were significantly less stiff; only 60-75% of normal rats’ stiffness. The injured rats adopt a stance strategy that isolates the hindlimbs from perturbation and may thus prevent hindlimb loadings. Such loadings could initiate reflex stepping, which we observed. This might activate lumbar pattern generators used in their locomotion. Adult spinalized rats never achieve independent hindlimb weight supported stance. The stance strategy of the P1 spinalized rats differed strongly from the behavior of intact rats and may be difficult for rats spinalized as adults to master.

Introduction

This paper compares stance control in rats which received spinal cord transections as neonates versus normal rats. Some neonatal spinalized rats (~20%) develop weight supported locomotion as adults despite the complete spinal transection (Stelzner et al. 1975), as do kittens Howland et al. 1995a, Robinson and Goldberger, 1986). Understanding the mechanisms of weight support and the control of locomotion and posture after spinal injury in such rats illuminates aspects of motor control and may provide a roadmap for the design of therapies for SCI.

Many spinal reflexes and compensatory mechanisms persist below the lesion after spinalization (Hiebert et al. 1996, Bouyer et al. 2001). Analyses of spinal circuits suggest that separate interacting interneuronal populations may play specific roles in stance and locomotion in spinal cord (see Jankowska and Edgely 1993). Thus these tasks may need to be trained differently after spinal cord transection. Indeed, adult spinalized cats trained to walk often do not stand well, and those that are trained to stand do not walk well (see Hodgson et al., 1994, DeLeon et al. 1999, and Tillakaratne et al. 2002), although with special training efforts some spinalized cats may accomplish both (see Edgerton et al., 1997 for review). However, cats spinalized as neonates and trained (Forssberg, Grillner and Rossignol 1975, Forssberg, Grillner, and Sjostrom, 1974, Grillner 1975; Smith et al. 1982; Howland et al. 1995a, Hiebert et al. 1996) can more often perform both locomotion and stance tasks autonomously and fairly competently as adults (e.g., Robinson and Goldberger, 1986). How such neonatal spinalized mammals integrate voluntary and brain controlled postural adjustments with spinal mechanisms in both stance and locomotor tasks is unknown.

We focus here on control of stance in rats spinalized P1/P2 which also had the the ability to walk independently using hindlimb weight support. Control of quiet stance requires integrated responses of both trunk and legs. Mapping of motor cortex in such rats suggested that voluntary postural control of the axial muscles may be critical for their weight-supported locomotion (Giszter et al. 1998). The task of quiet stance has not been examined in neonatal spinalized rats, nor have stance responses to external perturbations been tested in rats generally.

We trained all rats to walk on a treadmill and to stand quietly for rewards. They showed both weight-supported stance and weight-supported locomotion on all four limbs. Postural adjustments of normal and operate (spinal and transplant) rats were examined during a stance task using robot applied perturbations similar to jostling by cage mates. We examined coordination of limb forces during stance following perturbations applied using a small robot. Robots have previously been employed in rats primarily for training locomotion (e.g. Timoszyk et al. 2002, see De Leon et al. 2002a) and to assess its quality and plasticity (e.g., Timoszyk et al., 2005, DeLeon et al., 2002b).

Our data will show that operate and normal rats adapt their center of pressure to perturbations. However, their voluntary postural mechanisms are quite different. During quiet posture, spinalized rats miminize transmission of perturbation forces to the hindlimbs, while normal rats show forelimb-hindlimb cooperation. It is unknown if this strategy can be taught to adult injured rats. Learning to use functional motor strategies that differ from normal behaviors may aid clinical rehabilitation in some injuries and diseases.

Materials and Methods

All procedures were conducted in accordance with NIH and USDA guidelines and the approval of the Institutional Animal Care and Use Committee.

Neonatal transection/transplantation

25 rats in total were used in this study. 17 Sprague Dawley rats received midthoracic (T8-T9) transections on postnatal day 2 (P2). One or two segments of spinal cord tissue was removed with sharp dissection and gentle aspiration. In 8 of these rats, a 1-2 mm section of E14 fetal thoracic spinal tissue was transplanted into the lesion cavity (transplant rats). The remaining 9 rats underwent transection only with no transplantation (spinal rats). (Methods of transplantation described previously in Miya et al. 1997, Giszter et al. 1998). Eight additional rats served as normal controls (Normal rats). All operate rats were confirmed to have surgically complete transections using the standard histological techniques of Nissl-myelin and serotonergic immunohistochemistry (see Giszter et al. 1998, Miya et al. 1997). All rats received treadmill training and were tested in stance training.

Training

All rats entered the training program at post-natal day 21. Rats were trained biweekly to walk on a treadmill (speed 8cm/s) for five minutes sessions and 3 times per week to stand quietly on a platform for approximately 5 minutes for a water reward. Starting at post-natal day 28, water availability was limited to the test period and for an additional thirty minutes a day afterward. Rats were given water ad libitum from Friday afternoon until Sunday afternoon.

Testing Paradigm

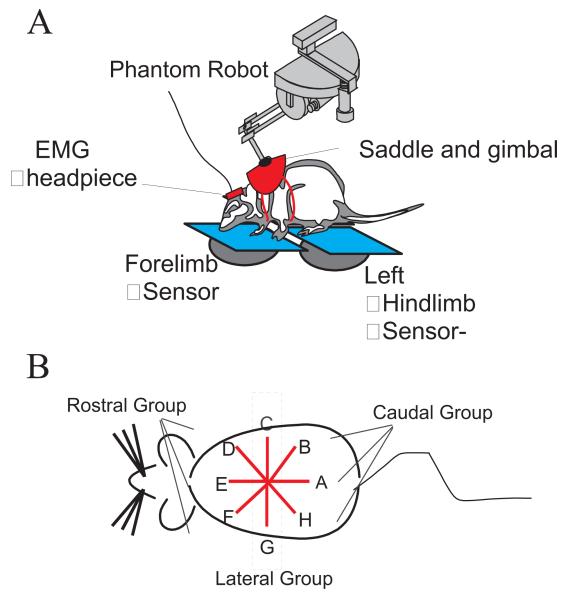
The testing platform consisted of 3 pieces of 0.5 inch thick, clear Plexiglas each attached to a FT3/10 force transducer (ATI Industrial Automation, Garner, NC; range of force = 3 lb, range of torque = 10 lb-in, resolution of force = 0.04 oz, resolution of torque = 0.08 oz-in). There was one sensor for each hindlimb (RHL sensor and LHL sensor) and a third for both forelimbs (FL sensor). Each force transducer, or sensor, recorded the 3 dimensional forces and torques exerted on the support plate, and thus allowed a calculation of the ground reaction forces resulting from the pressure of the limb or limbs on that sensor. Initial trials involved collecting ground reaction forces while the rat was standing freely and quietly. In later trials, a haptic interface device, the Phantom (SensAble Devices Inc., Cambridge, MA), attached to the rat via a saddle and jacket (made in house), was used to deliver perturbations to the rat. See Figure 1 A.

Figure 1.

A: Diagram of the testing paradigm. The Phantom™ robot was attached to the rat via a saddle and jacket mounted on the rat’s torso, near the shoulders. The saddle was attached to the robot with a gimbal. The rats stood with their two forelimbs on one force-plate sensor and each hindlimb on an individual force-plate sensor. The rat was motivated to drink from a drinking tube for a water reward. When active, the robot imposed a horizontal elastic field on the rat’s torso at the thorax. On perturbation trials the equilibrium of this field was moved in the commanded direction by a pre-specified distance. The rat either resisted and compensated for, or yielded to, the resulting directional interaction forces.

B: A diagram of a dorsal view of a rat depicting directions of perturbations. In all figures the rat’s head is to the left, and the perturbations are as indicated in A – H. The DEF group of directions constitute rostral perturbations and HAB group of direction are caudal perturbations. Perturbations began at A and proceeded to H. Perturbations were applied with increasing magnitude of the equilibrium motion in each set: first perturbation set 1.9cm, second 3.8cm, third 5.7cm.

Perturbations

A Phantom robot (Model T / A, Sensable Device Incorporated, and originally designed for human haptics applications) running in a control loop at 1.5KHz delivered perturbations to the rat. The robot was programmed to simulate isotropic Cartesian elastic fields in the horizontal plane with an extremely weak field component vertically. Field stiffness in the horizontal plane was 76.91 N/m. Perturbations consisted of a constant velocity motion of the elastic fields equilibrium, to the new target position specified by the perturbation direction. The velocity of the motion was proportional to the distance to be traversed (0.75 , 1.5 , or 2.25inches, 1.9cm, 3.8cm, 5.7cm ) so that all perturbations were completed in the same time (500 ms). Thus, in larger perturbations the equilibrium motion and rise in force were proportionally faster. If a rat yielded perfectly and moved to track the equilibrium, the interaction forces with the robot would be zero. If a rat completely resisted the perturbation and remained immobile, the interaction force with the robot would reflect the equilibrium motion and the rat’s distance from equilibrium. In this case (for an apparently infinitely stiff object) the peak horizontal plane force in the largest perturbation would have been 4.38 N ( ~429gm). Typical net horizontal forces generated at the force plates in large perturbations were ~150 to 200g. Our perturbation paradigm was in some regards (constant velocity motions set by the peak excursion) similar to Shadmehr and Mussa-Ivaldi (1993), but in their case a proportional derivative (PD) controller was used rather than a simple elastic field.

Data Collection

Using the robot, a cycle of eight perturbations was delivered. These were arranged uniformly, counterclockwise around a circle centered on the rest position of the rat. A perturbation caudal (toward the tail) was designated as zero degrees, while a 90-degree perturbation was toward the right side of the rat (see Figure 1 B). For all measures, results were separated into groups based on the direction of perturbation. These groups were rostral group, caudal group or lateral group. Responses to perturbations at 135, 180 and 225 degrees were classified as rostral group, those at 0, 45 and 315 degrees were classified as caudal group, and those at 90 and 270 degrees were classified as lateral. The cycle was repeated 3 times, utilizing a different size perturbation for each cycle, with excursions of the elastic field of 1.9, 3.8, or 5.7 cm. The Phantom recorded the resulting interaction force between the rat and the robot, i.e, the force that was delivered as a result of the location of the robot tip in the programmed elastic field. The force thus represented the difference between the field equilibrium and the robot tip position, and this force was experienced as a perturbation by the rat. Interaction force at the saddle was saved throughout the trial at a sampling rate of 63 Hz (i.e. synchronized to the three force plates data collection). Simultaneously, the reaction of the rat to the perturbation was measured from the ground reaction forces on the force plates and the EMG activity recorded. Ground reaction forces of the limbs were collected from the ATI force transducers at a sampling rate of 63 Hz. This was sufficiently rapid for the stance task and was also limited by the serial communication mode with 3 sensors which was employed in this set of experiments and version of our apparatus. The response of the rat to perturbation ramp onset and plateau was smooth and continuous. We believe this was essential to the tests here, because other perturbation tests could cause stepping. For example we observed that withdrawal or stepping motions could be induced with greater likelihood in operate rats by the more rapid release from applied force as the perturbation terminated. Ground reaction force data and the Phantom force data were all synchronized and collected simultaneously using in-house C programs. The data collection and control program lit an LED within the video camera field, allowing video data to be synchronized with the rest of the data. Video data was collected at 60 Hz single field rate with a shutter speed of 500 Hz.

Data Analysis

For this study, only the data collected from normal rats and weight supporting operate (including both spinal and transplant) rats were used. A weight-supporting rat is defined as a rat that underwent neonatal transection or transplantation surgery, but could stand and walk unassisted, and with more than 60% of it’s step cycles executed without its belly, knees or hips touching the support surface.

The three dimensional forces and torques collected from the force sensors were used to calculate the center of pressure (CoP), or foot placement, for each sensor. X and Y coordinates of the foot placement on each sensor were obtained using the following formula. The x and y coordinates, for each foot placement, were based on the center of the respective sensor. Offsets were added to the individual coordinates, based on the location of the sensors to each other, to have them all related to the same world coordinate system. The z value is the offset needed due to the thickness of the plexiglass.

$$\begin{array}{cc}\hfill & x=\frac{(z\ast F_x-T_y)}{F_z}\hfill \\ \hfill & y=\frac{(T_x-z\ast F_y)}{F_z}\hfill \end{array}$$

Where F are translation force components along, and T torque components about, their respective axes. These individual foot placements and the ground reaction forces were combined to obtain the resultant CoP of the entire rat.

$$\begin{array}{cc}\hfill & {\mathit{CoP}}_x=\frac{(F_{z1}\ast x_1+F_{z2}\ast x_2+F_{z3}\ast x_3)}{(F_{z1}+F_{z2}+F_{z3})}\hfill \\ \hfill & {\mathit{CoP}}_y=\frac{(F_{z1}\ast y_1+F_{z2}\ast y_2+F_{z3}\ast y_3)}{(F_{z1}+F_{z2}+F_{z3})}\hfill \end{array}$$

As a check on the completeness of our description and analysis, we examined the vector sum of horizontal plane ground reaction forces and Phantom interaction forces at the maximum of the perturbation. This sum was invariably close to zero, so that the resultant horizontal force of all limbs was opposite to the vector of perturbation and the rat’s body was at or very close to equilibrium. This is consistent with static equilibrium of the rat and similar to the results published in cat (Macpherson et al 1988).

Statistics

To compare distributions we used t-test parametric statistics, and Fisher distribution circular statistics, using unit vectors from data samples in planar circular or in spherical coordinates (Fisher 1993; Fisher, Lewis and Embleton, 1987).

RESULTS

Seventeen rats in this study received neonatal spinal surgery and entered the training and testing program. Six of these rats were able to maintain weight support while locomoting on the treadmill and while standing statically. Five rats did not consistently maintain weight support while standing statically in our apparatus, although they were able to achieve some weight supported locomotion on the treadmill. In contrast, in many years of work now on spinalized rats, we have never observed rats which could stand statically but could not walk. The remaining operate rats could not achieve weight support while standing or locomoting. 8 normal rats acted as controls. The results presented are from the 8 normal rats and the 6 operate rats that consistently weight supported during both tasks. These operates comprised 4 transplant receiving rats and 2 spinal rats. We could not readily distinguish the 2 untreated spinalized rats from the 4 transplant recipient rats based on either individual motor performance or motor strategy in this group of rats. Accordingly, in subsequent analyses, the untreated spinalized and transplant recipient rats are combined and examined together as ‘operate rats’. All operate rats used were confirmed to be histologically complete and similar to rats in Miya et al. 1997 and Giszter et al. 1998.

A. Center of Pressure (CoP)

A.1 Center of Pressure (CoP) in unperturbed initial trials

In initial trials, the rats stood freely on the platform and their ground reaction forces were recorded without the saddle. We then examined the effect of the saddle placement. Rats were attached to the phantom robot using the saddle, but no perturbations or forces were delivered (quiet stance). For both of these sets of data for each animal the individual foot placements on each force-plate and the resultant center of pressure (CoP) were calculated for comparison with subsequent test trials. The CoP’s small fluctuations through time during stance form the ‘stabilogram’ (e.g., Collins and DeLuca, 1993). The mean position of the CoP in the base of support, the statistics of the deviations of CoP and the time series of the motions of the CoP can all give insight into control (Collins and Deluca, 1995, Zatsiorsky and Duarte, 1999, Grzegorzewski and Kowalczyk, 2001). We focused here simply on the mean CoP location in unperturbed stance, deferring detailed analysis of CoP excursions to future work. There was no significant difference in CoP between the two sets of data for each individual rat when unencumbered and then when saddled prior to any use of the robot (p>0.3). This constancy indicates that neither the robot’s small unbalanced weight nor the sensation of the harness significantly perturbed the individual rat’s posture or stance in the unperturbed pre-trial condition.

There was a group difference in CoP between normal rats and operates during quiet stance. The position of the CoP relative to the individual foot placements ( Figure 2 and Table 1) showed a forward shift of the CoP in the injured rats. This shift in CoP is due to a change in the fore-hindlimb force distribution. This has also been seen in chronic spinal cats (Pratt, Fung and Mac Pherson 1994). In operate rats, the CoP is almost midway between the forelimb and hindlimb foot placement, while in normal rats the CoP is closer to the hindlimb foot position. This could arise from an altered mass distribution in the rat or represent a motor strategy. It is likely to reflect both. The hindlimbs are always significantly lighter in neonatal spinalized rats. We demonstrated this by testing the total hindlimb muscle mass in these rats, after our experiments were completed and the rats perfused for histology. Major muscles were removed and weighed and summed. The net hindlimb muscle mass as a fraction of body weight in the weight supporting operates differed significantly compared to the fractional weight of muscles in normal animals (two tailed t-test, p = 0.0032). The haunches were about 15-20% lighter in weight supporting operates.

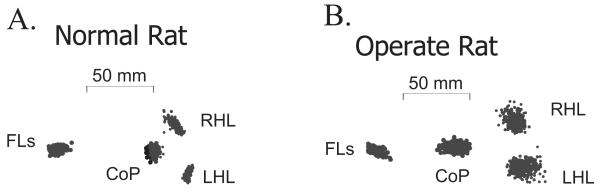
Figure 2.

Plots of the center of pressure and force application of the rat’s feet on each individual sensor (FLs: forelimb, RHL right hindlimb, LHL left hindlimb) and the resultant center of pressure (CoP) of the rat as a whole on the support surface. The CoP was computed from the individual sensor force applications. The CoP’s small fluctuations through time form the ‘stabilogram’. Data are shown for (A) a normal rat J494, and (B) an operate rat J490, in an unperturbed resting state before trials began. The CoP fluctuations observed over 500 ms are shown as unconnected dots. The CoP of the normal rat is more caudal than the operate rat’s CoP and shows less rostrocaudal variation in position or dispersion. The difference in position was statistically significant (see text and Table1). The points of application of force by the hindlimbs of the normal rat show directional variations that were absent in the injured rats, and probably associated with hindlimb postural differences between normal and operate rats.

Table 1.

Mean position of the resultant center of pressure position in the base of support. The CoP is measured from forelimbs, and this value is divided by the distance between the forelimbs and the hindlimbs placement. Thus a value of 0.5 is centered between the two limb pairs. High ratios indicate that the COP is near the hindlimbs, and low ratios that it is near the forelimbs.

Activity	Mean position ratio
Operates during quiet stance (n=6)	0.46
Normal Rats during quiet stance (n=8)	0.75
Operates with phantom attached prior to perturbation (n=6)	0.55
Normal Rats with phantom attached prior to perturbation (n=8)	0.65

Forces were resolved into the vertical or weight support forces and the horizontal plane (shear force) vectors for quiet unperturbed stance. We will refer to the latter as horizontal stabilizing force vectors. We found that the magnitudes of most horizontal force components did not differ between operates and normals after they were normalized to body weight. However, the hindlimb’s mediolateral components differed strongly between groups (two tailed t-test, p<0.0005) and were larger in operates, for quiet stance without any perturbations. We compared the horizontal forces of hindlimbs and forelimbs after they were normalized to the vertical loads on the individual limbs rather than overall body weight. This test showed that the ratio of mediolateral components to vertical components of both the forelimbs and the hindlimbs differed significantly between operates and normals (two tailed t-test, p<0.001). This difference in lateral forces could represent a difference in control or posture of the hindlimbs, or simply the altered load bearing of the hindlimbs as reflected in the CoP. Video and observation showed that the hindlimbs of operate rats often showed postural differences from normals, (for example splaying, and see Miya et al. 1997). The force component differences are likely to be due at least partly to these configuration differences.

A.2 Center of Pressure (CoP) in perturbed trials

For the test trials, when the Phantom was attached and producing perturbations to the rats’ stance, the center of pressure during rest periods or during the quiet stance in the first 0.5 seconds (pre-perturbation) was again calculated. During this time, the phantom was active but centered at the rat’s chosen posture. However, if the rat leaned, the robot would then apply small holding forces, but these were always well under 0.05N.

Rats quickly adapted their quiet stance posture, and shifted their CoP, once perturbation experiments had begun. This adaptation was made by rats in all sessions after about a week. It occurred prior to perturbation application, and also occurred in sessions where perturbations were not applied at all. It was an adaptation by the rats. We found that the CoP for the normal rats was now closer to midway (a ratio of 0.5) between the forelimb and hindlimb foot placements than before the phantom was attached. Normal rats had a mean CoP ratio of 0.65 compared to 0.75 before any perturbation testing with the robot. This change in their stabilogram’s mean or target posture was statistically significant (p <0.001, one-tailed t-test). Once the operates were attached to the phantom in perturbation experiments, and tested in rest periods, their CoP also moved. However, the resting CoP in operates moved caudally; it was 0.55 after testing began and 0.46 before testing (a significant difference, two tailed t-test, p < 0.0001). The significant difference between normal rats and operates in resting CoP described above before testing remained during testing with perturbations (during perturbation testing a two-tailed t-test showed a P-value <0.0001, and see Table 1). Both normal and operate rats adopted specific postural strategies, each adopting a posture which produced a more even load distribution between fore- and hindlimbs during perturbation testing (both moved closer to a ratio of 0.5). This weight distribution differed significantly from the initial quiet stance distributions recorded in the complete absence of perturbations and caused their CoP to move towards the center of the base of support when perturbations were expected.

B. Perturbation responses

The robot applied a directed elastic load to the rats during perturbation trials. The equilibrium of the elastic field generated by the robot moved gradually away from the rats’ resting position (velocity of equilibrium motion was proportional to perturbation size, 3.8cm/s, 7.6cm/s, or 11.4cm/s). The saddle then applied force to the rat if the rat did not comply with the motion. The force that the rat needed to generate in order to resist the perturbation ranged up to 400g but was easily within the rat’s capacity. To receive the water reward throughout the trial the rat had to stabilize its head at the drinking spigot. Rats continued drinking through both the perturbed and unperturbed trials. There were concomitant small rhythmic forces in the body induced by head bobbing and lapping motions, and these were sometimes large enough to be visible in the three force sensors in several rats. However, these internally generated force variations were negligible (<5%) compared to the responses to the perturbations. Rats generally responded smoothly and continuously to the perturbations. They used a combination of resistance and motion. Rats only rarely lost balance or exhibited steps or shifts of the feet. Trials with compensating steps were rejected. Thus foot placement was maintained in the data presented below. A typical perturbation response is shown in Figure 3 in which the robot motion, interaction force at the thorax and the ground reaction force in the hindlimb are shown for an operate rat.

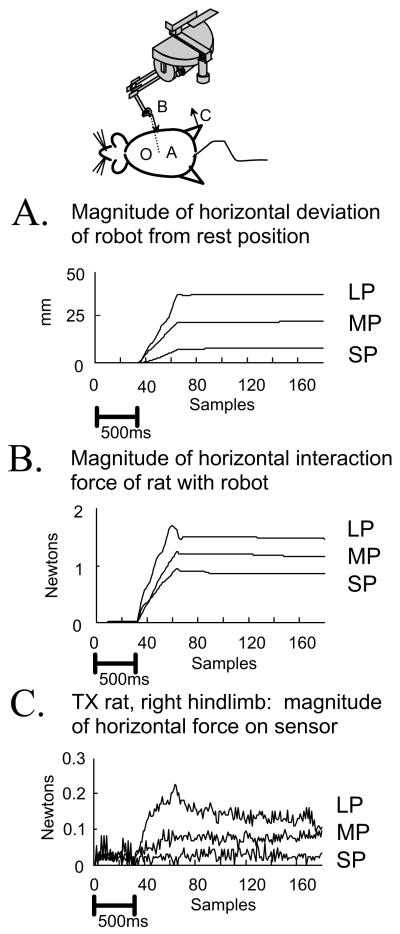
Figure 3.

Plots of the responses in perturbation trials for a single direction perturbation applied to an operate (TX) rat’s stance. LP large perturbation, MP medium perturbation, SP small perturbation. Shown are :(A) the distance over time of the position of the phantom tip from rest. (B), the magnitude of the horizontal plane interaction force between an operate rat and the Phantom. (C) the magnitude of the horizontal plane ground reaction force at the right hindlimb force-plate sensor. Rats picked a strategy for how to distribute horizontal (‘shear’) forces among the individual leg’s ground reaction forces. Data is shown for operate rat number J490 (CoP shown in Figure 2). Data are plotted during each size perturbation, all in direction D (See Fig 1). Bias resting force was removed from the ground reaction force sensor and position is referenced to the rest posture. Data is plotted at each force sample acquisition from the sensors (15.8ms increments). Time is displayed both as the sample count, and as a 500ms scale bar in panel A. Note the small hindlimb force responses in panel C relative to the applied force in panel B in this rat.

B.1 Force direction and magnitude

We evaluated the the motion of the saddle, and the direction and magnitude of the interaction force produced by the Phantom during the perturbations. The equilibrium of the robot elastic field moved in precise radial directions starting from a point centered on the rat’s resting position. Field stiffness was ~76 N/m in the horizontal plane, and 7.6N/m vertically. Prior to any perturbation the compliant elastic field was present, centered on the rest position at the start of the series. Therefore, it was possible for the rat to lean on the robot, before any perturbation. The degree of interaction with the force field generated by the robot prior to a perturbation varied among rats and from day to day. However the vertical component of the field interaction was usually under 5% of body weight of the rat (i.e., ~0.1N for a 200g / 1.962N) and less than the load of the saddle. The robot did not provide significant assistance against gravity. Thus the rat was almost wholly self supporting vertically. Leaning horizontal plane forces, if present, were usually less than 2-3% of forces during perturbations (5-6g, 0.06N). Despite this, the horizontal field force components delivered by the robot could provide the opportunity for additional external stabilization of the rats. If the initial horizontal interaction force was zero, then the rat was wholly self stabilizing at the beginning of a trial. If this interaction was small before the perturbation, then force vectors were, as expected, predominantly radially-directed (see below and Figure 5). If there was a larger interaction between the Phantom and the rat, the rat was using the Phantom harness as a partial means of horizontal stabilization and support in the period prior to the perturbation and the interaction force vectors were not predominantly radially-directed. Some rats always used the Phantom as a partial aid to horizontal stability, and all rats sometimes used the Phantom as a partial aid to stability. This occured in both normal and operated rats. The significant results presented here and below hold for data from both types of trials, but for clarity of presentation the Figures and analysis focus on those trials in which the rats did not use the Phantom as an aid.

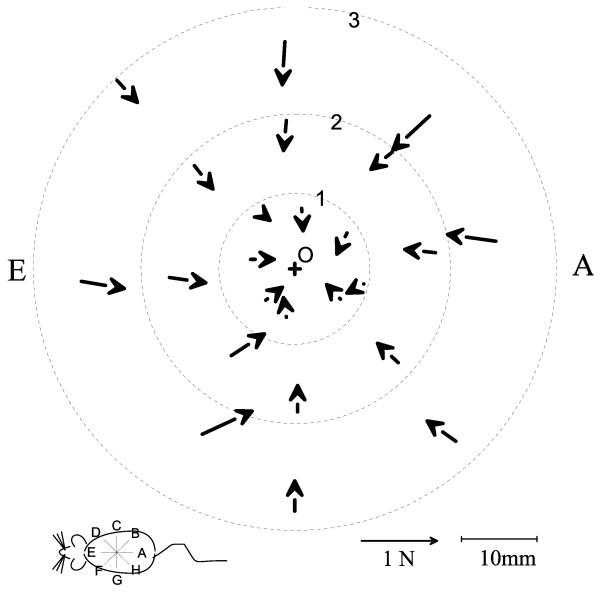
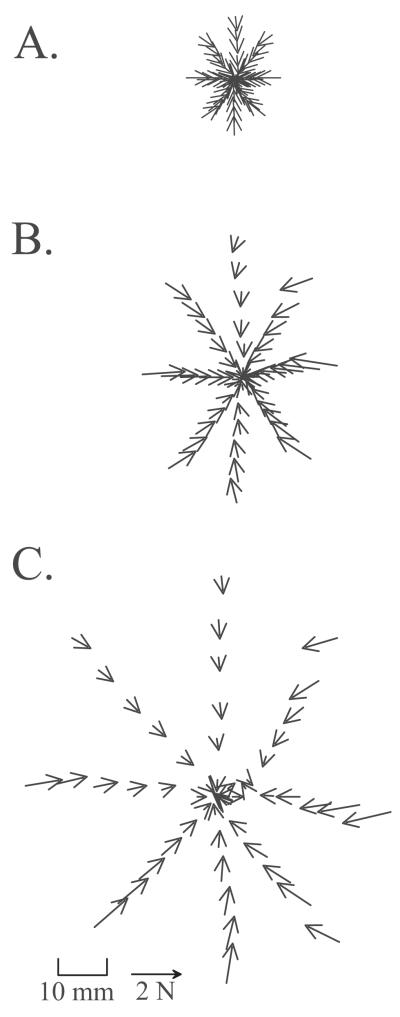
Figure 5.

The maximum active interaction force vectors between the rat and the robot (see also figure 2 and 4). Data from a normal rat, J494, in which the initial pre-perturbation interaction of the phantom and the rat was low on each set of trials. (+: location of robot equilibrium before perturbations, O: approximate rest location of rat before perturbations). The vectors show the peak forces generated by the rat after subtraction of resting forces. The vectors displayed were measured at the peak excursion produced by the Phantom for each perturbation. Each ring of vectors represents a perturbation size (1: 19mm, 2: 38mm, 3: 57mm ). Each line of 3 vectors represents a perturbation direction. The interaction forces are shown plotted as vectors at the measurement point to which the robot moved against the rat’s resistance. Force rises with the size of the perturbation, though not proportionately. Note also that forces converge approximately toward the rest position of the rat, but not precisely, since these represent active response forces.

In Figure 3 it can be seen that forces rose smoothly to a plateau. The phantom interaction forces in a normal rat are plotted as vectors in the horizontal plane at intervals of 30ms throughout the time course of perturbations in each of the 8 directions in Figure 4.

Figure 4.

Vector plots of the interaction force of rat and robot plotted at the robot tip position at intervals of 30ms through time. All directions in each of three perturbations sizes are shown [Commanded perturbation distances of elastic robot equilibrium : A) 19mm; B) 38mm; C) 57mm]. Data are for normal rat number J494 (CoP shown in Figure 2). Note the relatively larger excursion to force magnitude relationship that can be seen in C relative to A.

B.2 Ground Reaction Force Magnitude and tuning in response to perturbation

To test general compensatory responses of the rats to perturbation we examined the initial force vectors, the peak and plateau force vectors, the changes in ground reaction force vectors in the vertical direction and the horizontal plane, and the Center of Pressure. We found that the CoP did not move out of the range of the resting (stabilogram) measurements during the perturbation. Thus, CoP was stabilized. This was true of both normals and operate rats. Pre-perturbation period and plateau stabilograms were not statistically different. Vertical forces were not altered significantly. The CoP location was dominated by these vertical antigravity forces, which were far larger than horizontal plane forces. Accordingly, we focused subsequent analysis on the horizontal force components which showed perturbation responses.

The data for the individual animals in Figure 6 and subsequent figures are characteristic of the responses observed. Horizontal ground reaction force vectors of the forelimbs and each hindlimb were examined with regard to their direction and magnitude (Figure 6). The forces are plotted every 45 degrees around a circle centered on each sensor. The location of each force thus indicates the direction of the perturbation applied. For each rat the combined data from several days (6-8 days of complete testing) are depicted, each vector originating at a location representing a different day’s response to the perturbation in that direction.

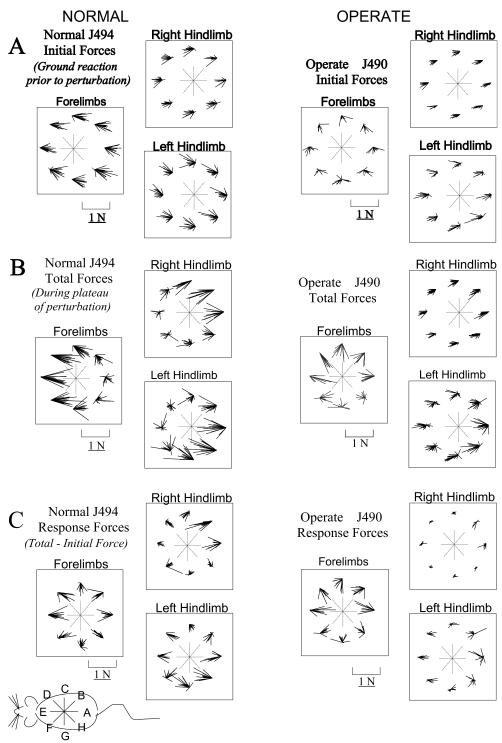
Figure 6.

Plots of raw A. Initial (pre-perturbation), B. Total (peak perturbation, see figure 3), and C. Response (Total-Initial) horizontal plane components of ground reaction force vectors measured from the force-plates. Groups of vectors are shown for the combined forelimbs force-plate and for each hindlimb forceplate. Within each group the measurements are organized into 8 clusters based on the direction of perturbation, as indicated by the central compass. Vectors originate at a common fixed point with no physical significance besides indicating direction of perturbation in the cluster trials. The small schematic of the rat in the lower left corner provides the orientation of the rat and the perturbations. Initial forces in A represent the horizontal plane shear forces before any perturbation. Total forces in B represent the peak interaction of rat and robot. Response forces in C represent the vector difference of forces in B and A. In A: Note variation of force trial to trial, but the clearly differing patterns of forelimb force in the operate and normal. In B: Note the tendency for horizontal shear loading to be concentrated in either the forelimbs (left clusters (perturbation directtions D, E, F in Figure 1) on forelimb plate) or hindlimbs (rightmost clusters (perturbation directtions B, A, H in Figure 1) on hindlimb plates) in the normal rat. Forces in the forelimbs of operate rats differ in direction, and this concentration of loading in either forelimb or hindlimb is largely absent. In C: Note that Hindlimb response forces in the operate are far smaller than in normals (Significantly so, two tailed t-test, p<0.05). In this data set there is some response in the left hindlimb in the operate.

We divided the analysis of forces and responses into three parts: first, analysis of the initial resting forces, next the total forces developed in response to perturbation, and finally the difference between these two, which we term ‘response forces’. The initial resting forces are the ground reaction forces exerted before the perturbation has begun, (in the 0.5s before perturbation onset) representing resting postural forces. During and following perturbation by the robot, the rat responded. The forces from 0.55 seconds after perturbation onset and beyond constitute the total response (or simply ‘total’) forces. At this point the perturbation shift in robot equilibrium was completed and holding steady. The Phantom was usually producing its maximum force during interaction with the rat at this time (e.g., Figure 3). The maximum force (~0.55s) and the subsequent stable plateau forces (times >0.55s) during perturbations did not differ significantly when compared statistically. We analyzed these further by subtracting the mean of initial resting forces from the mean of total plateau forces, to examine “response forces” in each trial. These represent the rat’s active change in response.. These response forces were thus the vector changes in the ground contact force applied by the limb as a result of the perturbation. The initial resting forces for a normal (J494) and an operate (J490) are shown in Figure 6 A, the total forces in Figure 6 B and the response forces in 6C.

For the normal rats’ initial resting horizontal forces (e.g., J494- Figure 6 A), the forelimb generated ground reaction forces were directed caudally while the hindlimb generated ground reaction forces were directed rostrally. For the operate rats (e.g., J490- Figure 6 A), in contrast, the direction of initial forelimb forces were sometimes not as consistent, although the hindlimb forces were all rostrally directed before all perturbations. Although CoP was closer to the center of the base of support in all rats, as remarked above, none of the animals anticipated the specific direction of the perturbation through the repeating cycle. None adjusted their pre-perturbation posture or horizontal limb forces trial by trial. This can be seen from the fact that there was no systematic variation in the direction and magnitude of initial forces with perturbation direction.

Total forces resulting from the perturbation are shown in Figure 6 B. In normal rats (e.g., J494- Figure 6 B), there was a difference between the distribution of forces produced for rostral perturbations and those produced for caudal perturbations. During rostral perturbations, the total horizontal forces were larger in the forelimbs, and during caudal perturbations, the total horizontal forces were larger in the hindlimbs. In contrast, in the operate rats (e.g., J490- Figure 6 B), this distinction between rostral and caudal perturbations was largely absent. Forelimb total forces were adjusted in all directions while hindlimb total forces were not very different from initial forces. The way in which rats compensated for perturbation forces thus differed in the normal and the spinal injured rats.

B.3 Active Responses forces

Active response forces in our analysis represent the change in force due to the perturbation. By examining active force responses we could assess in more detail how force alterations were distributed to the limbs in our animals. A range of response strategies are possible for rats in choosing total forces. The additional compensation by the rat was the vector sum of the changes in individual limb forces. Within a limb, the total horizontal ground reaction forces could be increased or decreased, or their direction could be altered. We evaluated response forces by subtracting initial from total force vectors, thus a decrease in total force vector from the initial force will be represented by an active response vector which is in the opposite direction from the initial force. It is important to keep in mind that, despite this convention, the actual total ground reaction force remained in the same direction and sense in both cases: in the one case total magnitude diminished and in the other it increased.

Response force analysis showed that in the normal rat (e.g., J494- Figure 6 C) the total force pattern observed resulted from two changes. There was (1) a rise in the forces in the limbs towards which perturbation occurred and (2) there was some decrease in the other limb pair’s force, e.g., forelimb force increased and hindlimb force decreased together. In contrast, we found that in the operate rats (e.g., J490 –Figure 6 C) the forelimb active response forces were always substantially larger than the hindlimb response forces, for all perturbations. Further, notice that the force changes in the right hindlimb in the operate rat J490 shown in Fig 6C were negligible. Routinely we observed a pattern of very small hindlimb force adjustments of this type in the operates. We tested this difference in magnitude in the pattern of compensation in operates compared to the normal rats and this was statistically significant (two-tailed t-test p<0.05,).

We plotted all total horizontal ground reaction forces to all perturbations as a population of vectors (Figure 7). In the normal rat (J494- Figure 7 A) total forces exhibited a strong directionality in both the forelimbs and hindlimbs. The forelimb forces were always directed caudally and the hindlimb forces were always directed rostrally. In the operate (J490- Figure 7 B), the hindlimb forces clearly exhibited a directionality of response, but the ground reaction forces were generated in all directions by the forelimbs of operates in contrast to normal rats. To analyze this further we examined tuning of response magnitudes.

Figure 7.

Plots of raw horizontal total response force vectors for all perturbations in all directions in a normal rat (A) and an operate (B). Forces are plotted for the forelimb (FL) sensor, the right hindlimb (RHL) and left hindlimb (LHL) sensors. These combined data show that there is clear directional clustering of hindlimb forces in both the normals and the operate rats, but clustering of forelimbs directions occurs only in normal rats. In contrast, there is wide directional variability of forelimb forces in operates. This is consistent with forelimb compensation dominating the response adjustment used in operates, which requires force production in all directions in the forelimbs and small or negligible active force changes in the hindlimbs (see Figure 8).

B4 Force Tuning

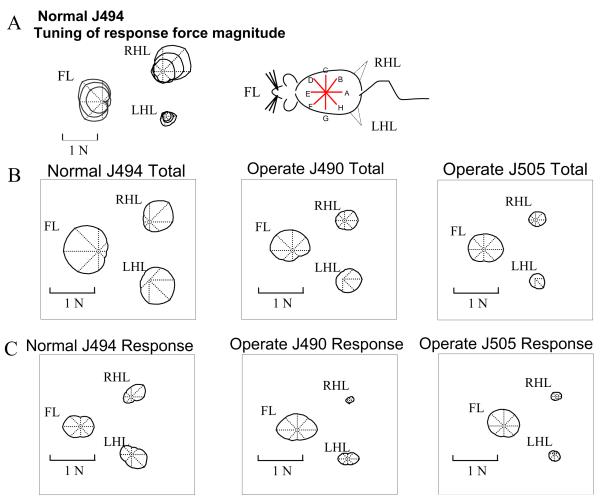
We averaged the data in Figure 6 across trials and perturbation strengths and constructed tuning curves of response magnitudes for each perturbation direction. We then used these curves in order to evaluate more precisely how the direction of perturbation modulated the magnitude of force in each limb. The tuning curve was produced by plotting the average magnitude in polar coordinates as a function of the perturbation direction, as described by MacPherson (1988a).The magnitudes of initial pre-perturbation forces showed no clear tuning to the subsequently applied perturbation direction. A tuning curve of the magnitude of the total horizontal force measured by each sensor was generated for different perturbation directions (Figure 8). Depth of modulation of force (largest -smallest force/largest force as a percentage) was 80-90% in forelimbs and 50-80% in hindlimbs. The tuning curves’ principal directions for the three different size perturbations that we used did not differ significantly as a result of perturbation magnitude in either rat group; the three perturbation magnitudes of a normal rat are overlaid in Figure 8 A. At each perturbation direction, we then combined all trials. We normalized magnitudes of the horizontal ground reaction forces to the peak response from the three different size perturbations, and then averaged these normalized responses for all three magnitude perturbation trials in each rat.

Figure 8.

Polar plots of tuning curves of the magnitude of the horizontal forces for different directions of perturbations. The polar plots are centered on the compass center. A: The tuning curves of the three different size perturbations for a single experiment in a normal rat. Tuning did not differ among perturbation sizes. B: The averages of the total force curves of the three different size perturbations for all experiments in a normal rat and in two operate rats. Note the greater directional tuning in the hindlimbs of normal rats as indicated by greater departure from a centered shape. C: The averages of the response force curves of the three different size perturbations for all trials in the normal and the two operate rats depicted in 5B. Normal rat forelimb and hindlimb responses are strongly tuned. In operate rats the hindlimbs show much less directional tuning and have very small hindlimb forces.

B4.1 Total forces

Average tuning curves for total forces in normal rats have a distinct shape and orientation, as shown in Figure 8 B. In normal rats (e.g., J494- Figure 8 B), largest forelimb total forces were seen in response to rostral perturbations while the largest hindlimb total forces were seen in response to caudal perturbations. Depth of modulation of force in the average tuning was ~85% in forelimbs and ~75% in hindlimbs. Thus in the normal rat, as suggested above, forelimb total forces were tuned to rostral or forward perturbations and hindlimb total forces tuned to caudal or backward perturbations. These tuning differences between hindlimbs and forelimbs were significant (p< 0.05, Fisher distribution test, Fisher 1993; Fisher, Lewis and Embleton, 1987).

In operate rats (J490 and J505- Figure 8 B), directional tuning of total forces was not at all strong in the forelimbs, (e.g., compare Operate 505 with Normal J494). Depth of modulation of forelimb force was usually ~20%, (rarely 50%, e.g. J490 in 8B). The forelimb forces were approximately the same magnitude whether the perturbation comprised rostral or caudal components (rostrocaudal modulation in both operate rats shown is under 20%). The hindlimb total forces in the operates were also tuned to both rostral and caudal perturbations, but more weakly directed than normal rats. (However the depth of modulation of hindlimb force was usually slightly larger than in the forelimbs, amounting to 25-35%). These differences in depth of modulation between normal and operate rats were significant (t-test, p<0.05). :

B4.2 Active Response forces

Tuning curves for active response magnitudes indicate the adjustments made, and are shown in Figure 8 C. In normal rats (J494-Figure 8 C) the magnitude of change of forelimb response was less dependent on whether the direction of the perturbation was rostral or caudal, or medial or lateral. Depth of force modulation was ~50%. (The two forelimb contributions were combined in our measurement system: any forelimb lateral tuning was averaged out). Modulation observed was mostly rostrocaudal because lateral perturbations showed less forelimb force change compared to a similar rostrocaudal perturbation. The hindlimb response force magnitudes in the normal rats were tuned to rostral and caudal perturbations. Depth of hindlimb force modulation in normal rats was ~80%. There was a rotation of the principal direction or axis of tuning of each hindlimb towards the midline.

The magnitude of the operate rats active response in the forelimb did not vary much whether the perturbation was rostral or caudal (compare forelimbs tuning in J490, J505 Figure 8 C). In this they were similar to the normal rats. The depth of modulation of force was ~50% and also similar. However, in contrast to the normal rats, in operate rats the hindlimb response forces were both small and poorly tuned. The depth of modulation of forces in operates was usually ~25% of the peak value, while it was ~80% of peak in normal rats.

Taken as a whole, the response tuning in Figure 8 C suggested that operate rats differ from normal in having poorly tuned and small active hindlimb responses. Instead they compensate mostly with the forelimbs for all directions of perturbation.

B5 Stiffness

Our experiments allowed us to coarsely evaluate the magnitude of the postural stiffness of the rats. Stiffness measures variations in the magnitude of restoring forces with change in position (negative stiffness is thus destabilizing). Stiffness can be linear, with force linearly related to position changes (as in a linear spring) or non-linear. Muscles for example exhibit non-linear stiffness during stretch. Stiffness can vary with direction, for example in a limb. This directional variation can be compatible with a linear model or incompatible. For example, if a rat behaved as a very stiff (but linear) system, and was uniform in its response to perturbation, it would not alter its posture much. As a result, it would strongly resist perturbations in all directions, and with similar magnitude. The resisting forces needed would be generated through the legs and observed as high ground reaction forces. Our data showed that there were significant nonlinearities in the rats’ stiffness. These did not allow a simple linear fitting procedure with our data. First, stiffness components did not vary linearly with vector direction. Second, the magnitude of apparent stiffness at plateau was lower for the larger (and faster) perturbation excursions. It was not possible to accurately express the measured stiffness of the rat in response to our perturbations as a single linear function (i.e., a graphical stiffness ellipse, as used in Mussa-Ivaldi et al. (1985) and as used for individual perturbations in Shadmehr and Mussa-Ivaldi (1993)). For a single extent and rate of perturbation, the magnitude of restoring forces were smallest for lateral perturbations. Rats were far less stiff mediolaterally than rostrocaudally. To evaluate stiffness coarsely, and without additional experiments, we proceeded as follows: we estimated the plateau magnitude of the stiffness of the rat in each perturbation direction by dividing the scalar magnitude of horizontal force exerted by the Phantom (during the perturbation plateau, e.g. see Figure 2 ), by the scalar magnitude of the horizontal excursion of the Phantom at the plateau. Thus significant vector information in, e.g. Figure 5, was lost in the approximation but our data could not readily support more complex analysis. All rats displayed a greater magnitude stiffness when a smaller perturbation was delivered. (See Figure 9). It is worth noting that in our experiments larger perturbations were delivered at a greater velocity than smaller perturbations, because all perturbations had the same total duration of 500ms. Force rise was almost linear (r ²> 0.9 ). Our results for larger excursions are thus similar to results described in Shadmehr, Mussa-Ivaldi and Bizzi (1993, Fig 2) in their evaluation of human arm stiffness. However, because we did not explicitly control for velocity we cannot discount velocity effects in our data. For all perturbation sizes in both rostral and caudal directions the normal rats were more stiff than the operate rats (two tailed t test, p<0.05, and see Table 2).

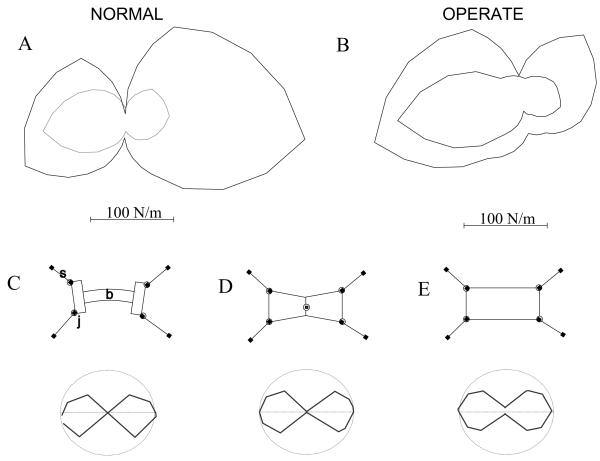
Figure 9.

A. A polar plot of the magnitude of stiffness of a normal rat J494. Stiffness magnitude is plotted at each direction of each perturbation. This should be distinguished from a linear fit stiffness ellipse, or a full non-linear fit. Our data did not support linear fits and was not sufficiently complete for a full non-linear fit. The inner curve represents the stiffness magnitude during the largest perturbations; the outer curve represents stiffness during the smallest perturbations. Rats exhibited less stiffness to larger perturbation. The polar plot of the magnitude of stiffness had an hourglass shape. The rat was much less stiff laterally. B. Stiffness plot for an operate rat J490. The stiffness of this rat showed rostrocaudal asymmetry as well as non-linearity, with lower stiffness in caudal directions. Nonlinear aspects of stiffness were at least partly attributable to the quadrupedal structure. To show this we tested 3 simple models of horizontal plane quadrupedal stiffness (C-E). Each showed an hourglass pattern magnitude response similar to the biological data. C Stiffness magnitude plot measured as in A and B for a structural model of a rat comprised of compression spring struts, springy rotary hip and shoulders and a stiff but flexible beam to represent the torso. D Stiffness magnitude in a model of rat comprised of legs as in C and a single central compliant trunk joint. This model could show symmetry breaking by flexure at the trunk joint leading to apparent lateral asymmetry of stiffness as sometimes also seen in the rats. E Stiffness of a structural model of a rat with legs as in C and D but using a rigid box as torso. Note persistence of hourglass shaped lateral stiffness, though less prominent compared to C and D.

Table 2.

A comparison of apparent mean stiffness (‘K’, measured in N/m) for different size caudal direction perturbations, in normal and operate rats. Rats appear less stiff for larger perturbations (e.g. 300 vs 900). The two mean values in each row are compared with one another using a t-test constructed with the raw measurements , where n is the number of trials across across animals in the group. The significance of the differences calculated in this way is given on the right. 8 normal rats or 6 operate rats data were pooled to obtain these trials (6-8 trials per rat) . Statistical comparisons between the perturbations and groups using only the mean values obtained from each rat in each of the tested conditions were also all significant (p<0.05). Operate rats show lower apparent stiffness for all similar perturbations. This is consistent with predominant forelimb responses in operates.

Trials	P Value
Normal Rats Caudal 300, n=57 K 1.32	1.9E-11
Normal Rats Caudal 900, n=54 K 0.71
Operate Rats Caudal 300, n=51 K 0.97	1.52E-7
Operate Rats Caudal 900, n=45 K 0.39
Normals Caudal 300, n=57  K 1.32	0.002
Operates Caudal 300, n=51  K 0.97
Normals Caudal 600, n=60  K 0.895	0.0003
Operates Caudal 600, n=51  K 0.6
Normals Caudal 900, n=54  K 0.71 1.39E-6
Operates Caudal 900, n=45  K 0.394

Magnitude of stiffness for each perturbation in a given direction is expressed in polar coordinates, in Figure 9. Whole body stiffness estimated in this way had an hour glass shaped tuning. This tuning could be partly attributed to the quadrupedal body structure of the rat and some axial yielding seen in video records for lateral perturbations. We evaluated several simple structural models of the rat, to identify those able to replicate the tuning of horizontal stiffness we observed. In order to represent the four limbs we used either linear or quadratic compressive springs constrained to act along struts attached to the body by rotary joints at the shoulder and hip with symmetric linear or quadratic stiffness in Working Model 2.0 software. This model produced the lateral inflections of the stiffness, capturing the hourglass shape in our data. In addition, if we added laterally flexing trunk joints, or a flexing beam representing the vertebral column in the body, on which the four compression struts representing the limbs attached, these further exaggerated the hourglass shape (Figure 9). The inclusion of more degrees of freedom in the body often led to a symmetry breaking in simulation of our measurement procedure. This could cause lateral bias of stiffness tuning depending on the trial. We also observed this behavior in measurements from some operate rats (e.g. Figure 9, B small perturbation has a caudal bias). Taken together, the presence of this hourglass shaped stiffness in all standing operate rats as well as normals and the simulation results support a largely structural basis for the hourglass shape of magnitude tuning.

Discussion

Previous studies of stance in rats have mostly examined vertical forces and self-generated perturbations to quadrupedal stance (e.g. Miklyaeva et al. 1997) or tested rats during rearing and bipedal balance tasks (Mulligan et al. 2002). Here we described the compensations for external perturbations to quadrupedal stance in normal and spinal injured rats, specifically those receiving spinal transection as neonates. These rats are interesting because a fraction succeed in developing autonomous weight support as adults (Stelzner et al., 1975; Miya et al. 1997). Understanding postural and locomotor mechanisms of rats which succeed in developing weight support despite spinal transection gives insights into the development and plasticity of spinal motor control mechanisms. In turn these may aid designing rehabilitative, or restorative interventions. Neonatal spinalized rats and transplant rats differ in various ways (e.g., see Giszter et al. 1998). However, our data here shows no difference in their biomechanical stance strategies. We selected injured rats that could both stand and locomote at better than 60% successfully weight supported steps as adults, and examined their postural controls compared to normal.

Our experimental paradigm is similar to the mutual jostling of rats in cages. We examine how stresses applied at the torso are resisted, and how the applied stress is distributed to the limbs. This method differs from that most frequently used for quadrupedal stance, which examines reactions to linear translation of support surfaces (Fung and MacPherson 1995, Pratt et al. 1994). In our task, the animal controlled how applied force was distributed among the limbs and thus to the force plates. Rats altered trunk posture to comply with the perturbation if they desired. In contrast, support surface translation causes unavoidable changes in the limbs, partly the goal of the method. Our method allowed us to test whether the compensating adjustments of ground reaction forces in response to trunk perturbations, on a timescale in which voluntary mechanisms could act, are distributed or localized to specific limbs in normal and operate rats. For example, we determined whether compensation is localized entirely in the forelimbs or distributed equally among all limbs.

Similarities of injured and normal rats

There were common features in the postural mechanisms characterized here in all our animals, both operates and normals: 1) Both adaptated by shifting of CoP toward the center of the base of support after a few trials of the perturbation experiments, although the robot was producing only a minimal holding force. (The CoP shifted rostrally in the normals and caudally in the operates.) 2) Both had qualitatively similar initial stance forces, when the animal was at rest prior to any perturbation. 3) Both had greater magnitude whole body stiffness in the rostral-caudal direction with an hourglass tuning overall.

The similar initial pre-perturbation forces demonstrated by all both normal and operate rats are consistent with MacPherson (1988a), the limbs working as inclined struts. They also mirror Lacquaniti and Maioli’s (1994a,b) finding of separate specification of limb configuration and postural ground reaction forces in mammals, since postures of injured and normal rats were quite different while stationary forces were similar. All rats showed small day to day variations in limb configuration. Rats varied their postures while preserving CoP location and ground forces, even in the absence of perturbations. In injured rats the consistent configuration changes we observed compared to normal rats probably represented one form of compensation (e.g. see Miklyaeva et al 1995,1997). MacPherson (1988b) considers the force vector produced as a result of a perturbation as a “high level, task-dependent controlled variable”, while the “selection of muscles to activate in order to produce the vector is controlled at a lower level”.

Whole body apparent stiffness and resistance to perturbations

Whole body stiffness in the rats in response to perturbations was non-linear. We had too few perturbation directions to identify the structure accurately, but we characterized the magnitude. Both normal and operate rats showed similarly tuned magnitudes of horizontal stiffness. Stiffness magnitude was larger for rostro-caudal perturbations and considerably smaller in lateral directions. The hourglass tuning pattern was probably due to the mechanical structure of the quadrupedal rat. Several simple planar mechanical models we tested captured the variation of stiffness magnitude. In part the pattern of stiffness is due to the fact that the base of support of the rat is narrower in the medio-lateral direction than in the rostro-caudal direction. The legs, acting as four inclined struts, also change their geometric relationship to the trunk during perturbations. This effect could be further exaggerated by adding a laterally more compliant ‘vertebral’ column. That similarity of stiffness tuning in operates and normals, despite dramatic differences in motor capability and posture, is consistent with the shape of stiffness variation being dominated by the mechanical structure.

We observed that rats showed a yielding behavior for larger perturbations, which in our design were also faster perturbations. These yielding patterns could represent local muscle properties and similar neuromechanical controls or they could represent voluntary compensations. In favor of the latter, normal rats sometimes showed additional and clearly voluntary trunk yielding. This yielding occured during the plateau phase following perturbation, and the perturbation duration of 500ms was clearly sufficiently long for a planned response.

Operates were less stiff than normals for caudal perturbations. The injured rats consistently had much reduced hindlimb contributions to postural adjustments. Finally, in operate rats we more often observed asymmetric stiffness magnitudes. Our simple models suggested that this could arise from symmetry breaking flexing in the trunk, or scoliotic bias in the trunk, which is a problem spinal injured rats are prone to. Injured rats might therefore show this behavior more often either due to skeletal distortion, or weakened trunk control and diminished trunk stability.

Strategies of compensation

The most significant differences between operates and normals were in the relationship between their forelimb and hindlimb forces. Force tuning curves of normal rats showed that the magnitude of their total forces after perturbations varied with the perturbation direction. Normal rats maintained their posture by varying the balance of horizontal forces in hindlimbs and forelimbs. The forelimbs mainly stabilized rostral group perturbations, while the hindlimbs mainly stabilized caudal group perturbations. In contrast, operates usually produced greater force changes with the forelimbs than with the hindlimbs in response to all perturbations. A reduced force generating capability of the hindlimbs contributed. However, hindlimb force responses were substantially smaller than could be accounted for in this way. The forelimbs also produced forces in atypical directions compared to normal rats. We speculate that operates employed a strategy which led to a different pattern of response, with compensation focused in the forelimbs. This would achieve two things: first, the forelimbs are more precise because they are under full voluntary control, and second, this strategy would avoid motion in the hindlimbs. It might be expected the local lumbar circuitry and resistance reflexes would be able to provide some predictable and useful hindlimb responses after initial loading, based on the research in cats (e.g., Ting and Macpherson, 2005). However, we believe that the strategy of minimizing any transmission of perturbation force to the hindlimbs that we observed here reduces the likelihood of inappropriate stepping or reflex motions induced by the perturbation. Operates which have lost all descending voluntary control of lumbar cord may lack the ability to control or suppress such spontaneous and reflex responses. Autonomous local pattern generation and reflexes play a central role in the weight supported locomotion of these spinally-injured rats, but their spurious activations during quiet stance could cause instability and stance failures. We sometimes saw such motions induced by the rapid release from the perturbation, at trial end. Specific stance or step training in spinal cats biases spinal excitation and inhibition systems up or down (DeLeon et al. 1999, Tillakaratne et al. 2002). If the spinal injured rats are to accomplish both stance and locomotion they must find compromise strategies where both can be achieved through largely reflex hindlimb use. Our study identifies important aspects of the stance strategy they employ.

Conclusions

We have quantified the responses of spinally injured rats to outside perturbations to stance. The data complements kinematic and kinetic analyses of locomotion. Results demonstrate that the voluntary motor strategies employed in stance differ between normals and operates. Within operates there were no obvious differences in motor strategy of spinal and transplant rats despite potential bridging effects of transplants. In all operate rats the active compensation for perturbations occured almost entirely in the forelimbs. Our data are consistent with a strategy of stance and compensation in the injured rats that organizes motor adjustments in forelimbs and trunk so as isolate the hindlimbs from perturbing forces. This strategy avoids involuntary hindlimb stepping during stance. Learning this strategy may be a key feature of developing function after complete spinal transection in rats, and these data may help guide future efforts to use motor training after adult spinal cord transection.