Structural and dynamic determinants of ligand binding and regulation of Cyclin-dependent Kinase 5 by pathological activator p25 and inhibitory peptide CIP

Abstract

The crystal structure of the cdk5/p25 complex has provided information on possible molecular mechanisms of ligand binding, specificity, and regulation of the kinase. Comparative molecular dynamics simulations are reported here for physiological conditions. This study provides new insight on the mechanisms that modulate such processes, which may be exploited to control the pathological activation by p25. The structural changes observed in the kinase are stabilized by a network of interactions involving highly conserved residues within the cdk family. Collective motions of the proteins (cdk5, p25, and CIP) and their complexes are identified by principal component analysis, revealing two conformational states of the activation loop upon p25 complexation, which are absent in the uncomplexed kinase and not apparent from the crystal. Simulations of the uncomplexed inhibitor CIP show structural rearrangements and increased flexibility of the interfacial loop containing the critical residue E240, which becomes fully hydrated and available for interactions with one of several positively charged residues in the kinase. These changes provide a rationale for the observed high affinity and enhanced inhibitory action of CIP when compared to either p25 or to the physiological activators of cdk5.

I. Introduction

Cyclin-dependent protein kinases (cdks) are a family of proline-directed Ser/Thr kinases that are largely involved in the control of the mitotic cycle¹. The kinases are expressed in most mature cells at relatively constant levels. However, their kinase activity is normally controlled by the level of expression of their activator proteins (the cyclins), which is in turn largely controlled by ubiquitinization via their half-lives. Cyclins bind to cdks via a globular domain in the cyclins termed the cyclin box. Cyclin-dependent kinase 5 (cdk5), although a member of the cyclin kinase family, is not directly involved in cell cycle control. Its activator proteins, p35 and p39, occur mostly in post-mitotic neurons and a few other specialized cell types, such as the insulin-secreting beta cells². Both p35 and p39 contain a globular C-terminal activator domain and N-terminal myristoylation and ubiquitinization sites. Activation by these proteins produces active kinases that bind to membranes and cytoskeletal elements³. Phosphorylation by cdk5/p35 and cdk5/p39 activities is involved in numerous regulatory pathways, some of which accept either activator. Deletion of both p35 and p39 produces severe defects of neuronal migration consisting of disorganization of the normal cerebral cortical neuron layers via effects on actin polymerization at neuronal growth cones⁴. Ca²⁺-dependent proteolysis of p35 removes residues 1–98 and produces a soluble and active cdk5/p25 complex. This also occurs in several neurodegenerative diseases and can be induced in cell cultures⁵ by various agents that elevate intracellular Ca²⁺. This soluble form of activated cdk5 phosphorylates less selectively than cdk5/p35. Within neurons cdk5/p25 occurrence is accompanied by ‘hyperphosphorylation’ of certain cytoskeletal and related proteins⁶. In several cases this leads to the formation of aggregates that are pathognomonic for certain neurodegenerative diseases, notably Alzheimer's, Parkinson's, and amyotrophic lateral sclerosis^{7; 8}. Because of the correlation between expression of these aggregate proteins and the expression of cdk5/p25 it is of considerable interest that a fragment of p35, consisting of residues 154–279 (CIP), binds with high affinity to cdk5 and potently inhibits cdk5/p25 kinase activity in vitro⁹. Moreover, when neurons are subjected to conditions that produce cdk5/p25, transfection of CIP suppresses the cdk5/p25 hyperphosphorylation and also the aggregate formation¹⁰. Understanding a mechanism that can suppress these pathological hallmarks has obvious therapeutic importance.

In an earlier study⁹ the GST derivatives of a series of N- and C-terminally truncated p35 molecules were examined for their ability to activate GST-cdk5 in vitro. Removal of the first 98 N-terminal residues of p35 (1–307) produces p25 (99–307); further truncations produced p16 (138–291), which can activate cdk5 as effectively as p35 or more so; however, further small truncations (154–291 or 138–287) produced only insignificant activation by this assay. This study also examined possible effects on the activation capability of p35 derivatives that do not activate cdk5. In this case both minimal C-terminal (154–291) and minimal N-terminal (138– 279) derivatives behave as if they are competitive with the activator p16 (K₅₀ = ~0.3 μM), and display moderately high affinities for cdk5 binding, yielding 0.9 and 2.2 μM, respectively, whereas the K₅₀ value for inhibition by CIP was ~0.04 μM. In experiments that estimated initial rates of activation by p16 as a function of CIP concentration, data were approximately hyperbolic with a K₅₀ of ~0.07 μM for binding to cdk5. Together, these data suggest that a complex initially forms reversibly and is followed by a much slower transition to an irreversible complex⁹.

Although the primary sequence of the cdk5 activators has little homology with cyclin box domains, their secondary structures consist of helices linked by loops that fold to form compact and partly similar tertiary structures. In the case of cyclin A, which activates cdk2, the tertiary structures of its free and cdk2-complexed forms are nearly identical, which demonstrates that the cyclin box is an intrinsically rigid structure¹¹. In the absence of an activator protein the cyclin-dependent kinases revert to an inactive conformation in which the activation loop blocks binding of peptide or protein substrates¹².

In this paper, comparative molecular dynamics simulations of the uncomplexed proteins (cdk5, p25, and CIP) and their complexes are carried out to elucidate the structural and dynamic properties that control ligand binding, and regulation and inhibition of the kinase by the pathological activator, p25, and the inhibitory peptide, CIP.

II. Results and Discussion

Structure and dynamics of cdk5 and its complex with p25

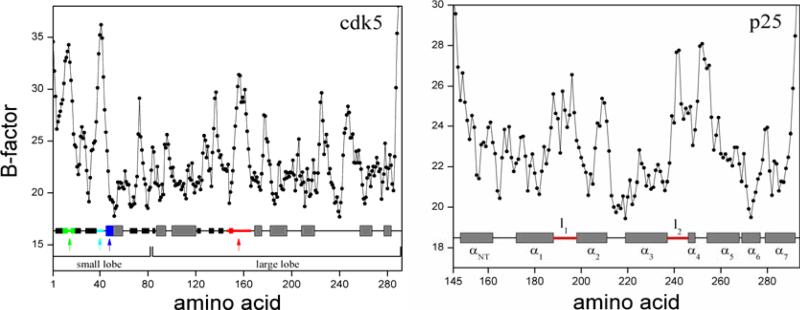
At physiological temperatures the uncomplexed kinase exists in two conformational states in equilibrium, one inactive and another active⁹. The inter-conversion involves a number of structural changes, most notably the rearrangement of the activation loop¹². Here, the structure of cdk5 in the complex was taken as the starting conformation for the dynamics simulation of the active state of the uncomplexed kinase. At the end of the 20-ns simulation the total C_α-rmsd of the uncomplexed cdk5 is ~2.1 Å with respect to the crystal. This departure is due to conformational changes within the lobes, mainly in loop regions, as well as a rigid-body-like rotation of one lobe with respect to the other. The small lobe shows the largest internal distortions, with a C_α-rmsd of ~2.6 Å, and is rather flexible (see below). All elements of secondary structure, mainly β-sheets, and tertiary arrangement are preserved during the simulation. The most significant structural changes in the small lobe involve the loop L37–G43 at the N-terminus of the PSSALRE helix (cf. Fig. 1a), which is at the cdk5/p25 interface. This short loop contains five acidic residues (DDDDE) that interact with p25 in the complex, but are exposed to the solvent in the absence of p25. The distortion of the loop appears to be the result of electrostatic repulsion between these side chains, which are likely unprotonated at physiological pH. In contrast to the small lobe, the large lobe shows less overall distortions, with a C_α-rmsd of ~1.5 Å. Secondary and tertiary structures are preserved during the simulation. The largest local distortions involve the long loop K232–L255, with the unstructured turn at the C-terminus end evolving into an α-helix turn. In contrast, the activation loop shows small changes with respect to the crystal (C_α-rmsd ~1 Å), which are expected as structural relaxations at physiological temperatures in the absence of p25.

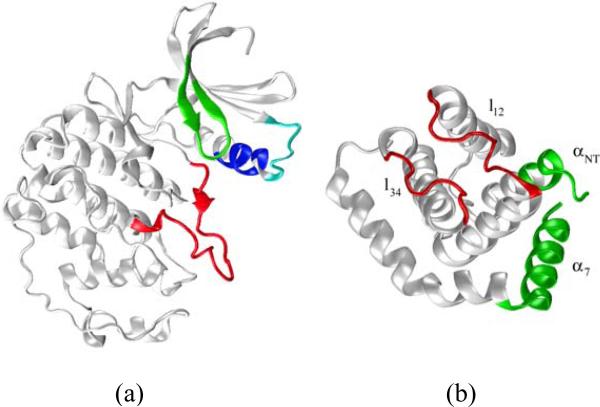
Figure 1.

Ribbon representations of a) cdk5 from the crystal structure of the cdk5/p25 complex (chain A of 1UNL). Critical structural motifs are identified in color: activation loop (red), Gly-rich loop (green), PSSALRE sequence of interfacial helix (blue), and acidic loop L37–G43 (cyan) containing the highly charged sequence DDDDE; b) p25 from the crystal structure of the cdk5/p25 complex (chain D). Helix definitions follow Ref.21; loops l₁₂ and l₃₄, both at the cdk5/p25 interface, are shown in red. The synthetic inhibitory peptide CIP results from truncation of the N- and C-terminus sequences of p25, shown in green.

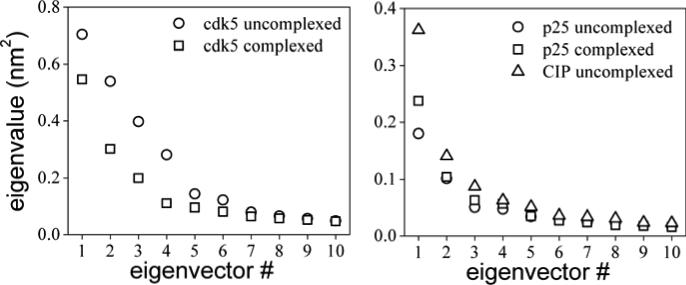
Protein conformational transitions are key determinants of biological function. These involve not only local structural adaptations typically needed during ligand binding or catalysis, but also large-scale collective motions, e.g., during allosteric regulation or inter-domain communication^{13; 14; 15}. A number of studies have related collective motions of proteins with their structural evolution across families¹⁶, suggesting that nature has coded specific dynamic patterns into macromolecular structure for optimal function during adaptation. Given the fundamental relationship between macromolecular dynamics and biological function, experimental techniques have been developed to probe specific aspects of protein dynamics. These include traditional diffraction methods to quantify thermal motion and structural disorder in crystals (e.g., temperature factors) to more recent spectroscopic-based assays to probe protein dynamics in solution¹⁷ and in the living cell^{18; 19}. Well established computational methods are also available to explore protein flexibility and uncover dynamic patterns hidden in the complex dynamics. One such technique is Principal Component Analysis (PCA)²⁰ (cf. Materials and Methods). To simplify the analysis only the subset of C_α atoms will be considered here. This analysis will be complemented later with a cross-correlation analysis of side-chain dynamics (cf. Materials and Methods). The ensemble average [cf. Eq. (1) in Methods] is approximated by a time average over the last half of the dynamics, when major conformational changes have already set in. An analysis of collective motions of the uncomplexed kinase shows that the first four eigenvector contain the most important structural fluctuations (cf. Fig. 2a). In the first mode the largest collective movements occur in the small lobe (cf. Fig. 3a, left). The movement of the acidic loop appears to be anticorrelated with respect to the rest of the lobe, and shows the largest fluctuations. This contrasts with the behavior of the activation loop, which shows relatively small overall fluctuations. The second mode also reveals large movements of the small lobe (cf. Fig. 3a, right), but in this case the acidic loop moves in sync with the rest of the lobe. In both modes the movement of the PSSALRE helix is in sync with the acidic loop. The Gly-rich loop, which contains part of the ATP-binding pocket (see below), displays substantial fluctuations as well, but these are smaller along the first eigenvector. In general, the overall displacements at the cdk5/p25 interface are quite different in the first two collective modes, suggesting that a substantial combination of movements is probably needed for proper structural adaptation during cdk5/p25 binding. Along the third and fourth eigenvectors (not shown) collective movements decrease overall, as indicated by the corresponding eigenvalues (cf. Fig. 2a), but the movements of the small lobe still dominate the fluctuations.

Figure 2.

Eigenvalues of the covariance matrix [cf. Eq.(1)] calculated from the last half of the dynamic trajectory of a) the kinase cdk5, and b) the pathological activator p25 and inhibitory peptide CIP.

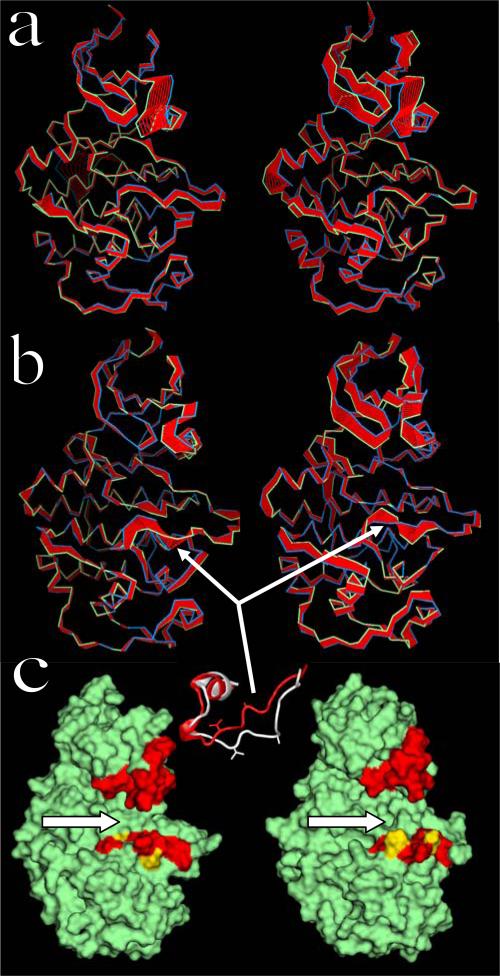
Figure 3.

Principal component analysis of the dynamics of cdk5: a) Collective motions of the uncomplexed kinase along the first (left) and second (right) eigenvectors. Blue and green ribbons correspond to the positions of the C_α atoms at opposite extremes of the fluctuations; red ribbons are interpolations that help visualize the range of movements. The orientations of the protein are similar to that in Figure 1; b) Same as in (a) but for cdk5 complexed with p25. The flexible segment R156–W166 of the activation loop, which defines the open and closed sub-states, is indicated by arrows. Inset: part of the activation loop containing the flexible segment R156–W166; closed sub-state from the crystal (red); open sub-state from the simulation (white); A160 and V163 side chains shown. c) Molecular surface representation of the uncomplexed (left) and complexed (right) kinase; similar orientations as in (a) and (b). Arrows point to the substrate-binding pocket, showing the enlargement induced by p25 binding. Regions lining the pocket are in red, and include the tips of the glycine-rich and acidic loops, and the flexible segment of the activation loop (cf. Fig. 1a); residues A160 and V163 are in yellow.

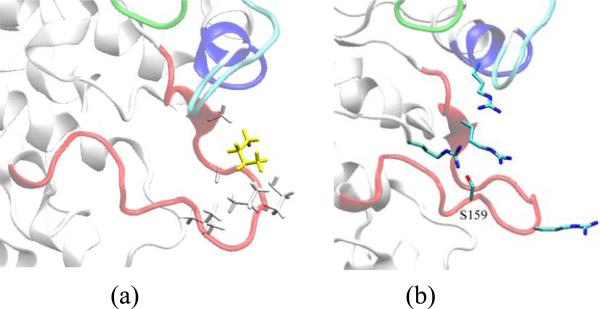
Based on crystallographic and biochemical data, residues I153 and S159 of cdk5 have been identified as critical for p25 and p35 binding, recognition, and selectivity²¹. In the crystal, I153 interacts with an extended network of non-polar residues in p25, namely, M237, A199, F282, I275, A277, and P279²¹. However, during the simulation of the uncomplexed kinase, I153 becomes partially buried as part of a non-polar moiety formed by A150, G152, P154, V155 (all in the activation loop), and, transiently, L178 (cf. Fig. 4a). An analysis of the behavior of water in the hydration shells of this group at the protein/solvent interface shows that it is kept in contact through hydrophobic forces. During the simulation of the uncomplexed kinase residue S159 forms a highly stable hydrogen bond (Hb) with R125. A multiple sequence alignment shows that R125 is strictly conserved among all members of the cdk family²². In the crystal, residues S159 and R125 do not interact directly but are bridged by a crystallographic water molecule (both in 1UNL and 1H4L). However, direct Hb interaction only requires rotation of single bonds and removal of the bound water, both thermodynamically favorable at physiological temperature, as shown by the simulation. The role of phosphorylation of S159 in the catalytic activity of cdk5 is controversial. In ²³, phosphorylation was shown to increase the rate of activation of cdk5, a finding supported in ²⁴, while data reported in ²⁵ show that phosphorylation does not contribute to maximal catalytic activity. The simulations suggest that a negatively charged group at position 159 of cdk5 may reinforce the Hb interaction with R125 (in cdk2, pdb code: 1QMZ, residue R126 forms a direct HB with the phosphate group of the phosphorylated residue S160), and also affect the structure and dynamics of two nearby arginine residues, R149 and R156 (both in the activation loop) and possibly also R50 (in the PSSALRE helix; cf. Fig. 4b). Both R149 and R50 are highly conserved residues within the cdk family²² (except in cdk7, where R149 is replaced by a homologous lysine residue); however, residue R156 is poorly conserved among cdks, but is homologous in both human and drosophila cdk5²². Since there are no acidic residues in the vicinity of S159 these positively charged residues may react strongly to a local electrostatic perturbation created by a negative charge at position 159. The orientations of these residues are similar in the simulation and in the crystal, except that in the latter R156 is extended away from S159 and in closer contact with p25, while K177 (also poorly conserved within the cdk family, but homologous in cdk5²²) is closer to S159. Therefore, mutations that prevent phosphorylation of S159, e.g., as reported in ^{21; 25}, may hinder or elicit structural or dynamic changes prior to activator binding, which may affect the kinase activity in non-obvious ways.

Figure 4.

a) Hydrophobic network formed by non-polar residues in the activation loop, including I153 (yellow) during the simulation of the uncomplexed kinase; side chains of A150, G152, P154, V155 and L178 are shown in white. In the cdk5/p25 complex I153 forms instead a compact hydrophobic network with several residues in p25; b) Side-chain orientations of positively charged residues surrounding S159 in the uncomplexed kinase; side chains of R50, R125, R149, and R156 also shown. A negative charge formed by phosphorylation of S159 may perturb the reorientations of these residues and affect ligand binding.

The substrate-binding pocket

In contrast to the uncomplexed kinase, during the simulation of the cdk5/p25 complex the small lobe shows little conformational change (C_α-rmsd ~1.6 Å), while the large lobe shows substantial distortions (C_α-rmsd of ~2.9 Å), most notably in the activation loop between residues R156 and W166. This segment includes residue S159 discussed above, but the Hb interaction between S159 and R125 observed in the uncomplexed kinase is preserved (cf. Fig. 4b). These local distortions of the activation loop results in an opening of the substrate-binding cleft (cf. inset of Fig. 3b), which occurs by a continuous zip-like shift of backbone dihedral angles from the C- to the N-terminus. Although the opening begins at ~10 ns, and is completed by the end of the simulation at 20 ns, the short sequence is quite flexible during the time leading up to the transition. This suggests that the active conformation of the activation loop may exist in two different sub-states, one open and another closed, both in thermal equilibrium, possibly undergoing interconversion in a time-scale longer than the simulation time. This result contrasts with the dynamics of the uncomplexed kinase, in which case the closed sub-state is highly stable (cf. Fig. 3a). Thus, the thermodynamic equilibrium between open and closed sub-states seems to shift towards the former when the activator binds the kinase. Further insight on this mechanistic hypothesis can be obtained from PCA. The eigenvalues of the covariance matrix (cf. Fig. 2a) show that the complexed kinase becomes less flexible overall upon complexation, particularly in the small lobe. However, critical structural motifs become much more flexible, most remarkably the portion of the activation loop between R156 and W166 (cf. Fig. 3b). This analysis supports the notion that the activation loop in the complexed kinase may indeed undergo conformational transitions between an open and a closed sub-state, and that these changes are induced by the activator. All four principal components show large fluctuations of this short segment. This hypothesis is consistent with crystallographic temperature factors of the complex (cf. Fig. 5a), which show large values within the sequence P154–V162. Other fluctuations evidenced by PCA are also consistent with the measured temperature factors in the crystal, including those in the Gly-rich and acidic loops. Opening of the activation loop upon complexation partially contributes to the enlargement of the substrate-binding cavity (cf. inset of Fig. 3b). This enlargement is compounded by the movement of the acidic loop away from the pocket and closer to the bound p25. Figure 3c shows a molecular-surface representation of the complexed and uncomplexed kinase, which illustrates the overall enlargement of the substrate-binding cleft in the open sub-state, enhanced by the shift of the acidic loop.

Figure 5.

Temperature factor of cdk5 and p25 from the cdk5/p25 crystal structure as reported in Ref.32 for chain A and D of 1UNL. Elements of secondary structure are shown at the bottom (gray: α-helix; black: β-strand). Colored segments and helix nomenclature are as in Fig. 1.

Understanding the specific pattern of interactions of the activation loop in the complex may help design kinase inhibitors that compete with the substrates. The open sub-state is stabilized by a network of Hb and hydrophobic interactions. Hydrogen bonds involve K128, T164, and D126, all intra to the kinase and conserved among all members of the cdk family²². The hydrophobic network includes V163 (conserved in all cdks²²), which is partially exposed to the solvent, and L147 (highly conserved except in cdk8, which is replaced by phenylalanine, another hydrophobic residue²²) in the kinase, and I241 in p25. In turn, these hydrophobic residues form an extended hydrophobic moiety with A160 in the kinase and the non-polar part of the side-chain of E240 in p25. Residue A160 is poorly conserved within the cdk family but conserved in human and drosophila cdk5²². During the dynamics of the cdk5/p25 complex A160 becomes partially exposed to the solvent, but is buried in the uncomplexed kinase. Residue E161 (poorly conserved in cdks but conserved in cdk5²²) in the open sub-state is fully exposed to the solvent, while it is buried and forming internal Hb with R168 (another strictly conserved residue among cdks) in the uncomplexed kinase. This analysis shows that there is a subtle balance of forces involving both Hb and hydrophobic interactions, some unique to cdk5 but others common to all cdks, which are quite different in the complexed and uncomplexed kinase. During the dynamics of the complex, these forces may compensate each other as the activation loop undergoes transitions between the open and closed conformations.

The crystal structure of cdk2 co-crystallized with cyclin A, the ATP molecule, and a substrate-mimetic peptide (PDB code: 1QMZ), shows that V163 in the kinase is deeply buried in the protein, which allows the conserved proline of the substrate to accommodate in the binding site¹². If the open sub-state of the activation loop plays a role in substrate binding it may be by exposing V163 to water to provide an extended non-polar patch on the protein surface (cf. Fig. 3c) towards which the proline can be dragged and stabilized by hydrophobic forces. Once the proline is oriented in the site, the activation loop would switch back to the closed sub-state, thus removing V163 and allowing better fit of the substrate into the pocket. These observations need to be reconciled with the fact that, in the absence of the substrate, the activation loop is in the closed sub-state, as the crystal shows. It is possible that at the conditions of the diffraction experiments enthalpic contributions play the dominant role, and the network of interactions just described favors the closed sub-state. At physiological temperatures, however, conformational entropy may be enough to shift the free energy balance and render the closed sub-state less favorable. Further computational studies would be necessary to explore the conformational space of the activation loop and draw quantitative conclusions. The replica path method²⁶ may be used to identify local minima (in this case, the open and closed sub-states) and the intervening transition barriers in the free energy landscape.

The ATP-binding pocket

The binding pocket of the ATP-antagonist may be defined as the set of residues with at least one atom within a distance of ~5 Å from any atom of the ligand. In the 1UNL structure these residues are I10–G13, V18, A31, K33, V64, F80–D86, Q130, L133, and A143–N144. Towards the end of the simulations of the complexed and the uncomplexed kinase the C_α-rmsd of this pocket is ~1.5 Å with respect to the crystal structure, while the orientations of the side chains show little change during the dynamics. No crystal structure of the cdk5 complexed with the ATP molecule is available, so a model was created here by superimposing the ATP molecule on the ATP-inhibitor, and subjecting the system to a short energy minimization. This shows that the binding pocket of the ATP molecule contains three additional residues, T14, K128, and N131, which surround the phosphate group. During the dynamics of the uncomplexed kinase the conformation of this enlarged pocket also shows little departure from the crystal.

The PCA analysis of backbone motion can be complemented with a local cross-correlation analysis of side-chain dynamics (cf. Materials and Methods). This analysis shows that, as a general rule, complexation with p25 reduces the cross-correlation between residues within cdk5, in particular between the lobes, between the activation loop and the rest of the kinase, and between the ATP-binding pocket and the rest of the kinase (cf. SM1 and SM2). For example, during the dynamics of the uncomplexed kinase, residues E51 and L55 in the PSSALRE helix show strong cross-correlation with F80 and N144 (both in the ATP-binding pocket). However, upon complexation, these correlations are reduced because the helix moves slightly away from the pocket towards p25. Moreover, although movements of p25 correlate with certain structural motifs in cdk5 (e.g., with the PSSALRE helix and with the activation loop) no element of p25 correlates directly with residues in the ATP binding pocket. Detailed analysis of individual amino acids shows that the motion of residues surrounding the phosphate group (T14, K128, Q130, N131, and N144) in the cdk5/p25 complex shows little correlation with residues outside of the pocket. This contrasts with the behavior of the uncomplexed kinase, where four of the residues surrounding the phosphate group correlate with six out-of-the-pocket residues (E51, L87, K88, H124, D126, and Y167). These observations may be of biological significance, and suggest that the activator exerts an indirect effect on the ATP-binding pocket by reducing perturbations on the catalytic site. This attenuation may be necessary for optimal atomic arrangement during catalysis, and to pass the control of the local dynamics to the demands required by the chemical reaction, free from deleterious effects of atomic motion outside of the catalytic site.

Structure and dynamics of p25 and CIP

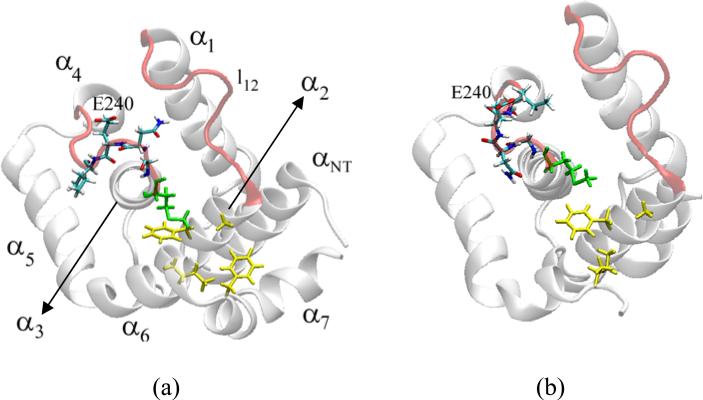
Comparative dynamic simulations of the uncomplexed p25 and CIP may help understand the contrasting differences observed in their binding affinities and effects on the kinase activity. Over the course of the simulation the uncomplexed p25 shows little departure from the crystal structure (C_α-rmsd ~1.5 Å). Structural changes are limited mostly to the N- and C-terminus, and to loop regions, mainly loop α₁–α₂ (l₁₂ hereafter) and loop α₃–α₄ (l₃₄) (cf. Fig. 1b). In the crystal, the loop l₃₄ is in direct contact with the kinase, filling the crevice between the PSSALRE helix and the activation loop. The conformation of the protein stabilizes at ~4 ns, with no major changes observed thereafter. The initial structure used for the simulation of the uncomplexed CIP is the structure of p25 after removing the corresponding N- and C-terminal residues (cf. Fig. 1b and Introduction). It is then assumed that the native folding of CIP in solution is not too different from the native folding of p25. In the absence of experimental data, ab initio prediction of the folding of CIP would be required. Given the limitation of current computational algorithms such an approach has been avoided here. The expectation is that CIP can reach its native conformation in solution by gradual changes during the course of the simulation. The native structure of CIP, however, may be quite different if serious misfolding occurs during synthesis of the protein, so data should be analyzed with caution. During the course of the simulation the uncomplexed CIP departs substantially from the starting conformation, reaching a C_α-rmsd of ~2.2 Å. Major structural changes are limited to loops l₁₂ and l₃₄, which also show larger fluctuations than in p25 (see below). Shifts of some of the helices are also observed. For example, helix α₂ in CIP is no longer constrained by α₇, and is then free to undergo structural relaxations; the absence of α₇ also relaxes α₅ and α₆, causing both helices to move slightly from their initial positions and undergo larger fluctuations. As a consequence of these rearrangements the inter-loop crevice between l₁₂ and l₃₄ opens slightly with respect to that in p25. Understanding the origin of these structural changes may help understand critical aspects of the folding mechanism of CIP and p25. In p25, either in solution or in the crystal, residue M237 at the C-terminus of α₃ is in close proximity to a number of non-polar residues, namely, A199 at the N-terminus of α₂, F203 in α₂, I275 at the C-terminus of α₆, and F282 in α₇ (cf. Fig. 6a). This group is at the protein/solvent interface, so it creates a hydrophobic environment that keeps the C-terminus end of α₃ close to both α₂ and α₆. During the simulation of the uncomplexed p25 the interactions between these non-polar residues show little variation from those in the crystal. However, in the uncomplexed CIP, this hydrophobic compactness is weakened due to the absence of F282 and to the outward relaxation of α₂. As a consequence, M237 detaches from the rest of the hydrophobic moiety, which leads to repositioning of the C-terminus of α₃, away from α₂ and α₆ (cf. Fig. 6b). This in turn triggers a rearrangement of backbone dihedral angles within l₃₄, which propagates upward in the sequence from G238 to I241, resulting in full exposure of E240 to the solvent. The result is a distorted loop l₃₄, with quite different side chain orientations when compared to p25, either in solution or in the crystal. These structural changes bring l₃₄ away from l₁₂, which broadens the inter-loop l₁₂–l₃₄ crevice, as mentioned. This is further enhanced by the outward relaxation of α₂, which stretches l₁₂. The uncomplexed CIP is quite stable after ~5 ns, while most of the structural changes occur very early in the dynamics, even during the equilibration phase. A recent study²⁷ of the dynamics of uncomplexed and complexed CIP has revealed similar local changes of this hydrophobic environment due to the absence of the C- and N-terminal helices of p25. These results were obtained with a different force field, and thus support the notion that the structural changes in CIP indeed originate in the disruption of the hydrophobic packing that keeps α₂, α₃, and α₆ in close proximity. These non-polar residues have been implicated in cdk5/p25 selectivity and binding²¹. In the crystal, I153 in cdk5 accommodates into a hydrophobic ridge formed by M237, A199, F282, I275, A277, and P279 in p25. Given the distortion of this hydrophobic moiety in the uncomplexed CIP and the structural changes in the interfacial loop l₃₄, it is expected that cdk5/CIP binding modes and affinity are governed by an entirely different set of interactions than in cdk5/p25, and that E240 may play an important role during complexation (this contrasts with the approach followed in ²⁷ where both CIP and p25 were assumed to share the same interface with cdk5 in their complexes). To explore this possibility, several independent dynamic simulations were carried out with CIP and cdk5 in close proximity. The starting conformations were taken from the dynamics of the uncomplexed proteins. The initial configurations of the complexes were obtained by first superimposing the backbones atoms on the corresponding atoms of the cdk5/p25 crystal, and then moving CIP away from cdk5 in the direction connecting their centers of mass. This resulted in initial configurations with approximately two to four hydration layers between cdk5 and CIP. In all of the simulations the exposed E240 rapidly formed highly-stable Hb with one of the positively-charged residues at the cdk5 interface, typically R50 or R149 (cf. Structure and dynamics of cdk5 and its complex with p25). The same protocol was repeated for the pair cdk5 and p25, but these proteins failed to come in close contact, and no specific interactions were identified during the total simulation times of ~20 ns. These results suggest that solvent exposure of E240 may increase the affinity of CIP for cdk5, and lead to the formation of an inactive cdk5/CIP complex in which CIP blocks binding of p25.

Figure 6.

Ribbon representation of the uncomplexed a) p25 and b) CIP at the end of the simulation. In p25, residue M237 (green) is part of a an extended patch of non-polar residues (yellow) at the protein/water interface that keeps helix α₃ close to α₂ and α₆ through hydrophobic forces. The absence of F282 in CIP weakens this hydrophobic interaction. As a result M237 detaches from the group, and α₃ relaxes and moves away from α₂ and α₆. This change induces important restructuring of loop l₃₄ and reorientation of side chains, most notably E240, which becomes fully exposed to the solvent.

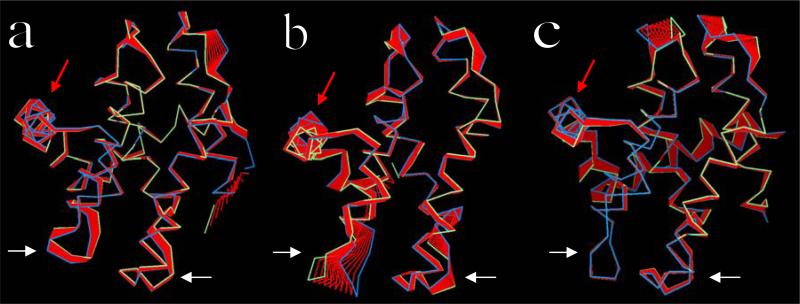
Principal component analysis of the uncomplexed p25 and CIP reveals differences in collective motions that may be required for structural adaptation during binding. The eigenvalues of the principal components (cf. Fig. 2b) show that the uncomplexed CIP not only undergoes larger structural rearrangements than p25, as discussed above, but also displays larger overall flexibility. The first three collective modes make important contributions to the dynamics of both proteins, and the main differences in the dynamics of both proteins can also be limited to these three modes. Figures 7a and 7b show the projections of the trajectories onto the first eigenvector for each protein. The largest eigenvalue in the uncomplexed p25 involves correlated movements of l₁₂ and l₃₄, and anticorrelated movements of the loops α_NT–α₁ and α₂–α₃. Helices display relatively minor overall displacements. The other principal components involve damped movements of essentially the same structural motifs (not shown), albeit with different cross-correlations. The large displacements observed in the N-terminus of p25 is probably of no biological significance since the protein contains a long sequence tethered at this terminus that is unresolved in the crystal and not modeled in this study. The main component in the uncomplexed CIP corresponds to large fluctuations of l₃₄, followed by fluctuations of l₁₂ and helices α₅ and α₆. Some movements are also apparent in the loops α_NT–α₁ and α₂–α₃, but these are smaller than in the uncomplexed p25. Overall, the principal components of the uncomplexed CIP show larger fluctuations of helices than in the uncomplexed p25. The principal eigenvalues of p25 complexed with cdk5 do not differ significantly from those of the uncomplexed p25 (cf. Fig. 2b). In the complex, however, p25 shows larger collective displacements in regions opposite to the interface (mainly α_NT and α₇, and loops α_NT–α₁ and α₂–α₃), while fluctuations of l₁₂ and l₃₄ are rather limited (cf. Fig. 7c). B-factors of l₁₂ and l₃₄ in the crystal are at least as large as in regions opposite to the cdk5/p25 interface (cf. Fig. 5b). These results suggest that the experimental B-factors reflect structural disorder rather than dynamic fluctuations of the interfacial loops.

Figure 7.

PCA of a) uncomplexed p25, b) uncomplexed CIP, and c) complexed p25. Ribbon colors as in Fig. 3. Only projections along the first eigenvectors are shown. White arrows indicate loops l₁₂ (right) and l₃₄ (left). Helix α₅ (at the cdk5/p25 interface) is indicated by the red arrows. Loops α_NT–α₁ (right) and α₂–α₃ (left) are at the top of the panels.

Local interactions in the uncomplexed p25 and CIP

The analyses of the uncomplexed proteins discussed above showed that the major differences between p25 and CIP are limited to loops l₁₂ and l₃₄. It is then expected that the differences in behavior observed in vitro between the proteins, i.e., inhibitory action of CIP and higher affinity of CIP when compared to p25, are likely to also originate in these loops. A comparison of the local networks of interactions involving l₁₂ and l₃₄ provides insight into the underlying mechanisms. In the uncomplexed p25 an extended network of non-polar residues is observed in the cleft formed between l₁₂ and l₃₄, which includes L185, W190, P244, and the non-polar portion of the side chains of Y243 and E240 (cf. Fig. 8a). This group is accessible to water and is then stabilized by hydrophobic forces. In addition to these hydrophobic interactions, a group of polar/charged residues form an extended Hb network (cf. Fig. 8b), including Y243, which tends to interact with Q191 and with the backbone atoms of N239 and E240 (both in l₃₄), and Y234, which interacts with D182. Residues D192 and Q193 (both in l₁₂), and N239, I241, and S242 (all in l₃₄) remain exposed to the solvent. In the uncomplexed CIP, the hydrophobic network is largely preserved (cf. Fig. 8c), although residue I241, which is solvent-exposed in p25, becomes part of the hydrophobic moiety in CIP, while E240, partially buried in the uncomplexed p25, becomes fully hydrated due to the structural changes in l₃₄. This is, in effect, an interchange of non-polar groups contributing to the hydrophobic packing, whereby I241 substitutes the non-polar portion of E240 side chain. More important differences, however, are observed in the Hb network connecting both loops, which is almost absent in CIP (cf. Fig. 8d). The inter-loop interaction between Y243 and Q191 in p25 is absent in CIP. Specifically, the distance between C_δ of Q191 and C₄ of the aromatic ring of Y243 fluctuates around ~10 Å in CIP, compared to ~6 Å in p25, both in its complexed and uncomplexed forms. In addition, residue Y243 in CIP forms Hb only with water molecules transiently entering the inter-loop crevice. Therefore, Y243 in CIP is readily available for direct binding to the kinase when water is removed during cdk5/CIP complexation. Similarly, the interaction between Y234 and D182 observed in p25 is absent in CIP, although Q191 tends to interact with D182 and, transiently, with Y234. The stacking between the aromatic rings of Y234 and F195 observed in the crystal is preserved both in CIP and p25. The disruption of this Hb network, which in p25 cross-links l₁₂ and l₃₄, is a direct consequence of the structural changes in these loops, and explains their enhanced flexibilities when compared to p25 (cf. Figs. 7a and 7b).

Figure 8.

a) Network of non-polar residues (yellow) at the cleft between loops l₁₂ and l₃₄ (in red; cf. Figs. 1b), from the simulation of the uncomplexed p25; these residues are accessible to water and interact through hydrophobic forces. b) Hydrogen-bonding network cross-linking l₁₂ and l₃₄, from the simulation of the uncomplexed p25. c) As in (a) but for the uncomplexed CIP; the hydrophobic network is largely preserved. d) As in (b) but for the uncomplexed CIP, showing the disruption of almost all Hb between the loops, which leads to increased loops flexibility (compare Figs. 7a and 7b) and reduced cross-correlation (compare Figs. SM3 and SM4). e) Hb interactions in cdk5/p25 complex (cdk5 in white; p25 in yellow; color of critical structural motifs as in Fig.1) obtained from the simulation, showing inter-loop interaction between E240 and the backbone of D192, and intra-loop interaction between E240 and Y243, and S159 from cdk5.

Local interactions in the uncomplexed and complexed p25

During the simulation of the cdk5/p25 complex, restructuring and fluctuations of l₁₂ and l₃₄ decrease substantially, not only because of the proximity to the kinase but also because of the development of new inter-loop Hb interactions not observed in the uncomplexed p25, and which are different in the crystal as well. During the dynamics of the cdk5/p25 complex the packing of non-polar residues observed in the uncomplexed p25 and CIP (cf. Fig. 8a and 8c) is preserved. These non-polar residues are mostly excluded from the solvent by the kinase, so they are no longer kept in close proximity by hydrophobic forces but merely by steric packing. The most notable difference in the Hb network with respect to the uncomplexed p25 involves E240, which becomes buried in the complexed p25. During the dynamics of cdk5/p25 an inter-loop Hb interaction develops between E240 and the backbone of D192, while an intra-loop Hb is formed between E240 and Y243 (cf. Fig. 8e). Both interactions are absent in the uncomplexed p25 and in the crystal; in the latter, E240 is away from l₁₂ and in closer contact with the kinase. The strong Hb between E240 and residues D192 and Y243 appear around ~3 ns in the dynamics. The behavior of E240 deserves particular attention as it was suggested that its orientation in the crystal is favorable for interaction with a protonated residue at position +3 of the substrate²¹. This observation led to the hypothesis that E240 plays the role of a phosphate group, so that there would be no need to invoke phosphorylation of S159 for optimal kinase activity²⁵ (cf. Structure and dynamics of cdk5 and its complex with p25). The strong interactions developed by E240 during the simulation of the complex, and the behavior of neighboring water molecules suggest that the inward reorientation of this side chain is physically reasonable at physiological temperatures. In the crystal, E240 is H-bonded to a crystallographic water molecule that bridges the side chain to the backbone of l₁₂. At higher temperatures, however, there may be a competition between the affinity of E240 for water molecules transiently entering the cavity and for residues in p25 with unsatisfied Hb (in this case D192 and Y243). The latter interactions seem to be favored during the dynamics. Still, experiments have shown that E240A and E240Q mutants of the shorter protein p20 bind the kinase with high affinity and severely impair substrate phosphorylation^{21; 25}. It is unclear at this point how these observations can be reconciled at the molecular level, but the simulations strongly suggest that there may not be a direct interaction between E240 and the substrate, but that a more intricate interplay of forces may be at work. An alanine at position 240 is in the vicinity of several non-polar residues in p25 (discussed above). It is possible that hydrophobic packing of A240 prior to complexation affects the binding mode to the kinase, impairing its ability to phosphorylate the substrate. Also, it is possible that a glutamine at position 240 develops weaker Hb interactions with residues in p25 than E240 does, and becomes solvent exposed prior to complexation. During the simulation of the uncomplexed CIP such exposure occurs for E240 itself, leading to inhibition of the kinase, as discussed above. Similarly, a residue at position 240 with the potential to form Hb with residues in cdk5 may affect binding modes and be deleterious to activation.

III. Materials and Methods

Simulations Setup

The simulations were carried out in a cubic box with sides of length ~60 Å or ~80 Å, containing ~6000 or ~14000 TIP3P water molecules, respectively, depending on the protein size. The all-atom (PAR22) representation of the CHARMM force field with the CMAP dihedral correction (version c31) was used²⁸. The simulations were carried out in the isothermal-isobaric ensemble at a temperature of 37 °C and pressure of 1 atm. The protonation states of titratable residues were fixed at standard values compatible with physiological pH, and ions were added to neutralize the system at zero ionic strength. Proteins were capped with acetylated and amidated groups. All proline residues were fixed in the trans conformation, as suggested by available crystallographic data, and no cis-trans isomerizations were allowed during the simulation. Neither the cdk5 nor p25 crystal structures used in this study appear to contain disulfide bonds (the closest S–S distance involves C208 and C229 in p25, which is ~4.7 Å, and fluctuate in the ~3.5–7.5 Å range during the dynamics). The Langevin temperature control algorithm was used in combination with a modified Nosé-Hoover constant pressure method. For computational efficiency simulations were performed in NAMD²⁹ using 16 parallel processors. Long-range electrostatic forces were treated with particle mesh Ewald summation using parameters suggested for the NAMD implementation and periodic boundary conditions. The non-bonded interactions were shut off at 12 Å, using a shift function applied to both electrostatics and van der Waals forces at 10 Å; a cutoff of 13.5 Å was used for the non-bonded list update. Water O–H bond lengths were kept fixed using the SHAKE facility in CHARMM, and a 2 fs time step was used for the calculations of forces with a Verlet integration algorithm. The entire system was first energy minimized; the solvent was then equilibrated for 0.5 ns, with the protein atoms constrained at fixed positions. The constraints were subsequently removed and the entire system equilibrated for 1 ns using temperature-rescaling. When the system reached a equilibrium, 20-ns and 10-ns molecular dynamics simulations were generated for the complex and the uncomplexed proteins, respectively; data were collected every 5 ps.

Choice of protein structures

A crystal structure of a cdk5/p25 complex was reported in²¹ at 2.65 Å resolution (PDB code: 1H4L). A few residues in the small lobe of cdk5, including part of the Gly-rich loop lining the ATP binding pocket, were not resolved. Although physics-based computational methods exist for structure calculation and refinement of missing segments in proteins^{30; 31}, a complete set of experimental coordinates, if available, is preferable for long dynamics simulations. Therefore, the study reported here is based on the crystal structure reported in³², determined at 2.2 Å resolution (PDB code: 1UNL), using chains A for cdk5 and D for p25. The amino acid sequences of 1UNL and 1H4L are identical except for a single mutation in cdk5^A199G. The asymmetric units of these crystals contain two cdk5/p25 complexes, but only one of the kinases in 1UNL contains the co-crystallized ATP-antagonist roscovitine. Despite the differences in crystallization and diffraction conditions the secondary and tertiary structures of cdk5 and p25 are quite similar in both 1UNL and 1H4L, with a total C_α-rmsd smaller than ~0.7 Å. In 1UNL the larger differences between the two complexes appear in the relative position of the lobes in cdk5, a rigid-body-like rotation probably induced by binding of the ATP inhibitor. The C_α-rmsd of the two p25 molecules in 1UNL is ~0.5 Å, while that of cdk5 is ~1 Å; local differences are limited mainly to the Gly-rich loop (residues ~9–19), although orientations of the side chains are similar. These structural differences are expected to lessen during the dynamics at physiological temperature.

Principal component analysis and cross-correlation of motion

In a principal component analysis (PCA)^{20; 33} an M × M covariance matrix is defined by

$$\mathbf{C}=<(\mathbf{R}-<\mathbf{R}>){(\mathbf{R}-<\mathbf{R}>)}^T>$$ (1)

where R is a M × 1 matrix (or column vector), and R^T is the corresponding 1 × M transposed matrix (or row vector). The brackets indicate either ensemble or time averages. If N is the number of atom in the system (or residues, or any subsets of atoms conveniently defined) and each atom i is assumed to have only three degrees of freedom (x_i, y_i, z_i), then M = 3N, the matrix may be defined explicitly by R^T = [x₁, y₁, z₁, x₂, y₂, z₂, ..., x_N, y_N, z_N], where each element depends on time (e.g., during dynamics) or on a suitable conformation index (e.g., in a Monte Carlo simulation or from a set of experimental coordinates). If i and j denote the i-th (r_i) and j-th (r_j) coordinate of R^T, the elements C_ij of C are given by C_ij = <(r_i–<r_i>)(r_j–<r_j>)>; the diagonal elements C_ii's are called variances of the coordinates r_i's.

The covariance matrix defined by Eq. (1) includes all possible correlations between the coordinates in the system, and can be used to identify their relationships during the dynamics. PCA is a linear technique which aims to identify collective motions hidden in the noisy and redundant data collected in an experiment or computer simulation²⁰. At ambient or physiological temperatures PCA is a more appropriate technique than a standard normal mode analysis^{34; 35; 36}, since the elements of the covariance matrix contain information of atomic displacements rather than forces evaluated at potential energy minima. Normal mode analysis is reasonable only at very low temperatures, and becomes weaker as the temperature increases. At high temperatures the system moves along complicated paths on the potential energy landscape, possibly jumping multiple barriers and minima³⁷, so non-harmonic behavior dominates the dynamics. As the temperature decreases, however, diagonalization of either the Hessian or the covariance matrix tends to identify similar collective motions. Identification of collective modes allows a substantial reduction in the number of degrees of freedom necessary to describe the system, from 3N to just a few fundamental modes p (with p << 3N), the so-called principal components. In general, macromolecular movements along these collective coordinates have been associated with biologically relevant dynamics³⁸, while the 3N–p remaining components are either irrelevant (rigid rotations and translations), constrained (usually associated with thermal noise), or dependent on the principal components (redundancy). To obtain the collective movements along the principal components, a linear transformation of the original coordinates R into new coordinates P is first defined as P = V^T(R – <R>), where V is a 3N × 3N matrix that transforms the covariance matrix C into a diagonal matrix E, that is E = V^TCV. Basic algebra shows that, if the k-th column of V is chosen as an eigenvector v_k of the symmetric matrix C, then the element e_kk of E is the corresponding eigenvalues λ_k, that is, Cv_k = λ_kv_k. The dynamic trajectory in the original space R corresponds to a transformed trajectory in the space P, such that a covariance matrix C' defined on this new space exhibit the convenient property that the covariances (or cross-correlations in P) are null. Moreover, the variances are equal to the eigenvalues λ_k, since C’ = <PP^T> = <V^T(R – <R>) (R – <R>)^TV> = V^TCV = E. The eigenvectors v_k form a new basis on which the trajectory can be mapped. The projection of the trajectory onto each of these eigenvectors corresponds to a collective movement on the original space obtained by the inverse transformation R = VP + <R>. The variances quantify the degree of displacements or fluctuations during the dynamics, so the eigenvalues contain information of the degree of collective movement along the corresponding eigenvector. Eigenvalues are typically arranged in decreasing order, λ₁ > λ₂ > ... >λ_3N, where the first p eigenvalues are usually much larger than the remaining 3N–p eigenvalues. Thus, the principal components are identified with the first p eigenvectors associated to the p largest eigenvalues of C. The dynamics of the system can then be assumed to be restricted mainly to this reduced subspace. For this reason the dynamics of a protein along the principal components is known as “essential dynamics”³⁸, conveying the idea that the remaining degrees of freedom are non-essential, i.e., redundant or noisy, and are not expected to carry biological information.

Cross-correlations of individual side chain movements can be estimated from a normalized covariance matrix C defined by³⁹

$$C_{ij}=<\Delta {\mathbf{r}}_i\cdot \Delta {\mathbf{r}}_j>∕{<\Delta {r_i}^2>}^{1∕2}{<\Delta {r_j}^2>}^{1∕2}$$ (2)

where i and j denote atoms (or any subset of atoms labeled by these indexes) in the system. In the residue-based analysis carried out here r_i and r_j define the geometric centers of residue i and j, and Δr_i and Δr_j are the corresponding displacements between time steps; brackets are calculated as time averages, as in Eq.(1). A positive correlation (C_ij > 0) indicates that atoms i and j move concertedly in the same direction, while negative correlation (C_ij < 0) indicate that the atoms move in opposite directions. If two atoms move in directions orthogonal to each other the covariance of Eq.(2) would vanish, so this definition may hide certain atomic correlations when compared to the more general, albeit more cumbersome to analyze, Eq.(1). However, this is not a serious limitation in the analysis carried out here.

IV. Conclusions

Dynamic simulations at physiological temperature of the uncomplexed proteins cdk5, p25, and CIP show conformational changes with potential implication for binding and regulation. An analysis of principal modes of collective motion demonstrates that the activation loop of the complexed cdk5 undergoes conformational transitions between two sub-states state. This behavior is not observed in the uncomplexed kinase, and is then triggered by the activator in close contact with the loop, and is obviously not apparent from the crystal structure. The relatively large temperature factors of amino acids in the activation loop when compared to other regions in the complexed protein suggest that such behavior is plausible. Upon complexation the kinase also undergoes structural rearrangements of two critical motifs, namely, the acidic and Gly-rich loops (cf. Fig. 1), and both contribute to the opening of the substrate-binding cleft. The conformational changes observed in the complexed and uncomplexed proteins are stabilized by extended networks of hydrophobic and hydrogen-bond interactions involving highly conserved residues within the cdk family, which suggests that the observed changes are beyond the limitations of the force field and/or computer simulation method. The uncomplexed inhibitor peptide CIP shows enhanced flexibility and large structural changes in the interfacial loop l₂. These changes reposition the critical residue E240, which becomes fully exposed to the solvent. During cdk5/CIP complexation, the orientation of this residue is such that may favor direct interaction with one or more protonated residues in the kinase. This may explain the higher affinity of CIP when compared to p25, and also its inhibitory power as a blocker of the activator. In fact, E240 is buried in the uncomplexed and complexed p25 and form strong intramolecular Hb interactions. These predictions can be tested by mutating E240 in CIP by a nonpolar or polar net-neutral residue, and measuring the reduced binding affinity and inhibition. The work reported in ²³ demonstrated that S159 of cdk5 is phosphorylated by a kinase activity in PC12 lysates and also by casein kinase I. However S159 phosphorylation does not increase the catalytic activity of cdk5 but it does markedly increase the rate of its activation by endogenous p35 (or p39). The effect of CIP on cdk5 activation by this system may be useful as a test of the extent that inhibition by CIP is competitive with p25-binding to cdk5.