Equilibrium conformational dynamics in an RNA tetraloop from massively parallel molecular dynamics

Abstract

Conformational equilibrium within the ubiquitous GNRA tetraloop motif was simulated at the ensemble level, including 10 000 independent all-atom molecular dynamics trajectories totaling over 110 µs of simulation time. This robust sampling reveals a highly dynamic structure comprised of 15 conformational microstates. We assemble a Markov model that includes transitions ranging from the nanosecond to microsecond timescales and is dominated by six key loop conformations that contribute to fluctuations around the native state. Mining of the Protein Data Bank provides an abundance of structures in which GNRA tetraloops participate in tertiary contact formation. Most predominantly observed in the experimental data are interactions of the native loop structure within the minor groove of adjacent helical regions. Additionally, a second trend is observed in which the tetraloop assumes non-native conformations while participating in multiple tertiary contacts, in some cases involving multiple possible loop conformations. This tetraloop flexibility can act to counterbalance the energetic penalty associated with assuming non-native loop structures in forming tertiary contacts. The GNRA motif has thus evolved not only to readily participate in simple tertiary interactions involving native loop structure, but also to easily adapt tetraloop secondary conformation in order to participate in larger, more complex tertiary interactions.

INTRODUCTION

Analogous to protein structure, nucleic acid structure is largely defined by specific, recurring structural motifs. The most ubiquitous of these motifs in RNA is the hairpin-loop that consists of a base paired stem region and a single-stranded loop region with independent sequence and structure (1). Such hairpins often facilitate the backbone inversions required for higher order structure formation, but their loop regions must consist of at least three nucleotides in order to avoid unfavorable sterics. Accordingly, ‘tetraloop’ regions composed of four single-stranded residues connecting the ends of a helical stem are a prevalent motif in RNA structure. In particular, loops of sequence GNRA, CUUG and UNCG (where N is any ribonucleotide and R is a ribonucleotide with a purine base) account for >70% of known tetraloops (2).

Despite their simplicity, however, tetraloops are known to participate in a variety of biochemical processes, including nucleation in RNA folding (1,3) and formation of tertiary contacts (4–8). Quite remarkably, the latter is sometimes accompanied by structural rearrangements in the native state of the tetraloop itself, potentially including a register shift in base pairing down the tetraloop-capped stem (9,10). Additionally, tetraloops are known to play roles in both transcription (3) and translation (11), as well as serving as recognition sites for RNA binding proteins (12). Indeed, tetraloops have even been identified as potential drug targets due to the differences in tetraloop geometry versus that of double-stranded nucleic acids (13,14). Clearly, the biochemical significance of this small structural motif, in conjunction with its amenability to both experimental (15,16) and theoretical (17,18) study, makes tetraloop systems of key interest within the biophysical community (19).

Still, a detailed understanding of the relevant conformational microstates, transitions between those microstates and folding kinetics of tetraloop regions remains largely unresolved, which has led to increasing interest in exploring these systems both experimentally and computationally in the last decade. Recent studies of such systems include those by Gruebele and coworkers (20), who probed the fast folding of a UUCG tetraloop hairpin via fluorescence; Deng and Cieplak (21), who employed molecular dynamics (MD) to study a UUUU tetraloop RNA hairpin; and Hoogstraten and coworkers (16), who have applied ¹³C NMR spin relaxation coupled with a metabolically based isotopic labeling strategy to study the backbone dynamics of the GCAA tetraloop (Figure 1), while avoiding the difficulties of accurately measuring relaxation parameters in uniformly labeled RNA. The findings of this latter study indicate that the structure of the backbone ribose groups in the GCAA tetraloop is dominated by an equilibrium between C3′-endo and C2′-endo conformations, and that the dynamics observed within the tetraloop correlate with shifts in the ribose pucker modes of individual tetraloop residues, thus supporting an observation posited in our initial computational study of this system (18). These insights, combined with experimentally determined kinetic data, provide a strong basis to which the results of computational and theoretical studies may be compared.

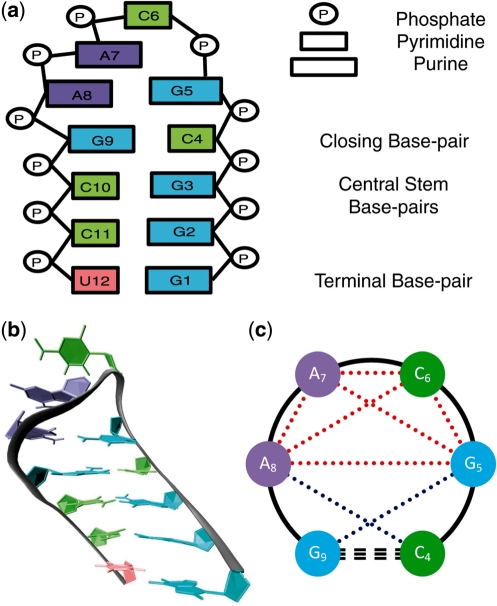
Figure 1.

(a) Schematic representation of the native starting structure of the GCAA tetraloop hairpin used in our ensemble simulations, with ribonucleosides colored by sequence (guanosine in cyan, cytidine in lime, adenosine in violet, and uridine in peach). Specifics of the structure, including base type and structure terminology, are included on the right. (b) Cartoon representation of the native state shown in (a). (c) Schematic representation of the loop region showing the six base separations within the tetraloop (dotted red) and the two base separations spanning the stem–loop interface (dotted blue) that comprise the 8D vector used in conformational clustering. The closing base pair (dashed) and tetraloop backbone (solid) are shown in black.

One such study, recently published by Zhang and coworkers (22), probes the conformational transition map of the GCAA tetraloop using temperature-jump replica exchange molecular dynamics (REMD) simulations. Although proven effective in characterizing the thermodynamics of small biomolecular systems, this method cannot be used to draw kinetic or mechanistic conclusions (23) and requires parallel simulations across a wide range of temperatures, many of which are inappropriate when applied to contemporary molecular models (24). We seek herein to build upon our previous studies of the GCAA tetraloop (18,25,26) in order to elucidate the thermodynamic, structural and kinetic characteristics of GNRA conformational equilibrium in all-atom detail using a massively parallel stochastic approach that employs 10 000 independent simulations. Our method yields orders of magnitude greater sampling at an experimentally and physiologically relevant temperature than any previous effort, providing valid kinetic and thermodynamic conclusions about GCAA tetraloop conformational dynamics for the first time. As the second part of our two-pronged approach, we conduct bioinformatical mining of the Protein Data Bank (PDB) and identify experimentally determined GNRA tetraloop structures in larger RNA systems in order to examine the roles of native and non-native tetraloop conformations in tertiary contact formation.

MATERIALS AND METHODS

Simulation protocols

The GNRA tetraloop hairpin shown in Figure 1, NMR model 1 from PDB 1ZIH (27) with sequence 5′-GGGC[GCAA]GCCU-3′, was simulated using the AMBER-94 all-atom potential (28), which has provided strong quantitative agreement with experimental metrics in our previous studies (18,25,26) and is one of the most well-characterized modern molecular mechanical potentials. The AMBER-94 force field was ported to the GROMACS MD suite (29) within the Folding@Home distributed computing infrastructure (30). The native tetraloop hairpin starting structure was centered in a 50 Å cubic box and neutralized with 11 randomly placed sodium ions with minimum ion–ion and ion–RNA separations of 5 Å, yielding [Na⁺] ∼150 mM. The system was then solvated in 3945 TIP3P water molecules (31), energy minimized via steepest descent, and annealed for 1 ns of MD with the solute held fixed. The resulting annealed system was used to initiate 10 000 independent MD trajectories, reaching an aggregate simulation time of over 110 µs. Simulations were carried out under constant pressure and temperature conditions (1 atm, 300 K), with the solute and ionic solvent independently coupled to external heat baths with a relaxation time of 0.1 ps (32). A cutoff of 10 Å was used to distinguish short- and long-range interactions, and long-range electrostatics were treated using the particle-mesh Ewald method (33). Non-bonded pair lists were updated every 10 steps with an integration step size of 2 fs in all simulations, and all bonds were constrained using the LINCS algorithm (34).

Conformational clustering

For each of the ∼1.1 million resulting RNA conformations, the centers-of-mass (COMs) of each purine and pyrimidine base in the loop region and closing base pair of the stem were calculated. As shown in Figure 1c, the six pairwise base COM separations within the tetraloop, as well as the C4–A8 and G5–G9 pairwise base separations spanning the stem–loop interface, were then used to build an 8D vector to represent the conformation of each simulation frame. These 8D vectors were then used to cluster the ∼1.1 million conformations according to a modified K_means algorithm (24), which allows for clustering without a priori knowledge of the number or distribution of clusters present in the dataset. This algorithm begins with a predetermined number of cluster centers (N) randomly placed within the multidimensional space populated by the data. Each datum is then assigned to the nearest cluster center, and void centers to which no conformations were assigned in any given iteration are replaced with new randomly placed cluster centers for use in the next iteration. Convergence is reached when the cluster assignments of all data points in this 8D space remain unchanged over 10 consecutive iterations.

To determine the proper number of starting clusters, this algorithm was run 100 times each with N values of 20, 30, 40 and 60, for a total of 400 trials. As low N values yielded significantly different cluster numbers and populations, the final value of N = 60 was chosen after observing convergence to similar cluster numbers and populations in the N = 40 trials. The final clustering result was then chosen from those 100 trials with N = 60 such that the mean-squared distance between data points and their second nearest cluster centers was maximized. As K_means clustering is inherently heuristic in nature, the resulting cluster centers were then compared both visually and numerically to identify and combine those containing highly similar conformational character. As described below, thermodynamic and kinetic assessment of the resulting clusters demonstrates steady-state behavior during the final portion of our ensemble simulation.

Database analysis

In addition, we used the advanced search options of the RCSB PDB at http://www.rcsb.org/pdb/search/advSearch.do to identify NMR and X-ray-based PDB structures containing the common GNRA tetraloop sequences GCAA, GAAA or GAGA. The eight COM base–base separations described above were calculated for each occurrence of these GNRA sequences and used to filter out non-tetraloop conformations. Visualization and characterization of hydrogen bonding was performed using VMD (35). Each GNRA tetraloop structure from the PDB was then assigned to the nearest cluster center found in our massive MD simulation database and also classified into one of three structural types based on participation in tertiary interactions: (i) helix tetraloops in which the loop protrudes into the solvent; (ii) minor groove-binding loops; and (iii) those that participate in multiple tertiary interactions.

RESULTS AND DISCUSSION

Ensemble simulation stability

Within our ∼110 µs sampling of the native GNRA hairpin, we observed a cumulative mean all-atom root mean-squared deviation (RMSD) of 1.81(±0.73) Å, demonstrating the stability of the hairpin topology. As specified in the ‘Materials and Methods’ section above, the ∼1.1 million structures taken from our simulation ensemble in 100 ps intervals were clustered using a modified K_means algorithm. After visual and numeric comparison of the resulting clusters, a total of 15 loop clusters were identified. While it is unconventional to identify these clusters as ‘microstates’ under the classical and formal definitions of this term, such clustering methods have been commonly employed to identify ‘structural microstates’ in simulated datasets of biomolecules, in which the number of true (energetically degenerate) microstates present is large and not easily defined. For that reason, we employ the terms ‘microstate’ and ‘cluster’ interchangeably in our discussion below. We also note that an analysis of the distribution of ions around the RNA solute showed no appreciable correlation with the solute shape or loop structure, and ion coordinates were thus omitted in our clustering scheme.

Sugar pucker was assessed in each simulation frame by calculating torsion angles within the ribose ring about the C2′ and C3′ carbons. As expected, contour plots of these torsions (data not shown) revealed two distinct conformational states associated with the 2′-endo and 3′-endo puckers (36). As observed in our previous studies of this system, the G5 residue is relatively immobile and, like stem residues, populates the 3′-endo pucker state nearly constantly, in agreement with the original Jucker et al. (27) NMR study of this hairpin–tetraloop. Other residues within the loop, however, exhibit equilibrium between these two pucker states. In further agreement with the NMR data of Jucker et al., residues A7 and A8 both highly favor the 3′-endo conformation, populating it ∼75% of the time. In contrast, the C6 residue, which has been observed to be the most mobile member of the ring in previous studies (18,22), favors 3′-endo pucker only ∼25% of the time in our simulation. This falls short of the C3′-endo population set forth by Jucker et al., but is in good agreement with the recent simulations of Zhang et al., which employed a different AMBER molecular potential than that used herein. More importantly, our observed favoring of a 2′-endo pucker in C6 is in good agreement with the spectroscopic study of Leulliot et al. (37), which strongly suggests that one of the loop residues adopts a primarily 2′-endo conformation. There is no evidence to suggest that the A7 or A8 residues, which are much less mobile than C6 and stabilized by base stacking, should favor a 2′-endo sugar pucker.

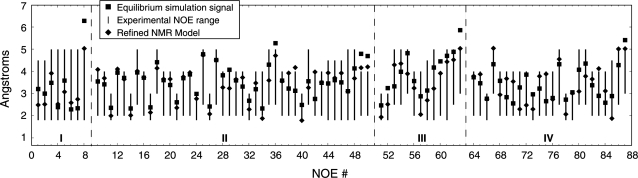
Following our previously reported assessment of the sampling of this RNA system using an implicit solvent model (25), we compare our simulation data to distance constraints determined by nuclear Overhauser effect (NOE) spectroscopy data (27) in Figure 2, which also includes the distances found in the refined NMR model used to initiate our simulations (diamonds). To best match the experimental data, mean inter-proton distances were weighted as 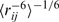and then classified as belonging to one of four categories within the hairpin stem and loop structure. As shown in Figure 2, we observe only a single NOE violation on the order of 1 Å in the stem region of the hairpin (Regions I and II in Figure 2), whereas three such violations were observed using the implicit solvent. Moreover, only a single NOE violation of approximately the same magnitude is observed within the stem–loop interface (Region III in Figure 2) and no appreciable violations are observed in the loop region itself (Region IV in Figure 2). In contrast, the results obtained using an implicit solvent model showed several violations and much greater deviation from the refined NMR model than seen in the explicit solvent simulations reported herein. This agreement serves as testament to the rigor of our methodology and demonstrates clearly that the use of an explicit solvent model does, in fact, help to stabilize the hairpin-loop structural motif by adequately capturing the structural role of water (26).

Figure 2.

Ensemble average inter-proton distances (squares) of the native hairpin for the four types of constraints used to derive the refined NMR models, plotted alongside the NOE-derived constraint ranges (bars) and values for the refined NMR model used to generate the relaxed starting structure (diamonds): (I) stem interstrand; (II) stem intrastrand; (III) stem–loop interface; and (IV) intraloop.

Tetraloop conformational clustering

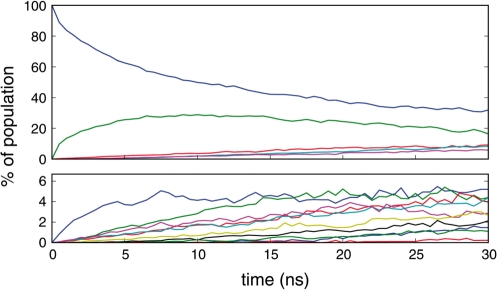
Figure 3 details the evolution of cluster populations within our simulated ensemble, where all simulations began in the native tetraloop microstate (blue curve in upper panel). As shown there, conformational equilibrium within the tetraloop region is established in ∼25 ns, with two dominant clusters observed. To err on the side of caution, we conservatively define our ensemble of equilibrium loop conformations as those occurring during the final 2 ns of the 30 ns ensemble simulation. It is clear that the observed equilibrium is an approximation of the absolute conformational equilibrium. However, in light of the large number of simulations contributing to this equilibrium and the sampling achieved, which is orders of magnitude greater than any previous study of this nature, we stress that this approximate equilibrium is the most accurate representation of tetraloop dynamics in silico to date.

Figure 3.

The ensemble of 10 000 simulations resulted in a total of 15 structural microstates, sorted from most populous (C0 in blue) to least populous (C14). Evolution of the 15 clusters to equilibrium populations is broken into two panels with the upper panel representing the five most populated loop conformations and the lower panel including the remaining conformations. For visual clarity, cluster labels are not shown.

In comparison, the recent study by Zhang et al. (22) that employed REMD to study this system reported total sampling time of 5.76 µs spread over 48 replicas at temperatures exponentially distributed between 300 and 575.5 K. While we do not criticize their methodology, two pitfalls of such REMD sampling are known. First is the limited amount of data that can be obtained at the relevant temperature, in tandem with the large quantity of data that must be collected at temperatures far outside the range for which common molecular mechanics force fields were derived, as described above. In the study by Zhang et al., each temperature was sampled for a total of 120 ns, with a mean exchange time between conformations in neighboring temperature levels of ∼8 ps, which is very short in comparison to the nanosecond to microsecond timescales on which the relevant dynamics of interest occur. In contrast, our sampling of tetraloop conformational dynamics over the final 2 ns of our 300 K simulation ensemble includes nearly 3 µs of data composed of ∼1500 simulations in absolute conformational equilibrium.

The second potential pitfall when employing replica exchange methodology is the inherent possibility of sampling high-temperature microstates not accessible at lower temperatures. Without the adequate follow-up sampling needed to allow these high-energy conformational states to properly anneal to the hyperdimensional free energy surface at the lower temperature(s) of interest, the data obtained at the lower temperatures will be inaccurately distributed in the conformational space sampled. Indeed, Hummer and coworkers (38) have recently published on artifacts involved in REMD sampling. In contrast to the study of Zhang et al. that reported a total of over 100 conformational clusters for the GNRA tetraloop—a number that seems in itself excessively high for such a small structural motif—we observe only 15 distinct clusters in our conformational equilibrium.

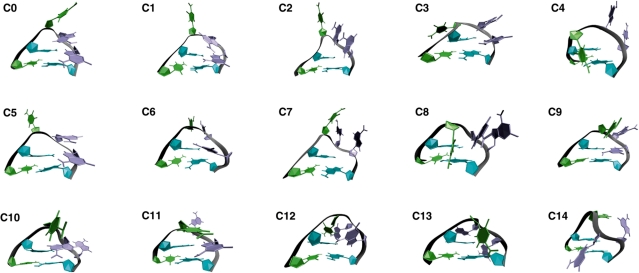
Figure 4 shows the resulting cluster centers observed in our sampling, numerically sorted from the most populated cluster (C0) to the least populated cluster (C14). These cluster centers are taken as the average structures within each populated area of the multidimensional space defined by the eight base–base separations used in our clustering and, therefore, serve only as general representations of each cluster.

Figure 4.

Cluster centers for each of the 15 resulting clusters are shown, sorted from the most stable (C0) to the least stable (C14). In each image, residues 4 through 9 in the sequence, the tetraloop and closing base pair, are shown from left to right, with the C4•G9 closing base pair at the bottom of each image. Residues are colored by type following the scheme of Figure 1.

• C0: native stacking of C6–A7–A8 and non-canonical base pairing of G5•A8
• C1: native state with C6 looped out into solvent, A7–A8 stacking and G5•A8 base pairing maintained
• C2: native-like conformation with C6–A7–A8 stack looped out into solvent and G5•A8 base pair broken
• C3: native-like conformation with C6 looped out far behind the loop
• C4: C6 looped in, A7 and A8 looped out in front and native G5•A8 base pair broken
• C5: G5•A8 base pair broken with C6 and A7–A8 stack independently looped out into solvent
• C6: native-like conformation with C6–A7 stacked and looped out together, G5•A8 base pair maintained
• C7: C6, A7 and A8 looped out fully into solvent with G5•A8 base pair broken
• C8: C6 looped in, A7–A8 stack looped out together in front of loop with G5•A8 base pair broken
• C9: C6–A7 stack more looped out in front
• C10: G5•A7 non-native base pairing, A8 looped out and back with C6 looped out in front
• C11: A7 looped out with C6–A8 stacking in front of the loop and G5•A8 base pair maintained
• C12: G9–G5–C6–A7 base stacking behind the loop with A8 looped out
• C13: G9–G5–A7 base stacking, C6 fully looped out in front and A8 fully looped out in back
• C14: C6 and A8 looped out behind loop with no stacking and A7 looped out in front.

Most notably, two dominant clusters are present in our data. The most populated cluster (>30%) is the native tetraloop conformation (C0), in which the non-canonical G5•A8 base pair is formed and the C6 base is stacked above the A7–A8 stack. C1, the second most prevalent cluster (∼20%), has similar base pairing and stacking structure, with the C6 base protruding into the solvent rather than stacking above A7 and A8. Our early work in this area denoted these two configurations as the ‘closed-loop’ and ‘open-loop’ conformations, respectively (18). In that work, which employed a generalized Born/surface area (GB/SA) implicit solvation model and included far less sampling than this report (100 ns in all, comparable to the 300 K dataset reported by Zhang et al.), a third conformation was also observed. Denoted as the ‘A8-extended’ conformation, this structure maintains C6–A7 base stacking with A8 breaking from the G5•A8 base pair and stacking interactions to protrude into the solvent.

In the more rigorous simulations reported herein, however, our ample sampling of conformational equilibrium within the tetraloop has reduced the observed prevalence of the A8-extended conformer. In its place, we observe three conformational clusters, each representing ∼10% of the equilibrium, which have free energies within ∼1 kcal/mol of the native structure: C2, a native-like conformation with the C6–A7–A8 stack looped out into solvent and the G5•A8 base pair broken; C3, a native-like conformation with C6 looped out far behind the loop; and C4, with C6 adopting a ‘looped-in’ conformation (base shifted into the loop), the A7–A8 stack looped out in front of the backbone, and the native G5•A8 base pair broken. The clear distinction between our early implicit solvent efforts and the current work employing an explicit water model, as highlighted by the prevalence of these newly identified conformational microstates, supports our previous conclusion that implicit solvent models lead to a significant divergence from all-atom modeling, even for this small RNA motif (26).

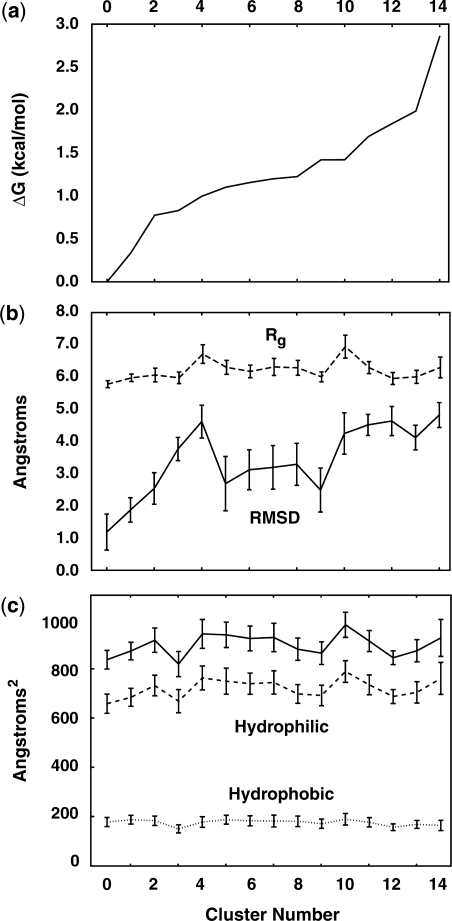
The relative free energy differences between the observed tetraloop clusters and the native state are shown in Figure 5a. Also shown are the structural characteristics of each cluster in Figure 5b, including the radius of gyration (R_g) and the all-atom RMSD of the loop region, with error bars representing one standard deviation within the equilibrium data in each cluster. While no strong correlation between free energy and overall size or native character is apparent, there are some clear distinctions between the ‘compact’ clusters and those that are more exposed to solvent. The extended loop conformations of clusters C4 and C10 are clear examples of this, both showing an average RMSD of ∼4 Å from the refined NMR model. As might be expected, the increase in R_g correlates well with increases in solvent accessible surface (SASA), as shown in Figure 5c. Notably, the hydrophobic SASA is nearly constant across all clusters, while increases in loop size appear to primarily affect the hydrophilic surface area that is exposed. This metric alone, however, is a poor indicator of overall stability, as increasing hydrophilic SASA does not necessarily provide a decrease in relative free energy. In fact, Figure 5 clearly shows that RMSD, R_g and SASA—three metrics that are often followed in simulation-based studies—do not serve as reliable predictors of overall stability. Thus, when used as a low-dimensional approximation of the free energy landscape, these metrics can provide a misleadingly simple energy landscape consistently composed of few microstates.

Figure 5.

(a) The free energy of each tetraloop microstate, relative to the native tetraloop, was calculated following standard thermodynamic relationships based on our statistical sampling. As shown above, only a few kcal/mol separate the most stable and least stable loop conformations from one another. (b) The all-atom RMSD and loop R_g are shown to indicate structural deviation from the native NMR starting structure. (c) The total, hydrophobic and hydrophilic components of the SASA are also shown for each cluster.

Dynamics in the GNRA tetraloop

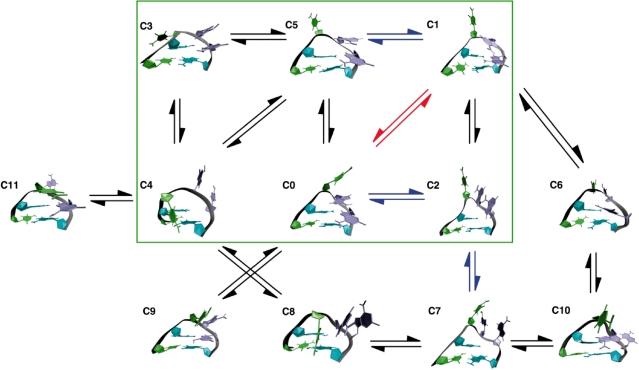
Figure 6 details the transitions observed within our equilibrium data, with arrows colored to represent the timescales on which these transitions occur. As should be the case for equilibrium ensemble simulations, the observed transition rate matrix was symmetric and steady-state behavior was observed with respect to cluster populations and transition probabilities between each pair of clusters, which represents the final stationary distribution of a Markovian model (17). For visual clarity, transitions that occurred less than 30 times in our sampling of over 6100 transitions (∼0.5%) were omitted, as were transitions from any microstate to itself. Clusters C12 through C14 were also excluded from the figure due to their low relative stability. For qualitative purposes, the predominant microstates (C0–C5) in this dynamic system, defined as those within ∼1 kcal/mol of the favored NMR model and representing >75% of the equilibrium, are boxed in green.

Figure 6.

Markovian transition model of the fast loop dynamics observed in our equilibrium ensemble simulations. Clusters are numbered as in Figure 4. Arrows represent observed transitions with rates on the order of 1/ns (red), 100/µs (blue) and 10/µs (black). Self-transitions and those that were observed in low quantities in our simulations were omitted for visual clarity. The green box highlights the six most predominant microstates contributing to the ‘native’ conformation.

Unlike the relatively simple and highly symmetric Markov state model reported by Zhang et al., the Markovian model presented in Figure 6 is relatively asymmetric, as one might expect of a biomolecular system in constant conformational fluctuation. It is clear from the figure that there is rich dynamics taking place in this system, even among only the most predominant of microstates. The ‘native state’ is a fluctuating combination of clusters C0 and C1, with alternative pathways connecting those native conformations via intermediates C2 and C5, and off-pathway intermediates C3 and C4. Interestingly, nearly all of the high-energy conformations occur through pathways that are not directly accessible from the native clusters C0 and C1.

In our initial study of this system, we posited that the looping out of bases into the solvent strongly correlated with a shift from the 3′-endo ribose puckers inherent to RNA structure to the 2′-endo conformation favored in DNA structure (18). This shift to the 2′-endo pucker mode allows the RNA backbone to expand, thus enabling the base to escape into solvent while only locally disrupting the backbone structure. This finding was supported by the IR study of Leulliot et al. (37), who concluded that one of the loop residues adopts a primarily 2′-endo conformation, and has been supported by subsequent studies, including the micro- to millisecond dynamics study of Johnson and Hoogstraten (16) using ¹³C NMR spin relaxation and the simulation-based studies of Zhang et al. (22).

While Johnson and Hoogstraten probed the tetraloop on the micro- to millisecond timescales, they were unable to observe dispersion effects for the C2′ atom in residue C6. One possibility put forth in their publication was that the increased mobility of C6 in comparison to other loop residues could lead to transitions too fast to be detected within their range of study. This hypothesis is strongly supported by our simulations, in which the looping-out and subsequent return of the C6 base to stack on A7 occurs much faster than any other motion observed. Indeed, conversion between 3′-endo and 2′-endo pucker modes for C6 in our equilibrium ensemble simulations occurs at a rate of ∼150/µs. While Johnson and Hoogstraten also hypothesize that ring pucker mode shifts in one residue may be correlated with pucker shifts in neighboring residues, we have searched for such correlations within our data to no avail; these pucker transitions appear to occur independently on a per-residue basis.

Analysis of PDB conformational trends

As GNRA tetraloops are known to participate in tertiary structure formation within large RNA structures, it is a natural progression to consider how the conformational microstates, and the dynamics between them, may play a role in forming long-range structural contacts. To investigate this topic, the advanced search options of the PDB were used to identify 164 NMR and 223 X-ray structures that included any of the three prominent GNRA sequences: GCAA, GAAA and GAGA. These structures were then filtered, leaving only those in which the indicated sequences formed tetraloop structures with a closing base pair below the loop, and were then numerically assigned to one of the 15 clusters defined above. In cases in which multiple refined models were produced from a single set of NMR constraints, each distinct conformation was counted only once and additional models that contained the same conformation were ignored. For example, when considering the PDB file for the hairpin-tetraloop simulated in this work [PDB 1ZIH (27)], which contains two different loop structures (C0 and C1), our assessment included both loop structures once, but not the additional NMR models containing C0 or C1 loop conformations. In addition, identical loops present in PDB files generated via X-ray crystallography in which multiple chains resulted from the crystallization process (i.e. dimerization) were also counted only once.

Table 1 shows the breakdown of tetraloop structures downloaded from this PDB search following the filtering process, as well as the resulting number of structures assigned to each cluster. Remarkably, a number of examples of relatively high-energy loop conformations were found, including numerous cases of clusters C8, C9, C12 and C13 in downloaded NMR structures and clusters C3 through C7 in downloaded X-ray structures. Additionally, while the majority of identified tetraloops served only as terminating caps on RNA helices (>90% of NMR and ∼60% of X-ray tetraloop structures) numerous examples of tetraloops participating in tertiary contacts were also identified.

Table 1.

Tetraloops mined from PDB

Cluster	NMR		X-ray
	N	(%)	N	(%)
0	34	68.6	59	74.7
1	1	2.0	3	3.8
2	0	0.0	0	0.0
3	0	0.0	6	7.6
4	0	0.0	5	6.3
5	0	0.0	3	3.8
6	0	0.0	2	2.5
7	0	0.0	1	1.3
8	2	4.0	0	0.0
9	7	14.0	0	0.0
10	0	0.0	0	0.0
11	0	0.0	0	0.0
12	3	6.0	0	0.0
13	3	6.0	0	0.0
14	0	0.0	0	0.0
Total	50	100	79	100

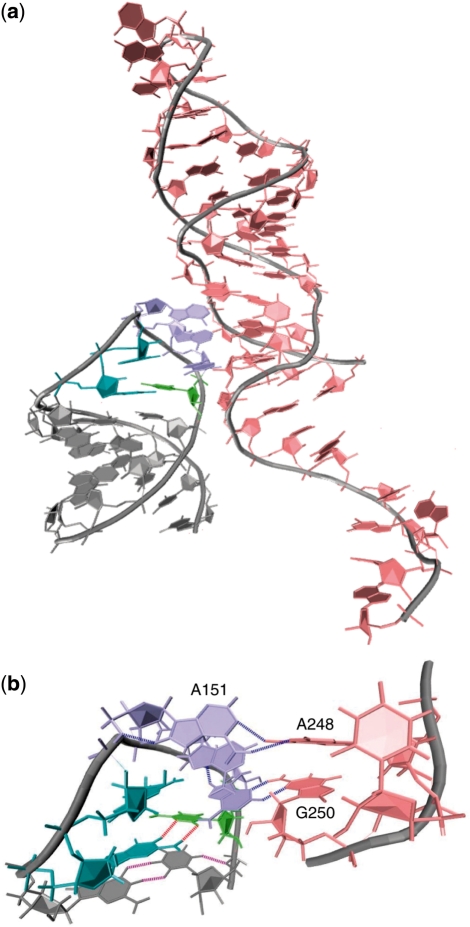
Of these, the majority included docking of native state (C0) tetraloops inside the minor groove of adjacent helical structures. This phenomenon, seen in loops of sequence GCAA and GAAA (but not GAGA), lends support to the notion that these GNRA tetraloops evolved to most adequately form tertiary contacts with nearby stem regions. Figure 7a depicts such tertiary contact by a GAAA tetraloop within the Group I self-splicing intron from the large ribosomal subunit of Tetrahymena thermophila, commonly known as Tetrahymena ribozyme [PDB 1X8W (39)]. A magnification of this interaction is shown in Figure 7b. Analogous minor groove binding interactions involving GCAA tetraloops, such as in ribonuclease P [PDB 2A2E (40)], were also observed.

Figure 7.

(a) Minor groove binding, in which the native C0 conformation of the loop docks into the minor groove of an adjacent helix, is illustrated by the GAAA tetraloop region of Tetrahymena ribozyme (PDB 1X8W). Expansion of the tetraloop docking is shown in (b) with the closing G•C base pair shown in cyan and lime, and hydrogen bonds shown in red. Base stacking in the loop from A151 through A153 is apparent, as is the formation of multiple tertiary hydrogen bonds (blue) between the A151–A248 and A153–G250 pairs.

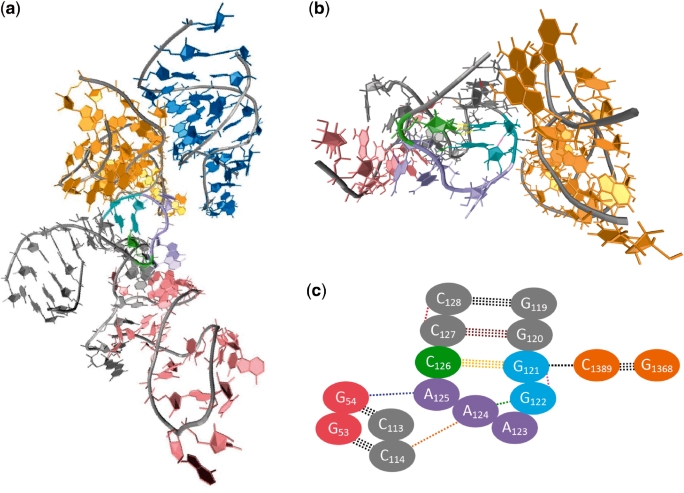
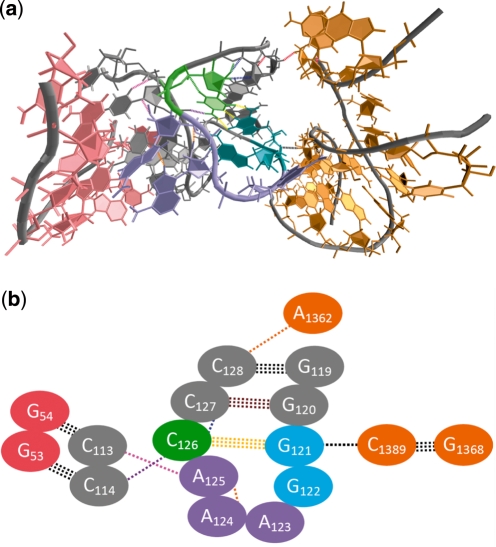
In contrast to the relatively simple interaction scheme observed in minor groove-binding of these GNAA species, ∼5% of GNRA tetraloops found in the PDB participate in more complex tertiary contacts involving multiple adjacent stem regions, which typically involve non-native tetraloop conformations that are 1–2 kcal/mol higher in energy than the native loop structure. An example of such ‘multiple tertiary contact’ is shown in Figure 8a that depicts a portion of the crystal structure of the 23S ribosomal RNA from Deinococcus radiodurans [PDB 1P9X (41)]. Figure 8b shows a magnification of the tetraloop region that has adopted a C4 conformation and demonstrates hydrogen bonding between the backbone of the tetraloop and adjacent bases, as well as between tetraloop bases and guanosine bases in the minor groove of a second adjacent helix. An alternative C5 conformation of the same GAAA tetraloop [PDB 2O45 (42)] is shown in Figure 9. In contrast to the C4 tetraloop conformation, this second conformation shows significantly different intraloop and stem–loop hydrogen bonding that affect the contour of the backbone to allow hydrogen bonding of A125 with its adjacent residue and prevent its interaction with the nearby helix. In fact, though these two conformations share a common tertiary contact, their overall hydrogen bonding schemes are almost entirely different, as are the RNA–RNA interactions that they can facilitate. While these two conformations are higher in energy than the native tetraloop conformation, the adaptability of the tetraloop in assuming multiple conformations during participation in complex tertiary interactions, as demonstrated by independent experimental structure determination studies, allows for greater conformational entropy within the loop that can only serve to stabilize such interactions between non-native loops and adjacent bodies.

Figure 8.

(a) Participation of the GNRA loop in multiple tertiary contacts involves non-native tetraloop conformations, such as the C4 conformation seen in the crystal structure of the 23S rRNA from D. radiodurans (PDB 1P9X). Expansion of the tetraloop and its multiple tertiary interactions is shown in (b) and a schematic version of this interaction is shown in (c). Note that the coloring of bases and hydrogen bonds is consistent throughout, and that each oval represents both base and corresponding backbone in the schematic representation. The GAAA tetraloop and closing base pair residues are shown in cyan (G), violet (A) and lime (C), with the hydrogen bonds of the closing G121•C126 base pair in yellow. Intraloop hydrogen bonding is evident between G122 and A124 (green), and G121 and G122 (pink). Furthermore, interaction of A124 and A125 in the tetraloop with C114 and G54, respectively, provides for two tertiary contacts between the tetraloop and the nearby pink helical region. Additionally, G121 forms a third tertiary contact (black) with C1389 in the adjacent orange helical region.

Figure 9.

(a) The same GNRA tetraloop from D. radiodurans also takes on a C5 conformation (PDB 2O45) while participating in multiple tertiary contacts. The overall hydrogen bonding scheme both within the tetraloop and between the tetraloop and nearby helical regions, as illustrated in (b), is significantly different than in the docking conformation shown in Figure 8. Within the tetraloop and stem, hydrogen bonding is evident between A124 and A125 (orange), and between C126 and C127 (blue). While the G121–C1389 tertiary contact (black) is formed in the same manner as in the C4 conformation pictured in Figure 8, the other tertiary contacts are different. In this C5 conformation, C128 of the stem forms a tertiary contact with A1362 of the nearby helical region (orange). Additionally, both A125 and C126 form contacts with the pink helical region via interactions with C113 and C114 of the stem, respectively, giving a total of four tertiary contacts.

Though these two modes of forming tertiary contact dominate the interactions of GNRA tetraloops within larger structures, additional interactions were identified to a much lesser extent as well. One example of this is the ‘self-interaction’ scheme observed in the NMR structure of the malachite green-binding RNA aptamer [PDB 1Q8N (43)], in which a GAGA tetraloop adopts a compact, but non-native, loop conformation that allows the loop backbone to form hydrogen bonds with the stem region several residues away from the loop. We speculate that the presence of the malachite green moiety bound within the RNA stem is responsible for the non-native loop conformation that results, which again suggests that the flexibility of the GNRA moiety is a primary factor in stabilizing larger RNA structure.

A second example of deviation from the trends discussed above was found in the ATP-binding RNA aptamer in complex with AMP [PDB 1RAW (44)], in which no closing base pair is present and the ‘loop’ appears more as a bulge region that interacts with the major groove of an adjacent helix, rather than the more ubiquitous minor groove binding. In this study, we investigate only situations in which the closing base pair is well-defined and, therefore, speculate that interactions of GNRA sequences that form bulges rather than tetraloops may offer alternative tertiary contact formation modes of greater flexibility within the binding GNRA region and less energetic penalty than the high energy microstates observed in this study.

CONCLUSION

We have studied the conformational dynamics of the statistically predominant GNRA tetraloop motif that participates in a variety of tertiary contact schemes in larger RNA systems. Using tens of thousands of CPUs around the world, our ensemble simulations include 10 000 independent all-atom trajectories in an explicit solvent model. This sampling offers a clear picture of the equilibrium thermodynamics and structural dynamics within this system that is comprised of 15 microstates, many of which are >1 kcal/mol higher in energy than the native loop conformation. Unlike a recent study that took a vastly different approach in silico (22), our data provides a highly asymmetric Markovian State Model that includes transitions ranging from the nanosecond to microsecond timescales. Indeed, the dynamics are complex and include a combination of six loop structures contributing to the ‘native’ state, as well as a number of misfolded and off-pathway intermediate microstates. Such rich dynamics can lead to structural adaptation that is known to stabilize larger RNA structure, as highlighted recently by Bailor et al. (45).

Mining of the PDB for GNRA sequences in experimental RNA structures was also pursued. Filtering of the resulting structures to include only proper tetraloop structures provided significant insight into how this small but highly dynamic structural motif contributes to tertiary structure. Most predominantly observed are interactions between GNRA tetraloops in their lowest energy, native configuration and the minor groove of adjacent RNA helical segments, supporting the notion that these statistically dominant sequences evolved most readily to form tertiary contacts. Several exceptions to this rule were also observed, including a significant number of structures in which the GNRA tetraloop takes on high energy, non-native conformations in order to participate in multiple tertiary contacts. We have illustrated one specific example of this, in which the tetraloop is observed to take on two possible conformational microstates identified via X-ray crystallography. The ability of the GNRA moiety to sample multiple conformational states while participating in tertiary contacts is thus expected to counteract the higher energy inherent to non-native loop conformational microstates by introducing conformational entropy to allow for tertiary contacts with more than a single adjacent helical region. This motif is thus well-suited not only for simple stem–stem interactions involving native loop structure, but also easily adapted to participate in larger, more complex tertiary interactions, which we propose as a significant factor in the molecular evolution of RNA to favor GNRA loop sequences.

This study, while focusing on the dynamics of a small RNA motif, provides proof-of-concept for our multi-pronged computational approach and highlights the potential of future studies of this nature. As computing power continues to increase, the pairing of all-atom rigor and equilibrium sampling will allow us to pursue detailed studies of larger, more complex structural motifs and their inherent dynamics.

FUNDING

Women & Philanthropy Undergraduate Research and Creative Activity Scholarship (to A.J.D.); Provost’s Undergraduate Student Summer Research Stipend (to E.J.T.); Research Corporation Cottrell College Science Award (to A.J.D., E.J.T., E.J.S.). Funding for open access charge: CSU Long Beach.

Conflict of interest statement. None declared.