Finite-temperature critical point of a glass transition

Abstract

We generalize the simplest kinetically constrained model of a glass-forming liquid by softening kinetic constraints, allowing them to be violated with a small rate. We demonstrate that this model supports a first-order dynamical (space–time) phase transition between active (fluid) and inactive (glass) phases. The first-order phase boundary in this softened model ends in a finite-temperature dynamical critical point, which may be present in natural systems. In this case, the glass phase has a very large but finite relaxation time. We discuss links between the dynamical critical point and quantum phase transitions, showing that dynamical phase transitions in d dimensions map to quantum transitions in the same dimension, and hence to classical thermodynamic phase transitions in d + 1 dimensions.

As a liquid is cooled through its glass transition, it freezes into an amorphous solid state, known as a glass (1, 2). The transition from fluid to solid typically requires only a small change in temperature and is accompanied by characteristic large fluctuations, known as dynamical heterogeneity (3). Based on these observations, several theories invoke analogies between the glass transition and phase transitions that occur in model systems (4–8). Some theories are based on equilibrium phase transitions at finite temperatures (4, 5, 7), although these seem to be unobservable in experiments and computer simulations. An alternative idea (8) is that supercooled liquids and certain model systems both exhibit dynamical phase transitions (9–14), controlled by biasing fields that drive the system away from equilibrium. Here, we demonstrate the existence of a nontrivial critical point associated with such a dynamical transition.

The phase transition that we consider occurs in trajectory space. We bias the system toward an “ideal glass” phase by enhancing the probability of trajectories where particle motion is slow. The parameter that controls this bias—the field s—can be varied continuously in computer simulations. For models of glass-forming liquids, the response to this change can be large and discontinuous, corresponding to a first-order phase transition. Such transitions between an active state (analogous to a fluid) and an inactive state (analogous to a glass) were first demonstrated (11) for kinetically constrained lattice models (KCMs) (15). More recently, evidence for such a transition has been found in the molecular dynamics of an atomistic model of a supercooled liquid (13).

In KCMs, the transition to the inactive phase takes place when the biasing field s is infinitesimally small, and this result is independent of the temperature. However, very general arguments based on ergodicity breaking, e.g., refs. 14, 16 and 17, indicate that transitions in ergodic molecular fluids should take place at nonzero s. In this context, the essential difference between KCMs and molecular systems is that forces constraining dynamics in the former are infinite (i.e., hard) whereas those in the latter are finite (i.e., soft). Infinitely long-lived inactive metastable states exist in KCMs because the constraints are hard. The dynamic first-order phase transition detailed in refs.  11 and 12 coincides with a nonequilibrium biasing that stabilizes these inactive states. But because constraints in molecular systems are soft, it is not obvious that this first-order transition will persist in natural systems. Here, we address this issue by considering the effects of softening constraints in the simplest of all KCMs—the one-spin facilitated Fredrickson–Andersen (FA) (18) model.

In this softened FA (sFA) model, we find two main results, illustrated in Fig 1. Firstly, we prove that the dynamic phase transition found in the original FA model still occurs when the constraint forces are finite, but the transition now takes place at nonzero s. Thus, the sFA model—a system with finite short-ranged forces of interaction, one that exhibits long relaxation times and dynamic heterogeneity without equilibrium thermodynamic transitions of mode-coupling theory (7) and random first-order theory (4, 5)—has a dynamical nonequilibrium glass transition. The solution of the sFA model is therefore a concrete, if overly simplified, illustration of the picture of the glass transition proposed in refs. 9 and 21, and later supported by the results of refs. 10–13. This study demonstrates all of these features in a single model.

Fig. 1.

Space–time phase diagrams. (A) Generic space–time phase diagram for KCMs (11). There is a first-order phase boundary that occupies the s = 0 axis, separating an active fluid phase from an inactive “glass.” The critical point s = T = 0 is identified with a filled circle: No motion takes place in this state, and the approach to this point is characterized by scaling behavior and slow dynamical relaxation (22, 23). (B) Sketch of the space–time phase diagram for the softened FA model, under the assumption that the probability of violating constraints ϵ has an Arrhenius form, as described in the main text. The first-order phase boundary moves away from the s = 0 axis and ends in a new finite-temperature critical point, identified with an open circle. The scaling behavior in the vicinity of this point is analogous to the critical behavior near liquid–vapor transitions and is different from the scaling near s = T = 0.

Our second main result is that the sFA model supports a new finite-temperature critical point that only appears when the constraints are softened. More specifically, we show that the first-order dynamical phase boundary in the sFA model ends at a critical point, with universal scaling behavior that maps to that of a quantum-Ising model in a transverse field (19), and hence to a classical liquid–vapor (or liquid–liquid) critical point. The existence of such a critical point is consistent with the requirement that models of glass formers should recover simple liquid behavior at high temperatures. It also means that the relaxation time in the inactive (glass) phase of the sFA model must be finite, although it may be many orders of magnitude larger than the relaxation time of the active phase. This contrasts with the behavior in other model systems, where the inactive phase never relaxes (11, 12, 14).

Softened FA Model

Dynamics in supercooled liquids is heterogeneous (3): Particle motion is relatively significant in some regions of space, and relatively insignificant in others. We associate mobile regions with “excitations” that facilitate local motion. Near such excitations, motion takes place through fast processes with rate λ, whereas motion in immobile regions takes place with a slower rate λ ϵ. To arrive at KCMs, one sets ϵ = 0, for which the physical picture is that relaxation in the system is dominated by correlated sequences of fast processes and that the slow processes are irrelevant (21, 20).

The sFA model consists of a set of binary variables (spins) n_i = 0, 1, where n_i = 1 denotes the presence of an excitation. The rate for flipping spin i from 1 → 0 is [r_i]_1→0 = λC_i, where C_i is a constraint function that depends on the neighbors of spin i, taking a value of order ϵ if the site is in a slow region, and a value of order unity if the site is in a fast region. The reverse process, 0 → 1, takes place with a slower rate [r_i]_0→1 = γλC_i. To ensure detailed balance at a temperature T, we take γ = exp(-J/T) = c/(1 - c), where J is the energy associated with creating an excitation, and c = 〈n_i〉₀ is the equilibrium average concentration of excitations. (We use units of temperature such that Boltzmann’s constant k_B = 1.) The case ϵ = 0 would be a KCM, and we refer to models with ϵ > 0 as “softened” KCMs. We expect that violating a kinetic constraint should require a large activation energy U > J, so that ϵ ∝ exp(-U/T).

In the sFA model, we take 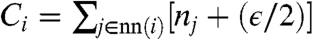, where the sum runs over the nearest neighbors j of site i. We also allow excitations to hop (diffuse) between adjacent sites: The process where the state (1,0) of two nearest neighbors changes to (0,1) occurs with rate λ D. The value of the (dimensionless) diffusion constant D has no qualitative effect on the behavior of the model, but it makes some of our later calculations more tractable because it allows us to solve analytically for the position of the critical point shown in Fig. 1 B. (This technical aspect is detailed below and in the SI Text.) We fix the units of time by setting λ = 1, so the state of the sFA model is specified by the three dimensionless parameters γ, ϵ, and D. The one-spin facilitated FA model is recovered by setting ϵ = D = 0. In constructing Fig. 1, we assumed that γ and ϵ both depend on temperature as described above, and we take U > 3 J, so that the model behaves as a KCM in the limit where T → 0.

Finally, we specify an observable K, which measures the (extensive) amount of dynamical activity in a trajectory. We work in continuous time where successive configurations differ by exactly one local change (diffusion of an excitation or flipping of a spin). We define the dynamical activity K (9, 11, 24–27) to be the total number of such configuration changes in a trajectory.

Active and Inactive Space–Time Phases

Fig. 1 shows two space–time phase diagrams. The idea of a space–time phase is at the heart of this work. In statistical mechanics, a “phase” (such as a liquid or crystal) is a region of phase space in which configurations are macroscopically homogeneous and share similar qualitative properties. By analogy, a “space–time phase” is a region of trajectory space (a set of trajectories) with similar qualitative features.

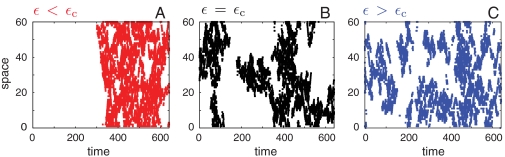
Two space–time phases are depicted in Fig. 2 A. Using computational methods that we will discuss below, we obtained many trajectories for the sFA model, covering a wide range of K. Keeping (γ, ϵ, D) constant, we then restrict ourselves to trajectories where the value of K is equal to approximately half of its equilibrium average. For the parameters of Fig. 2 A, this restriction leads to “phase separation in time”: the trajectory that we show is representative of the ensemble, and it has an early part that is inactive (very few spin flips), whereas its later part is much more active (many spin flips). (The ensemble is time-reversal symmetric, so one might similarly have observed a trajectory where the early part is active and the later part inactive.)

Fig. 2.

Trajectories obtained by constraining the activity K, for the three state points identified in Fig. 3. Active sites (n_i = 1) are colored; inactive sites (n_i = 0) are white. (A) For small ϵ, we observe phase separation in time. (B) At a specific value ϵ = ϵ_c, the system is critical, with large self-similar clusters of active sites. (C) For large ϵ, the system exhibits only one phase, and all correlations have finite range.

In ref. 11, it was proven that phase separation in time occurs for the FA model (i.e., the model with ϵ = 0). The main subject of our current article is how this behavior is affected by a finite value for ϵ, because this relaxes the assumption of infinite forces of constraint that was used in ref. 11. The three panels of Fig. 2 summarize these effects. Phase separation in time is clear in Fig. 2 A, even though ϵ is nonzero. On the other hand, there is no such effect in Fig. 2 C: Whatever restriction we place on K, phase separation never occurs for the values of γ, ϵ, and D used in that figure. The qualitatively different situations shown in Fig. 2 A and C are separated by a critical point in space–time: A representative trajectory from the critical system is shown in Fig. 2 B. There are active and inactive domains with a range of sizes, and the interfaces between them are diffuse and complex.

Biased Ensembles of Trajectories.

We introduce a biasing field s which couples to K in the same way that the inverse temperature couples to the energy in the canonical ensemble of equilibrium statistical mechanics. In so doing, we define nonequilibrium ensembles of trajectories (9–11, 24, 25, 28) known as s ensembles, that can be studied both analytically and computationally. A detailed description of the application of our methods to KCMs is given in ref. 12. In the s ensemble, 〈 A〉_s denotes the mean value of a function of system history, A. Denoting unbiased equilibrium averages by 〈 A〉₀, we have

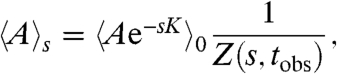[1]

where Z(s, t_obs) = 〈 exp(-sK)〉₀ is the partition function for the s ensemble. The ensemble with s = 0 is simply the unbiased equilibrium dynamics of the sFA model.

We define a dynamical free energy (per unit time)

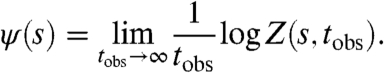[2]

With these definitions, ensembles with fixed K and biased ensembles with fixed s are equivalent, in the same sense as equivalence of ensembles in statistical mechanics. Thus, although the field s does not have a direct physical interpretation, it plays the same role as a constraint on the activity K.

In the sFA model, this formalism yields ensembles of trajectories that depend on four parameters γ, ϵ, D, and s. Such ensembles may exhibit phase coexistence in space–time. For an sFA model specified by γ, ϵ, and D, we show in the SI Text that ensembles of trajectories have a hidden symmetry if s = s^∗, where s^∗ satisfies

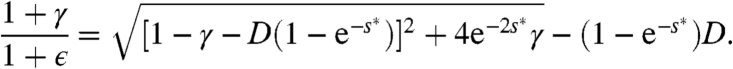[3]

If the model supports coexisting active and inactive phases then they are related by this symmetry, and the coexistence point is s = s^∗, with the inactive phase being found for s > s^∗ and the active one for s < s^∗. We emphasize that the symmetry condition s = s^∗ is necessary for space–time phase coexistence, but it is not sufficient.

Computational Sampling of Space–Time Phases.

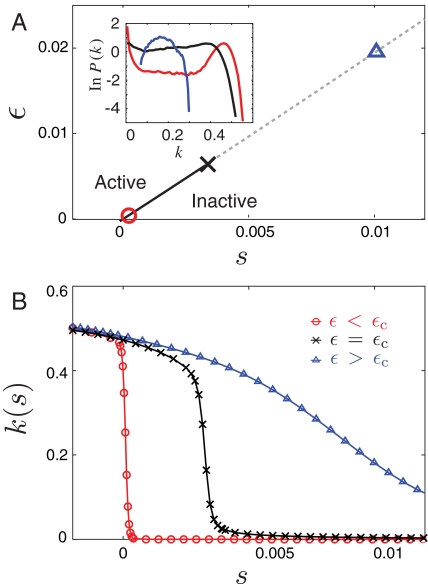
We have investigated the s ensemble computationally, using transition path sampling (TPS) (29). The procedure is similar to that used in ref. 13: We run standard TPS simulations with shooting and shifting moves, and a Metropolis acceptance criterion based on values of s and K. As discussed above, the behavior of the sFA model does depend on the parameter D, but qualitative features are largely independent of D. We have verified this by performing numerical simulations for several values of D, including D = 0. However, in Figs. 2–4, we take advantage of this adjustable parameter. We fix γ and vary ϵ, taking

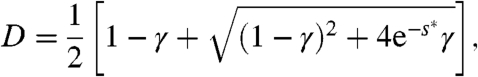[4]

where the value of s^∗ is obtained by solving Eq. 3 simultaneously with Eq. 4. This leads to the phase diagram of Fig. 3 A, in which the parameter D depends on ϵ, so that Eqs. 3 and 4 hold both on the (solid) phase coexistence line and on the (dashed) symmetry line. We can then solve for the position of the critical point shown in Figs. 2 B and 3 A.

Fig. 3.

Space–time phase behavior of the sFA model. (A) Phase diagram of the 1d sFA model. For γ = 0.25, we show the (s, ϵ) plane, varying the diffusion constant D as a function of ϵ, as discussed in the text. The solid line is a first-order phase boundary between active and inactive states. It ends at a critical point. The dashed line shows the extension of the symmetry line (Eq. 3) into the one phase region. The symbols show the parameters for which we present data, which are ϵ = 1.9 × 10^-4, 6.3 × 10^-3, and 1.9 × 10^-2. (Inset) Histograms of the (intensive) activity k = K/(Nt_obs), in symmetrized s ensembles corresponding to the three symbols in the main figure. (B) Plots of the activity k(s), in the vicinity of the state points identified in A.

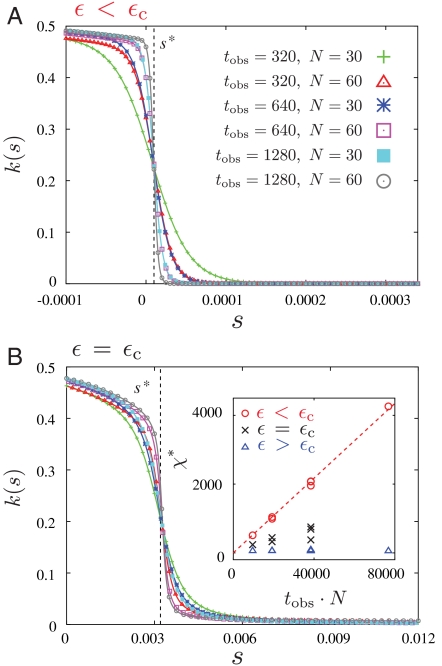
Fig. 4.

Finite-size scaling in the s ensemble. We show the dependence of the mean activity on the biasing field s, for various system sizes and observation times. Dashed vertical lines show the positions of first- and second-order transitions predicted by Eq. 3. (A) Data for ϵ < ϵ_c, at the state point marked by a circle in Fig. 3 A. (B) Data for ϵ = ϵ_c, for the state point marked by a cross (×) in Fig. 3 A. The values of N and t_obs are the same in A and B. (Inset) The derivative of the activity with respect of the field s, evaluated at s = s^∗, for the three state points shown in Fig. 3 A, varying N and t_obs.

As in standard Monte Carlo simulations near phase coexistence, sampling of the s ensemble may be frustrated by large free-energy barriers between coexisting phases. To avoid this, we work at s = s^∗ and ensure that the system explores both active and inactive phases within each TPS run (13).

Other obstacles to accurate characterization of phase coexistence include the possibility of large boundary effects. Although periodic boundary conditions are used for the spatial degrees of freedom in the sFA model, it is not possible to use periodic boundaries in time within our computational approach (for an analytic treatment, see ref.  17). If s > 0, then this means the initial and final parts of the trajectory are biased toward the active phase (12). To reduce this effect and more accurately characterize phase coexistence in the sFA model, we introduce a refinement to the method of ref. 13. We bias the initial and final conditions in our ensembles of trajectories, arriving at a “symmetrized s ensemble” that fully respects the symmetry between active and inactive phases in the sFA model (see SI Text). Expectation values in this ensemble are given by

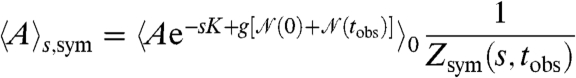[5]

with 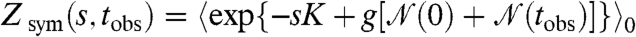. Here, 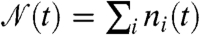is the total number of excitations in the system at time t, and the parameter g depends on γ, ϵ, and D through an expression given in the SI Text. For large enough t_obs, bulk properties of the s ensemble and symmetrized s ensemble are the same. In particular, the mean activity density within the symmetrized s ensemble is

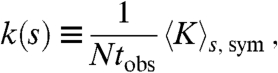[6]

which depends implicitly on N and t_obs as well as the parameters of the model. However, as t_obs → ∞, then the activity densities in symmetrized and original (unsymmetrized) s ensembles approach the same limit, which is -N^-1dψ(s)/ds.

We show both first- and second-order dynamical phase transitions in Fig. 3. For fixed γ, we show a space–time phase diagram in the (s, ϵ) plane, with D being adjusted as in Eq. 4. The overall structure mirrors that of Fig. 1 B, but we are now working at fixed γ and varying ϵ, whereas both of these parameters were varying separately with temperature in Fig. 1 B, as discussed above. The condition of Eq. 3 is shown as a dashed line, together with a solid first-order phase boundary that follows this line from the origin to the (known) position of the critical point. We also show histograms of the activity K obtained from s ensembles at the coexistence point s = s^∗, and the behavior of k(s). We emphasize the analogy between the data of this figure and the behavior of a ferromagnetic model at phase coexistence: The bimodal distribution P(K) is analogous to the bimodal distribution of the magnetization at zero magnetic field, whereas the sharp change in k(s) as s is increased is analogous to the jump in the magnetization as the field is varied through zero.

Pursuing this analogy with ferromagnetic phase transitions, we expect a true jump discontinuity in k(s) at s = s^∗ only in the limit N, t_obs → ∞. (The order of the limits of N and t_obs is discussed in the SI Text.) We show a finite-size scaling analysis of k(s) in Fig. 4. The data in Fig. 4 A show an increasingly sharp jump in k(s) as N and t_obs are increased. On the other hand, Fig. 4 B shows the behavior found at the critical point, and the inset shows how the maximal susceptibility χ^∗ = -dk(s)/ds|_s=s^∗ scales with the system size. For ϵ < ϵ_c, the data in the inset are consistent with the behavior at a first-order phase transition: χ^∗ = (Δk)²Nt_obs/2, with Δk being the size of the jump in k(s) at the phase transition. For ϵ = ϵ_c, the dependence of χ^∗ on N and t_obs is weaker, consistent with a second-order phase transition; for ϵ > ϵ_c, the susceptibility χ^∗ is independent of the system size.

Theoretical Analysis

We now analyze the sFA model through its master equation. We write this compactly as

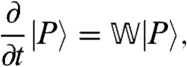[7]

where |P〉 represents a probability distribution over the configurations of the system, and is a linear operator whose matrix elements are the transition rates of the sFA model. The s ensemble may then be studied by defining an operator 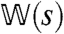such that 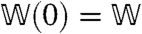, and the largest eigenvalue of 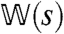is the dynamical free energy ψ(s). Details are given in the SI Text. Because the sFA model obeys detailed balance, one may write 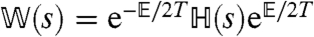, where 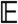is an energy operator, and 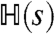is a symmetric (Hermitian) operator with the same eigenvalues as .

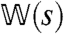These observations allow properties of large deviations in space–time to be obtained from ground-state properties of a quantum many-body system with Hamiltonian 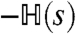. Such mappings between stochastic classical systems and deterministic quantum ones are well established (30, 32), and a recent review (31) covers the relevant cases for this article. As well as the mathematical mapping, there is also a useful physical analogy: The phase boundaries shown in Fig. 1 are points at which the dynamical free energy ψ(s) has a nonanalytic dependence on s and on the parameters of the model. In the quantum systems, such singularities are quantum phase transitions (QPTs) (21), which have been studied extensively. Relations between large deviations in classical systems and QPTs were discussed in ref. 33, and other possible connections between QPTs and glass transitions have also been proposed recently (34).

Mapping to Quantum and Classical Spin Systems.

As discussed in the SI Text, we use a spin-half representation of the binary spins of the sFA model, following refs. 23 and 31. The result is

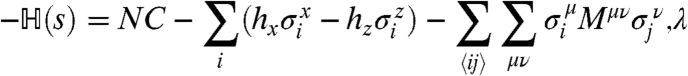[8]

where μ, ν∈{x, y, z} and the 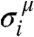are Pauli matrices associated with site i, and C = [D + (1 + γ)(1 + ϵ)]d/2. The scalars h_x and h_z and the coupling matrix M depend on the sFA parameters γ, ϵ, D, and s, through expressions that are given in the SI Text. The sum over 〈ij〉 runs over pairs of nearest neighbor sites on a d-dimensional lattice.

This operator may be analyzed in a mean-field approximation, following ref. 11. We replace operators in Eq. 8 by numbers: 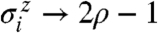and 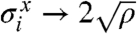, where ρ ≪ 1 is the mean density of excitations. We also take D = 0 and γ ≪ 1 although these conditions may be relaxed at the expense of some algebra. The result is a space–time Landau free energy:

[9]

We have 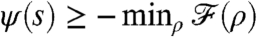(11, 12) and we use this bound to estimate ψ(s). The function 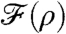is quartic in 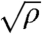, and may have either one or two minima. At this mean-field level, the point where the single minimum bifurcates into two is the critical point, whereas cases where 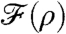has two degenerate minima correspond to space–time phase coexistence. For fixed γ, the mean-field estimate of the position of the critical point is 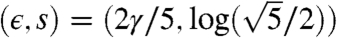, at which .

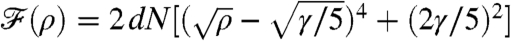To move beyond this mean-field level, we interpret 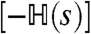as a quantum Hamiltonian and diagonalize the matrix M. That is, we let 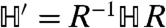where R is a uniform rotation of the spins (see SI Text), so that

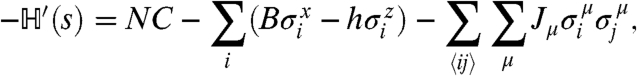[10]

with B, h, and J_x,y,z being new constants that depend on (γ, D, ϵ, s) through expressions given in the SI Text. For the quantum spin system described by 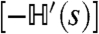, h and B are magnetic field terms: We have h > 0 but B may have either sign. The most interesting behavior of the quantum system occurs when B = 0, in which case the field h tends to align the spins along the -σ ^z direction, while the ferromagnetic coupling J_x promotes ferromagnetic ordering along ± σ ^x directions. For B = 0 and small h/J_x, there is a single ground state with 〈σ ^x〉 = 0. However, for B = 0 and large J_x/h, there are two degenerate ground states, with the symmetry of 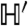under σ ^x → -σ ^x being spontaneously broken. These two regimes are separated by a quantum phase transition.

There is a standard exact mapping between quantum spin systems in d dimensions and classical spin systems in (d + 1) dimensions (19). One takes a small time increment δt and considers the operators 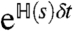and 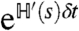as transfer matrices that generate ensembles of configurations for (d + 1)-dimensional Ising systems. We denote the ensembles defined by these two transfer matrices as S and S^′, respectively, with details given in the SI Text. The ensembles are defined for classical Ising systems on anisotropic (d + 1)-dimensional lattices, but we concentrate here on symmetries and universal properties of the models, which do not depend on its underlying lattice. The weights of configurations in ensemble S are identical to those of corresponding trajectories of the sFA model in the s ensemble, with the time axis in the sFA model being interpreted as the (d + 1)th spatial axis in the classical Ising system.

Consequences for the sFA Model.

Under the mapping from 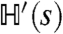to 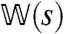, the condition B = 0 in the quantum spin model corresponds to a symmetry condition for the sFA model, which is Eq. 3. If B = 0 then 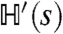is unchanged by the global transformation 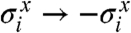, and the classical ensemble S^′ is also symmetric under global spin inversion, except for possible boundary effects that are discussed below. This symmetry of 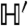corresponds to a symmetry transformation of the sFA model that relates active and inactive phases, and was used to derive Eqs. 3 and 5. Thus, the dashed line shown in Fig. 3 A for the sFA model corresponds to a zero-field condition for the quantum and classical spin systems. When distinct active and inactive phases exist in the sFA model, they correspond to ferromagnetic phases in these spin systems.

As usual, coexistence between ferromagnetic phases is associated with a critical point. The ensemble S^′ has the symmetry properties of an Ising model in (d + 1) dimensions. Thus, the finite-temperature critical point shown in Fig. 1 B is in the universality class of a (d + 1)-dimensional Ising model. For this critical point, the (upper) critical dimension of the sFA model is d_c = 3, whereas the dynamical exponent that sets the relative scaling of space and time is z = 1 in all dimensions (21). This is in contrast with the zero-temperature critical points in Fig. 1, where z = 2 and d_c = 2 (23).

The classical ensemble S^′ also motivates our definition of the symmetrized s ensemble. As we discuss in the SI Text, the s ensemble of Eq. 1 corresponds to an ensemble S^′ in which boundary conditions are biased toward one of the ferromagnetic phases. However, the symmetrized s ensemble defined in Eq. 5 corresponds to an ensemble S^′ that is invariant under global spin inversion. Thus, the symmetrized s ensemble removes biases toward active or inactive phases in the sFA model by ensuring that ensemble S^′ has no symmetry-breaking bias. This property enabled the accurate finite-size scaling analysis shown in Fig. 4. Our choice of the parameter D given in Eq. 4 is also motivated by properties of 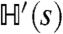: We show in the SI Text that, if both Eqs. 3 and 4 are satisfied, then B = J_z = 0. In one dimension, 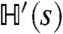may then be diagonalized by a Jordan–Wigner transformation (31), allowing us to locate the critical point in Fig. 3.

Finally, it is useful to generalize concepts of equilibrium thermodynamic phases to those of nonequilibrium space–time phases in the s ensemble. For example, if ensemble S^′ contains coexisting phases, one may calculate the surface tension Γ between them. In the sFA model, Γ gives the value of a space–time surface tension whose interpretation will be given in the final section. Away from phase coexistence (B ≠ 0), ensemble S^′ is dominated by a single phase, but one may still investigate metastable phases with opposite magnetization. In particular, the free-energy difference between phases and the spinodal limit of stability of the metastable phase may be calculated approximately. Variational and mean-field methods for estimating such space–time free-energy differences and spinodals in s ensembles for KCMs were discussed in ref. 12 and we summarize them in the SI Text.

Implications of These Results for the Glass Transition

The critical point we have uncovered appears as kinetic constraints are softened, and its discovery has implications for natural systems even though experimental methods to directly access the s ensemble are not yet known. To explain this, we return to our analogy between sFA and ferromagnetic systems.

Consider an ordered ferromagnetic system, below its critical temperature and in a small magnetic field. Within the ordered equilibrium state (which has positive magnetization), the dominant fluctuations are small domains of the minority phase (with negative magnetization). The probability of observing such a domain depends on the surface tension and the free-energy difference between majority and minority phases.

Dynamical heterogeneities can occur by a similar mechanism: The dominant fluctuations in the (active) supercooled liquid state come from domains of the inactive space–time phase. In that case, the probability of observing inactive behavior in a region of space–time is set by several factors: the spatiotemporal extent of the region and the surface tension and free-energy difference between dynamical phases. In the unbiased equilibrium dynamics of the system, one expects the dominant contributions to this probability to take the form (10)

[11]

where ℓ ^d and τ are the spatial and temporal extents of the inactive domain, Γ_1,2 are surface tensions, and Δψ is the difference in free energy between the space–time phases, evaluated at s = 0.

We have shown (9, 10) that KCMs (with ϵ = 0 = s^∗) lie naturally at phase coexistence so that Δψ = 0. However, for models with s^∗ > 0 (including the sFA model) we expect Δψ > 0. In either case, the probability of observing large dynamical heterogeneities in the system is set by the space–time surface tensions and free energies. Of course, in defining the distribution P(ℓ ^d,τ), one assumes the existence of two space–time phases, which is strictly valid only at phase coexistence. However, one may use a mean-field spinodal condition for the classical spin model to estimate whether the minority (inactive) space–time phase is sufficiently stable to form fluctuating domains within the stable active state, as in the magnetic case.

Based on these arguments, we return to Fig. 1 B. For high temperatures in the sFA model, there is only a single phase, which we identify with a simple liquid. As the system is cooled, a new inactive phase comes into existence at a critical point, where s > 0. Whether the inactive phase has observable consequences in the liquid depends on its stability at equilibrium (s = 0) and on the free-energy difference and surface tension between active and inactive phases. For the sFA model, these factors are estimated via mean-field arguments. Within the theoretical picture presented here, the stability of the inactive space–time phase and the parameters Γ₁, Γ₂, and Δψ are the key quantities that determine the nature of the dynamical heterogeneities in supercooled liquids.

Finally, the phase diagram of Fig. 1 B connects our work to different theoretical scenarios for the glass transition. First, if cooling a supercooled liquid is analogous to reducing both γ and ϵ in the sFA model, then both the dynamical free-energy difference and the surface tension between the phases vanish as T → 0. This corresponds to a zero-temperature ideal glass transition for the liquid (22). Such transitions are accompanied by increasing dynamical heterogeneity because the probability of large inactive space–time regions increases, according to Eq. 11.

Second, if molecular liquids support a finite-temperature ideal glass transition along the lines of the thermodynamic glass transition in spin glasses (4, 5), one expects the dynamical free-energy difference and surface tension to vanish at that point. Ref. 14 provides a mean-field analysis of that case. Further, if molecular liquids do support dynamical transitions in the presence of the field s, this does not imply the existence of any finite-temperature thermodynamic transition, but nor does it preclude such a possibility.

Third, for the active–inactive phase boundary of Fig. 1 B to end at a critical point as it does for the sFA model, the two phases must have the same symmetry properties. (Critical points for phase boundaries separating crystalline and liquid phases are forbidden for this reason.) In a molecular system, it is not clear a priori whether the inactive phase should be a true amorphous solid that spontaneously breaks translational symmetry, or a yet-to-be-observed liquid phase with an extraordinarily large but finite relaxation time. In the former case, the critical point shown in Fig. 1 B cannot occur, and any active–inactive phase boundary must separate the (s, T) plane into distinct regions. (This was the case in the spin-glass model considered in ref. 14). However, the latter possibility—a liquid–liquid transition that is relevant for the glass transition (6, 35, 36)—can be consistent with the critical point discussed here, provided that the liquid– liquid transition is a nonequilibrium transition.