Abstract
The complex etiology of common diseases like cardiovascular disease, diabetes, hypertension, and rheumatoid arthritis has led investigators to focus on the genetics of correlated phenotypes and risk factors. Joint analysis of multiple disease-related phenotypes may reveal genes of pleiotropic effect and increase analytical power, but at the cost of increased analytical and computational complexity. All three data sets provided for analysis at the Genetic Analysis Workshop 16 offered multiple quantitative measures of phenotypes related to underlying disease processes as well as discrete measures of affection status. Participants in Group 6 addressed the challenges and possibilities of association analysis of these data sets on multiple levels, including phenotype definition and data reduction, multivariate approaches to gene discovery, analysis of causality and data structure, and development of predictive models. These approaches included combinations of continuous and discrete phenotypes, use of repeated measures in longitudinal data, and models that included multiple phenotypic measures and multiple single-nucleotide polymorphism variants. Most research teams regarded the use of multiple related phenotypes as a tool for increasing analytical power, as well as for clarifying the underlying biology of complex diseases.
Keywords: multivariate analyses, quantitative traits, longitudinal data, instrumental variables, association analysis, genetic risk scores, data reduction, correlation
Introduction
While clinical outcomes are the ultimate concern of medical genetics, the complex etiology of common diseases (e.g., cardiovascular disease (CVD), diabetes, hypertension, and rheumatoid arthritis (RA)) has led many investigators to focus on the genetics of correlated phenotypes and risk factors. Such endophenotypes [Gershon et al., 1998, Almasy and Blangero, 2001] representing specific physiological or biochemical processes are expected to be closer to gene action and therefore more amenable to genetic analysis; in addition, known risk factors can be measured in unaffected as well as affected individuals, increasing sample size and providing insight into the distribution of genetic susceptibility for future disease. Not surprisingly, many of these endophenotypes are correlated and may represent pleiotropic effects of common genetic pathways, such that joint analysis of several phenotypes may offer more power for detection of causal variants than separate analysis of each. In addition, longitudinal study designs provide multiple measurements of each phenotype in each individual, and the time course of changes in a phenotype may provide additional information about underlying risk.
Eight research groups participated in Genetic Analysis Workshop 16 (GAW16) Group 6: Multi-Phenotype Analyses. These investigators presented work using all three data sets: discrete and quantitative phenotypes in unrelated individuals recruited by the North American Rheumatoid Arthritis Consortium; longitudinal CVD risk-related phenotypes from three generations of Framingham Heart Study (FHS) participants; and a simulated data set using the pedigree structure and genotype data from FHS. While many participants focused on methods for gene discovery, the presentations addressed a wide range of other topics, including phenotype definition, correlation of genetic and other disease risks, and mechanistic and/or predictive models of genetic risk.
Approaches to the Data
The three population data sets provided for GAW16 are described in detail in the conference proceedings. The following brief discussion focuses on the approaches that Group 6 investigators took with respect to data selection and preparation.
Problem 1 [Amos et al., 2009]
Two groups used the RA data comprising unrelated cases and controls were provided by the North American Rheumatoid Arthritis Consortium. These data included one discrete phenotype (RA affection status) and two continuous phenotypes correlated with RA: anti-cyclic citrullinated protein (anti-CCP) and IgM. The continuous measures were available only for the cases. Because both groups sought to combine discrete and continuous data, they chose to impute the continuous phenotypes in the controls using published data on the distribution (mean, variance, and covariance) of these clinical markers in unaffected individuals [Hu et al., 2007; Keskin et al., 2008]. The effect of this decision on the studies is discussed below.
Problem 2 [Cupples et al., 2009]
Five groups used the de-identified FHS single-nucleotide polymorphism (SNP) Health Association Resource (SHARe) data provided through dbGaP. These data include several continuous clinical measures related to CVD risk, including fasting blood glucose levels, systolic and diastolic blood pressure (S/DBP), total cholesterol, high density lipoprotein cholesterol (HDL-C), and triglycerides (TG). Body mass index (BMI) was calculated from height and weight. Several groups calculated low density lipoprotein cholesterol (LDL-C) based on the other lipid measures. Data were available for three generations of FHS participants; repeated measures from several clinical examinations were available for the Original Cohort and the Offspring Cohort. Three groups [Baker et al., 2009; Hamid et al., 2009; Waaijenborg and Zwinderman, 2009] used phenotype data from the Offspring Cohort only, while Morris et al. [2000] and Piccolo et al. [2009] used data from all cohorts (Table I). Three groups [Hamid et al. 2009; Morris et al., 2009; Waaijenborg and Zwinderman, 2009] made use of the repeated measures as described below. Most groups prepared phenotype data by removing extreme values, performing loge or other transformation to meet the assumption of normality, and correcting for age, sex, and medication. In particular, all but one [Hamid et al., 2009] of the groups that analyzed BP data corrected for antihypertensive medication by adding 10 mm Hg to SBP and 5 mmHg to DBP measures in the medicated subjects, as recommended [Cui et al., 2003].
Table I. Comparison of study designs and SNP selection protocols.
| Study | Cohort | SNP selection protocol | SNP exclusion criteria | Adjustment for family data |
|---|---|---|---|---|
| Baker et al. | FHS offspring, unrelateds, and sibpairs, 7th exam | GWAS using 50k panel | Mendelian inconsistencies1 | Mixed model |
| Cui et al. | NARAC | Candidate regions | Missing ≥ 5% MAF < 5% HWE P < 0.001 |
Not applicable (unrelated individuals) |
| Hamid et al. | FHS offspring, multiple exams, unrelated only | Candidate SNPs | Not applicable | Analysis limited to unrelated individuals |
| Huang et al. | FHS simulated data, 1st replicate | Known SNPs from correct model | Missing > 10% MAF < 1% |
Not described |
| Morris et al. | FHS, all generations, age stratified | Candidate SNPs | Not applicable | Mixed model |
| Piccolo et al. | FHS, all generations, first examination | Pre-selected by 2-stage GWAS, 500k panel | Missing > 2% HWE P < 0.001 |
No adjustment (GWAS); mixed model (GRS) |
| Qin et al. | NRAC | Multi-stage GWAS, 550k panel | Not described | Not applicable (unrelated individuals) |
| Waaijenborg and Zwinderman | FHS, offspring generation, multiple exams | Pre-selected by GWAS, 50k panel | Missing > 5% MAF < 1% |
No adjustment |
For a family in which segregation of a particular marker was inconsistent with Mendelian inheritance, genotypes for that marker were marked as ‘missing’ for all family members.
Problem 3 [Kraja et al., 2009]
Huang (unpublished) made use of the simulated data based on the FHS pedigree structure and SNP genotypes. This investigator was testing methods for identifying pleiotropic variants and made use of known pleiotropy in the simulated data, and thus chose to work with knowledge of the correct model.
Among investigators using the FHS and FHS-derived simulated data, various methods were used for dealing with family structure. Several investigators used mixed model-based association tests that estimated random effects of familiality as well as the fixed effects of SNP genotypes implemented in PLINK [Purcell et al., 2007, http://pngu.mgh.harvard.edu/purcell/plink/] or the ASSOC routine in S.A.G.E. [http://darwin.cwru.edu] (Table I).
Table I describes the varied approaches to study design and selection of the SNP data by all eight research teams.
Multivariate Versus Univariate Phenotypes
While metabolic syndrome (MetSyn), a predictor of CVD risk, has been defined in various ways [Day, 2007; López-Alvarenga et al., 2008], all definitions acknowledge that obesity, type 2 diabetes, and CVD share common risk factors and are themselves intercorrelated. Baker et al. [2009] examined the component phenotypes of the World Health Organization's 1999 definition of MetSyn (TG, HDL-C, SBP, DBP, fasting blood glucose, and BMI) in the Offspring Cohort of the FHS. (The World Health Organization definition was chosen over the more recent NCEP-III definition because fasting insulin levels and waist circumference were not included in the FHS SHARe data.) Using the 50k Affymetrix SNP panel, variants were tested for association using the ASSOC routine in S.A.G.E.: a SNP covariate (number of minor alleles) was included in a mixed model that also accounted for the random effects of familiality. The MetSyn component phenotypes were tested for association in separate univariate tests and also jointly in a multivariate association test. Because of the extensive correlation among the component phenotypes, the authors expected that the multivariate test might reveal pleiotropic variants – and potentially increased power to detect associations (although the authors did not present a formal test of power as part of this study). Among the strongest associations in this study, two SNPs on TCP11L1 showed significant association with fasting blood glucose and HDL-C, respectively, in univariate analysis, providing evidence of pleiotropy at this gene locus. The strongest candidates in multivariate analysis were two SNPs on CETP, which had been associated with HDL-C levels in other studies [Dullaart and Sluiter, 2008]. These SNPs were also significantly associated with HDL-C in the univariate test, but not strongly associated with any other MetSyn trait; in this case, inclusion of the other phenotypes seems simply to have increased the evidence for an already significant locus for HDL-C in spite of the additional degrees of freedom in the multivariate test. Perhaps a better example of pleiotropy appeared in the third-highest multivariate finding: rs9901139 in PMP22 appeared to be strongly associated with the vector of MetSyn traits although there was no strong evidence of association in any univariate test.
High-Dimensional Analyses
Four groups addressed the complexity of combining multiple correlated phenotypes and/or multiple SNPs in the same model. Cui et al. [2009] proposed a multivariate combinatorial searching method (MCSM) to search for gene-gene interactions. In contrast to previous combinatorial methods [Nelson et al., 2001; Sha et al., 2006], the MCSM examines both multiple SNPs and multiple traits. Given a predetermined set of SNPs (selected, for example, from candidate genes) and a matrix of correlated traits, the MCSM proceeds by performing multivariate association analysis of subsets of SNPs with a vector of traits and retaining subsets that explain a significant proportion of trait variance, validating the retained subsets and ranking them by Akaike information criterion, and assessing the significance of the final retained set by permutation.
The authors applied their method to the RA data, taking as their matrix of traits the discrete measure of RA affection status and the continuous endophenotypes anti-CCP and IgM. (As noted above, this application required imputation of the continuous measures in the unaffected controls. It is not clear how the imputation might have affected the results because the traits were not analyzed separately in this study.) The search was conducted using a set of 137 SNPs in three candidate genes for RA: PTPN22, STAT4, and TRAF1-C5. Due to computational limitations, this study considered only sets of one or two SNPs. The best set consisted of variant rs7037673 in TRAF1-C5 and rs2476601 in PTPN22. All significant sets contained rs2476601, which was also significantly associated by itself with the trait vector; however, the evidence for association was much greater for two-locus sets than for rs2476601 alone. This result suggests the presence of interlocus interaction between rs2476601 and variants in the other candidate genes.
Where Cui et al. [2009]. Searched for patterns of gene interaction, Qin, Ye, Fang, Zhang, and Sha (unpublished) addressed the issue of pleiotropy by comparing association of individual SNPs with various combinations of the three traits available in the RA data: the discrete measure of affection status and the continuous phenotypes anti-CCP and IgM. The authors proposed a multiple correlation method to integrate multiple one- and two-stage scans based on single, double, and more traits (Qin, Ye, Fang, Zhang, and Sha; unpublished). The method proposed to use the information in different parts of the total dataset to increase power to detect association [Qin, 2008], but the results from the RA data were somewhat equivocal (in several cases, inclusion of multiple traits reduced rather than enhanced evidence of association). As in Cui et al. [2009], the unmeasured continuous traits in the controls were imputed by the protocol described above; unfortunately, in this case these partially imputed data may not have offered the best test of the proposed method.
Multivariate models increase computational demand due to the large number of parameters that must be estimated at each iteration. Huang (unpublished) took the novel approach of combining test statistics from multiple univariate analyses to construct a joint measure of pleiotropy while accounting for multiple testing. Given a vector of test statistics for association of a SNP with multiple traits, two combined test statistics are proposed: one testing whether the individual test statistics are different from zero on average, and another testing whether at least one is. Each of the proposed joint test statistics has a null distribution with degrees of freedom equal to the number of univariate analyses to account for the multiple testing. The method was applied to measures of HDL-C, LDL-C, and TG in Replicate 1 of the simulated FHS data (GAW16 Problem 3). Because the true genetic model was known, analysis was limited to SNPs truly associated with all three traits or with HDL-C and TG; the combined evidence was consistently greater for the composite test than for the univariate tests. This must be regarded as a preliminary demonstration of the method: because true-positive univariate associations were pre-selected for analysis, no conclusions can be drawn about the type I or type II error rates for the method.
The first joint test proposed by Huang is said to be most powerful if the effects of the SNP on all of the traits have the same sign, and it seems to be a clear test for pleiotropy. The data presented at GAW16 are less clear about how the second test should be interpreted, or whether either test should be applied only if there is a priori evidence of correlation among the traits that would lead to an expectation of pleiotropy. The authors note that a particular advantage of their method is the considerable reduction in computational complexity due to the much smaller dimensionality of the individual tests – and this technical advantage alone should suffice to encourage further exploration of this approach.
Longitudinal Data and Correlation Structure
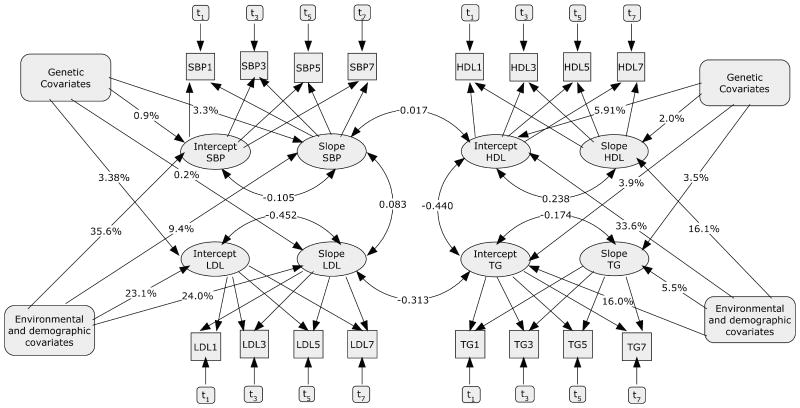
The effects of individual SNPs on total phenotypic variance are typically quite small, and most complex diseases are expected to result from a combination of genetic and non-genetic factors. Hamid et al. [2009] sought to combine a set of previously identified genetic and environmental factors into a single model that estimated the relative contribution of each. To incorporate an additional level of information, a latent growth curve, based on repeated measurements of individuals at sequential clinical examinations, provided two measures of the temporal progression of the phenotypes of interest: the intercept and slope. These authors used four correlated phenotypes (SBP, HDL-C, LDL-C, and TG) in the Offspring Cohort of FHS, with a set of repeated measures of the phenotypes and time-variant covariates (smoking, hypertension, and medication) for each individual. Sex and baseline age, BMI, and diabetes status were taken as time-independent covariates. The analysis was limited to unrelated individuals. The genetic factors incorporated in the model were chosen by meta-analysis: eight SNPs associated with lipid measures in GWA studies [Kathiresan et al., 2008a, Willer et al., 2008] plus the two SNPs most highly associated (albeit not at genome-wide significance) with SBP or hypertension status in the Wellcome Trust Case Control GWAS [The Wellcome Trust Case Control Consortium, 2007]. Figure 1 shows the complex structure of the resulting model and clearly shows that the effect of environmental and demographic factors on the traits is quite large compared with the measured genetic factors. It should be noted, however, that because family data were not included, the model did not quantify unmeasured (random) genetic effects representing the aggregate impact of genetic variants not yet detected by GWAS.
Figure 1. Path diagram describing growth curve parameters (intercept and slope) of repeated measures of SBP, HDL, LDL, and TG made at FHS Exams 1, 3, 5, and 7.
Environmental and demographic covariates, sex, age, baseline BMI and diabetic status; genetic covariates, 10 selected markers. The numbers on the lines connecting these covariates with the intercepts and slopes are percentages of explained variation and correlations. Paths with one arrow indicate causal relationships, whereas those with two show correlations. The ti values represent time varying covariates hypertensive and cholesterol medication as well as number of cigarettes smoked. (Reprinted from Hamid et al. [2009] with permission of the authors. Copyright 2009 by J. S. Hamid, N. M. Roslin, A. D. Paterson, and J. Beyene.)
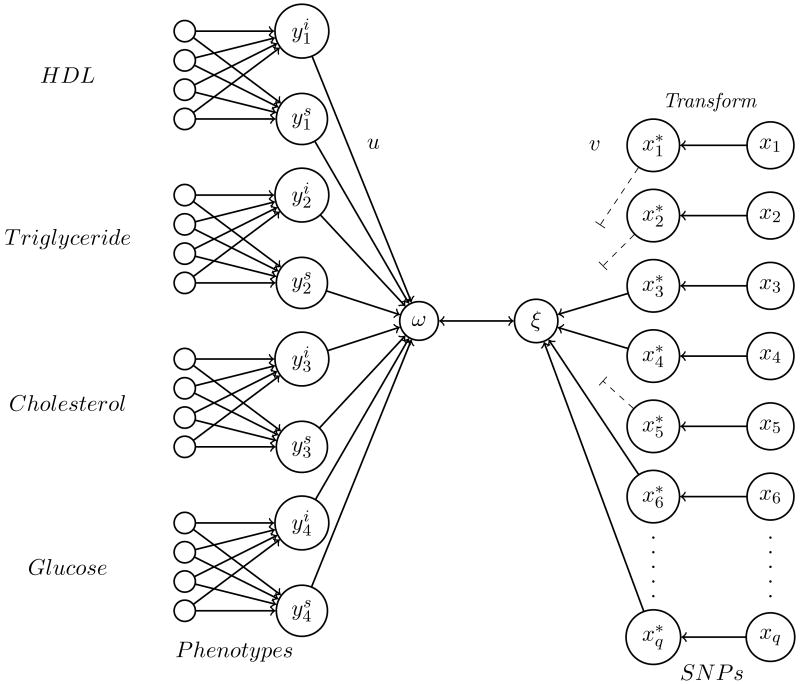
Like Hamid et al. [2009], Waaijenborg and Zwinderman [2009] sought to combine temporal patterns in repeated measurements of FHS study subjects with information on multiple genetic variants in a comprehensive model. Each of several MetSyn phenotypes (total cholesterol, HDL-C, TG, and fasting blood glucose) was summarized as the intercept and slope of a regression across measurements at multiple (two to four) clinical examinations. (In contrast to Hamid et al. [2009], these summary parameters were estimated in advance rather than at the same time as other parameters of the model.) Due to computational time constraints, prior association was conducted between intercepts and the Affymetrix 50k SNP panel, and the canonical correlation model was limited to the top 10% of SNPs by association with any of the underlying phenotypes, yielding a set of 12,682 SNPs. Because intercept and slope estimates were highly correlated, intercept alone was included in the model. A penalized nonlinear canonical correlation analysis was performed with cross-validation to identify an optimal set of SNPs, and this set was then tested for significance by permutation. A schematic of the canonical correlation structure is given in Figure 2. The method proposed in this study resembles that of Hamid et al. [2009] in attempting simultaneous modeling of the interactions of many phenotypes and genetic variants. However, Waaijenborg and Zwinderman [2009] saw their comprehensive approach primarily as a tool for gene discovery: given sufficient computing power, their method could be applied genome-wide.
Figure 2. Penalized nonlinear canonical correlation analysis.
Association between repeatedly measured phenotypes and a large number of SNPs. The longitudinal measured phenotypes are summarized into two measures, one representing the intercept Yi and one the slope (Ys). The effect of each SNP genotype (X) is expressed as a continuous variable (X*) by optimal scaling [de Leeuw et al., 1976]. (Reprinted from Waaijenborg and Zwinderman [2009] with permission of the authors. Copyright 2009 by S. Waaijenborg and A. H. Zwinderman.)
Causality and Prediction
Morris et al. [2009] effectively stood the usual practice of genetic epidemiology on its head: in their own words, their study was designed “not to detect genetic factors of disease, but rather to use genetic factors of disease to uncover causal relationships between phenotypes.” The authors implement an instrumental variable (IV) approach [Bowden and Turkington, 1984] to explore patterns of causality in association data. This approach – sometimes described as “Mendelian randomization” because genetic recombination offers a natural, quasi-experimental randomization of phenotypes over genotypes [Davey Smith and Ebrahim, 2003; Didelez and Sheehan, 2007] – seeks to determine whether a genetic variant influences a particular trait B entirely or partly via its direct effect on a correlated trait A. If the first case is true – the variant affects B solely through its effect on A – this provides evidence for a causal effect of A on B. Thus, the goal is a better understanding of causal relationships among physiological or biochemical processes with genetic variants serving an instrumental role in this discovery. The specific contribution of Morris et al. [2009] was to formulate the dependent relationship B ← A as a novel phenotype that could be tested for association in a mixed-model framework including the random effect of kinship.
To demonstrate their method, Morris et al. [2009] took as instrumental variables SNPs on LDLR and APOB identified in the literature as candidate causal variants for blood levels of LDL-C [Benn et al., 2008]. The small set of instrumental variables was used to explore causal relationships between LDL-C and BMI, SBP, HDL-C, and TG. The SNPs appeared to be associated with TG only through their direct effect on LDL-C, although (as in many association studies) their effect sizes were quite modest.
Where Morris et al. [2009] used known genetic associations to reveal causal relationships among phenotypes, Piccolo et al. [2009] proposed to use gene discoveries to aid in risk prediction. Their focus here was on correlated lipid phenotypes (LDL-C, HDL-C, and TG) that are themselves risk factors, or “intermediate risk phenotypes” (IRPs), for CVD. Previous studies had proposed to exploit the correlation between IRPs (and the putative pleiotropy of their genetic causes) to develop genetic risk scores (GRS) as a sum of genotype scores for IRP-associated SNPs [Kathiresan et al., 2008b]. Piccolo et al. [2009] took this proposal one step further by weighting the genotype scores by the empirical effect size of the respective variants to reflect the relative importance of the genetic ‘risks’. The study used data from the earliest examination of each FHS participant from which all three lipid measures were available, and conducted a two-stage GWAS (using the 500k SNP panel) in PLINK for each lipid IRP. A separate haplotype analysis provided additional information on genetic risk factors. For each lipid trait, sets of associated SNPs were used to construct GRS, with and without weighting by effect size, which were then tested for association with their respective traits in a mixed model that included random effects of familiality. The weighted GRS gave consistently stronger evidence of association than the unweighted GRS. The authors suggest that such GRS could be used in a clinical setting to predict genetic risk of these IRPs and future CVD.
Discussion
All of the studies presented in GAW16 Group 6 sought to exploit the additional information provided by joint analysis of multiple correlated phenotypes. Many studies were motivated by the expectation that methods that combined information from multiple correlated phenotypes should increase power for detection of genetic variants, whether the phenotypic correlation results from pleiotropy or from repeated measures. Unfortunately, while several authors presented favorable anecdotal comparisons of multivariate versus univariate methods, a potential limitation of all studies was the lack of formal power analysis. Power analysis should be considered as part of any future development of these methods.
Some groups [Cui et al., 2009; Hamid et al., 2009; Waaijenborg and Zwinderman, 2009] attempted joint analysis not only of multiple phenotypes but also of multiple SNPs to better reflect the complex genetic architecture of the traits. In the process, they confronted the increased computational demands imposed by high-dimensional analysis. These and other investigators also examined strategies for reducing the dimensionality of analysis to avoid the computational demands and the penalty for multiple tests. Data-reduction strategies included stepwise selection of SNPs [Cui et al., 2009; Waaijenborg and Zwinderman, 2009], construction of genetic risk scores [Piccolo et al., 2009], and post-analytical construction of composite test statistics (Huang, unpublished).
The studies presented here spanned the genetic epidemiological program: phenotype definition [Baker et al., 2009; Piccolo et al., 2009], inclusion of growth curves for repeated measures [Hamid et al., 2009; Waaijenborg and Zwinderman, 2009], gene discovery (most studies), exploration of etiological complexity and causation [Hamid et al., 2009; Morris et al., 2009; Waaijenborg and Zwinderman, 2009] and clinical prediction [Piccolo et al., 2009]. The results of Hamid et al. [2009] are especially noteworthy for quantifying the relatively large effect size of non-genetic factors in complex traits. These latter studies point to the maturation of quantitative genetics: there are now sufficient prior genetic discoveries in the literature to support meta-analytical investigations, including – potentially – clarification of biological processes and improved prediction of patient outcomes.
Acknowledgments
We thank the Group 6 authors and meeting participants for a lively and productive discussion. Andrew D. Paterson's insightful comments helped guide our group discussions. We thank the National Heart, Lung, and Blood Institute; the Framingham Heart Study participants and investigators; and the North American Rheumatoid Arthritis Consortium for providing the data sets. JWK's participation in GAW16 was supported by R01 MH059490 from the National Institute of Mental Health. The Genetic Analysis Workshops are supported by R01 GM031575 from the National Institute of General Medical Sciences.
References
- Almasy L, Blangero J. Endophenotypes as quantitative risk factors for psychiatric disease: Rationale and study design. Am J Med Genet B Neuropsychiatr Genet. 2001;105:42–4. [PubMed] [Google Scholar]
- Amos CI, Chen WV, Seldin MF, Remmers E, Taylor KE, Criswell LA, Lee AT, Plenge RM, Kastner DL, Gregersen PK. Data for Genetic Analysis Workshop 16 Problem 1, association analysis of rheumatoid arthritis data. BMC Proc. 2009;3(Suppl 7):S2. doi: 10.1186/1753-6561-3-s7-s2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker AR, Goodloe RJ, Larkin EK, Baechle DJ, Song YE, Phillips LS, Gray-McGuire CL. Multivariate association analysis of the components of metabolic syndrome from the Framingham Heart Study. BMC Proc. 2009;3(Suppl 7):S42. doi: 10.1186/1753-6561-3-s7-s42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benn M, Stene MCA, Nordestgaard BG, Jensen GB, Steffensen R, Tybjaerg-Hansen A. Common and rare alleles in apolipoprotein B contribute to plasma levels of low-density lipoprotein cholesterol in the general population. J Clin Endocrinol Metabol. 2008;93:1038–45. doi: 10.1210/jc.2007-1365. [DOI] [PubMed] [Google Scholar]
- Bowden RJ, Turkington DA. Instrumental variables. Cambridge: Cambridge University Press; 1984. [Google Scholar]
- Cui JS, Hopper JL, Harrap SB. Antihypertensive treatments obscure familial contributions to blood pressure variation. Hypertension. 2003;41:207–10. doi: 10.1161/01.hyp.0000044938.94050.e3. [DOI] [PubMed] [Google Scholar]
- Cui X, Sha Q, Zhang S, Chen HS. A combinatorial approach for detecting gene-gene interaction using multiple traits of Genetic Analysis Workshop 16 rheumatoid arthritis data. BMC Proc. 2009;3(Suppl 7):S43. doi: 10.1186/1753-6561-3-s7-s43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cupples LA, Heard-Costa N, Lee M, Atwood LD, Framingham Heart Study Investigators Genetics Analysis Workshop 16 Problem 2: The Framingham Heart Study data. BMC Proc. 2009;3(Suppl 7):S3. doi: 10.1186/1753-6561-3-s7-s3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davey Smith G, Ebrahim S. ‘Mendelian randomization’: Can genetic epidemiology contribute to understanding environmental determinants of disease? Int J Epidemiol. 2003;32:1–22. doi: 10.1093/ije/dyg070. [DOI] [PubMed] [Google Scholar]
- Day C. Metabolic syndrome, or what you will: Definitions and epidemiology. Diab Vasc Dis Res. 2007;4:32–8. doi: 10.3132/dvdr.2007.003. [DOI] [PubMed] [Google Scholar]
- De Leeuw J, Young FW, Takane Y. Additive structure in qualitative data: An alternating least squares method with optimal scaling features. Psychometrika. 1976;41:471–503. [Google Scholar]
- Didelez V, Sheehan N. Mendelian randomization as an instrumental variable approach to causal inference. Stat Methods Med Res. 2007;16:309–30. doi: 10.1177/0962280206077743. [DOI] [PubMed] [Google Scholar]
- Dullaart RP, Sluiter WJ. Common variation in the CETP gene and the implications for cardiovascular disease and its treatment: An updated analysis. Pharmacogenomics. 2008;9:747–63. doi: 10.2217/14622416.9.6.747. [DOI] [PubMed] [Google Scholar]
- Gershon ES, Badner JA, Goldin LR, Sanders AR, Cravchik A, Detera-Wadleigh SD. Closing in on genes for manic-depressive illness and schizophrenia. Neuropsychopharmacology. 1998;18:233–42. doi: 10.1016/S0893-133X(97)00145-0. [DOI] [PubMed] [Google Scholar]
- Hamid JS, Roslin NM, Paterson AD, Beyene J. Using a latent growth curve model for an integrative assessment of the effects of genetic and environmental factors on multiple phenotypes. BMC Proc. 2009;3(Suppl 7):S44. doi: 10.1186/1753-6561-3-s7-s44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu ZD, Lu JQ, Yan BY, Xin N, Fu L, Wei G, Chen XC. The value of anticyclic citrullinated peptide antibody and vascular endothelial growth factor in the diagnosis of rheumatoid arthritis. Lab Med. 2007;22:41–3. [Google Scholar]
- Kathiresan S, Melander O, Guiducci C, Surti A, Burtt NP, Rieder MJ, Cooper GM, Roos C, Voight BF, Havulinna AS, Wahlstrand B, Hedner T, Corella D, Tai ES, Ordovas JM, Berglund G, Vartiainen E, Jousilahti P, Hedblad B, Taskinen MR, Newton-Cheh C, Salomaa V, Peltonen L, Groop L, Altshuler DM, Orho-Melander M. Six new loci associated with blood low-density lipoprotein cholesterol, high-density lipoprotein cholesterol or triglycerides in humans. Nat Genet. 2008a;40:189–97. doi: 10.1038/ng.75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kathiresan S, Melander O, Anevski D, Guiducci C, Burtt NP, Roos C, Hirschhorn JN, Berglund G, Hedblad B, Groop L, Altshuler DM, Newton-Cheh C, Orho-Melander M. Polymorphisms associated with cholesterol and risk of cardiovascular events. N Engl J Med. 2008b;358:1240–9. doi: 10.1056/NEJMoa0706728. [DOI] [PubMed] [Google Scholar]
- Keskin G, Inal A, Keskin D, Pekel A, Baysal O, Dizer U, Sengul A. Diagnostic utility of anti-cyclic citrullinated peptide and anti-modified citrullinated vimentin antibodies in rheumatoid arthritis. Protein Pept Lett. 2008;15:314–7. doi: 10.2174/092986608783744153. [DOI] [PubMed] [Google Scholar]
- Kraja AT, Culverhouse R, Daw EW, Wu J, Van Brunt A, Province MA, Borecki IB. The Genetic Analysis Workshop 16, Problem 3: Simulation of heritable longitudinal cardiovascular phenotypes based on actual genome-wide single-nucleotide polymorphisms in the Framingham Heart Study. BMC Proc. 2009;3(Suppl 7):S4. doi: 10.1186/1753-6561-3-s7-s4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- López-Alvarenga JC, Solís-Herrera C, Kent JW, Jr, Jaju D, Albarwani S, Al Yahyahee S, Hassan MO, Bayoumi R, Comuzzie AG. Prevalence and clusters for diagnostic components of metabolic syndrome: The Oman Family Study. Metab Syndr Relat Disord. 2008;6:129–35. doi: 10.1089/met.2007.0039. [DOI] [PubMed] [Google Scholar]
- Morris NJ, Gray-McGuire C, Stein CM. Mendelian randomization in family data. BMC Proc. 2009;3(Suppl 7):S45. doi: 10.1186/1753-6561-3-s7-s45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson MR, Kardia SLR, Ferrell RE. A combinatorial partitioning method to identify multilocus genotypic partitions that predict quantitative trait variation. Genome Res. 2001;11:458–70. doi: 10.1101/gr.172901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piccolo SR, Abo RP, Allen-Brady K, Camp NJ, Knight S, Anderson JL, Horne BD. Evaluation of genetic risk scores for lipid levels using genome-wide markers in the Framingham Heart Study. BMC Proc. 2009;3(Suppl 7):S46. doi: 10.1186/1753-6561-3-s7-s46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, Sklar P, de Bakker PIW, Daly MJ, Sham PC. PLINK: a toolset for whole-genome association and population-based linkage analysis. Am J Hum Genet. 2007;81:559–75. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin HZ. PhD dissertation. Houghton, MI: Michigan Technological University; 2008. Statistical approaches for genome-wide association study and microarray analysis. [Google Scholar]
- Sha Q, Zhu X, Zuo Y, Cooper R, Zhang S. A combinatorial searching method for detecting a set of interacting loci associated with complex traits. Ann Hum Genet. 2006;70:677–92. doi: 10.1111/j.1469-1809.2006.00262.x. [DOI] [PubMed] [Google Scholar]
- The Wellcome Trust Case Control Consortium. Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature. 2007;447:661–78. doi: 10.1038/nature05911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waaijenborg S, Zwinderman AH. Associating multiple longitudinal traits with high-dimensional single-nucleotide polymorphism data: Application to the Framingham Heart Study. BMC Proc. 2009;3(Suppl 7):S47. doi: 10.1186/1753-6561-3-s7-s47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willer CJ, Sanna S, Jackson AU, Scuteri A, Bonnycastle LL, Clarke R, Heath SC, Timpson NJ, Najjar SS, Stringham HM, Strait J, Duren WL, Maschio A, Busonero F, Mulas A, Albai G, Swift AJ, Morken MA, Narisu N, Bennett D, Parish S, Shen H, Galan P, Meneton P, Hercberg S, Zelenika D, Chen WM, Li Y, Scott LJ, Scheet PA, Sundvall J, Watanabe RM, Nagaraja R, Ebrahim S, Lawlor DA, Ben-Shlomo Y, Davey-Smith G, Shuldiner AR, Collins R, Bergman RN, Uda M, Tuomilehto J, Cao A, Collins FS, Lakatta E, Latrop GM, Boehnke M, Schlessinger D, Mohlke KL, Abecasis GR. Newly identified loci that influence lipid concentrations and risk of coronary artery disease. Nat Genet. 2008;40:161–9. doi: 10.1038/ng.76. [DOI] [PMC free article] [PubMed] [Google Scholar]