Perturbation analysis analyzed - Mathematical modeling of intact and perturbed gene regulatory circuits for animal development

Abstract

Gene regulatory networks for animal development are the underlying mechanisms controlling cell fate specification and differentiation. The architecture of gene regulatory circuits determines their information processing properties and their developmental function. It is a major task to derive realistic network models from exceedingly advanced high throughput experimental data. Here we use mathematical modeling to study the dynamics of gene regulatory circuits to advance the ability to infer regulatory connections and logic function from experimental data. This study is guided by experimental methodologies that are commonly used to study gene regulatory networks that control cell fate specification. We study the effect of a perturbation of an input on the level of its downstream genes and compare between the cis-regulatory execution of OR and AND logics. Circuits that initiate gene activation and circuits that lock on the expression of genes are analyzed. The model improves our ability to analyze experimental data and construct from it the network topology. The model also illuminates information processing properties of gene regulatory circuits for animal development.

Introduction

The main task of the embryo specification process is the formation of distinct territories that are defined by unique regulatory states. Regulatory state is the total set of active transcription factors in a cell nucleus at a given developmental time. (Davidson, 2006; Ben-Tabou de-Leon and Davidson, 2007). Distinct regulatory states are established by the cis-regulatory interactions of the relevant regulatory genes, and these interactions constitute the linkages of developmental gene regulatory networks (GRNs). It is now apparent that the architecture of gene regulatory circuits determines their information processing functions (see, e.g., (Medina and Singh, 2005; Olson, 2006; Ben-Tabou de-Leon and Davidson, 2007; Davidson and Levine, 2008; Oliveri et al., 2008; Smith and Davidson, 2008; Bryantsev and Cripps, 2009)). The computation performed by any given gene regulatory circuit is complex. It incorporates the linkages between the circuit genes (architecture), the function the cis-regulatory modules of the genes execute on their inputs (logic), and the dynamic expression patterns of the circuit genes. Any change in the expression of a gene in a circuit affects the expression of the other genes, and therefore these systems are highly interdependent while yet surprisingly accurate. The complexity of GRNs presents a great challenge of constructing a realistic model out of experimental data.

One of the most comprehensive models of GRN for development is the sea urchin embryo specification network (Oliveri et al., 2008; Peter and Davidson, 2010; Su et al., 2009). The network was constructed based of inclusive perturbation analysis where the expression of every gene in the network was perturbed and the effect on the expression of every other gene in the network was measured by quantitative PCR (QPCR) or by new instrumental technology (NanoString Technologies nCounter Analysis System) (Su et al., 2009). For key nodes in the network a detailed cis-regulatory analysis was conducted to verify which network linkages are direct and to find the logic function a given cis-regulatory module executes on its inputs (see e.g. (Yuh et al., 1998; Yuh et al., 2001; Ransick and Davidson, 2006; Smith and Davidson, 2008)). A novel technique was recently developed to test more than hundred of cis-regulatory elements in one experiment (Nam et al., 2010). The development of reliable RNA sequencing will extend the perturbation analysis from the known GRN genes to the entire genome (Mortazavi et al., 2008; Wang et al., 2009). These exceedingly advanced high throughput techniques generate high quality data and demand an advanced analysis tools for accurate construction of a network model from the data.

The use of computational tools that incorporate gene expression, perturbation and transcription factor-DNA binding data into large scale GRN models can significantly enhance the ability to generate GRN models from experimental data (reviewed e.g. in (Kim et al., 2009) for prokaryotes and metazoan GRN and in (Long et al., 2008) for plants GRN.). The success of these computational tools as well as of any other method to generate a realistic GRN models depends on the correct translation of the experimental data into network architectures and logic. Mathematical modeling of the dynamics of gene regulatory circuits in wild type and under perturbed conditions can advance the ability to infer regulatory connections and logic function from experimental data.

There are different approaches to study the kinetics of gene regulatory circuits, and each has its advantages. One approach is to study the general properties of possible regulatory circuits without the limitation of specific kinetic parameters (see e.g., (Glass and Kauffman, 1972; Kaufman and Thomas, 1987; Thomas et al., 1995; Thomas and Kaufman, 2001)). In this approach the general properties of sets of differential equations that describe regulatory circuits are analyzed. This analysis is very useful in predicting circuit architectures that are necessary to obtain observed regulatory behavior. For example, such analysis showed the necessity of positive feedback loops architecture to enable multi-stationary states (Plahte et al., 1995; Demongeot, 1998; Gouze, 1998; Snoussi, 1998; Thomas and Kaufman, 2001). In other words, it showed that positive feedback loops are necessary for the establishment of multiple distinct regulatory states that are the basis of cell fate specification. The strength of this approach is its generality; no assumptions are made about specific interactions or kinetic parameters in the regulatory circuit, the deduction are made based on pure mathematical analysis with dimensionless variables. However, in order to apply these general principles to explain experimental observation it is necessary to introduce the specific interactions and parameters of the system in study.

Parameters dependent approaches usually consider specific regulatory circuitry that is based on real examples found experimentally (see, e.g., (Ackers et al., 1982; Bolouri and Davidson, 2003; Zak et al., 2003; Brandman et al., 2005; Perkins et al., 2006; Ben-Tabou de-Leon and Davidson, 2009b)). Simple kinetic models are frequently used to estimate the scale of biological kinetic parameters such as mRNA turnover rates, transcription initiation rates, transcription factor – DNA binding strength and protein – protein binding cooperativity (see e.g., (Galau et al., 1977; Ackers et al., 1982; Cabrera et al., 1984; Calzone et al., 1991; Kohler and Schepartz, 2001; Fan et al., 2002; Wang et al., 2002; Howard-Ashby et al., 2006; Walsh and Carroll, 2007)). Parameter dependent network models use this data to study the function of typical network circuits and provide insights to their actual behavior in developing embryos (Zak et al., 2003; Brandman et al., 2005; Lin et al., 2005; Perkins et al., 2006; Ben-Tabou de-Leon and Davidson, 2009b). In these works, the scale of the kinetic parameters is estimated from the experimental available data and the dynamic behavior of a given circuit is analyzed. The use of realistic biological parameters makes this approach very helpful for experimental data analysis and for generating predictions for measurable quantities. Once the dependence of the results in the kinetic variables is considered, general conclusions can be drawn from these analyses. This is the approach that we take in this paper.

We use the mathematical model developed earlier (Davidson, 1986; Bolouri and Davidson, 2003; Ben-Tabou de-Leon and Davidson, 2009b) to simulate the dynamics of typical circuits that are found in GRNs for development. The effect of knockdown of an upstream gene on its downstream genes in different circuits’ architectures and logic functions is simulated. We study various circuits’ architectures that lead to gene activation as well as lock-down establishment by single and coupled positive feedback loops. The effect of the perturbation of a direct input is compared to the effect of indirect input perturbation. The results show that different architectures that appear to execute the same developmental task respond differently to perturbation. The logic functions executed at the circuit nodes are critical for the perturbation propagation in the network and hence for the buffering of upstream level variations. This analysis therefore enhances the ability to derive GRN models from gene expression and perturbation data and provides predictions that can be tested experimentally.

Methods

General formalism

The objective of this work is to simulate the effect of a perturbation of an input on the expression level of its downstream genes and by that improve the experimental perturbation analysis and gain insights into the function of GRN circuits. An appropriate model would be the simplest one where all the prominent features of the system are explicitly considered. The experimental measurement of a perturbation effect is done by extracting the mRNA of a group of embryos and then quantitatively measuring the mRNA level by various techniques such as QPCR (Oliveri et al., 2008; Peter and Davidson, 2010), nanostring (Su et al., 2009) or microarrays (Guimbellot et al., 2009; Hu et al., 2009). The expression level of the wild type system is then compared to that of a perturbed one, where the expression of one of the regulatory genes is down regulated. The mathematical model therefore has to explicitly describe the dependence of the mRNA level of the output on the protein level of the input. An important question in this analysis is how much time after the perturbation is made the effect is observable experimentally. To answer this question the model has to include time as a variable. Since these measurements are usually done with whole embryos, spatial regulation will not be considered in the model.

An important aspect of gene regulation is the mode of action of multiple inputs. Some transcription factors function additively, each of them contributing to the overall expression level. This behavior can be described as OR logic executed on multiple inputs (reviewed in (Istrail and Davidson, 2005)). Some transcription factors require at least one additional transcription factor to induce transcription so when one factor is absent the others are unable to activate transcription. This behavior can be described as AND logic executed on multiple inputs (Istrail and Davidson, 2005). The outcome of perturbing the expression of a given transcription factor depends on the logic executed by the cis-regulatory apparatus. Hence, the model should describe explicitly the logic function the cis-regulatory module executes on its inputs.

The formalism developed previously (Davidson, 1986; Bolouri and Davidson, 2003; Ben-Tabou de-Leon and Davidson, 2009b) contains all these aspects of gene regulation and is applied here to study the dynamics of perturbation analysis. This formalism describes populations of molecules and cis-regulatory modules of given genes in a cell expressing them. That is, the model variables are average concentrations, and the model parameters are the average rates for a cell in a given territory. Since the actual measurements are averages over many embryos, an average approximation model is directly useful for understanding and simulating perturbation analysis. Below we present the set of differential equations that we use to describe the dynamics of gene regulatory circuits.

The mRNA level of gene C that has two inputs, the transcription factors A and B, is described by the following expression when the inputs are additive (OR logic) (Ben-Tabou de-Leon and Davidson, 2009b):

$$\frac{\mathit{\text{dmC}}(t)}{\mathit{\text{dt}}}=\frac{I_{\text{max}}}{2}\left\{\left(1-\text{exp}\left(-\frac{k_{\mathit{\text{bA}}}{Y}_A(t-T_m)}{I_{\text{max}}}\right)\right)+\left(1-\text{exp}\left(-\frac{k_{\mathit{\text{bB}}}{Y}_B(t-T_m)}{I_{\text{max}}}\right)\right)\right\}-k_{\mathit{\text{dmC}}}\mathit{\text{mC}}(t).$$ (1)

That is, each transcription factor contributes to the overall transcription synthesis rate independent of the presence of the other factor. The following expression describes two necessary inputs (AND logic) (Ben-Tabou de-Leon and Davidson, 2009b):

$$\frac{\mathit{\text{dmC}}(t)}{\mathit{\text{dt}}}=I_{\text{max}}\left\{1-\text{exp}\left(-\frac{k_{\mathit{\text{bAB}}}{Y}_A(t-T_m)Y_B(t-T_m)}{I_{\text{max}}}\right)\right\}-k_{\mathit{\text{dmC}}}\mathit{\text{mC}}(t).$$ (2)

That is, if either one of the inputs is absent the transcription is off. In Eqs. (1) and (2) mC(t) is the number of mRNA molecules of gene C per cell at time t, I_max is the maximal possible initiation rate (mRNA per minute) which depends on the RNA polymerase translocation rate, since the next polymerase cannot bind to the promoter before the currently transcribing polymerase has cleared about 100 bp of DNA (see (Davidson, 1986, p142–149) and (Bolouri and Davidson, 2003; Ben-Tabou de-Leon and Davidson, 2009b) for further explanations). k_bA and k_bB are the activation strengths of transcription factors A and B respectively, T_m is the delay due to mRNA transcription, processing and export (Ben-Tabou de-Leon and Davidson, 2009b), k_dmC is the mRNA turnover rate of C (time⁻¹), and Y_p is binding site occupancy (Bolouri and Davidson, 2003):

$$Y_P(t)=\frac{K_{r}P(t)}{D_n+K_{r}P(t)}.$$ (3)

Here P (t) can be either the number of transcription factor A or B per cell, K_r is the relative equilibrium constant which can be measured experimentally and is of the order 10⁴–10⁶ (Calzone et al., 1988; Calzone et al., 1991; Hoog et al., 1991), and D_n the available chromatin, which can be estimated as about 90% of the total genome (Felsenfeld and Groudine, 2003). The equation that describes protein synthesis for all genes is (Davidson, 1986; Ben-Tabou de-Leon and Davidson, 2009b)

$$\frac{\mathit{\text{dP}}(t)}{\mathit{\text{dt}}}=k_t\mathit{\text{mP}}(t)-k_{\mathit{\text{dP}}}P(t).$$ (6)

Here P(t) is the number of protein molecules per cell at the time t, and mP(t) is the number of mRNA molecules of this gene per cell. k_dP is the protein turnover rate constant, k_t is the translation rate constant, and the units of both constants are time⁻¹.

Down regulation of a gene is achieved by different techniques depending on the system. In many systems, injection of specific morpholino antisense oligonucleotides (MASO) is used to down-regulate the expression of a gene. These are morpholino sequences about 20 bp long that match the antisense of the coding sequence of the studied gene. When MASO is injected to a fertilized egg it binds to the mRNA of the gene and blocks its translation. That means that the translation rate of the perturbed gene is decreased significantly, and this is how we model it here. In the perturbed condition we assume that only one percent of the mRNA molecules are free to be translated. This is an arbitrary choice that represents a significant reduction in translation but not entire elimination of the protein, which is what we expect to happen in a MASO experiment.

This formalism is also suitable to simulate the effect of RNAi perturbation that is used in other systems to knock the level of a gene down. In systems where gene deletion in the genomic DNA is possible the perturbation should be simulated by fixing the mRNA generation to zero.

Estimation of the values of the model parameters

There are many possible temporal profiles and kinetic parameters of the circuits described below. To obtain a guide for the expected dynamic behavior we use typical values that were measured experimentally. mRNA and protein turnover rates vary significantly between different genes and are in the range of 10 minutes to many hours (Kenney and Lee, 1982; Cabrera et al., 1984; Davidson, 1986; Ouali et al., 1997; Herdegen and Leah, 1998; Hirata et al., 2002; Howard-Ashby et al., 2006). Transcription factors usually have relatively short turnover rates that are of the order of few hours or less (Cabrera et al., 1984; Davidson, 1986; Herdegen and Leah, 1998; Hirata et al., 2002; Howard-Ashby et al., 2006). For simplicity we assigned a turnover rate of about two hours (K_d=0 .005 min⁻¹) for both protein and mRNA products of all genes.

Transcriptional delays due to mRNA elongation and processing depend on the RNA polymerase translocation rate and mRNA processing. The translocation rate is expected to obey the Q10 law and increase by 2–2.5 for an increase of 10° C. In sea urchin (S. purpuratus) embryos that are cultured at 15° C, the RNA polymerase translocation rate was measured to be 6–9 nucleotides per second (Aronson and Chen, 1977; Davidson, 1986). At this rate it takes about 56 min to complete the first primary transcript of a 30Kb gene. mRNA export from the nucleus to the cytoplasm requires about 10–30 min depending on the mRNA (Schroder et al., 1989; Fuke and Ohno, 2008). In the simulations presented below we assumed transcriptional delay of one hour for all genes.

The translation rate for sea urchin cultured in 15° C was measured to be k_t=2 protein molecules per mRNA molecule per minute (Davidson, 1986). The translation rate is expected to obey the Q10 law and increase by 2–2.5 for an increase of 10° C. Indeed, Zak et. al. (Zak et al., 2003) estimated the translation rate of metabolic enzymes in rat liver cells to be about 20 protein molecules per mRNA molecule per minute, based on Kenney and Lee experimental work (Kenney and Lee, 1982). In the simulations below the translation rate is k_t=2 protein molecules per mRNA molecule per minute.

Transcription initiation rates for various transcription factors were measured in sea urchin embryos (Howard-Ashby et al., 2006). The rates vary from 0.3 – 9 transcript per minute per embryo. At the developmental times where the experiments where done the maximal number of cells per embryo is about 500 and the genes expression is usually restricted to a specific lineage in the embryo. Hence we can estimate the range of transcription initiation rrates to be 0.001–1 transcripts per minute per cell (two DNA copies). Transcription initiation rates for two metabolic enzymes in rat liver cells were estimated to be 0.08 and 1.5 transcripts for two DNA copies per minute (Zak et al., 2003). In the model presented above, the transcription initiation rate depends on the binding site occupancy, Y_p, Eq.(3), and the activation strength k_b which represents the enhancer strength (see e.g., Eq.(1)). At low occupancy the initiation rate increases linearly with occupancy, with a slope of k_b. For low enhancer strength (k_b/I_max<1) the initiation rate is in the linear region even at maximal occupancy, Y_P=1. For strong activation (k_b/I_max>2) at high occupancy the initiation rate approaches the maximal initiation rate, I_max, that depends on the RNA polymerase translocation rate (Bolouri and Davidson, 2003; Ben-Tabou de-Leon and Davidson, 2009b). Considering translocation rate of 6–9 nucleotides per second, it takes the RNA polymerase about 11–17 seconds to transcribe 100 bp, and enable the next RNA polymerase to bind to the promoter. This results with a maximal initiation rate of about 5.5 initiations per minute, for one DNA copy of a gene. There are two copies of each gene in every cells, therefore in the simulations presented below we assume I_max=11 initiations per minute. Considering this value of I_max and the measurements of the transcription initiation rates described above we assumed k_b=2 for all genes, so the maximal number of initiations per two DNA copies at maximal occupancy Y_p=1 is about 1.8 transcripts per minute per two DNA copies.

The total genome size affects the binding site occupancy Eq. (3). Assuming that 90% of the chromatin is available for binding and considering a genome size of 8 ×10⁸ bp (sea urchin), we obtain D_n=7.2 ×10⁸ bp.

The results presented below depend on the choice of parameters described here. We explicitly discuss this dependence in the results section; in particular, we discuss the effect of changing the parameters values on the dynamic behavior we observe.

Results

Regulatory state initiation

As the specification process progresses, genes are activated differentially by a flow of regulatory events. Various circuit architectures are used by GRNs to initiate regulatory states. In this section we analyze the effect of perturbation of a regulatory gene on its targets under different activation architectures and cis-regulatory logic.

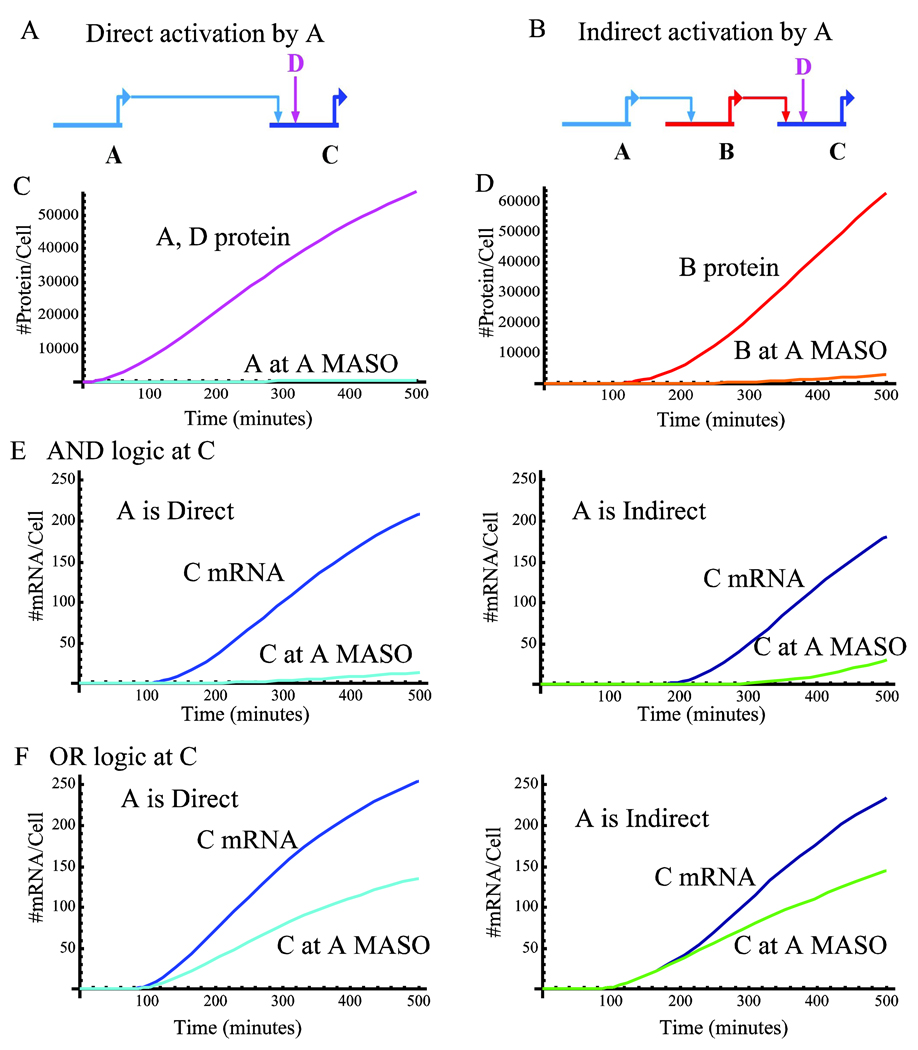
One of the challenges in constructing a network model from perturbation data is to distinguish between direct and indirect targets. Transcription factor A is a direct input into gene C if it binds to the cis-regulatory module of C and activates C expression, Fig. 1A. Transcription factor A is an indirect input into gene C if it activates gene B directly, and transcription factor B activates C directly, Fig. 1B. Strictly linear cascades are very rare in GRNs for development. It is always a combination of activators that drive a gene in a specific lineage. Therefore in both direct and indirect cases gene C usually has another input, D. The inputs C and D can be either additive, and approximated by OR logic, Eq. (1), or both necessary and approximated by AND logic, Eq. (2). In this section we use the formalism described above to model the effect of a knock-down of an activator on the dynamic expression of its target gene and study the expected behavior of direct versus indirect links under different logic operations.

Figure 1.

The effect of MASO perturbation on the expression of a downstream gene through time, direct versus indirect activation. A. Schematic diagram of direct activation. Transcription factor A binds to the cis-regulatory module of gene C and activates its expression. Gene C has another input, D and the logic the cis-regulatory module of B applies on A and D can be either AND or OR. B. Schematic diagram indirect activation. Transcription factor A activates gene B directly. Gene B encodes a transcription factor that activates gene C directly. Gene C has another input, D, and the logic applied on B and D can be either AND or OR. C. The expression levels of the inputs, protein number per cell. Genes A and D turn on at t=0 and stay on (fucsia) The protein level of A at A MASO treatment is in cyan. D. The protein level of gene B in WT (red) and under A MASO treatment (orange). E. The mRNA level of the downstream gene, C, at different conditions, OR logic. Left – direct connectivity, Blue - WT, cyan – C at A MASO. Right – indirect connectivity. Dark blue – WT, green – C at A MASO. F. The mRNA level of the downstream gene, C, at different conditions, AND logic. Same structure and color scheme as in E. Kinetic parameters for all simulations: K_dm=K_dp=0.005 min⁻¹, T_m = 60 minutes, K_b= 2, I_max=11, I₀=1, K_r=10⁵, D_n=90% of the genome, which for sea urchin is 7.2×10⁸.

For simplicity we assume that the transcriptional activation of the inputs A and D starts at the same time with similar initiation rate. The expression for their mRNA generation is therefore:

$$\frac{\mathit{\text{dmA}}(t)}{\mathit{\text{dt}}}=I_0-k_{\mathit{\text{dmA}}}\mathit{\text{mA}}(t),$$ (7)

$$\frac{\mathit{\text{dmD}}(t)}{\mathit{\text{dt}}}=I_0-k_{\mathit{\text{dmD}}}\mathit{\text{mD}}(t),$$ (8)

where k_dmA and k_dmD are the mRNA turnover rate of gene A and gene D respectively, and I₀ is the initiation rate (mRNA × time⁻¹). C mRNA is described by either Eq. (1) for OR logic or Eq. (2) for AND logic, and the indices in the equations are either A and D for direct connectivity or B and D for indirect connectivity. The equation for all proteins is Eq.(6) for the intact condition. For the MASO condition the translation rate k_t is multiplied by 0.01, as discussed above.

The results of the simulation for the parameters defined in the method section and I₀ = 1 transcript per minute, are presented in Fig. 1C–F. The protein levels of the inputs A and D, are depicted in Fig. 1C for the wild type (WT) and for MASO against gene A. The protein levels of the transcription factor B for the WT and for A MASO are depicted in Fig. 1D. The mRNA level of the downstream gene C in the WT and perturbed cases is presented in Fig. 1E for AND logic and Fig. 1F for OR logic.

The logic applied by the cis-regulatory module on its inputs makes a clear difference in the response to A perturbation. When AND logic is executed, A MASO reduces C level significantly. The difference of the mRNA level of gene C between the WT and the A MASO condition is apparent immediately after C is on. There is a clear delay between the activation of C in the indirect circuit compared to the direct. If we consider a two-fold difference as the cut-off for the detection by QPCR, the effect of A MASO on C is detectible immediately after C is on and the lag due to the indirect connection is measurable. On the other hand, C under OR logic behaves quite differently. The maximal difference in C mRNA between the WT and the perturbed situation in the direct connectivity is two-fold and it can be observed after about one hour from C initiation. The indirect connectivity does not induce a lag in the initiation of gene C translation since the additional input D is still driving gene C expression. In the indirect connectivity the difference between the WT and A MASO reaches the maximal value of one and a half fold after several hours from C initiation.

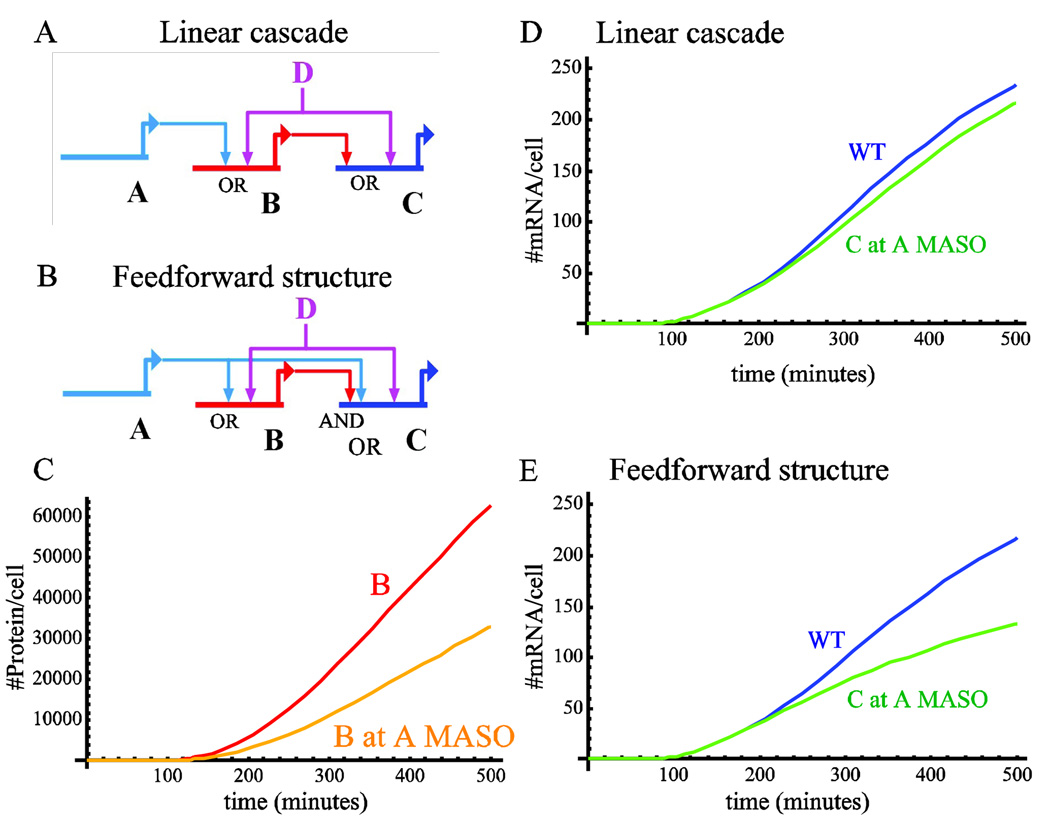
This exercise shows that OR logic has buffering effect on perturbation propagation, which is even more apparent when we assume that there is an additional factor activating gene B under OR logic, Fig. 2A. The equation describing the kinetics of gene B mRNA is Eq. (1) replacing mC(t) with mB(t) and Y_B with Y_D. The resulting kinetic profiles of B protein in the WT and A MASO conditions are presented in Fig. 2C. The effect of A knock-down on B protein level is not as significant as in the case presented in Fig.1, due to the additional input, D. As a result, B together with D are sufficient to drive C close to its’ wild type level, Fig. 2D. In this circuitry the downstream targets of B are almost unaffected by variation in the level of one of B inputs. This means that two steps of OR logic can eliminate variations in the upstream input level. Some of the sensitivity to A knock-down is recovered in a feedforward structure where in addition to the indirect link through B, there is also a direct link between A and C and the logic is [(A AND B) OR D], Fig. 2B. The equation for C mRNA synthesis has the form:

$$\frac{\mathit{\text{dmC}}(t)}{\mathit{\text{dt}}}=\frac{I_{\text{max}}}{2}\left\{\left(1-\text{exp}\left(-\frac{k_{\mathit{\text{bAB}}}{Y}_A(t-T_m)Y_B(t-T_m)}{I_{\text{max}}}\right)\right)+\left(1-\text{exp}\left(-\frac{k_{\mathit{\text{bD}}}{Y}_D(t-T_m)}{I_{\text{max}}}\right)\right)\right\}-k_{\mathit{\text{dmC}}}\mathit{\text{mC}}(t).$$ (9)

Figure 2.

Linear cascade with OR logic versus feedforward structure. A. Schematic diagram of linear cascade where both genes B and C have multiple inputs and the cis-regulatory modules execute OR logic on these inputs. B. Schematic diagram of feedforward structure where transcription factor A activates gene B and together they activate gene C in AND logic. C. The protein level of gene B in WT condition (red) and in A MASO treatment (orange). D. The mRNA level of the downstream gene, C, for linear cascade at WT condition (blue) and at A MASO treatment (green). E. The mRNA level of the downstream gene, C, for feedforward structure at WT and A MASO treatment. Same color scheme as in D. Kinetic parameters for all simulations are the same as in Fig. 1.

The resulting kinetics of gene C mRNA is presented in Fig. 2E. The behavior is very similar to the indirect OR logic presented in Fig. 1F and this is since even though B is less sensitive to the knock-down of gene A, gene C is sensitive due to the direct link from A.

GRNs are composed of multiple circuits such as the ones described here, which are interconnected. In some cases gene D can depend on transcription factor A in a feedforward structure. In that case the downstream gene C has no additional independent input and the effect of A MASO on C expression is similar to that of AND logic, i.e., a significant immediate reduction of the level. If there is any additional independent input, the effect on the downstream input depends on the logic applied on the inputs, similar to the cases described in Figs. 1 and 2.

In the examples presented here, perturbation analysis is sufficient to distinguish between the execution of AND and OR logic on the inputs, and in the case of AND logic, between direct and indirect connectivity. However, these results depend on the choice of parameters and on the assumption of 99% efficiency of the MASO. When the translation rate or the enhancer efficiency are higher, or the turnover rates slower, the 99% MASO efficiency assumed in this simulation is not enough to prevent protein accumulation and the effect on the downstream gene is less significant even for AND logic. Therefore, in the general case when the MASO efficiency in not known it is hard to distinguish between AND and OR logic from perturbation data alone. On the other hand, in systems where knock-out of a gene can be introduced genetically, the knock-out efficiency is off course, 100%, and the difference between AND and OR logic is even more prominent than in our simulations.

The lag that the indirect connectivity induces when AND logic is executed depends mostly on the transcriptional delay, T_m. The transcriptional delays depend on RNA polymerase translocation rate, the gene size and the mRNA export from the nucleus. All these could vary significantly between different genes and be either shorter or longer than the delay we consider in these simulations. For example, in mammalian cells in culture the delay between mRNA generation and protein production for the gene Hes1 was measured to be 15 minutes (Hirata et al., 2002). Due to these variations in temporal delays it could be hard to distinguish between direct and indirect linkages from expression kinetics and perturbations data alone even for AND logic. The exact connectivity and logic needs to be verified by cis-regulatory analysis where the binding sites on the downstream genes are mutated in a reporter construct.

Another parameter that the results depend on is the genome size, Eq. (3). This is since all the open chromatin is competing with the specific binding site on binding the transcription factor (Bolouri and Davidson, 2003; Ben-Tabou de-Leon and Davidson, 2009b). This means that for a given binding site the larger the genome is the higher is the required concentration of a transcription factor to achieve a given occupancy, Eq. (3), and therefore, the slower is the accumulation curves of mRNA Eqs. (1)–(2). This observation indicates that large genomes could acts as buffers to biochemical fluctuations and by that increase the reliability of gene regulatory circuits.

Regulatory states lock-down – positive feedback circuits

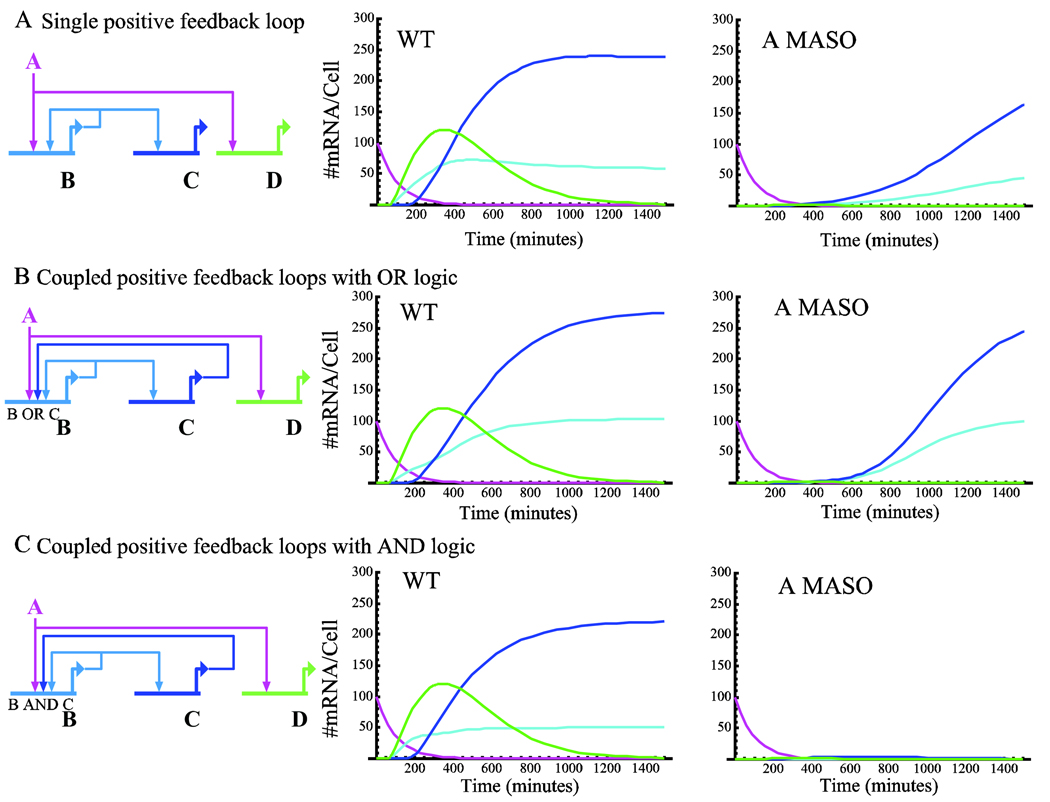
Once a specific regulatory state is established in a given domain, it is maintained by various mechanisms. One prominent mechanism is the installation of chromatin states which “lock down” conditions of activity or inactivity that were initially mandated by cis-regulatory modules interactions (for review see (Davidson, 2006; Ng and Gurdon, 2008; Mohn and Schubeler, 2009)). Another mechanism that is used by GRNs to maintain the expression of regulatory genes is positive feedback. The necessity of positive feedback loops architecture for the establishment of multiple distinct regulatory states was shown theoretically, which demonstrates the generality of this architecture (Plahte et al., 1995; Demongeot, 1998; Gouze, 1998; Snoussi, 1998; Thomas and Kaufman, 2001). In the left panel of Fig. 3A we present a schematic diagram of a feedback circuit that contains a single positive feedback loop. In this circuit, a transient input, A, activates gene B which encodes a transcription factor that binds to gene B cis-regulatory module and activates its own transcription. The logic that the cis-regulatory module of B applies on its inputs is A OR B, so once A is off, gene B expression is maintained by the transcription factor it encodes.

Figure 3.

Positive feedback circuitry. A. Single positive feedback loop circuit. Left: Schematic diagram of a single positive feedback circuit. The transient input A activates gene B, which encodes a transcription factor that feeds back into gene B and activates gene C. Middle and right: mRNA expression levels of single feedback circuit in the wild type condition (middle) and under A MASO treatment (right). Genes A and B mRNA and protein decay with K_dm=K_dp=0.01 min⁻¹. Gene A is depicted in magenta, gene B in cyan, gene C is in depicted blue. For illustration of the maintenance function of the feedback circuitry we plot also the mRNA of gene D (green) that is downstream of A but does not execute positive feedback. B. Coupled positive feedback loops executing (A OR B OR C) logic. Left: Schematic diagram of the coupled circuit. It is similar to the circuit presented in A but gene C encodes a transcription factor that feeds back and activates gene B. middle and right: mRNA expression levels of coupled feedback circuit executing (A OR B OR C) logic, middle: wild type, right: A MASO. Same color scheme as in A. C. Coupled positive feedback loops executing [A OR (B AND C)] logic. Left: Schematic diagram of the coupled circuit. Middle and right: mRNA expression levels of coupled feedback circuit executing [A OR (B AND C)] logic, wild type: middle, A MASO: right. Same color scheme as in A. Kinetic parameters for all simulations are the same as in Fig. 1 (except from genes A and B as stated above.).

Many examples of positive feedback circuitry are observed in GRNs that control cell fate specification. In the sea urchin GRN feedback circuits maintain the specification state of the skeletogenic lineage (Oliveri et al., 2008), the pigment cells (Ransick and Davidson, 2006), the endoderm specification (Peter and Davidson, 2010) and the aboral ectoderm (Su et al., 2009). Positive feedback loops control heart development in multiple organisms (Olson, 2006), muscle cell fate specification in mammalian cells (Thayer et al., 1989; Kaneko et al., 2002; Brandman et al., 2005) and retinal determination in Drosophila (Kumar, 2009). In all of these examples there are multiple genes that feed back to each other, forming coupled feedback loops. In Figs. 3B and 3C we present schematic diagrams of coupled feedback circuits. These circuits are similar to that in Fig. 3A except from an additional activation link between gene C and gene B. Gene C is a downstream target of transcription factor B and it encodes a transcription factor that activates gene B transcription. The logic the cis-regulatory module of B applies on its input can be either (A OR B OR C), Fig. 3B left panel, or [A OR (B AND C)], Fig. 3C left panel.

The extensive use of positive feedback circuits in GRNs raises the question about their stability. In principle, a few copies of mRNA of a gene that positively feeds back to its own expression could lead to the constitutive activation of this gene expression. However, the positive feedback circuits that were detected experimentally are reliably activated in the exact domain and time of their required function. MASO treatment against the initiating input prevents the positive feedback circuit from turning on (Ransick and Davidson, 2006; Su et al., 2009; Croce and McClay, 2010). Here we study the dynamics of the three architectures of feedback circuits presented above in order to test which architecture has the best agreement with the experimental observations. The three circuits’ architectures are simulated in wild type condition and under MASO treatment of the transient input that initiates the circuit activation.

We assume that the transient input A has an initial finite mRNA level and is decaying with time:

$$\frac{\mathit{\text{dmA}}(t)}{\mathit{\text{dt}}}=-k_{\mathit{\text{dmA}}}\mathit{\text{mA}}(t).$$ (10)

The equation for the mRNA synthesis of gene B in the case of single positive feedback loop is similar to Eq. (1) where gene B is activated by the transcription factors A and B. In the case of a coupled feedback loop where the logic executed is (A OR B OR C) the equation for B mRNA synthesis is:

$$\frac{\mathit{\text{dmB}}(t)}{\mathit{\text{dt}}}=\frac{I_{\text{max}}}{3}\left\{\begin{array}{c}\left(1-\text{exp}\left(-\frac{k_{\mathit{\text{bA}}}{Y}_A(t-T_m)}{I_{\text{max}}}\right)\right)+\left(1-\text{exp}\left(-\frac{k_{\mathit{\text{bB}}}{Y}_B(t-T_m)}{I_{\text{max}}}\right)\right)\hfill \\ +\left(1-\text{exp}\left(-\frac{k_{\mathit{\text{bC}}}{Y}_C(t-T_m)}{I_{\mathit{\text{max}}}}\right)\right)\hfill \end{array}\right\}-k_{\mathit{\text{dmB}}}\mathit{\text{mB}}(t).$$ (11)

In the case of a coupled feedback loop where the logic is [A OR (B AND C)] the equation for B mRNA synthesis is similar to Eq. (9) with the relevant indices replacement. The equation for C mRNA synthesis for all the above cases is

$$\frac{\mathit{\text{dmC}}(t)}{\mathit{\text{dt}}}=I_{\text{max}}\left(1-\text{exp}\left(-\frac{k_{\mathit{\text{bB}}}{Y}_B(t-T_m)}{I_{\text{max}}}\right)\right)-k_{\mathit{\text{dmC}}}\mathit{\text{mC}}(t).$$ (12)

To illustrate the preservation function of the feedback circuit we also simulate the expression of gene D that is activated by Transcription factor A but is not regulated by a feedback loop. The equation for the mRNA synthesis of D is similar to Eq. (12) where D is activated by A. The equations for all protein synthesis are Eq. (6) with the relevant index.

Simulations of the dynamics of the three feedback circuits are presented in Fig. 3A–C, middle (WT) and right (A MASO treatment) panels. While the wild type behavior of the three circuits is quite similar there is a significant difference in the response to A MASO treatment between AND logic coupled circuit and the other two. While the activity of the other feedback circuits is not eliminated by A MASO treatment, the [A OR (B AND C)] logic does not allow the circuit to turn on when A protein level is significantly down-regulated. This makes this architecture more reliable than the other two, since the other two circuits turn on at very low levels of transcription factor A. The AND logic enables activation only when transcription factor A is at a significant level and for long enough time and therefore is the only circuit architecture that agrees with the experimental observations described above.

The behavior of these circuits depends strongly on the model parameters. When the turnover rates of mRNA A and B are two times slower or more, or when the translation rate is two time higher or more, or when the enhancer efficiency is two times higher or more, even the AND logic circuitry does not prevent the coupled feedback circuit from turning on at low levels of transcription factor A. (These modifications of parameters are well within the biological range, see method section.) On the other hand, low binding site affinities (i.e., low K_r) or larger genomes will make all circuitries described here more reliable as higher concentrations of all transcription factors are required to establish significant binding site occupancies. For example, for the parameters considered in this simulation, reducing K_r from 10⁵ to 10⁴ makes all the architectures in Fig. 3 reliable in the sense that the circuits are not turned on at A MASO. Large genome size of the scale of the human genome (3×10⁹) has the same stabilizing effect on the circuits’ activity. Interestingly, neither shortening the transcriptional delays to five minutes nor extending it to three hours did not change the stability of the three circuits described here. We can conclude from this analysis that the factors that increase the reliability of positive feedback circuits are low binding site affinities (K_r) and low enhancer efficiencies (K_b). Factors that reduce the reliability are slower turnover rate and higher translation rate. For a given combination of these parameters, AND logic applied on coupled positive feedback loops increases the reliability of the circuit. It would be fascinating to study experimentally what combinations of these strategies are used by GRNs to ensure the reliable activation of positive feedback circuits.

Discussion

In this work we used mathematical modeling of GRN circuits to promote the ability to analyze perturbation data and construct reliable GRNs. We studied the response to perturbation of direct and indirect linkages executing AND or OR logic. The response to MASO treatment, and therefore the performance of a given circuit architecture depends on the logic applied on the inputs and on the kinetic parameters. As expected, AND logic is very sensitive to a change in each input level; efficient MASO treatment of inputs has a major effect on the downstream genes which is immediately observed. Considering the intact circuit function, AND logic offers a reliable mechanism to prevent a gene from turning on ectopically and “correct” for over or ectopic expression of upstream transcription factors. The use of AND logic in coupled positive feedback circuits can prevent the circuit from turning on ectopically. Other possible mechanisms that can prevent ectopic expression in positive feedback circuitry are low binding sites affinities and low mRNA and protein synthesis rates. Interestingly, large genome size can also buffer biochemical fluctuation since it competes with the specific binding sites on binding transcription factors. This decreases the response of cis-regulatory modules to low concentrations of transcription factors and creates a threshold for gene activation.

OR logic is much less sensitive than AND logic to a change of the level of its inputs; after two OR logic steps MASO treatment of one of multiple inputs is completely buffered. Considering intact circuit function, when an input is expressed ectopically, OR logic could propagate this miss-expression forward in the network. Therefore in actual nodes in the network OR logic is usually applied together with a repression mechanism that restricts the expression of the genes to a specific domain. For example, foxa, a key endodermal regulator, is activated by multiple additive inputs and is restricted spatially by TCF-Groucho repression (Ben-Tabou de-Leon and Davidson, 2010). When considering the evolvability of the network, OR logic offers another advantage. Clearly the developmental price of adding or removing a link that operates by OR logic is lower than the price of changing an AND logic link. Therefore circuits that are wired heavily by AND logic are more rigid to changes, and are predicted to be more conserved. Interestingly positive feedback circuits seem to be highly conserved compared to other network components, e.g., the echinoderm gut specification circuit (Hinman et al., 2003; Hinman and Davidson, 2007; Hinman et al., 2007; Ben-Tabou de-Leon and Davidson, 2009a) and the circuit regulating the bilaterian heart progenitor field specification (Davidson, 2006; Olson, 2006).

In summary, the kinetic analysis of typical network circuits provides a better understanding of the results of perturbation analysis. It also gives insights to the function of the intact circuits and to GRN plasticity and conservation.