An Association Test for Multiple Traits Based on the Generalized Kendall’s Tau

Abstract

In many genetics studies, especially in the investigation of mental illness and behavioral disorders, it is common for researchers to collect multiple phenotypes to characterize the complex disease of interest. It may be advantageous to analyze those phenotypic measurements simultaneously if they share a similar genetic mechanism. In this study, we present a nonparametric approach to studying multiple traits together rather than examining each trait separately. Through simulation we compared the nominal type I error and power of our proposed test to an existing test, i.e., a generalized family-based association test. The empirical results suggest that our proposed approach is superior to the existing test in the analysis of ordinal traits. The advantage is demonstrated on a data set concerning alcohol dependence. In this application, the use of our methods enhanced the signal of the association test.

1 Introduction

Recent publication of the human genome sequence has generated a great deal of interest in the genetic factors that underpin common disease and has resulted in publicly available resources that have set the stage for the modern association study. Taking advantage of high throughput genomic data, association analysis has emerged as a more powerful alternative to linkage analysis for identifying genes for complex disease (e.g., Klein et al. 2005, Arking et al. 2006, Duerr et al. 2006, Frayling et al. 2007). The association studies commonly utilize a case-control design with unrelated individuals, but may be family based, mostly when the families have already been recruited. We describe a method for testing association between multivariate (quantitative or ordinal) traits and genetic variants. This is important because in the investigation of mental illness and behavioral disorders, it is common for researchers to collect multiple phenotypes to characterize the complex disease of interest. Progress made so far (Lange, Silverman, Xu, Weiss, and Laird 2003; Lambertus, Dianna, Devlin, and Roeder 2008; Zhu and Zhang 2009) has demonstrated the benefit of conducting genetic association analysis of multivariate traits.

Human beings have 23 pairs of chromosomes. Each chromosome is a long strand structure in which deoxyribonucleic acid (DNA) molecules are tightly coiled many times around proteins called histones that support its structure. DNA molecules are a double-stranded sequence consisting of complementary nucleotides. Human DNA has about 3 billion bases, and more than 99 percent of those bases are believed to be identical in all people. The ones that may be different between any two persons are called single nucleotide polymorphisms (SNPs). Even though SNPs are less than 1 percent of the human genome, they are the most common form of variant and relatively easy to assay. It has been observed that the alleles at the nearby SNPs tend to be correlated as measured by linkage disequilibrium.

Most of the genetic association analyses use either the case-control study design with unrelated individuals or nuclear families (two generations); however, some are family based. The case-control studies are cost effective due to easy recruitment, but they employ population-based sampling and may be vulnerable to confounding such as population substructure due to the presence of clusters of individuals with a common ancestry. On the other hand, family-based association studies utilize pedigree data. Through proper conditioning (Rabinowitz and Laird 2000), the analysis result is robust to population stratification and ascertainment. However, unless pedigrees already exist, it is very difficult and expensive to recruit families. In addition, the power increment (per person) in family-based association analyses is less than that in case-control analyses, and hence increase the genotyping costs.

In the last decade, there have been many useful methodological developments in association studies to separate genetic contributions from potential confounding factors such as population admixture. Spielman, McGinnis and Ewens (1993) introduced a transmission/disequilibrium test (TDT) using affected offspring-parent trios. The test compares the frequencies of transmitted and nontransmitted alleles from heterozygous parents to their affected children. This creates an artificially but ideally matched case-control study design so that the TDT is robust to the effect of population admixture. Many approaches have followed TDT to relax the restrictive requirement of trios and either to allow other study designs such as sibships or to propose a new approach (e.g., Allison, 1997 and Rabinowitz, 1997; Spielman and Ewens 1998; Knapp 1999; Martin, et al. 2000; Abecasis, Cardon, and Cookson, 2000). Most of these extensions can be unified into a general framework of so-called family-based association tests (FBATs) (Rabinowitz and Laird 2000; Laird, Horvath, and Xu 2000), which are applicable to any type of traits. Liu, Tritchler, and Bull (2002) proposed a similar framework with their distributions belonging to the exponential family. Recently, the importance of ordinal traits has been recognized, and there are efforts to extend the TDT for ordinal traits (Zhang, Wang, and Ye 2006; Wang, Ye and Zhang 2006). Interestingly, the test statistic for the ordinal traits can also be expressed in a form of the FBATs, and it also performs well for quantitative traits with a robustness property to trait outliers. In summary, the existing work focuses on a single trait analysis or multivariate quantitative traits. The objective of this work is to propose a test for association involving multivariate traits (quantitative and/or ordinal).

Based on the generalized Kendall’s tau, we propose a novel association test to study multiple complex traits which may be quantitative and/or categorical, or even ordinal. We exploit a traditional nonparametric method of analyzing differences between pairs of individuals to obtain test statistics in the form of U-statistics, which are the generalizations of Kendall’s tau (called Generalized Kendall’s tau). Similar ideas have also been applied in different genetic analyses (Risch and Zhang 1995; Dudoit and Speed, 2000; Tzeng, Devlin, Wasserman, and Roeder 2003; Schaid, Mc-Donnell, Hebbring, Cunningham, and Thibodeau 2005). The generalized Kendall’s tau provides more flexible forms of test statistics even for a hybrid of traits of different types. In the next section, following an introductory description of the underlying genetic model, we define the generalized Kendall’s tau. We present simulation studies to assess the accuracy of the nominal p-value for our test and to compare the performance with another existing method in Section 3. We then conclude this paper with discussion in section 5 following an application to an important data set in Section 4.

2 Method for Multiple Traits

2.1 Genetic Model

Let D and M denote the trait locus of interest and a marker locus, respectively, and A_D and A_M the alleles at D and M, respectively. When two alleles, A_D and A_M, are on the same gamete, they form a haplotype. In the presence of linkage disequilibrium, having A_D and A_D on a haplotype is not an independent event. The coefficient of linkage disequilibrium, δ = P(A_D, A_M ) − P (A_D)P (A_M ), is one measure of how far apart the joint and independent distributions are (Ott, 1999). We test the null hypothesis, H₀, that there is no linkage disequilibrium (δ = 0) between the alleles at the marker and trait locus of interest.

Let Z = (S, M^O), where M^O represents the set of marker alleles of all offspring and S consists of all observed trait values T and the set of parental marker alleles M^P. Let A^T be the set of alleles at the trait locus for all study subjects. Let f(·) refer to a generic probability function that depends on certain parameters. Then,

$$\begin{array}{l}f(\mathbf{Z}=\mathbf{z})=f({\mathbf{M}}^O={\mathbf{m}}^O,{\mathbf{M}}^P={\mathbf{m}}^P,\mathbf{T}=\mathbf{t})\\ =\sum f({\mathbf{M}}^O={\mathbf{m}}^O,{\mathbf{M}}^P={\mathbf{m}}^P,\mathbf{T}=\mathbf{t},A^T)\\ =\sum f(\mathbf{T}=\mathbf{t}\mid {\mathbf{M}}^O={\mathbf{m}}^O,{\mathbf{M}}^P={\mathbf{m}}^P,A^T)f({\mathbf{M}}^O={\mathbf{m}}^O,{\mathbf{M}}^P={\mathbf{m}}^P,A^T),\end{array}$$

where z = (m^O, m^P, t), and the summation is over all combinations of the alleles at the trait locus.

Under the null hypothesis,

$$f({\mathbf{M}}^O={\mathbf{m}}^O,{\mathbf{M}}^P={\mathbf{m}}^P,A^T)=f({\mathbf{M}}^O={\mathbf{m}}^O,{\mathbf{M}}^P={\mathbf{m}}^P)f(A^T),$$

provided that the marker alleles of one parent are independent of those of the other parent. Note that the joint marker probability, f(M^O = m^O, M^P = m^P), is characterized by the allele frequency, f(M^P = m^P), and Mendalian transmission f(M^O = m^O|M^P = m^P). Also note that f(T = t|M^O = m^O, M^P = m^P, A^T) = f(T = t|A^T) because the distribution of the trait depends on the alleles at the trait locus only, if given. This dependence is referred as the penetrance function. Therefore, we have

$$\begin{array}{l}f(\mathbf{Z}=\mathbf{z})=\sum f(\mathbf{T}=\mathbf{t}\mid A^T)f({\mathbf{M}}^O={\mathbf{m}}^O,{\mathbf{M}}^P={\mathbf{m}}^P)f(A^T)\\ =f(\mathbf{T}=\mathbf{t})f({\mathbf{M}}^O={\mathbf{m}}^O,{\mathbf{M}}^P={\mathbf{m}}^P).\end{array}$$

In other words, the assumption under the null hypothesis is equivalent to the independence of the trait distribution and the marker distribution. In the following, we will introduce a U-statistic to test this independence assumption.

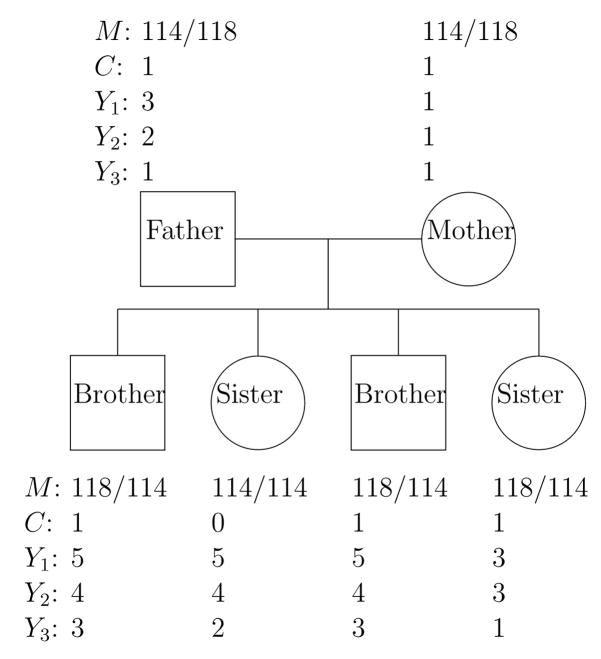
As discussed above, the association test is vulnerable to confounding due to population substructure. When parents are available as depicted in Figure 1, we use the same approach as in Rabinowitz and Laird (2000) by conditioning on the minimal sufficient statistics to ensure correct type I error rates regardless of patterns of population admixture, the sampling plan, and the genetic model. We show in Appendix A that the minimal sufficient statistics consist of the parental marker alleles and trait values provided that the conditional distribution of offspring marker alleles given parental marker alleles is completely determined by the Mendelian laws. The derivation of the conditional distribution of offspring markers is illustrated in Table 5.

Figure 1.

A Nuclear Family with Observed Data. The genotype at one marker (M) is presented as an example, and the three trait values (Y₁, Y₂, Y₃) and the count (C) for allele 118 are also given.

Table 5.

Conditional distributions given the both parental genotypes are observed

	Probability
Parental genotypes	AA	Aa	aa	Joint Probability
(AA, AA)	1	0	0	P(AA, AA) = 1
(AA, Aa)	1/2	1/2	0	P(Aa,AA)=1/2 P(Aa,Aa)=P(AA,AA)=1/4
(AA, aa)	0	1	0	P(Aa, Aa)=1
(Aa, Aa)	1/4	1/2	1/4	P(AA,aa)=1/8 P(Aa,Aa)=1/4 P(AA,AA)=P(aa,aa)=1/16 P(AA, Aa)=P(aa, Aa)=1/4
(Aa, aa)	0	1/2	1/2	P(Aa,aa)=1/2 P(Aa,Aa) = P(aa,aa) =1/4
(aa, aa)	0	0	1	P(aa, aa) =1

2.2 Generalized Kendall’s τ

Kendall’s τ is a classic nonparametric measure of correlation between two variables. It is based on the difference between the probability of observing the two variables in the same order in two observations and the probability of observing the two variables in the opposite order. Specifically, for a sample of n observations (X₁, Y₁),···, (X_n, Y_n), two observations (X_i, Y_i) and (X_j, Y_j) are called concordant if (X_i − X_j)(Y_i − Y_j) > 0 and discordant if (X_i − X_j)(Y_i − Y_j) < 0. Then Kendall’s τ is based on the difference between the numbers of concordant pairs and discordant pairs.

First, let us consider the following kernel function

$$\varphi ((X_i,Y_i),(X_j,Y_j))=\text{sign}\{(X_i-X_j)(Y_i-Y_j)\}=\{\begin{array}{ll}1,\hfill & \text{if}(X_i-X_j)(Y_i-Y_j)>0,\hfill \\ -1,\hfill & \text{if}(X_i-X_j)(Y_i-Y_j)<0,\hfill \\ 0,\hfill & \text{if}(X_i-X_j)(Y_i-Y_j)=0,\hfill \end{array}$$

and the corresponding U-statistic

$$U={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\sum _{i<j}\varphi ((X_i,Y_i),(X_j,Y_j)).$$ (1)

Then, Kendall’s τ is

$$\tau =\frac{U}{\sqrt{{\text{Var}}_0(U)}},$$ (2)

where Var₀(U ) is the variance of U under the null hypothesis of no correlation between X and Y, and equal to n(n − 1)(2n + 5)/18 if X and Y are continuous variables (Hollander and Wolfe, 1999).

The Kendall’s τ has been extended beyond a simple measure of bivariate correlation to include a trend test, Wilcoxon’s rank sum test, and the Jonckheere-Terpstra test. See Hollander and Wolf (1999) for more discussion. In this study, we generalize the Kendall’s τ to test associations between genetic markers and traits. For this purpose, we choose a multiplicative kernel as follows

$$\varphi ((X_i,Y_i),(X_j,Y_j))={\varphi }_1(X_i,X_j){\varphi }_2(Y_i,Y_j),$$ (3)

where ϕ₁(X_i, X_j) and ϕ₂(Y_i, Y_j) are some measures of the dissimilarity of (X_i, X_j) and (Y_i, Y_j), respectively. These kernel functions shall be defined shortly.

2.3 Association tests of multiple traits and genetic markers

Suppose we observe a vector of measured or coded traits T = (T⁽¹⁾,···, T^(p))′ and a vector of markers M = (M⁽¹⁾,···, M^(g))′ for each of n study subjects. In general, we perform the association test for one marker at a time. Thus, without loss of generality, we only need to consider g = 1 and use M to refer to the marker. Let M^P represent the parental marker information, although it may be unavailable for some parents. We refer to Rabinowitz and Laird (2000) for the details on how to deal with the situations where parental markers are not available. The basic idea is that we need to consider the distribution of parental genotypes conditional on the observed sibling genotypes, and then we need to integrate over the distribution of parental genotypes.

For individuals i and j, let T_i and T_j be their vectors of traits, respectively. We can define

$${\mathbf{u}}_{ij}={\left(f_1(T_i^{(1)}-T_j^{(1)}),\cdots ,f_p(T_i^{(p)}-T_j^{(p)})\right)}^{\prime },$$

where function f_k(·) can be the identity function for a quantitative or binary trait (Rabinowitz 1997) or the sign function for an ordinal trait (in fact, the sign function is applicable to any trait) (Zhang et al. 2006). This formulation allows us to consider mixed traits: some quantitative and some qualitative.

Let C be a function of marker M such as the count of any chosen allele or genotype. Also, let C_i refer to the C for the i-th subject. For a population-based study, the marker kernel is chosen as v_ij = C_i − C_j. For a family-based study, as discussed in Section 2.1, we condition the test statistic on the minimal sufficient statistics. Hence, C is replaced with Ĉ = C − E[C|M^P] and v_ij = Ĉ_i − Ĉ_j.

Now, we choose the trait kernel, ϕ₂(T_i, T_j), to be u_ij. For example, if the traits are quantitative, as discussed above, ϕ₂(T_i, T_j) can simply be ${(T_i^{(1)}-T_j^{(1)},\cdots ,T_i^{(p)}-T_j^{(p)})}^{\prime }$. Use of trait difference is quite common in genetic studies of quantitative traits (e.g., Risch and Zhang 1995), although there exist other choices including the use of the sign function and Gaussian kernel. The impact of different kernels warrants further investigation.

Similar to (1), by replacing X with marker M and Y with the trait vector T, we define the U-statistic as

$$\begin{array}{l}\mathbf{U}={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\sum _{i<j}\varphi (({\mathbf{M}}_i,{\mathbf{T}}_i),({\mathbf{M}}_j,{\mathbf{T}}_j))\\ ={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\sum _{i<j}{\varphi }_1({\mathbf{M}}_i,{\mathbf{M}}_j){\varphi }_2({\mathbf{T}}_i,{\mathbf{T}}_j)[\text{by}(3)]\\ ={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\sum _{i<j}{v}_{ij}{\mathbf{u}}_{ij}.\end{array}$$

Then the association test statistic is $W={\mathbf{U}}^{\prime }{\text{Cov}}_0^{-1}(\mathbf{U}\mid \mathbf{T})\mathbf{U}$, where Cov₀(U|T) is the co-variance matrix of U given trait T under the null hypothesis that there is no association between marker alleles and any linked locus that influences the trait T (Rabinowitz and Laird 2000). Note also that for a family-based study, the calculation of U is already conditioned on parental marker alleles M^P.

Our test statistic focuses on one marker locus at a time. However, we need to correct for the multiple testing problem when we test all genotyped markers, because we test many null hypotheses, and the chance of falsely rejecting one of them increases as the number of the null hypotheses increases. See Storey and Tibshirani (2003) and Benjamini and Hochberg (1995) for more detailed discussion of the multiple testing issue.

2.4 Properties of the proposed test

Recall that the null hypothesis that there is no association between marker alleles and any linked locus that influences traits T, implying that E₀[C_i − C_j|T] = 0 and hence $E_0(\mathbf{U}\mid \mathbf{T})={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}{\sum }_{i<j}{\mathbf{u}}_{ij}{E}_0[C_i-C_j\mid \mathbf{T}]=0$. Next, we discuss how to estimate the conditional variance of U, Cov₀(U|T), under the null hypothesis.

For a population study, let ${\overline{\mathbf{u}}}_i=\frac{1}{n}{\sum }_{j=1}^n{\mathbf{u}}_{ij}$, and then U can be rewritten as follows (see Appendix B for the derivations),

$$\mathbf{U}=\frac{2}{n-1}\sum _{i=1}^n{C}_i{\overline{\mathbf{u}}}_i.$$

If data come from nuclear families and suppose that there are S sibships and s_k siblings in the k-th sibship, then following Appendix B, we have

$$\mathbf{U}=\frac{2}{n-1}\sum _{k=1}^S\sum _{i=1}^{s_k}{C}_{d_k(i)}{\overline{\mathbf{u}}}_{d_k(i)},$$

where d_k(i) is the mapping function, implying that the i-th member in the k-th sibship is the d_k(i)-th subject in the entire study cohort.

For a population study,

$${\text{Cov}}_0(\mathbf{U}\mid \mathbf{T})=\frac{4}{{(n-1)}^2}\sum _{i=1}^n\sum _{j=1}^n{\overline{\mathbf{u}}}_i{{\overline{\mathbf{u}}}^{\prime }}_j{\text{Cov}}_0(C_i,C_j\mid \mathbf{T}).$$

For a family study,

$${\text{Cov}}_0(\mathbf{U}\mid \mathbf{T})=\frac{4}{{(n-1)}^2}\sum _{k=1}^S\sum _{1\le i,j\le s_k}{\overline{\mathbf{u}}}_{d_k(i)}{{\overline{\mathbf{u}}}^{\prime }}_{d_k(j)}{\text{Cov}}_0(C_{d_k(i)},C_{d_k(j)}\mid \mathbf{T}).$$

The calculation of covariance Cov₀(C_{dk (i)}, C_{dk (j)}|T) is illustrated in Appendix C. Analogous to Kendall’s τ, $\sqrt{n}(\mathbf{U}-E(\mathbf{U}\mid \mathbf{T}))$ is asymptotically normal under some mild conditions. This is a corollary of Theorem 1 below, which is proved in Appendix D.

Theorem 1 Suppose C₁, C₂,... is a bounded sequence, and m = max{s_k|1 ≤ k ≤ S} ≤ m₀ for some positive integer m₀. Let ${\mathbf{A}}_i=\sqrt{n}{C}_i{\overline{\mathbf{u}}}_i/(n-1)$ and $\mathbf{A}(n)={\sum }_{i=1}^n{\mathbf{A}}_i=\sqrt{n}\mathbf{U}/2$. If for almost any t, Var(A(n)|T = t) → V_A(t) < ∞ as n → ∞, then $\mathbf{A}(n)\mid \mathbf{T}=\mathbf{t}\stackrel{d}{\to }N(0,V_A(\mathbf{t}))$.

In our application, C_i is between 0 and 2, and m₀ is usually smaller than 10. Thus, the assumptions for the theorem are satisfied. This theorem implies that the association test statistic, $W={\mathbf{U}}^{\prime }{\text{Cov}}_0^{-1}(\mathbf{U}\mid \mathbf{T})\mathbf{U}$, is asymptotically ${\chi }_{\nu }^2$-distributed where ν = rank(Cov₀(U|T)).

3 Simulation Study

The objective of our simulation studies is two-fold. First, we shall use simulation to validate the asymptotic behavior of our test statistic under the null hypothesis by assessing the accuracy of the nominal p-value for our test in practical settings. Also, we shall compare the power of our test with an existing approach, FBAT-GEE (Lange et al., 2003).

Specifically, let A, a and D, d, denote the alleles at a SNP marker and the trait locus, respectively. In our simulation, we set P(D) = 0.3 and P(A) = 0.3 as in Zhang et al. (2006). These choices are representative and illustrative. The parental genotypes at the marker locus are generated according to the allele frequency under the Hardy-Weinberg equilibrium. The offspring genotypes at the marker locus are generated by randomly selecting either copy of the alleles from each parent. Although our test does not use the information at the trait locus, we need to generate the data at the trait locus to simulate the trait values. The parental genotypes at the trait locus are generated according to the allele frequency and the linkage disequilibrium coefficient δ between the alleles at the marker and trait loci (e.g., δ = 0 under the null hypothesis defined in Section 2.1). Also, we assume the marker and trait loci are linked with the genetic distance of 1 centimorgan (cM). In other words, when we generated the four gametes from any parent, we allowed the crossover to take place between the marker and trait loci with a chance of one percent. This would allow us to generate the genotype for an offspring at the trait locus. After the trait genotype is determined for the offspring, the trait values are generated from the penetrance function that is introduced in Section 2.1. Specifically, for an ordinal trait with K ordered categories, a non-proportional odds model is used to generate the trait values as delineated in Table 2.

Table 2.

Conditional and marginal distributions for ordinal traits generated from nonproportional odds models

K = 3
P(Y <= 1 | dd) = 0.70	P(Y <= 1 | dD) = 0.30	P(Y <= 1 | DD) = 0.10	P(Y = 1) = 0.48
P(Y <= 2 | dd) = 0.90	P(Y <= 2 | dD) = 0.60	P(Y <= 2 | DD) = 0.50	P(Y = 2) = 0.26
			P(Y = 3) = 0.26
K = 4
P(Y <= 1 | dd) = 0.70	P(Y <= 1 | dD) = 0.30	P(Y <= 1 | DD) = 0.10	P(Y = 1) = 0.48
P(Y <= 2 | dd) = 0.80	P(Y <= 2 | dD) = 0.50	P(Y <= 2 | DD) = 0.35	P(Y = 2) = 0.16
P(Y <= 3 | dd) = 0.90	P(Y <= 3 | dD) = 0.70	P(Y <= 3 | DD) = 0.60	P(Y = 3) = 0.16
			P(Y = 4) = 0.21
K = 5
P(Y <= 1 | dd) = 0.70	P(Y <= 1 | dD) = 0.20	P(Y <= 1 | dd) = 0.05	P(Y = 1) = 0.43
P(Y <= 2 | dd) = 0.77	P(Y <= 2 | dD) = 0.45	P(Y <= 2 | dd) = 0.35	P(Y = 2) = 0.17
P(Y <= 3 | dd) = 0.85	P(Y <= 3 | dD) = 0.65	P(Y <= 3 | dd) = 0.55	P(Y = 3) = 0.14
P(Y <= 4 | dd) = 0.92	P(Y <= 4 | dD) = 0.80	P(Y <= 4 | dd) = 0.75	P(Y = 4) = 0.12
			P(Y = 5) = 0.15
K = 6
P(Y <= 1 | dd) = 0.60	P(Y <= 1 | dD) = 0.20	P(Y <= 1 | DD) = 0.05	P(Y = 1) = 0.38
P(Y <= 2 | dd) = 0.68	P(Y <= 2 | dD) = 0.32	P(Y <= 2 | DD) = 0.35	P(Y = 2) = 0.12
P(Y <= 3 | dd) = 0.72	P(Y <= 3 | dD) = 0.52	P(Y <= 3 | DD) = 0.48	P(Y = 3) = 0.12
P(Y <= 4 | dd) = 0.76	P(Y <= 4 | dD) = 0.68	P(Y <= 4 | DD) = 0.60	P(Y = 4) = 0.09
P(Y <= 5 | dd) = 0.80	P(Y <= 5 | dD) = 0.80	P(Y <= 5 | DD) = 0.72	P(Y = 5) = 0.08
			P(Y = 6) = 0.21

Two sets of simulations were performed. In both, we considered three choices of the number of nuclear families (200, 400 and 600) and three nominal levels of significance (0.05, 0.01, and 0.001), and replicated 1,000 times. The ordinal traits were generated according to the penetrace probability given in Table 2.

The first simulation is to assess type I error. The results of simulation are shown in Table 3. This table indicates that the empirical type I errors estimated from our simulation numerically approximate the pre-determined nominal levels, although some deviation from empirical results and nominal levels is observed.

Table 3.

Type I error comparison for ordinal traits. τ-FBAT refers to our proposed test and FBAT the FBAT-GEE method.

		α = 0.05		α = 0.01		α = 0.001
#(family)	K	τ-FBAT	FBAT	τ-FBAT	FBAT	τ-FBAT	FBAT
200	3	0.043	0.044	0.009	0.009	0.001	0.001
	4	0.049	0.051	0.008	0.007	0.001	0.001
	5	0.059	0.062	0.013	0.010	<0.001	<0.001
	6	0.047	0.043	0.005	0.005	<0.001	<0.001
400	3	0.049	0.051	0.012	0.009	0.002	0.002
	4	0.055	0.054	0.009	0.011	0.001	0.001
	5	0.042	0.041	0.006	0.006	0.001	0.002
	6	0.045	0.045	0.006	0.008	0.001	0.001
600	3	0.036	0.038	0.006	0.006	<0.001	<0.001
	4	0.054	0.055	0.013	0.010	0.001	0.001
	5	0.061	0.055	0.005	0.009	0.001	<0.001
	6	0.038	0.038	0.006	0.007	<0.001	<0.001

The second set of simulations evaluates the power of the proposed approach as compared to an existing approach, FBAT-GEE (Lange et al., 2003). Now, the marker and trait loci are in linkage disequilibrium, as presented in Table 1, which yields δ = P(AD) − P(A)P(D) = 0.11. Table 4 demonstrates the superiority of our proposed method in our simulated data sets. It can be seen that as the number of categories increases, the additional power of our proposed approach also increases.

Table 1.

Haplotype frequencies with P(D) = P(A) = 0.3 and δ = 0.11

Haplotype	AD	Ad	aD	ad
Frequency	0.2	0.1	0.1	0.6

Table 4.

Power comparison for ordinal traits that are characterized in Table 2. τ-FBAT refers to our proposed test and FBAT the FBAT-GEE method.

		α = 0.05		α = 0.01		α = 0.001
#(family)	K	τ-FBAT	FBAT	τ-FBAT	FBAT	τ-FBAT	FBAT
200	3	0.783	0.778	0.553	0.541	0.261	0.249
	4	0.732	0.702	0.492	0.456	0.213	0.184
	5	0.760	0.672	0.541	0.429	0.277	0.193
	6	0.504	0.403	0.266	0.184	0.076	0.042
400	3	0.980	0.982	0.922	0.916	0.757	0.752
	4	0.961	0.946	0.882	0.857	0.664	0.627
	5	0.978	0.949	0.914	0.839	0.757	0.604
	6	0.792	0.664	0.584	0.437	0.328	0.203
600	3	0.999	0.999	0.989	0.991	0.958	0.954
	4	0.996	0.988	0.978	0.970	0.920	0.885
	5	0.999	0.990	0.987	0.957	0.935	0.837
	6	0.947	0.859	0.826	0.658	0.582	0.379

4 Application on COGA Data

We applied the proposed approach to alcohol dependence data from the Collaborative Study on the Genetics of Alcoholism (COGA).

4.1 Background

Alcohol dependence, influenced by genes, environmental factors and the interaction between them, is a widespread psychiatric disorder throughout the world. In the United States, 12.5% of adults have alcohol dependence problems at some point in their lifetime (Hasin, Stinson, Ogburn, and Grant 2007).

The COGA is a nine-site national collaboration to identify genes related to alcohol dependence. In their recruitment, every entering proband must meet two alcohol dependence diagnostic criteria based on DSM-III-R (APA, 1994) and Feighner et al. (1972) to ensure that the data population represents a severely alcohol-dependent population. The COGA also invited first-degree relatives of probands into the study. More detailed information can be found in Begleiter et al. (1995). The total sample included in our study consisted of 143 families, with a total of 1614 individuals.

4.2 Data Analysis

The traits of primary interest are the degree of study subjects’ alcohol dependence. Specifically, we consider three phenotypes (1) Alcohol DX-DSM3R+Feighner (ALDX1: Y₁), (2) maximum number of drinks in a 24 hour period (MaxDrink: Y₂), and (3) “spent so much time drinking, had little time for anything else” (TimeDrink: Y₃). All of these three variables were coded in ordinal scales. Variable ALDX1 has 4 categories (pure unaffected, never drank, unaffected with some symptoms, and affected). Variable MaxDrink has 4 categories as well (0–9, 10–19, 20–29, and more than 30 drinks). The last variable, TimeDrink, has 3 categories, including “no”, “yes and lasted less than a month”, and “yes and lasted for one month or longer”. To illustrate the data, Figure 1 presents an example from one family. The example shows a typical nuclear family, and for each family member, we delineate one method of defining C at one marker (i.e., the indicator of genotype 114/118) and his or her three trait values (Y₁, Y₂, Y₃). In a nutshell, we try to assess whether the C value affects the trait values.

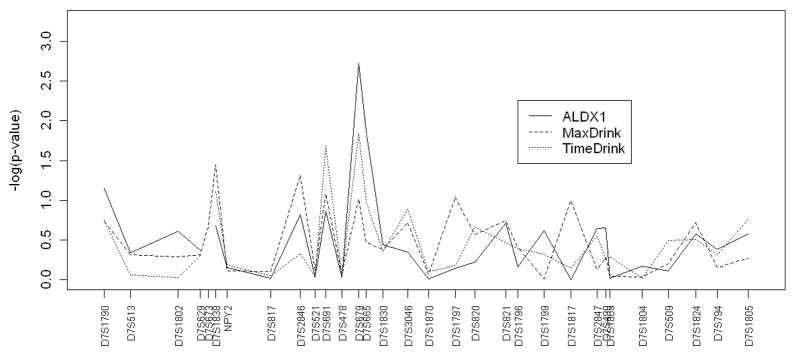
Here, we focus on chromosome 7 because it is suggested to have a linkage signal with alcohol dependence [Reich et al. (1998) and Zhu et al. (2005)]. First, we performed an association analysis for each of the three traits separately. The results are plotted in Figure 2. The figure shows a peak at marker D7S679 for trait ALDX1, with a p-value of 0.0019. However, if we consider that the three traits were analyzed separately and we tested 30 markers, this p-value must be adjusted for multiple comparisons. Applying the Bonferroni correction, none of the associations remain statistically significant in this analysis (the threshold is α_Bonferroni = 0.05/(3 × 30) = 0.00056).

Figure 2.

These plots display the log p-values in association analysis between alcohol dependence and markers on chromosome 7 using each of the three traits: ALDX1 (solid line), MaxDrink (dot-dash line), and TimeDrink (long-dash line), individually.

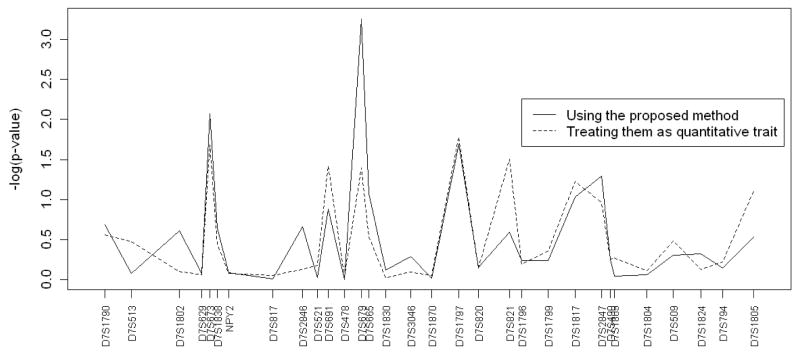
Next, we used the proposed approach to test for association between the three traits and the markers. The distributions of the p-values considering the three traits together are shown in Figure 3. As in the single trait analysis, the peak is also at marker D7S679. The uncorrected p-value at marker D7S679 on chromosome 7 is 0.00055, which is statistically significant at the 5% significance level. In this case, even after the Bonferroni adjustment (α_Bonferroni = 0.05/30 = 0.0016), the association remains statistically significant.

Figure 3.

These plots display the log p-value in association analysis between alcohol dependence and markers on chromosome 7 using the three traits together. Two approaches are considered: the proposed method (solid line) and FBAT-GEE by treating the ordinal traits as if they are quantitative traits (dot-dash line).

To evaluate the performance of FBAT-GEE, the ordinal traits were taken as quantitative. The resulting p-values are plotted in Figure 3. Specifically, the uncorrected p-value for FBAT-GEE is 0.040248. This suggests that the simple use of FBAT-GEE may not be appropriate when the traits are ordinal.

5 Discussion

Comorbidity is a major issue in mental health research. Traditionally, genetic studies of mental disorders focus on a single trait, such as obsessive and compulsive disorders (e.g., Zhang et al. 2002; Shugart et al. 2006), Tourette Syndrome (TSAICG 2007), nicotine dependence (e.g., Ma et al. 2005, Zhang et al. 2006), or cocaine dependence (e.g., Gelernter et al. 2005). Because of the complexity, genetic studies thus far have focused on mapping genes for a single trait at a time. Recently, Zhu and Zhang (2009) examined a variety of genetic models and underscored the importance of analyzing multiple traits. In this report, we propose a novel method to conduct association analysis of multiple traits simultaneously and demonstrate the advantages of our method over existing strategies. We first performed a simulation study and showed the superior power of our method over an existing approach that treats ordinal traits as if they were quantitative. Then, using the alcohol dependence genetic data, we demonstrated that analyzing multiple traits together enhanced the significance of the association test as well as alleviated the necessity for multiple comparison adjustments.

In the presence of comorbidity or multiple traits, our approach can be used to test the overall association, and then for the markers with significant associations, to examine the association of the individual traits. In the case of the alcohol dependence study, ALDX1 was the main contributor to the association signal among the three traits studied. However, when all three traits were analyzed simultaneously, the other two traits enhanced the association significance level. It is noteworthy that Reich et al (1998) reported linkage evidence on Chromosome 7 near marker D7S1793, which is about 1 cM away from D7S679, identified in this study. These findings suggest that there exists a trait locus in this region that is in linkage disequilibrium with marker D7S679.

Our numeric results confirm that our proposed method is superior to FBAT-GEE for multiple ordinal traits. Another alternative method in dealing with multiple ordinal traits (especially when there are many) is to perform a principal component analysis on the ordinal scale. While this alternative is worthy of further study, we should also note the caveat that the interpretation based on a composite score may be challenging.

As we pointed out earlier, few authors (Lange et al. 2003 and Lambertus et al. 2008) have considered the challenge of examining multiple traits in genetic studies. Unlike the existing methods, our proposed test can be applied when the properties of the multiple traits are mixed; namely, some or all can be binary, quantitative, or ordinal. However, while this unified property is appealing, our method may be improved by taking into account specific relationships among the traits, especially when the relationships are known or can be readily characterized. In addition, in the current implementation we have not considered covariates. We should note that the multiplicative kernel in (3) is critical to simplifying the calculation, but it may not be optimal for all applications. It remains to be seen as to whether there exist tractable and more efficient alternatives. We believe these issues are of great interest and importance that warrant thorough and further investigation.

Appendix A. Minimal Sufficient Statistics in Nuclear Families

If the conditional distribution of offspring marker alleles given parental marker alleles is completely determined by the Mendelian laws, we prove here that the minimal sufficient statistic consists of parental marker alleles and trait values.

Under the null hypothesis, it follows from Section 2.1 that

$$f(\mathbf{Z}=\mathbf{z})=f({\mathbf{M}}^O={\mathbf{m}}^O\mid {\mathbf{M}}^P={\mathbf{m}}^P)f({\mathbf{M}}^P={\mathbf{m}}^P)f(\mathbf{T}=\mathbf{t}).$$

Because f(M^O = m^O|M^P = m^P) does not depend on any parameters, according to the factorization criterion (Theorem 5.2) in Lehmann (1983), S is a sufficient statistic.

Next, for any sufficient statistic U, according to Corollary 5.1 of Lehmann (1983), f(Z = z|θ)/f(Z = z|θ₀) is a function of U(z) for any fixed θ and θ₀ Note that

$$f(\mathbf{Z}=\mathbf{z}\mid \theta )/f(\mathbf{Z}=\mathbf{z}\mid {\theta }_0)=\frac{f({\mathbf{m}}^P\mid \theta )f(\mathbf{t}\mid \theta )}{f({\mathbf{m}}^P\mid {\theta }_0)f(\mathbf{t}\mid {\theta }_0)},$$

which is a function of (m^P, t). Thus, S is minimal sufficient.

Appendix B. Expression of U

$$\mathbf{U}=\frac{2}{n-1}\sum _{i=1}^n{\overline{\mathbf{u}}}_i{C}_i=\frac{2}{n-1}\sum _{k=1}^S\sum _{i=1}^{s_k}{\overline{\mathbf{u}}}_{d_k(i)}{C}_{d_k(i)}.$$

Proof.

For a population-based study, U is defined as

$$\mathbf{U}={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\sum _{i<j}{\mathbf{u}}_{ij}{v}_{ij}.$$

Let ${\overline{u}}_i=\frac{1}{n}{\sum }_{j=1}^n{\mathbf{u}}_{ij}$. Then,

$$\begin{array}{l}\left(\begin{array}{c}n\\ 2\end{array}\right)\mathbf{U}=\sum _{i<j}{\mathbf{u}}_{ij}{v}_{ij}=\sum _{i<j}{\mathbf{u}}_{ij}(C_i-C_j)=\sum _{i<j}{\mathbf{u}}_{ij}{C}_i-\sum _{j<i}{\mathbf{u}}_{ji}{C}_i\\ =\sum _{i<j}{\mathbf{u}}_{ij}{C}_i+\sum _{j<i}{\mathbf{u}}_{ij}{C}_i=\sum _{i=1}^n\sum _{j=1}^n{\mathbf{u}}_{ij}{C}_i=n\sum _{i=1}^n{\overline{\mathbf{u}}}_i{C}_i.\end{array}$$

As a result, U can be rewritten as $\frac{2}{n-1}{\sum }_{i=1}^n{\overline{\mathbf{u}}}_i{C}_i$ for the population-based study. For a family-based study, recall that there are S sibships and s_k siblings in the k-th sibship. The U can be written as $\frac{2}{n-1}{\sum }_{k=1}^S{\sum }_{i=1}^{s_k}{\overline{\mathbf{u}}}_{d_k(i)}{C}_{d_k(i)}$.

Appendix C. Calculation of Covariance

We sketch the calculation of the covariance of C d_k(i)and C d_k(j)in the case where both parental genotypes are observed. Recall that the distribution is under the null hypothesis and conditional on the parental marker alleles and trait values.

¿ From the definition, we can write the covariance of Cd_k(i) and Cd_k(j) as

$$\sum _g\sum _{g^{\prime }}{C}_i(g)C_j(g^{\prime })P(g_i=g,g_j=g^{\prime })-\sum _g{C}_i(g)P(g_i=g)\sum _{g^{\prime }}{C}_j(g^{\prime })P(g_j=g^{\prime }),$$

where Σ_g denotes the sum over all offspring genotypes that are possible in the family, g_i is the i-th individual’s genotype, and P (g_i = g) is the conditional probability under the null hypothesis.

What remains is to derive the probability P(g_j = g) and the joint probability P(g_i = g, g_j = g′), which are displayed in Table 5.

When parents are missing, the general idea is similar but the calculation is more tedious.

Appendix D. Proof of Theorem 1

Proof. In order to prove the assertion of Theorem 1, it suffices to show that ${\mathbf{v}}^{\prime }\mathbf{A}(n)\mid \mathbf{T}=\mathbf{t}\stackrel{d}{\to }N(0,{\mathbf{v}}^{\prime }{\mathbf{V}}_A(\mathbf{t})\mathbf{v})$, for any constant vector v of p elements. (4)

Without loss of generality, we can rearrange the index i such that the subjects from the same family have the consecutive index numbers. With this rearrangement, conditional on T = t, the sequence A₁, A₂,... is a m₀-dependent sequence of random vectors. That is, A_i and A_i+m₀+1 are independent for any i. Recall that m0 is defined in Theorem 1 as the maximum size of all families in a family study, and it is 1 for a population study. Denote ξ_i = v′A_i − E(v′A_i|T = t), then ξ₁, ξ₂,... is a m₀-dependent sequence of random variables, conditional on T = t. Furthermore, ${\sum }_{i=1}^n{\xi }_i={\mathbf{v}}^{\prime }\mathbf{A}(n)$ since E(v′A(n)|T = t) = 0.

Now we check the assumptions of Theorem 6.6 in Bergstrom (1970) to prove (4). First, E(ξ_i|T = t) = 0. Second, the boundedness of the sequence C₁, C₂,... implies that $E({\xi }_i^2\mid \mathbf{T}=\mathbf{t})<\infty$ and that the conditions B̂ and C in Bergstrom (1970) are satisfied. Third, under the assumption of Var(A(n)|T = t) → V_A(t), it follows that

$$E\left[\sum _{i=1}^n{\xi }_i^2\mid \mathbf{T}=\mathbf{t}\right]\to {\mathbf{v}}^{\prime }{\mathbf{V}}_A(t)\mathbf{v}.$$

Thus (4) holds by applying Theorem 6.6 in Bergstrom (1970) to the m₀-dependent sequence ξ₁, ξ₂,....