Using patient data similarities to predict radiation pneumonitis via a self-organizing map

Abstract

This work investigates the use of the self-organizing map (SOM) technique for predicting lung radiation pneumonitis (RP) risk. SOM is an effective method for projecting and visualizing high-dimensional data in a low-dimensional space (map). By projecting patients with similar data (dose and non-dose factors) onto the same region of the map, commonalities in their outcomes can be visualized and categorized. Once built, the SOM may be used to predict pneumonitis risk by identifying the region of the map that is most similar to a patient’s characteristics. Two SOM models were developed from a database of 219 lung cancer patients treated with radiation therapy (34 clinically diagnosed with Grade 2+ pneumonitis). The models were: SOM_all built from all dose and non-dose factors and, for comparison, SOM_dose built from dose factors alone. Both models were tested using ten-fold cross validation and Receiver Operating Characteristics (ROC) analysis. Models SOM_all and SOM_dose yielded ten-fold cross-validated ROC areas of 0.73 (sensitivity/specificity = 71%/68%) and 0.67 (sensitivity/specificity = 63%/66%), respectively. The significant difference between the cross-validated ROC areas of these two models (p < 0.05) implies that non-dose features add important information toward predicting RP risk. Among the input features selected by model SOM_all, the two with highest impact for increasing RP risk were: (a) higher mean lung dose and (b) chemotherapy prior to radiation therapy. The SOM model developed here may not be extrapolated to treatment techniques outside that used in our database, such as several-field lung intensity modulated radiation therapy or gated radiation therapy.

1. Introduction

Lung radiation pneumonitis (RP) is one of the major toxicities experienced by cancer patients receiving thoracic radiation therapy (RT) (Kocak et al 2005a). It occurs in approximately 13–37% of patients who undergo radiotherapy for lung cancer (Rodrigues et al 2004). Identification of factors that predict for the incidence of RP is important for reducing its probability of occurrence. For example, should adjuvant chemotherapy be identified as a risk factor, then alteration of chemotherapy regimens can be considered to reduce RP incidence.

Various predictors have been identified to predict the risk of RP (Rodrigues et al 2004). Three such predictors, derived from the lung dose–volume histogram, are frequently reported to be significantly correlated with RP: V_x, the volume above x Gy, for example V₂₀ (Kong et al 2006, Tsujino et al 2006, 2003, Chang et al 2006, Rancatiet al 2003, Jenkinset al 2003, Moiseenko et al 2003) and V₁₅ (Tsujino et al 2006, Schallenkamp et al 2007), mean lung dose (MLD) (Kong et al 2006, Chang et al 2006, Graham et al 1999, Jenkins et al 2003, Hernando et al 2001, Martel et al 1994, Kwa et al 1998, Theuws et al 1998b) and the Lyman (1985) normal tissue complication probability (NTCP) (Kong et al 2006, Tsujino et al 2006, Hernando et al 2001, Seppenwoolde et al 2003,Marks et al 1997). These predictors, while important for understanding the causes of RP, generally only have poor-to-fair predictive ability (Rodrigues et al 2004).

Dose factors alone may not be ideal predictors (Marks 2002). Non-dose factors such as age, gender, tumor location, chemotherapy, etc, although nonsignificant by themselves, could likely contribute significantly when combined with other dose and non-dose factors in a multivariate model. This synergestic enhancement of predictive capability is suggested by the findings in Marks et al (1997), who reported that the correlation of Lyman NTCP and V₃₀ with RP improved when patients with the poorest pre-RT pulmonary function were excluded. In a similar vein, Lind et al (2006) reported that the correlation of V₂₀ with RP was greater in patients younger than 55 years of age. This appears to warrant a predictive model that is somehow capable of discerning and quantifying these interactions. For example, Das et al (2007) developed a decision tree model to predict the risk of RP, and demonstrated that the model including non-dose factors is superior to that using dose factors alone. The aim of this work is to develop and test an RP predictor based on self-organizing maps (SOM) (Kohonen 1995), a technique that is potentially capable of extracting and quantifying the underlying synergistic interactions.

SOM is a type of artificial neural network that is trained using unsupervised leaning, capable of projecting and visualizing high-dimensional data in a low-dimensional space (Kohonen 1995). The SOM technique clusters and classifies patients into neurons based on similarities in the patient input data, unlike other techniques which additionally take patient outcomes into consideration. By searching for data similarities, the SOM is capable of extracting synergistic interactions between factors that are more powerfully predictive than the individual factors (Guyon and Elisseeff 2003). SOM has been previously applied in medicine (e.g. computer-aided detection of breast cancer (Markey et al 2003, Chen et al 2000)). To the best of our knowledge, SOM has never been applied to predict the risk of radiation pneumonitis.

In this work, the SOM model was built with input features selected from the total available set of factors, using a unique methodology. Predictive capability of the model was realistically tested using ten-fold cross validation (Hastie et al 2002). The effect of non-dose variables on predictive capability was assessed by comparing the SOM model built from dose alone to that including non-dose factors. Model comparison used receiver operating characteristic (ROC) curves (Das et al 2005, Lind et al 2002, Swets and Pickett 1982). Lastly, the importance of individual input features in the SOM model was evaluated.

2. Materials and methods

2.1. Input data

The patient database used in this study was previously described by Kocak et al (2005b). The database consists of 235 patients with lung cancer who received three-dimensional conformal, external-beam RT at Duke University Medical Center on an Institutional Review Board approved protocol (protocol title: prospective study of the influence of external beam radiation on pulmonary function (whole organ and regional) with radiographic correlations; protocol number: IRB 1698). Table 1 lists the patient and treatment characteristics. The patient population in this database was treated with RT delivered via parallel opposed anterior–posterior fields, followed by off-cord oblique fields. Most patients (70%) were treated at 1.8–2.0 Gy/fraction, once daily. The remaining were treated at 1.25 Gy/fraction to the clinical target volume and 1.6 Gy/fraction to the gross volume, twice daily (minimum interval was 6 h between two fractions). Dose distributions were three-dimensionally computed based on computed tomography (CT) scans of patients in the treatment position. The left and right lungs were considered as a paired organ (excluding planning target volume).

Table 1.

Patient and treatment characteristics.

Characteristic	Percentage of all patients or mean (range)
Radiation pneumonitis	15.5
No radiation pneumonitis	84.5
Age (years)	64 (27–87)
Gender: male/female	54/56
Race: white/others	83/17
Pre-RT FEV1%	64 (15–127)
Pre-RT DLCO%	63 (11–129)
Fractionation: once/twice daily	70/30
RT dose (Gy)
Once daily treatment	63.0 (30.0–86.4)
Twice daily treatment	72.3 (45.0–86.4)
Histological type
SCLC	11
NSCLC (squamous/adeno/other)	88 (27/19/42)
Other	1
Tumor stage
I–II	17
III–IV	81
Recurrent	2
Tumor location
Central/peripheral	61/39
Upper/lower/middle	60/22/18
Right/left location	58/42
Chemotherapy schedule (relative to RT)
Concurrent with RT	14
Pre-RT	48
Pre-RT + concurrent RT	6
Concurrent RT+ post-RT	3
Post-RT	1
No chemotherapy	28

SCLC, small cell lung cancer; NSCLC, non-small cell lung cancer; FEV1, forced expiratory volume in 1 second; DLCO, diffusion capacity of carbon monoxide.

Radiation-induced symptomatic pneumonitis was assessed at 1, 3 and then every 3–4 months post-RT. Based on the modified National Cancer Institute Common Toxicity Criteria (NCICTC) (table 2), pneumonitis was graded from 0 to 4. These NCICTC criteria are similar to the Southwestern Oncology Group (SWOG) toxicity criteria (Green and Weiss 1992) (table 2), often used in other studies (Kwa et al 1998, Seppenwoolde et al 2003). The toxicity endpoint of this study, Grade 2+ pneumonitis, is equivalent in both sets of criteria. Of the 235 patients in this analysis, 37 and 13 patients experienced Grade 2 and Grade 3 RP, respectively, and none experienced Grade 4 RP. Among patients with Grade 2 RP, 16 patients were classified as ‘hard-to-score’ due to uncertain diagnosis (Kocak et al 2005a). For the purpose of this study, 34 patients (excluding hard-to-score patients) were considered as having contracted Grade 2+ pneumonitis.

Table 2.

Radiation pneumonitis grading system.

Grading system	Grade	Definition
The modified National	0	No increase in symptoms
Cancer Institue Common	1	Symptoms not requiring initiation or increase in steroids and/or oxygen
Toxicity Criteria (NCICTC)	2	Symptoms requiring initiation or increase in steroids
	3	Symptoms requiring oxygen
	4	Symptoms requiring assisted ventilation or causing death.
Southwest Oncology	1	Radiographic changes are observed but the symptoms do not require steroids
Group Toxicity Criteria	2	Requiring steroids
	3	Oxygen required
	4	Assisted ventilation is necessary
	5	Fatal

A large number of factors were extracted from the patient database, explained next. This large set comprised all factors that we believed might have potential to be selected as factors by the SOM. No preliminary prospective analysis was employed to include/exclude factors, since such an analysis may not necessarily identify factors that could be selected by the SOM as strongly synergistic with other factor(s) in the database.

A total of 27 non-dose factors (biological, clinical and other factors) were collected for each patient. These factors included race, age, gender, tumor stage, tumor location (central (mediastinal) or peripheral; upper, middle or lower lobe; right or left lung), chemotherapy schedule (none, pre-RT, concurrent, pre-RT and concurrent, post-RT or concurrent and post-RT), histology type (squamous cell, adenocarcinoma, non-small cell, small cell, large cell or other), surgery (yes versus no), once or twice daily RT, pre-RT FEV₁ (forced expiratory volume in 1 s), FEV₁% (as percentage of predicted normal), pre-RT DLCO (carbon monoxide diffusion capacity in lung) and pre-RTDLCO%(as percentage of predicted normal). FEV₁ and DLCO% were not collected for approximately 20% of patients. In accordance with statistical treatment of missing values (Hastie et al 2002, Setiono 2001), they were assigned the average of non-missing values.

The lung cumulative dose–volume histogram (DVH) was calculated for each patient, for a bin size of 2 Gy. The lung DVH was also reduced to the generalized equivalent uniform dose (EUD) (Niemierko 1999) with the equation

$$\text{EUD}={\left({\displaystyle \sum _i{\upsilon }_i{D}_i^a}/{\displaystyle \sum _i{\upsilon }_i}\right)}^{1/a},$$ (1)

where υ_i is the lung volume receiving dose D_i. EUDs were generated for the exponential parameter a ranging from 0.4 to 4, in increments of 0.1. Note that for a = 1, EUD is equivalent to MLD. In addition to the lung DVH and lung EUDs, the biological mean lung dose (NTD_mean) was also included as a factor. NTD_mean was calculated by normalizing the lung DVH to a fraction size of 2 Gy (Lebesque and Keus 1991):

$${\text{NTD}}_i=\frac{{\mathit{\text{nd}}}_i\{1+d_i/(\alpha /\beta )\}}{1+2/(\alpha /\beta )},$$ (2)

where n is the number of fractions, d_i is the dose per fraction for lung volume υ_i and α/β is the linear quadratic model parameter (assumed to be α/β = 3 Gy (Dubray et al 1995, Kwa et al 1998) in this study). Similar to the physical mean lung dose, the biological mean lung dose, NTD_mean, was calculated as

$${\text{NTD}}_{\text{mean}}={\displaystyle \sum _i{\upsilon }_i{\text{NTD}}_i}/{\displaystyle \sum _i{\upsilon }_i}.$$ (3)

Thus, the lung dose factors considered in this analysis were the DVH points, V_x (volume above x Gy), for x ranging from 6 Gy to 60 Gy in increments of 2 Gy, EUDs for the exponents a = 0.4 to 4 (increments of 0.1) and NTD_mean.

Luijk et al (2005) reported that the tolerance dose for early lung function damage also depends on the concomitant irradiation of the heart. Consequently, we included the mean dose received by the heart as a factor in this analysis.

2.2. Data partitioning for model creation and testing: cross validation

For small datasets, K-fold cross validation is the recommended method to assess the performance of a prediction model (Hastie et al 2002). In this technique, the data are randomly split into K approximately equal-sized groups. K − 1 groups (training data) are used to create (train) the model and the remaining group (cross-validation data) is used as a test to measure the performance of the prediction model. The procedure is repeated K times, with each group, in turn, serving as the cross-validation data. The typical choices of K are 5 or 10 (Hastie et al 2002). In this analysis, we chose ten-fold cross validation (K = 10).

2.3. Model creation and testing: self-organizing map

The basic idea behind the SOM is to construct a nonlinear transformation to project high-dimensional input data onto a low, often two-dimensional space, termed a feature map. This makes it particularly useful for patient data, i.e. since it is difficult to search for similarities in high dimensions, SOM provides a ‘collapsed’ view that is easier to interpret. The disadvantage of SOM is that this reduction from high to low dimensions might also inadvertently conceal similarities that exist in high dimensions. In this work, similar patient input vectors in the higher dimensional input space were clustered into the same region or neuron of the feature map. The entries in the input vector, termed features, are a subset of all available factors. The algorithm for selection of input features is detailed later in this section. For example, if the input features constituting the input vector are ‘a’ and ‘b’, patients with similar values of a and b were clustered into the same region (neuron). Each neuron in the map contains two parts of information. The first part is its relative physical location, i.e. proximity to other neurons, and the second part is its reference vector or weight vector, which can be thought of as the ‘typical’ feature values for that neuron.

During the course of SOM training, patients were assigned to neurons with reference vectors most similar to the patient input vector. Following each such patient assignment, the reference vector of the assigned neuron and its immediate neighboring neurons were updated to reflect the change to the patient population at the neuron. The neighboring neurons were identified as neurons whose distances to the assigned neuron were less than the neighborhood distance (nd). The neighborhood distance (nd) decreased from a large number to 0 during training, such that the neighborhood neurons included all neurons at the beginning and only the assigned neuron at the end. The learning rate (lr) determined the amount of information passed from the patient input vector to the assigned neuron, which decreased from 1 to 0 during training. Similarity was judged by the Euclidean distance between a patient input vector and the neuron reference vector (a smaller distance implies greater similarity). Since SOM is an unsupervised learning method, patients were assigned to each neuron without knowledge of their toxicity classification (RP versus no RP). The training algorithm for SOM with M neurons is briefly summarized by the following steps:

1. Initialize the reference vector of each neuron to random values, and set the initial neighborhood distance (nd) and initial learning rate (lr).

2. for i = 1 to N (N is the number of patients used to train SOM)

   1. Randomly select one unused patient (input vector x).

   2. for j = 1 to M, calculate the Euclidean distance (d_j ) between the patient and the reference vector for neuron j (w_j ), d_j = ‖x − wj ‖.

   3. Determine the best matching neuron o with the minimal distance, $d_o=\underset{j=1:M}{\text{min}}(d_j)$.

   4. for j = 1 to M, update the reference vector of the neuron j : w_j → w_j + lr · f (d_oj) · (x − w_j)

      $$f(d_{\mathit{\text{oj}}})=\{\begin{array}{l}1,d_{\mathit{\text{oj}}}=0\\ 0.5,0<d_{\mathit{\text{oj}}}\le \mathit{\text{nd}}\\ 0,d_{\mathit{\text{oj}}}>\mathit{\text{nd}},\end{array}$$

      where d_oj is the Euclidean distance between neuron j and the best matching neuron o.

   5. Decrease the neighborhood distance (nd) and the learning rate (lr):nd = nd − Δnd, and lr = lr − Δlr.

3. Repeat step 2 until convergence.

The default values of SOM toolbox in MATLAB (Math Works, Inc., Natick, MA) were used for the initial neighborhood distance (nd), the initial learning rate (lr), step Δnd and step Δlr.

Input features were selected from the list of 93 dose and non-dose factors by a trial addition/substitution process, as follows. In the ten-fold cross-validation scheme described in the previous subsection, nine groups of data were used to train the SOM. To optimally select the input features, the SOM was trained (MATLAB, The Math Works, Inc., Natick, MA) using eight of the nine training groups and then evaluated on the remaining training group by ROC analysis (greater model accuracy implies a higher area under the ROC curve, which plots sensitivity versus 1-specificity for varying values of the threshold separating cases with and without RP (Swets and Pickett 1982)). The eight training groups used to build the SOM were collectively termed the training-construction set, and the one training group used for evaluation was termed the training-evaluation set. This evaluation process was internal to the training group and only served to build the list of selected features, i.e. it was not used as an unbiased test of SOM performance. The added or substituted factor was accepted as an input feature if the area under the training-evaluation ROC curve increased. SOM construction was stopped if no new factor was accepted as an input feature. To prevent the selection of multiple highly correlated dose factors as features, the SOM disallowed selection of any dose factor having correlation >0.95 with any of the already selected features.

Once the SOM was trained, the probability of RP at every neuron was computed as

$$P=\frac{N_p}{N_n+N_p},$$ (4)

where N_n and N_p are the numbers of patients suffering RP and not suffering RP, respectively, at that neuron. For prospective use (i.e. to predict the risk of RP for patients outside the database used to build the SOM), the SOM-predicted risk of a patient suffering RP is the probability associated with the closest matched neuron (neuron most resembling the patient).

Unbiased testing of the SOM followed construction, wherein each test group was evaluated using the SOM built from the training set. Since each of the ten patient groups sequentially served as the test group, ten SOMs were built for the purpose of unbiased testing. The combined results of all ten test groups were then analyzed to evaluate SOM predictive ability using the metrics: area under the ROC curve (AUC), sensitivity and specificity.

2.4. Model comparison and evaluation of importance of input features

To evaluate the influence of non-dose factors in modeling the risk of RP, two SOM models were built: SOM_dose and SOM_all, with input features selected from dose factors alone and all factors, respectively. ROCKIT software (Metz et al 1998) from the Department of Radiology, University of Chicago, was used to evaluate the statistical significance of the difference in areas between the ROC curves from the two models. Statistical significance was based on a univariate z-score test (null hypothesis: the datasets arose from binormal ROC curves with equal areas beneath them).

The importance of input features was evaluated in the SOM_all model by individual exclusion. Each time a feature was excluded from SOM_all, the model was retrained and tested. The cross-validated ROC area decrement resulting from feature exclusion was used to rank its importance: a larger decrement signifies a more important feature. Statistical significance of the feature was judged by statistical significance of the area decrement (ROCKIT (Metz et al 1998)).

3. Results and discussion

3.1. Model building

The optimal SOM configuration was chosen as a 4 × 3 neuron map after evaluating various configurations (see table 3). The AUC for training data continuously increases with increasing neurons, whereas the AUC for training-evaluation data decreases beyond 12 neurons (the 4 × 3 map). Training evaluation provides an effective way to avoid model under-training (model is not complex enough) or over-training (model is too complex—it fits the signal as well as the noise).

Table 3.

The area under the ROC curve (AUC) of models SOM_all and SOM_dose, for various SOM topologies.

	AUC of SOMall		AUC of SOMdose
Topology of SOM	Training construction	Training evaluation	Training construction	Training evaluation
3 × 2	0.76	0.67	0.72	0.63
3 × 3	0.81	0.73	0.78	0.66
4 × 3	0.85	0.82	0.82	0.74
4 × 4	0.87	0.78	0.85	0.72

The input features selected by models SOM_all and SOM_dose are shown in table 4. The table displays the input features selected by all ten of the SOMs used for cross validation (one SOM for each test set). Since the training data for each SOM is slightly different (two of nine groups are different for any two SOMs), the selected input features vary slightly between the SOMs. Statistical significance of the features selected by model SOM_all is discussed in the next subsection.

Table 4.

The input features selected by model SOM_all and SOM_dose. V_x is the lung volume above x Gy. Higher values of the dose variables are indicative of greater risk of radiation pneumonitis. Arrows next to the non-dose variables indicate higher (↑) or lower (↓) risk.

SOMall	SOMdose
EUD a = 0.9	EUD a = 0.7
EUD a = 1.0	EUD a = 0.8
EUD a = 1.1	EUD a = 0.9
Chemotherapy prior to RT (yes↑ versus no↓)	EUDa = 1.0
Histology (squamous cell↑ versus other histology↓)	V40
Tumor location (lower lobe↑ versus other location↓)	V42
	V44

For model SOM_all, the ten cross-validation SOMs selected three equivalent uniform doses (EUD) as input features, with exponents a = 0.9, 1.0 and 1.1. These three dose factors, while highly correlated to each other, were selected by different cross-validation SOMs, i.e. no two of these dose features were selected by the same cross-validation SOM. Since EUD a = 1 corresponds to MLD, the dose features selected by SOM_all can be approximately characterized as MLD. MLD frequently appears as a strong predictor of RP risk in the literature (Kong et al 2006, Chang et al 2006, Graham et al 1999, Jenkins et al 2003, Hernando et al 2001, Martel et al 1994, Kwa et al 1998, Theuws et al 1998b). For model SOM_dose, the ten cross-validated SOMs also selected EUDs similar to the MLD (exponents a = 0.7, 0.8, 0.9 and 1.0). Additionally, SOM_dose also selected three V_x values (x = 40, 42, 44 Gy). Again, no two EUD values or two V_x values with correlation >0.95 were selected by the same cross-validated SOM. (Note that the selected features did not change for dose bin sizes <2 Gy.) In the literature, V_x for x = 20, 30, 15 Gy, lower than those selected by SOM_dose, are reported as predictive for RP (Kong et al 2006, Tsujino et al 2006, Lind et al 2006, Chang et al 2006, Graham et al 1999, Tsujino et al 2003, Rancati et al 2003, Jenkins et al 2003, Moiseenko et al 2003). It is likely that SOM_dose selected volumes above higher doses to complement the relatively lower MLD dose. It is also likely that SOM_all, in contrast to SOM_dose, did not select V_x features because they are more weakly complementary than the non-dose features. The distinction between MLD and V_x features is that MLD summarizes the entire DVH curve, whereas V_x is a single point on the curve. The frequently reported correlation of V_x to RP may be because of the association of V_x with the entire DVH shape. It is probable that the relative diversity of treatments in our database decreased V_x’s association with the DVH shape.

The non-dose features selected by model SOM_all are chemotherapy prior to RT (yes versus no), histology (squamous cell versus other histology) and tumor location (lower lobe versus other location). Our results indicate that patients who underwent chemotherapy prior to RT are more likely to have RP. Chemotherapy schedule has been previously reported as associated with the occurrence of pneumonitis (Theuws et al 1998a, 1998b, McDonald et al 1995). McDonald et al (1995) reported that some chemotherapeutic drugs can not only induce lung injury such as pneumonitis, but also enhance radiation-induced lung injury. Tumor location (lower lobe) was found to be associated with increased risk of pneumonitis. This has also been noted in the literature (Graham et al 1999, Hope et al 2006, Yorke et al 2002). Mice experiments have also suggested that tumor location is correlated to RP (Liao et al 1995, Travis et al 1997). In our model, patients with squamous cell lung cancer have higher risk of suffering RP (however, its correlation is weak; see discussion in the next subsection). To the best of our knowledge, there have been no reports from outside our institution associating tumor histology with RP (Das et al (2007), from our institution, also report this association in a decision tree model).

3.2. Evaluation of feature importance

Table 4 lists the input features selected by model SOM_all. The importance of each feature, measured by the AUC decrement resulting from its exclusion, is summarized in table 5. The most important features are approximately equivalent to the MLD (EUD a = 0.9, 1.0 and 1.1). Excluding these features resulted in the largest AUC drop of 0.12, from 0.73 to 0.61 (p = 0.033). The second most important factor in our model, chemotherapy prior to radiotherapy, resulted in an AUC decrement of 0.09 (p = 0.041). Exclusion of tumor location or histology resulted in only small drops in the AUC (AUC decrement <0.01, p > 0.05). Because neither tumor location nor histology is individually highly correlated with RP, their statistical significance is low. It is, however, not surprising that a more sophisticated model such as SOM selects input features with weak univariate correlation, since a factor that is not useful by itself can provide significant performance improvement when taken with others (Guyon and Elisseeff 2003).

Table 5.

Evaluation of importance of input features by individual exclusion.

Input feature excluded	AUC decrement	p-Value
EUD a = 0.9, 1.0, 1.1	0.12	0.033
Chemotherapy prior to radiotherapy (yes or no)	0.09	0.041
Tumor position (lower lobe or not)	<0.01	0.166
Histology (squamous cell or not)	<0.01	0.236

3.3. Model testing and comparison

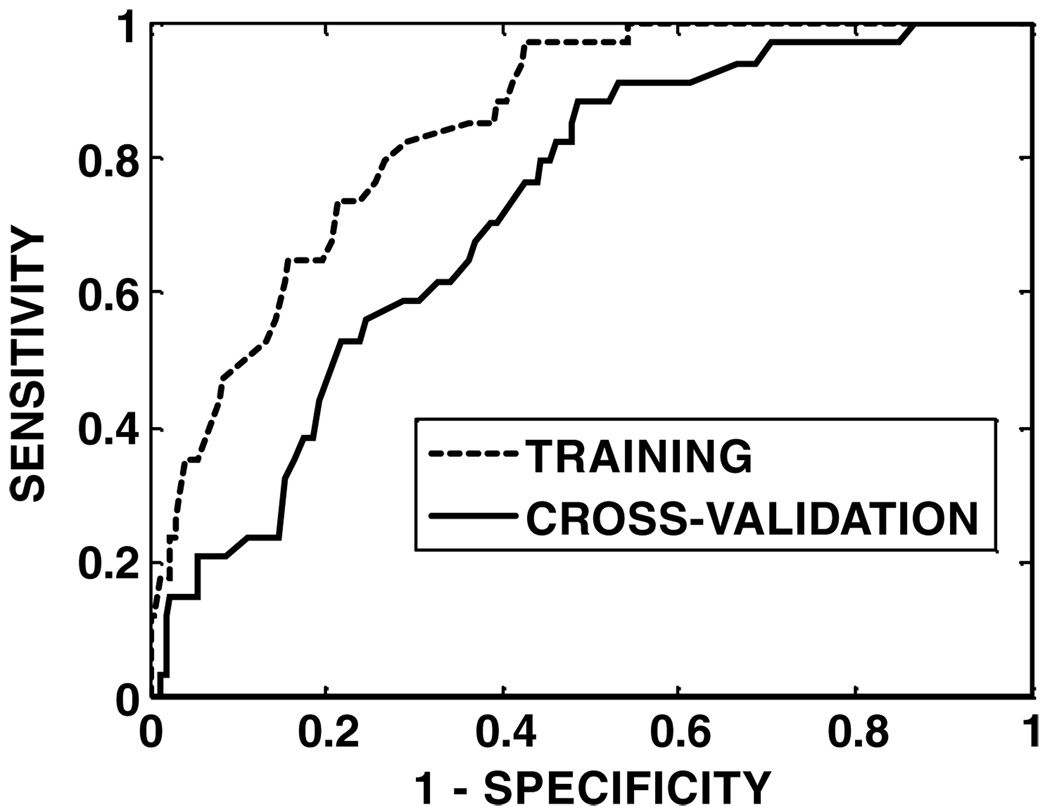
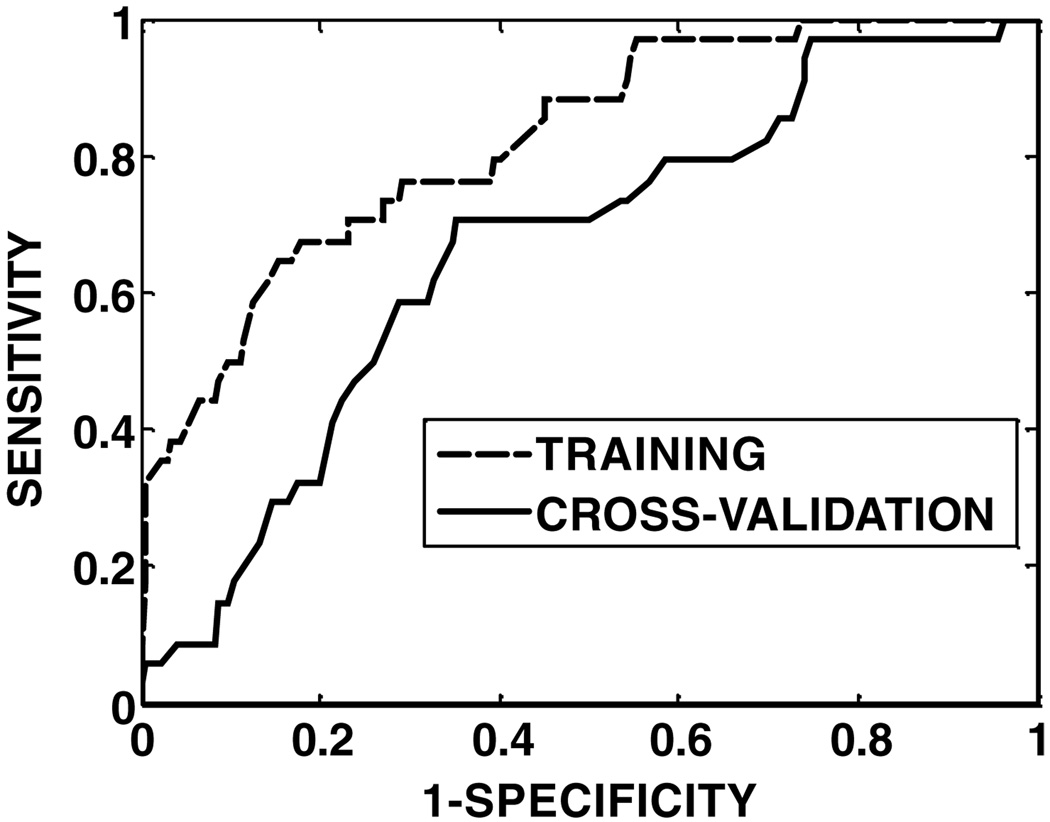
The cross-validated ROC curves are shown in figure 1 and figure 2 for models SOM_all and SOM_dose, respectively. The results of ROC analysis are shown in table 6. The AUC for training is notably lower than 1 because of the overfitting prevention resulting from the use of a training-evaluation set within the training set. The cross-validated AUC of model SOM_all (0.73) is higher than that of model SOM_dose (0.67), and the accuracy of model SOM_all (sensitivity: 71%, specificity: 68%) is better than that of model SOM_dose (sensitivity: 63%, specificity: 66%). The difference between the ROC areas from the two models was significant (p =0.048), indicating superiority of model SOM_all over model SOM_dose. Statistical significance also implies that the addition of non-dose factors improved the predictive ability of the SOM model.

Figure 1.

ROC curves for the model SVM_all on training (ROC area = 0.85) and cross-validation (ROC area = 0.73) data.

Figure 2.

ROC curves for the model SVM_dose on training (ROC area = 0.82) and cross-validation (ROC area = 0.67) data.

Table 6.

The results of ROC analysis for model SOM_all and SOM_dose.

		SOMall	SOMdose
Training	AUC	0.85	0.82
	Sensitivity	76%	71%
	Specificity	76%	74%
Cross validation	AUC	0.73	0.67
	Sensitivity	71%	63%
	Specificity	68%	66%

The combination of multiple dose factors and non-dose factors into a single predictive model follows from previous works that have indicated synergism between dose and non-dose factors (Marks et al 1997, Lind et al 2002, Das et al 2007, Rodrigues et al 2004). Rodrigues et al (2004) reviewed 12 refereed publications and 2 conference abstracts with regard to three dose predictors: V_x, MLD and NTCP. Their review indicated that, although these three factors are associated with RP risk, they do not have high predictive power. This review suggested that a model based on several factors may improve our ability to predict the risk of clinically relevant RP. Marks et al (1997) state that ‘the use of NTCP/DVHs and patient-specific biologic factors (e.g. PFTs) represent the state-of-the-art in predictive measures of post-RT whole-lung function’, indicating possible synergy between dose and non-dose factors. Previous studies from our institution have suggested that combining a dose–volume factor with a pulmonary function test factor was more predictive than a model based on dose–volume factors alone (Marks et al 1997, Lind et al 2002). Lind et al (2006) observed that the area under the ROC curve for predictor V₂₀ increased when the analysis was restricted to patients below 55 years of age.

3.4. Impact of data splitting on ten-fold cross-validation results

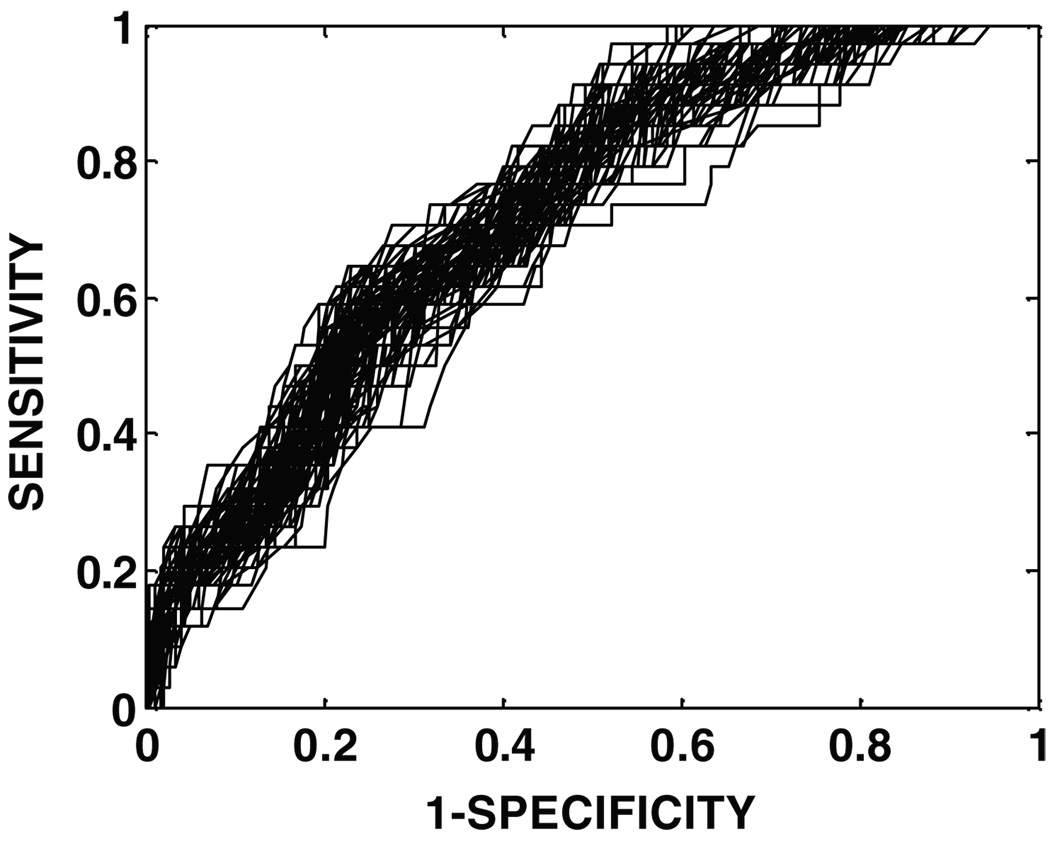
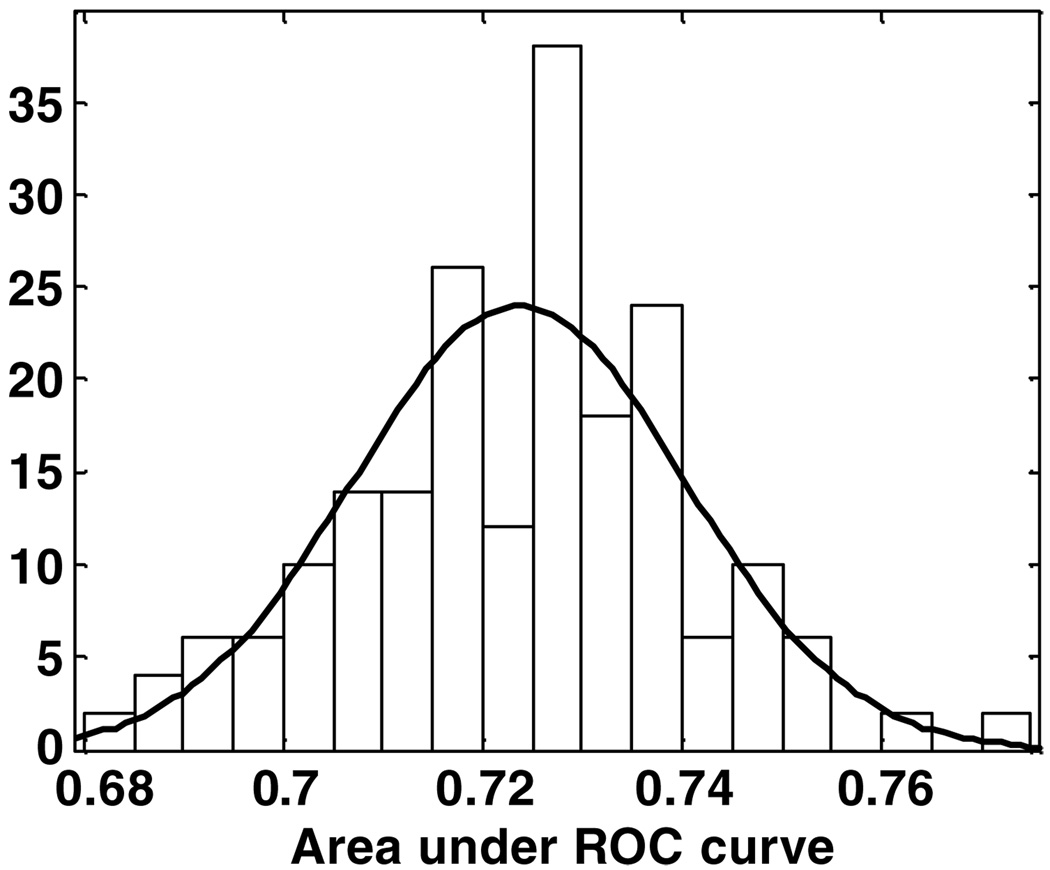
To evaluate the dependence of the cross-validated results on the assignment of patients to the ten groups, cross validation for SOM_all was run 200 times (each time, the data were randomly split ten-fold). The ROC curves for each of these 200 cross validations are shown superimposed in figure 3. The distribution of the areas under the 200 ROC curves is shown in figure 4 (mean = 0.724, standard deviation = 0.017). The small variance implies that the SOM_all model results are robust for ten-fold cross validation.

Figure 3.

The cross-validated ROC curves for model SVM_all, for 200 random splits of the ten cross-validation groups (area under ROC curves = 0.724 ± 0.017).

Figure 4.

The distribution of the areas under the cross-validated ROC curves, for model SVM_all, for 200 random splits of the ten cross-validation groups (mean = 0.724, standard deviation = 0.017).

3.5. Biological mean lung dose (NTD_mean)

The physical mean lung dose, MLD, does not take the effect of the dose per fraction into account. To gauge the impact of this effect in predicting RP, model SOM_all was run with ‘MLD’ (EUDs with exponents a = 0.9, 1.0 and 1.1) replaced by the biological mean lung dose, NTD_mean. The results with NTD_mean (cross-validated AUC: 0.72, sensitivity: 71%, specificity: 68%) were similar to those with ‘MLD’ (cross-validated AUC: 0.73, sensitivity: 68%, specificity: 71%). This would indicate that ‘MLD’ and NTD_mean may be considered as equivalent features in predicting RP.

3.6. Limitations on the applicability of the predictive model

The SOM model developed here to predict lung RP is only applicable within the scope imposed by the limitations of the database used to build the model (number and orientation of treatment fields, treatment field margins, total dose and fractionation). The database is limited to lung cancer patients who received radiation therapy via parallel opposed anterior-posterior fields followed by off-cord oblique fields. No gating technique was applied for reduction of margins. Approximately 70% of patients were treated once daily at 1.8–2.0 Gy per fraction, and the remaining were treated twice daily at 1.6 Gy per fraction. Therefore, for example, the SOM model may not necessarily be applicable to lung cancer patients receiving intensity-modulated radiation therapy (IMRT) from a larger number of fields, where much higher lung volumes are usually irradiated to low dose and lower lung volumes receive high dose.

4. Conclusion

The self-organizing map (SOM) technique appears to be an effective, robust predictor of lung radiation pneumonitis. The model (SOM_all) developed from all factors is superior to the model (SOM_dose) developed from dose factors alone. The addition of non-dose factors improved model predictive ability. Among the selected input features in model SOM_all, the two most important features contributing to increased radiation pneumonitis risk are: doses approximately equivalent to the mean lung dose and chemotherapy prior to radiotherapy. Since the SOM model was built from the database at our institution, it may be poorly extrapolated to treatment techniques outside that contained in the database.