Minimal Clinically Important Difference based on Clinical Judgment and Minimally Detectable Measurement Difference: A rationale for the SF-36 Physical Function scale in the SPORT Intervertebral Disc Herniation Cohort

Abstract

Design

A proof of concept case study.

Objective

To introduce and evaluate a method for identifying what constitutes a minimal clinically important difference (MCID) in the SF-36 Physical Function scale at the patient level.

Background

MCID has become increasingly important to researchers interested in evaluating patient care. Over the last 30 years, an array of approaches for assessing MCID has evolved with little consensus on which approach applies in any given situation.

Methods

Three approaches for estimating standard errors of measurement (s_e) and a 30% change approach for establishing MCID were evaluated for the PF scale with SPORT patients in the IDH cohort. MCIDs for each s_e approach were then developed based on 1) these standard errors and 2) clinically relevant factors including: a) baseline PF score, and b) acceptable risk for type I error.

Results

IDH patients (N=996) identified from the SPORT database met inclusion criteria. The s_e for the CTT-based test level approach was 9.66. CTT-score-level and IRT-pattern-level standard errors varied depending on the score, and ranged from (2.73–7.17) and (5.96–16.2), respectively. As predicted, CTT-score-level s_e values were much smaller than IRT-pattern-level s_e values at the extreme scores and IRT-pattern-level s_e values were slightly smaller than CTT score-level s_e values in the middle of the distribution. Across follow-up intervals, the CTT-score-based approach consistently demonstrated greater sensitivity for identifying patients who were Improved or Worsened. Comparisons of CTT-based-score-level s_e and 30% improvement rule MCID estimates were as hypothesized: MCID values for 30%-gains demonstrated substantially lower sensitivity to change for baseline PF scores in the 0–50 range but were similar to CTT-score-level-based MCIDs when baseline scores were above 50.

Conclusion

The CTT-based-score-level approach for establishing MCID based on the clinical relevance of the baseline PF score and the tolerance for erroneously accepting an observed change as reliable provided the more sensitive and theoretical compelling approach for estimating MCID at the patient level, which in turn will provide fundamentally important to the clinician regarding treatment efficacy at the patient level.

INTRODUCTION

When a body of research has reached a certain level of maturity, exhibited for the concept of Minimal Clinically Importance Difference (MCID) by a history of almost 30 years of study,^{1,2,3,4,5,6,7} but implementation and integration into the fields of study have generally not been very successful, there comes a time when researchers in the field need to question the viability of their endeavors. Perhaps the time has come to reframe the problem.

MCID has two basic components: 1) evaluation of the magnitude of change, for which a wide variety of options have been suggested; and 2) clinical implications or importance of that change, or lack there-of, which is dependent on treatment and timing issues related to both patient and/or clinician expectations. These clinical factors have not been systematically studied in conjunction with the evaluation of the magnitude of change. Further, the will to integrate these two concepts does not seem strong. The logical approach would be to disattenuate these two issues by calling the magnitude of change one thing and the clinical implications of change another.

Recently, Dhawn, et al ⁸ introduced the notion of minimally detectable measurement difference (MDMD) to describe what others have called standard errors of measurement-based approaches for assessing MCID.^9–11 The difference between MDMD and MCID is that MDMD simply seeks to determine if the change is reliable, meaning larger than can be explained due to measurement error. Education and psychology has a rich literature in this area generally under the key words “reliable change”.^12–14 In contrast, MCID attempts to determine if the change is “Important” or “Clinically Relevant.” Thus, MDMD or reliable change is a necessary but not a sufficient condition for establishing MCID.

The issue then becomes, what should constitute the criteria for determining if the change that is reliably measurable (MDMD) is also clinically important (MCID)? The proposed method of establishing MCID combines the notion of MDMD with the clinical relevance of a given change considering: 1) a patient factor (i.e., patient baseline level on the outcome of interest); and 2) a clinician judgment factor, namely the clinician’s risk tolerance for judging an observed change as clinically important when, in fact, it is not.

METHODS

Target Population

This study uses the SF-36 Physical Function score from SPORT patients diagnosed with an intervertebral disc herniation. The methods used to select this sample have been described in detail by Birkmeyer.¹⁵ Patients with complete scores at baseline, 6-week, 3-month, 6-month and 1-year follow-ups were evaluated.

The Standard Error of Measurement

The standard error of measurement is the index that estimates the consequence of the lack of perfect reliability within the metric of the survey score. Thus, it is important for the clinician to understand that: 1) all instruments come with a standard error particular to that population responding to the instrument; and 2) that error must be taken into account when interpreting the change in any given patient’s score.

Classical Test Theory (CTT) and Item Response Theory (IRT)-based Approaches

The CTT-based standard error of measurement for an instrument is defined by Equation 1:

$$s_{e-GL}=S_X\sqrt{1-r_{xx}}$$ Equation 1

where s_e-GL (GL = Group level) is the standard error of measurement for the survey instrument as a whole, or at the group level, based on classical test theory, r_XX is an estimate of the stability of the trait being assessed by the instrument, and S_X is the standard deviation of the scores obtained by administering the tool to a sample from the cohort of interest.

Although Equation 1 is the most commonly used definition of s_e, Standard 2.10 in the 1985 Standards for Educational and Psychological Testing calls for reporting standard errors at the score level.¹⁶ CTT-based score-level standard errors (s_e-SL) were computed using a modification of the Thorndike¹⁷ method proposed by Feldt and Qualls.¹⁸ The details of these procedures as applied to these data are provided in Appendix A.

In contrast, Item Response Theory (IRT) derives its standard error of measurement (s_e-IRT) from the pattern of responses across the items.¹⁹ Each unique pattern results in a unique standard error of measurement. Bjorner²⁰ provides a basic “clinician-friendly” primer for IRT within a medical context; a more extensive, but not overly mathematic, view is provided by Embreton.¹⁹

Estimating Physical Function and Standard Errors

CTT and IRT methods were each used to determine PF scores and the standard error of measurement associated with that score for the 10-item physical function subscale of the SF-36. Under CTT methods, the ability estimate was determined using the standard scoring algorithm from the SF-36 version 1.0. The standard deviation was estimated across baseline and all follow-ups and test-retest reliability was set at .89. The group level standard error was then computed using Equation 1.

Under IRT-methods the 2-parameter generalized partial credit model (G-PCM)²¹ was used to estimate each patient’s latent or underlying PF ability level (by convention symbolized by the Greek letter theta - θ) using Parscale 4.1.²¹ Thetas, which are arbitrarily scaled to have mean 0 and standard deviation 1, were linearly transformed to have the same mean and standard deviation as the CTT-based scores to facilitate comparison of IRT- and CTT-based ability estimates and standard errors of measurement. Person-level standard errors of measurement were estimated using the Bayesian EAP (expected a posteriori estimation) method.²² Readers who wish more details regarding IRT methods are referred to an article by Bjorner et al,²³ which provides a detailed summary of the polytomous IRT approach written for a clinical audience.

Defining and Estimating Minimally Detectable Measurement Difference (MDMD)

Charters and Feldt³² provide a compelling argument that establishing confidence intervals around the observed score X remains the most appropriate approach for evaluating the potential distinction between the observed score (X) and the underlying true score (T), though others have been suggested. ^24–31

In this study, the X of interest is the difference between the patient’s reported PF score atfollow-up and at baseline (Delta_PF = PF_Follow-up − PF_Baseline). Evaluating the magnitude of Delta_PF involves two steps:

1. Estimating the standard error of measurement for the observed PF scores using the three methods summarized above (i.e. s_e-GL, s_e-SL, and s_e-IRT denoting the standard error estimated by classical test theory at the group-level, by classical test theory conditioned at the score-level, and by item response theory, which produces estimates at the response pattern-level); and

2. Estimating the standard error of measurement for Delta_PF from Equation 2

   $$s_{e-D}=\sqrt{s_{eB}^2+s_{eF}^2-2r_{BF}{s}_{eB}{s}_{eF}}$$ Equation 2

   where s_e-D represents the standard error of measurement associated with the change score Delta_PF, S_eB and S_eF are the standard error of measurement at baseline and follow-up and r_BF is the Pearson correlation of baseline and follow-up scores for the population. Equation 2 applies to all three standard error of measurement estimates being evaluated.

From MDMD TO MCID: When is MDMD clinically relevant?

Evaluating clinical relevance requires simultaneously considering the nature of the scale and the importance of the observed clinical change for a particular patient. First, one needs to understand what change means on the instrument. In the case of the PF scale, the responses to the 10 3-choice items making up the scale are summed and then transformed to range from 0 to 100 by 5s. This means that the granularity of the rescaled PF scale is 5 points. In other words, a single change of one level on a single item will change the PF score by 5 points.

Second, one needs to understand the meaning of change relative to the precision of the instrument, which is reflected by the standard error of measurement. Since the granularity of the PF is 5, if the standard error of measurement is 10, then the granularity to s_e ratio (i.e., 5/10 or .5) provides a basic sensitivity scale. For this sensitive scale, values less than 1 are generally considered weak evidence for scale sensitivity, meaning that one unit of change on the scale (5 points on the PF scale) represents a small amount relative to the precision of the scale.

A Rational for Defining Clinical Importance

For the sake of simplicity, let’s limit our discussion to a patient’s baseline PF score. Average PF scores for surgical candidates for IDH at baseline typically range from 30–40.³³ In this IDH SPORT sample, the average baseline PF score was 35.8 with a standard deviation of 24.1. Such a high standard deviation indicates a great deal of variability in the sample. Thus, the mean score for the group may not be reflective the PF levels of many patients in the group.

Given the large variability in the sample, at the patient level a relatively large number of patients are likely to have low scores (0 – 25) and many will have high scores (85–100). At the patient level, the standard error of measurement can be thought of for a single patient’s score the same way that the standard deviation of the mean can be though of for a group’s average score. If the standard error of measurement is large, our confidence that the observed score for that patient is precise is low, if the error is small, our confidence that the observed score is precise is high.

For extreme scores (both low and high) it should be clinically interesting to detect any change at follow-up. For low and high scores, any worsening is likely to reflect important loss of function and any improvement likely to reflect important function gain. In the middle of the distribution, small changes are more likely to reflect multiple items changes with some items showing gain and others worsening. Thus, the importance of a small net gain or loss when PF scores are more in the middle of the distribution is more difficult to evaluation based on change alone. It is for this reason that score-level standard errors of measurement should be preferred relative to test level standard errors and IRT-base standard errors of measurement since theory dictates that group level standard errors of measurement are constant across all scores and IRT-based standard errors of measurement tend to be larger for extreme scores compared to scores in the middle of the distribution. In contrast, score-level standard errors of measurement in well constructed scales tend to display smaller standard errors of measurement for extreme scores compared to scores in the middle of the distribution.

From this logic, clinical importance for detecting change for extreme scores on the PF scale seems clear. A clinically important change is a function of the: 1) size of the change (Delta_PF), 2) standard error of measurement associated with the change (s_e-D) and 3) clinical importance of detecting change, which, here is defined by the baseline PF score. Again, considering the baseline PF score is important because, it is difficult know where you’re going if you don’t know where you started.

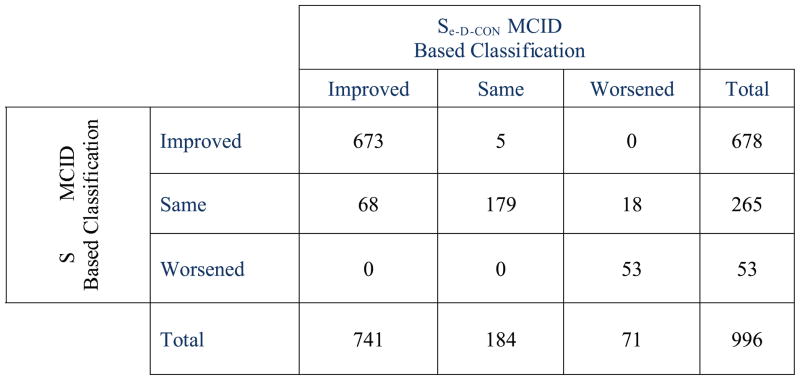
Figure 1 summarizes the different decision rules associated with making a clinical evaluation of whether or not Delta_PF is considered clinically important when baseline PF scores are in the 0–25, 30–80, or 85–100 range. When Delta_PF is positive and above the cut point the patient is judged to have demonstrated reliable and clinically important improvement. When DeltaPF is negative and below the cut point, the patient is judged to have demonstrated reliable and clinically important worsening. Otherwise, no reliable change has been demonstrated and the patient is judged to be the same.

Figure 1.

Summary of Cut Points for establishing MCID in the three PF scale ranges (0–25, 30–80, 85–100). In each Panel, if Delta_PF/s_e-D is less than the lower limit then that loss is considered clinically important. If Delta_PF/s_e-D is greater than the upper limit then that gain in PF is considered clinically important. The different cut points for the different baseline PF score ranges reflect different interpretations of the importance of change based on the patient’s starting point.

It is hypothesized that:

• 1. The s_e-SL based MCID approach will be more sensitive in classifying both Improvement and Worsening when baseline scores are near the extremes compared to either the s_e-GL and s_e-IRT approaches.

• 2. The se_-IRT-based MCID approach will be more sensitive in classifying both Improved and Worsening results when scores are near the center of the scale compared to the s_e-GL approach, but will demonstrate no greater sensitivity compared to the s_e-SL approach.

Implementing the 30% change rule at the patient level

The 30% change rule defines MCID as 30% change in the possible gain (for improvement) and 30% change in the possible loss (for worsening). Thus, for a PF baseline of 30, which has a possible gain of 70 points, the 30% rule would define MCID for improvement as 21 (i.e. .30 × 70) and MCID for worsening as 9 (.30 × 30). From this definition, improvement in low scores, where there is a lot of possible improvement will be associated with large MCID values (e.g., 30 points if PF at baseline is 0) improvement for large scores, where possible improvement is small, will be associated with small MCID values. Similarly, MCIDs will be small for low extreme scores and large for high extreme scores.

Based on this 30% gain rule approach for defining MCID, it is hypothesized that:

• 3. In comparison with the s_e-SL approach: the 30% change rule MCID estimates will be:

  1. Less sensitive in detecting improvement when baseline PF scores are low and worsening when baseline PF scores are high; and

  2. More sensitive in detecting improvement when baseline PF scores are high, and worsening when baseline PF scores are low.

RESULTS

Sample

A total of 1411 patients diagnosed with intervertebral disc herniations (IDH) were identified from SPORT. Of these, 996 patients had complete data at baseline and across all follow-ups. The average age was 53.6 with standard deviation 16.0, and ranged from 18 to 92 years of age. A little over half of the patients (50.2%) were female.

Comparing CTT- and IRT-based PF Scores

Pearson correlations between CTT- and IRT-based PF scores were .976, 981, .980, .980, .980 at baseline, 6-weeks, 3-Months, 6-Months, and 1-Year follow-up, respectively. Table 1 summarizes average CTT- and IRT-based PF scores as well as follow-up from baseline change scores at each follow-up interval. The pattern of results was quite similar for the CTT- and IRT-based scoring. Overall, change from baseline was statistically significant at each follow-up interval, but the large standard deviations for these change scores indicate that at the patient level change was quite variable, as clearly observed by noting the magnitudes of the minimum and maximum scores at each follow-up interval.

Table 1.

Summary statistics for the CTT- and IRT-Scaled PF scores from the SF-36 Version 1.0 across Assessment Times and the CTT- and IRT-based Change Scores from Baseline to Time of Follow-up Assessment

		CTT-Based Scoring				IRT-Based Scoring*
Assessment Time	N	Mean	SD	Min	Max	Mean	SD	Min	Max
Initial Visit	996	35.32	24.83	0	100	35.79	24.13	−7.40	110.68
6-Weeks	996	53.81	26.28	0	100	53.90	25.37	−7.40	110.68
3 Months	996	61.33	27.14	0	100	61.10	27.06	−7.40	110.68
6 Months	996	63.86	27.89	0	100	63.93	28.34	−7.40	110.68
1 Year	996	66.37	28.17	0	100	66.44	29.56	−7.40	110.68
Total	4980	56.23	29.13	0	100	56.23	29.13	−7.40	110.68
PF Change Score DeltaPF
6-Weeks - Baseline	996	18.48	26.60	−55	95	18.1	26.0	−63.3	108.6
13-Weeks - Baseline	996	26.00	29.20	−60	100	25.3	28.6	−53.7	118.1
26-Weeks - Baseline	996	28.53	29.99	−90	100	28.1	29.9	−95.6	118.1
52-Weeks - Baseline	996	31.04	30.50	−90	100	30.6	30.9	−92.3	118.1

^*Note that the linear transformation of the IRT-based scores to have the same mean and standard deviation as the CTT-base scores resulting in IRT-based scores where extreme values that could be less than 0 or more than 100

Estimating Standard Errors of Measurement

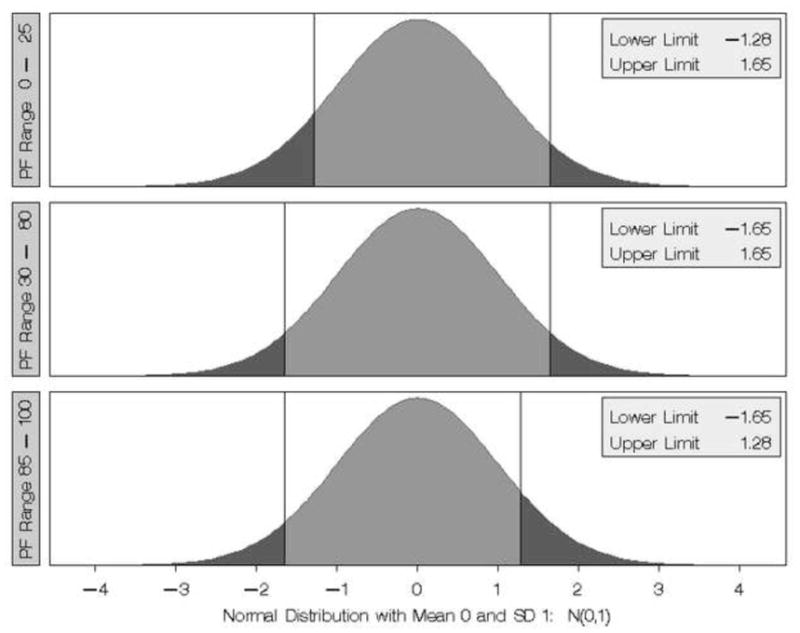
Figure 2 summarizes the s_e-GL, s_e-SL and s_e-IRT based standard errors of measurement. As required by Equation 1, the s_e-GL value is constant at 9.66 across all score levels, and as would be expected, the s_e-SL values are smaller at the extremes and somewhat larger in the center of the distribution and the s_e-IRT values are larger at the extremes and smaller in the center of the distribution.

Figure 2.

Summary of Standard Errors of Measurement using the classical test theory survey-level (s_e-GL) and conditioned on score-level (s_e-SL) and the item response theory (s_e-IRT) response-level Estimation defined as the inverse of the test characteristic curve.

Note 1. The differences in the s_e-SL and s_e-IRT differences in the middle of the distribution are much smaller than these differences at the extreme scores.

Note 2. The shaded areas reflect the score levels were the measurement error tolerances are different.

Stand Error of Measurement for the Difference in Two PF Scores

Estimating the standard error of measurement for a difference score requires some notion of the magnitude of the correlations between scores across time. The correlations summarized in Table 2 were used in conjunction with the baseline and follow-up standard errors of measurements (s_e-GL, s_e-SL, and s_e-IRT) to estimate s_e-D for each baseline to follow-up difference based on Equation 2.

Table 2.

Summary of Pearson Correlations Across Times of Assessment for the CTT- and IRT-based Physical Function Scores

	Time of Assessment
Time	Baseline	6-weeks	3 Months	6 Months	1 Year
Baseline		.46	.37	.36	.34
6-weeks	.45		.75	.66	.59
3 Months	38	.77		.79	.70
6 Months	36	68	.78		.77
1 Year	.35	.61	70	.77

Correlations in the unshaded cells for the CTT-based PF scores, shaded cells are correlations for the IRT-based PF scores

MCID Sensitivity

Table 3 summarizes MCID cut points for determining Improved or Worsened change relative to baseline PF score and time to follow-up for each of the three s_e approaches. Table 4 summarizes the percentages of patients classified as Improved, Same, or Worse from baseline to 1-year follow-up based on the s_e-GL s_e-SL and s_e-IRT methods with the same rules for establishing risk tolerance across the methods. The heavy lines in Table 4 serve as a reminder of the cut points where risk tolerance was adjusted to reflect the clinician’s notion of clinical importance. As depicted in Table 4, when using the s_e-SL approach, at 1-year follow-up 74.4% of the 996 patients demonstrated clinically relevant improvement, 18.5% no change and 7.1% clinically relevant worsening. Clinically relevant improvement ranged from 81.2–89.7% when baseline PF was 0–35, from 54.8–70.5% when baseline PF was 40–80, and from 40–53.3% when baseline PF was 85–100. Results for the 6-week, 3-month and 6-month follow-ups were consistent with these 1-year follow-up results (data not presented).

Table 3.

Summary of MCID Cut Points for defining Clinically Important Differences (Improvement and Worsening) based on Baseline PF Score and the Length of Time to Follow-up

	6 Weeks						3 Months						6 Months						One Year
Baseline PF Score	Standard Error of Measurement Method						Standard Error of Measurement Method						Standard Error of Measurement Method						Standard Error of Measurement Method
	se-GL		se-SL		se-IRT		se-GL		se-SL		se-IRT		se-GL		se-SL		se-IRT		se-GL		se-SL		se-IRT
	I*	W	I	W	I	W	I	W	I	W	I	W	I	W	I	W	I	W	I	W	I	W	I	W
0	15	.	5	.	20	.	15	.	5	.	20	.	15	.	5	.	20	.	15	.	5	.	20	.
5	15	.	10	−5	15	.	15	.	10	−5	15	.	15	.	10	−5	20	.	15	.	10	−5	20	.
10	15	.	10	−5	15	.	15	.	10	−5	15	.	15	.	10	−5	15	.	15	.	10	−5	15	.
15	15	−15	10	−10	10	−15	15	−15	10	−10	15	−15	15	−15	10	−10	15	−15	15	−15	10	−10	15	−15
20	15	−15	10	−10	10	−10	15	−15	10	−10	10	−10	15	−15	10	−10	10	−10	15	−15	10	−10	10	−10
25	15	−15	10	−10	10	−10	15	−15	10	−10	10	−10	15	−15	10	−10	10	−10	15	−15	10	−10	10	−10
30	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15
35	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15
40	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15
45	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15
50	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15
55	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15
60	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15
65	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	15	−15
70	20	−20	10	−15	15	−15	20	−20	15	−15	15	−15	20	−20	15	−15	20	−15	20	−20	15	−15	20	−15
75	20	−20	10	−15	20	−15	20	−20	10	−15	20	−15	20	−20	10	−15	20	−15	20	−20	15	−15	.	−15
80	20	−20	10	−10	.	−15	20	−20	10	−15	.	−15	20	−20	10	−15	.	−15	20	−20	10	−15	.	−15
85	15	−20	5	−10	15	−15	15	−20	5	−10	.	−15	15	−20	10	−10	.	−20	15	−20	10	−15	.	−20
90	.	−20	5	−10	.	−20	.	−20	5	−10	.	−20	.	−20	5	−10	.	−20	.	−20	5	−10	.	−20
95	.	−20	5	−10	.	−20	.	−20	5	−10	.	−20	.	−20	5	−10	.	−20	.	−20	5	−10	.	−25
100	.	−20	.	−10	.	−25	.	−20	.	−10	.	−25	.	−20	.	−10	.	−30	.	−20	.	−10	.	−30

^*I = Improved, W = Worsened

MCID cut points in this table indicate that the difference from baseline to follow-up must be equal to or greater than the indicated score.

Blacked out boxed indicate that no cut point exists because the MCID value is larger than the score range remaining and shaded cells indicate the lowest MCID value.

Table 4.

Summary of the Number and Percentage of Patients Who Were Classified As Improved, The Same, Or Worse at 1 Year Compared To Baseline for the Three Standard Error Of Measurement Approaches Broken Down By Baseline PF Scores

Baseline PF Score	se-GL						se-SL						se-IRT
	Improved		Same		Worse		Improved		Same		Worse		Improved		Same		Worse
	N	Pct	N	Pct	N	Pct	N	Pct	N	Pct	N	Pct	N	Pct	N	Pct	N	Pct
0	52	80.0	13	20.0			57	87.7	8	12.3			53	81.5	12	18.5
5	52	80.0	13	20.0	.	.	57	87.7	6	9.2	2	3.1	57	86.4	9	13.6	.	.
10	65	77.4	19	22.6	.	.	70	83.3	7	8.3	7	8.3	60	76.9	14	18.0	4	5.1
15	68	87.2	9	11.5	1	1.3	70	89.7	7	9.0	1	1.3	63	81.8	13	16.9	1	1.3
20	55	75.3	15	20.6	3	4.1	62	84.9	7	9.6	4	5.5	57	77.0	13	17.6	4	5.4
25	64	82.1	14	18.0	.	.	67	85.9	10	12.8	1	1.3	63	80.8	15	19.2	.	.
30	54	78.3	13	18.8	2	2.9	56	81.2	10	14.5	3	4.4	48	76.2	13	20.6	2	3.2
35	50	71.4	17	24.3	3	4.3	57	81.4	10	14.3	3	4.3	58	78.4	13	17.6	3	4.1
40	34	57.6	20	33.9	5	8.5	37	62.7	16	27.1	6	10.2	45	65.2	21	30.4	3	4.4
45	29	58.0	21	42.0	.	.	33	66.0	16	32.0	1	2.0	31	57.4	20	37.0	3	5.6
50	22	56.4	14	35.9	3	7.7	24	61.5	10	25.6	5	12.8	27	60.0	12	26.7	6	13.3
55	29	48.3	27	45.0	4	6.7	35	58.3	18	30.0	7	11.7	22	53.7	16	39.0	3	7.3
60	28	63.6	16	36.4	.	.	31	70.5	11	25.0	2	4.6	31	59.6	18	34.6	3	5.8
65	20	47.6	15	35.7	7	16.7	23	54.8	10	23.8	9	21.4	22	55.0	12	30.0	6	15.0
70	13	43.3	16	53.3	1	3.3	19	63.3	8	26.7	3	10.0	13	54.2	7	29.2	4	16.7
75	5	20.0	17	68.0	3	12.0	14	56.0	7	28.0	4	16.0	12	36.4	18	54.6	3	9.1
80	2	13.3	10	66.7	3	20.0	9	60.0	3	20.0	3	20.0	2	11.8	12	70.6	3	17.7
85	7	36.8	9	47.4	3	15.8	8	42.1	6	31.6	5	26.3	8	50.0	6	37.5	2	12.5
90	.	.	15	100.0	.	.	8	53.3	6	40.0	1	6.7	5	35.7	9	64.3	.	.
95	.	.	8	80.0	2	20.0	4	40.0	3	30.0	3	30.0	1	10.0	7	70.0	2	20.0
100	.	.	5	83.3	1	16.7	.	.	5	83.3	1	16.7	.	.	5	83.3	1	16.7
All	649	65.2	306	30.7	41	4.1	741	74.4	184	18.5	71	7.1	678	68.1	265	26.6	53	5.3

Shaded cells denote the standard error of measurement approach that resulted in the highest identification of Improved or Worsened PF HRQOL Status from baseline.

Within the table the dark lines indicate the zones where different probability cut points were used to define MCID-based classifications of Improved, Same or Worsened, as specified in Figure 1.

Table 5 summarizes the consistency of classification, symmetry, and relative discrimination of the score-level and response-level standard error of measurement approaches for establishing MCID at all follow-up intervals. The weighted Kappa estimates were all quite high, and percent agreements were all above 84%. Not surprisingly, given the similarly of the weighted Kappa’s, the test for equal weighted Kappa’s across the four follow-up times was not significant, ${\chi }_3^2=4.58$, p < .21. On the other hand, Bowker’s symmetry index (Figure 3) was also quite high; indicating that although the two methods agreed much of the time, when there was disagreement, the pattern of disagreement was not similar across the two methods. The percent asymmetry index, which is designed to estimate the relative discrimination of the two approaches, indicates that when disagreements between the two methods were observed, the likelihood was that patients classified as Same by the IRT approach were more likely to be classified as either Improved or Worsened when using the s_e-SL approach.

Table 5.

Weighted Kappa Agreement and Symmetry of Disagreements for s_e-SL and s_e-IRT based MCID classifications of Improved, Same and Worse

Interval	Weighted Kappa*	95% CI	Pct Agreement	Bowker’s Symmetry**	df	p <	Pct Asymmetry*** CON > IRT
Baseline – 6-Weeks	0.883	0.860 – 0.906	90.3	46.54	3	0.0001	69.1
Baseline – 13-Weeks	0.875	0.849 – 0.901	90.6	55.46	3	0.0001	78.0
Baseline – 26-Weeks	0856	0.828 – 0.885	89.9	64.98	3	0.0001	80.2
Baseline – 52-Weeks	0.870	0.843 – 0.898	90.9	72.37	3	0.0001	89.1

^*Weighted Kappa using Fleiss-Cohen weights

^**Bowker’s Symmetry test evaluates for a differential distribution of off-diagonal counts in square cross-classification tables. In a consistency of response model, lack of symmetry indicates that disagreements tend to be more likely in a given direction. In this study the significant lack of symmetry in disagreements between s_e-SL and s_e-IRT based MDMD classifications of Improvement, Same or Worsening were reflective of the CTT-SL-based estimates being more aggressive, (i.e., more likely to detect a change in outcome from baseline.

^***

Pct Asymmetry for SL > IRT is computed by observing: 1) Total disagreements: the total number of disagreements and 2) the difference in the frequency of Same responses for the two approaches. Thus, from Figure 2, if there were 91 total off diagonal ratings (disagreements) and s_e-SL-based and s_e-IRT-based “Same” responses were 184 and 265, respectively, then

$$\text{PCT}\text{Asymmetry}\text{SL}>\text{IRT}=(265-184)/91=.891\text{or}89.1\%$$

Figure 3.

Cross Classification of S_e-D-SL with s_e-D-IRT based MCID estimates of Clinically Important change from Baseline at 1-Year Follow-up.

Table 6 summarizes the differences between the CTT-based score-level standard error approach for estimating MCID for improvement and for worsening vs. the 30% change rule.

Table 6.

Comparison of CTT-based score-level standard error of measurement and clinical relevance approach for MCID with the 30% change rule for Gains and Loss from baseline on PF Scores

					6-Week		3-Month		6-Month		1-Year
PFB	Possible Gain	Required Gain**	PFF*	30% MCID (PFF - PFB)	MCID	DELTA	MCID	DELTA	MCID	DELTA	MCID	DELTA
0	100	30.0	30	30	5	25	5	25	5	25	5	25
5	95	28.5	35	30	10	20	10	20	10	20	10	20
10	90	27.0	40	30	10	20	10	20	10	20	10	20
15	85	25.5	45	30	10	20	10	20	10	20	10	20
20	80	24.0	45	25	10	15	10	15	10	15	10	15
25	75	22.5	50	25	10	15	10	15	10	15	10	15
30	70	21.0	55	25	15	10	15	10	15	10	15	10
35	65	19.5	55	20	15	5	15	5	15	5	15	5
40	60	18.0	60	20	15	5	15	5	15	5	15	5
45	55	16.5	65	20	15	5	15	5	15	5	15	5
50	50	15.0	65	15	15	0	15	0	15	0	15	0
55	45	13.5	70	15	15	0	15	0	15	0	15	0
60	40	12.0	75	15	15	0	15	0	15	0	15	0
65	35	10.5	80	15	15	0	15	0	15	0	15	0
70	30	9.0	80	10	10	0	15	−5	15	−5	15	−5
75	25	7.5	85	10	10	0	10	0	10	0	15	−5
80	20	6.0	90	10	10	0	10	0	10	0	10	0
85	15	4.5	90	5	5	0	5	0	10	−5	10	−5
90	10	3.0	95	5	5	0	5	0	5	0	5	0
95	5	1.5	100	5	5	0	5	0	5	0	5	0
PFB	Possible Loss	Required Loss***	PFF*	30% MCID (PFF - PFB)	MCID	DELTA	MCID	DELTA	MCID	DELTA	MCID	DELTA
5	5	1.5	0	−5	−5	0	−5	0	−5	0	−5	0
10	10	3.0	5	−5	−5	0	−5	0	−5	0	−5	0
15	15	4.5	10	−5	−10	5	−10	5	−10	5	−10	5
20	20	6.0	10	−10	−10	0	−10	0	−10	0	−10	0
25	25	7.5	15	−10	−10	0	−10	0	−10	0	−10	0
30	30	9.0	20	−10	−15	5	−15	5	−15	5	−15	5
35	35	10.5	20	−15	−15	0	−15	0	−15	0	−15	0
40	40	12.0	25	−15	−15	0	−15	0	−15	0	−15	0
45	45	13.5	30	−15	−15	0	−15	0	−15	0	−15	0
50	50	15.0	35	−15	−15	0	−15	0	−15	0	−15	0
55	55	16.5	40	−15	−15	0	−15	0	−15	0	−15	0
60	60	18.0	45	−15	−15	0	−15	0	−15	0	−15	0
65	65	19.5	45	−20	−15	−5	−15	−5	−15	−5	−15	−5
70	70	21.0	45	−25	−15	−10	−15	−10	−15	−10	−15	−10
75	75	22.5	50	−25	−15	−10	−15	−10	−15	−10	−15	−10
80	80	24.0	55	−25	−10	−15	−15	−10	−15	−10	−15	−10
85	85	25.5	60	−25	−10	−15	−10	−15	−10	−15	−15	−10
90	90	27.0	60	−30	−10	−20	−10	−20	−10	−20	−10	−20
95	95	28.5	65	−30	−10	−20	−10	−20	−10	−20	−10	−20
100	100	30.0	70	−30	−10	−20	−10	−20	−10	−20	−10	−20

^*PF_F = the actual PF possible that is equal to or greater than the required Gain or less than or equal to the possible loss. Thus, for PF_B = 5, although the required gain by the 30% rule is to 6.5, the granularity of the PF scale (units of 5) dictates that the next possible PF_B score after 5 is 10.

^**Required Gain = .3 * Possible Gain. Thus for PF_B = 5 Required Gain = .3 * 5 = 1.5

^***Required Loss = .3 × Possible Loss. Thus for PF_B = 10, Required Loss = .3 * 10 = 3.0

Note 1. Shaded cells reflect a smaller MCID value (closer to zero) for the s_e-SL approach

Note 2 Cells with bolded numbers reflect a smaller MCID value for the 30% change rule

DISCUSSION

This study compared classical test theory and item response theory approaches for scoring the physical function (PF) scale of the SF-36 and found that both scoring approaches provided very similar results. The pattern of mean scores indicated that, on average, the patients reported initially large and then incremental improvement in physical function from baseline. These high correlations, similar distributions, and nearly identical point estimates (means) at each assessment, and similar change scores indicate that the interpretation of CTT- and IRT-based estimates of the SF-36 PF scales produced similar interpretations at the group level. However, the PF score standard deviations were large and at each time point, at least some patients reported PF scores of 0 and 100, which indicated a wide diversity of PF scores at the patient level at baseline and at each follow-up assessment.

Standard Error of Measurement Approaches

As clearly demonstrated in Figure 2, the expected patterns of results were consistent with theory. As expected, MCID values defining both Worsening and Improvement varied by baseline PF score and were typically smaller for the CTT score-level approach compared to the CTT group-level and the IRT response-level approach for extreme PF scores.

The hypothesis that the s_e-SL approach would be more sensitive to change at the extremes compared to the s_e-IRT approach, and that the s_e-IRT approach would be more sensitive to change when PF changes scores were nearer the middle compared to the s_e-SL approach was only partially supported. Overall, the s_e-SL approach was consistently more likely to identify more patients as Improved or as Worsened compared to the s_e-GL and s_e-IRT approaches regardless of the location of the PF score relative to its scale. When the s_e-IRT was as good as or better than the s_e-SL approach, the trend was for the baseline and follow-up PF scores to be near the center of the distribution.

Clinical Relevance Criteria

Tables 4 and 5 provide clear evidence of the effects that grouping baseline PF scores and specifying different probability cut points for estimating MCID. When applying the s_e-SL approach, the threshold for establishing MCID was a 5-point loss when baseline PF scores were 5 or 10, and a 5-point gain when baseline PF scores were 90 or 95, thus providing maximum sensitivity when making clinical judgments at these extremes. In contrast, demonstrating worsening for baseline PF scores of 5 or 10 or improvement when baseline PF scores were 90 or 95 was not possible when applying the s_e-GL or s_e-IRT approaches.

The 30% Change Rule

The differences between the CTT-based score-level standard error approach for estimating MCID with the 30% improvement criterion suggested by Dworkin et al ⁶ and Ostelo et al⁷ were generally as hypothesized. MCID values for 30%-gains demonstrated substantially lower sensitivity to change for baseline PF scores in the 0–50 range but were similar to CTT-score-level-based MCIDs when baseline scores were above 50. As expected, the reverse held true when evaluating the 30% loss rule: MCID values for 30%-losses demonstrated substantially lower sensitivity to change for baseline PF scores when at or above 50 but were similar to CTT-score-level-based MCIDs when baseline scores were below 50.

MCID values for gains clearly demonstrated substantially lower sensitivity to change in PF scores in the 0 – 50 range were 30% improvement MCID values range from 15 to 25. In comparison s_e-SL based MCIDs for PF scores at these levels were 5 or 10. The 30% Gain approach estimated MCID values continued to be larger than the score-level standard of error approach until Baselines PF scores reached 50. When baseline PF scores were 50–65, the two approaches for estimating MCID were similar. Contrary to expectation, the s_e-SL based MCIDs for PF scores generally continued to be smaller than for the 30% gain rule even when PF scores were 70 or greater. Only 6.25% (6/36) of the MCIDs were smaller for the 30% Gain rule, and in each case, the difference was 5 points, the smallest difference possible. The same pattern of results was observed when comparing the s_e-SL based MCID approach with the 30% loss rule.

The smaller MCID values based on the s_e-SL approach compared to the s_e-GL and s_e-IRT approach compares “apples to apples”. Based on the notion that smaller standard errors of measurement estimates will result in smaller MCID values, and therefore, greater sensitivity in identifying change, are the smaller MCID values necessarily better? In the few cases where the 30% change rule produced smaller MCID values compared to the s_e-SL approach, the argument against the 30% change rule seems obvious. Why would a clinician feel comfortable judging a change to be important when the change is thought to be no greater than would be expected due to measurement error? The argument that the generally smaller MCID values for observed for the s_e-SL approach represent a better way for estimating change depends on the clinician’ strength of belief that the cut points established for defining change reflected sound clinical judgment. As a new approach, the soundness of the suggested cut-scores provided in this paper are strictly theoretical and the validity of this framework can be evaluated empirically just as others may question the validity of a 30% gain rule as apposed to a 10%, 20% or even 50% rule.

Conditioning on Baseline

The clinical importance of change is undoubtedly related to a multitude of factors including, but not limited to: 1) patient baseline score; 2) individual factors associated with the patient such as age, gender, general health, health-related habits such as smoking, alcohol use, medications; and 3) personality factors such as their general mood or ability to comply with treatment requirements. Some would argue that baseline level might be a reasonable proxy for many of these factors. In fact, in the various SPORT papers, baseline status was often the single strongest predictor of follow-up performance. Furthermore, little if any research is currently available that provides a framework by which the clinician can integrate these various factors into a coherent and reproducible estimate of patient prognosis.

Limitations

Standard errors of measurement are instrument- and cohort-specific. The pattern of results observed for the PF scale in the IDH cohort may not hold for other scales (e.g, Bodily Pain, Oswestry) or with other cohorts (e.g., Degenerative Spondylolisthesis or Spinal Stenosis). As demonstrated in this study, for the PF scale within the IDH cohort, standard errors of measurement and, as a consequence, MDMD and MCID estimates, can vary depending on the:

1. location on the baseline score;

2. approach used to estimate the standard error of measurement;

3. The cut points established for indentifying sufficient change; and

4. time interval between the two scores being compared.

As a consequence, these study results are limited to the IDH cohort, the three methods of estimating s_e used in this study, the probability levels used to define MCID; and the time intervals from baseline specified (i.e., baseline to 6 weeks, 3 months, 6 months and 1 year).

Future Directions

Expansion of these methods to other scales commonly used for studying treatment efficacy and to the other two diagnostic cohorts enrolled in the SPORT trials would allow a first look at the possible generalizability of the s_e-SL approach for establishing MCID cut points across patient diagnostic categories.

Demonstrating that patient-level results based on MCID-related classification of patients change status (Worse, Same, Better) will provide more relevant guidance to the clinician when forming clinical judgments is an important next step. In these data, the average gain in PF from baseline to one year (from Table 1) was 31.04 with a standard deviation of 30.5 and change scores ranging from −90 to 100. Consider that these same data, interpreted at the patient-level, suggest a different picture. From Table 4 consider than when using the s_e-SL approach, overall 74.7% (741/996) showed improvement, 18.5% (184/996) no change and 7.1% (71/996) worsening. Furthermore, of the 50 patients whose baseline PF scores were high (85–100), 40% demonstrated improvement; of the 364 patients with baseline PF scores between 40–80, 62% demonstrated improvement; and of the 582 patients whose baseline PF scores were between 0–35, 85% demonstrated improvement. These results would suggest that, not withstanding the overall 75% improvement rate on the PF scale, the likelihood of patients experiencing this magnitude of success is not very likely if their baseline PF scores are already high. Which information provides the clinician and the patient with a better understanding of the possible treatment outcomes for a given patient, the group-level mean or the patient-level summary of Improved, Same, Worsened, broken down by baseline PF levels?

As for implementing this patient level approach into clinical practice, a subset of Table 3 just showing the s_e-SL results would be sufficient to allow the practicing clinician to estimate the MCID for any given IDH patient at 6-weeks, 3-Months, 6-Months or 1 year.

Conclusions

This study was undertaken as a proof of concept for using a standard error or measurement approach in conjunction with clinical judgment based on clinically relevant criteria known at baseline to establish a general approach for establishing MCID. CTT-based score-level standard errors of measurement in conjunction with cut score decisions based on the clinical relevance of the baseline PF score and the clinician’s risk tolerance provided a more sensitive approach for estimating MCID compared to the CTT-based group-level or the IRT-based pattern-level approaches. The computational rigor of this approach compared to a more simple approach such as defining MCID as a 30% change represents a poor choice as one is trading ease of use for lack of accuracy, especially when in estimating gain when baseline scores are above 50 or estimating loss when baseline scores are less than 50. The future of this approach depends on demonstrating the value added for clinical decision-making when patient level MCID information is used to help guide clinical decision making.

Key Points.

• Classical test theory (CTT) and Item Response Theory (IRT) scoring of the PF scale from the SF36 produced very similar results

• The CTT-based score-level standard error of measurement was superior than the CTT-based group-level and the IRT-based response-level approaches for estimating smaller minimally detectable measurement differences (MDMD), which in turn resulted in greater sensitivity in MCID for classifying patient’s change in PF scores as Improved, Same or Worse.

• Using the modified 30% gain approach for estimating MCID on the PF scale; resulted in substantially lower sensitivity to change for baseline PF scores in the 0–50 range but were similar to CTT-score-level-based MCIDs when baseline scores were above 50. As expected, the reverse held true when evaluating the 30% loss rule.

• Use of MCID to classify each patient as Improved, Same or Worse can lead to substantially different understandings of the potential outcomes associated with a given treatment when compared with the group average change.

Appendix A

Estimating Score-Level Standard Errors of Measurement using Classical Test Theory Computing CTT-based score level standard errors of measurement is a four-step process:

1. Create two ½ length parallel forms from then 10 items each with 3-choices PF scale

2. Compute the Part 1 and Part 2 means (X̄₁ and X̄₂) variances and internal consistency reliability estimates

3. Compute the conditional standard error of the sum of the two part tests, which will equal the value of the original 10 item PF scale using equation (3)

   $$s_{e-\mathit{CON}}=\sqrt{{[(S_{i1}-S_{i2})-({\overline{X}}_1-{\overline{X}}_2)]}^2}$$ (3)

4. Smooth the estimates using polynomial regression, regressing s_e-SL on PF, PF², and PF³.

Table A1 provides all of the information needed to estimate the s_e-SL based standard error of measurement and evaluate the credibility of the parallelism of part tests 1 and 2. The similarity in the part 1 and 2 means and standard deviations and coefficient alpha internal consistency reliability estimates along with the high Pearson correlation between the two scores were sufficient to consider these part tests as being reasonable parallel forms.

Table A1.

Summary statistics for the 10 item PF scale and the Part 1 and Part 2 parallel ½ forms of the scale used to estimate score-level standard errors of measurement

PF Scale Item No.	Content	Item Mean	Part 1	Part 2
PF1	Vigorous activities	1.43	1
PF2	Moderate activities	1.86		1
PF7	Walking more than a mile	1.93		2
PF6	Bending, kneeling or stooping	1.97	2
PF4	Climbing several flights of stairs	2.09	3
PF3	Lifting or carrying groceries	2.13		3
PF8	Walking several blocks	2.18		4
PF5	Climbing one flight of stairs	2.47	4
PF9	Walking one block	2.50	5
PF10	Bathing or dressing yourself	2.66		5
Mean Score* (1–3) scaling		21.23	10.46	10.76
SD (1–3) scaling		5.86	2.90	3.10
Mean (Rescaled**)		56.14	27.3	28.8
SD (Rescaled)		29.13	14.5	15.5
Test-Retest reliability r(xx)		.890
Coefficient Alpha Reliability		.926	.853	.862
Pearson Correlation of Part 1 & 2 r(Part1, Part2)			.889

^*The mean score indicated the average score in the group where the score is defined as the sum of the 10 PF items for the full text and the 5 items in each of the part tests.

^**Rescaled scores are when the 1–3 scores are transformed to the 0–100 scale such that 1 = 0, 2 = 50 and 3 = 100.

For example, a PF score of 55 could be split into two part tests 1 and 2 with part 1 score 25 and part 2 score 30. If the overall means of the part 1 and part 2 tests were 25.6 and 27.4, then by equation (3): s_e-SL = SQRT ([(25–30)−(27.3–28.8)]²) = SQRT(−3.5²) = 3.5.