Abstract
A biophysical, computational model of cell pharmacokinetics (1CellPK) is being developed to enable prediction of the intracellular accumulation and transcellular transport properties of small molecules using their calculated physicochemical properties as input. To test if 1CellPK can generate accurate, quantitative hypotheses and guide experimental analysis of the transcellular transport kinetics of small molecules, epithelial cells were grown on impermeable polyester membranes with cylindrical pores and chloroquine (CQ) was used as a transport probe. The effect of the number of pores and their diameter on transcellular transport of CQ was measured in apical-to-basolateral or basolateral-to-apical directions, at pH 7.4 and 6.5 in the donor compartment. Experimental and simulation results were consistent with a phospholipid bilayer-limited, passive diffusion transport mechanism. In experiments and 1CellPK simulations, intracellular CQ mass and the net rate of mass transport varied <2-fold although total pore area per cell varied >10-fold, so by normalizing the net rate of mass transport by the pore area available for transport, cell permeability on 3µm pore diameter membranes was more than an order of magnitude less than on 0.4µm pore diameter membranes. The results of simulations of transcellular transport were accurate for the first four hours of drug exposure, but those of CQ mass accumulation were accurate only for the first five minutes. Upon prolonged incubation, changes in cellular parameters such as lysosome pH rise, lysosome volume expansion, and nuclear shrinkage were associated with excess CQ accumulation. Based on the simulations, lysosome volume expansion alone can partly account for the measured, total intracellular CQ mass increase, while adding the intracellular binding of the protonated, ionized forms of CQ (as reflected in the measured partition coefficient of CQ in detergent-permeabilized cells at physiological pH) can further improve the intracellular CQ mass accumulation prediction.
Keywords: Systems Biology, Epithelial Cells, Membrane Transport, Mathematical Models, Pharmacokinetics, Cell Permeability
Introduction
The cell permeability of a small molecule (Pcell) is its rate of mass transport across an individual cell, as a function of the transcellular concentration gradient, normalized by the area over which transport occurs. Pcell is an important factor affecting the distribution of lipophilic nutrients (e.g. fat soluble vitamins), metabolites and signaling molecules (e.g. prostaglandins) inside and outside cells. Pcell can also influence the effects of lipophilic growth factors and morphogens (e.g. retinoids) affecting cell growth, differentiation, and motility. At the systemic level, Pcell can also affect the synthesis, uptake, distribution, metabolism and activity of lipophilic hormones (e.g. estrogen, testosterone), as well as that of xenobiotics and drugs.1 Several different molecular mechanisms may mediate transcellular mass transport including passive diffusion across membranes and protein channels, ATP-dependent transmembrane carriers and transporter proteins, paracellular transport, and vesicle-mediated transcytosis.2 Independently, the permeability of the matrix to which the cells are attached and the patterns - size and microscopic distribution of aqueous pores on this matrix - could affect the routes and rates of mass transport across cells.2
Here, we tested a biophysical model3, 4 by comparing simulation results and experimental measurements of the transcellular transport route of a small molecule under a variety of different conditions. Certainly, cell-substratum interactions can affect cell morphology, differentiation, gene expression and apoptosis,5–7 and can impose steric constraints to the passive diffusion of small lipophilic molecules. Hence, we took into account how cell monolayer architecture, as well as apical-to-basolateral (AP→BL) and basolateral-to-apical (BL→AP) transport routes, may be influenced by the porosity properties of the underlying polyester membrane film to which cells are attached. For transport experiments, a metabolically stable small molecule drug with high lipophilicity, high solubility and well-characterized subcellular transport properties (CQ) was selected as a probe. Varying extracellular pH in drug donor or acceptor compartments and performing detailed measurements using a wide range of concentrations and time points, we aimed to identify a domain of applicability and the limitations of the model. Our results help establish how a biophysical model like 1CellPK can be used to guide quantitative experimental analysis of transcellular transport properties of small molecules and to identify key mechanisms governing cellular pharmacokinetics, while pointing to practical applications and constraints of 1CellPK as a framework for computational ab initio prediction of drug ADME properties.
Materials and Methods
Confocal Microscopy of Cells on Pores
Madin-Darby canine kidney (MDCK) cells were purchased from ATCC (CCL-34™) and maintained in DMEM (Gibco 11995) plus 10% FBS (Gibco 10082), 1X non-essential amino acids (Gibco 11140) and 1% penicillin/streptomycin (Gibco 15140), at 37°C with 5% CO2. Transwell® inserts (12-well, pore size is 3µm or 0.4µm) were purchased from Corning Incorporated (Cat No. 3460 and 3462). For confocal microscopy, a Zeiss LSM 510 microscope (Carl Zeiss Inc.) was used for both membrane and cells imaging with a 60X water immersion objective. Inserts (with or without cells) were put directly in the wells of two-well Lab-Tek®II chamber #1.5 coverglasses (Nalge Nunc International Corp., Naperville, IL) for imaging. Cells were pre-stained with 5 µg/mL Hoechst 33342 (Molecular Probes H3570) for 30 minutes. LysoTracker® Green DND-26 (LTG, Molecular Probes L7526) and MitoTracker® Red (MTR, Molecular Probes M7512) were diluted with transport buffer (HBSS, 10mM HEPES, 25mM D-glucose, pH 7.4) to 2.5 µM and 1 µM respectively. The insert with cells was put onto the Lab-Tek®II chamber’s cover glass. 1.5 mL of diluted dyes solution was added into the chamber, and 0.5 mL of dyes free transport buffer was added into the apical compartment of the insert. After 10 minutes, the cells on the insert were imaged with the confocal microscope using enterprise laser (364 nm), argon laser (488 nm), helium neon 1 laser (543 nm) and the corresponding emission filters (BP 385–470, BP 505–530, and LP 560).
Polyester Membrane Permeability Analysis
Polyester membranes without pores were purchased from AR Brown-US (One Oxford Centre 301 Grant Street, Ste: 4300, Pittsburgh, PA) and glued on the 12-well Transwell® inserts using ELMER’s instant glue. Trypan blue was used to test the leakage of the edges. Transport experiments of CQ and LY (Lucifer yellow, Sigma L0144) were performed at 8 different initial concentrations ranging from 0 to 7500 µM.
Permeability Measurements of CQ on Membranes with MDCK Cells
Cells were seeded on Transwell® inserts (12-well, polyester membranes with 3µm or 0.4µm pores) with density at least 2×105 cells/cm2 for 1 or more days to form a monolayer. Transepithelial electrical resistance (TEER) values were measured both before and after transport experiments by Millipore Millicell® ERS. Cell monolayers were considered intact if both TEER values (background subtracted) were higher than 100 Ω·cm2. CQ diphosphate (Sigma C6628) was dissolved in transport buffer, HBSS (Sigma H1387) without phenol red and sodium bicarbonate, supplemented with 25 mM D-glucose (Sigma G7021) and buffered with either 10 mM HEPES (pH 7.4) or 10 mM MES (pH 6.5). Inserts with cell monolayers were washed with drug free transport buffer (pH 7.4) twice, and then incubated for 20 minutes with 0.5 mL/1.5 mL transport buffer in apical/basolateral compartment (pH 7.4/7.4) respectively. After measuring TEER values, 0.5 mL/1.5 mL of CQ solutions (concentration ranges from 0–10 mM, pH 7.4 or 6.5) was added into the apical/basolateral compartment and 1.5 mL/0.5 mL of drug free buffer (pH 7.4) was added into basolateral/apical compartment. 0.75 mL/0.4 mL of the donor solutions was taken out and replaced with the same volume of drug free transport buffer (pH 7.4) every 30 minutes. Transport experiments were performed at 37 °C with shaking. Transport experiments were ended at various time points (5 min to 4 hours) and both apical and basolateral solutions were collected for analyses. Every insert was washed twice with fresh buffer and TEER values were measured again. CQ concentration was determined with a standard curve, by absorbance measurement at 343 nm wavelength using a BioTek Synergy 2 plate reader (BioTek Instruments, Inc.).
Intracellular CQ Mass Measurements
Cells on membrane inserts were quickly washed with buffer and then lyzed 1% Triton X-100 in transport buffer (pH7.4, 1.5 mL) for 1.5 hours following 5 minutes to 4 hours CQ transport experiments in transwell inserts. CQ uptake was measured with 1mM concentration in the donor compartment The lysis solutions were centrifuged at 12,000 rpm for 8 minutes. CQ concentration was measured with the aid of a standard curve, by absorbance at 343 nm wavelength using BioTek Synergy 2 plate reader. To normalize the intracellular mass by the density of cells on membranes, cell counts were performed by staining the cells on inserts with Hoechst dye. Cells were then imaged by Nikon TE2000S epifluorescence microscope using a 20X objective at DAPI channel. At least five 12-bit images were taken for every insert. Cell counts were automated with an imaging algorithm programmed in Metamorph® software (Molecular Devices Corporation, Sunnyvale, CA).
CQ Binding Measurements
Inserts were incubated with 1 mM CQ (pH 6.5 and pH 7.4) for 4 hours. Then inserts were washed with buffer for twice and incubated with 1.5 mL 1% Triton X–100 for 1.5 hours. The solution was centrifuged at 12,000 rpm for 8 minutes and CQ absorbance in the supernatant was measured at 343 nm and the concentration established with a standard curve. In order to measure the binding of CQ to MDCK cells, cells were permeabilized with 60 µg/mL digitonin in HBSS-HEPES buffer (pH 7.4) or 1% Triton X–100 for 5 minutes on ice. Cells then were stained with trypan blue and checked under microscope to ensure that more than 95% cells were permeabilized with digitonin or Triton X–100 based on the appearance of stained nuclei. Cells were diluted with buffer and the same volume of CQ solutions (pH 7.4) were added into cell solutions. The mixture solutions of cells and CQ were incubated at 4°C for 4 hours. The cells were centrifuged at 12,000 rpm for 8 minutes and the supernatant’s CQ absorbance was measured at 343 nm. CQ concentration in the supernatant was then calculated with a standard curve. The difference of the initial CQ mass and the final CQ mass in the supernatant was used as a measure of CQ binding to cells.
Assessment of CQ Metabolism in MDCK Cells
A 1200 Series HPLC system (Agilent Technologies, Santa Clara, CA) coupled with a QTRAP 3200 mass spectrometer (Applied Biosystems, Foster City, CA) was employed for chemical analysis. Separation was performed on a Zorbax RX–C18 column (5 µm, 150 mm × 2.1 mm) (Agilent Technologies, Santa Clara, CA). The isocratic elution profile was 35% (v/v) of aqueous solution containing 5 mM ammonium acetate and 0.1% formic acid and 65% (v/v) of MeOH, maintained for 2.5 minutes. The flow rate was 1 mL/min and injection volume was 10 µL. An electrospray ionization source was used under positive ionization mode. Multiple reaction monitoring (MRM) scan was employed and ion transition is m/z 320.2→247.2. Data acquisition and processing were performed using Analyst® software (Applied Biosystems, Foster City, CA). To construct the linear calibration curves, the mixed working standard solutions at each concentration (0, 51, 102, 204, 408, 816, 1020 ng/mL) were injected in triplicate. A 30 minutes gradient elution (the percentage of MeOH increased from 10% to 90% in 16 minutes and then maintained at 90% for additional 4 minutes and dropped to 10% at 21 minutes and maintained at 10% for another 9 minutes) and a full scan (m/z 150–500) were used to detect any possible metabolites of CQ. The MS parameters for full scan were similar with those of MRM scan except that CE is decreased to 20 units. The product ions of protonated CQ at m/z 179.1 and 247.1 were selected as the daughter ions for two precursor scans to detect the possible metabolites which also generate a product ion at m/z 179.1 or 247.1 or both of them. The scan range is m/z 150–800 and CE is 51 units. All the other LC and MS parameters of precursor scans were the same as those of full scan. Furthermore, based on a literature search,8–10 34 previously reported biotransformation processes were considered for CQ, such as mono- (+16 Da), di- (+32 Da), trihydroxylation (or oxidation) (+48 Da), dehydrogenation (−2 Da) and oxidative dechlorination (−18 Da). The 4 most abundant product ions (m/z 247.1, 179.1, 142.2 and 86.1) of protonated CQ were selected to generate 272 MRM scan channels by using Metabolite ID software (Applied Biosystems, Foster City, CA). With this method, no significant metabolism was detected through any one of the 34 possible CQ biotransformation processes.
Modeling CQ Transport
In 1CellPK 3, 4 we modeled five compartments: apical, cytosol, mitochondria, lysosomes, and basolateral compartment. Simulations consider compartment volumes, pH, and membrane potential, and areas as constant. Equations 1–4 are the concentration changing over time in each compartment express by net fluxes (J).
| (1) |
| (2) |
| (3) |
| (4) |
In the above equations, C indicates the total concentration, J indicates the flux, A and V indicate the membrane surface area and volume respectively. The subscripts a, c, m, l, and b indicate apical compartment, cytosol, mitochondria, lysosomes, and basolateral compartment respectively. The directions of fluxes are indicated by the orders of the subscripts, e.g. Jc,m represents the flux from cytosol to mitochondria. Equation (1) to (4) expressed apical to basolateral transport. Basolateral to apical transport can be easily derived. A molecule with two ionizable groups can be an ampholyte, a diacid or a dibase. In the case of CQ, it is a bivalent base and the pKa values of the two ionizable groups are 7.47 and 9.96 calculated by ChemAxon®. Three main species exist in solutions with pH ranging from 0 to 14, the neutral form, ionized forms with one positive charge or two positive charges (Table 1). Thus the total flux across each membrane is contributed by those three species freely dissolved in solutions.
Table 1.
Calculated distribution and logP values for each microspecies of CQ at pH 6.5 and pH 7.4, used as input for 1CellPK. The numbers 7.47 and 9.96 correspond to the pKa values of the protonation sites of the molecule, calculated by ChemAxon®.
| Structure | calculated logP |
fraction at pH6.5 (%) |
fraction at pH7.4 (%) |
|---|---|---|---|
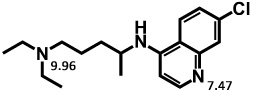 |
3.93 | 0.00 | 0.04 |
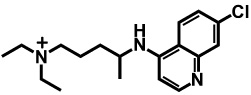 |
0.43 | 5.49 | 31.55 |
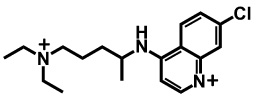 |
−0.91 | 94.49 | 68.33 |
Considering membrane permeation as the main rate limiting step governing the intracellular distribution and transcellular transport of CQ, mass transport across the membranes delimiting each compartment can be calculated with Fick’s equation and Nernst-Planck equation11:
| (5) |
where, subscripts o and i indicate outer- and inner- respectively. o could be a, b and c; i could be a, c, m, l, and b. Subscripts n, d1, and d2 indicate neutral form, ionized form with one charge, and ionized form with two charges, respectively. P represents the permeability across the bilayer membranes of each species and can be calculated from lipophilicity (logP) of that species 11, 12; f is the calculated activity coefficient of each species that can be calculated as described previously 11, 12; N = zEF/(RT), where z = +1 for Nd1 (ionized base with one charge), and z = +2 for Nd2 (ionized base with two charges); E, F, R, and T are membrane potential, Faraday constant, universal gas constant, and absolute temperature, respectively. Calculated CQ logP values are 3.93, 0.43, and −0.91 for the neutral form, ionized form with one charge, and ionized form with two charges, respectively (Table 1), as calculated by ChemAxon®. After plugging in all parameters on the right hand of equation (1) to (4), the ordinary differential equations can be numerically solved. Once the concentration in the receiver compartment is calculated, the permeability of one cell (Pcell) can be calculated with equation 6:
| (6) |
Where, Cr and Vr are the concentration in the receiver compartment and volume of the receiver compartment respectively; Apore is the pore area underneath one cell; and Cd is the initial concentration in the donor compartment. The effective permeability can be calculated by equation 7:
| (7) |
Where, cellNo is the total cell number per insert, and Ainsert is the total area per insert. Parameter sensitivity analysis was performed by varying each parameter and simulating CQ transport in AP → BL direction to calculate dM/dt, intracellular CQ mass, Papp, and Pcell (see Supporting Information).
Monte Carlo Simulations
Monte Carlo simulations were performed with MATLAB®. In 1CellPK the input parameters can be categorized into biological parameters and physicochemical parameters of the compounds. Physicochemical properties of CQ that used as input parameters are lipophilicity of neutral form and ionized forms with one or two charge (logPn, logPd1 and logPd2), and pKa values of two ionizable groups (pKa1 and pKa2). Biological parameters were apical membrane area (Aa), basolateral membrane area (Ab), cytosol membrane area (Am), lysosome membrane area (Al), cytosol volume (Vc), cytosol volume (Vm), lysosome volume (Vl), volume of the receiver compartment (Vb for AP → BL transport and Va for BL → AP transport), pH value in the donor compartment (pHa for AP → BL transport and pHb for BL → AP transport), pH value in the receive compartment (pHb for AP → BL transport and pHa for BL → AP transport), pH value in mitochondria and lysosomes (pHm and pHl), apical membrane potential (Ea), basolateral membrane (Eb), cytosol membrane potential (Em), lysosome membrane potential (El), lipid fraction in cytosol (Lc), mitochondria (Lm), and lysosomes (Ll), cell density, and pore density. Independent Monte Carlo simulations were performed for pH 6.5 and pH 7.4, on 0.4µm- and 3µm- membranes, and in AP → BL and BL → AP transport directions. For each condition, 10,000 simulations were performed. In each simulation parameters were randomly sampled from uniform distributions (Table S1 of Supporting Information). Lipophilicity (logP) values for both neutral and ionized forms of CQ varied ± 0.5 log units based on weighted method prediction provided by ChemAxon®. Boundaries of lysosome volume and pH were determined based on experimental measurements. Details of the calculations are described in Supporting Information.
Analysis of CQ binding to the non-aqueous cellular fraction
The concentration of CQ associated with the non-aqueous cellular fraction after detergent extraction was estimated by dividing the mass CQ bound per cell by the estimated non-aqueous volume remaining after detergent extraction. In turn, the partition coefficient of the protonated forms of CQ was calculated, by dividing this calculated concentration in the non-aqueous volume fraction by the concentration of CQ in the buffer. The log of this partition coefficient was used to calculate a single sorption values for both ionized forms of CQ, which was then used as input for Monte Carlo simulations (based on equation 17 of reference 3).
Measurement of Lysosome Volume Changes
MDCK cells were seeded on 96-well optical bottom glass-based plates (Nunc™ Cat. 164588) at the density of 1×105 cells/cm2 and let grown for 1 or 2 days in 150 µL fully supplemented DMEM. CQ diphosphate was dissolved in DPBS buffer (Gibco 14190) to a final concentration of 50 mM and diluted in cell culture medium to 50 µM. Cells were incubated with 150 µL DMEM-CQ for 3.5 hours. LTG was added to CQ-treated and untreated cell culture to a final concentration of 0.5 µM for another 30 minutes incubation. For fluorescence microscopy, a Nikon TE2000S microscope with a 100X oil immersion objective was used to image the lysosomes using the FITC filter set. Image analysis was carried out with MetaMorph® software. In calibration experiments, we determined this system could accurately resolve and measure objects >200 nm diameter, using fluorescent bead standards (Molecular Probes T14792) ranging from 100 to 4000 nm diameters. We also determined the objective was capable of capturing fluorescent signals within 2 µm vertical spaces. For analysis, images were background subtracted, and each individual lysosome vesicle of each individual cell was manually outlined with the Circular Region Tool. Next, assuming spherical shape, the diameter of each individual lysosome was estimated from the area of the regions. Because the height of cell monolayer was estimated to be 5 to 7 µm (Figure 1) and the depth of the focal plane is in the order of 2 µm, the total number of lysosomes associated with one cell was calculated by multiplying the region count by a factor of 2.5. The average diameter and total number of lysosomes in treated and untreated cells was calculated as the average value of those acquired from at least 5 images under the corresponding condition.
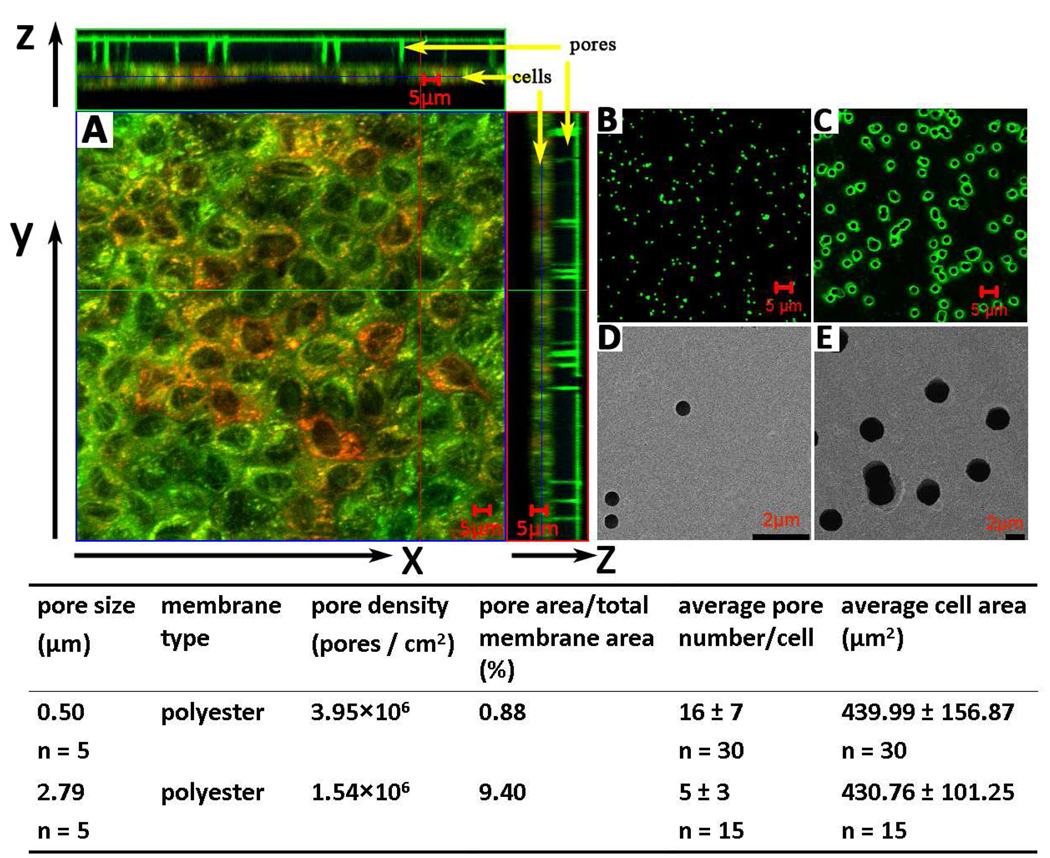
Figure 1.
Microscopic images of polyester membranes and MDCK cells grown on a 0.4µm-membrane. (A) Orthogonal planes of 3D reconstructions reveal cross-sections of MDCK monolayers grown on a polyester membrane with 0.4 µm pores. Cells were stained with LTG, MTR and Hoechst and imaged as detailed in the methods. (B) Confocal microscope images of membranes with 0.4µm pores. C) Confocal microscope images of membranes with 3µm pores. (D) Scanning electron microscope (SEM) images of membranes with 0.4µm pores. E) Scanning electron microscope (SEM) images of membranes with 3µm pores. The table details microscopic measurements of pore geometry, density and cell monolayer characteristics, as analyzed in this study.
Lysosome pH Measurements
MDCK cells were seeded on 96-well optical bottom polymer-based plates (Nunc™ Cat. 165305) at the density of 1×105 cells/cm2 and let grown for 1 to 2 days in 150 µL fully supplemented DMEM. FITC-dextran (FD, Sigma FD150S) was dissolved in DPBS buffer to a final concentration of 10mg/mL and diluted in cell culture medium to 0.2 mg/mL. Cells were incubated with 150 µL DMEM-FD for 24 hours to allow cell uptake of FD via endocytosis. To measure lysosome pH during 50 µM CQ treatment, cells were washed twice with 100 µL DPBS buffer before incubation in 150 µL FD-free medium with or without CQ. At the end of 1 to 4 hours incubation, cells were washed with 100 µL DPBS buffer twice, immersed in 150 µL buffer, and scanned for fluorescent signal with BioTek Synergy 2 plate reader using Ex.485/20 and Em.528/20 filter set as well as Ex.450/50 and Em.528/20 filter set. For pH standard curves, FD pretreated cells were washed with 100 µL DPBS buffer twice, immersed in 150 µL DPBS-based solutions (pH 3 to 10) with 10 µg/mL Nigericin (Sigma N7143), let equilibrate for 10 minutes and scanned for fluorescent signal with the same settings. Background fluorescence from MDCK cells without FD treatment was also recorded after wash. The fluorescence ratio (FR) was calculated based on equation 8:
| (8) |
where F485i and F450i standard for integrated fluorescent intensity from the ith well of cells under Ex.485 nm and Ex.450 nm, respectively, and subscript bg indicates background fluorescence signal without FD treatment. FR values were plotted against known pH values to create a standard curve, or compared with the standard curve to calculate the lysosome pH.
Results
Morphometric Analysis of Cells on Pores
Optically-transparent track-etched polyester membranes of similar membrane thickness (~10 µm) were used for experiments. The fractional pore area of the 3µm-membranes was about 28 times higher than the 0.4µm-membranes based on the manufacturer’s specification, and >10 times higher based on our measurements (Figure 1). TEER values of 0.4µm-membrane was similar to that of 3µm-membranes (mean ± SD: 126 ± 8 vs. 118 ± 9 Ω·cm2, n = 8; p value = 0.0784). MDCK cells grown on polyester 0.4µm- or 3µm-membranes formed regular monolayers (Figure 1). By visual inspection, no difference in monolayer architecture was apparent on 0.4µm- and 3µ4m-membranes. TEER value of cells grown on 0.4µm-membrane was higher than on 3µm-membrane (mean ± SD: 221 ± 16 vs. 117 ± 16 Ω·cm2, n = 48, background subtracted; p value < 10−4). This behavior can be explained by the difference in pore area available for transport or by differences in tightness of intercellular junctions. Seeded at the same density (2×105cells/cm2) and grown for two days, the cell number on 0.4µm-membrane was slightly higher than the cell number on 3µm-membrane (mean ± SD: 4.9×105 ± 6.4×104 vs. 3.9×105 ± 4.5×104, n = 8), which almost corresponded to the difference in surface area available for cell attachment (Figure 1). We did not observe any MDCK cells migrating through the pores.
CQ Transcellular Transport Is Nonsaturable and Directly Proportional to the Transcellular Concentration Gradient
CQ and Lucifer Yellow (LY) transport across polyester membranes without pores is negligible: in the absence of pores, the amount of CQ or LY in the receiver compartment was undetectable after a 6 hour transport experiment (data not shown). Therefore, transport of small molecules across cell monolayers on nucleopore polyester membranes is driven primarily by the flux of molecules through the pores (not through the polyester film). On 0.4µm- and 3µm-membrane, CQ mass transport rate linearly correlated with the initial concentration in the donor compartment at pH 7.4 or 6.5, both over low concentration range (Figure 2) and even at higher concentrations (data not shown). The intercepts of the regression lines were all zero, after statistical testing for the intercept values. LY, a hydrophilic, cell membrane-impermeant small molecule, was used as a control probe to assess paracellular transport. Average apparent permeability of LY (AP → BL) was 0.70 ± 0.33 nm/sec (mean ± SD, n = 27) and 1.7 ± 2.1 nm/sec (mean ± SD, n = 23) measured on MDCK cells grown on 0.4µm- and 3µm-membranes, respectively (p value = 0.0273) with an apical pH value of 7.4. This is consistent with LY transport occurring mostly through a paracellular route. The Papp of CQ was approximately two orders of magnitude greater than the Papp of LY. We conclude that CQ traverses MDCK cells mainly through a transcellular pathway, with the rate of transport being directly proportional to the concentration gradient in either AP → BL or BL→ AP directions.
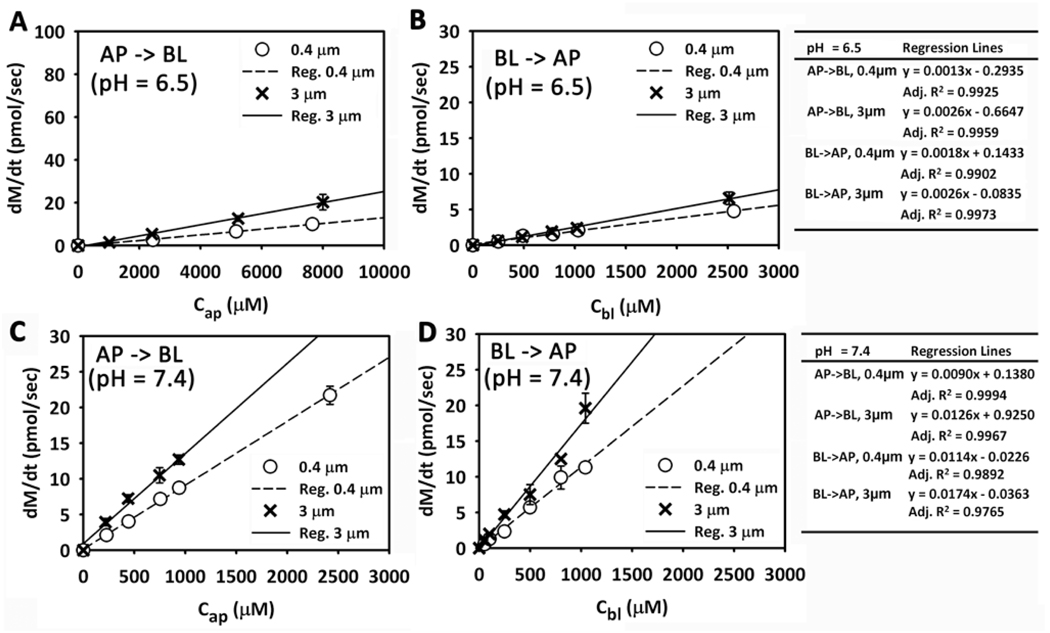
Figure 2.
The relationship between mass transport rate and the initial concentration of CQ in the donor compartment. (A) AP → BL transport (pHa = 6.5). (B) BL → AP transport (pHb = 6.5). (C) AP → BL transport (pHa = 7.4). (D) BL → AP transport (pHb = 7.4). The linear regression equations are included in the tables.
Effects of pH and Pore Geometry on CQ Transport Routes and Cellular Uptake
Based on measurements, the time course of the appearance of chloroquine (dM) in the receiver compartment under all conditions tested is linear (Figure S1 of Supporting Information), and consistent with simulation results. Comparing cells on 3µm- or 0.4µm-diameter pore membranes was used to study how differences in the porosity of the substratum can affect the transport route small molecules through epithelial cells (Figure 2). Comparing the regression coefficients, if the other conditions are the same (such as the pH and the transport direction), the mass transport rate of CQ on 3µm diameter pore membranes was only slightly greater (< 2-fold) than on 0.4µm-membranes. However, the total pore area of the 3µm diameter pore membranes is >10-fold greater than that of a 0.4µm-membrane. If Pcell was an intrinsic, invariant property of the cells, one would have expected the mass transport rate to be directly proportional to the total pore area available for transport. Thus, Pcell is greatly affected by the porosity of the substratum.
CQ is a weak base, with two amine groups that can be protonated within physiological pH values. The fraction of CQ with two charges is higher at pH 6.5 relative to pH 7.4 (Table 1). Conversely, the proportion of neutral CQ species is higher at pH 7.4 than at pH 6.5. Consistent with transmembrane transport being a function of the charge and lipophilicity of CQ, the pH of the donor compartment exerted a major effect on CQ transcellular transport rate (Figure 2) with the rate of transport at pH 7.4 being seven times greater than that at pH 6.5, as expected if diffusion across phospholipid bilayers was the rate limiting step of CQ transport across cells.
For CQ, the BL → AP transport rate is only slightly higher than AP → BL transport rate for the same pH values and same membranes. Linear relationship of transport rate with initial concentration in the donor compartment was observed as well. Thus, unidirectional active transport mechanisms cannot be invoked to explain CQ transport across MDCK cells. Overall, the experiments are consistent with passive diffusion and transmembrane gradients being primarily responsible for driving the bulk of CQ transport across MDCK cells.
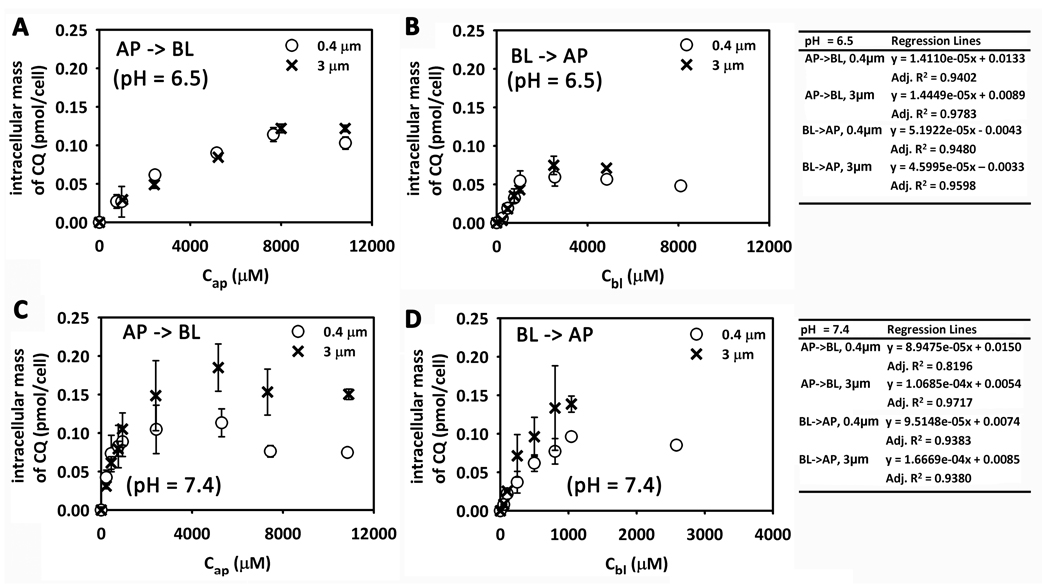
During transport experiments, intracellular mass accumulation of CQ was linearly correlated with the initial concentration when the concentration in the donor compartment was lower than 1 mM and reached a plateau when the concentration in the donor compartment was higher (Figure 3) after 4 hours exposure to the drug. This plateau was related to adaptive changes induced by CQ at high concentrations, apparent as nuclear shrinkage, chromatin condensation and irregular nuclear spacing in the cell monolayer (Figure S2 of Supporting Information). At pH 6.5, the CQ accumulation plateau is reached when the apical concentration is higher than 8 mM for AP → BL transport (Figure 3A); however the plateau is reached when the basolateral concentration is higher than 2 mM (Figure 3B). When the pH is 7.4, the plateau is reached when the concentration in the donor compartment is higher than 1 mM for both AP → BL and BL → AP transport (Figure 4C and 4D). This pH sensitivity of the intracellular accumulation is consistent with higher CQ lipophilicity at higher apical pH values, leading to greater influx from the donor compartment into the cytosol, and presumably, higher cytosol concentration. Comparing AP → BL transport with BL → AP transport for the same conditions, the intracellular accumulation is similar for pH 6.5 and pH 7.4 (Figure 4). Intracellular accumulation of CQ on 3µm-membranes and 0.4µm- membrane is similar for the same conditions (Figure 4), except for BL → AP transport when pH = 7.4 (Figure 4D) where it is slightly different (which could be due to an experimental measurement outlier, evident in the larger error bars).
Figure 3.
The relationship between intracellular CQ mass and the initial concentration of CQ in the donor compartment. (A) AP → BL transport (pHa = 6.5). (B) BL → AP transport (pHb = 6.5). (C) AP → BL transport (pHa = 7.4).(D) BL → AP transport (pHb = 7.4). The linear regression equations shown in the table (right) were obtained from the four lowest concentrations tested.
Figure 4.
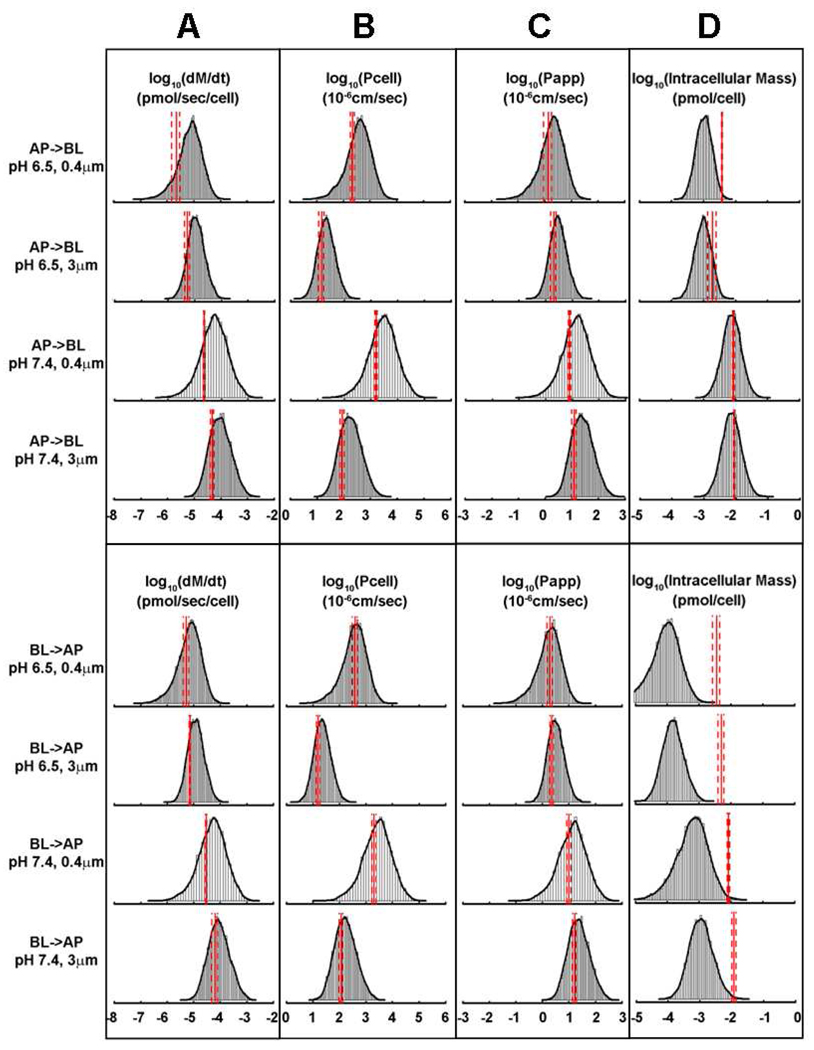
Histogram plots of Monte Carlo simulations showing calculated dM/dt (A), Pcell (B), Papp (C), and intracellular CQ mass accumulation at 5 minutes incubation (D), for the indicated experimental conditions analyzed in this study. The solid red lines indicate experimentally-measured mean values and the dashed red lines indicate measured standard deviation.
Simulation-Driven Quantitative Analysis of CQ Transport and Uptake
Monte Carlo simulations were used to assess the effect of measurement variability, experimental errors and other uncertainties in the input variables of the 1CellPK model, on the calculated mass transport rate (dM/dt; Figure 4A), Pcell (Figure 4B), Papp, (Figure 4C) and total intracellular mass accumulation (Figure 4D). Because of the adaptive cellular changes occurring upon 4 hours exposure to CQ (Figure 3 and S2) mass accumulation of CQ was measured after 5 minutes incubation with 1mM CQ in the donor compartment. Results showed that CQ uptake after 5 minutes incubation (Figure 4D, red lines) is much lower than that after 4 hours transport experiment (Figure 3) under the same conditions.
For simulations, the apparent permeability (Papp) was calculated from measured dM/dt by normalizing over the initial concentration in the donor compartment and the total insert area. Unlike Pcell measurements which normalize mass transport rate over the aqueous pore area of the polyester membrane, Papp measurements normalize the mass transport rate over both pore and non-pore regions of the polyester membrane. Comparing permeability normalized by the pore area (Pcell; Figure 4B, red lines) with the permeability normalized by total insert area (Papp; Figure 4C, red lines), Pcell of CQ on 0.4µm-membrane is at least an order of magnitude higher than that on 3µm-membrane. However, Papp of CQ on 3µm-membrane is only slightly higher than on 0.4µm-membrane (<2-fold). Per cell, the total pore area on 3µm-membrane is more than an order of magnitude greater than on 0.4µm-membrane. Arguably, Pcell most accurately reflects a difference in the actual flux of CQ molecules across the basolateral membrane of cells on 0.4µm- vs. 3µm-membrane, at the single cell level.
Most importantly, for the measured transcellular transport kinetics and permeability values, the simulation results were largely consistent with experimental measurements. In the case of dM/dt (Figure 4A), Pcell (Figure 4B), and Papp (Figure 4C) most of measured values fell between 10% and 90% quantiles of simulated distributions, and very close to the median (Table S2). Predictions were accurate irrespective of whether transport experiments were carried out at pH 7.4 or 6.5, on 0.4µm- vs. 3µm-membrane, or in the AP → BL or BL → AP directions. Simulations were also predictive of CQ uptake after 5 minutes incubation for AP → BL transport at pH 7.4 (Figure 4D; Table S2), although measured CQ uptake at pH 6.5 or in the BL → AP direction was greater than predicted by the model (Figure 4D, rows 5 – 8 and Table S2).
Probing the Adaptive Mechanisms of CQ Mass Accumulation upon Prolonged Exposure
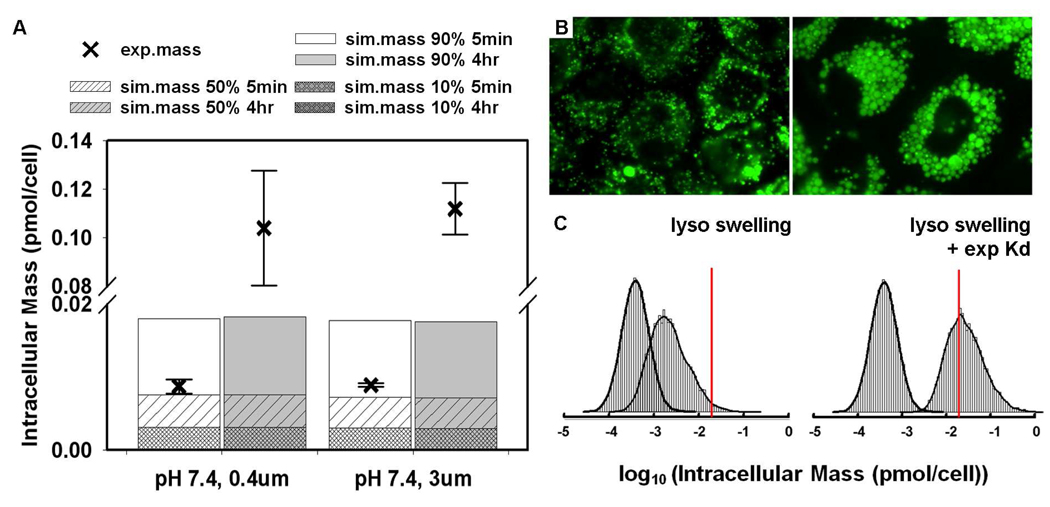
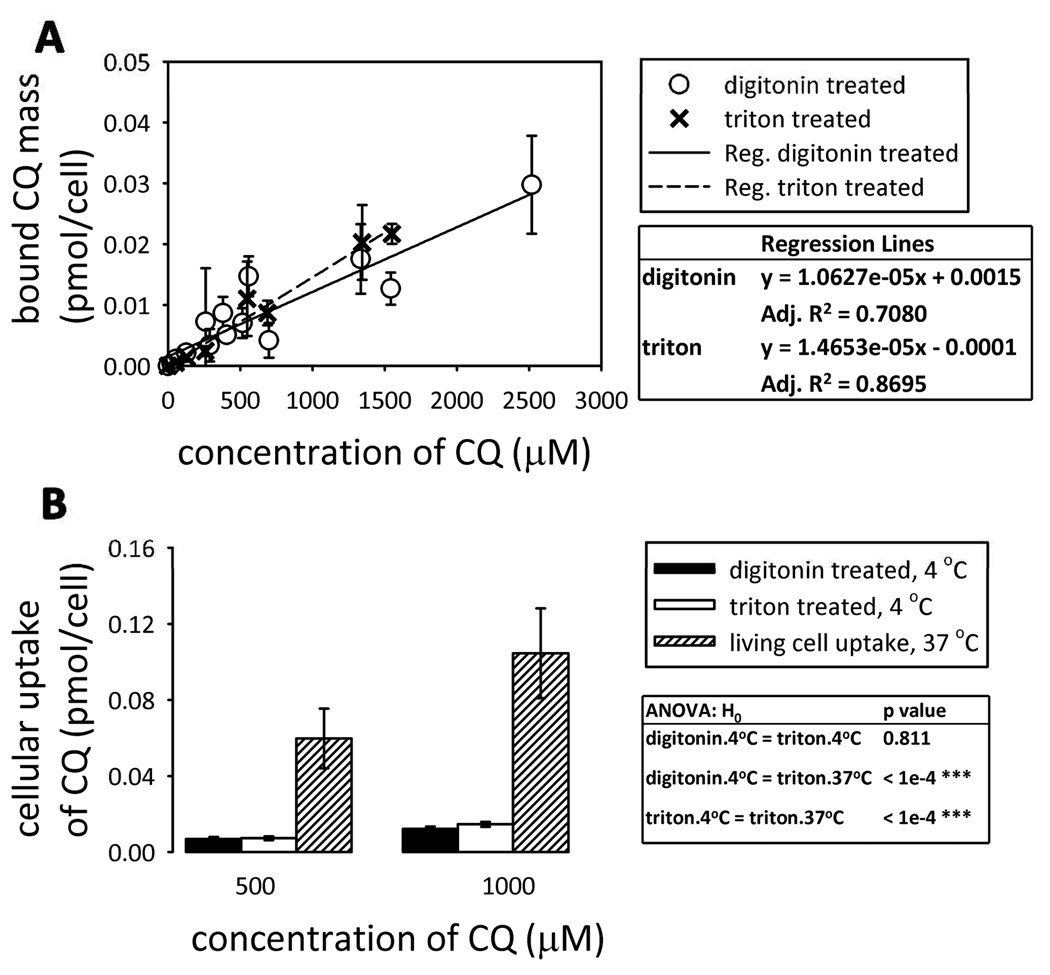
Although the initial input parameters for the simulations yielded dM/dt, Pcell, Papp values and CQ uptake after 5 minutes incubation consistent with experimental measurements, they consistently underestimated the intracellular mass of CQ after 4 hour exposure (Figure 6A). Biochemical analysis with LC/MS reveals no metabolites of CQ, with all the intracellular CQ present in intact form (data not shown). Based on the simulation, intracellular CQ mass should reach steady state levels by 5 min incubation, but this was not observed experimentally (Figure 6A). We also measured the passive binding of CQ to detergent-extracted (triton-treated) or permeabilized (digitonin-treated) cells. Binding of CQ to detergent extracted cells was proportional to the concentration of CQ in the buffer, and was lower than its measured uptake by live cells (Figure 5), while binding to digitonin- and triton-treated cells were similar.
Figure 6.
Effects of lysosome swelling on CQ intracellular mass accumulation. (A) Comparison of simulated intracellular mass and experimental data at the end of a 5 minute and 4-hour AP→BL transport experiment. (B) Lysotracker Green (LTG) staining of MDCK cells treated with CQ free medium (left) and 50 µM CQ diluted in medium (right) for 4 hours. (C) Histograms of Monte Carlo simulation of lysosome expansion and pH effect on intracellular CQ mass accumulation, excluding (left) or including (right) the measured partitioning component of the ionized CQ species with initial concentration of 50 µM. The left curves in each panel were generated from Monte Carlo simulations without considering lysosome expansion and pH effect. All model parameters were kept the same as in Figure 4 except that the measured lysosome volume and pH values were used as input (as median values of a uniform distribution, see Supporting Information for boundary calculation). The simulations performed to generate the right histogram were described in Supporting Information (Figure S3) except that the initial concentration used for this plot was 50 µM. The red lines show intracellular mass accumulation of CQ with initial concentration of 50 µM extrapolated from regression lines of experimental measurements (Figure 3C).
Figure 5.
CQ binding experiments. (A) The bound CQ mass digitonin- and triton-treated cells as a function of CQ concentration in buffer; (B) comparison of passive CQ binding at 4°C (digitonin-treated and triton-treated cells) and CQ uptake by live cells. The values and standard deviations were calculated from the regression lines using CQ concentration equal to 500 or 1000 µM.
CQ is a weakly basic molecule that accumulates in lysosomes through an ion trapping mechanism dependent on the acidic microenvironment (pH 4.5 to 5.5) of lysosomes. CQ incubation gradually expanded the lysosome compartment in MDCK cells (Figure 6B). The average number of lysosomes per cell was slightly lower in CQ-treated cells as compared with untreated cells: 200 ± 35 (n = 6) vs. 253 ± 45 (n = 5) (mean ± SD, p-value = 0.059). However, the diameter of lysosomes is significantly increased in treated cells in comparison with untreated cells: 1.74 ± 0.19 µm (n = 6) vs. 0.50 ± 0.03 µm in untreated cells (n = 5) (mean ± SD, p-value = 7.8E-12). Based on these numbers, the calculated, total lysosome volume was 16.5 ± 4 µm3 in untreated cells and 551.4 ± 205 µm3 after 4 hours treatment with 50 µM CQ. Overall, there was a 33.5-fold increase in the total lysosome volume. The measured lysosome pH of untreated cells was 5.03 ± 0.18 (mean ± SD, n = 4) and the lysosome pH of CQ-treated cells gradually increased from 5.2 ± 0.2 at 1 hour incubation to pH 6.0 ± 0.3 at 4 hour incubation (mean ± SD, n = 6).
Given that CQ exposure alters the lysosome volume and pH over a 4 hour period, simulations were repeated with an average lysosome pH value of 5.5 and the measured, expanded lysosome volume (Figure 6C). The experimental, measured intracellular mass accumulation of CQ was extrapolated down to 50 µM CQ using the regression equations in Figure 3 for different conditions. After taking lysosome swelling and pH increase into account, the predicted intracellular CQ mass is closer to experimental measurement for AP →BL transport with pH 7.4 in apical compartment (Figure 6C). However, in BL→AP transport, the measured intracellular accumulation of CQ still exceeded the simulated distributions by more than an order of magnitude, at least as much as was observed during the shorter, 5 minutes exposure (Figure 4D). To account for this missing mass, we considered the measured amount of CQ binding to digitonin-permeabilized cells. At pH 7.4, most the CQ is in a mono- or di-protonated state (Table 1). Based on the CQ mass per cell vs. CQ concentration curve, 1.0×10−5 pmol CQ binds in a 1 µM CQ solution (Figure 5). Accordingly, using an estimate of the non-aqueous volume fraction per cell of ≤ 50 µm3 (≤ 5% of the total cellular volume) the partition coefficient of the mono and di-protonated species of CQ was calculated to be about 200. In contrast, the octanol:water partition coefficient of the protonated and diprotonated forms of CQ (based on Chemaxon calculations) were two or more orders of magnitude lower (0.43 for the mono-protonated form and −0.91 for the di-protonated form; Table 1). After incorporating the higher sorption values of protonated CQ species in Monte Carlo simulations, the gradual increase of intracellular CQ mass could be accounted for by the induced changes in lysosome volume coupled to the partitioning of the protonated forms of CQ to a non-aqueous volume fraction (Figure 6C and S3.
Discussion
1CellPK is a biophysical model 11–13 that can be used to analyze the transport route of CQ across an MDCK monolayer, while studying how extracellular pH, substratum porosity, and transcellular concentration gradients affect CQ’s transport behavior. As a fixed-parameter model, all input variables including compartmental volumes, areas, pH, membrane potentials and lipid fractions are held constant from the start of a simulation, and only the calculated drug concentrations vary in the different compartments. With 1CellPK, the effects of the porosity of the substratum on the permeability and transport properties of CQ were readily accounted for by considering the pores as a steric constraint on the basolateral membrane surface area (Ab) and the effective cell cross sectional area (Aaa) over which flux effectively occurred. Biological variability, experimental errors, and other uncertainties (such as the effective basolateral surface area over which transport takes place, and the absolute concentration and permeability of different ionic species of CQ at any given pH) were readily accounted for in Monte Carlo simulations, yielding probabilistic distributions of 1CellPK results that were reasonably accurate with respect to experimental measurements.
Geometric constraints on cell adhesions can profoundly impact cell structure and function with cell-substratum interactions potentially affecting cellular transport in many different ways. But perhaps most importantly, the non-pore area of polyester membranes is impermeant. Thus the only route for molecules to go through the membrane is the pores. Therefore, pore area, diameter and arrangements affect the number of cells per membrane area, the number and area of pores per cell, and the effective basolateral membrane area over which flux actually occurs. We found that cell density on 3 µm membranes is less than cell density on 0.4 µm membranes, and that TEER values on 3 µm membranes were lower than on 0.4 µm membranes. Whether the filter or the cell monolayer is rate limiting step, depends on the pore area available for transport, in relation to the physicochemical properties of the molecules, the permeability of the apical and basolateral membranes and the direction of transport. For example, in basolateral to apical transport studies using custom-manufactured polyester membranes, when the pore areas are small, the filter becomes the rate limiting step (N. Zheng manuscript in preparation). Because of the close relationship between simulation and experimental results, the current study suggests that, in the case of chloroquine and the commercially available 0.4 and 3 µm membranes, the cells (not the polyester) behave as the rate limiting step. However, explicit consideration of pore area vs. non-pore area makes the model applicable to other situations.
With 1CellPK, our analysis demonstrates how the logP and pKa of ionizable functional groups of small molecules can serve as a starting point for predicting transcellular, passive transport properties. With 1CellPK, CQ is postulated to undergo very fast (instantaneous) mixing within the each subcellular compartment, with the transport of CQ across cellular membranes being the rate-limiting step determining the net rate of mass transport across the cell monolayer. The experimental results were largely consistent with this compartmental model, with CQ traversing MDCK cell monolayers via a passive, transcellular, phospholipid bilayer-limited diffusion route. The 1CellPK model captured the effects of cell biological variables (pH values in donor and receiver compartment, pore size and density of the support filter, transmembrane concentration gradients, organellar volumes and intracellular pH) on passive transport routes. However, discrepancies between simulation results and CQ uptake measured during a 4-hour exposure point to a physiological mechanism responsible for the gradual intracellular mass accumulation of CQ that is not captured by the model. Our measurements indicate that CQ accumulated intracellularly to a level higher than expected by nonspecific partitioning, ion trapping or membrane potential dependent sequestration in cytosol, lysosomes or mitochondria –all of which were included in the model or were controlled for in the experimental measurements. Other amine-containing molecules also accumulate to very high concentrations inside cells 14.
Certainly, one of the limitations of a fixed-parameter model like 1CellPK is that the compartment volumes, pH, membrane potentials are held constant from the start of the simulations. Thus, the gradual biological effects of a drug on cell physiological parameters are not taken into account. CQ induced a gradual but significant increase in lysosome volume and pH in MDCK cells. By using an expanded lysosome volume (and an increased lysosome pH) as input, simulations revealed that this lysosome volume change could partly account for an increase in the total intracellular CQ mass especially in the AP → BL with pH 7.4 (Figure 6C). In BL → AP direction, the volume expansion cannot account for the excess CQ mass observed even during a five minute drug exposure, so an unknown factor affecting much higher-than-expected BL → AP mass sequestration remained to be identified.
CQ exists as ionic species at physiological pH and thus electrostatic interactions with negatively charged lipids and intracellular proteins and macromolecules can exert a dominant effect in terms of binding the protonated form of the base15. Thus we considered whether such interactions might explain the discrepancy in CQ mass accumulation observed after a 4-hour incubation period. Based on results obtained with detergent-permeabilized cells, the measured partition coefficient of the ionized CQ species between the non-aqueous and aqueous cellular volume fractions were at least two orders of magnitude greater than the octanol:water partition coefficients predicted with cheminformatics software (Table 1). Therefore, by adjusting the sorption coefficients in the Monte Carlo simulations, the interaction of protonated CQ species with cellular macromolecules or anionic phospholipids, together with the measured changes in the volume of acidic organelles, could explain the higher-than-expected, gradual intracellular accumulation of CQ. Nevertheless, to confirm this hypothesis, it will be necessary to analyze the concentration of CQ in the lysosomes, the binding interaction between the protonated forms of CQ and resident cellular phospholipids and macromolecules, as well as the associated changes in organelle volumes and pH.
In summary, for monovalent weak acids and bases, the biophysical modeling approach here presented was previously tested in terms of predicting passive transcellular permeability3. In this study we further elaborated 1CellPK to analyze the transcellular transport of dibasic molecules, to study the effects of pore size and density on transport, and more importantly, to test the model’s predictions of intracellular drug accumulation in the presence of a transcellular concentration gradient. Unlike empirical models which rely on a training data set, biophysical mechanism-based models can be used to make predictions irrespective of training data, if those predictions are aimed to guide experimental design and discover new mechanisms. When discrepancies between model predictions and observations are found, the model can point to new discoveries. Thus, although the current version of 1CellPK has been tested and validated only with CQ, it can be used to generate quantitative hypothesis and guide experimental analysis of other dibasic compounds.
To conclude, as related to drug discovery and development, permeability measurements, including in vitro, in situ, and in vivo methods are low throughput and costly.16–18 Permeability assays on cell monolayers are usually done in vitro, growing cells on semi-permeable support membranes, and monitoring the rate of mass transport across the membranes, through time.19–21 Cell permeability measurements often show huge variability between laboratories.22, 23 and many factors have been proposed to contribute to these experimental variations. Indeed, mathematical models are being increasingly used to facilitate empirical interpretation of cell-based transport mechanisms24, 25. The ability to make predictions by using a molecule’s physicochemical properties (e.g. logP and pKa) as input may allow biophysical modeling approaches like 1CellPK to be applied at the earliest phases of drug development, to facilitate the rational design of drug candidates with the most desirable, cell pharmacokinetic characteristics.3, 4, 13 In terms of drug mass accumulation, the fixed-parameter modeling approach here presented may be most accurate for predicting the behavior of drugs with short tissue residence times (for example, inhaled fast-acting bronchodilators or other inhaled, fast-acting medications intended to be rapidly absorbed). For predicting pharmacokinetics of drug candidates with prolonged, systemic exposures, it will be important to elucidate the mechanisms underlying gradual intracellular drug sequestration to capture the key physiological changes associated with long term exposure to drugs.
Supplementary Material
Acknowledgments
This work was funded by NIH grants RO1GM078200 and P20HG003890 to G.R.R, and by grant number GM007767 from NIGMS. Its contents are solely the responsibility of the authors and do not represent the official views of NIGMS. The authors thank Drs. Gordon L. Amidon, Steven P. Schwendeman, and Shuichi Takayama for their excellent suggestions. Supporting information is available free of charge via the internet at http://pubs.acs.org/
References
- 1.Malkia A, Murtomaki L, Urtti A, Kontturi K. Eur J Pharm Sci. 2004;23(1):13–47. doi: 10.1016/j.ejps.2004.05.009. [DOI] [PubMed] [Google Scholar]
- 2.Yu H, Sinko PJ. J Pharm Sci. 1997;86(12):1448–1457. doi: 10.1021/js960524q. [DOI] [PubMed] [Google Scholar]
- 3.Zhang X, Shedden K, Rosania GR. Mol Pharm. 2006;3(6):704–716. doi: 10.1021/mp060046k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhang X, Zheng N, Rosania GR. J Comput Aided Mol Des. 2008;22(9):629–645. doi: 10.1007/s10822-008-9194-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen CS, Mrksich M, Huang S, Whitesides GM, Ingber DE. Science. 1997;276(5317):1425–1428. doi: 10.1126/science.276.5317.1425. [DOI] [PubMed] [Google Scholar]
- 6.Dike LE, Chen CS, Mrksich M, Tien J, Whitesides GM, Ingber DE. In Vitro Cell Dev Biol Anim. 1999;35(8):441–448. doi: 10.1007/s11626-999-0050-4. [DOI] [PubMed] [Google Scholar]
- 7.Chen CS, Alonso JL, Ostuni E, Whitesides GM, Ingber DE. Biochem Biophys Res Commun. 2003;307(2):355–361. doi: 10.1016/s0006-291x(03)01165-3. [DOI] [PubMed] [Google Scholar]
- 8.Projean D, Baune B, Farinotti R, Flinois JP, Beaune P, Taburet AM, Ducharme J. Drug Metab Dispos. 2003;31(6):748–754. doi: 10.1124/dmd.31.6.748. [DOI] [PubMed] [Google Scholar]
- 9.Kostiainen R, Kotiaho T, Kuuranne T, Auriola S. J Mass Spectrom. 2003;38(4):357–372. doi: 10.1002/jms.481. [DOI] [PubMed] [Google Scholar]
- 10.Anari MR, Sanchez RI, Bakhtiar R, Franklin RB, Baillie TA. Anal Chem. 2004;76(3):823–832. doi: 10.1021/ac034980s. [DOI] [PubMed] [Google Scholar]
- 11.Trapp S, Rosania GR, Horobin RW, Kornhuber J. Eur Biophys J. 2008;37(8):1317–1328. doi: 10.1007/s00249-008-0338-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Trapp S, Horobin RW. European Biophysics Journal With Biophysics Letters. 2005;34(7):959–966. doi: 10.1007/s00249-005-0472-1. [DOI] [PubMed] [Google Scholar]
- 13.Balaz S. Chem Rev. 2009;109(5):1793–1899. doi: 10.1021/cr030440j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chanteux H, Paternotte I, Mingeot-Leclercq MP, Brasseur R, Sonveaux E, Tulkens PM. Pharm Res. 2003;20(4):624–631. doi: 10.1023/a:1023203017300. [DOI] [PubMed] [Google Scholar]
- 15.Rodgers T, Leahy D, Rowland M. J Pharm Sci. 2005;94(6):1259–1276. doi: 10.1002/jps.20322. [DOI] [PubMed] [Google Scholar]
- 16.Balimane PV, Chong S. Drug Discov Today. 2005;10(5):335–343. doi: 10.1016/S1359-6446(04)03354-9. [DOI] [PubMed] [Google Scholar]
- 17.Winiwarter S, Bonham NM, Ax F, Hallberg A, Lennernas H, Karlen A. Journal Of Medicinal Chemistry. 1998;41(25):4939–4949. doi: 10.1021/jm9810102. [DOI] [PubMed] [Google Scholar]
- 18.Bohets H, Annaert P, Mannens G, Van Beijsterveldt L, Anciaux K, Verboven P, Meuldermans W, Lavrijsen K. Curr Top Med Chem. 2001;1(5):367–383. doi: 10.2174/1568026013394886. [DOI] [PubMed] [Google Scholar]
- 19.Artursson P, Karlsson J. Biochem Biophys Res Commun. 1991;175(3):880–885. doi: 10.1016/0006-291x(91)91647-u. [DOI] [PubMed] [Google Scholar]
- 20.Walter E, Janich S, Roessler BJ, Hilfinger JM, Amidon GL. Journal Of Pharmaceutical Sciences. 1996;85(10):1070–1076. doi: 10.1021/js960110x. [DOI] [PubMed] [Google Scholar]
- 21.Irvine JD, Takahashi L, Lockhart K, Cheong J, Tolan JW, Selick HE, Grove JR. J Pharm Sci. 1999;88(1):28–33. doi: 10.1021/js9803205. [DOI] [PubMed] [Google Scholar]
- 22.Artursson P, Palm K, Luthman K. Advanced Drug Delivery Reviews. 2001;46(1–3):27–43. doi: 10.1016/s0169-409x(00)00128-9. [DOI] [PubMed] [Google Scholar]
- 23.Braun A, Hammerle S, Suda K, Rothen-Rutishauser B, Gunthert M, Kramer SD, Wunderli-Allenspach H. Eur J Pharm Sci. 2000;(11 Suppl 2):S51–S60. doi: 10.1016/s0928-0987(00)00164-0. [DOI] [PubMed] [Google Scholar]
- 24.Gonzalez-Alvarez I, Fernandez-Teruel C, Garrigues TM, Casabo VG, Ruiz-Garcia A, Bermejo M. Xenobiotica. 2005;35(12):1067–1088. doi: 10.1080/00498250500354469. [DOI] [PubMed] [Google Scholar]
- 25.Tran TT, Mittal A, Aldinger T, Polli JW, Ayrton A, Ellens H, Bentz J. Biophys J. 2005;88(1):715–738. doi: 10.1529/biophysj.104.045633. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.