Remodeling of Engineered Tissue Anisotropy in Response to Altered Loading Conditions

Abstract

Structural and mechanical anisotropy are critical to the function of many engineered tissues. This study examined the ability of anisotropic tissue constructs to overcome contact guidance cues and remodel in response to altered mechanical loading conditions. Square tissues engineered from dermal fibroblasts and type-I collagen were uniaxially loaded to induce cell and matrix alignment. After an initial time, t*, of 5 to 72 hrs, loading was switched from the x-axis to the y-axis. Cell alignment was examined throughout the experiment until a steady state was reached. Before t*, cells spontaneously aligned in the x-direction. After t*, the strength of alignment transiently decreased then increased, and mean cell orientation transitioned from the x- to the y-direction following an exponential time course with a time constant that increased with t*. Collagen fiber orientation exhibited similar trends that could not be explained by passive kinematics alone. Structural realignment resulted in concomitant changes in biaxial tissue mechanical properties. The findings suggest that even highly aligned engineered tissue constructs retain the capacity to remodel in response to altered mechanical stimuli. This may have important functional consequences when an anisotropic engineered tissue designed in vitro is surgically implanted into a mechanically complex graft site.

INTRODUCTION

In recent years, important advances have been made in the effort to engineer living tissue substitutes for the purpose of repairing or replacing irreversibly damaged tissues and organs ²⁸. The promise of engineered tissues is particularly attractive for applications such as ligaments, heart muscle and cartilage, which have a limited ability to regenerate, and for which there is a critical shortage of donor tissue available. One major challenge for orthopedic and cardiovascular applications in particular is that the engineered replacement tissues must function in complex and demanding mechanical environments, which can lead to implant failure under adverse conditions ⁹.

On the other hand, normal physiologic loading is obviously compatible with healthy tissue function, and has ultimately influenced the evolution of highly specialized three-dimensional tissue architectures--hence the tenet, “form follows function” ^{20, 36}. This principle is often assumed to also operate in reverse ¹⁷, such that the objective of many tissue engineering efforts has been to develop substitutes that resemble natural tissues with the idea that they will then function like natural tissues. While this may be valid to some degree, it requires (among other things) that tissues designed in the laboratory will not adversely remodel under altered loading conditions, i.e. that the tissue structure will be stable after implantation. Unfortunately, the prediction of such an outcome is difficult because the predominant factors and mechanisms that guide tissue alignment and remodeling remain poorly understood.

One approach to better understand candidate factors is to study tissue remodeling in an experimental system with controlled environmental cues. In particular, a number of investigators have shown that the organization of most anchorage dependent cells may be impacted by principles of contact guidance, in which cells orient themselves in alignment with topographical cues from the substrate or other neighboring cells ^{23, 33}. It has also been demonstrated that mechanical loading constraints can be used to guide cell and matrix alignment ^{2, 13, 14, 21}. However, in most cases the loading and topographical cues are concomitant factors that act synergistically.

Few studies have attempted to uncouple the effects of contact guidance and mechanical stimulation in the tissue remodeling process. In particular, Wang and Grood found that contact guidance from a deformable substrate with fabricated microgrooves could prevent fibroblasts from realigning in response to cyclic stretch ³⁵, demonstrating the strong effects of substrate topography. In contrast, Barocas et al. ¹ have shown that smooth muscle cells suspended in gels with magnetically prealigned collagen fibrils can overcome the effects of contact guidance by reorganizing the matrix in response to mechanical constraints imposed during tissue culture, revealing that loading effects can predominate. More recently, Mudera et al. demonstrated that on large fibronectin strands embedded within a fine collagen matrix, fibroblasts aligned with the fibronectin, whereas the alignment of neighboring cells in the surrounding collagen was governed by the applied mechanical loading ²⁴, indicating that substrate feature size may be a key factor. Based on this background, it remains unclear how contact guidance and mechanical stimulation independently impact structural alignment in living replacement load-bearing tissues. Moreover, no previous studies have examined the remodeling of highly anisotropic engineered tissues in which cell and matrix structures were already strongly aligned in response to mechanical stimulation.

From the tissue engineering perspective, it is important to understand what happens when a highly aligned tissue construct is subjected to an abrupt change in loading conditions that may conflict with the mechanical and contact guidance cues established in the laboratory, as might arise due to surgical implantation in a site with abnormal biomechanics due to injury or disease ¹⁶. One must determine whether the pre-existing structure will adequately sustain the functional characteristics designed in the laboratory, or whether the living engineered replacement tissue (or the surrounding native tissue) is sufficiently adaptable to undergo an appreciable degree of remodeling that might result in adverse structural and mechanical properties after implantation. In this study, extended from our previous work on the use of boundary constraints to guide engineered tissue alignment and anisotropy ¹³, we tested the hypothesis that mechanically pre-aligned tissue constructs retain the ability to remodel their structure in response to altered loading conditions. Using a biaxially-loaded fibroblast-populated collagen gel system ¹⁹, we found that even strongly aligned engineered tissue constructs (ETCs) were highly adaptable, and dramatic changes in cellular and matrix organization occurred within hours to days following a step change in mechanical loading conditions. The resulting biaxial mechanical properties of the tissue also changed drastically. Since material anisotropy is considered essential for normal function of the heart and other load-bearing tissues ^{5, 6, 10, 12, 22} the potential for such rapid and extensive remodeling has important implications for the in vitro design of living tissue substitutes.

MATERIALS AND METHODS

Materials

Human foreskin fibroblasts (HFFs) were obtained as a generous gift from Dr. S. Nicoll, (University of Pennsylvania). Dulbecco’s Modified Eagle Medium (DMEM) from Sigma-Aldrich (St. Louis, MO) was supplemented with 10% fetal bovine serum (FBS) from Atlanta Biologicals (Norcross, GA), and 1% penicillin-streptomycin from Gibco BRL (Carlsbad, CA). Purified Type I bovine dermal collagen (Vitrogen 100) was from Cohesion Technologies (Palo Alto, CA). Minimum Essential Medium (MEM) was from Gibco BRL. Phosphate-buffered saline (PBS), bovine serum albumin (BSA), HEPES, sodium deoxycholate, and titanium oxide were from Sigma-Aldrich (St. Louis, MO). Collagenase type II was from Worthington Biochemical (Lakewood, NJ). Porous polyethylene sheet, vacuum grease and cell culture supplies were from Fisher Scientific (Pittsburgh, PA). Monofilament 5-0 sutures were from Med-Vet International (Mettawa, IL).

Cell Culture

Cells were cultured using previously reported techniques ¹³. Briefly, secondary HFF cultures were cultivated in tissue culture treated polystyrene flasks using DMEM supplemented with 10% FBS and 1% penicillin-streptomycin, and maintained in an incubator at 37 °C, 5% CO₂, and 100% humidity. Fresh culture medium was exchanged every 3 days. HFFs of passage 9 to 14 were used in this study.

Collagen Gel Preparation and Loading Protocol

As described in detail elsewhere ¹⁹, square ETCs were created from fibroblast-populated collagen gels in custom polysulfone molds (40 mm × 40 mm). Autoclaved molds were placed in 100-mm Petri dishes that were pre-coated with 2% BSA for 1 hr at 37 °C and rinsed twice with PBS to inhibit cell attachment to the dish. Hydrophilic porous polyethylene bars (20 mm × 6 mm × 3 mm) were threaded with 5-0 monofilament suture and secured at the edges of the mold with vacuum grease.

Ice-cold sterile collagen solution (1:1:8 mixture of HEPES: 10× MEM: collagen) was prepared using purified type I collagen and mixed with cell suspension in a 4:1 ratio yielding a final concentration of 2.0 mg ml⁻¹ collagen and 2 × 10⁵ cells ml⁻¹. Five milliliters of the cell-collagen solution was pipetted into each mold and incubated for 2 hours at 37 °C and 5% CO₂ (Fig. 1A), during which time the cells began forming attachments to the collagen matrix, and the edges of the gel polymerized into the porous polyethylene bars.

FIGURE 1.

Altered boundary condition experiment. (A) Tissue construct, T, with integrated polyethylene bars, B, following 2 hrs incubation in the casting mold, M. (B) After replacing the mold with a custom loading frame, L, constructs were initially loaded in the x-direction (arrows) with 200 mg weights to induce structural alignment. (C) The loading direction was switched to the y-direction at time t* and maintained until steady state was achieved, as shown. Scale bar, 1 cm.

The mold was then removed, and a custom loading frame was placed over the tissue and seated on the Petri dish (see ¹⁹ for further details). The free end of each suture attached to the four polyethylene bars was carefully threaded through a corresponding slot in each edge of the loading frame. After the tissues were floated in 20 ml of culture medium, a uniaxial 200 mg load was applied by hanging calibrated clay weights from the ends of two sutures defining the x-direction, and leaving the y-axis sutures unloaded. The dish and loading frame were placed in a 150 × 25 mm cell culture dish to maintain sterility and facilitate transporting the assembly during media exchanges and periodic videomicroscopy, as described below. The ETC was incubated at 37 °C and 5% CO₂ for an initial loading time, t*, during which the entrapped cells spread out, exerted tension on the collagen matrix, and remodeled the tissue in response to the uniaxial load in the x-direction (Fig. 1B). Note that the loading frame is designed to limit displacement of the bars due to loading by the weights, essentially enforcing a displacement constraint on the x-axis while leaving the y-axis free to deform due to endogenous cell traction forces.

Following a pre-determined initial loading time, t*, of 5, 24, 48, or 72 hours for a given tissue construct (n = 3 to 5 for each value of t*), the uniaxial load was switched from the x-axis to the y-axis by moving the 200 mg weights from one pair of sutures to the other under sterile conditions. The ETC was then returned to the incubator for an additional 72 hours or longer (up to 216 hours) until a steady-state configuration was achieved (Fig. 1C), based on periodic microscopic evaluation of the cell distribution (see details below).

Cell Alignment

At multiple time points before and after t*, the loaded tissue assembly was briefly removed from the incubator and phase contrast videomicrographs of living tissue constructs were acquired at 1280×1024 pixel resolution with a digital video camera (Sensicam, Cooke Corp., Auburn Hills, MI) and inverted microscope (IX70, Olympus America, Melville, NY) at four arbitrary locations in the central region of each tissue at 100× magnification (10× objective).

The digital images were transferred to a UNIX workstation (O2, Silicon Graphics Inc, Mountain View, CA), scaled by 50%, contrast enhanced, and converted to grayscale 8-bit TIFF format. The orientation of cells within each image was analyzed using public software (fiber3, available at http://cmrg.ucsd.edu) designed for measuring alignment based on a gradient detection algorithm applied sequentially to 20-pixel square subregions of the image ¹⁸. This automated analysis determines the predominant orientation of features in each subregion. The resulting distribution of cell orientation data was analyzed using circular statistics to properly account for the fact that measurements are only unique within a 180° range ³. In circular statistics, each angle measurement is represented as a unit vector, and the vector components are averaged. The angle of the resulting mean vector, θ, indicates the average orientation (−90° < θ ≤ 90°, with 0° being parallel to the x-axis), while the mean vector length, r, indicates the strength of alignment. The value of r ranges from 0 for a random distribution to 1 for a perfectly aligned sample. For each tissue at each time point, circular statistics were performed on angle measurements pooled from the four separate image locations, with each image typically yielding around 650 measurements.

Our preliminary studies suggested the tissue remodeling process followed an approximately exponential time course, and that the transient mean cell orientation, θ(t), was not necessarily synchronized with the changing degree of alignment, r(t). Thus, we used the following two equations to quantify this remodeling behavior:

$$\theta (t)={\theta }_{\infty }+({\theta }_o-{\theta }_{\infty })e^{-(t-t^{\ast })/{\tau }_{\theta }}$$ (1a)

$$r(t)=r_{\infty }+(r_o-r_{\infty })e^{-(t-t^{\ast })/{\tau }_r}$$ (1b)

In Equation (1a), θ_o is the initial mean cell angle before the transient, θ_∞ is the steady state mean angle, t* is the time at which the uniaxial loading condition was switched from the x-axis (0°) to the y-axis (90°), t is elapsed time, and τ_θ is the time constant for the mean angle transient. Similarly, in Equation (1b), r_o is the initial mean vector length before the transient, r_∞ is the mean vector length at steady state, and τ_r is the time constant for the transient in strength of cell alignment. For each experiment, the initial and steady state parameter values (θ_o, θ_∞, r_o, and r_∞) were measured directly from the time course data, and the time constants (τ_θ and τ_r) were estimated by fitting Equations (1a) and (1b) to the corresponding data using a standard least-squares minimization algorithm implemented using Microsoft Excel.

Collagen Fiber Alignment

At the end of each study, the tissue construct was fixed overnight with 3.7% formaldehyde in PBS while still on the loading frame to minimize potential distortion caused by unloading and handling. Samples were then transferred to a large (35 X 50 mm) glass coverslip and placed on the stage of an inverted laser scanning confocal microscope (Olympus IX-70 with Fluroview software). Images of collagen fibers were acquired using confocal reflected light microscopy ⁷. Briefly, the sample was illuminated with 488-nm wavelength laser light with all downstream filters removed from the light path, and four non-overlapping images were acquired with a 60× oil immersion objective from the central region of the gel in a focal plane slightly above the cellular layer. The 1024 × 1024 pixel images were scaled by 70%, processed and analyzed as described above to quantify the distribution of collagen fiber orientation in each image, and circular statistics were performed on angle measurements pooled from the four separate images from each gel. Each collagen image typically yielded about 900 measurements.

Because confocal reflection microscopy required removal of tissue constructs from the loading device and examination under non-sterile conditions, it was not possible to follow the time course of collagen remodeling in a single living ETC. Therefore, to obtain snapshots of the dynamic collagen remodeling process, a separate set of gels was prepared using identical conditions to those described above, except that the uniaxial loading experiment was terminated at specific time points (0, 5, 24, 48, and 72 hours after the initial 2-hr incubation period) and the ETCs (n = 3 to 4 per time point) were fixed and analyzed as described above.

Estimating the Passive Response to Altered Loading Conditions

When the applied load is switched from the x-axis to the y-axis at time t*, there is an associated macroscopic deformation of the tissue (e.g. from Fig. 1B to 1C) which would tend to pull the underlying microstructure toward the y-axis. In theory, it is possible to predict the associated passive changes in tissue structure if the applied macroscopic tissue deformation is known. Therefore, deformation of the tissue was monitored throughout the loading experiment for a representative case of t* = 24 hours (n = 4). Before culture media was added to float the gel, a 3 × 3 array of nine titanium oxide markers was carefully painted with a fine sterile brush tip on the central third of the exposed tissue surface, where the strain field has been shown to be relatively homogeneous ³². Throughout the course of the experiment, the construct and dish were intermittently moved to a photography copy stand for imaging with a digital camera (PowerShot G2, Canon Inc.). Images of the tissue constructs (1024 X 768 pixels) were transferred to a personal computer, and the titanium oxide marker centroids were detected semi-automatically by threshholding the binary image (Scion Image, Frederick, MD). As described elsewhere ³², homogeneous, two-dimensional finite Lagrangian strains (i.e., normal strains E_xx and E_yy, and shear strain E_xy) were computed from the digitized marker coordinates at each time point after t* referenced to the pre-switch configuration immediately prior to t*. In the steady state, the final deformation relative to the pre-switch reference configuration (i.e. from Fig. 1B to 1C) was characterized by the stretch ratios ${\lambda }_x=\sqrt{2E_{xx}+1}$ and ${\lambda }_y=\sqrt{2E_{yy}+1}$.

Assuming the entire macroscopic deformation was translated to the underlying structural components according to the affine transformation model ⁴, the final cell alignment was predicted from the pre-switch reference cell alignment using the following equation:

$${\text{R}}^{\prime }(\theta )=\text{R}(\theta )\ast 1/{\lambda }_{\text{x}}{\lambda }_{\text{y}}[{{\lambda }_{\text{x}}}^2{cos}^2(\theta )+{{\lambda }_{\text{y}}}^2{sin}^2(\theta )]$$ (2)

where R(θ) and R′(θ) represent reference and deformed angle distributions.

The passive change in tissue structure due to the measured λ_x and λ_y was also estimated using a published non-affine kinematics model, in which the underlying fibrous tissue structures deform to establish stress equilibrium at fiber interconnections ¹¹. The resulting network behavior in such non-affine models can differ substantially from that predicted by affine transformation ¹¹.

For comparison with these modeling studies, additional experiments were performed to characterize the passive response to altered loading conditions. In one set of tissue constructs (n = 4), immediately after the load was switched at t* = 24 hrs, the tissue was treated with 0.1% sodium deoxycholate in PBS to lyse the cells and eliminate active traction forces on the collagen matrix. Tissue constructs with disrupted cells were maintained in the culture system for an additional 72 hrs and then fixed. For completeness, acellular control constructs were also created (n = 3), loaded in the x-direction for t* = 24 hrs, switched to the y-direction for 72 hrs, and then fixed. Confocal reflection microscopy was performed to obtain collagen fiber orientation on all fixed samples.

Biaxial Mechanics

Biaxial mechanical testing of the engineered tissues required interruption of the loading protocol and non-sterile manipulation that may have interfered with subsequent tissue remodeling. Therefore, two more groups of gels (n = 5 per group) were prepared specifically for mechanical testing using identical conditions to those described above. In one group (the “SW” group), the 200-mg uniaxial load was switched from the x-axis to the y-axis at t* = 48 hours, and then allowed to remodel to a new steady-state (144 hours after the switch), followed by mechanical testing as described below. For comparison, the second group of gels was incubated for an equivalent total length of time (192 hours) under a 200-mg uniaxial load, and then tested to determine the mechanical properties of tissues that underwent no switch in boundary conditions (the “NS” group).

Biaxial mechanics of the engineered tissues was measured using static, isotonic (i.e., constant force), equibiaxial loading conditions as follows. After completing either the NS or SW experimental protocol described above, the loading assembly was removed from the incubator. The 200 mg weights were then disconnected from the sutures to unload the tissue, and the loading frame assembly was removed from the petri dish. Culture media was extracted and a 3 × 3 array of titanium oxide markers was applied as described above. The construct and dish were then moved to a photography copy stand for imaging. Culture media was added until the ETC floated to the very top of the petri dish, and the construct was photographed in this unloaded reference configuration. The ETC was then loaded incrementally from 0 to 1400 mg in steps of 200 mg by carefully adding calibrated weights to the four sutures that hung freely over the edges of the petri dish. Independent preliminary studies by our group demonstrated that in a biaxial creep test, the response of similar tissue constructs was viscoelastic and appeared to reach an equilibrium configuration within approximately 10 to 15 seconds (S. Thomopoulos, unpublished observations). Therefore, following each 200 mg load increment, the ETC was photographed after a 30-second equilibration period to minimize short-term viscoelastic effects. All testing was performed at room temperature. Two-dimensional finite Lagrangian strains referred to the unloaded configuration were computed from the digitized marker coordinates as described above. Piola-Kirchhoff stress was computed from the loading force divided by the cross-sectional area of the embedded polyethylene bars (60 mm²), as established previously using the same tissue loading apparatus ³².

Statistical Analysis

As described above, circular statistics were used to characterize the distributions of cell and collagen fiber alignment in engineered tissue constructs in terms of a mean vector angle, θ, and a mean vector length, r. Descriptive statistics for θ and r were then computed assuming a standard normal distribution. Results are presented as mean ± SEM to help account for variations in sample size. Effects of initial loading time, t*, were tested by single-factor analysis of variance (ANOVA) using SuperANOVA software (Abacus Concepts, Inc., Berkeley, CA), and post-hoc comparisons were based on Scheffe’s S test, which is a conservative procedure for paired comparison that allows unequal sample sizes among groups ²⁷. Statistical significance was accepted for p < 0.05.

RESULTS

Cell Alignment

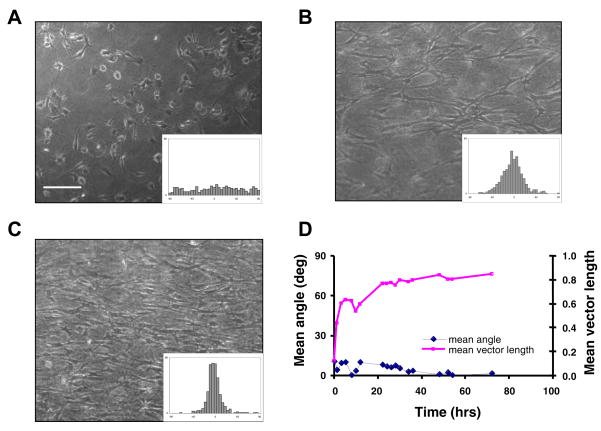
Figure 2 shows the development of structural alignment in a representative uniaxially loaded ETC without any switch in boundary conditions, illustrating the standard tissue remodeling response in our experimental system. In these tissues, an initially random cell distribution (Fig. 2A) became aligned with a mean orientation parallel to the loaded x-direction (θ ~ 0°). The mean vector length, which indicates the degree of alignment, gradually increased from r < 0.2 to r > 0.8 over the course of 72 hours of incubation time (Fig. 2D), resulting in highly aligned tissues (Figs. 2B, 2C). Such uniaxially loaded collagen gels shortened to approximately 60% of their original dimension in the unconstrained direction by 24 hrs, although endogenous cell traction forces persisted and continued to remodel and compact the tissue such that the microstructural alignment and cell density were visibly different by 72 hrs.

FIGURE 2.

Remodeling response of a representative uniaxially loaded engineered tissue construct (ETC) with no switch in boundary conditions. (A) Phase contrast micrograph of the ETC at 0 hr. Scale bar, 200 μm. Inset histogram shows distribution of cell orientation in this image (θ = 10.8°, r = 0.12). (B) Corresponding image and histogram of the same tissue at 24 hrs (θ = −5.6°, r = 0.77), and (C) at 72 hrs of incubation (θ = −4.0°, r = 0.88). (D) Mean angle, θ, and mean vector length, r, versus incubation time obtained for the same tissue construct combining data from four images at each time point.

Analysis of fibroblast concentration in similar engineered tissue constructs, using collagenase digestion (0.45 mg/mL) and manual cell counting every other day up to 12 days, showed n00o significant change in cell number with culture time based on one-way ANOVA (p = 0.77, n = 12), consistent with published reports of depressed fibroblast proliferation in 3-D collagen gels ^{15, 26}. Therefore, tissue compaction, rather than cell proliferation, was primarily responsible for the higher cell density apparent at 72 hrs.

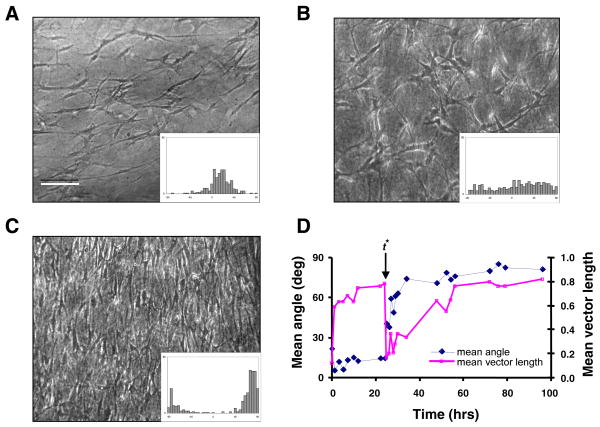
Engineered tissue constructs subjected to a sudden change in the uniaxial loading direction from the x-axis to the y-axis exhibited a striking remodeling response. Figure 3 shows an example tissue in which the loading direction was changed at t* equal to 24 hrs. Prior to t*, the cells were becoming aligned in the x-direction (θ < 15 °, r ~ 0.8), following a time course similar to that described above. Within one hour after the switch in load there was an abrupt drop in the mean vector length as cell alignment was substantially reduced (θ ~ 40°, r ~ 0.2). Cells subsequently reoriented themselves toward the direction of the newly applied load and eventually reached a steady state that was highly aligned in the y-direction (θ > 80°, r ~ 0.8). Both θ and r exhibited approximately exponential transient behavior, but were not necessarily synchronized (Fig. 3D).

FIGURE 3.

Remodeling response of a representative engineered tissue construct (ETC) in which uniaxial loading was switched from the x-axis (0°) to the y-axis (90°) at t* = 24 hrs. (A) Phase contrast micrograph with corresponding histogram of cell alignment at 24 hrs, just prior to the load switch (θ = 14.6°, r = 0.77). Scale bar, 200 μm. (B) Image and histogram of the same tissue at 25 hrs of incubation, or 1 hour post-switch (θ = 40.7°, r = 0.17). (C) Image and histogram at 96 hrs, or 72 hours post-switch (θ = 82.7°, r = 0.82). (D) Mean angle, θ, and mean vector length, r, versus incubation time, with t* indicating time of load switch.

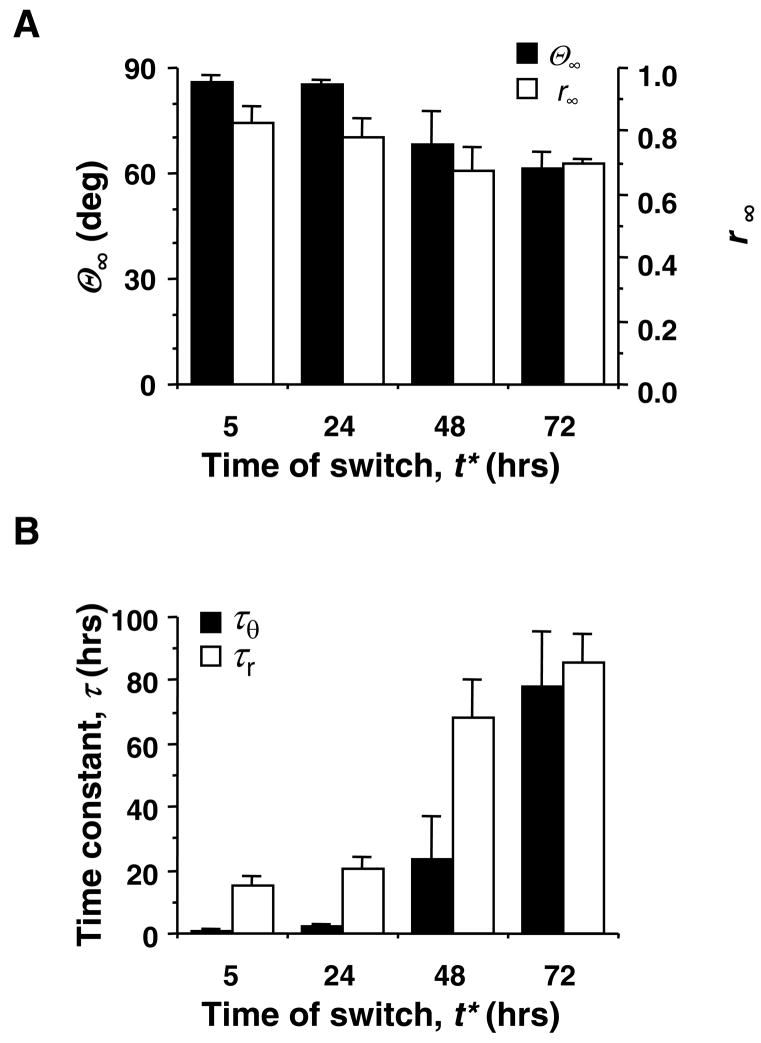
A substantial cell remodeling response was observed in all samples tested, in which the time of switch in the loading direction, t*, varied from 5 to 72 hours. However, the time required for remodeling was longer in tissues with larger values of t*. Least-squares fitting of the exponential equations (Eqs. 1a and 1b) to the data yielded correlation coefficients, r², ranging from 0.93 to 0.99, and typical RMS errors of less than 10 degrees for θ(t) and of 5% to 10% for r(t). Steady-state values of mean cell orientation (θ_∞) and strength of alignment (r_∞) at the end of each experiment are plotted against the time of switch (t*) in Fig. 4A. Both parameters indicate a strong remodeling response, with the final tissue structure being highly aligned toward the y-direction (θ_∞ 65°, r_∞ 0.7). While there was a trend toward reduced remodeling (reduced θ_∞ and r_∞ with increasing t*, this trend was only significant for θ_∞ p = 0.013).

FIGURE 4.

Mean values (± SEM, n = 4 for t* = 24 hrs, n = 3 otherwise) of exponential model parameters from fits to the cell remodeling time course data (see text for details). (A) Post-switch steady-state mean cell orientation, θ_∞, and strength of alignment, r_∞, versus time of switch, t*. (B) Estimated time constants, τ_θ and τ_r, versus t*.

Figure 4B shows the relationship between the fitted exponential time constants (τ_θ and τ_r) and the time of load switch (t*). The effect of t* was significant for both τ_θ (p = 0.0017) and τ_r (p = 0.0002). The average time constant for mean cell orientation, τ_θ, increased from less than 1 hour to greater than 60 hours as t* increased from 5 to 72 hours. The average time constant for mean vector length, τ_r, also increased from approximately 12 to 75 hours for the same range of t* values.

Collagen Alignment

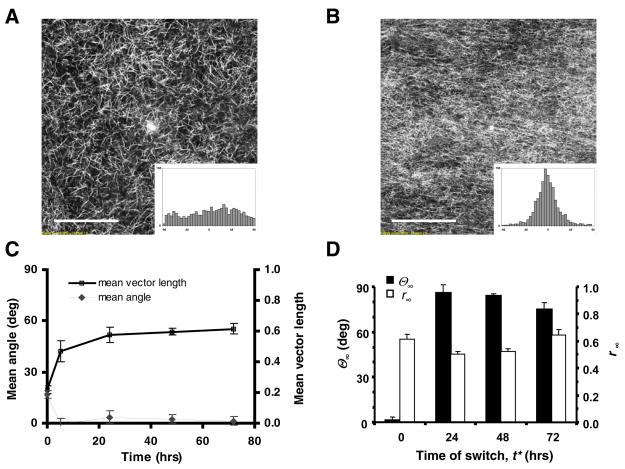
From the above cell remodeling response it appears that contact guidance from pre-aligned neighboring cells was insufficient to prevent realignment due to altered mechanical loading conditions. However, the underlying collagen matrix also imparts alignment cues that may differ from cell-cell contact guidance. To examine the role of contact guidance from the extracellular matrix, collagen fiber orientation was measured using confocal reflectance microscopy as described earlier. Figures 5A and 5C show that collagen fibers were essentially randomly distributed at time zero (r ~0.25), and as the ETCs were loaded uniaxially in the x-direction, collagen fibers gradually became aligned with a mean vector angle near 0° and a mean vector length ~ 0.6 (Figs. 5B and 5C).

FIGURE 5.

Collagen fiber remodeling response. (A) Confocal reflectance image of collagen fibers at 0 hrs (θ = 18.1°, r = 0.25), and (B) at 72 hrs of uniaxial loading in the x-axis (θ = 1.36°, r = 0.61). Scale bar, 50 μm. (C) Mean angle (θ) and mean vector length (r) versus incubation time (mean ± SEM, n = 3 at each time point) of collagen fiber alignment in response to uniaxial loading, reconstructed from multiple samples fixed and analyzed at each time point. (D) Post-switch steady-state mean (± SEM, n = 3) collagen fiber orientation (θ_∞) and mean vector length (r_∞) versus time of load switch (t*).

Figure 5D shows that when the loading direction was switched to the y-axis at t* values of 24, 48, or 72 hours, the collagen fibers eventually reoriented towards the y-direction. The steady-state mean vector length was in the range of 0.5 to 0.6, indicating a moderate level of structural alignment similar to non-switched gels. The average steady-state value of the mean collagen orientation was greater than 80° for values of t* ≤ 48 hours, but dropped below 70° for the longest t* value of 72 hours, indicating incomplete remodeling as found with the cells (Fig. 4A). Overall, collagen fibers exhibited similar trends in structural organization and remodeling as the cells, although the strength of alignment of collagen fibers remained lower than that of the cells.

Passive Response to Altered Loading Conditions

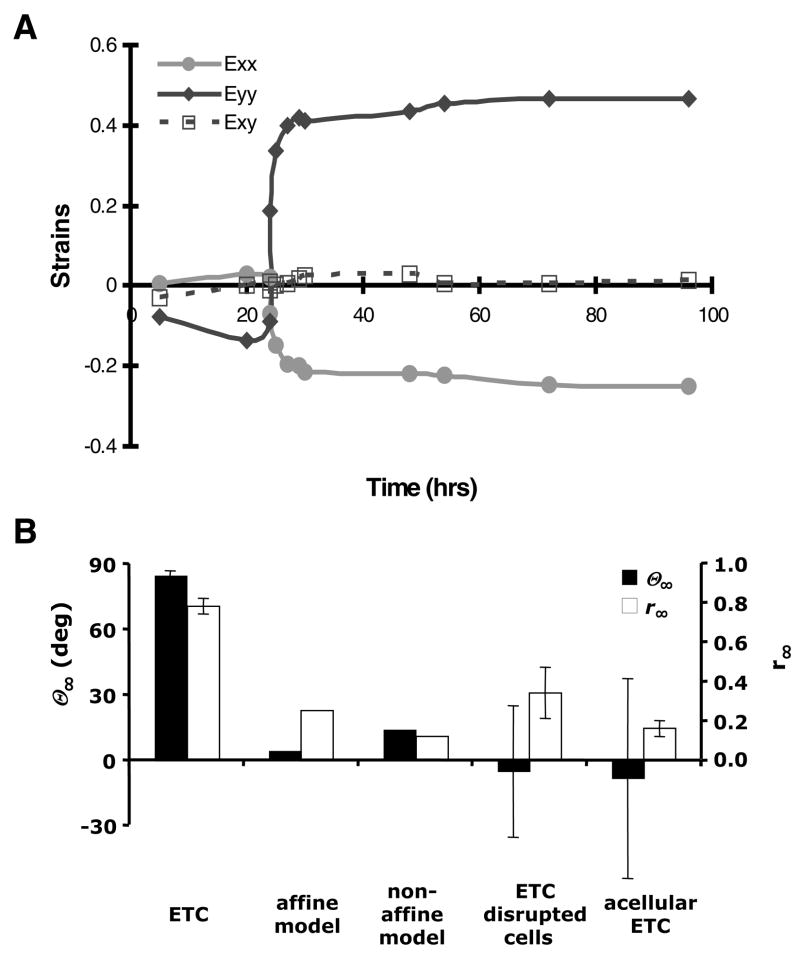
As shown in Figure 6A, initial loading caused negligible strain in the x-axis and shortening in the y-axis as cells compacted the gel. After the load axis was switched at t* = 24 hrs, the tissue deformation pattern transitioned to stretching in the y-axis and shortening in the x-axis (with negligible shear strain throughout the experiment). In the steady state, the final deformation relative to the pre-switch reference configuration was characterized by stretch ratios of λ_x=0.66 ± 0.015 and λ_y=1.42 ± 0.046 (n=4). Although this deformation did not occur instantaneously upon alteration of the loading, but rather took several hours to develop (similar to the cell reorientation time course), the final deformation was used in the theoretical analysis to assess the maximum potential impact on the underlying tissue structure.

FIGURE 6.

(A) Time course of two-dimensional finite strain throughout the loading experiment referred to the unloaded state (t = 0 hr) for a representative tissue with boundary conditions altered at t* = 24 hours. E_xx and E_yy are normal strains in the x- and y-axes, respectively, and E_xy is the shear strain. (B) Mean (± SEM) steady state cell/fiber orientation (θ_∞) and vector length (r_∞) measured in t* = 24 hrs ETCs, predicted by affine and non-affine kinematic models based on the biaxial deformation from panel A, and measured in ETC with cells disrupted during altered loading, and in acellular control tissue constructs.

According to the affine transformation model, the average initial cell alignment pattern with θ = 1.8° and r = 0.6 would change to θ_∞ 4.6° and r_∞ 0.25, which represents a substantial decrease in strength of alignment due to passive loading, and is very different from the experimentally observed steady state cell alignment with θ_∞ 85.1 ± 1.8° and r_∞ = 0.78 ± 0.04. In comparison, the non-affine model predicted a final cell alignment with θ_∞ = 14.4° and r_∞ = 0.12. Consistent with these model findings, in ETC experiments with the cell component chemically disrupted immediately after the load switch at t* = 24 hrs, the final steady state alignment parameters were θ_∞ = −5.0 ± 30.1 and r_∞ = 0.34 ± 0.13. Furthermore, acellular gels subjected to the same loading protocol yielded θ_∞ = −8.2 ± 45.8 and r_∞ = 0.16 ± 0.04. Both the models and the experimental findings suggest the passive kinematic response to the switch in loading conditions cannot explain the experimentally observed changes in tissue structural alignment in normal ETCs (Fig. 6B), implicating a substantial effect of active cell-directed remodeling.

Biaxial Mechanics

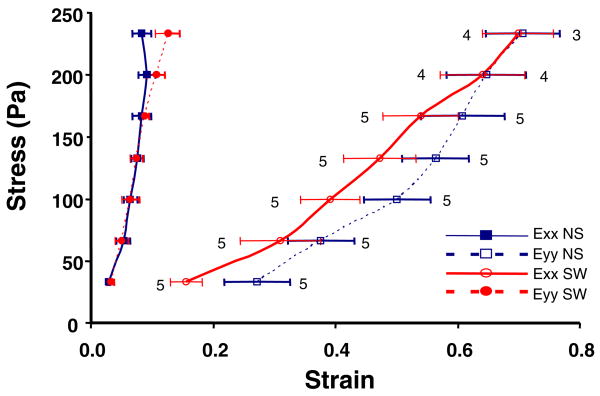
Biaxial testing of ETCs was performed to determine whether the remodeling of cellular and matrix structures was also accompanied by changes in material anisotropy that might impact mechanical function of the engineered tissues. The biaxial stress versus strain curves for the no-switch group, NS, were highly anisotropic, with the x-axis being stiffer (i.e. smaller strains at a given stress) than the y-axis (Fig. 7). The switched group, SW, was also mechanically anisotropic, but the y-axis was stiffer than the x-axis. These findings are consistent with the aforementioned structural data indicating cell and collagen alignment in the x-axis for NS, and comparable post-remodeling structural alignment in the y-axis for SW. The shear strain was independent of load and not significantly different from zero for both sets of gels (data not shown), indicating the biaxial tests were performed with the loading directions closely aligned with the underlying mean structural axes of the cells and collagen ²⁵.

FIGURE 7.

Piola-Kirchhoff stress versus finite strain, E_xx and E_yy, (mean ± SEM, n = 3 to 5 as shown) during equibiaxial isotonic mechanical testing of non-switched, NS, and switched, SW, engineered tissue constructs (see text for details). Although the tissues are highly anisotropic in both conditions, the preferred material axis changes from the x-axis for NS to the y-axis for SW.

Due to the strong correlation between structural and mechanical anisotropy in these tissues, we also compared mechanics in the fiber direction (x-axis for NS, y-axis for SW) with the cross-fiber direction (y-axis for NS, x-axis for SW) at an arbitrary load of 800 mg (stress of 133 Pa). The data indicated no significant difference in either the fiber strains or the cross-fiber strains between the two groups (p > 0.2). Consequently, the relative anisotropy of the tissue was comparable in the NS and SW constructs, although the preferred material axis direction was rotated by 90 degrees.

DISCUSSION

The objective of this study was to examine the effects of contact guidance and mechanical loading on the remodeling response of engineered tissue constructs. In particular, we tested the hypothesis that highly anisotropic ETCs retain the ability to remodel their structural and mechanical properties in response to an altered loading environment. The findings demonstrated that living 3-D tissue constructs with highly aligned cells and collagen fibers readily remodeled in response to an abrupt change in loading conditions, resulting in extensive alteration of structural and mechanical anisotropy of the tissue. This demonstrates that the cell remodeling response to mechanical loading can be strong enough to overcome the influence of contact guidance imposed by highly-aligned neighboring cells or the underlying extracellular matrix.

Our findings differ from some previous studies that have examined the effects of contact guidance and mechanical stimulation on cellular realignment. In particular, Wang and Grood showed that fibroblasts could be prevented from reorienting in response to cyclic deformation when cultured on an elastic substrate with fabricated microgrooves ³⁵. However, the use of an inert synthetic substrate made it impossible for the cells to modify the contact guidance cues. Thus, it is unclear how those findings on a coarse synthetic surface relate to cells growing in a fine 3D matrix. Interestingly, the actin cytoskeleton did reorient in the microgroove studies ³⁵, suggesting the cells remained responsive to mechanical cues, but their overall morphology was restricted by the patterned substrate.

In another related study, Mudera and co-workers devised a composite matrix of large fibronectin cables embedded in a fibrous collagen gel and oriented perpendicular to the direction of uniaxial mechanical loading ²⁴. Locally, fibroblasts attached and spontaneously aligned along the fibronectin cables and remained thus during mechanical stimulation, even though neighboring cells in the collagen matrix realigned parallel to the mechanical stimulus. It is possible that the fibronectin strand provided contact guidance cues that dominated the mechanical cues. Alternatively, the thick fibronectin strand may have shielded its attached cells from mechanical cues, such as substrate deformation, presented to cells in other regions of the collagen gel, leading to a heterogeneous remodeling response. The investigators did not examine the cytoskeleton of cells attached to the fibronectin cables, and hence it is unclear whether the cells were responding in any morphological way to the mechanical stimulus. However, the cells on fibronectin exhibited trends in matrix protease gene expression indicative of a mechano-active state ²⁴.

Our results are consistent with the findings of Barocas et al., who demonstrated that smooth muscle cells cultured in magnetically aligned collagen gels can overcome existing contact guidance cues and remodel in a manner governed by the external mechanical boundary constraints ¹. The present study extends that work in several ways. In the study by Barocas et al., suspended cells were only subjected to a single loading condition associated with the cylindrical casting mold ¹. In the present study, cells were first subjected to a mechanical stimulus that resulted in spontaneous alignment of the initially isotropic cell and matrix architecture. The resulting structurally and mechanically anisotropic tissues were then exposed to an altered mechanical stimulus that conflicted with the existing cell-cell and cell-matrix contact guidance cues, which more realistically represents what might occur during surgical implantation of an engineered tissue graft.

In addition, the present study demonstrates a change in biaxial mechanical properties as a direct consequence of cell and matrix remodeling in such engineered tissue constructs. From a functional standpoint, changes in mechanical properties of the tissue are critical, especially for applications in which the tissue must survive in a mechanically demanding environment. The reorientation of fibroblasts was accompanied by a reorganization of the collagen matrix and realignment of the material axes of the anisotropic tissue construct. This led to a 90-degree rotation in the direction of greatest stiffness of the tissue indicating the potential for major fundamental changes in the biaxial mechanical properties of engineered tissue constructs in response to alterations in loading conditions. Efforts to develop structurally-based constitutive equations describing the mechanical properties of such model tissues are ongoing ³¹.

The protocol of subjecting model tissues to a step change in uniaxial loading from the x-axis to the y-axis was designed to provide a convenient mechanical stimulus that clearly conflicted with structural cues developed prior to the load switch, making the individual effects on remodeling easier to distinguish. While this loading protocol was not intended to represent a particular pathologic or surgical scenario, there are realistic examples of altered loading conditions that may give rise to comparable levels of tissue remodeling. For instance, a similar transition in mechanical environment could arise due to surgical implantation of a statically cultured vascular graft or myocardial patch into the dynamic host tissue, since most cell types align parallel to a static mechanical stretch but perpendicular to cyclic stretching ^{8, 30, 34}. Nevertheless, the relevant message from this work is that when designing living tissues, one cannot necessarily rely on contact guidance cues to sustain structural and functional anisotropy. It is important to accurately characterize and mimic the intended in vivo environment during the process of culturing living tissue replacements to prevent unwanted remodeling and improper function after surgical implantation.

An interesting caveat was the finding of a significant increase in the time constant for remodeling as the initial loading time was increased, indicating that it takes longer for more strongly pre-aligned ETCs to remodel after a change in loading conditions. It might be extrapolated that native tissues, which have been loaded for extremely long time periods, will likely require a long time to remodel as well. Indeed, the process of structural remodeling in healing myocardial infarcts occurs over a timeframe of weeks ¹⁶. This is also consistent with a study by Sipkema and co-workers ²⁹ in which four hours of cyclic axial deformation of rat renal arteries caused no apparent change in endothelial cell alignment, although actin stress fibers within the cells did reorient 90° from the axial to the circumferential direction.

We have interpreted the observed changes in ETC cell and matrix structure as an active remodeling response to the applied loading conditions. This is certainly valid for the initial alignment represented in Figure 2, since our loading device is designed so that essentially all of the observed deformation (e.g. from Fig. 1A to 1B) and associated structural changes result from endogenous cell traction forces acting over time. However, passive stretch due to loading perpendicular to the initial fiber direction (e.g. from Fig. 1B to 1C) would tend to reduce this initial alignment, potentially redirecting the associated contact guidance cues. While the non-affine model predicted greater disruption of alignment than the affine model, mean alignment remained predominantly oriented in the x-direction in both cases. Both experimental and modeling results support the conclusion that while the passive response to altered loading conditions can decrease the initial cell and matrix alignment, x-directed contact guidance cues persist, and the extensive reorientation of cells and collagen into the y-direction requires a substantial active cell-directed remodeling response.

Limitations of the Study

One limitation of the methods of this study is that the time course of cell and collagen remodeling had to be reconstructed from snapshots of the tissue structure at selected time points. That is, individual cells or collagen fibers were not tracked in time. To account for variability within a given gel, multiple images were acquired from the same general region of each tissue. Images of cells were obtained using phase contrast microscopy at relatively low magnification (10× objective) in order to sample a large number of cells. Because collagen fibers were not visible using this method, collagen fiber alignment was measured using confocal reflection microscopy at higher magnification (60× objective) in fixed gels either at the end of the loading study to determine the final collagen orientation, or in a separate set of gels in which the experiment was terminated prematurely to capture the instantaneous collagen structure. The consistency between cell and collagen alignment suggests this was not a major limitation of the study. The major source of error in the alignment measurements was in the accuracy with which the tissue was placed on the microscope stage. We conservatively estimate this error to be within ±10 degrees, which was not sufficient to impact the detection of remodeling from the x-axis to the y-axis, nor was it sufficient to obscure detection of incomplete reorientation observed with longer initial loading periods.

CONCLUSION

We have examined the structural and mechanical remodeling of anisotropic fibroblast-populated 3-D model tissues. This study points out for the first time that even in highly aligned engineered tissues with strong contact guidance cues, cells remain highly responsive to mechanical loading conditions, and may retain the capacity to adversely remodel a tissue when those loading conditions are altered, leading to significant changes in structural and functional anisotropy of the tissue construct. This could have important practical implications when designing functional engineered tissues for surgical implantation where the mechanical environment may be abnormal and complex. Therefore, it is critical that mechanical conditioning is carefully controlled when culturing tissues in vitro, and carefully matched to the environment of the intended implantation site.