A Mechanochemical Model Explains Interactions between Cortical Microtubules in Plants

Abstract

Microtubules anchored to the two-dimensional cortex of plant cells collide through plus-end polymerization. Collisions can result in rapid depolymerization, directional plus-end entrainment, or crossover. These interactions are believed to give rise to cellwide self-organization of plant cortical microtubules arrays, which is required for proper cell wall growth. Although the cell-wide self-organization has been well studied, less emphasis has been placed on explaining the interactions mechanistically from the molecular scale. Here we present a model for microtubule-cortex anchoring and collision-based interactions between microtubules, based on a competition between cross-linker bonding, microtubule bending, and microtubule polymerization. Our model predicts a higher probability of entrainment at smaller collision angles and at longer unanchored lengths of plus-ends. This model addresses observed differences between collision resolutions in various cell types, including Arabidopsis cells and Tobacco cells.

Introduction

Many vital cell functions, from cell division to organelle positioning (1) and aster formation (2), require complex interactions among microtubules (MTs). An exquisite model system for MT-MT interaction is the two-dimensional cortex of elongating plant cells, where MTs self-organize into parallel arrays that are required for unidirectional cell wall expansion (3). This cellwide order, on the length scale of microns, is hypothesized to result from molecular interactions involving individual microtubules, microtubule-associated proteins, and the cell membrane.

MTs are stiff, polar polymers composed of tubulin. In plant cortical MTs, photobleaching studies show that individual tubulin subunits remain mostly fixed relative to the cell cortex (4). However, MTs are highly dynamic due to polymerization at the so-called plus-end, which randomly switches between states of growth and rapid shrinking (5) as well as intermittent pauses (4). Transition from growth to shrinkage is known as a “catastrophe”.

Because cortical MTs are approximately confined to a two-dimensional surface, the growing plus-end of one MT (herein referred to as the “incident MT”) can collide along the length of another (the “barrier MT”). The collision may result in several possible outcomes. The incident MT may undergo a catastrophe, or it may continue to grow unperturbed, crossing over the barrier MT. These outcomes have been reported at predominantly steep angles of collision (6). At shallow angles of collision, the incident MT may become entrained with the barrier MT, after which the plus-end grows parallel to the barrier MT, resulting in a sharp bend in the MT at the site of collision. This phenomenon is commonly referred to as zippering (6) or plus-end entrainment (7). Other collision outcomes are possible: the incident MT may buckle before the barrier (8); it may cross over the barrier and continue in a perturbed direction (9); or, it may become severed at the crossover point (8).

Two scales of questions about cortical MT self-organization remain to be elucidated.

First are cell-level questions:

• How do molecular interactions between MTs give rise to cell-scale order?

• How do changes in the molecular interactions affect self-organization?

This aspect has received recent attention (6,7,10–12). These models have assumed phenomenological descriptions of MT-MT interaction.

A second scale of questions is molecular:

• How do interactions such as entrainment and collision-induced catastrophe occur?

• Why do they occur at different frequencies for different collision angles?

• How are MTs held to the cortex and how does this anchoring affect MT-MT interactions?

Here, we present a mechanochemical model of cortical MTs to address the second-scale questions.

The first section of this article introduces a kinetic model for MT anchoring to the cortex, which allows us to infer chemical rate constants from experimentally measured free lengths. This model is used in subsequent sections of MT-MT interactions. The second section introduces mechanical models for collision-induced catastrophe, crossover, and plus-end entrainment. For collision-induced catastrophe, a dimer-level model leads to an estimate of its probability, P_cat. For crossover, we present an energetic model independent of details of the crossover pathway. For entrainment, we present an energetic model as well as a dynamic (torque-based) model. In the final section we use the energetic models of crossover and entrainment in an adiabatic approximation to compute probabilities for these collision resolutions. Through these models, entrainment is explained by a competition between cross-linkers, which tend to bundle adjacent MTs, and the bending stiffness of the incident MT, which opposes entrainment. We find this energetic competition is sufficient to explain the angle-dependence of entrainment and crossover.

MT-cortex anchoring

Although the molecular identity of the anchor linking MTs to the cortex is unknown, the process involves phospholipase-D (13,14) and the CLASP protein (15). One or both of these may form the physical anchor. MTs in CLASP null mutants remain attached to the membrane, although with longer free ends (15). Here, we refer to the physical anchor without speculation regarding its components. As an MT grows, the anchor protein chemically attaches and detaches along its length. If the MT were a long, stationary rod adjacent to the membrane, and anchors attached with rate constant k_on (with units μm⁻¹ min⁻¹) and detached with rate k_off (in min⁻¹), then the density of attachments, a(x, t), would be governed by the equation

$$\partial a/\partial t=k_{\text{on}}-k_{\text{off}}a\text{.}$$ (1)

Here we assume that the binding rate k_on is uniform along the length of the filament. In reality, the free plus-end can fluctuate away from the membrane, in principle reducing k_on near the tip compared to near the anchored regions, where the filament is always close to the membrane. However, two facts suggest that nonuniformity of k_on is insignificant. First, the persistence length of a MT is millimeters, whereas the free length is typically 3 μm, so thermal undulations are small. Second, below we estimate k_on ∼ 0.3 min⁻¹ μm⁻¹, suggesting that anchor attachment is reaction-limited as opposed to diffusion-limited; thus, fluctuation of the filament is not the bottleneck. Note that the anchor kinetics may be different tens of microns behind the plus-end, where the MT is older and other MAPs may act. Our model is only concerned with anchors near the plus-end. Consistent with this, the data we use below to estimate the kinetic rates only incorporates anchor spacings at the tip of the MT.

In steady state, the density of anchors is a = k_on/k_off ≡ a_c. This density corresponds to a spatial Poisson process (16), and the distance between anchors, L, would have cumulative probability distribution G(l) = 1 − exp(− a_cl) (that is, G(l) is the probability that L < l). Thus, lengths would be exponentially distributed. However, if the plus-end of the MT is growing at constant velocity v^p_g, then the density of anchors is lower near its growing tip, as this region of MT has not been present for as long as the region further back. The anchor density is governed by same differential equation, Eq. 1, but with boundary condition a($v_g^p$t, t) = 0. The solution is

$$a\left(x,t\right)=a_c\left(1-e^{-k_{\text{off}}\left(t-x/v_g^p\right)}\right),$$

or, as measured a distance l = x – v^p_gt from the growing tip, a(l) = a_c(1 – e^−λl), where λ ≡ k_off/$v_g^p$. This varying density gives rise to a nonhomogeneous Poisson process (16), and the distance between the growing tip and the first anchor, L, is a random variable with cumulative density

$$P(L<l)=G\left(l\right)=1-\exp \left(-{\int }_0^{l}a\left(l^{\prime }\right){dl}^{\prime }\right)\text{.}$$ (2)

The probability density, g(l), is found by differentiating Eq. 2. There are two competing length scales—the mean spacing in absence of growth, a_c⁻¹ and the length of growth before detachment, λ⁻¹.

The tip-length distribution has been experimentally measured by Ambrose and Wasteneys (15) in both wild-type (WT) cells and the clasp-1 mutant and is shown in Fig. 1. We estimate a_c and λ in the probability density by fitting Eq. 2 to the data using the method of maximum likelihood and a bootstrap. The fit is shown in Fig. 1. Note that the exponential distribution predicted by the stationary model would not reproduce the nonzero maximum seen in the experimental data, whereas the model including growth does. Furthermore, given $v_g^p$ = 3.5 μm/ min (17), we can back-engineer the kinetic rate constants near the tip. These are shown in Table 1.

Figure 1.

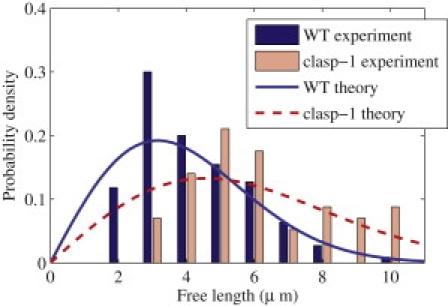
The free lengths L from the MT tip to the last anchoring site. Experimental data from Ambrose and Wasteneys (15). The nonhomogeneous distribution predicted by Eq. 2 provides qualitative agreement for both WT and clasp-1 data.

Table 1.

Chemical kinetic rate constant for the anchor protein in WT and clasp-1 mutants

	kon (min−1μm−1)	koff (min−1)
WT	0.34 ± 0.13	(5.5 ± 1.3) × 10−5
clasp-1	0.16 ± 0.08	(4.5 ± 1.0) × 10−5

The small detachment rate predicts that once an anchor has attached, it will be, on average, weeks before it detaches—anchoring appears to be an effectively irreversible process. However, near the tip, the density of anchors is limited not by dissociation but by the growth of the MT tip. Further back, the anchor density will be limited by MT catastrophe. Note we are modeling growing MTs only, and the experimentally observed free lengths are from growing MTs, thus the rates in Table 1 are only relevant while the MT is in the growing state.

MT-MT interactions

In this section, we consider the interaction between two MTs after collision, in which the growing plus-end of an incident MT collides along the length of a barrier MT. There are several possible resolutions to a collision. The incident MT may switch to the shrinking state, which we refer to as collision-induced catastrophe. It may cross over the barrier MT and continue growing (9), or it may become entrained. We consider these three resolutions, depicted in Fig. 2, neglecting other possible resolutions, such as buckling before the barrier or becoming severed at the crossover point (8).

Figure 2.

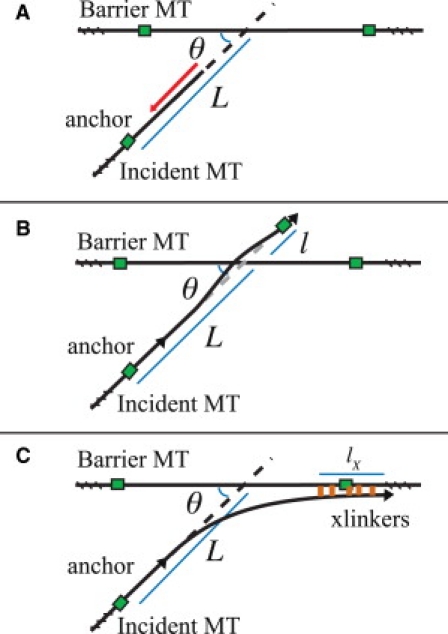
Three possible collision resolutions. The incident MT collides with a barrier at an angle θ and with free length L. Possible resolutions are (A) catastrophe, in which the incident MT begins shrinking, (B) crossover, in which the incident MT develops a small bend to overpass the barrier and continue growing unperturbed, and (C) plus-end entrainment, in which the incident MT becomes entrained by the barrier via cross-linking proteins (orange online). MTs are shown in black, whereas anchors are shown as green squares.

In the following, we assume the incident MT is colliding with the barrier at collision angle θ ∈ [0, π/2], where θ = 0 for parallel MTs and we ignore the polarity of the barrier MT. The distance from the collision site to the closest anchor on the incident MT is L.

The remainder of the article is organized as follows. Anchoring and catastrophe are slow processes and effectively irreversible but mechanical relaxation and MAP cross-linking are fast and reversible. When a collision occurs, it is resolved as soon as an anchor attaches, either on the distal side of the target on in an entrained configuration, or if the incident MT “catastrophes”. The catastrophe probability is described by a dimer-level model we describe in the next section.

We then consider the conditional probabilities of crossover and entrainment, given no catastrophe occurred during the collision (either natural catastrophes or collision-induced catastrophes). The incident MT has a large configuration space to explore thermally, including some configurations in which its tip is far from the membrane, some in which it is crossed over the barrier and close to the membrane, and finally, configurations in which it is entrained by the barrier MT. Assuming these are explored in quasiequilibrium, at the moment of anchoring, the probabilities of being in a crossover configuration or an entrained configuration only depend upon the energies of those states. Therefore, we compute the energy of crossover configurations, and the energy of entrained configurations. To be certain that the entrained configurations are indeed explored in quasiequilibrium, we present a mechanistic (torque-based) model of entrainment describing how an incident MT is progressively entrained by a barrier MT and the action of cross-linking MAPs. In the final section, we use the crossover and entrainment state energies to compute overall angle-dependent probabilities of entrainment and crossover.

Collision-induced catastrophe

Catastrophe is the spontaneous switch of the MT plus-end from a state in which growth dominates, to a state in which shrinkage dominates, due to the loss of the polymerization-promoting GTP-tubulin cap. VanBuren et al. (18) developed a model for MT polymerization and catastrophe at the dimer level. In this model, dimers associate at a rate k⁰₊ and dissociate at a rate

$$k_{-}=k_{+}^0\times \text{exp}\left(-\Delta G/k_{\mathrm{B}}T\right),$$

where ΔG is the energy required to remove the dimer from the MT lattice. This energy is different for GTP-tubulin dimers, which favor growth, and GDP-tubulin dimers, which favor disassembly. Newly associated dimers are GTP-tubulin, and they switch to GDP-tubulin through GTP hydrolysis at rate k_hyd.

We fit the bond energies and hydrolysis rate parameters in the model of VanBuren et al. (18) to the growth rate, shrinkage rate, and catastrophe rate of Arabidopsis at 31C from Kawamura and Wasteneys (17) and found parameters listed in Table 2. These parameters are comparable to the parameters reported in VanBuren et al. (18). We modify the model to consider collision with a barrier MT as follows. A growing MT that encounters a barrier will have the same k_hyd and k_–, but for protofilaments in contact with the barrier, k₊ will be modulated by a prefactor α, that is, k₊ = αk⁰₊. We compute α as follows. When the incident MT encounters the barrier, its tip is undergoing thermal fluctuations and is a distance ρ away from its equilibrium position. Its energy, E_jump(ρ), is the minimum of the linear elastic rod energy,

$$E=\frac{B}{2}{\int }_0^L\kappa {\left(s\right)}^{2}ds,$$ (3)

where B is the bending modulus of a MT, L is the MT's free length, κ(s) is the curvature, and arc length s of the incident MT is measured from the last anchor. For small deformation, κ(s) ≈ y″(x), where y is the height of the MT above the membrane and x is distance along the membrane. From this we obtain the familiar beam equation y^(iv)(x) = 0 for x ∈ (0, L), where L is the distance from the anchor to the barrier and we measure from the anchor. We use boundary conditions y(0) = y′(0) = 0, y″(L) = 0 and y(L) = ρ and find

$$E_{\text{jump}}\left(\rho ,L\right)=6B{\rho }^2/\left(25L^3\right)\text{.}$$

The prefactor α, which depends on L, is the probability that thermal fluctuations allow the incident MT tip to clear the barrier, allowing the addition of a subunit, as opposed to subunit addition being blocked by the barrier (see Fig. 3 A). We compute the fraction

$$\alpha \left(L\right)=\frac{{\iint }_{\text{clear}}{e}^{-E_{\text{jump}}/k_{\text{B}}T}dA}{{\iint }_{\text{clear}}{e}^{-E_{\text{jump}}/k_{\text{B}}T}dA+{\iint }_{\text{block}}{e}^{-E_{\text{jump}}/k_{\text{B}}T}dA},$$ (4)

where the block region is 0 < y < d and the clear region is y > d (both regions with infinite width in the direction parallel to the barrier), ρ is the radial coordinate, and d is the diameter of a MT.

Table 2.

Parameters used in the dimer-level model modified from VanBuren et al. (18)

Parameter	Value
k+0 (s−1μm−1)	4
c (μM)	5
ΔGLat (kBT)	10
ΔG∗Long (kBT)	6.8
ΔGkink (kBT)	6
khyd (s−1)	1.3

Figure 3.

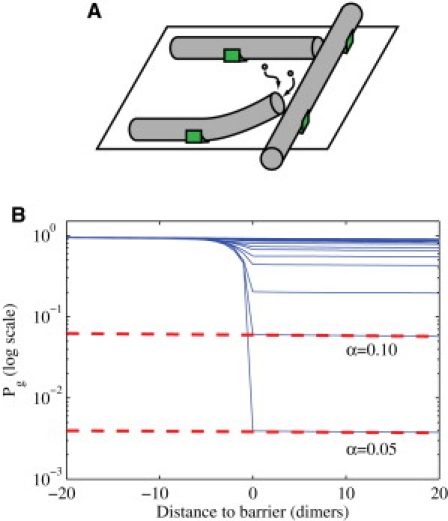
Collision-induced catastrophe. (A) Two MTs approach a barrier MT. Thermal fluctuations at their tips allows them to either clear the barrier (bottom incident MT), or get temporarily blocked (top incident MT). Anchors are shown as green boxes. (B) Probability of being in the growth stage, i.e., that catastrophe has not yet occurred, versus distance to the barrier MT, for various values of α (log-linear scale). The drop between the prebarrier curve and the postbarrier curves (shown as dashed lines for some α) provides the probability of collision-induced catastrophe.

For α = 1 (no barrier), we simulate MT growth in this way 1000 times and observe that the probability of still being in the growth state P_g decays exponentially as a function of space. That is, fitting to ∂P_g/∂x = –r(x)P_g, we find a constant r(x) = r₀. The catastrophe rate is

$$f_{\text{cat}}=r\left(x\right){\overline{v}}_g^p=0.2{\text{min}}^{-1}$$

by construction. If α << 1, P_g exhibits a rapid drop near the barrier, shown in Fig. 3 B, which corresponds to a temporary increase in catastrophe rate near the barrier. The width of the drop represents MTs that either influence the barrier and depolymerize GTP dimers before undergoing catastrophe, or MTs that overcome the barrier but have a weakened GTP-cap, and thus undergo a collision-induced catastrophe beyond the collision site. As α → 0, the r(x) resembles a δ-function. The width of the drop depends on how the precise time of catastrophe is defined. As in VanBuren et al. (18), we use the moment when the MT has lost its entire GTP cap, after which we find the MT always enters the shrinking state. To compute a catastrophe probability independent of the arbitrarily-defined beginning and end of the collision, we plot P_g on a log-linear plot and take the drop, P_cat(α), to be the difference in y intercepts of the line before and after the collision site, as shown in Fig. 3 B. Note this quantity is distinct to the experimentally measured probabilities of catastrophe (6,8), which may include spontaneous catastrophes. Using the relationship between α and L from Eq. 4, we compute the probability of collision-induced catastrophe as a function of the free length L. Convolving this with the anchoring model

$$P_{\text{cat}}={\int }_0^{\infty }{P}_{\text{cat}}\left(L\right)g\left(L\right)dL,$$

we find P_cat = 0.03 for WT Arabidopsis. A low probability agrees with experiments on petiole cells of A. thaliana, where the probability of catastrophe during a steep collision is 9% (8). However, a study of Tobacco BY-2 cells (6) reported collision-induced catastrophe in up to 50% of collisions. Interpreting this in light of our model, it suggests differences in anchoring properties between cell lines: Denser anchors would disfavor crossover and entrainment, favoring catastrophe. As a demonstration of this concept, increasing the anchor attachment rate k_on to 10 times the value we found for A. thaliana, leads to a mean length of 1.2 μm (i.e., one-third of WT). This tighter anchoring leads to P_cat = 0.47, roughly in agreement with Dixit and Cyr (6).

In our model, dimer addition at any protofilament requires the entire MT tip to fluctuate above the barrier. In reality, heterogeneity in the way each protofilament confronts the barrier may lead to the incident MT getting stuck near the cortex, or partially or entirely above the barrier. These effects are neglected in our model. We also assume all protofilaments encounter the barrier at the same depth in the lattice, which neglects the cylindrical shape of the barrier as well as the slight offset of protofilaments in a B-lattice (18). To test the sensitivity on the latter assumption, we ran simulations in which protofilaments encountered the barrier at different depths and found the effect to be weak. A more detailed model of protofilament and barrier geometry may explain the strong angle-dependence observed experimentally in Dixit and Cyr (6), but would be computationally taxing.

Crossover

For crossover, the MT must bend to surpass the barrier. Note that in many eukaryotic cells, the fluid membrane may undulate, allowing a hypothetical MT to crossover without bending. In the plant case, turgor pressure and the stiff cell wall (with a Young's modulus of several hundred pN/nm² (19)) render membrane undulations insignificant. The configuration of the incident MT is determined by minimizing the linear elastic rod energy, similar to Eq. 3, except with

$$x\in \left(-L,0\right)\cup \left(0,l\right)$$

and boundary conditions

$$y\left(-L\right)=y^{\prime }\left(-L\right)=y\left(l\right)=y^{\prime }\left(l\right)=0,\text{and}y\left(0\right)=d,$$

where d is the diameter of a MT. We find the energy associated with crossover to be

$$E_{\text{cross}}\left(l,L\right)=\frac{3B{d}^2{\left(L+l\right)}^3}{L^3{l}^3}\text{.}$$ (5)

Note that there are many pathways to this final state, some of which involve prolonged contact between the barrier and incident MT (8). However, in energetic terms, the final state of these distinct pathways is assumed to be the same.

Plus-end entrainment

Although plus-end entrainment (commonly called zippering) has been reported frequently (4,6,15), its molecular mechanism remains unclear. After a MT is entrained by another, the MTs form a bundle most likely mediated by members of the MAP65 class of MAPs, which cross-link adjacent MTs together with a spacing of 20–30 nm (20). Once bundled, MTs remain dynamic (4), although possibly with different polymerization properties (21). In our model, depicted in Fig. 2 C, we refer to a cross-linker protein that preferentially bundles adjacent MTs with a rest length of l₀ between MTs, and a spacing of δ between adjacent cross-linkers. The chemical bonding energy gained by the cross-linker associating with two MTs is μ_X. The cross-linker is stiff, with a Hookean spring stiffness of k_X ∼10⁻² pN/ nm (22).

In this section, we present a model for how an incident MT can be progressively bundled into a parallel orientation with the barrier MT, as subsequent cross-linkers provide a torque reorienting its plus-end. Its final configuration will minimize the energy

$$E_{ME}=\frac{B}{2}{\int }_0^{l+L}\kappa {\left(s\right)}^{2}ds+\frac{k_X}{2\delta }{\int }_0^{l_X}y{\left(s\right)}^{2}ds,$$ (6)

where y is the distance from the incident MT to the barrier MT and l_X is the length of incident MT that is cross-linked, so n_X ≡ l_X/δ is the number of associated cross-linkers. In this case, it is convenient to measure the arc length s of the incident MT back from its plus-end. On the length-scale of interest, L, Eq. 6 can be nondimensionalized to

$$\tilde{E}={\int }_0^1{\left({\tilde{y}}^{″}\left(\tilde{x}\right)\right)}^{2}dx+K{\int }_0^r{\tilde{y}}^{2}d\tilde{x},$$ (7)

where r = l_X/L and K = (k_XL⁴)/(δB) ≈ 10³ using the parameters in Table 3. The mechanical energy in the cross-linked region is 1/K relative to the energy in the MT bending energy, so in the region of MT that is cross-linked, deflection is insignificant. Thus, we restrict our treatment to the un-cross-linked region. For small collision angles, the minimal energy is

$$E_{ME}=2B{\theta }^2\left(l^{\ast 2}+{3l}^{\ast }L+3L^2\right)/l^{\ast 3},$$

where l^∗ = L + l – l_X. For larger collision angles, we minimize Eq. 6 numerically.

Table 3.

Parameters used in the biophysical model of MT-MT interactions

Parameter	Meaning	Value	Reference
Parameters used in computing entrainment probability
B	Bending modulus of MT	3–20 × 106 pN nm2	(31)
d	Width of MT	25 nm	(20)
δ	Mean spacing between cross-linkers	35 nm	(20)
μX	Chemical bonding energy of cross-linker	14 kBT	(32)
vpg	MT growth velocity	3.5 μm/min	(17)
Other parameters
fcat	Free-space catastrophe rate	0.2 min−1	(17)
l0	Mean spacing between cross-linked MTs	35 nm	(20)
kX	Cross-linker spring constant	10−3–10−2 pN/nm	(22)

The chemical bonding energy of a cross-linker is calculated from the dissociation constant K_d measured in tobacco MAP65-1b by Wicker-Planquart et al. (32) using μ_X = k_BT ln K_d (33).

In addition to the mechanical energy, E_ME, of the bent MT and stretched cross-linkers, there is also the chemical bonding energy of the cross-linkers,

$$-{\mu }_X{n}_X=-{\mu }_X{l}_X/\delta ,$$

which acts favorably (negatively). The energy associated with entrainment is thus

$$E_{\text{ent}}\left(l,L,n_X\right)=E_{ME}\left(l,L,n_X\right)-{\mu }_X{n}_X\text{.}$$ (8)

The energy in Eq. 8 describes the final state of an entrained MT, without mentioning the pathway through which it arrived there. As mentioned above, the adiabatic approach we use in the next section to compute the probability of entrainment is independent of the details of the pathway, provided that such a pathway exists and that there are no energetic barriers preventing entrainment. Here, we describe a possible mechanistic model for entrainment via torque provided by cross-linkers to demonstrate a pathway free of energetic barriers to the entrained state. This model is similar to the model of actin bundling proposed in Yang et al. (23).

The mechanistic model below is presented as follows. The incident MT tip has an initial deflection making its angle at the collision site θ_X (which is distinct from θ, the angle between the undeflected portion of the incident MT and the barrier MT; see Fig. 4). We compute the torque τ with which the bending rigidity of the MT resists entrainment. We then compute the torque τ_X with which putative cross-linkers promote further entrainment. If τ_X > τ, then θ_X decreases. If θ_X = 0 is an attractive steady state of this process, the MT becomes entrained.

Figure 4.

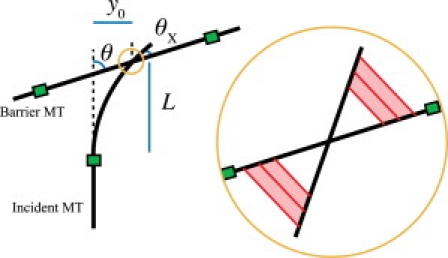
A mechanical pathway to entrainment. An incident MT encounters a barrier MT at an approach angle θ. The incident MT is slightly bent due to thermal fluctuations and, at the point of intersection, makes an angle θ_X with the barrier MT. (Inset) Cross-linkers (red online) attach two intersecting MTs. The cross-linkers vary in length, l_i ∈ [l₀, l_M] and are spaced δ apart. Distance along the bisector to the i^th cross-linker is x_i.

Suppose the straight, anchored section of an incident MT makes an angle θ with a barrier MT, while its free length bends slightly, so that the angle between the two MTs at the collision site is θ_X, as shown in Fig. 4. The MT acquires an initial deflection before the first cross-linker attaches. Here we assume this initial deflection is due to thermal fluctuations, under which the average tip deflection and tip angle (24) are

$$y_0=0.57\sqrt{L^3/L_p},$$ (9)

$$\tan (\theta -{\theta }_X)=1.90\sqrt{L/L_p},$$ (10)

where L_p = B/k_BT is the persistence length of a MT. Cytoplasmic streaming (4) may further promote initial deflection, so our assumption in this section is an underestimate.

At the collision site, the incident free-end is subject to torque τ, caused by cross-linkers elaborated upon below. The MT's shape is described by the beam equation with boundary conditions

$$y\left(L\right)=y^{\prime }\left(L\right)=0,y^{\prime }\left(0\right)=\tan (\theta -{\theta }_X)\text{and}{y}^{″}\left(0\right)=\tau /B\text{.}$$

We find the relationship among the tip deflection y₀, cross-linker torque, and intersection angle,

$$y_0=(L/6)(4\tan (\theta -{\theta }_X)-\tau L/B)\text{.}$$ (11)

A particular Hookean cross-linker at position i provides a torque

$${\tau }_i=x_i{k}_X(l_i-l_0),$$

where l_i is the length of cross-linker i and x_i is its position along the bisector of the MTs (see Fig. 4). Whereas cross-linkers have a chemical bond energy μ_X favoring attachment, this attachment cannot pull distant MTs together that have been separated by tens of nanometers of cytoplasm, even if it is energetically favorable. Therefore we assume a cross-linker will attach only if the MT bond sites are separated by no more than l_M given by the equipartition theorem,

$$k_{\mathrm{B}}T/2=(k_X/2){(l_M-l_0)}^2\text{.}$$

The total torque from all cross-linkers is

$$\begin{array}{c}{\tau }_X=2\int x\left(s\right)\frac{k_X}{\delta }(l\left(s\right)-l_0)ds,\\ =\frac{k_X}{\delta }\left(\frac{1}{3}{l}_M^3+\frac{1}{6}{l}_0^3-\frac{1}{2}{l}_0{l}_M^2\right)\frac{\cos ({\theta }_X/2)}{{\sin }^2({\theta }_X/2)},\\ =C\frac{\cos ({\theta }_X/2)}{{\sin }^2({\theta }_X/2)},\end{array}$$ (12)

where the characteristic torque C ≈ 2–5 pN nm contains the molecular properties of a cross-linker, using ranges from Table 3. The torque is unbounded as θ_x → 0. This divergence occurs because as the angle between the MTs shrinks, the number of cross-linkers that pull them together increases.

In mechanical equilibrium, the elastic restoring torque of the MT τ, found by solving Eqs. 10 and 11, will balance with the cross-linker torque τ_X from Eq. 12. Out of mechanical equilibrium, the angle θ_X obeys

$$d{\theta }_X/dt=v\left({\theta }_X\right)({\tau }_X\left({\theta }_X\right)-\tau \left({\theta }_X\right)),$$

where ν is the rotational mobility. If τ_X < τ, the incident MT will straighten. If τ_X > τ, the incident MT will bend toward the barrier MT and another cross-linker can attach. We find that τ_X(θ_X) – τ(θ_X) < 0 for θ_X > 0 and passes through the origin (not shown). That is, attachment of a cross-linker increases the torque and, because of the geometry, allows yet another cross-linker to attach. Thus, the MT becomes entrained.

For L = 3 μm, the MT can access the entrained state through this pathway at collision angles up to 90°. At L = 1 μm, this pathway leads to entrainment for θ < 65°. These angles are comparable to angles at which entrainment occurs. This tells us that thermal fluctuations in the pre-entrained free tip are sufficient to allow the cross-linkers to entrain the incident MT. Bending induced by the drag force of cytoplasmic streaming (15) will increase the range of angles that can be entrained; however, it is not necessary.

This calculation tells us when entrainment may occur; to find out the probability that it will occur, we use an adiabatic approach described below.

Entrainment and crossover probabilities

Entrainment and crossover do not occur deterministically but rather, for each collision angle θ, there is a probability that the incident MT will entrain, p(ent|θ) or crossover, p(cross|θ). In this section, we derive a model to compute these probabilities.

In thermodynamic equilibrium, a pair of collided MTs will exhibit collision resolution j ∈ {ent, cross} with probability given by the Maxwell-Boltzmann distribution

$$P_j=\frac{1}{Z}\exp \left(-E_j/k_{\text{B}}T\right),$$ (13)

where Z is a normalizing factor. The MTs in living cells are open systems far from equilibrium. However, a separation of timescales allows us to make an adiabatic approximation and use a modified version of Eq. 13. The elastic relaxation timescale of the MT is τ_relax⁻¹ ≈ 10³ s⁻¹ (24), and typical values for MAP kinetics are s⁻¹ (25,26). Meanwhile, on the relevant length scale of L ∼3 μm, MT growth is slow $v_g^p$/L ≈ 1 min⁻¹, and we found above that MT-cortex anchoring is also slow, k_onL ≈ 1 min⁻¹, k_off ≈ 10⁻⁴ min⁻¹. Thus, mechanics and cross-linking kinetics occur on a fast timescale of seconds, while MT growth and anchoring kinetics occur on a slow timescale of minutes or longer.

On the slow timescale of MT growth and anchoring, the incident MT has free length L + l(t), which grows at rate v^p_g. Mechanics and cross-linking are reversible and occur on the fast timescale, so an ensemble will have a distribution of n_X, the number of cross-linkers attaching the incident and barrier MTs, given by

$$\begin{array}{c}p\left(n_X\ge 1|\theta ,l,L\right)=\frac{1}{Z}\sum _{n_X=1}^{\infty }\exp \left(-E_{\text{ent}}\left(l,L,n_X\right)/k_{\text{B}}T\right),\\ p\left(n_X=0|\theta ,l,L\right)=\frac{1}{Z}\exp \left(-E_{\text{cross}}\left(l,L\right)/k_{\text{B}}T\right)\text{.}\end{array}$$ (14)

In this case, the normalizing factor is

$$Z=\sum _{n_X=1}^{\infty }\exp \left(-E_{\text{ent}}\left(l,L,n_X\right)/k_{\text{B}}T\right)+\exp \left(-E_{\text{cross}}\left(l,L\right)/k_{\text{B}}T\right)\text{.}$$ (15)

We think of n_X ≥ 1 as states that, if anchored, would be entrained, while n_X = 0 states would cross over the barrier. We measure time on the slow scale, t, from the time the incident MT's plus-end arrives at the collision site, so l = $v_p^g$t. In the time interval (t, t + dt), a portion g(v^p_gt)dt of the ensemble is anchored, as described in Eq. 2. At any time t, the mechanics and cross-linking remain in equilibrium, so Eqs. 14 are satisfied. For a given free length of L,

$$p\left(ent|\theta ,L\right)={\int }_0^{\infty }p\left(n_X\ge 1|\theta ,l,L\right)g\left(l\right)dl\text{.}$$ (16)

The overall probability of entrainment at collision angle θ is given by the following equation, the principal result of this article:

$$p\left(ent|\theta \right)={\int }_0^{\infty }{\int }_0^{\infty }p\left(n_X\ge 1|\theta ,l,L\right)g\left(l\right)g\left(L\right)dldL\text{.}$$ (17)

In a similar manner, we calculate the overall probability of crossover at collision angle θ as

$$p\left(cross|\theta \right)={\int }_0^{\infty }{\int }_0^{\infty }p\left(n_X=0|\theta ,l,L\right)g\left(l\right)g\left(L\right)dldL\text{.}$$ (18)

The collision resolution probabilities p(ent|θ) is shown in Fig. 5 A for both WT and clasp-1 anchoring kinetics. Crossover probability p(cross|θ) is the complement, 1 − p(ent|θ). The model parameters are listed in Table 3.

Figure 5.

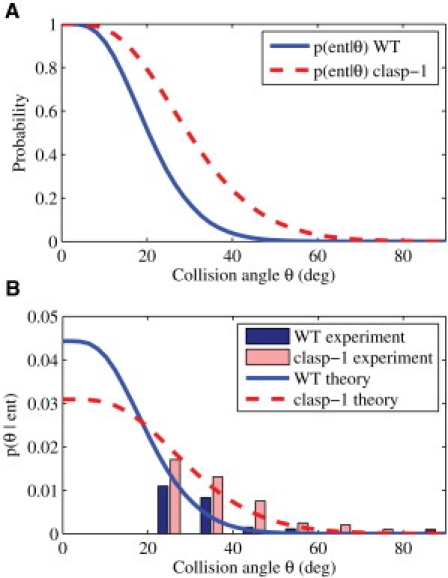
Collision resolution probabilities. (A) Probability of entrainment given by Eq. 17 for WT (solid) and clasp-1 (dashed) anchoring kinetics. (Dashed lines) Upper bound for probability of collision-induced catastrophe. (B) Distribution of zippering angles for WT and clasp-1 anchoring kinetics, along with experimental histograms from Ambrose and Wasteneys (15). These are calculated from the results in panel A using Bayes' rule. In the experimental histograms, we exclude entrainment events at <20° as low-angle entrainment events are difficult to resolve experimentally.

Some experimental studies measure p(θ|ent) rather than p(ent|θ), that is, the angular distribution of all entrainment events. We convert between the two using Bayes' rule,

$$p\left(\theta |ent\right)=p\left(ent|\theta \right)p\left(\theta \right)/\int p\left(ent|{\theta }^{\prime }\right)p\left({\theta }^{\prime }\right){d\theta }^{\prime },$$

with the approximating assumption that collisions are uniformly distributed in collision angle. These are shown in Fig. 5 B. The experimental observations from Ambrose and Wasteneys (15) are also shown. To dismiss coincidences, the authors only reported readily noticeable changes in orientation, which would underreport low-angle collisions. For this reason, we assume the uncertainties are large for collisions at <20° and omit them from the figure.

The results are insensitive to model parameters. Varying parameters k_on, k_off, δ_‖, μ_X, E_cat, B, and d by ±10% led to no significant change in the collision resolution probabilities.

Discussion

We propose a mechanism for collision-induced interactions between cortical MTs that gives rise to plus-end entrainment. The energetics of this mechanism give rise to an angle-dependent entrainment probability, based on a competition between the chemical bonding of a cross-linking MAP and the bending energy of the incident MT.

A major prediction of our model is the limited significance of collision-induced catastrophe, in agreement with observations in A. thaliana. However, Dixit and Cyr (6) report significant collision-induced catastrophe in Tobacco BY2 cells. As noted above, one possible explanation is a difference in anchoring in different organs and species. Another possible explanation is the action of an unknown MAP at collision sites, which may promote catastrophe.

This model makes several testable predictions concerning MT-cortex anchoring. The parameter fits found in Table 1 demonstrate that the association and dissociation rates in WT and clasp-1 of A. thaliana are slow. Furthermore, these parameters suggest how CLASP affects anchoring. The clasp-1 mutant has roughly half the WT k_on, but leaves k_off unaffected. This suggests CLASP is involved in promoting anchor association between MTs and the cortex, while it is not involved in dissociation of anchors. The model also predicts that faster anchoring kinetics lead to higher rates of collision-induced catastrophe.

This model predicts that the probability of entrainment decreases monotonically with collision angle. This is in agreement with observations of Dixit and Cyr (6), but contrasts with the results of Ambrose and Wasteneys (15) (see Fig. 5 B), where entrainment at small angles is not reported. However, as mentioned above, to dismiss coincidences, the authors only reported readily noticeable changes in orientation, which would underreport low-angle collisions.

The adiabatic approach we use here allows us to produce collision resolution probabilities with only a few, and experimentally well-constrained, parameters: the MT bending modulus, cross-linker spacing, and the cross-linker bonding energy. Moreover, it is independent of the details of the pathway a particular MT follows to its proper collision resolution, which remains to be experimentally elucidated. However, the approach has several drawbacks. It relies heavily on slow anchoring and implicitly assumes there are no impediments to the rapid exploration of the energy landscape. A dynamic approach involving either Langevin equations (27,28) or Fokker-Planck equation (29,30) remains desirable; however, this will require kinetic rate constants for all processes and other presently unmeasured experimental details.