Abstract
The self-assembly of clathrin proteins into polyhedral cages is simulated for the first time (to our knowledge) by introducing a coarse-grain triskelion particle modeled after clathrin's characteristic shape. The simulations indicate that neither this shape, nor the antiparallel binding of four legs along the lattice edges, is sufficient to induce cage formation from a random solution. Asymmetric intersegmental interactions, which probably result from a patchy distribution of interactions along the legs' surfaces, prove to be crucial for the efficient self-assembly of cages.
Introduction
Three long curved legs endow the clathrin protein with the remarkable ability to self-assemble into polyhedral cages with a hub centered at every vertex and four legs running along all edges of the pentagonal and hexagonal faces. Clathrin plays important structural and regulatory roles in endocytosis, the process in which living cells internalize large molecules by building a clathrin coat at the cytosolic side of the plasma membrane to collect the external cargo in a membrane pit which subsequently grows into a clathrin-coated vesicle encapsulating the cargo (1–4). In vivo and in vitro experiments have resolved clathrin's conformation in three-dimensional cages (5–9) and explored several dozen assisting proteins (10). Interestingly, whereas in vivo cage formation is localized at the cell membrane and requires adaptor proteins, in vitro self-assembly is already observed for clathrins dissolved in slightly acidic, pH ∼6.5, buffers containing neither adaptor proteins nor membranes (11). Understanding the latter assembly process and its products (11–13) provides important insights toward elucidating the complex endocytic process, which is difficult to access with current experimental techniques (14–20).
Another obstacle to comprehending clathrin-mediated endocytosis is the still-elusive interaction mechanism responsible for the self-assembly and the subsequent stabilization of the lattice, even though the atomic structure of clathrins in a hexagonal barrel, a cage of 36 clathrins with D6h symmetry, has been resolved down to 12 Å by cryo-electron microscopy (6,8). Besides the omnipresent attractive and repulsive van der Waals interactions between atoms, which may be enhanced by complementary packing of ridges and grooves (21), the speculated interactions include salt bridges (22), pH-dependent Coulombic interactions between paired histidine residues (22), weak hydrophobic interactions (13), and an ankle brace (8). The binding energy per clathrin, which probably reflects the cumulative effect of many weak interactions (13,23), has not been measured but is expected to be of approximately the thermal energy kBT (24,13), with kB denoting Boltzmann's constant and T the absolute temperature.
Computer simulations of clathrinlike particles offer the possibility of establishing whether hypothesized interaction mechanisms are capable of self-assembly into polyhedral cages, and thereby yield new suggestions for probable locations and strengths of putative interaction sites. Here we present what to our knowledge are the first computer simulations of clathrin cage assembly in solution, using coarse-grain models of increasing complexity to determine the key structural and interaction elements of self-assembling triskelia. The simulations indicate that a radial asymmetry of the leg-leg interactions is crucial for the successful assembly of ordered cages, and the possible origins of this asymmetry are discussed.
Simulation Model
During self-assembly, clathrin molecules, to a good approximation, behave as rigid particles—the structure of which is well known (5–8). The characteristics of this structure are captured by the cartoon shown in Fig. 1. Three legs radiate from a hub at a pucker angle χ relative to a threefold rotational symmetry axis, each making a bend with corresponding dihedral change at their respective knees and terminating at the ankles. The combination of bended legs, a pucker angle >90°, and a threefold symmetry axis admits two possible enantiomers, of which only the right-handed one occurs in nature.
Figure 1.
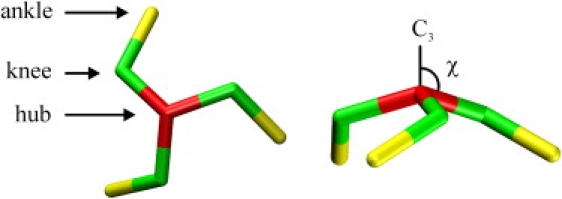
The triskelion simulation model, shown here in top view (left) and side view (right), is based on the idealized structure of clathrin. Three proximal legs run from the central hub (red) to a knee (green), under a pucker angle χ relative to the threefold rotational symmetry axis (C3), followed by three distal legs running from the knees to the ankles (yellow). In all simulations, the pucker angle was set equal to 101°. The particle is simulated as a rigid unit with proximal and distal legs of equal length.
In clathrin cages, a single hub is situated at each vertex, and two proximal legs, i.e., upper leg segments, gather in antiparallel alignment along the edges between neighboring vertices (5–8). These two segments are accompanied by two antiparallel distal legs, i.e., lower leg segments, connected to proximal legs along two neighboring edges. Excluded volume effects prevent the accumulation of more than four leg segments along one edge. All of these features are effectively reproduced in our simulation model by introducing four-site interaction potentials based on the averaged separations of the two pairs of end-points of neighboring leg segments. For instance, the attractive interaction potential between two antiparallel proximal segments is represented by a function of the average of the two hub-knee distances. Detailed information about these potential energy functions is provided in the Appendix. The smooth shape of the potential allows small displacements of leg segments perpendicular and along one another, permits a modest misalignment of the segments, provides some leeway for the slight variations of edge lengths in a polyhedron, and accounts for small shape fluctuations (7,25) of the legs. We note that this definition of the potential, because it is based on mean distances, makes the segmental interactions invariant under rotations of leg segments around their long axis. There are no solvent particles in the simulations—the potential models the effective interactions between leg segments, including both direct and solvent-induced interactions. An important feature of the potential, without which the current simulations would be excessively demanding computationally, is the omission of direct excluded volume interactions between the leg segments. This expedient is not expected to affect the conclusions of this study significantly, because the model contains the key elements of the free energy landscape, i.e., the decrease in energy and the concomitant loss of entropy upon binding of clathrins into lattices. Furthermore, the simulations indicate that lattices grow predominantly at their edges, where the steric restrictions on the movements of attaching clathrins are modest (see Appendix for a more detailed discussion). All simulations are performed using the Monte Carlo technique. In every step, a randomly selected particle is randomly translated and rotated by a small amount and the resulting trial configuration is accepted or rejected with a probability based on the Boltzmann factor of the accompanying energy change to obey detailed balance (26,27).
Besides geometric parameters like the pucker angle and the related bending angle at the knees, the potential contains just one parameter ε representing the segmental binding energy per pair of well-aligned proximal or distal legs. This binding strength is expected to be of the order of the thermal energy kBT (13,24), with kB denoting Boltzmann's constant and T the absolute temperature. The binding energy of mixed pairs has been put equal to ε/2. Several alternative attributions of binding energies to mixed pairs have been considered, as described in the Appendix. We have checked that all findings with the chosen potential are qualitatively generic in the full class of potentials described there, with only minor variations in the numerical values given below.
The cubic simulation boxes contain 1000 or 10,000 particles, always at a concentration of 1 particle per 10−3 σ−3, with σ the length of the proximal and distal leg segments. This concentration is close to the experimental critical assembly concentration at room temperature of ∼100 μg/ml, below which no assembly occurs and above which the number of self-assembled cages quickly increases. Similarly, keeping the concentration fixed at this particular value and varying the temperature results in no self-assembly at temperatures slightly above room temperature and exuberant cage formation slightly below room temperature. The relevant dimensionless parameter entering the simulations is the ratio ε/kBT of binding strength to thermal energy. Raising this parameter beyond a critical value—by strengthening the attractive interactions and/or cooling the system—initiates the assembly of cages, whereas lowering its value to below the critical value—by weakening the attractions and/or heating the system—shifts the equilibrium toward disassembly.
Simulation Results
Simulations with the above model yield small short-lived assemblies for weak binding interactions and disordered aggregates for strong interactions. With binding energies of seven times the thermal energy, ε = 7 kBT, for the first time aggregates are formed spontaneously. An example of such a cluster, isolated from its surroundings, is shown in Fig. 2 together with a similar example from a simulation with a segmental binding energy of eight times kBT. To test whether the structures so obtained represent kinetically trapped states resulting from a large oversaturation or a deep temperature quench, we performed simulations with boxes seeded with a few preassembled half-cages, using binding energies of 5 kBT. All of the half-cages disintegrated into single triskelia. Similarly, we performed simulations with preassembled half-cages at binding energies equal to 6 kBT. In these cases, the hemispherical cages started to grow slowly, but finally developed disordered appendages akin to the structures observed in the nonseeded simulations. During long simulations with preassembled complete cages and segmental binding energies of 6 kBT, all cages kept their integrity, only rarely losing and capturing a triskelion. From these results, we conclude that the model presented above is capable of describing cages, but still misses an essential ingredient necessary to achieve spontaneous self-assembly of cages. Apparently, clathrin's characteristic shape and the antiparallel binding of like leg segments are not sufficient by themselves to promote cage formation.
Figure 2.
Triskelia of the first simulation model, at segmental binding energies ε = 7 kBT (A) and ε = 8 kBT (B), have a tendency to self-assemble into chainlike structures. The number of branch points increases with the segmental binding energy, and thereby changes the shape of the aggregates.
A closer look at the relative positions and orientations of the various leg segments of clathrin molecules in experimentally observed cages (5–8), as reproduced in Fig. 3, and building on the extensive discussions of possible locations and mechanisms of interaction in the literature (7,13,21,23), suggests the schematic binding concept of Fig. 4. In Fig. 4 A, one edge is shown schematically as it occurs in experimentally observed clathrin cages. Two antiparallel proximal and two antiparallel distal legs gather along this edge. In Fig. 4 B, a perpendicular cut is shown through this edge. Two proximal legs are drawn, one with its hub above the paper and one with its hub below the paper; similarly two distal legs are shown, one with its knee above the paper and one with its knee below the paper. The elliptic cross section of a leg gradually rotates as one goes from the hub to the knee and next to the ankle (see Fig. 3), roughly such that the distal leg is a repetition of the proximal leg rotated over 90° (8,23). The dark areas in the cartoon of Fig. 4 have been introduced to indicate that the cross sections of the legs are not fully symmetric. Stated differently, they indicate that the chemical constitution of the leg's surfaces varies as one goes around the circumference of the leg's cross section. The dark patches have been chosen such that the experimental configuration of the four legs along one edge brings them together in the center of the edge; note that this requires the shaded area to follow the 90° rotation between proximal and distal leg segments. In Fig. 4, C and D, one of the molecules has been rotated over 180° around the central edge. The resulting edge configuration does not occur in experimentally observed clathrin cages, and in the cartoon, this edge configuration does not bring all dark areas together. We will now assume as our working hypothesis that incorrectly oriented leg segments do not lead to binding and set forth to explore the consequences of this asymmetry on the assembly process. This concept of radial asymmetric interactions is introduced into the simulation model by multiplying each attractive segmental interaction by a function which is equal to one in case the corresponding segments are oriented correctly and zero when they are oriented incorrectly. For details of the potential energy functions, we refer to the Appendix. We will call this more-detailed model the “patchy model”, as it has interacting patches on its surface.
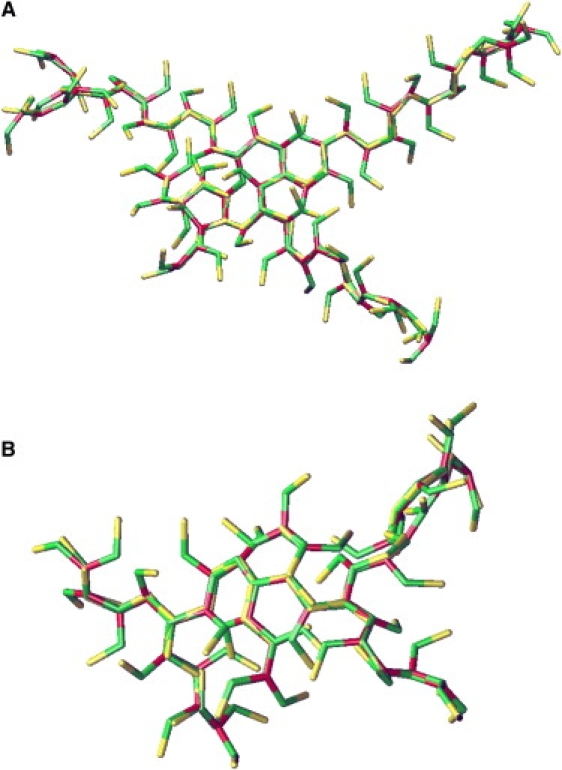
Figure 3.
Experimentally resolved structure of a lattice edge in a hexagonal barrel viewed (A) from the top, (B) from the side, and (C) in cross section. The two antiparallel proximal leg-segments (red and green) are in the front of the top view and on top in the side view and cross section, the two antiparallel distal leg-segments (blue and amber) are in the back of the top view and at the bottom of the side view and cross section. Proximal and distal legs are similar in structure and are clearly asymmetric, with two faces made of α-helices and two faces made of connecting loops. A gradual right-handed twist along the leg has rotated the elliptic cross sections of the distal legs by ∼90° relative to those of the proximal legs. The cartoons in Figs. 4 and 7 are based on this structure. (Reproduced with permission from the authors and Macmillan Publishers from the supplementary material to Fotin et al. (8).)
Figure 4.
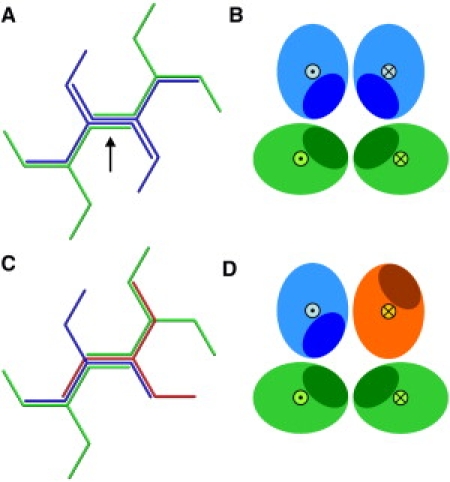
Schematic of the probable edge structure in a clathrin cage, based on the experimental structure (5–8) provided in Fig. 3. An edge (marked by an arrow in panel A) combines two antiparallel proximal legs (dark blue) of the two clathrins centered at the flanking vertices with two antiparallel distal legs (light green) of two clathrins centered at next-nearest vertices. In the cross section (B), the hub-to-knee and knee-to-ankle directions are indicated by the symbols ⊙ and ⊗ for segments pointing out of and into the paper, respectively. The diagram illustrates that the asymmetric segments are preferentially oriented with the shaded regions (schematically representing the segmental interactions) oriented toward the center of the edge. Rotating the upper-right dark blue clathrin by 180° around the direction of the marked edge yields the upside-down red clathrin (C), whose poor binding is explained in cross section (D) by a mismatch of the shaded areas. The latter configuration is very common, however, in the simulations with the nondirectional model, where it gives rise to the typical stringlike structures of Fig. 2 with alternating up-down orientations for consecutive pairs of particles.
Nonseeded simulations with this patchy model first show spontaneous cage formation at segmental binding energies of 8 kBT. Movie S1, illustrating the self-assembly of two cages over the course of ∼7 × 106 Monte Carlo trial moves per particle, is available in the Supporting Material. A snapshot of the simulation box is shown in Fig. 5, together with a snapshot obtained with the original nonpatchy model. Two examples of the cages formed are shown in Fig. 6. Cage assembly is found to proceed by a nucleation and growth mechanism: small clusters formed by chance often disintegrate readily, but sometimes a cluster crosses the stability barrier and then continues to grow, by consecutive additions of monomers, into a full cage with hexagonal and pentagonal faces. Performing seeded runs as with the first model, we found that preassembled half-cages disintegrate at 5 kBT, whereas most seeds finally grow into complete cages at binding energies of 6 kBT.
Figure 5.

Snapshots after ∼5,000,000 Monte Carlo trial moves per particle, starting from a random initial configuration, for the interaction models with nonpatchy (A) and patchy (B) segmental interactions at a segmental interaction energy of ε = 8 kBT. Whereas the model with nondirectional interactions yields chainlike aggregates of various shapes (two isolated clusters are shown in Fig. 2), the model with directional interactions readily self-assembles into near-spherical cages of fairly uniform size (two isolated cages are shown in Fig. 6). The actual simulation boxes are approximately four times as large, containing 104 particles at a density of 10−3σ−3 corresponding to the critical assembly concentration of ∼100 μg/ml.
Figure 6.
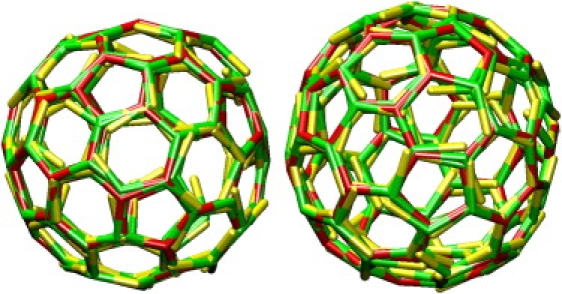
Two typical self-assembled cages grown at ε = 8 kBT with the patchy model. Closed polyhedral cages formed by triskelia with a pucker χ = 101° contain ∼60–70 particles, forming exactly 12 pentagonal faces and ∼20 hexagonal faces. The cage on the left is rotated to create a coalescence of the edges in the front with those in the rear.
Discussion
We conclude from the computer experiments described above that incorporation of asymmetry of the segmental interactions has large consequences for the efficiency of cage formation, even when the various leg segments have already been forced to bind in antiparallel fashion. It is not difficult to understand why this is so. With the original model, both cases in Fig. 4 lead to the full binding energy along the central edge, whereas with the patchy model only the configuration in panels A and B leads to optimal binding along this edge. As a result, the nonpatchy model quickly leads to a proliferation of structures. Moreover, the configuration in Fig. 4, C and D, gives rise to a change of curvature along the central edge, whereas the one in Fig. 4, A and B, conserves curvature. This means that the additional configurations generated with the original model readily lead to disordered aggregates, whereas the patchy model has a propensity for configurations that lead to the uniform curvature required for cage formation. The consequences of this difference are twofold. First, many pathways to kinetically trapped disordered aggregates are cut off in the patchy model. Second, even if the energy per molecule in the cages is lower than in the disordered aggregates, the latter are so abundant when effects of patchiness are ignored that they appreciably deplete the cages in equilibrium. This entropic effect is largely ruled out in the patchy model. Asymmetric interactions resulting from patchy surfaces thus prove crucial to successful self-assembly of triskelia into cages.
Although we have introduced the anisotropy of the segmental interaction without further chemical motivation, it is supported by the resolved cage edge structure (8) displayed in Fig. 3. A leg consists of eight clathrin heavy chain repeats, each containing ∼145 residues forming five helical hairpins (8,21,23). The resulting leg cross section is slightly elliptical, with two opposite faces made of α-helices connected by two faces made of loops (8,21,23), as is clearly visible from Fig. 3 C. One readily envisages how the various face-face combinations result in distinct binding energies (23), and thereby create the asymmetric potential crucial to self-assembly. Note that, when considering interaction energies, it is important to include solvation energies that may give rise to hydrophobic attractions (13), which in the simulations have been included in the effective intersegmental interaction potential. The 90° drift of the interaction asymmetry on going from the proximal leg to the distal leg (see Fig. 4) is supported by the gentle right-handed twist of the helical zigzags by ∼90° between these two segments (8,23), as clearly seen in Fig. 3 C. This ensures that the same faces are opposing each other, or directed toward the solvent, along the length of the skewed edge.
In summary, the simulations show that clathrin's characteristic shape and the antiparallel binding of like leg segments are not sufficient to induce cage formation, whereas clathrin's asymmetric segmental interactions emerge as the key to efficient self-assembly.
Contributor Information
Wouter K. den Otter, Email: w.k.denotter@utwente.nl.
W.J. Briels, Email: w.j.briels@utwente.nl.
Appendix: Simulation Details
Structure
The proximal segments of the three legs α = 1, 2, 3 of particle i are at an angle χ relative to the threefold rotational symmetry (C3) axis of the particle. This angle is fixed at 101° in this study. A unit normal vector is associated with the hub (h), running parallel to the symmetry axis in the direction from the center of mass toward the hub and hence pointing outward in a completed cage. The introduction of distal leg segments involves choosing a proximal-distal bending angle and a proximal-proximal-distal dihedral angle. We constructed the orientation of the distal segment to leg (i, α) by mirroring the proximal segment of the clockwise next leg (i, α + 1) in the midplane of the (i, α) proximal segment. The mirror image of the hub coincides with the knee to leg (i, α), and the knee of the neighboring leg (i, α + 1) is mirrored onto the ankle position of leg (i, α). Both proximal and distal legs have the same length σ. A consequence of this relative orientation of the distal legs is that a second particle j, when positioned with its hub at the knee of leg (i, α) of the primary particle, can be oriented such that two of its proximal legs coalesce with the proximal and distal leg segments of leg (i, α). At the same time, one of the distal legs of j overlaps with a proximal leg of i (as illustrated by the two blue triskelia in Fig. 4). Note that it is not possible to create a pentagon or hexagon of five or six adjacent perfectly overlapping particles (a perfect hexagon requires χ = 90°, a perfect pentagon χ = 110.9°). The particles are treated as rigid bodies in the simulations, and interact by the force field detailed below. Note that the leg index α to the hub will be maintained for notational uniformity only.
The free energy landscape created by the attractive and repulsive interactions detailed in this Appendix describes a smoothed representation of the expected (but largely still unknown) free energy landscape for real clathrins. Assembly and disassembly of clathrin cages are driven, in both Monte Carlo simulations and experiments, by a minimization of the total free energy and hence are governed by a balance between the lower energy of bound clathrins and the higher translational and rotational entropy of unbound clathrins. An important assumption in the simulation model is the omission of direct excluded volume interactions between the leg segments. The frequent collisions between particles in an assembled lattice, compounded by the complex shape of the particle, make a simulation with excluded volume interactions extremely computer-time consuming—the uninteresting collisions would completely dominate the simulations, thereby relegating the interesting assembly process to a rare and obscured side-show. Furthermore, the simulations presented here—which include repulsive interactions (see below) permitting only one particle per lattice position—indicate that clathrin lattices grow predominantly at their edges, where there is ample room for the approaching triskelia to move around and slot in. We note that the final few clathrins to complete a nearly finished cage are more restricted in their movements, and hence that their incorporation in the simulated cages will be easier than in real clathrin cages.
Attraction
Although in the schematic picture of Fig. 1 the leg segments are drawn as solid cylinders, in reality they are slightly flexible (7,25) and their slightly elliptic cross sections gradually twist as one moves along the leg (8,21,23), as can be seen in Fig. 3. It is therefore plausible that the binding of two leg segments depends strongly on the relative orientation of the two (7,13,23), as discussed in the main text. In the simulation model, we assume that the αth proximal leg of particle i binds to the βth proximal leg of particle j only if they are close to each other and oriented in an antiparallel manner. That is, the hub (h) of leg (i, α) is close to the knee (k) of leg (j, β) and simultaneously the knee of leg (i, α) is close to the hub of leg (j, β). In a simulation force field, this may be expressed by introducing a pair potential depending on the average distance between the neighboring unlike ends of these proximal segments,
| (1) |
with xiα,h and xiα,k the positions of the hub and knee, respectively, of leg (i, α). In the upper and lower indices to the average distance r, the first two labels identify the leg and the last two labels specify the leg segment and its direction. The proximal-proximal (pp) interaction potential in the current simulations is of the form
| (2) |
where ε denotes the strength of the segmental interaction. The function
| (3) |
was chosen to describe the variation of the potential with the average distance, and runs from unity at zero distance to zero at the cutoff distance rc, with A determining the steepness of the potential. Similar interactions
| (4) |
are implemented between pairs of distal legs (dd), again promoting antiparallel orientations by using average knee to ankle (a) distances defined as
| (5) |
Interaction energies of mixed pairs of leg segments seem to be less restricted in the alignment of the segments. Expressed most generally, we have implemented the following contribution of such proximal-distal (pd) pairs to the potential energy
| (6) |
with the mean distances
| (7) |
| (8) |
between the upper segments of leg (i, α) and the lower segment of leg (j, β). Note that the orientation of the lower segment, relative to the upper segment, differs for these two proximal-distal interactions.
Repulsion
Because there is no excluded volume in our model, we must prevent the accumulation of more than four leg segments along one edge by other means. This should be done such that the general interaction scheme described so far will not be frustrated. This leaves the freedom to associate repulsive interactions with all or some of the segmental leg pairs that do not contribute to binding in the model constructed so far. We therefore associate positive energies with parallel pairs of proximal legs and with parallel pairs of distal legs. Therefore, we add two more contributions to the potential energy,
| (9) |
| (10) |
with average distances
| (11) |
| (12) |
The bars are used to highlight that the repulsion is of the same functional form as the attraction but differs in the numerical values for the strength, steepness, and cutoff distance. These repulsions are intended to outweigh the attraction that an approaching fifth leg segment will experience with some of the four segments already assembled. We have found that with
the repulsions are sufficiently strong to prevent the undesired aggregation of more than four segments along a cage edge.
Asymmetry
To introduce the effects of patchiness, as discussed in the main text, we associate with each leg segment a unit vector as indicated in Fig. 7. In mathematical terms, the -vector of the αth proximal (p) leg of particle i is then defined as
| (13) |
with vector liα, p = xiα, k – xiα, h pointing along the leg segment from hub to knee, and the previously introduced normal vector at the hub.
Figure 7.
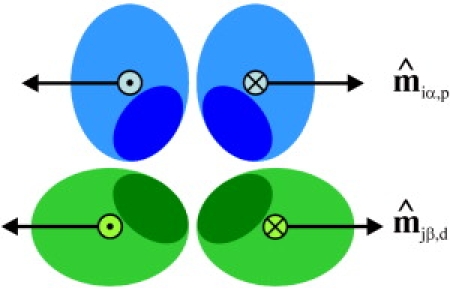
Cross section of a cage edge showing the preferred orientations of the -vectors for maximum binding between the leg segments. The two proximal-proximal -vectors are antiparallel, as are the two distal-distal -vectors, whereas combinations of a proximal and a distal segment can yield both parallel and antiparallel -vectors depending on the segments involved.
To define the compatible vector for the distal (d) segment of the (i, α) leg, one first needs to determine the appropriate normal vector at the knee. In line with the definition of the orientation of the distal segments, is readily calculated by mirroring the normal at the hub, , in the midplane of the (i, α) proximal leg. Consequently, this knee-based normal vector coincides with the hub-based normal vector of a second particle j positioned such that its hub resides at the (i, α) knee and two of its proximal leg segments coincide with the proximal and distal leg segments of the (i, α) leg. The three distal -vectors of particle i are then calculated as
| (14) |
where the vector liα, d = xiα, a – xiα, k points along the leg segment from knee to ankle.
Patchiness of the interactions demands that both proximal-proximal and distal-distal attractions only occur when the corresponding -vectors are antiparallel, as illustrated in Fig. 7. Therefore, we introduce the function
| (15) |
and replace the original attractive interactions by
| (16) |
| (17) |
Here Θ is the Heaviside function, so Θ(x) is equal to one in case x > 0 and equal to zero otherwise, and denotes the dot product of the -vectors of the proximal legs (i, α) and (j, β). Similar arguments make us replace the proximal-distal attractions by
| (18) |
where the minus signs with the argument of g in the first line accounts for the fact that the corresponding -vectors must be parallel for optimal binding, as illustrated in Fig. 7. We note that the introduction of patchiness, i.e., the function g, weakens the segmental interactions relative to those of the nonpatchy model at the same ε. Replacing the smooth function g(x) by the step function g(x) = Θ(– x) had no qualitative influence on the simulation results. No changes are made to the repulsive parts of the potential.
Setup
All simulations were run with a dedicated Monte Carlo algorithm (26,27). The simulated systems contain 104 particles for homogeneous starting configurations, or 103 particles when including hemispherical lattices to nucleate growth, at a density of one particle per 10−3σ−3 in a cubic box with periodic boundary conditions (26,27), where σ denotes the length of a leg segment. The pucker χ was fixed at 101°. The potential parameters were set at A = 4σ−1 and rc = 0.4σ, whereas the segmental binding strength ε varied between the simulations. Simulation runs typically range from 1010 to 1011 Monte Carlo trial moves. In every trial move, a randomly selected particle is subjected to small rigid body translations and rotations, and the trial configuration is accepted or rejected (26,27) with a probability p = min [1, exp(– ΔΦ/kBT)]. To accelerate the calculation of the potential energy change ΔΦ, we make extensive use of grid and neighbor lists.
Binding strengths
In the main text, we have described results obtained with
| (19) |
We have performed simulations with several other combinations, in view of the uncertainty at present about the interactions strengths (13). Simulations with
| (20) |
| (21) |
| (22) |
| (23) |
were all observed to lead to qualitatively similar results to those discussed in the main text.
Supporting Material
Movie S1. The spontaneous self-assembly of two clathrin cages at ε = 8 kBT over the course of >>7 × 106 Monte Carlo moves per particle
Document S1. Movie legend
References
- 1.Edeling M.A., Smith C., Owen D. Life of a clathrin coat: insights from clathrin and AP structures. Nat. Rev. Mol. Cell Biol. 2006;7:32–44. doi: 10.1038/nrm1786. [DOI] [PubMed] [Google Scholar]
- 2.Royle S.J. The cellular functions of clathrin. Cell. Mol. Life Sci. 2006;63:1823–1832. doi: 10.1007/s00018-005-5587-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Young A. Structural insights into the clathrin coat. Semin. Cell Dev. Biol. 2007;18:448–458. doi: 10.1016/j.semcdb.2007.07.006. [DOI] [PubMed] [Google Scholar]
- 4.Ungewickell E.J., Hinrichsen L. Endocytosis: clathrin-mediated membrane budding. Curr. Opin. Cell Biol. 2007;19:417–425. doi: 10.1016/j.ceb.2007.05.003. [DOI] [PubMed] [Google Scholar]
- 5.Vigers G.P.A., Crowther R.A., Pearse B.M.F. Three-dimensional structure of clathrin cages in ice. EMBO J. 1986;5:529–534. doi: 10.1002/j.1460-2075.1986.tb04242.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Smith C.J., Grigorieff N., Pearse B.M.F. Clathrin coats at 21 Å resolution: a cellular assembly designed to recycle multiple membrane receptors. EMBO J. 1998;17:4943–4953. doi: 10.1093/emboj/17.17.4943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Musacchio A., Smith C.J., Pearse B.M. Functional organization of clathrin in coats: combining electron cryomicroscopy and x-ray crystallography. Mol. Cell. 1999;3:761–770. doi: 10.1016/s1097-2765(01)80008-3. [DOI] [PubMed] [Google Scholar]
- 8.Fotin A., Cheng Y., Walz T. Molecular model for a complete clathrin lattice from electron cryomicroscopy. Nature. 2004;432:573–579. doi: 10.1038/nature03079. [DOI] [PubMed] [Google Scholar]
- 9.Cheng Y., Boll W., Walz T. Cryo-electron tomography of clathrin-coated vesicles: structural implications for coat assembly. J. Mol. Biol. 2007;365:892–899. doi: 10.1016/j.jmb.2006.10.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schmid E.M., McMahon H.T. Integrating molecular and network biology to decode endocytosis. Nature. 2007;448:883–888. doi: 10.1038/nature06031. [DOI] [PubMed] [Google Scholar]
- 11.Zaremba S., Keen J.H. Assembly polypeptides from coated vesicles mediate reassembly of unique clathrin coats. J. Cell Biol. 1983;97:1339–1347. doi: 10.1083/jcb.97.5.1339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Greene B., Liu S.-H., Brodsky F.M. Complete reconstitution of clathrin basket formation with recombinant protein fragments: adaptor control of clathrin self-assembly. Traffic. 2000;1:69–75. doi: 10.1034/j.1600-0854.2000.010110.x. [DOI] [PubMed] [Google Scholar]
- 13.Wakeham D.E., Chen C.-Y., Brodsky F.M. Clathrin self-assembly involves coordinated weak interactions favorable for cellular regulation. EMBO J. 2003;22:4980–4990. doi: 10.1093/emboj/cdg511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gaidarov I., Santini F., Keen J.H. Spatial control of coated-pit dynamics in living cells. Nat. Cell Biol. 1999;1:1–7. doi: 10.1038/8971. [DOI] [PubMed] [Google Scholar]
- 15.Rappoport J.Z., Simon S.M. Real-time analysis of clathrin-mediated endocytosis during cell migration. J. Cell Sci. 2003;116:847–855. doi: 10.1242/jcs.00289. [DOI] [PubMed] [Google Scholar]
- 16.Wu X., Zhao X., Greene L.E. Adaptor and clathrin exchange at the plasma membrane and trans-Golgi network. Mol. Biol. Cell. 2003;14:516–528. doi: 10.1091/mbc.E02-06-0353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ehrlich M., Boll W., Kirchhausen T. Endocytosis by random initiation and stabilization of clathrin-coated pits. Cell. 2004;118:591–605. doi: 10.1016/j.cell.2004.08.017. [DOI] [PubMed] [Google Scholar]
- 18.Merrifield C.J., Perrais D., Zenisek D. Coupling between clathrin-coated-pit invagination, cortactin recruitment, and membrane scission observed in live cells. Cell. 2005;121:593–606. doi: 10.1016/j.cell.2005.03.015. [DOI] [PubMed] [Google Scholar]
- 19.Loerke D., Wienisch M., Klingauf J. Differential control of clathrin subunit dynamics measured with EW-FRAP microscopy. Traffic. 2005;6:918–929. doi: 10.1111/j.1600-0854.2005.00329.x. [DOI] [PubMed] [Google Scholar]
- 20.Kirchhausen T. Imaging endocytic clathrin structures in living cells. Trends Cell Biol. 2009;19:596–605. doi: 10.1016/j.tcb.2009.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ybe J.A., Brodsky F.M., Hwang P.K. Clathrin self-assembly is mediated by a tandemly repeated superhelix. Nature. 1999;399:371–375. doi: 10.1038/20708. [DOI] [PubMed] [Google Scholar]
- 22.Ybe J.A., Greene B., Brodsky F.M. Clathrin self-assembly is regulated by three light-chain residues controlling the formation of critical salt bridges. EMBO J. 1998;17:1297–1303. doi: 10.1093/emboj/17.5.1297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wilbur J.D., Hwang P.K., Brodsky F.M. New faces of the familiar clathrin lattice. Traffic. 2005;6:346–350. doi: 10.1111/j.1600-0854.2005.00277.x. [DOI] [PubMed] [Google Scholar]
- 24.Nossal R. Energetics of clathrin basket assembly. Traffic. 2001;2:138–147. doi: 10.1034/j.1600-0854.2001.020208.x. [DOI] [PubMed] [Google Scholar]
- 25.Ferguson M.L., Prasad K., Nossal R. Conformation of a clathrin triskelion in solution. Biochemistry. 2006;45:5916–5922. doi: 10.1021/bi052568w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Allen M.P., Tildesley D.J. Oxford University Press; Oxford, UK: 1987. Computer Simulation of Liquids. [Google Scholar]
- 27.Frenkel D., Smit B. Academic Press; San Diego, CA: 1996. Understanding Molecular Simulation. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Movie S1. The spontaneous self-assembly of two clathrin cages at ε = 8 kBT over the course of >>7 × 106 Monte Carlo moves per particle
Document S1. Movie legend


