Actin Filament Length Tunes Elasticity of Flexibly Cross-Linked Actin Networks

Abstract

Networks of the cytoskeletal biopolymer actin cross-linked by the compliant protein filamin form soft gels that stiffen dramatically under shear stress. We demonstrate that the elasticity of these networks shows a strong dependence on the mean length of the actin polymers, unlike networks with small, rigid cross-links. This behavior is in agreement with a model of rigid filaments connected by multiple flexible linkers.

Introduction

The actin cytoskeleton is a composite intracellular biopolymer network. To tune the mechanical properties of the cytoskeleton for such diverse processes as cell division, locomotion, and shape, a large number of actin binding proteins organize network structure (1). Nucleating and capping proteins regulate the polymerization of monomeric actin into filamentous actin (F-actin). Cross-linking proteins bind the actin filaments together to form elastic gels or bundle structures, such as in stress fibers and filopodia. Motor protein assemblies control tension within the networks by pulling on actin filaments cross-linked to the network (2–4). Even though the important molecular components are known, relatively little is understood of how this large ensemble of proteins collectively contributes to the mechanical response of the cytoskeleton.

The complex and composite structure of the cytoskeleton makes studying the origins of the mechanical response difficult. One approach has been to study reconstituted in vitro F-actin networks in the presence of purified binding proteins (3,5–9). Reconstituting the network allows precise control of its chemical composition and systematic investigation of its properties. A ubiquitous feature of these networks is that they stiffen with increasing applied stress. When F-actin is cross-linked by small rigid cross-links, the stiffening arises from the properties of the filaments themselves. F-actin is a semiflexible polymer; the persistence length is 17 μm (10). Thermal fluctuations cause transverse bending in the F-actin, which decreases its end-to-end distance. Application of a force stretches out these fluctuations. For small extensions, the force is proportional to the extension, whereas for large extensions approaching the contour length, the force diverges, leading to strain-stiffening (11). Both the linear and nonlinear network elasticities are consistent with the theoretical predictions for a network of semiflexible polymers, provided the deformation is affine (5,7,12). However, this picture of network elasticity implicitly assumes that the elasticity is controlled by one component, the actin filaments. It ignores any contribution of the cross-linking proteins; these can be both large and compliant, and therefore can themselves contribute to the elasticity.

One example of a large and flexible cross-link is filamin, which is abundant in cells. Filamin cross-links F-actin into orthogonal networks in the cortex, connects F-actin to integrins, and may play a role in mechanotransduction (13–17). F-actin networks cross-linked by filamin exhibit a mechanical response that is qualitatively different from networks formed with rigid cross-links (6,8,18,19). Filamin-F-actin networks are compliant, weakly elastic solids. Nevertheless, they can support large shear stresses because of their pronounced nonlinear strain-stiffening. Their nonlinear behavior is inconsistent with predictions for an affinely deformed network with rigid cross-links (5,6,19). In comparison to networks with rigid cross-links, networks cross-linked by filamin exhibit mechanical properties that more closely mimic the properties of cells (3,6,18).

Recent experimental reports show that the unusual nonlinear elasticity of these networks is consistent with a model of rigid polymers connected by multiple flexible cross-links (19–21). The rigid polymer of length L constrains the deformation profile of the n flexible cross-links bound along its length, as shown in Fig. 1; thus, polymer length is predicted to be an important parameter controlling the linear and nonlinear properties of the network (21). Indeed, the linear viscoelasticity and rupture stress of F-actin networks cross-linked by filamin are sensitive to the addition of gelsolin (19,22), an actin-capping and severing protein that shortens the average filament length. While these previous data support the view that F-actin length affects the rheology of these networks, fully elucidating the physical principles of this mechanism demands a more systematic investigation of the linear and nonlinear behavior of filamin-gelsolin-F-actin networks.

Figure 1.

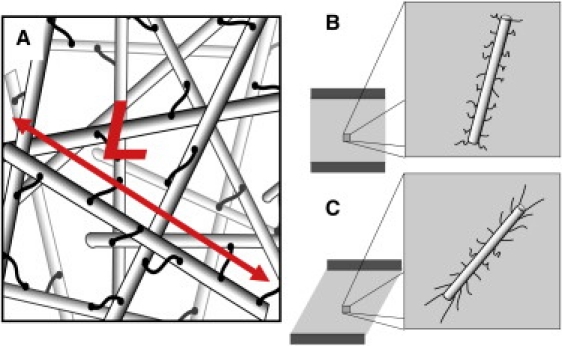
(A) Schematic of network of stiff polymers of mean length L connected by flexible cross-links. (B and C) Schematic of stiff polymer and attached cross-links in a network before (B) and after (C) shear.

In this article, we investigate the mechanical response of networks of F-actin cross-linked by filamin as we systematically decrease L by adding gelsolin. Using bulk rheology, we show that the linear modulus increases proportional to L². The critical strain, which marks the onset of stiffening, decreases with increasing L. In the nonlinear regime, the maximum stress before breaking is proportional to L. These results are contrasted with the rheology of a network formed with rigid cross-links to demonstrate that these behaviors are unique features of the filamin-F-actin system. Thus, we show that the linear and nonlinear elastic behavior of F-actin cross-linked by filamin is indeed tuned by varying L, in a manner that is consistent with the theoretical predictions for a network of stiff polymers connected by flexible linkers.

Materials and Methods

Proteins

We purify monomeric (G) actin from rabbit skeletal muscle (23), followed by gel-filtration (HiLoad 16/60 Superdex 200pg; GE Healthcare, Little Chalfont, Buckinghamshire, UK). Aliquots of purified G-actin in G buffer (2 mM Tris HCl, 0.2 mM ATP, 0.2 mM CaCl₂, 0.2 mM DTT, and 0.005% NaN₃, pH 8.0) are frozen in liquid nitrogen and stored at −80°C. Recombinant human filamin A is purified from Sf9 cell lysates (24). Recombinant human plasma gelsolin is purified (25) or purchased (Biogen, Cambridge, MA). For rigidly cross-linked networks, we incorporate biotinylated actin monomers (Cytoskeleton, Denver, CO) that can be cross-linked by NeutrAvidin protein (Pierce, Rockford, IL).

Network formation

We form networks with an actin concentration, c_A = 0.5 mg/mL, unless otherwise noted, and control network microstructure by varying the molar ratio of filamin dimers/actin monomers, R_F. We regulate the actin-filament length distribution with gelsolin. The molar ratio of gelsolin/actin monomers, R_G, sets the mean actin filament length (26). Samples are prepared by mixing solutions of 10× polymerization buffer (20 mM Tris-HCl, 20 mM MgCl₂, 1 M KCl, 2 mM DTT, 2 mM CaCl₂, and 5 mM ATP, pH 7.5), gelsolin, filamin, and G-actin.

For rigidly cross-linked networks, biotinylated actin monomers are incorporated in actin filaments at a molar ratio of biotinylated G-actin to nonbiotinylated G-actin, R_B. Cross-linking is mediated by NeutrAvidin protein. Samples are prepared by mixing 10× polymerization buffer, gelsolin, biotinylated G-actin, and G-actin. After 3 min, NeutrAvidin at a 1:1 molar ratio to biotinylated actin is gently mixed in.

The sample is loaded into a microscopy chamber, consisting of two coverslips with a 1-mm spacer, or between rheometer plates and polymerized for 1 h at 25°C.

Characterization of F-actin length distribution

To characterize the actin-filament length distribution, we polymerize 0.3 mg/mL F-actin in the presence of gelsolin. After 1 h, the filaments are labeled and stabilized with a 1:1 molar ratio of Alexa-488 phalloidin and incubated at 25°C for 30 min. The filaments are diluted to a concentration of 2 nM, and 5 μL of the suspension is pipetted onto a coverslip functionalized with poly(acrylamide-co-diallyldimethylammonium chloride). A second coverslip is placed on top and the sample sealed. Nearly all filaments stick to the coated coverslip. Immobilized filaments are imaged using a confocal microscope (model No. TCS SP5; Leica, Wetzlar, Germany); image pixel size is 160 nm. Filament contour lengths, l, are measured manually in ImageJ (National Institutes of Health, Bethesda, MD); the minimum distance measurable using this method is 0.5 μm. For each gelsolin concentration, the width of the distribution of filament lengths

$$\sigma =\sqrt{\langle l^2\rangle -{\langle l\rangle }^2}$$

is nearly equivalent to the mean (Fig. S1 in the Supporting Material).

For network formation, we polymerize F-actin in the presence of gelsolin and filamin. In previous work, addition of α-actinin to gelsolin-regulated F-actin narrowed the width of the length distribution without significantly affecting the mean length L (27). Similarly, we expect that filamin should not significantly change the values of L we measure here.

Imaging

For confocal microscopy, samples are fluorescently labeled by polymerizing in the presence of 0.6 μM Alexa-488 phalloidin and examined (model No. TCS SP5; Leica). For transmission electron microscopy, a 10 μL drop of assembled network is applied to a 400-mesh carbon-coated nickel grid and incubated for 30 s, stained with 1% uranyl acetate, rinsed by passing a drop of distilled water over the grid, then air-dried and imaged (model No. 2100; JEOL USA, Peabody, MA).

Rheology

We use a stress-controlled rheometer with 40-mm stainless steel parallel plates and a 160-μm gap (AR-G2; TA Instruments North America, New Castle, DE; or C-VOR; Bohlin Instruments/Malvern Instruments, Malvern, Worcestershire, UK). We polymerize samples in situ and use a solvent trap, applying a thin layer of low-viscosity mineral oil around the sample to minimize evaporation. We confirm the results are independent of gap and reproducible within and between different protein preparations.

The linear viscoelastic response is measured by applying a frequency-dependent, sinusoidal stress, σ_osin(ωt), and measuring the strain, γ_osin(ωt + δ). We maintain γ_o < 2% to ensure linear response. The elastic modulus is

$$G^{\prime }\left(\omega \right)=\left({\sigma }_{\text{o}}/{\gamma }_{\text{o}}\right)\text{cos}\left(\delta \right);$$

the viscous modulus is

$$G^{″}\left(\omega \right)=\left({\sigma }_{\text{o}}/{\gamma }_{\text{o}}\right)\text{sin}\left(\delta \right).$$

We measure the response in the nonlinear regime with a differential or “prestress” measurement; a small amplitude oscillatory stress, δσ, is superposed on a steady prestress, σ_o, to measure the differential modulus,

$$K^{\ast }\left({\sigma }_{\text{o}},\omega \right)={\delta \sigma /\delta \gamma |}_{{\sigma }_{\text{o}}}.$$

The elastic and viscous components are K′ and K″, respectively. We confirm there is no time dependence in K′ at various levels of prestress and minimal hysteresis in K′(σ_o) (Fig. S5). In a complementary strain ramp approach, we increase the strain at a fixed rate and measure the resulting stress. Both σ(t) and γ(t) are smoothed using a cubic spline algorithm to compute the differential modulus

$$K=\frac{d\sigma }{d\gamma }$$

by applying a numerical derivative to the stress-strain curve.

Results and Discussion

F-actin length distribution in the presence of gelsolin

Within the cell, the contour lengths, l, of actin filaments are highly regulated. Typical lengths range from 100 nm to a few microns (28,29). In vitro, high enough concentrations of pure monomeric actin will polymerize spontaneously in the presence of divalent salt and ATP. Yet, these in vitro filaments are typically much longer than those in the cell, with contour lengths that can be up to 50 μm (Fig. S1).

To better mimic the conditions in cells, we use the F-actin capping and severing protein gelsolin to vary the mean length, L = 〈l〉, of our in vitro actin filaments. To characterize the filament length distribution in the presence of gelsolin, we image a diluted sample of F-actin stabilized with fluorescent phalloidin (Fig. S1). For the ratio of gelsolin/actin, R_G = 0, the unregulated F-actin has a mean length of L = 14.8 μm. Upon adding a small amount of gelsolin, R_G = 1:3700, the length distribution is dominated by the presence of the gelsolin and L decreases to 10.4 μm. Increasing R_G decreases L further. We find that L scales linearly with R_G⁻¹, as shown in Fig. 2; it varies as L = (330 R_G)⁻¹, with L measured in microns. This is consistent with a model where each gelsolin molecule associates with one actin filament. Each actin monomer adds 2.7 nm to the filament length (30), so that 1 μm of filament is composed of 370 monomers, predicting L = (370 R_G)⁻¹. Some inactivation of gelsolin during storage may account for the slightly larger observed filament lengths compared to the prediction. These findings are consistent with previous studies of actin-filament length distributions (26,27,31).

Figure 2.

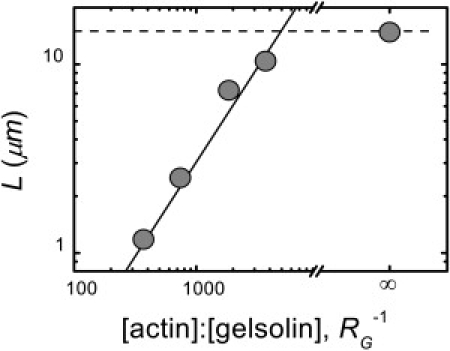
Mean F-actin length L as a function of the molar ratio of actin/gelsolin, R_G⁻¹. L decreases from its unregulated value (dashed line) as gelsolin is added. (Solid line) Linear scaling.

Microstructure of filamin-gelsolin-F-actin networks

We form in vitro networks of actin filaments whose lengths are regulated with gelsolin and which are cross-linked by filamin. In vitro, filamin efficiently cross-links F-actin into orthogonal networks, which are soft but support large stresses (6,13). These networks mimic several key features of cell mechanical properties (3,6,18). The microstructure of these networks varies as we change L and the molar ratio of filamin/actin, R_F.

For R_F ≲ 0.01, the networks are a homogeneous mesh of F-actin as seen by electron microscopy (Fig. S2) and confocal microscopy (Fig. 3, A and B). For R_F > 0.01, large bundles appear within the mesh (Fig. 3, C and D). The value of R_F ≈ 0.01 above which bundles appear is roughly independent of L (19). From electron microscopy, the bundles appear as loose, branching structures with diameters ∼100 nm (Fig. 3 C, inset). These observations are consistent with reports for networks with filamin from chicken gizzard (22,32,33). We confirm this bundling transition by tracking the thermal motion of particles within the networks (Fig. S3).

Figure 3.

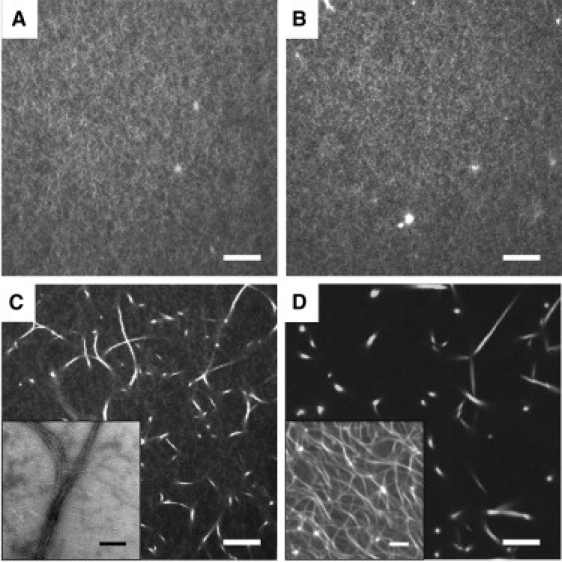
Microstructure of filamin-gelsolin-F-actin networks. (A and B) For R_F ≲ 0.01, networks are a homogeneous mesh of F-actin. (C and D) Large bundles are present at high R_F. (A) Confocal image, R_F = 0.002, R_G = 0 (L = 15 μm). (B) Confocal image, R_F = 0.01, R_G = 1:370 (L = 1 μm). (C) Confocal image, R_F = 0.01, R_G = 0. (Inset) TEM image. (D) Confocal image, R_F = 0.04, R_G = 1:370. (Inset) Confocal image at lower magnification to show network connectivity. Scale bars are 10 μm for confocal images and 0.5 μm for TEM image.

Varying L has little effect on the visual appearance of the nonbundled networks (Fig. 3, A and B). However, in the bundled networks, F-actin partitions more readily into the bundles at high R_G, forming networks of pure bundles without a background F-actin mesh, as visible in confocal microscopy (Fig. 3 D) or detectable by particle tracking (data not shown). This may be due to increased diffusion and decreased entanglements for shorter filaments, allowing them to more easily associate into bundles (32).

Linear response

To probe the mechanical properties of the filamin-gelsolin-F-actin networks, we use a stress-controlled rheometer. For an actin concentration c_A = 0.5 mg/mL and L = 15 μm, a weakly cross-linked network having R_F = 0.001 is a soft, viscoelastic solid (Fig. 4 A, squares). The elastic modulus G′ is two- to threefold larger than the viscous modulus G″, and G′(ω) increases as a weak power-law with the frequency, ω, over a broad frequency range. This network is only slightly stiffer than purely entangled actin (triangles). Increasing R_F further to 0.01 only modestly increases G′ and has little impact on the frequency response.

Figure 4.

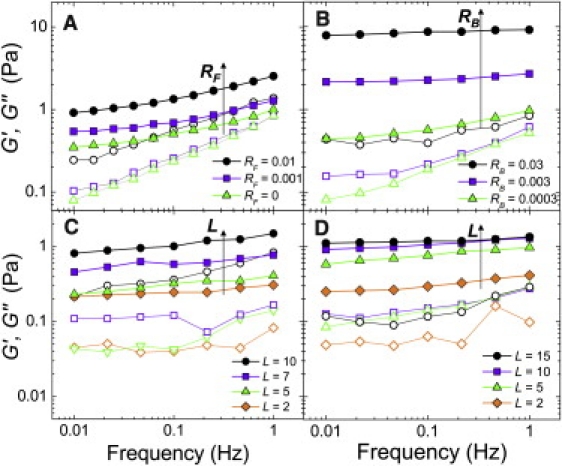
Linear viscoelasticity of cross-linked F-actin networks. Elastic moduli G′ (solid) and viscous moduli G″ (open). Filamin cross-linked networks are soft, viscoelastic solids that become stiffer with increasing R_F or L: (A) L = 15 μm with various R_F and (C) R_F = 0.01 with various L (in μm). Rigidly cross-linked networks become stiffer with increasing L and significantly stiffer and more solidlike with increasing R_B: (B) L = 15 μm with various R_B, and (D) R_B = 0.01 with various L.

This is in contrast to F-actin with rigid cross-linking induced by addition of NeutrAvidin to networks with a small fraction, R_B, of biotinylated actin monomers incorporated into the F-actin. Increasing R_B leads to a drastic increase in the stiffness of the network, as shown in Fig. 4 B; this is accompanied by a decrease in the slope of the weak power-law frequency response of G′(ω), consistent with more solid-like behavior (Fig. S4).

In the filamin networks, as we systematically decrease the mean filament length L from 10 to 2 μm by adding increasing amounts of gelsolin, G′ decreases from 1 to 0.2 Pa (Fig. 4 C). For rigidly cross-linked networks, G′ also decreases with L (Fig. 4 D). For both types of cross-links, the slope of G′(ω) does not vary drastically with L.

Dependence of the linear modulus on filament length

To quantify the changes in the elasticity of these networks as we decrease L, we plot G_o, defined as

$${G_{\text{o}}=G^{\prime }|}_{\omega =0.1\text{Hz}},$$

as a function of L (Fig. 5 A). For R_F = 0.001, G_o is 0.2 Pa for the networks with the shortest filaments, L = 1–2 μm. As we increase L to 15 μm, G_o increases to 0.5 Pa. For increasing values of R_F, G_o starts out at roughly the same value for short filaments, but increases more strongly with L. Interestingly, at each R_F, G_o increases stronger than linearly with L.

Figure 5.

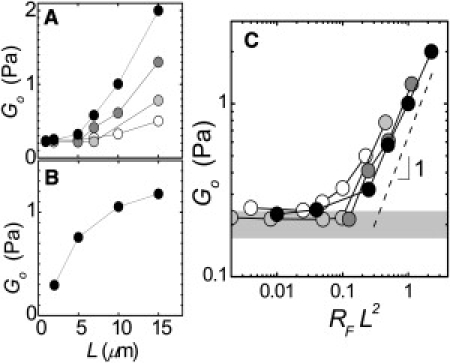
Dependence on L of the linear elastic modulus measured at a frequency of 0.1 Hz, G_o. (A) For filamin networks G_o increases stronger than linearly with L. R_F = 0.001 (open), 0.002 (light shaded), 0.005 (medium shaded), and 0.01 (solid). (B) Rigidly cross-linked networks show qualitatively different behavior. R_B = 0.01. (C) G_o for networks cross-linked with filamin at different R_F collapse onto a single curve when plotted versus R_FL² with nearly linear scaling above R_FL² = 0.1. Shaded bar represents the range of moduli measured for F-actin solutions with 2 < L < 7 μm.

This strong dependence on L is not expected from an affine theory (11) that has been used to describe the linear and nonlinear elasticity of actin cross-linked with pointlike rigid cross-links such as heavy meromyosin and scruin (5,7,12). In this theory, network elasticity is governed by the thermal compliance of the semiflexible F-actin polymers; thermal fluctuations of the F-actin get stretched-out as the network is deformed (11). This model predicts

$$G_{\text{o}}=6\rho k_{\text{B}}T\frac{l_p^2}{l_c^3},$$

where ρ is the linear density of polymer, k_B is Boltzmann's constant, T is the temperature, l_p is the persistence length of F-actin, and l_c is the distance between cross-links. Thus, in this theory the network elasticity is controlled by the distance between cross-links rather than by the length of the actin filaments, in disagreement with our results for filamin-F-actin.

Alternatively, the elasticity of our networks can originate from the compliant nature of the filamin cross-links. The large 160-nm chain between the actin binding domains of a filamin protein is quite flexible and can be modeled as a linear polymer with l_p = 20 nm (34). As a result, a filamin cross-link is soft compared to an F-actin segment of length l_c, which ranges from 0.3 to 2 μm. This suggests a model in which the compliance of the network is governed by the flexible cross-links. The actin polymers are treated as rigid rods linked by many flexible linkers, as depicted in Fig. 1 A. When the network surrounding a rigid rod is deformed, the linkers get stretched by an amount that increases linearly in the distance from the center of the rod, as shown in Fig. 1 C. Provided the network deformation is uniform on the length scale of L,

$$G_{\text{o}}=\frac{1}{8}\rho nkL\sim R_F{L}^2,$$

with k the stiffness of the flexible cross-links and n the average number of cross-links per actin filament (21). The explicit L dependence arises as a direct result of the nonuniform deformation profile of the cross-links. The average number of cross-links per actin filament is proportional to both R_F and L and is given by n = 370 R_FL; thus, the overall prediction is that G_o will increase proportional to R_FL².

To test this mechanism, we plot G_o as a function of R_FL² (Fig. 5 C). The data for different cross-linking densities collapses onto a single curve. For R_FL² ≥ 0.1, G_o scales nearly linearly with R_FL², consistent with the prediction. This supports the model of crosslink-dominated elasticity. Below R_FL² = 0.1, which corresponds to n = 7 cross-links for a 5-μm filament, the values of G_o are roughly equivalent to the elasticities we measure for F-actin solutions in the absence of cross-linking, as shown in Fig. 5 C (shaded bar). This suggests that the linear elasticity of these weakly cross-linked networks is dominated by the solution elasticity, not by the cross-links. The threshold of R_FL² = 0.1 corresponds to typical physiological conditions (L = 2 μm, R_F = 0.02) (35,36), suggesting that by spatially or temporally regulating L, cytoskeletal elasticity could be adjusted from essentially that of entangled F-actin to a network with tunable stiffness.

By contrast, the dependence of G_o on L for the rigidly cross-linked networks is of a qualitatively different form; G_o increases linearly with L for small L but approaches a plateau for large L (Fig. 5 B). Simulations of two-dimensional (37) and three-dimensional (38) stiff polymer networks reveal a dependence on L qualitatively similar to our results. The departure from the plateau for decreasing L in simulations has been attributed to an increase in the nonaffinity in the deformation of the network, where the affine thermal theory is expected to break down.

Nonlinear response

The dependence of G_o on R_F and L is consistent with network elasticity that is governed by the filamin cross-links. We further test the origin of the elasticity by measuring the nonlinear elastic properties of the filamin-F-actin gels with two complementary techniques—strain ramps and prestress measurements.

Strain ramps

In the first approach, we increase the strain, γ, at a fixed rate and measure the resulting stress, σ. From the derivative of the stress-strain curve, K = dσ/dγ, we quantify the nonlinear behavior. This technique has been used to study nonlinear behavior of both entangled and cross-linked F-actin networks (39–41). For a filamin cross-linked network with L = 15 μm and R_F = 0.01, K normalized by its initial value, K_o, is equal to 1 for small strains (Fig. 6 A). At the critical strain, γ_c = 0.06, K/K_o increases above 1, and the network begins to stiffen. It stiffens 30-fold before breaking at γ_m = 0.9. Networks with shorter filaments initially display weakening behavior, where K/K_o decreases below 1, due to their lower network connectivity, but eventually stiffen. As we decrease L, γ_c increases markedly, as shown in Fig. 6 A.

Figure 6.

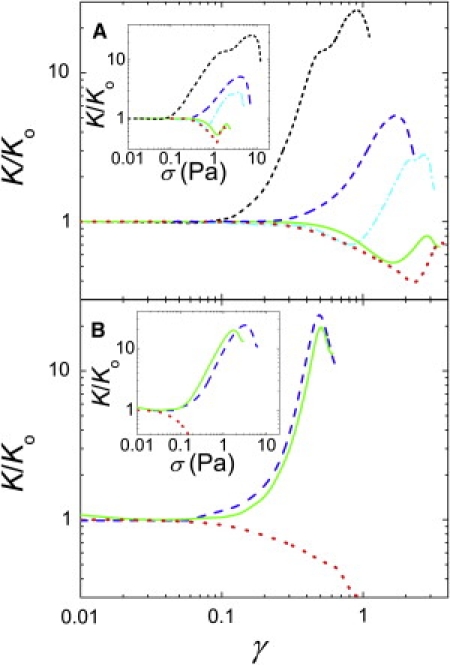
Nonlinear stiffening in strain ramps with a rate of 0.1/s. The derivative of the stress-strain curve, K, normalized by its initial value, K_o, as a function of strain. (A) Filamin with R_F = 0.01 and L = 15 (short dash), 10 (long dash), 7 (dash-dot), 5 (solid), and 2 (dot) μm. For the network with L = 15 μm, K/K_o = 1 at small strains before beginning to stiffen above γ_c = 0.06. Networks with shorter filaments initially display weakening behavior, where K/K_o decreases below 1, due to their lower network connectivity, but stiffen at higher strains where the slope of the curve becomes positive. The value γ_c increases with decreasing L. (B) Rigid cross-links with R_B = 0.01 and L = 10 (dash), 5 (solid), and 2 (dot) μm. Networks with long filaments display stiffening behavior that is independent of L, while networks with short filaments display weakening behavior. (Insets) Same data plotted versus stress.

By contrast, rigidly cross-linked networks with L > 5 μm stiffen at small strains, independent of L (Fig. 6 B). Networks with L ≤ 2 μm do not stiffen and display weakening behavior. This is consistent with a transition from stiffening behavior arising from pulling out fluctuations in F-actin, where

$${\gamma }_c=\frac{1}{6}\left(\raisebox{1ex}{$l_c$}\!\left/ \!\raisebox{-1ex}{$l_p$}\right.\right)$$

is set only by l_c and l_p, to weakening behavior, where the network becomes too sparsely connected to stiffen. However, the strong dependence of γ_c on L for filamin-F-actin is inconsistent with such a nonlinear response arising from thermal fluctuations of the actin filaments being stretched-out.

We propose instead that the nonlinear response for filamin-F-actin originates from the stiffening behavior of the cross-links. Single molecule experiments indicate that filamin proteins stiffen markedly as they are stretched toward their contour length l_o (42). When the network surrounding a rigid rod is deformed strongly, linkers bound at the ends of the polymers are stretched most, as depicted in Fig. 1 C. These linkers will be the first to reach full extension and stiffen, setting the critical strain at which the network begins to stiffen. These end-bound linkers reach full extension at a strain (21):

$${\gamma }_c=4l_{\text{o}}/L.$$

The L-dependence arises because the amount an end-bound cross-link must stretch to accommodate a given macroscopic network strain increases with the length of the rigid rod to which it is bound.

Plotting γ_c as a function of L⁻¹ in Fig. 7 A, the dependence of γ_c on L⁻¹ is in stark contrast to the stiffening behavior of rigidly cross-linked networks, which display no dependence of γ_c on L. The increase of γ_c with increasing L⁻¹ is qualitatively consistent with the prediction of the model. We see similar behavior for γ_m (Fig. 7 B), suggesting that the nonuniform deformation profile of the linkers prevails up to large strains. Interestingly, the γ_c data from the two systems converge at small L⁻¹ (Fig. 7 A). In this limit of large L, the model of rigid rods with flexible linkers predicts that the smallest of strains would lead to stiffening. However, this model relies on the linkers being the softest mode in the system. When the prediction for stiffening by the linkers would yield a lower γ_c than by the F-actin segments themselves, this picture breaks down, and it is no longer valid to assume the F-actin behave as rigid rods. In this limit, the compliance of the F-actin would contribute to the stiffening behavior of the system, consistent with our observation.

Figure 7.

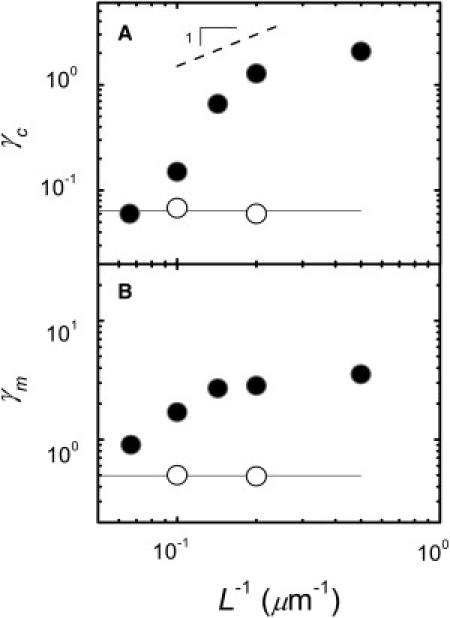
Dependence of the critical and maximum strains on L. Filamin with R_F = 0.01 (solid). Rigid cross-links with R_B = 0.01 (open). (A) The value γ_c of the filamin networks increases with increasing L⁻¹. In contrast, γ_c for rigidly cross-linked networks is independent of L, with mean value denoted (solid line). (B) The value γ_m versus L⁻¹.

Prestress measurements

In our second technique for probing nonlinear response, we apply a steady prestress, σ_o, and probe the differential elastic modulus, K′(σ_o,ω), with a small oscillatory stress. This technique has been used in cross-linked F-actin networks to study nonlinear stiffening behavior (5,6,12,41). Rigidly cross-linked F-actin networks display stiffening with K′ ∼ σ_o^3/2 (5); we see the same behavior for networks cross-linked by biotin-NeutrAvidin (Fig. 8 B). This is consistent with the predictions for the affine thermal model in which the nonlinear response is due to pulling out thermal bending fluctuations in the semiflexible actin filaments within the network (5,11).

Figure 8.

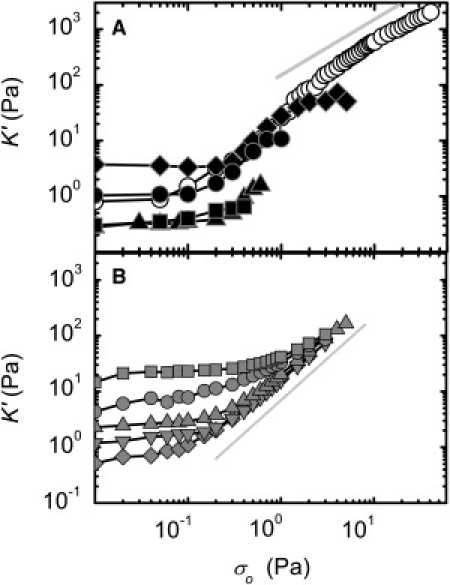
Nonlinear stiffening in prestress measurements. (A) Filamin networks with R_F = 0.003 and L = 1 (squares), 5 (triangles), 15 μm (solid circles); R_F = 0.005 with L = 15 μm (diamonds); and R_F = 0.01 with L = 15 μm (open circles, bundled network). K′ is independent of prestress, σ_o, for small prestresses before beginning to increase with σ_o at a critical stress, σ_c. Networks with higher R_F and L stiffen more and support larger stresses before breaking. (Line) Linear scaling predicted by the model. (B) Rigidly cross-linked network with L = 15 μm and R_B = 0.0003 (diamonds), 0.001 (inverted triangles), 0.003 (triangles), 0.03 (circles), and 0.3 (squares). These networks also display stiffening behavior, but the maximum stiffness and stress are roughly the same for every sample. (Line) The σ_o^3/2 scaling predicted by the affine thermal model.

Our model of rigid filaments connected by multiple flexible linkers predicts a qualitatively different stiffening behavior that arises from the stiffening of the filamin cross-links. The theoretical model is extended to the nonlinear regime by employing a self-consistent effective medium approach (19–21). The linkers are bound on one side to the rigid rod and on the other to an elastic continuum with a nonlinear elasticity that is required to self-consistently represent a uniform and isotropic collection of such elements. As the network is deformed, the linkers get stretched and stiffen one-by-one as they approach full extension and start pulling back on the effective medium. This model predicts K′ ∼ σ_o in the limit of a dense network.

To test this prediction, we measure K′(σ_o) for the networks cross-linked by filamin. For a network with R_F = 0.003 and L = 15 μm (solid circles, Fig. 8 A), K′ increases with σ_o above a critical stress, σ_c = 0.1 Pa, and reaches a stiffness, K′_m = 10 Pa, before breaking at σ_m = 1 Pa. Networks with higher R_F and L stiffen more and support larger stresses. For these networks, K′ increases more strongly than linear in σ_o just above σ_c, whereas at high σ_o, K′ ∼ σ_o (Fig. 8 A). This unusual stiffening behavior is in agreement with the prediction of the model. Rescaling K′ by its initial value and σ_o by σ_c, the K′(σ_o) data for networks formed with different R_F and L collapse onto a single curve, provided the network is not highly bundled (Fig. 9). Our rescaled data agrees well with the nonlinear response calculated with the effective medium model (Fig. 9), with only one fit parameter that represents the coupling of a rigid rod to the effective medium. In contrast, the rescaled data from networks rigidly cross-linked by biotin-NeutrAvidin fall on a separate curve, which is well described by the prediction of the affine thermal theory of cross-linked semiflexible networks (Fig. 9). These data support the model of crosslink-dominated elasticity in the filamin-F-actin networks.

Figure 9.

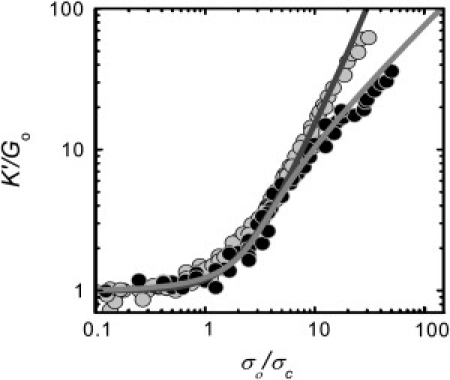
Rescaled nonlinear stiffening of nonbundled networks with filamin (solid) or rigid cross-links (light shaded) at various values of R_F or R_B, L, and c_A. Filamin data is consistent with model of rigid rods connected by flexible linkers (20) (medium shaded line), while rigid cross-linking data is consistent with model of semiflexible filaments connected by rigid linkers (5) (dark shaded line).

Interestingly, although the filamin-F-actin networks are all quite compliant, the maximum stiffness before breaking, K′_m, increases strongly with R_F, presumably because network failure is due to filamin unbinding (19,43). Thus, the overall magnitude of stiffening, K′_m/G_o, increases with R_F (Fig. 8 A and Fig. S6 B). Of these networks the highly bundled ones show the most dramatic stiffening (open symbols). The opposite behavior is observed for the rigidly cross-linked networks; G_o increases significantly with R_B, while K′_m is nearly independent of R_B (Fig. 8 B and Fig. S6 B), presumably because network failure is due to F-actin rupture (12).

Dependence of the maximum stress on filament length

Assuming cross-link unbinding as the dominant failure mode for these networks, a scaling argument based on the theoretical model predicts how σ_m scales with c_A, R_F, and L. Essentially, each cross-link will unbind from F-actin at a force, f_m. With multiple cross-links per filament, the cross-links act in parallel, and the total rupture force per filament increases linearly with n. From the density of filaments and assuming an isotropic orientation of filaments within the network, the maximum stress is (20,21)

$${\sigma }_m=\frac{1}{45}\rho n{f}_m.$$

Thus, as we increase L at fixed R_F, the number of filamins per actin filament will increase, and the prediction is

$${\mathit{\sigma }}_m\sim n\sim R_{F}L.$$

We first look at σ_m measured in prestress experiments. In Fig. 8 A, we see that σ_m supported by the R_F = 0.003 networks increases as we increase L. To quantify this, we plot σ_m as a function of L in Fig. 10 A. Above a critical value of L, the maximum stress increases with L. This critical value of L decreases with increasing R_F. Similarly, for fixed L, σ_m increases roughly linearly with R_F over a broad range of R_F (Fig. S6 A). For the highest values of R_F, where the networks are highly bundled, σ_m increases dramatically (open symbols, Fig. S6 A). For R_F below a critical value, σ_m is roughly independent of R_F. This critical value of R_F decreases with increasing L (19).

Figure 10.

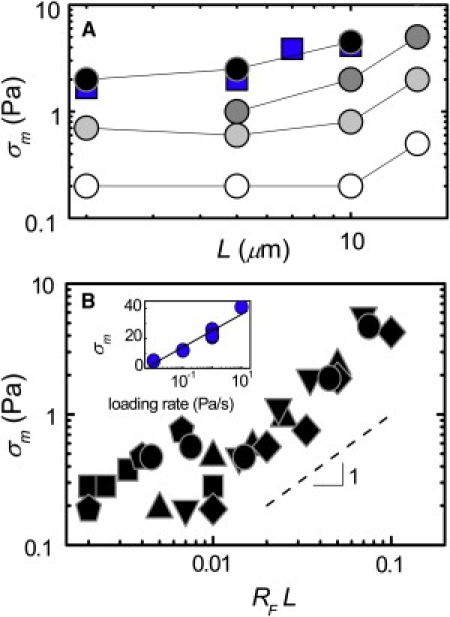
Scaling of the maximum stress, σ_m, with L for nonbundled filamin networks. (A) The value σ_m increases with L. From prestress measurements (circles) or 0.1/s strain ramps (squares): R_F = 0.001 (open), 0.003 (light shaded), 0.005 (medium shaded), and 0.01 (solid). (B) The value σ_m for samples of different compositions collapse onto a single curve when plotted versus R_FL. Above R_FL = 0.01, the data scale roughly linearly with R_FL. L = 15 (circles), 10 (diamonds), 7 (inverted triangles), 5 (triangles), 2 (pentagons), and 1 (squares) μm. (Inset) The value σ_m grows as the logarithm of loading rate in stress ramps for networks with L = 15 μm, R_F = 0.005.

We can collapse all the filamin data onto a single curve by plotting σ_m as a function of R_FL (19), as shown in Fig. 10 B. For R_FL > 0.01, σ_m grows nearly linearly with R_FL, consistent with the prediction of the model. For smaller values of R_FL, the network is rather weakly connected and breaks at very low levels of stress. The value of R_FL ≈ 0.01 corresponds to n ≈ 4. At physiological conditions, n ≈ 15—suggesting that the cytoskeleton operates in a regime where it has high enough connectivity to support large external stresses or internal tensions compared to purely entangled F-actin without rupturing. The linear scaling with R_FL or n suggests that failure of these networks is indeed determined by unbinding of cross-links (19,43). In contrast, σ_m for rigidly cross-linked networks is nearly independent of R_B for R_B > 0.001 (Fig. S6 A); this is consistent with rupture of F-actin at network failure (12).

We can also determine σ_m from the strain ramp measurements. In Fig. 6 A (inset), we see that σ_m also increases with L for strain ramps conducted at a rate of 0.1/s. Plotting σ_m determined in this way as a function of L (squares, Fig. 10 A) for R_F = 0.01, we find that these measurements of σ_m show similar scaling to the prestress measurements, and at this strain rate the values from the two methods nearly match. More generally, we expect that σ_m will depend on the rate of the measurement. The unbinding force for a single cross-link is expected to increase as the logarithm of the loading rate (40,44). In an analogous macroscopic measurement, we find that σ_m increases as the logarithm of the loading rate on the network, again consistent with cross-link unbinding at network failure (inset, Fig. 10 B).

Conclusions

The linear and nonlinear elastic behavior of filamin-gelsolin-F-actin networks support a model of crosslink-dominated elasticity. The F-actin behaves as a rigid filament that constrains the deformation profile of the flexible cross-links bound along its length; this leads to the unusual L dependence in the rheology of these networks. Our data suggest that the lengths of actin filaments within cross-linked cytoskeletal networks may be an important determinant of cell mechanics.

Large, flexible cross-links like filamin form compliant gels that can nonetheless support stresses that are orders-of-magnitude larger than those of purely entangled F-actin. The stiffness of these networks can be tuned over a broad range by external stress or internal tension (3,6,19). In contrast, rigid cross-links form networks with a linear stiffness that is highly tunable by increasing the cross-link concentration, but show less dramatic nonlinear stiffening and tend to break at smaller strains (5,7). Interestingly, the mechanical response of F-actin networks can be tuned between these two cases by systematically varying the molecular weight of a cross-link (8).

Many physiological cross-links are smaller and expected to be more incompliant than filamin; within the cell these cross-links typically organize F-actin into bundles rather than orthogonal meshworks. For example, the α-actinin dimer forms an antiparallel rod of ≈30 nm, and fimbrin has two actin binding domains in tandem and is only ≈12 nm. Indeed, rheological studies show that α-actinin-F-actin networks have highly tunable linear stiffness (45), suggesting α-actinin behaves predominantly as a rigid cross-link. This also suggests that the cell may use large, compliant cross-linking proteins like the 160-nm-long filamin dimers precisely because of the unique mechanical properties of the networks they form. In support of this view, filamin-F-actin networks mimic many key rheological features of cells (6,18). This highlights the potential value of these results in providing insight into the behavior observed in cells.