A model of hypertension and proteinuria in cancer patients treated with the anti-angiogenic drug E7080

Abstract

Hypertension and proteinuria are commonly observed side-effects for anti-angiogenic drugs targeting the VEGF pathway. In most cases, hypertension can be controlled by prescription of anti-hypertensive (AH) therapy, while proteinuria often requires dose reductions or dose delays. We aimed to construct a pharmacokinetic–pharmacodynamic (PK–PD) model for hypertension and proteinuria following treatment with the experimental VEGF-inhibitor E7080, which would allow optimization of treatment, by assessing the influence of anti-hypertensive medication and dose reduction or dose delays in treating and avoiding toxicity. Data was collected from a phase I study of E7080 (n = 67), an inhibitor of multiple tyrosine kinases, among which VEGF. Blood pressure and urinalysis data were recorded weekly. Modeling was performed in NONMEM, and direct and indirect response PK–PD models were evaluated. A previously developed PK model was used. An indirect response PK–PD model described the increase in BP best, while the probability of developing proteinuria toxicity in response to exposure to E7080, was best described by a Markov transition model. This model may guide clinical interventions and provide treatment recommendations for E7080, and may serve as a template model for other drugs in this class.

Introduction

Over the last few decades, various pharmacological approaches to the inhibition of angiogenesis have been investigated. So far, suppression of vascular endothelial growth factor (VEGF) signaling has shown the most prominent clinical success. This can be achieved by drugs that inhibit signaling by binding the tyrosine kinase domains of the VEGF-Receptor (VEGFR) such as sorafenib, or binding to VEGF by monoclonal antibodies (e.g. bevacizumab) or decoy receptors (VEGF-Trap). While drugs acting on the VEGF pathways are generally well tolerated at doses that achieve pharmacologically active plasma levels, especially in comparison with classical cytotoxic drugs, toxicities are still a major problem. This may partially be explained by the fact that VEGF-signaling is not specific to tumor-induced angiogenesis, but is also involved in various other physiological mechanisms. Furthermore, most small-molecule VEGF(R)-inhibitors are not specific for the tyrosine kinase domain of one specific receptor, but may interfere with multiple pathways. The most commonly reported side effects for VEGF(R)-inhibitors are hypertension and proteinuria [1]. While the observed hypertension can generally be managed with anti-hypertensive (AH) drugs, proteinuria is often treatment limiting, and necessitates dose interruptions or dose reductions. Several mechanisms are assumed to be involved in the development of hypertension, including the decrease of NO and/or PGI₂ production, rarefaction of blood vessels, vascular stiffness and disturbed endothelin function, although the exact mechanisms has not been clarified yet [2]. Proteinuria may be caused directly by drug action through inhibition of VEGF’s effects on glomerulal endothelial function, or indirectly through increase of blood pressure, but most probably a combination of both factors is involved.

Although tyrosine kinase inhibitors (TKI) are targeted molecules, and often show efficacy at lower concentrations than achieved using the approved doses, it is recognized that dosing should be aimed at obtained as high exposure as possible [3]. Therefore, clinical development of these agents often adheres to comparable strategies as those of cytotoxic anti-cancer agents, i.e. aimed at finding a maximum tolerable dose (MTD). This implies that still a significant number of patients will experience toxicities in treatment with these agents, thereby potentially limiting treatment efficacy due to dose reductions or dose delays. The management and if possible avoidance of these toxicities is therefore of key importance. Moreover, a positive correlation has been shown between the development of hypertension and treatment effect, and, therefore, it has been proposed that hypertension might function as a biomarker to guide individual dosing strategies [4–7].

In this article we report the development of a pharmacokinetic–pharmacodynamic (PK–PD) model that describes the effects of exposure to a novel drug targeting the VEGF pathway (E7080) on blood pressure and the probability of developing different grades of proteinuria, in patients with cancer. E7080 is an oral anti-cancer agent, inhibiting angiogenesis by its capacity to bind tyrosine kinase domains of several receptors, mainly VEGF-R2 and VEGF-R3 [8]. In preclinical trials, it has shown promising activity, and was shown to be more potent than bevacizumab in reducing angiogenesis and lymph angiogenesis in xenograft models [8, 9]. E7080 has been tested in several Phase I trials, in which both hypertension and proteinuria were commonly observed and were the major dose limiting toxicity. By developing this model, we aim to provide a tool to investigate the influence of dosage, exposure, time, and patient characteristics on the development of these toxicities. The model will allow evaluation of dosing regimens for reduction of adverse events or optimizing efficacy, support clinical decision making, and aid in further clinical development of this drug.

Methods

Data

Data was obtained from a two-site phase I dose finding study of E7080 in patients with advanced malignancies, as described elsewhere [10–12]. In summary, patients were ≥18 years of age with solid tumors or lymphoma, and a Karnofsky score ≥70%. Patients were treated with E7080 once daily (qd), using fixed doses. No other anti-cancer drugs were administered during or less than 4 weeks before start of treatment. Doses were escalated from 0.2 mg day⁻¹ up to 32 mg day⁻¹ in cohorts of 3–6 patients. Intra-patient dose escalation was not allowed. Relevant exclusion criteria were brain tumors, uncontrolled infections, reduced bone marrow reserve, clinically significant cardiac impairment, and bleeding or thrombotic disorders. Excluded were patients using therapeutic dosages of anti-coagulants, patients treated with other investigational drug within 30 days prior to start of study, patients with proteinuria ≥2+ (CTC grade ≥2), and patients with poorly controlled hypertension (repeated measurements higher than 160/90 mmHg) at screening.

AH therapy was offered to all patients who had a confirmed blood pressure (BP) of 160/100 mmHg during treatment with E7080. If BP during treatment was >160/100 mmHg, AH therapy was initiated according to local guidelines, with the aim of reducing BP to ≤140/90 mmHg. E7080 dose reductions following adverse events were performed per protocol, to 75 or 50% of the former dose, or discontinuation of treatment, depending on the grade of toxicity and the number of times the toxicity grade occurred before.

PK samples were obtained after the first dose at day 1 of cycle 1 and cycle 2. Trough samples were obtained on days 8, 15 and 22 of cycle 1, and on the first day of each subsequent schedule. Plasma concentrations were determined using a validated LC/MS/MS method. Blood pressure (BP) measurements were carried out weekly using standard manual sphygmomanometers. From all patients, the medication prescriptions were recorded during the study. Prescription of anti-hypertensive (AH) drugs, or drugs that were known to induce anti-hypertensive effects was recorded.

Urinalysis was performed weekly during therapy using commercially available strip tests, and consisted of (at least) pH, glucose, protein measured by dipstick, presence of ketones, and presence of blood. Protein in urine was reported as ‘negative’, ‘trace’, ‘+/−’, ‘+’, ‘2+’, ‘3+’ or ‘4+’, but treated as a four category scale, corresponding to the CTC (NCI, version 3.0) grades: PU₁ = <1+, PU₂ = 1+, PU₃ = 2+ or 3+, PU₄ = 4+.

PK–PD analysis

The statistical data analysis was performed with non-linear mixed effects modeling using NONMEM, version VI, level 2.0 (Icon Development Solutions, Ellicott City, MD, USA) with g77 as Fortran compiler, using several functions from the PsN toolkit [13], and Piraña [14] as modeling environment. The first order conditional estimation method with interaction (FOCE-I) was used throughout the analysis. The Laplacian method was uses for modeling the categorical data. When continuous and categorical data were modeled simultaneously, the F_FLAG option was used to switch between observations and likelihoods. Standard errors for model parameters were estimated from the covariance step in NONMEM.

Judgement of model fit was done using goodness-of-fit plots, the likelihood ratio test (LRT), and measures of model stability and adequacy (condition number, successful convergence, significant digits, matrix singularity). Nested models were tested for significant improvement in fit at a significance level of P < 0.01, corresponding to a decrease in objective function value (OFV) of 6.67. Plots of conditional weighted-residuals (CWRES) versus time and versus predicted values were used to evaluate model bias.

Performance of candidate and final models for the BP model was evaluated using visual predictive checks (VPC), by simulation of 500 simulated datasets [15]. Since observations were spread around nominal time points, bin separators in the VPC were set at the lowest densities of sample points over time, i.e. this positions the bins such that the periods with densest sampling were in the middle of the bins. Shrinkage in between subject variability (BSV) and residual errors was calculated to assess the informativeness of the data for using individual predications in the evaluation of model fit. The adequacy of the model for prediction of probabilities of developing proteinuria grades was also evaluated by VPCs, i.e. the observed percentage of patients experiencing a specific CTC grade were compared with those simulated from the model in simulated datasets of which median, and 95% prediction interval (PI) were calculated. The ability of the model to predict individual patterns of proteinuria grades in patients was evaluated, by comparing longitudinal plots of several simulated datasets for proteinuria with the observed data. Also, predictive checks were performed by simulating 200 new datasets with the same design, and comparing the simulated number of transitions from one grade to another, with the observed.

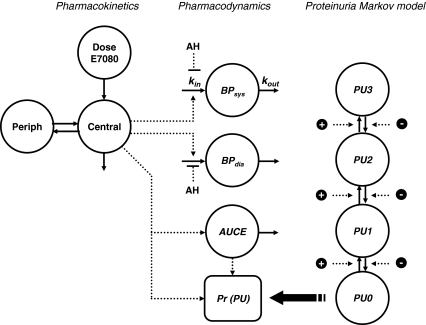
The PK–PD model was developed using a sequential approach, i.e. the empirical Bayesian estimates (EBE) from a previously developed PK model [7] were used to drive the BP model. Briefly, the PK model consisted of a central and a peripheral compartment, with a sequential zero- and first-order absorption process and first order elimination. E7080 was rapidly absorbed (ka = 0.348) with maximum concentrations typically observed from 1 to 3 h post dose, and clearance was linear over the studied dose range (CL_pop = 6.07 l h⁻¹, V _centr = 11.3 l, Q = 3.95, V _per = 45.3). After development of the BP model, the EBEs from the BP model were used in the development of the model for proteinuria. In a final step, both PD models (hypertension and proteinuria) were also fitted simultaneously.

BP model

Several structural models were tested for the BP model, expressed as direct effects or indirect responses. The indirect response models were implemented as differential equations (ODE): an effect-compartment model [16], a turnover-model [17], or a combined effect-compartment and turnover model. Since the BP data consisted of systolic (BP_S) and diastolic (BP_D) blood pressure data, we evaluated two methods of incorporating both data sources. Firstly, BP_S was modeled as function of drug effect, with BP_D data assumed to be proportional to BP_S, or the other way around. Secondly, we evaluated a model that incorporated two separate indirect effect models for BP_S and BP_D.

Additive, proportional, combined additive and proportional, and exponential (using untransformed data) residual error models were evaluated. As residual errors for BP_S and BP_D recorded at the same timepoint might be expected to show correlation, the L2 data item implemented in NONMEM was used, which groups these data in a second level of random effects, allowing the estimation of this correlation magnitude. Several approaches for implementing BP at baseline were tested, as described by Dansirikul et al. [18].

Drug effect (E _E7080) and effect of AH medication (E _AH) were incorporated as slope effect on rate constants in the BP indirect effect model as shown in Eq. 1 for the systolic compartment:

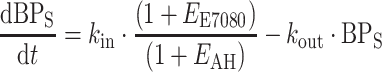1

In this equation, both baseline and k _in were estimated, and k _out was fixed to k _in/BP_S, thereby not allowing for spontaneous increase or decrease from baseline. E _E7080 was defined as a slope function: E _E7080 = θ_x · c _p,E7080, and E _AH was estimated as a slope function on cumulative AH prescription, while E _max models were also evaluated. At baseline, the system was assumed to be at steady state, i.e. k _out was set to k _in/BP_s,base Models that incorporated E _E7080 and E _AH on k _out instead of on k _in were also assessed. A cumulative measure of AH prescription as ‘defined daily dose equivalents’ was constructed, as

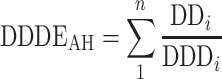2

scaling the daily prescribed dose (DD) to its WHO defined daily dose (DDD, http://www.whocc.no/atcddd/indexdatabase/, accessed November 11, 2008), over the n different AH medications that the patient was using at a certain timepoint. It was also evaluated if the inclusion of the effect of AH treatment as a direct effect, i.e. on the error model, resulted in similar or improved model fit. The equation thus uses as differential equation for BP_S and BP_D was:

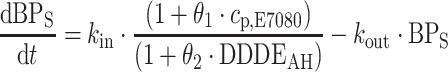3

with θ₁ and θ₂ being the estimated slopes of the effects of drug and anti-hypertensive treatment.

Proteinuria

For describing the observed categorical PU data, two approaches were evaluated. First, a proportional odds model was implemented in which three probabilities had to be estimated, as proteinuria was divided in four ordered categories (the fourth can be deducted as one minus the cumulative probabilities of the other grades). A logit transformation was applied to constrain estimated probabilities between 0 and 1, using:

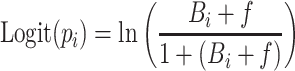4

with 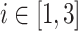, and B _i the offset probabilities for the different CTC grades (on a logit scale). The function f was used to link drug effects to probabilities of developing proteinuria, in which both linear and E _max equations were investigated.

Secondly, a Markov transition model was implemented. Study protocol indicated that urinalyses were to be performed weekly, however in clinical practice it was observed that the observations were not equally spaced. To be able to calculate the probabilities of observing each grade at every timepoint, the probabilites were incorporated in the model as differential equations (see Fig. 1). The probability at t = 0 was set to 1 for the observed proteinurea state at baseline, and updated after each observation. To reduce the number of parameters to estimate, only transitions between neighboring states were included in the model. Evaluation of the effects of drug exposure, blood pressure, and AH medication on transition were implemented in the Markov model using as proportional factors on the transitions rate parameters.

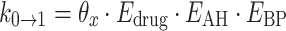5

All effect parameters were tested on each transition parameter separately, and in combination. The effects were included on the transitions for increasing transitions (k _0→1, k _1→2, k _2→3), and on the transitions for decreasing transitions (k _1→0, k _2→1, k _3→2) separately. It was tried to reduce the number of parameters, by including the same factors reciprocally for the transitions for decreasing grades, e.g.:

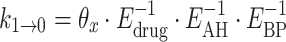6

Drug effect on probability of developing proteinuria was tested in several ways. A direct drug effect was incorporated by relating predicted plasma concentrations (c _p) using slope or E _max factors to probabilities (in the proportional odds model) or transition rates (in the Markov model). An indirect effect was incorporated as an exposure compartment, i.e. the area under the concentration–time curve, with- (AUCE_E7080, “effect compartment”) and without (AUC_E7080, “cumulative exposure”) an estimated first-order recovery rate. Increases in BP_D and BP_S from baseline were also evaluated as covariate on the transition rates. Co-medication that were plausible to have an effect on proteinuria were included as a binary covariate (use or no-use of medication). These included: anti-hypertensive medication, aldosterone-blocking drugs, diuretic drugs, non-steroidal anti-inflammatory drugs and bisphosphonates [19]. Furthermore, a number of additions to the PK–BP–proteinuria base model were considered. These included e.g. the development of tolerance, and the incorporation of lag-times before onset of the hypertensive effect of exposure to E7080 improved model-fit, either related to time, cumulative AUC or both).

Fig. 1.

PK–PD model for E7080. At t = 0, proteinuria (PU) compartment amounts are set to 0 or 1 according the observed proteinuria grade at baseline

Results

Patients and data

Patient characteristics are given in Table 1. BP and data from urinalysis were recorded over a mean period of 24 weeks (range 1–77 weeks). None of the patients experienced grade 4 hypertension or grade 4 proteinuria toxicities. The maximum tolerable dose (MTD) was established at 25 mg day⁻¹.

Table 1.

Patient and study characteristics

	N/Mean	Range
Male	38
Weight (kg)	79.3	48.3–121
Female	29
Weight (kg)	73.9	51.4–114
Age (years)	55	25–84
Race
Caucasian	66
Black	1
BPS at baseline (mmHg)	130.7	99–170
BPD at baseline (mmHg)	76.5	51–105
Time in study (weeks)	24	1–77
Patients using AH medication at baseline	3
Patients using AH medication in study	8
Proteinuria toxicities (n observations)
Grade 0/no toxicity	1042
Grade 1	202
Grade 2	75
Grade 3	9
Grade 4	0

BP model

In Fig. 1, the final structural PK–PD model is shown. It was found that indirect response models provided better fit than direct effect models. Two separate indirect-effect models for BP_S and BP_D best described the data. A combination of direct and indirect response models did not provide better fit than indirect response alone. Baseline BP_S and BP_D were estimated at 126 and 77.2 mmHg (RSE <5%) respectively, with 10% (RSE 12%) BSV for both BP_S and BP_D. The plasma concentration of E7080 (c _p,E7080) was linked to the input rate of the indirect effect model by a slope factor, which could be estimated separately for BP_S and BP_D. These effects differed significantly for BP_S and BP_D, but lead to approximate similar absolute effect sizes (in mmHg). An E _max model for the concentration–effect relationship was not supported by the data. BSV on drug effect was estimated almost three times larger for BP_S (72%, RSE 40%) than for BP_D (26%, RSE 50%), with a positive correlation of 42% (RSE 62%) between the effects. The AH effect was described using AH daily dose equivalents. The effect of AH therapy was linked to the input rates of the indirect response model for BP by a slope factor, estimated at 0.036 DDDE⁻¹, which could not be estimated separately for BP_S and BP_D. Due to the low number of patients (n = 8) receiving AH medication in the study, BSV could not be estimated for the effect of AH drugs. Moreover, for the same reason, and since the prescribed medication was too diverse, class differences in effects between AH drug classes could not be assessed.

From the hospital information system we could retrieve the actual time of day at which the BP recordings were taken for about 25% of the dataset. However, all of these measurements, and therefore likely also the actual times of BP recordings that were not retrievable, were obtained in a narrow time window (between 9 AM and 12 AM). This precluded an informative assessment of 24-h blood profiles [20].

An exponential residual error model best fitted the model prediction to the data. The overall exponential residual error magnitude for BP_S and BP_D was 12.8% (RSE 3%), with 53% (RSE 3%) correlation between systolic/diastolic residual errors recorded at the same timepoint. Residual error magnitude was the same for BP_S and BP_D. The inclusion of BSV on the residual error magnitude improved fit of the model significantly, and was estimated at 12% (RSE 23%). The model for BP did not show significant bias judged by inspection of plot of CWRES vs time or predicted BP (not shown).

Proteinuria

In the proportional odds model, AUCE_E7080 (“effect compartment”) was a significant better predictor for the probability of developing proteinuria than AUC_E7080 (“cumulative exposure”). Furthermore, BP_D was a significant better predictor than BP_S, and inclusion of both AUCE_E7080 and BP_D parameters simultaneously showed significantly better fit than when included separately. Both predictors could only be related to the probabilities using a slope model, E _max models were not supported by the data. Development of tolerance or lag-times in the onset of proteinuria did not significantly improve the model. A VPC of the proportional odds model (not shown) showed good agreement between observed and model predicted numbers of patients experiencing different proteinuria grades. However, a predictive check of the number of transitions revealed that the number of transitions between grades was significantly overpredicted by the model for most transitions.

Therefore, a Markov transition model was also implemented and evaluated. Since the number of observed grade 3 proteinuria toxicities was low (n = 9), transition rates to- and from grade 3 could not be estimated independently, and k _2→3 was fixed to 0.2 weeks⁻¹, which allowed estimation of all other transition rates. By inspection of predictive checks, it was assured that the correct number of transitions to and from grade 3 were predicted by the model. BSV in the drug effect or in the transition rates could not be estimated. Addition of parameters to describe the drug effect more specifically in the Markov model, e.g. separately on each transition and/or differentiating the effect for transitions up one grade/down one grade did not improve the model.

In the Markov model, as in the proportional odds model, an indirect drug effect (AUCE_E7080) described the data significantly better than when no drug effect or only a direct effect was implemented. The half-life for the recovery rate of the exposure compartment was estimated at 98.1 days, suggesting an almost cumulative effect (AUC) of drug exposure on proteinuria. The exposure was however significantly better than when included as an effect of total AUC. Blood pressure, either BP_S or BP_D included as covariate on transition rates, improved model fit, although the improvement was not significant nor relevant, and destabilized the Markov model, and was therefore not included as predictor in the proteinuria model. Incorporation of AH medication as protective time-changing covariate improved the fit slightly in both the Markov model and the proportional odds model, but the effect was not significant. Co-medication did not affect the probabilities for experiencing proteinuria.

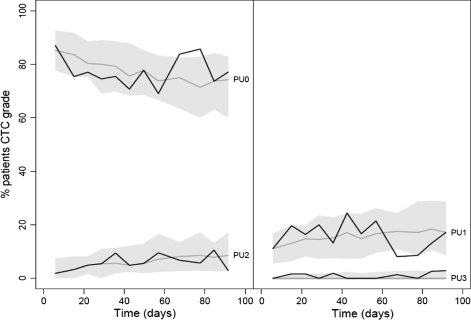
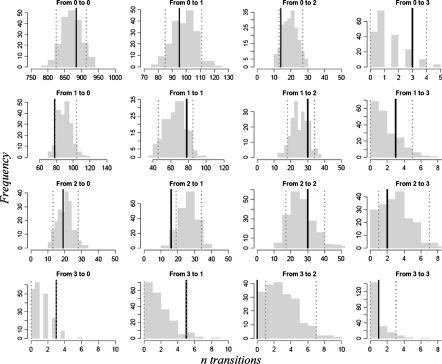
A VPC (Fig. 3) of the Markov model showed that on a population level, the model predicted the % of patients experiencing the PU grades just as good as the proportional odds model. However, a predictive check for all transitions of the Markov model, shown in Fig. 4, showed much better agreement between observed and predicted number of transitions between toxicity grades than the proportional odds model. For almost all transitions, the observed number was within the 90% (PI) of the model. Therefore the Markov model was chosen as final model for describing PU toxicities.

Fig. 3.

VPC of the Markov transition model for proteinuria grades (split in two to avoid overlap of the prediction intervals). The grey areas show the 90% prediction interval for the % of patients experiencing PU, while the dotted line represents the model predicted median. Solid lines are observed % of proteinuria grades

Fig. 4.

Predictive check of Markov model transitions. Histograms represent the model simulated (n = 200) transitions. The dashed lines represents the 5th and 95th percentiles of the simulated number of transitions

Parameter estimates for the final model are presented in Table 2, together with their relative standard errors. The %RSE of both fixed effects parameters were low to intermediate, indicating that the model parameters could be estimated with adequate precision. Model stability of the final model was indicated by successful convergence of the estimation procedure, successful implementation of the covariance step, and low condition numbers of the model (62 for the BP model, 63 for the proteinuria Markov model). For the random effects the amount of shrinkage is also shown in Table 2, which was low for BSV in baseline BP, but intermediate to high for residual error and BSV in E_E7080.

Table 2.

Model estimates

Parameter	Description	Estimate	RSE	Shrinkage (%)
BP model
BPS,base	Baseline systolic BP	126 mmHg	(1%)
BPD,base	Baseline diastolic BP	76.8 mmHg	(1%)
k in	Input rate indirect effect model	0.304 mmHg h−1	(18%)
E E7080,S	Drug effect on systolic input rate	0.543 ng−1 ml	(19%)
E E7080,D	Drug effect on diastolic input rate	0.904 ng−1 ml	(13%)
E AH	Effect of AH medication	36 DDDE−1	(–)
Markov PU model
E indir	Indirect effect size	1.09 × 10−3 ng−1 h−1 ml	(51%)
E dir	Direct effect size	2.2 ng−1 ml	(–)
t 1/2,indir	Half-life of recovery	98 days	(47%)
k 0→1	Transition rate from state 0 to 1	0.141 week−1	(22%)
k 1→0	Transition rate from state 1 to 0	1.19 week−1	(19%)
k 1→2	Transition rate from state 1 to 2	0.361 week−1	(40%)
k 2→1	Transition rate from state 2 to 1	1.90 week−1	(41%)
k 2→3	Transition rate from state 2 to 3	0.20 week−1	(fixed)
k 3→2	Transition rate from state 3 to 2	4.97 week−1	(74%)
BSV
BSV: BPS	BSV in systolic blood pressure	10%	(12%)	4.9
BSV: BPD	BSV in diastolic blood pressure	9%	(13%)	6.2
BSVcorr,BP	Correlation in baseline between BPsys–BPdia	8%	(16%)
BSV: E E7080,S	BSV in drug effect on systolic input rate	66%	(41%)	45
BSV: E E7080,D	BSV in drug effect on systolic input rate	39%	(47%)	51
BSVcorr,E	Correlation in drug effect sizes BPsys–BPdia	32%	(71%)
BSVRE	BSV in RE	12.4%	(22.8%)	32
RE
RE	Exponential residual error	12.8%	(3%)	28
Corr RES–RED	Correlation residual errors for BPsys–BPdia	53.5%	(3%)

Discussion

Hypertension and proteinuria are commonly observed side effects of mAbs and TKIs directed against VEGF or the VEGF receptor. Meta-analysis showed a 22.5–57.7% incidence of hypertension in studies with angiogenesis inhibitors, and a 7.5, 6.1 and 22.7 relative risk of developing hypertension for bevacizumab, sorafenib and sunitinib, respectively [21–23]. The mechanisms through which the hypertensive effect is mediated are still subject of discussion. Physiologically, VEGF stimulates the production and release of vasodilatory stimulants NO by endothelial cells through stimulatory action on endothelial nitric oxide synthase (eNOS). Inhibition of VEGF signaling will hence lead to decreased release of NO and higher vascular resistance. Rarefaction of microvascularity, i.e. a reduced density of microvessels in tissues and organs, is also speculated to be involved in hypertension [24]. For sorafenib, it has been postulated that increased vascular stiffness is the primary cause of elevated blood pressure [25].

Hypertension is known to be strongly correlated to the development of proteinurea [26]. Moreover, since VEGF has an important role in the homeostasis of glomerulal endothelial cells, VEGF inhibitors may have direct effects on the development of proteinurea, apart from their effect through BP elevation. In a meta-review of clinical trials of bevacizumab, the occurrence of hypertension and proteinuria was investigated [21]. Although an association between hypertension and proteinuria was found, the authors were unable to dissect if proteinuria was caused by hypertension, or directly by exposure to bevacizumab resulting from VEGF blockade, or through both mechanisms.

The development and approval of several new angiogenesis inhibitors over the last few years, and the shared toxicity profile, has prompted us to construct a model that describes hypertension and proteinuria toxicities observed for agents in this class of drugs. In treatment with TKIs it is attempted to achieve as high exposure as possible, i.e. dosing at the MTD. Moreover, hypertension is recognized to be a biomarker for treatment efficacy with angiogenic agents. Investigation of strategies to avoid, cope with or diminish toxicities will help to maximize exposure to these drugs, and consequently increase treatment response. Recently, a model was presented describing time profiles of blood pressure and pharmacodynamic biomarkers in response to administration of sunitinib [27]. This model was shown to be predictive of blood pressure profiles in patients treated with sunitinib [28], although it did not incorporate the occurrence of proteinuria, nor interventions with AH medication.

The model presented in the current article was constructed on the basis of clinical data, and was able to capture the rise in blood pressure, and the increased probability of experiencing grades of proteinuria, in response to treatment with E7080, an inhibitor of VEGF. We expect this model to be applicable to other anti-angiogenic agents as well. If so, this will require the collection of PK, BP and proteinurea data from treatment with those compounds. As the link between exposure and PD effects in our model is not mechanistic, these cannot easily be extrapolated from preclinical data. However, as no mechanisch link is present, the model structure presented in this article may be applied to other exposure–effect relations as well, such as changes in biomarkers or disease states due to drug treatment.

PK–PD analysis

An issue that may have inflated the residual error of the model is the fact that the BP recordings are not a truly continuous data source: clinicians and nurses tend to round BP to the nearest 5 mmHg unit. In theory, this should not introduce bias, although it may decrease precision. Furthermore, since BP shows pronounced diurnal patterns, the time of day of BP measurement is important, not only in diagnosing hypertension, but also in fitting models for BP, since this will introduce bias and imprecision if not accounted for. Addition of circadian variation to the current template model may be a valuable addition, if exact times of measurement are available.

The number of patients that were prescribed AH medication at some point during the treatment course was low (n = 8) in this study. This was partially because data were obtained from a dose escalation study: a considerable portion of the patients were treated at E7080 dose levels that did not show hypertension or proteinuria toxicities. Due to this low number of patients and the diversity in their AH medication (four different classes, doses ranging from 0.25 to 4 DDDE), a thorough assessment of the effect of AH medication was not possible from the current data. Therefore, if this model is used in a simulation analysis, e.g. to assess the effect of different hypertension intervention strategies, these results should be interpreted with some caution.

Proteinuria

In our analysis we found a probability at baseline of experiencing ≥1 + proteinurea (CTC grade ≥1) as measured by dipstick that was 15%. It has been shown that incidence of proteinuria is significantly higher in patients with malignancies than in healthy controls [29]. In our analysis of proteinuria data we could distinguish an effect of E7080 plasma concentration on the occurrence of this toxicity, as well as a separate effect mediated by an increased BP_D. The latter effect was however only significant when a proportional odds model was used, and not when the Markov model was used. Analysis of data from future trials with the current model may be able to address in more detail how the effect on proteinuria is mediated.

Treatment with AH drugs, especially ACE-inhibitors and agiotensin II receptor blockers, is known to reduce proteinuria in both hypertensive [30] and normotensive patients [31]. Due to the low overall size of the study and the percentage of patients that were prescribed AH medication, we were unable to show any significant effect of AH medication on the development of proteinuria, let alone assess class differences between AH drugs. Data from subsequent trials will be needed to assess the influence of covariates, such as genetic predispositions and/or baseline characteristics that might predispose patients to developing proteinuria. The number of patients experiencing grade 3 neutropenia was low, thereby limiting the ability to rigorously test the validity of our model for predicting grade 3 PU toxicity. Although we considered lumping the grade 2 and grade 3 toxicities in one category, it was chosen not do so because clinically, the distinction between grade 2 and grade 3 PU is important for interventions. The probabilities associated with developing grade 4 proteinuria could not be estimated, since this grade was not observed in the clinical trial.

Overall, although the dataset was obtained from a single phase I study, the dose range that was studied provided enough data to capture an exposure–response relationship, both for BP and for the probability of experiencing proteinuria. The predictive checks that were generated (Figs. 2, 3, 4) showed that the model was describing the observed clinical data with satisfactory precision, which is especially important if the model is to be used for simulation purposes, e.g. the evaluation of dosing strategies. Such simulations have been planned, and include e.g. the evaluation of a hypertension intervention scheme, and the evaluation of an adaptive treatment design, using BP to guide intra-patient dose escalation.

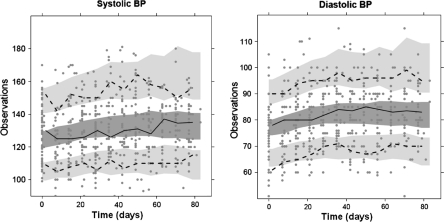
Fig. 2.

Visual predictive checks of systolic (a) and diastolic (b) BP, for patient treated at the MTD of 25 mg E7080 qd. Solid line and dark grey area represents median observed and predicted 95% CIs. Dashed lines and light grey areas represent the 10 and 90% percentiles of the observed values, and the 95% CI of the model predicted percentiles

Conclusion

In this article we presented a model that was able to capture the pharmacodynamic characteristics of a novel oral anti-cancer agent (E7080) targeting the VEGF pathway. This model, will allow the investigation of clinical strategies for optimizing treatment with E7080. The current model was constructed using data from a single anti-angiogenic TKI, but may serve as a template model for hypertension and proteinuria toxicity in treatment with drugs targeting the VEGF pathway.