Mathematical Modeling of Endocytic Actin Patch Kinetics in Fission Yeast: Disassembly Requires Release of Actin Filament Fragments

We report time courses of the accumulation and loss of 16 fluorescent fusion proteins at sites of clathrin-mediated endocytosis in fission yeast. Mathematical modeling shows that dendritic nucleation hypothesis can account for the kinetics of actin assembly in vivo and disassembly requires actin filament severing along with depolymerization.

Abstract

We used the dendritic nucleation hypothesis to formulate a mathematical model of the assembly and disassembly of actin filaments at sites of clathrin-mediated endocytosis in fission yeast. We used the wave of active WASp recruitment at the site of the patch formation to drive assembly reactions after activation of Arp2/3 complex. Capping terminated actin filament elongation. Aging of the filaments by ATP hydrolysis and γ-phosphate dissociation allowed actin filament severing by cofilin. The model could simulate the assembly and disassembly of actin and other actin patch proteins using measured cytoplasmic concentrations of the proteins. However, to account quantitatively for the numbers of proteins measured over time in the accompanying article (Sirotkin et al., 2010, MBoC 21: 2792–2802), two reactions must be faster in cells than in vitro. Conditions inside the cell allow capping protein to bind to the barbed ends of actin filaments and Arp2/3 complex to bind to the sides of filaments faster than the purified proteins in vitro. Simulations also show that depolymerization from pointed ends cannot account for rapid loss of actin filaments from patches in 10 s. An alternative mechanism consistent with the data is that severing produces short fragments that diffuse away from the patch.

INTRODUCTION

Fungal actin patches are sites of clathrin-mediated endocytosis, where a network of actin filaments appears and turns over in ∼20 s during internalization of the endocytic vesicle. Several lines of evidence are consistent with actin assembly and turnover in actin patches by a mechanism similar to the dendritic nucleation model for the leading edge of motile cells (Pollard and Borisy, 2003). 1) Actin patches depend on the proteins included in the dendritic nucleation model (Kaksonen et al., 2006; Galletta and Cooper, 2009). 2) In both budding yeast and fission yeast the order of protein assembly in actin patches is consistent with the hypothesis (Kaksonen et al., 2003, 2005; Sirotkin et al., 2005). 3) Electron microscopy revealed the presence of short branched filaments, as expected for Arp2/3 complex–mediated actin assembly (Young et al., 2004; Rodal et al., 2005). However, none of this evidence constitutes a rigorous test of whether the mechanism assumed by the dendritic nucleation hypothesis can account for rapid assembly and disassembly of actin patches in cells.

As in any complex, biochemical pathway kinetic analysis offers a powerful approach to test mechanistic hypotheses. The data required for kinetic analysis of actin patches are counts of the numbers of protein molecules in patches over time, the concentrations of the participating proteins in the cytoplasmic pool, and estimates of the rate constants for the reactions. The accompanying article by Sirotkin et al. (2010) used a spinning disk confocal microscope calibrated with internal standards (Wu and Pollard, 2005) to measure the time courses of the accumulation and disappearance in actin patches of 16 proteins tagged with fluorescent proteins in fission yeast including WASp (Wsp1p), a subunit of the Arp2/3 complex (ARPC5), a subunit of the capping protein (Acp2p), and actin (Act1p). The highly reproducible time courses for the accumulation and disappearance of each protein place stringent constraints on the underlying biochemical mechanisms, but the complexity of the process makes it impossible to interpret those data intuitively.

Therefore we formulated a mathematical model of the actin filament component of the process and used simulations constrained by the quantitative kinetic data to interpret the mechanism. The simulations showed that three modifications to the mechanism are required for the model to account for the observed time course of actin patch assembly and disassembly. First, binding of the ternary complex of actin monomer-WASp-Arp2/3 complex to the side of a preexisting actin filament is faster in cells than in vitro. Excluded volume effects, reduced dimensionality and participation of additional proteins provide reasonable explanations for this difference. Second, binding of capping protein to actin filament barbed ends is also faster in cells. Excluded volume effects may explain this difference. Third, depolymerization of the filaments from free pointed ends is too slow to account for the rapid turnover of actin patches in 10 s. Therefore, we propose an alternative mechanism based on severing filaments into fragments that diffuse away before depolymerizing. This analysis supports the general features of the dendritic nucleation hypothesis and also gives a rare example of estimates of reaction rates inside cells. The conclusions from this analysis of actin patches also provide clues about actin assembly and turnover in motile cells where quantitative measurements are more difficult owing to asynchronous events superimposed in time and space.

MATERIALS AND METHODS

Assumptions Regarding the Mechanism

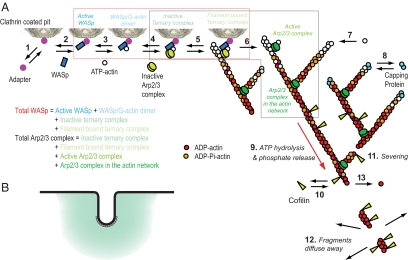
We assumed the pathway of actin assembly and disassembly illustrated in Figure 1. The following paragraphs describe our initial assumptions. See Results for an explanation of two of these assumptions that had to be modified to account for the experimental observations.

Figure 1.

Diagram illustrating the reactions assumed in the mathematical model and simulations of actin filament assembly and disassembly at sites of endocytosis. (A) Numbered reactions in the model: 1, adapter binds clathrin; 2, Wsp1p binds adapter; 3, actin binds Wsp1p; 4, Arp2/3 complex binds Wsp1p (ternary complex); 5, inactive ternary complex binds filament; 6, filament activates ternary complex to initiate a branch; 7, ATP-actin elongates filament barbed ends; 8, capping protein blocks barbed ends; 9, actin hydrolyzes bound ATP and dissociates phosphate; 10, cofilin binds ADP-actin filaments; 11, filaments sever; 12, filament fragments diffuse away; and 13, ADP-actin subunits dissociate from free pointed ends. The red box encloses all WASp species in the model (Active WASp, dark blue; WASp/G-actin monomer, light blue; Inactive ternary complex, turquoise; Filament bound ternary complex, light green) for comparison with the amount of Wsp1p measured experimentally. The black box encloses all Arp2/3 complex species in the model (Inactive ternary complex, turquoise; Filament bound ternary complex, light green; Active Arp2/3 complex, green; Arp2/3 complex in the actin network, dark green) for comparison with ARPC5 measured experimentally. (B) A schematic diagram of actin network assembly at the site of endocytosis. Black line represents cell membrane, gray boxes represent clathrin at the tip of invagination, and teal represents actin network in a 300-nm sphere around endocytic invagination. The intensity of teal shading represents postulated gradient of density of actin network.

Reaction 2: Recruitment and Activation of Nucleation-promoting Factors.

Our starting assumption was that WASp is the primary activator of Arp2/3 complex in patches in budding and fission yeast. This assumption is consistent with timing, biochemical analysis, and effect of mutations (Sirotkin et al., 2005; Sun et al., 2006; Galletta et al., 2008). We recognize that myosin-1 Myo1p and Pan1p can activate Arp2/3 complex in the absence of Wsp1p and are likely to contribute to Arp2/3 complex activation in the presence of Wsp1p (Sun et al., 2006; Galletta et al., 2008). Wsp1p also recruits verprolin (Vrp1p) to patches in excess of their ratio in cytoplasm (Table 1 of Sirotkin et al. (2010)), and Vrp1p may help to regulate Wsp1p and Myo1p. Our model subsumed these contributions of Myo1p, Pan1p and Vrp1p under Wsp1p, because they have lower nucleation-promoting factor activity in biochemical assays.

Table 1.

Reactions and parameters used in the model

Reaction number	Reaction	Reaction rate	Forward rate constant (μM−1 s−1)a	Reverse rate constant (s−1)	References
3	ActiveWASp + G ⇆ WASpGDimer	kWASpGBinding+[ActiveWASp][G]-kWASpGBinding−[WASpGDimer]	42.9	25.7	Beltzner et al. (2008) and this study
4	WASpGDimer + Arp ⇆ ArpTernaryComplex	kArpComplexFormation+[WASpGDimer][Arp]-kArpComplexFormation−[ArpTernaryComplex]	0.8	0.74
5	ArpTernaryComplex + FADP ⇆ FilamentBoundTernaryComplex	kARPGWBindingF+[ArpTernaryComplex][FADP]-kARPGWBindingF− [FilamentBoundTernaryComplex]	0.3 (1.5 × 10−4)	1 × 10−3
5	ArpTernaryComplex + FATP ⇆ FilamentBoundTernaryComplex	kARPGWBindingF+[ArpTernaryComplex][FATP]-kARPGWBindingF−[FilamentBoundTernaryComplex]
6	FilamentBoundTernaryComplex → ActiveArp	kArpActivation+[FilamentBoundTernaryComplex]	0.5 [s−1]	—
7	ActiveArp + G → BEa + ArpInFilament	kPolymerisation+[G][ActiveArp]	11.6	—	Fujiwara et al. (2007)
7	G → FATP	kPolymerisation+[G][BEa]	11.6	—	Fujiwara et al. (2007)
8	BEa + C ⇆ BEc	kCap+[BEa][C]-kCap−[BEc]	7 (0.11)	4 × 10−3	Kuhn and Pollard (2007)
9	FATP → FADP	kHydrolysis[FATP]	0.3 [s−1]	—	This study
10	COF + FADP ⇆ FCOF	kCOFBinding+[COF][FADP]-kCOFBinding−[FCOF]	8.5 × 10−3	5 × 10−3	Blanchoin et al. (1999)
11 and 12	FATP → Ø	kChop[FCOF][FATP]	3 × 10−3b	—	This study
	PE → Ø	kChop[FCOF][PE]
	ArpInFilament → Ø	kChop [FCOF][ArpInFilament]
	BEa → Ø	kChop[FCOF][BEa]
	BEc → Ø	kChop[FCOF][BEc]
	FCOF → Ø	kChop[FCOF][FCOF]
	FADP → Ø	kChop[FCOF][FADP]
13	FATP → Ø	kDepolymerisation−[PE][FATP]/Ftot	—	0.25	Fujiwara et al. (2007)
	FADP → Ø	kDepolymerisation−[PE][FADP]/Ftot
	FCOF → Ø	kDepolymerisation−[PE][FCOF]/Ftot
	PE + BEc → Ø	kDepolymerisation−[PE][BEc]/Ftot

^a Boldface values were obtained in this study. Values in parentheses are from the literature. Brackets note units different from μM⁻¹ s⁻¹.

^b For a concentration of active cofilin of 1 μM, k_Chop = 4 × 10⁻² μM⁻¹ s⁻¹ (this study).

Because the Wsp1p binding sites and the mechanisms triggering recruitment and activation of Wsp1p are unknown, we simply assumed that recruitment and disappearance of active WASp (reaction 2) follows a Gaussian (see Figure 2D) that drives the other reactions. The simulations give sums of all the WASp molecules in the pathway from reaction 2 to reaction 6 (see red curves, Figures 2 and 3) for comparison with the experimental counts of Wsp1p.

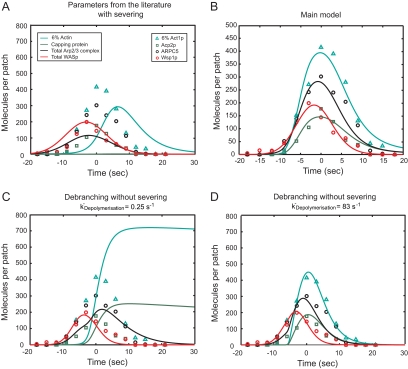
Figure 2.

Comparison of experimental and simulated time courses of actin patch assembly and disassembly for the following species: simulated WASp (red curve); measured Wsp1p (red circles); simulated Arp2/3 complex (black curve); measured ARPC5 (black circles); simulated 6% of polymerized actin subunits (teal curve); measured 6% of Act1p (teal triangles); simulated capping protein (green curve); and measured Acp2p (green squares). (A) Simulation of the main model with parameter values measured in biochemical experiments and severing k_Chop at 0.25 μM⁻¹ s⁻¹. (B) Main model with optimized parameters from Tables 1 and 2. (C) Simulation with optimal parameters from the main model and dissociation of subunits from pointed ends at 0.25 s⁻¹ but without severing and with Arp2/3 complex debranching k_Debranch at 0.2 s⁻¹. (D) Same as C but with k_Debranch optimized to 0.3 s⁻¹ and actin subunit dissociation rate from pointed ends at 83 s⁻¹ to give the best fit with the experimental data without severing.

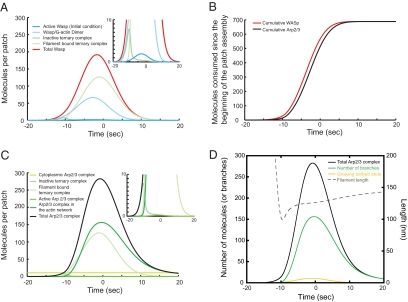
Figure 3.

Time courses of protein species calculated in simulations of the main model. (A) WASp species. Color code for protein species: red, Total WASp; dark blue, Active WASp; light blue, WASp/G-actin dimer; turquoise, Inactive ternary complex; and light green, Filament bound ternary complex. (B) Accumulated numbers of WASp and Arp2/3 complex consumed during patch assembly, calculated as the integral of the rate of reaction 3 and 4, respectively. Color code for protein species: red, total WASp; black, total Arp2/3 complex. (C) Arp2/3 complex species. Color code for protein species: black, Total Arp2/3 complex; turquoise, Inactive ternary complex; light green, Filament bound ternary complex; green, Active Arp2/3 complex; and dark green, Arp2/3 complex in the actin network. (D) Number of actin filament ends and filament length. Color code for protein species: black, Arp2/3 complex; green, number of branches, also equal to Arp2/3 complex in the actin network: yellow, number of growing barbed ends; and gray dashed line, average length of branches calculated as the ratio of F-actin over the number of branches.

Reactions 3–6: Recruitment and Activation of Arp2/3 Complex.

We assumed that WASp sequentially binds an actin monomer (reaction 3) and an Arp2/3 complex (reaction 4) from the bulk cytoplasm to form an inactive ternary complex that is activated to form a branch when it binds (reaction 5) to the side of a filament (Marchand et al., 2001; Beltzner and Pollard, 2008). We assumed that Arp2/3 complex dissociates quickly from WASp and the membrane after branch formation (Marchand et al., 2001) to allow polymerization to expand the network away from the membrane. We assumed that our microscopic count of Arp2/3 complex molecules (see black symbols in Figure 2) includes all species of Arp2/3 complex in this pathway, from inactive complex recruited by WASp to Arp2/3 complex in actin branches (between reactions 4 and 7 in Figure 1 and black curves in Figures 2 and 3).

Reaction 7: Actin Filament Elongation.

We assumed that free barbed ends of actin filaments elongate by adding subunits from the cytoplasmic pool of 22 μM ATP-actin monomers (Table 1 of Sirotkin et al. (2010)).

Reaction 8: Actin Filament Capping.

We assumed that binding of cytoplasmic capping protein to barbed ends stops elongation.

Reaction 9: ATP Hydrolysis by Polymerized Actin.

We assumed that polymerized actin hydrolyzes bound ATP randomly with the first order rate constant of 0.33 s⁻¹ reported for muscle actin (Blanchoin and Pollard, 2002), because the active sites of actins are nearly identical and this parameter has never been measured for a fungal actin. We also assumed that P_i-release from ADP-P_i-actin is fast, as estimated for budding yeast actin (Bryan and Rubenstein, 2005), and keeps pace with hydrolysis.

Reactions 10–12: Patch Disassembly.

Assuming branching nucleation by Arp2/3 complex and termination by capping proteins, most of the filaments will be capped on both ends. In vitro these caps dissociate slowly (Mullins et al., 1998; Kuhn and Pollard, 2007), limiting subunit dissociation. Therefore, patch disassembly must depend on the activity of ADF/cofilin (called cofilin hereafter), as expected from the observation that actin patches turn over slower in cells with mutant cofilins (Lappalainen and Drubin, 1997; Nakano and Mabuchi, 2006; Okreglak and Drubin, 2007).

We assumed that cofilin binds ADP-actin subunits in filaments according to mass-action kinetics (reaction 10). Because fission yeast cofilin tagged with a fluorescent protein is not fully functional (Chen, Q., and Pollard, T. D., unpublished data), we did not measure the number of cofilins in actin patches. However our simulations indicate that cofilin bound to <10% of polymerized actin subunits in all cases. Therefore, we ignored cooperative binding (Blanchoin and Pollard, 1999).

When we discovered that dissociation from pointed ends does not account for the disappearance of actin from patches, we added the assumption that severing releases a fragment of the actin network into bulk cytoplasm. The rates of severing and disassembly are proportional to the concentration of cofilin bound to the filaments ([F_COF]) and the concentration of each species. The rate constant for severing (k_chop) is the same for the disassembly of all actin nucleotide species, so that the rate of loss of ADP-actin subunits (F_ADP) due to severing equals k_chop[F_COF][F_ADP]. We used the same formula for the loss of ATP-actin subunits, cofilin-bound subunits, capped and active barbed ends, and Arp2/3 complex bound to the side of filaments, by substituting the concentration of these species for [F_ADP].

Initial Assumptions about Numerical Parameters

We assumed the rate constants measured in dilute solution with purified proteins and constant bulk concentrations of proteins at the values measured experimentally in the cytoplasm (Table 1; Tables S2 and S3 in Sirotkin et al. (2010)). We assumed that proteins in the bulk cytoplasmic phase penetrate the patch, because the volumes occupied by the membrane invagination and the actin filament network are negligible. Before the onset of patch assembly the initial numbers of assembled proteins were zero. When considering concentrations, we assumed that all proteins in patches were distributed homogenously in a sphere 300 nm in diameter.

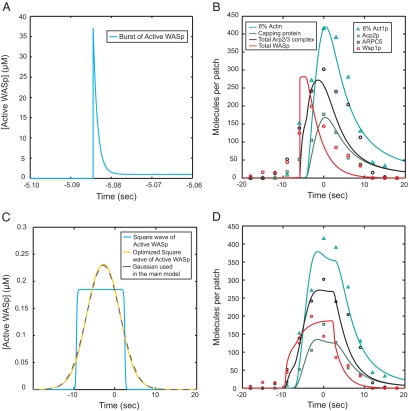
We assumed that the accumulation and disappearance of active WASp (between reaction 2 and 3) follows a Gaussian curve over time and that this pulse of WASp (gray dashed line in Figure 4C and dark blue curve in Figure 3A) drives the other reactions. The parameters of this Gaussian were estimated by comparing the total amount of WASp (intermediates between reactions 2 and 6; red curve in Figures 2B and 3A) to the counts of Wsp1p (red circles in Figure 2B) measured experimentally in Sirotkin et al. (2010).

Figure 4.

Effects of alternative assumptions for the accumulation and disappearance of active WASp on the simulated time courses. Color code for protein species: teal, actin; green, capping protein; and black, Arp2/3 complex. (A) All WASp molecules required for patch assembly are assumed to be activated suddenly in a burst and then consumed by the process. (B) Output of the simulation of the model with the driving function in (A) and the parameters from the main model in Table 1 except, k_{ArpActivation}⁺ + 0.41 s⁻¹, k_Cap⁺ + 6.7 μM⁻¹ s⁻¹. (C) Model driven by rectangular pulse of activated Wsp1p. The blue curve is a square wave of activated WASp described by the equation, ActiveWASp + WASp_Max 1/(1 + exp(−2k(t − time_ON))) (1 − 1/(1 + exp(−2k(t − time_OFF))), with k + 5 s⁻¹, WASp_max + 0.18 μM, time_ON + − 9.4 s, and time_OFF + 2.5 s. The yellow curve is the result of optimizing the parameter k along with the other parameters for this function to give simulations with the best fit to the experimental time courses for Arp2/3 complex, actin and capping protein. The optimal parameters are k + 0.27 s⁻¹, WASp_max + 0.29 μM, time_ON + −6.9 s, and time_OFF + 1.3 s and give a time course for active WASp indistinguishable from the Gaussian used in the main model (gray dashed curve). (D) Output of the simulation of the model with the artificial square wave from C as the driving function and the parameters from the main model in Table 1.

Alternative Models without Severing

For comparison, we assumed no severing, but substituted a debranching reaction (ArpInFilament → ArpPE), followed by dissociation of Arp2/3 complex release from pointed ends (ArpPE → PE) at the same rates that actin dissociates from pointed ends, i.e., 0.25 s⁻¹ in Figure 2B or 83 s⁻¹ in Figure 2C. Optimization produced a rate constant for debranching (0.2–0.3 s⁻¹) close to values measured in vitro in the presence of cofilin (Chan et al., 2009).

Mathematical Model and Computer Simulations

We formulated a temporal model with the following ordinary differential equations. Table 2 defines the protein names.

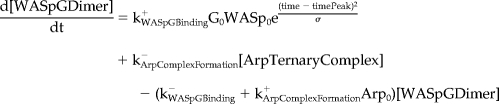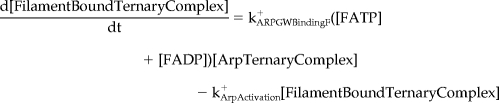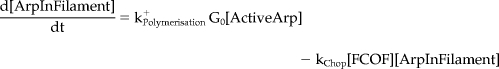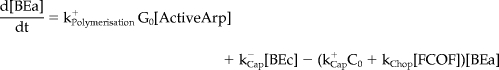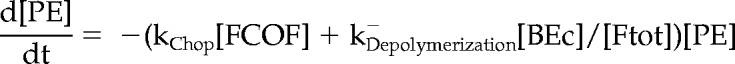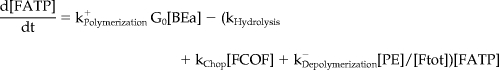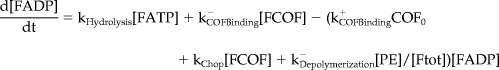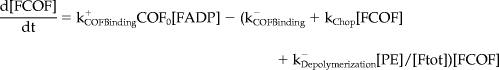We performed numerical simulations and fit parameters and carried out a sensitivity analysis with Matlab 7.6 (MathWorks, Natick, MA) and the SimBiology plugin 2.3. We compared simulations of these reactions with cellular measurements of the time courses of the accumulation and loss of the following species: 1) actin (the sum of the simulated concentrations of all polymerized actin species, i.e., FATP + FADP + FCOF + Bea + BEc + PE) compared with the experimental measurement for Act1p; 2) Arp2/3 complex (the sum of all species of Arp2/3 complex along the modeled pathway, i.e., ArpTernaryComplex + FilamentBoundTernaryComplex + ActiveArp + ArpInFilament; the species between reaction 4 and 7 in the black box in Figure 1) compared with the experimental measurements of ARPC5; 3) capping protein (the simulated concentration of capped barbed ends, BEc) compared with the experimental measurement of Acp2p; and 4) WASp (sum of the all the species of WASp along the modeled pathway, i.e., ActiveWASp + WASpGDimer + ArpTernaryComplex + FilamentBoundTernaryComplex, the species between reactions 2 and 6 in the red box in Figure 1) compared with the experimental measurement of Wsp1p.

Table 2.

Initial and bulk concentrations used in the model

Name	Description	Localization	Initial Concentration (μM)
G	Bulk actin monomer-ATP	Bulk	21.6 (Constant)
COF	Bulk cofilin	Bulk	40 (Constant)
C	Bulk capping protein	Bulk	0.8 (Constant)
Arp	Bulk Arp2/3 complex	Bulk	1.3 (Constant)
Active WASp	Active WASp bound to the membrane/vesicle	Membrane/vesicle	WASp0*e−(t-TimePeak)^2/σ with WASp0 = 0.23 μM, TimePeak = −2.8 s, σ = 33.5 s2
WASpGDimer	Dimer of WASp and actin monomer bound to the membrane/vesicle	Membrane/vesicle	0
ArpTernaryComplex	Ternary complex of WASp, actin monomer and Arp2/3 complex	Membrane/vesicle	0
FilamentBoundTernary Complex	Ternary complex bound to the side of a filament	Membrane/vesicle	0
ActiveArp	Arp2/3 complex ready to initiate a branch	Membrane/vesicle	0
ArpInFilament	Arp2/3 complex at the base of a branch	Membrane/vesicle	0
FATP	Polymerized actin with ATP	Bulk	0
FADP	Polymerized actin with ADP	Bulk	0.01
FCOF	Polymerized actin with bound cofilin	Bulk	0
PE	Pointed end	Bulk	0.01
BEa	Active barbed end	Bulk	0
BEc	Capped barbed end	Bulk	0.01
Ftot	Total polymerized actin	Bulk	FATP + FADP + FCOF + PE + BEa + BEc
Arptot	Total Arp2/3 complex	Membrane/vesicle and bulk	ArpTernaryComplex + FilamentBoundTernaryComplex + ActiveArp + ArpInFilament
WASptot	Total WASp	Membrane/vesicle	ActiveWASp + WASpGDimer + ArpTernaryComplex + FilamentBoundTernaryComplex

We optimized the parameters with the function “sbioparamestim” of SimBiology using the least square method “lsqcurvefit” from the Matlab Optimization Toolbox 4.0. We normalized the target data (the experimental data for Act1p, ARPC5, Acp2p, and Wsp1p) and their equivalents in the model to peak at the same value to allow each of these species to have an equal influence during the optimization process.

RESULTS

Formulation of a Model for Assembly and Disassembly of the Actin Filament Network

Sirotkin et al. (2010) collected enough quantitative information about the time courses of protein accumulation and loss in actin patches to formulate and test a mathematical model of the assembly and disassembly of actin and associated proteins (Figure 1). We based our model on the dendritic nucleation hypothesis, the leading hypothesis for actin endocytic patch formation (Kaksonen et al., 2006; Galletta and Cooper, 2009). Because the detailed arrangement of molecules in actin patches is not known and diffusion is fast enough to consider the cytoplasm in the tiny patch to be homogeneous (see below), we made a temporal model with ordinary differential equations and did not attempt a spatial or mechanical model with partial differential equations.

In our simplified macroscopic model the reactions take place in a dimensionless compartment representing the endocytic patch. Only for the purpose of converting the number of molecules to local concentrations, we assumed that patches are spheres with diameters of 300 nm (Figure 1B), the size of “filasomes” observed by electron microscopy (Kanbe et al., 1989; Takagi et al., 2003), although we understand that some proteins are not distributed homogenously in this space (Idrissi et al., 2008). We assume that this patch is suspended in another dimensionless compartment representing the cytoplasm, which supplies reactants whose concentrations remain constant over time.

Comparison of Simulations with Observations of Actin Filament Assembly in Live Cells

Using the starting set of assumptions, cytoplasmic protein concentrations measured in live cells (Table 1 and Tables S2 and S3 in Sirotkin et al. (2010)) and rate constants measured in diluted solution with purified proteins (Blanchoin and Pollard, 1999; Fujiwara et al., 2007; Kuhn and Pollard, 2007; Beltzner and Pollard, 2008), numerical simulations of the model assembled, and disassembled actin filaments. However, the amplitudes and timings of the protein peaks were not the same as observed in cells (Figure 2A). The simulated time courses were even worse if severing was not included and actin filament disassembly depended entirely on dissociation of subunits from pointed ends at 0.25 s⁻¹ (Figure 2C).

To obtain good agreement between the simulated and measured time courses of protein accumulation and loss, we varied model parameters and tested alternative hypotheses about mechanism of patch disassembly. After adjusting two parameters and one mechanistic assumption, the simulated time courses for assembly and disassembly of multiple patch proteins were close to observations in live cells; Figure 2B shows the main model with optimized parameters from Tables 1 and 2. Two association reactions must be faster to account for events in the cell. These enhanced association reactions are binding of the ternary complex of actin monomer-WASp-Arp2/3 complex to actin filaments (reaction 5) and barbed end capping (reaction 8). The most dramatic departure of the model from current beliefs is that dispersal of short filament fragments augments the disassembly of the actin filament network (reaction 12). The first-order rate constant for ATP hydrolysis measured in vitro did not need to be adjusted. The following paragraphs consider what the simulations revealed about each of the reactions.

Reaction 2: Recruitment and Activation of Nucleation-promoting Factors.

The available evidence indicates that recruitment and/or activation of WASp is the first step in the actin assembly process, although little is known about the mechanisms. Driving the following reactions with a Gaussian time course of active WASp accumulation and disappearance gave simulated time courses for the other components similar to the experimental observations. These simulations showed that only a small fraction of the total WASp is “active” free WASp, because most of the protein is bound to actin monomers, Arp2/3 complex, or filaments (see below; Figure 3A).

For comparison with this assumed Gaussian wave, we tested two extreme variations of the time course for WASp accumulation and loss: sudden activation of all WASp in the patch at a specific time point (Figure 4A) and a square wave (Figure 4C). Subsequently active WASp is consumed, inactivated, and/or released. Simulations of time courses for the other proteins using these extreme initial conditions did not fit the observations as well as those obtained with a Gaussian initial condition, but shared the fundamental features of the process (Figure 4, B and D). This leeway was important for our simulations, because microscopic measurements (Sirotkin et al., 2010) document only the total amount of Wsp1p associated within the patches, not the numbers of active WASp.

When we started with a square wave of Wsp1p and optimized the parameter-driving process, the shape of the Wsp1p wave converged on an almost perfect Gaussian (Figure 4C). Thus our choice of a Gaussian curve to drive the reactions was optimal but not crucial.

Reactions 3–6: Recruitment and Activation of Arp2/3 Complex.

We assumed that WASp sequentially binds an actin monomer (reaction 3) and an Arp2/3 complex (reaction 4) from the bulk cytoplasm to form an inactive ternary complex that is activated (reaction 6) to form a branch after it binds (reaction 5) to the side of a filament (Marchand et al., 2001; Beltzner and Pollard, 2008). The source of filaments to initiate the first branches at the onset of patch assembly is not known, but the simulations indicated that only a few short filaments are required to start the autocatalytic branching process that rapidly builds the filament network, as shown by direct observations in vitro (Achard et al., 2010).

For the simulations to assemble actin filaments as fast as observed in patches, the ternary complex of actin monomer-WASp-Arp2/3 complex must bind to actin filaments ∼400 times faster than calculated from the local protein concentrations and the very slow association rate constant of the purified proteins measured in bulk in vitro (Beltzner and Pollard, 2008). Although this difference from initial expectations may seem alarming, this difference is quite informative and entirely reasonable in light of the factors considered in the Discussion.

Reaction 7: Actin Filament Elongation.

The elongation rate constant measured in vitro and the cytoplasmic pool of 22 μM ATP-actin monomers (Table 1 in Sirotkin et al., 2010) accounted for the time course of actin assembly.

A simple calculation, the difference between the experimental measurements of the numbers of Arp2/3 complex (ARPC5) and capping protein (Acp2p) molecules in a patch (Figure 6D in Sirotkin et al., 2010), established that patches could contain up to 140 free barbed ends, but the simulations showed that actual number is much less, because at every point in time, a large fraction of the Arp2/3 complex has not initiated a branch (Figure 3C). In fact, a rough estimate showed that only eight barbed ends are required to account for the maximum polymerization rate of about 2000 subunits per second (i.e., eight ends × 22 μM actin monomers × 12 μM⁻¹ s⁻¹). The number of filaments growing at each point (Figure 3D) in time is small, because the rate of nucleation is finite and capping barbed ends rapidly terminates elongation. In wild-type cells the unpolymerized actin monomer concentration is expected to be ∼40 μM, so the filaments should grow twice as fast and the total polymerized actin per patch is expected to be about twofold higher than in mGFP-act1/act1⁺ diploids (Figure S1). This difference has a modest effect on the other reactions in the model.

Reaction 8: Actin Filament Capping.

We assumed that binding of cytoplasmic capping protein to barbed ends stops elongation. If all of the capping protein assembled in patches is bound to barbed ends, simulations showed that the binding reaction rate in patches is similar to the rate measured for mouse capping protein (Schafer et al., 1996) and about 10-fold faster than expected from the cytoplasmic concentration of capping protein and the rate constant measured for Schizosacchromyces pombe capping protein binding chicken actin filaments (Kuhn and Pollard, 2007).

Capping at the rate observed in cells terminated elongation in ∼0.2 s when the average filament was only a couple hundred of nanometers long. The ratios of polymerized actin to the number of filament ends in our simulations gave a similar estimate of 100–150 nm (Figure 3D), a length that varied little during patch assembly and disassembly. Filament lengths estimated by these simulations are similar to average lengths observed by electron microscopy of budding yeast patches: 50 nm (corresponding to ∼19 subunits) in isolated actin patches (Young et al., 2004) and 100 nm (38 subunits) in patches on plasma membranes (Rodal et al., 2005).

Reaction 9: ATP Hydrolysis by Polymerized Actin.

Fast disassembly of actin patches was consistent with the hydrolysis of ATP bound to polymerized actin at 0.3 s⁻¹, but P_i-release had to be much faster than measured in vitro for muscle actin (0.003 s⁻¹; Blanchoin and Pollard, 1999). Thus we assumed that P_i-release from ADP-P_i-actin is fast, as estimated for budding yeast actin (Bryan and Rubenstein, 2005), and keeps pace with hydrolysis.

Reactions 10–12: Patch Disassembly.

The rapid disappearance of actin and all associated proteins in less than 10 s provided the greatest challenge to explain mechanistically. Assuming branching nucleation by Arp2/3 complex and termination by capping protein, most of the filaments will be capped on both ends. In vitro these caps dissociate slowly (Mullins et al., 1998; Kuhn and Pollard, 2007), limiting subunit dissociation.

Therefore, we postulated that patch disassembly depends on actin filament severing. Cofilin is expected to be a major contributor to severing, because cofilin mutations slow actin patch turnover (Lappalainen and Drubin, 1997; Nakano and Mabuchi, 2006; Okreglak and Drubin, 2007). However, simulations showed that filament severing by cofilin and subsequent actin subunit dissociation from the ends were not sufficient to account for the rapid disappearance of actin from patches, owing to the intrinsically slow rates of ADP-actin dissociation from filament ends. Even if cofilin mediates rapid debranching and Arp2/3 complex dissociates rapidly, to depolymerize the actin in 10 s ADP-actin would have to dissociate from pointed ends at 83 s⁻¹(Figure 2D) rather than the rate of 0.25 s⁻¹ observed in vitro (Fujiwara et al., 2007).

A simple solution is to assume that oligomers of actin severed from the ends of filaments diffuse out of patches into the cytoplasm (reaction 12), whereas the proximal stump remains anchored in the patch, as observed in vitro (Michelot et al., 2007; Roland et al., 2008). We tested several reaction rates to account for the time course of actin subunit loss from patches, and because they all gave the same qualitative results, we chose a simple kinetic mechanism for the loss of subunits. We assumed that the probability of severing is proportional to the concentration of polymerized actin subunits with bound cofilin. We assumed that fragments severed from a filament consist of the same uniform mixture of subunits (actin-ATP, actin-ADP/actin-ADP-P_i, and actin-ADP-cofilin) as the whole population of filaments.

In simulations using dissociation of severed oligomers and an estimate of ∼40 μM cytoplasmic cofilin measured on immunoblots (V. Sirotkin, unpublished observation), actin patches disassembled as quickly as in cells, if the rate constant for subunit loss by severing k_Chop was 0.003 μM⁻¹ s⁻¹ (Figure 2B). Thus the modeling and simulations show that depolymerization alone cannot account for the turnover of actin and associated proteins, but severing and fragment dissociation is a reasonable alternative hypothesis consistent with the experimental measurements.

Diffusion of Molecules Does Not Limit Patch Assembly

Our model does not take into account the geometry of the actin network around the patch, but the actin filament network might influence diffusion of the reactants and limit the rates of the reactions. However, the following calculations show that diffusion of small proteins does not limit actin patch assembly. We estimate from our simulations that proteins from the cytoplasm are consumed at the maximum following rates: actin monomers 4462 s⁻¹, Arp2/3 complex 70 s⁻¹, capping protein 60 s⁻¹, and cofilin 510 s⁻¹. On the other hand, if we approximate the geometry of the membrane where polymerization occurs as a sphere of radius r + 25 nm, a minimum value for the flux of proteins reaching its surface can be estimated from the diffusion equation as 4πDArC_max, where D is the diffusion coefficient, A is Avogadro's number, and C_max is the bulk concentration of each protein. If we use a low estimate for D + 2 μm² s⁻¹ in a crowded environment, the following numbers of proteins collide with the surface of the sphere each second: ∼8000 actin monomers, 500 Arp2/3 complexes, 300 capping proteins, and 15,000 cofilins. In the worst case, this is 2–30 times more than the numbers of proteins consumed in the reactions. Thus our assumption regarding diffusion is valid even if crowding reduces diffusion up to one order of magnitude. However, this is unlikely, because we estimate that the actin network occupies <3% of the volume of the patch. This idea agrees well with estimates of diffusion and actin assembly in similar actin networks (Plastino et al., 2004; Rafelski et al., 2009).

Robustness of the Model

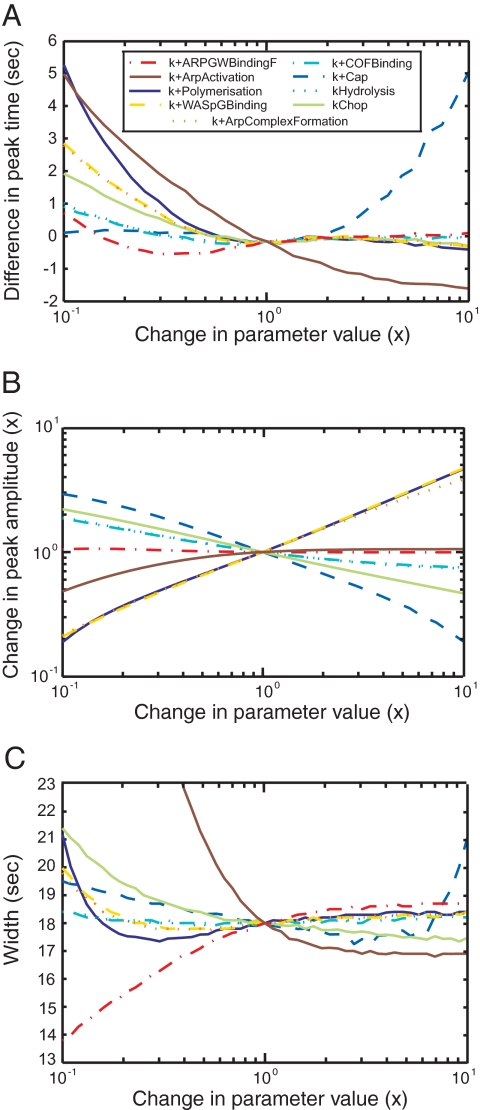
To test the robustness of the mechanism based on the dendritic nucleation hypothesis, we varied each parameter value, one at a time from 0.1 to 10 times the best value and simulated the time courses of actin, WASp, Arp2/3 complex, and capping protein. For each protein, we calculated for each peak three characteristic values: amplitude (Figure 5B and Figure S2, E–H), time (Figure 5A and Figure S2, A–D), and width, defined as the difference in time between the points when the protein number was 25% of the peak value during the assembly and the disassembly phases (Figure 5C and Figure S2, I–L).

Figure 5.

Sensitivity analysis. The model was simulated with each parameter varied ± 1 order of magnitude to determine the sensitivity of the time course of actin accumulation and dispersal on parameter values. (A) Times of protein peaks. (B) Amplitudes of protein peaks. (C) Widths of protein peaks, defined as the difference between the times when the signal reaches 25% of its peak value during the assembly and during the disassembly. Color code for varied parameters: yellow dashed line, k_WASpGBinding⁺; orange dotted line, k_{ArpComplexFormation}⁺; red dotted and dashed line, k_{ARPGWBindingF}⁺; brown plain line, k_{ArpActivation}⁺; dark blue plain line, k_{Polymerization}⁺; blue dashed line, k_Cap⁺; light blue dotted line, k_Hydrolysis; light blue dotted and dashed line, k_COFBinding⁺; plain light green line, k_Chop. Parameters for the reverse reactions are not shown, because varying these parameters has little effect on the time courses of proteins in patches.

Simulations showed that the mechanism in Figure 1 is robust, because it assembles and disassembles actin filaments over at least this hundred-fold range of individual parameter values. Nevertheless, these parameter scans showed that some parameter values influence the amplitudes and times of the protein peaks, especially for actin and capping proteins (Figure 5 and Figure S2).

The peak amplitude for polymerized actin increases with the rates of ternary complex formation (k_WASPGBinding⁺, k_{ArpComplexFormation}⁺) and with the rate of elongation (k_{Polymerization}⁺), whereas the rate of capping (k_Cap⁺) has the opposite effect. The aging and severing parameters (k_Hydrolysis, k_COFBinding⁺, k_Chop) have little influence on the size of the actin peak. The position in time of the actin filament peak is most sensitive to the last step of Arp2/3 complex activation (k_{ArpActivation}⁺) and the barbed end parameters (k_{Polymerization}⁺ and k_Cap⁺). The duration of the actin filament peak depends mainly on the rate of the ternary complex binding to the side of a filament (k_{ARPGWBindingF}⁺) and its subsequent activation step (k_{ArpActivation}⁺) and less on the severing parameter (k_Chop) and the barbed end parameters.

Two-dimensional parameter scans (with two parameters varied at the same time) showed that simulations produce reasonable fits to the data if both the polymerization and capping rates vary in parallel up to 10-fold (Figure S3A) and that variation of the rates of cofilin binding to filaments, filament severing, or ATP hydrolysis ± 10-fold can be compensated for by varying either of the two other rates (Figure S3, B–D). Variation in the rates of WASp binding actin monomers and formation of the ternary complex can compensate for each other over a limited range (Figure S3E).

DISCUSSION

Insights about the Mechanism of Actin Patch Assembly and Disassembly

We used the stoichiometry of components over time to analyze the mechanism of patch assembly and to constrain simulations of a mathematical model of actin filament assembly and disassembly. Two bimolecular reactions are faster in the cell than in vitro: capping barbed ends of growing filaments and nucleation of branches.

Capping protein binds filaments in actin patches about ten times faster than fission yeast capping protein binds muscle actin filaments in vitro. The yeast protein may bind its own actin faster, but excluded volume effects may contribute to the higher rate in cells, as observed for actin filaments where elongation is 3.3 times faster in 20% ovalbumin than in buffer alone (Drenckhahn and Pollard, 1986).

To obtain simulations of our model that agree with the kinetics of Arp2/3 complex, actin and capping protein in actin patches, the ternary complex of Arp2/3 complex-Wsp1p-actin must bind the sides of actin filaments much faster in actin patches than the pure proteins in vitro. In addition to the effect of excluded volume, geometric factors and missing proteins may increase the rate of the reaction.

Geometry.

Concentrating both the ternary complex and growing actin filaments on the cytoplasmic surface of the membrane invagination reduces the dimensionality, raises the effective concentrations, and increases reactions rates. The local concentrations of the ternary complex and of actin filaments may be higher than the average concentrations calculated from the number of molecules in a 300-nm sphere as in our calculations (Figure 1B). If Wsp1p is anchored to a membrane and can react with Arp2/3 complex up to 25 nm from the membrane, the local concentration of ternary complex is ∼10 times higher on a cylindrical membrane tubule or ∼20 times higher on a sphere than the value used in our model. Furthermore, the process of actin nucleation, growth, and turnover may create a gradient of polymerized actin where the filament concentration is highest at the site of polymerization near the membrane and is diluted as the network of capped filaments expands radially. We can show that the concentration of capped actin filaments varies with 1/R² around a sphere and 1/R around a cylinder of radii R (Figure S4 and Supplemental Text). Thus the actin filament concentration near the plasma membrane is seven times higher on the surface of an internal tubule and 20 times higher on the surface of an internal sphere than the average concentration of ∼0.9 mM in the whole patch. Disassembly of older filaments away from the membrane should enhance this concentration gradient. Polymerization may increase reaction rates by producing force to press filaments against the membrane (Noireaux et al., 2000).

Taking the local concentrations into account, the rate of ternary complex binding to actin filaments (rate + k_{ARPGWBindingF}⁺[ArpTernaryComplex][F-actin]) will be at least 70–600 times higher than in our bulk model even without considering the effects of excluded volume and reduced dimensionality on the rate constants. The observations and modeling of Achard et al. (2010) also argue for rapid branching in a reconstituted system.

Although not considered here, the F-BAR proteins Bzz1p and Cdc15p are required for normal actin assembly in patches and Bzz1p stimulates the nucleation promoting activity of Wsp1p (R. Arasada and T. D. Pollard, unpublished data). We expect that both of these proteins contribute to the much higher rate of branching in cells than in simplified systems with only Arp2/3 complex and Wsp1p.

Our quantitative data and computer simulations also revealed that subunit dissociation from pointed ends at the rate 0.25 s⁻¹ observed in biochemical experiments (Fujiwara et al., 2007) cannot account for the turnover of actin filaments in actin patches. The rate constant for dissociation of ADP-actin from pointed ends would have to be ∼300–1000 times faster than measured in vitro. Cofilins were postulated to promote dissociation from both ends of filaments 22-fold (Carlier et al., 1997); however, even this effect would not be sufficient to account for rapid disassembly of actin patches. Furthermore, cofilin actually inhibits dissociation at barbed ends and has no effect at pointed ends (Andrianantoandro and Pollard, 2006).

This situation puts the focus on the alternative hypothesis used in our simulations that severing releases short pieces of the filament network. If these severing events were coupled to capping by capping proteins or Aip1p (Okada et al., 2002), these fragments would not elongate and could depolymerize slowly from their pointed ends outside patches. We did not include debranching explicitly in the main model, but note that because debranching is equivalent to severing in taking the network apart and the rates of both debranching and severing depend on cofilin concentration (Blanchoin et al., 2000; Chan et al., 2009), their contributions are difficult to distinguish.

Uniqueness of the Model

Analysis of our model began with parameters measured biochemically with purified proteins in dilute solution. Simulations of our model with these parameters from the biochemical literature gave poor fits to the protein kinetics in cells (Figure 2, A and C), so we varied the parameters until we obtained good fits simultaneously for the numbers of Arp2/3 complex and actin and capping proteins. We are aware that this set of parameters is not unique in giving a good fit of the experimental data, as illustrated by two-dimensional parameter scans (Figure S3) with many pairs of parameters giving good fits. However, we think that the optimized set of parameters are the most reasonable, because they all can be explained with simple arguments and are close to the experimental parameters.

Mathematical Analysis Was Required to Interpret the Data

Initially we thought that we could use the quantitative data (Sirotkin et al., 2010) to understand intuitively the pathway and the molecular mechanisms, but while formulating and testing the mathematical model described in this article, we learned that this intuitive approach is difficult or impossible. For a system of this complexity one must take into account all of the reactions, which can only be done with a formal mathematical model.

Here we note two of many examples where intuition failed. Guessing stoichiometries directly from the measurements is risky. For example, simulations show that Arp2/3 complex and WASp are consumed in parallel over time (Figure 3B), but at each moment in time only half of the WASp is bound to an Arp2/3 complex (Figure 3A) and about half of Arp2/3 complex is not bound to WASp (Figure 3C). The simulations show that <8 barbed ends are active at the same time (Figure 3D), whereas a simple calculation based the numbers of Arp2/3 complexes and capping proteins in patches indicated that a patch could contain up to 140 free barbed ends (Figure 6D in Sirotkin et al. (2010)).

Thus a simple biochemical model can provide insights that substantially enhance the value of quantitative experimental measurements. Liu et al. (2009) proposed a complementary model of actin patches that considers the interplay between the mechanics and the chemistry during endocytic vesicle formation but does not focus on the precise biochemical reactions. When more information is available in the future, stochastic simulations of spatial models including mechanics will provide additional insights.