Population Decoding of Motor Cortical Activity using a Generalized Linear Model with Hidden States

Abstract

Generalized linear models (GLMs) have been developed for modeling and decoding population neuronal spiking activity in the motor cortex. These models provide reasonable characterizations between neural activity and motor behavior. However, they lack a description of movement-related terms which are not observed directly in these experiments, such as muscular activation, the subject's level of attention, and other internal or external states. Here we propose to include a multi-dimensional hidden state to address these states in a GLM framework where the spike count at each time is described as a function of the hand state (position, velocity, and acceleration), truncated spike history, and the hidden state. The model can be identified by an Expectation-Maximization algorithm. We tested this new method in two datasets where spikes were simultaneously recorded using a multi-electrode array in the primary motor cortex of two monkeys. It was found that this method significantly improves the model-fitting over the classical GLM, for hidden dimensions varying from 1 to 4. This method also provides more accurate decoding of hand state (lowering the Mean Square Error by up to 29% in some cases), while retaining real-time computational efficiency. These improvements on representation and decoding over the classical GLM model suggest that this new approach could contribute as a useful tool to motor cortical decoding and prosthetic applications.

1. Introduction

Recent developments in biotechnology have given us the ability to measure and record population neuronal activity with more precision and accuracy than ever before, allowing researchers to study and perform detailed analyses which may have been impossible just a few years ago. In particular, with this advancement in technology, it is now possible to construct a brain-machine interface (BMI) to bridge the gap between neuronal spiking activity and external devices that help control real-world applications (Donoghue, 2002; Lebedev and Nicolelis, 2006; Schwartz et al., 2006). The primary goal of this BMI research is to be able to restore motor function to physically disabled patients (Hochberg et al., 2006): spike recordings would be “decoded” to provide an external prosthetic device with a neurally-controlled signal in the hope that the movement can be restored in its original form. However, there are still various issues that need to be addressed, such as long-term stability of the micro electrode array implants, efficacy and safety, low power consumption, and mechanical reliability (Donoghue, 2002; Chestek et al., 2007).

Many mathematical models have been proposed to perform this decoding of spiking activity from the motor cortex. Commonly-used linear models include population vectors (Georgopoulos et al., 1982), multiple linear regression (Paninski et al., 2004), and Kalman filters (Wu et al., 2006; Pistohl et al., 2008; Wu et al., 2009). These solutions have been shown to be effective and accurate, and have been used in various closed loop experiments (Taylor et al., 2002; Carmena et al., 2003; Wu et al., 2004). However, one caveat is that these models all make the strong assumption that the model for the firing rate has a continuous distribution (such as a Gaussian distribution) which apparently is not compatible with the discrete nature of spiking activity.

In addition, various discrete models have been developed to characterize spike trains. These formulations allow us to model the spiking rate using a discrete distribution, often a Poisson function with a “log” canonical link function, for the conditional density function at each time. In particular, recent research has focused on Generalized Linear Models (GLMs) which allow us to model non-linear relationships in a relatively efficient way (Brillinger, 1988, 1992; Paninski, 2004; Truccolo et al., 2005; Yu et al., 2006; Nykamp, 2007; Kulkarni and Paninski, 2007a; Pillow et al., 2008; Stevenson et al., 2009). The online decoding methods in a GLM framework include particle filters (Shoham, 2001; Brockwell et al., 2004, 2007) and point process filters (Eden et al., 2004; Truccolo et al., 2005; Srinivasan and Brown, 2007; Kulkarni and Paninski, 2007b).

Some very recent methods have also been proposed to perform population neuronal decoding. (Yu et al., 2007) focused on appropriate representation on the movement trajectory. They proposed to combine simple trajectory paths (each path to one target) in a probabilistic mixture of trajectory models. (Srinivasan et al., 2006; Srinivasan and Brown, 2007; Kulkarni and Paninski, 2007b) recently developed methods that incorporate goal information in a point process filter framework, and showed corresponding improvements in the decoding performance. This idea of incorporating goal information was further examined by Cunningham et al. (Cunningham et al., 2008), who investigated the optimal placement for targets to achieve maximum decoding accuracy.

While all of these non-linear models have attractive theoretical and computational properties, they do not take into account other internal or external variables that may affect spiking activity, such as muscular activation, the subject's level of attention, or other factors in the subject's environment. Collectively, we call these unobserved (or unobservable) variables hidden states, or common inputs, using the terminology from (Kulkarni and Paninski, 2007a); see also (Yu et al., 2006; Nykamp, 2007; Brockwell et al., 2007; Yu et al., 2009) for related discussion. Similarly, recent studies in the nonstationary relationship between neural activity and motor behaviors indicate that such nonstationarity may be accounted for by the fact that the spike trains also encode other states such as muscle fatigue, satiation, and decreased motivation (Carmena et al., 2005; Chestek et al., 2007). Moreover, a nonparametric model for point process spike trains has been developed using stochastic gradient boosting regression (Truccolo and Donoghue, 2007); it was found that the model fit with minor deviations and that these deviations may also result from other (unobservable) variables related to the spiking activity. Thus we would like to include these “hidden variables” as an important adjustment for modeling neural spiking processes in the context of neural decoding and prosthetic design. The effects of these variables for neural decoding of hand position has been examined in our recent investigation under a linear state-space model framework (Wu et al., 2009); significant improvement in both data representation and neural decoding were obtained.

In this paper, we apply a GLM-based state-space model that includes a multidimensional hidden dynamical state, to analyze and decode population recordings in motor cortex taken during performance of a random target pursuit task. This new model is a natural extension of our recent investigation in the linear case (Wu et al., 2009). The parameters in the model can be identified based on a recent version of the Expectation-Maximization (EM) algorithm for state-space models (Smith and Brown, 2003; Yu et al., 2006; Kulkarni and Paninski, 2007a). Finally, decoding in this model can be performed using standard efficient point process filter methods (Brown et al., 1998; Truccolo et al., 2005), and can therefore be applied in real-time online experiments. We find that including this hidden state in our analysis leads to significant improvements in the decoding accuracy, as discussed in more detail below.

2. Methods

2.1. Experimental Methods

Electrophysiological recording

The neural data used here were previously recorded and have been described elsewhere (Wu and Hatsopoulos, 2006). Briefly, silicon microelectrode arrays containing 100 platinized-tip electrodes (1.0 mm electrode length; 400 microns inter-electrode separation; Cyberkinetics Inc., Salt Lake City, UT) were implanted in the arm area of primary motor cortex (MI) in two juvenile male macaque monkeys (Macaca mulatta). Signals were filtered, amplified (gain, 5000) and recorded digitally (14-bit) at 30 kHz per channel using a Cerebus acquisition system (Cyberkinetics Neurotechnology Systems, Inc.). Single units were manually extracted by the Contours and Templates methods, and units with very low spiking rate (< 1 spike/sec) were filtered to avoid non-robustness in the computation. One data set was collected and analyzed for each monkey; the number of distinct units was 100 for the first monkey, and 75 for the second. The firing rates of single cells were computed by counting the number of spikes within the previous 10 ms time window. We found approximately 99.9% of these counts are either 0 or 1, which essentially enforces a binary sequence of spike counts for most time bins in the study.

Task

The monkeys were operantly trained to perform a random target pursuit task by moving a cursor to targets via contralateral arm movements. The cursor and a sequence of seven targets (target size: 1cm × 1cm) appeared one at a time on a horizontal projection surface (the workspace is about 30cm × 15cm). At any one time, a single target appeared at a random location in the workspace, and the monkey was required to reach it within 2 seconds. As soon as the cursor reached the target, the target disappeared and a new target appeared in a new, pseudo-random location. After reaching the seventh target, the monkey was rewarded with a drop of water or juice. One example trial is shown in Figure 1. A new set of seven random targets was presented on each trial. The hand positions were recorded at a sampling rate of 500 Hz. 100 successful movement trials were collected in each data set. To match time scales, the hand position were down-sampled every 10 ms and from this we computed velocity and acceleration using simple differencing. Taking into account the latency between firing activity in MI and hand movement, we compared the neural activity with the instantaneous kinematics (position, velocity, and acceleration) of the arm measured 100 ms later (i.e. a 10 time bin delay) (Moran and Schwartz, 1999; Paninski et al., 2004; Wu et al., 2006).

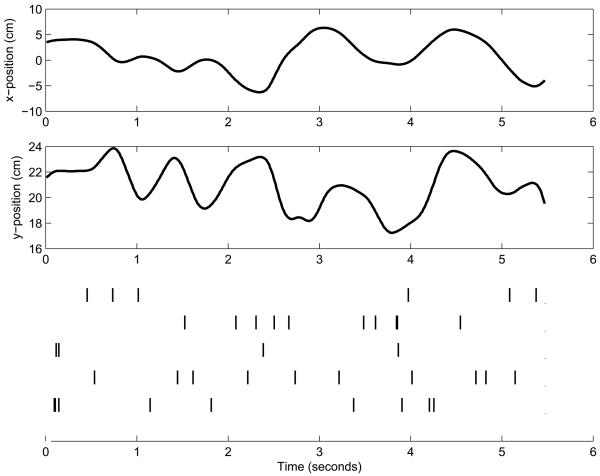
Figure 1.

Upper two panels: True hand trajectory, x- and y-position, for one example trial in the study. Bottom panel: A raster plot of spike trains of 5 simultaneously-recorded neurons during the same example trial. We plot the hand trajectory as one-dimensional plots to help show the temporal correspondence between the hand trajectory and the spike trains.

2.2. Statistical Methods

2.2.1. Independent State Model

In motor cortical decoding models, the system state typically includes the hand kinematics. We use the hand position, velocity, and acceleration to fully describe the movement. The state over time is assumed as a simple autoregressive (AR) model with order 1 which essentially imposes the continuity of the hand movement. Mathematically, the state is described using the following equation:

$${\mathbf{x}}_{k+1}={\mathbf{m}}_x+{\mathbf{A}}_x{\mathbf{x}}_k+{\xi }_k$$ (1)

where x_k ∈ ℜ^p is the hand kinematics (i.e. the position, velocity, and acceleration for x- and y-coordinates, grouped together to form a vector), m_x ∈ ℜ^p is the intercept term, A_x ∈ ℜ^p×p is the transition matrix, and ξ_k ∈ ℜ^p is the noise term. We assume ξ_k ~ N(0, C_x), with C_x ∈ ℜ^p×p.

In this study, we add a multi-dimensional hidden state to the system. For simplicity, the hidden state, q_k ∈ ℜ^d, is also assumed as an AR(1) model (Smith and Brown, 2003; Kulkarni and Paninski, 2007a), and the transition is described as:

$${\mathbf{q}}_{k+1}={\mathbf{A}}_q{\mathbf{q}}_k+{∊}_k$$ (2)

where A_q ∈ ℜ^d×d is the transition matrix, and ε_k ∈ ℜ^d is the noise term. We assume ε_k ~ N(0, C_q), with C_q ∈ ℜ^d×d. Here, ε_k and ξ_k are also assumed independent of each other.

In addition to the two system equations (Eqns. 1 and 2), a measurement equation is used to characterize the discretized firing activity (spike count) of the recorded C neurons. Here, we use a Poisson distribution to describe the spike count for each neuron at each time conditioned on the hand state, spike history, and hidden state. That is,

$${\mathbf{y}}_k^c\mid {\mathbf{x}}_k,{\mathbf{H}}_k^c,{\mathbf{q}}_k~P\left({\lambda }_k^c\Delta t\right)$$ (3)

where ${\mathbf{y}}_k^c$ is the spike count of the cth neuron at the kth time bin for c = 1, ⋯ , C, and ${\mathbf{H}}_k^c$ denotes the spike history. Δt denotes the bin size. Based on the GLM framework, the conditional intensity function (CIF), ${\lambda }_k^c$ has the form:

$${\lambda }_k^c=\exp ({\mu }_c+{\beta }_c^T{\mathbf{x}}_k+{\gamma }_c^T{\mathbf{y}}_{k,N}^c+{\mathbf{l}}_c^T{\mathbf{q}}_k)$$ (4)

where ${\mathbf{y}}_{k,N}^c={(y_{k-1}^c,\cdots ,y_{k-N}^c)}^T$ is the most recent N history steps from the kth bin of the cth neuron, μ_c ∈ ℜ is the intercept for this model, and β_c ∈ ℜ^p, γ_c ∈ ℜ^N, and l_c ∈ ℜ^d are coefficients for the hand state, spike history, and hidden state, respectively.

Note that the history term in the density function implies the dependence for the spike train over time. The spike train is, therefore, a non-Poisson process (NPP) albeit the distribution at each time is Poisson. However, if this term is excluded from Equation 4; that is,

$${\lambda }_k^c=\exp ({\mu }_c+{\beta }_c^T{\mathbf{x}}_k+{\mathbf{l}}_c^T{\mathbf{q}}_k),$$ (5)

then the spike train is a commonly-used inhomogeneous Poisson process (IPP) (Brown et al., 1998; Gao et al., 2002; Brockwell et al., 2004), given the system states x_k and q_k; on the other hand, if we integrate over the unobserved hidden state q_k, then the spike train may be considered a log-Gaussian Cox process, a doubly stochastic Poisson process where the logarithm of the conditional intensity function is a Gaussian process (Snyder and Miller, 1991; Moeller et al., 1998; Kulkarni and Paninski, 2007a).

We also note that we have an intercept term in Equation 1 as the kinematic data may not be centered at 0. However, we do not use an intercept term for the hidden state (Eqn. 2). This is to assure the identifiability of the model. It is easy to verify that the intercept is equivalent to a centralization shift in the hidden state and the shift can be absorbed in the intercept term, μ_c, in the CIF in Equation 4 or 5.

2.2.2. Dependent State Model

Equations 1 and 2 independently describe the hand state and hidden state, respectively. This independent description provides an easy-to-access framework to investigate their dynamics. However, in general the hidden states may actually have a direct, dynamic impact on the hand state and vice versa (Wu et al., 2009). Taking into account this dependency, the system model can be written as:

$$\left(\begin{array}{c}\hfill {\mathbf{x}}_{k+1}\hfill \\ \hfill {\mathbf{q}}_{k+1}\hfill \end{array}\right)=\mathbf{A}\left(\begin{array}{c}\hfill {\mathbf{x}}_k\hfill \\ \hfill {\mathbf{q}}_k\hfill \end{array}\right)+{\mathbf{v}}_k$$ (6)

where A ∈ ℜ^(p+d)×(p+d) is the transition matrix, and v_k ∈ ℜ^(p+d) is the noise term. We assume v_k ~ N(0, V), with V ∈ ℜ^(p+d)×(p+d). There is no intercept term here as the center of the hidden state can be absorbed in the measurement equation and the hand kinematics can be easily centralized before being used in the model. Note that if A = diag(A_x, A_q), and V = diag(C_x, C_q), then Equation 6 can be simplified to two independent equations (as Eqns. 1 and 2 except the intercept term m_x). Here diag(·) denotes a block-diagonal matrix by putting all components in the main diagonal.

Coupling the dependent state model (Eqn. 6) and the measurement model (Eqn. 3), we also form a state-space model to represent the neural activity and hand kinematics. We denote this GLM with hidden states using a dependent state model as GLMHS-DS, and the one using an independent state model (Eqns. 1, 2, and 3) as GLMHS-IS. As in the GLMHS-IS, the CIF, ${\lambda }_k^c$, in the GLMHS-DS can have either an NPP (Eqn. 4) or IPP (Eqn. 5) form.

2.3. Model Identification of GLMHS-IS

Based on Equations 1, 2, and 4, the parameters in the GLMHS-IS are (m_x, A_x, C_x, A_q, C_q, {μ_c}, {β_c},{γ_c}, {l_c}) where bracket {·} denotes the set of parameters with all values of the subindex; for example, {μ_c} = (μ₁, ⋯, μ_C). At first, we need to identify the new model using a training set where firing rates of all neurons, {y_k}, and hand states, {x_k}, are observed. As the hand kinematics is independently formulated in Equation 1, the parameters (m_x, A_x, C_x) can be identified using the standard Least Squares estimates (Wu et al., 2006). Let θ = (A_q, C_q, {μ_c}, {β_c}, {γ_c}, {l_c}). The identification of θ needs more computations as it involves the unknown hidden state. Here we propose to identify θ based on an approximate EM algorithm for this state-space model (Smith and Brown, 2003; Shumway and Stoffer, 2006; Kulkarni and Paninski, 2007a).

2.3.1. EM Algorithm for GLMHS-IS: E-Step

The EM algorithm is an iterative method. Let the parameter be θ_i at the ith iteration. In the E-step, we need to calculate the expectation of the complete (i.e. firing rates, hand state, and hidden state) log-likelihood, denoted by ECLL, with the parameter θ, given as:

$$\mathit{ECLL}=E_{P(\left\{{\mathbf{q}}_k\right\}\mid \{{\mathbf{x}}_k,{\mathbf{y}}_k\},{\theta }_i)}\log P(\{{\mathbf{y}}_k,{\mathbf{x}}_k,{\mathbf{q}}_k\};\theta )$$ (7)

where the expectation is on the posterior distribution of the hidden state conditioned on the entire observation with the current parameter θ_i.

Using the Markov properties and the independence assumptions formulated in Eqns. 2 and 3, we have:

$$\begin{array}{cc}\hfill \mathit{ECLL}& =E_{P(\left\{{\mathbf{q}}_k\right\}\mid \{{\mathbf{x}}_k,{\mathbf{y}}_k\},{\theta }_i)}[\underset{k=1}{\overset{M-1}{\Sigma }}\log P({\mathbf{q}}_{k+1}\mid {\mathbf{q}}_k;\theta )+\underset{k=1}{\overset{M}{\Sigma }}{E}_{P({\mathbf{q}}_k\mid \{{\mathbf{x}}_k,{\mathbf{y}}_k\},{\theta }_i)}\log P({\mathbf{y}}_k\mid {\mathbf{x}}_k,{\mathbf{H}}_k,{\mathbf{q}}_k;\theta )]+\mathit{const}.\hfill \\ \hfill & =\underset{k=1}{\overset{M-1}{\Sigma }}{E}_{P({\mathbf{q}}_{k+1},{\mathbf{q}}_k\mid \{{\mathbf{x}}_k,{\mathbf{y}}_k\};{\theta }_i)}\log P({\mathbf{q}}_{k+1}\mid {\mathbf{q}}_k;\theta )+\underset{k=1}{\overset{M}{\Sigma }}{E}_{P({\mathbf{q}}_k\mid \{{\mathbf{x}}_k,{\mathbf{y}}_k\},{\theta }_i)}\log P({\mathbf{y}}_k\mid {\mathbf{x}}_k,{\mathbf{H}}_k,{\mathbf{q}}_k;\theta )+\mathit{const}.\hfill \end{array}$$ (8)

where M denotes the total number of time bins in the data, and ${\mathbf{H}}_k=\left\{{\mathbf{H}}_k^c\right\}$ denotes the spike history of all neurons. The constant term includes the hand state transition probability and the initial condition, P(q₁), on the hidden state. The computations of these terms are independent of the parameter θ. The initial state q₁ can be simply set to zero; we have found that the initial value has a negligible impact on the data analysis (Wu et al., 2009).

To estimate the expected log-likelihood in Equation 8, we need to to know the distributions of P(q_k+1, q_k|{x_k, y_k}; θ_i) and P(q_k|{x_k, y_k}; θ_i). Assuming normality on these quantities, we only need to compute their first and second order statistics E[q_k|{x_k, y_k}; θ_i], Cov[q_k|{x_k, y_k}; θ_i], and Cov[q_k+1, q_k|{x_k, y_k}; θ_i] (labeled as q_k|M, W_k|M, and W_k+1,k|M, respectively). These terms can be computed via a standard approximate forward-backward recursive algorithm (Brown et al., 1998; Smith and Brown, 2003; Kulkarni and Paninski, 2007a). See Appendix A for details.

Likelihood Computation

With all conditional probabilities of the hidden state estimated in the E-step, we can compute the joint likelihood of the observed firing rates and hand state in the training data with current parameters θ_i. Letting x_1:M denote the set (x₁, ⋯, x_M) and y_1:M denote the set (y₁, ⋯, y_M), we can compute

$$P({\mathbf{x}}_{1:M},{\mathbf{y}}_{1:M};{\theta }_i)=c\prod _{k=2}^{M}P({\mathbf{x}}_k,{\mathbf{y}}_k\mid {\mathbf{x}}_{1:k-1},{\mathbf{y}}_{1:k-1})$$ (9)

where the initial condition (i.e. P(x₁, y₁)) is assumed as a constant, c, over the iterations. For convenience, we remove θ_i and use 1:n to denote sub-indices (1, ⋯, n). This notation simplification will be used in all future conditional probabilities in this paper. For each k,

$$P({\mathbf{x}}_k,{\mathbf{y}}_k\mid {\mathbf{x}}_{1:k-1},{\mathbf{y}}_{1:k-1})={\int }_{{\mathbf{q}}_k}P({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1})P({\mathbf{y}}_k\mid {\mathbf{x}}_k,{\mathbf{H}}_k,{\mathbf{q}}_k)P({\mathbf{q}}_k\mid {\mathbf{x}}_{1:k-1},{\mathbf{y}}_{1:k-1})d{\mathbf{q}}_k$$

The integrand is a product of two Gaussian distributions (first and third terms) and one Poisson distribution (second term). There is no closed-form expression for this integration. Here we use a Monte-Carlo method to estimate its value as q_k|x_1:k−1, y_1:k−1 ~ N(q_k|k−1, W_k|k−1) (see Appendix A). Let ${\mathbf{q}}_k^{\left(1\right)},\cdots ,{\mathbf{q}}_k^{\left(I\right)}$ be I independent samples from this distribution. Then

$$P({\mathbf{x}}_k,{\mathbf{y}}_k\mid {\mathbf{x}}_{1:k-1},{\mathbf{y}}_{1:k-1})\approx \frac{1}{I}\underset{i=1}{\overset{I}{\Sigma }}\left[P({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1})\prod _{c=1}^{C}P({\mathbf{y}}_k^c\mid {\mathbf{k}}_k,{\mathbf{H}}_k^c,{\mathbf{q}}_k^{\left(i\right)})\right]$$

Note that as the likelihood in Eqn. 9 is calculated over all time steps, the randomness of samples at each time is offset. In practice, we found a very stable likelihood value even with a small sample size (I = 10 in this study) at each time.

2.3.2. EM Algorithm for GLMHS-IS: M-Step

In the M-step, we update θ_i by maximizing ECLL with respect to θ. To simplify notation, we use P(·|⋯) to denote P(·|{x_k, y_k}; θ_i) and remove the subindex i for all parameters. The log-likelihood in Equation 7 can be partitioned in the following form:

$$\mathit{ECLL}=E_1+E_2+\mathit{const}.,$$

where

$$E_1=\underset{k=1}{\overset{M-1}{\Sigma }}{E}_{P({\mathbf{q}}_{k+1},{\mathbf{q}}_k\mid \cdots )}\log P({\mathbf{q}}_{k+1}\mid {\mathbf{q}}_k;{\mathbf{A}}_q,{\mathbf{C}}_q)$$ (10)

$$E_2=\underset{k=1}{\overset{M}{\Sigma }}{E}_{P({\mathbf{q}}_k\mid \cdots )}\log P({\mathbf{y}}_k\mid {\mathbf{x}}_k,{\mathbf{H}}_k,{\mathbf{q}}_k;\{{\mu }_c,{\beta }_c,{\gamma }_c,{\mathbf{l}}_c\})$$ (11)

Here E₁ and E₂ contain different parameters. We can maximize E₁ to identify A_q and C_q, and maximize E₂ to identify {μ_c}, {β_c}, {γ_c}, and {l_c}. The solution for A_q has a closed-form expression given by:

$$\begin{array}{cc}\hfill {\mathbf{A}}_q^{(i+1)}& =\left(\underset{k=1}{\overset{M-1}{\Sigma }}E({\mathbf{q}}_{k+1}{\mathbf{q}}_k^T\mid \cdots )\right){\left(\underset{k=1}{\overset{M-1}{\Sigma }}E({\mathbf{q}}_k{\mathbf{q}}_k^T\mid \cdots )\right)}^{-1}\hfill \\ \hfill & =\left(\underset{k=1}{\overset{M-1}{\Sigma }}{\mathbf{W}}_{k+1,k\mid M}+{\mathbf{q}}_{k+1\mid M}{\mathbf{q}}_{k\mid M}^T\right){\left(\underset{k=1}{\overset{M-1}{\Sigma }}{\mathbf{W}}_{k\mid M}+{\mathbf{q}}_{k\mid M}{\mathbf{q}}_{k\mid M}^T\right)}^{-1}.\hfill \end{array}$$ (12)

Similarly, using the measurement model in Equation 3, we have

$$E_2=\underset{k=1}{\overset{M}{\Sigma }}\underset{c=1}{\overset{C}{\Sigma }}{\int }_{{\mathbf{q}}_k}P({\mathbf{q}}_k\mid \cdots )[-{\lambda }_k^c\Delta t+y_k^c\log \left({\lambda }_k^c\right)]d{\mathbf{q}}_k+\mathit{const}.,$$

where ${\lambda }_k^c$ is described in Equation 4 or 5. There is no closed-form expression for the maximization of the parameters {μ_c, β_c, γ_c, l_c}. Here we use a Newton-Raphson algorithm to update these parameters. It can be shown that the Hessian matrix of E₂ is negative-definite (Kulkarni and Paninski, 2007a), indicating that E₂ is a strictly concave function with respect to all parameters. Therefore, the Newton-Raphson method rapidly converges to the unique root of the equation (i.e., the global maximum of E₂) within a few iterations (typically around 5 in the given data). The detailed procedure is described in Appendix B.

2.4. Model Identification of GLMHS-DS

Based on Equations 4 and 6, the parameters in the GLMHS-DS are θ = (A, V, {μ_c}, {β_c}, {γ_c}, {l_c}). Similar to the identification of the GLMHS-IS, we use an EM algorithm to identify the GLMHS-DS.

2.4.1. EM Algorithm for GLMHS-DS: E-Step

In the ith iteration, we estimate the expected complete log-likelihood

$$\begin{array}{cc}\hfill \mathit{ECLL}& =E_{P(\left\{{\mathbf{q}}_k\right\}\mid \{{\mathbf{x}}_k,{\mathbf{y}}_k\};{\theta }_i)}\log P(\{{\mathbf{x}}_k,{\mathbf{y}}_k,{\mathbf{q}}_k\};\theta )\hfill \\ \hfill & =E_{P(\left\{{\mathbf{q}}_k\right\}\mid \{{\mathbf{x}}_k,{\mathbf{y}}_k\};{\theta }_i)}[\underset{k=1}{\overset{M-1}{\Sigma }}\log P({\mathbf{x}}_{k+1},{\mathbf{q}}_{k+1}\mid {\mathbf{x}}_k,{\mathbf{q}}_k;\theta )+\underset{k=1}{\overset{M}{\Sigma }}{E}_{P({\mathbf{q}}_k\mid \{{\mathbf{x}}_k,{\mathbf{y}}_k\};{\theta }_i)}\log P({\mathbf{y}}_k\mid {\mathbf{x}}_k,{\mathbf{H}}_k,{\mathbf{q}}_k;\theta )]+\mathit{const}.\hfill \\ \hfill & =\underset{k=1}{\overset{M-1}{\Sigma }}{E}_{P({\mathbf{q}}_{k+1},{\mathbf{q}}_k\mid \cdots )}\log P({\mathbf{x}}_{k+1},{\mathbf{q}}_{k+1}\mid {\mathbf{x}}_k,{\mathbf{q}}_k;\theta )+\underset{k=1}{\overset{M}{\Sigma }}{E}_{P({\mathbf{q}}_k\mid \cdots )}\log P({\mathbf{y}}_k\mid {\mathbf{x}}_k,{\mathbf{H}}_k,{\mathbf{q}}_k;\theta )+\mathit{const}.\hfill \end{array}$$ (13)

This decomposition is the same as that in Equation 8 except that the hand state and hidden state are in one probability transition as they are dependent on each other. To utilize the observed hand state in training data, we let

$$\mathbf{A}=\left(\begin{array}{cc}\hfill {\mathbf{A}}_{11}\hfill & \hfill {\mathbf{A}}_{12}\hfill \\ \hfill {\mathbf{A}}_{21}\hfill & \hfill {\mathbf{A}}_{22}\hfill \end{array}\right),\text{and}{\mathbf{v}}_k={({\xi }_k^T,{∊}_k^T)}^T,\mathbf{V}=\mathit{diag}({\mathbf{C}}_x,{\mathbf{C}}_q),$$

where A₁₁ ∈ R^p×p, A₁₂ ∈ R^p×d, A₂₁ ∈ R^d×p, and A₂₂ ∈ R^d×d are four sub-matrices, and ξ_k, ∈_k, C_x, and C_q follow the same definition in the GLMHS-IS model. Then Equation 6 can be reorganized in the following form:

$${\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}{\mathbf{x}}_k={\mathbf{A}}_{12}{\mathbf{q}}_k+{\xi }_k$$ (14)

$${\mathbf{q}}_{k+1}={\mathbf{A}}_{22}{\mathbf{q}}_k+{\mathbf{A}}_{21}{\mathbf{x}}_k+{∊}_k$$ (15)

Here the hidden state transition (Eqn. 15) has a linear Gaussian form with A₂₁x_k as a control input. The hand kinematics (Eqn. 14) can be thought of as a measurement in addition to neural firing rate of each observed neuron in Equation 3. With this extra measurement, the estimation of posteriors of the hidden state conditioned on the full observation, P(q_k+1, q_k|{x_k, y_k}; θ_i) and P(q_k|{x_k, y_k}; θ_i), involves more computations than that in the GLMHS-IS model (Appendix A). Assuming the normality on the posteriors, we also compute the means and covariances, Eq_k|{x_k, y_k}; θ_i], Cov[q_k|{x_k, y_k}; θ_i,], and Cov[q_k+1, q_k|{x_k, y_k}; θ_i] (labeled as q_k|M, and W_k|M, and W_k+1,k|M, respectively).

Likelihood Computation

We compute the joint likelihood of the observed firing rates and hand state in the training data with parameters θ_i. The likelihood can then be written as

$$P({\mathbf{x}}_{1:M},{\mathbf{y}}_{1:M};{\theta }_i)=\mathit{cP}({\mathbf{y}}_M\mid {\mathbf{x}}_{1:M-1})\prod _{k=1}^{M-1}P({\mathbf{x}}_{k+1},{\mathbf{y}}_k\mid {\mathbf{x}}_{1:k},{\mathbf{y}}_{1:k-1})$$ (16)

Here the initial probability, P(x₁), is assumed as a constant c. For each k,

$$\begin{array}{cc}\hfill & P({\mathbf{x}}_{k+1},{\mathbf{y}}_k\mid {\mathbf{x}}_{1:k},{\mathbf{y}}_{1:k-1})\hfill \\ \hfill =& {\int }_{{\mathbf{q}}_k}P({\mathbf{x}}_{k+1}\mid {\mathbf{x}}_k,{\mathbf{q}}_k)P({\mathbf{y}}_k\mid {\mathbf{x}}_k,{\mathbf{H}}_k,{\mathbf{q}}_k)P({\mathbf{q}}_k\mid {\mathbf{x}}_{1:k},{\mathbf{y}}_{1:k-1})d{\mathbf{q}}_k\hfill \\ \hfill \approx & \frac{1}{I}\underset{i=1}{\overset{I}{\Sigma }}\left[P({\mathbf{x}}_{k+1}\mid {\mathbf{x}}_k,{\mathbf{q}}_k^{\left(i\right)})P({\mathbf{y}}_k^c\mid {\mathbf{x}}_k,{\mathbf{H}}_k^c,{\mathbf{q}}_k^{\left(i\right)})\right]\hfill \end{array}$$

where we use a Monte-Carlo method in the last step in that q_k|x_1:k, y_1:k−1 ~ N(q_k|k−1, W_k|k−1) (see Appendix C).

The first term in Equation 16 can be computed in the same way except that there is no transition in the hand state; that is,

$$P({\mathbf{y}}_M\mid {\mathbf{x}}_{1:M},{\mathbf{y}}_{1:M-1})={\int }_{{\mathbf{q}}_k}P({\mathbf{y}}_M\mid {\mathbf{x}}_M,{\mathbf{H}}_M^c,{\mathbf{q}}_M)P({\mathbf{q}}_M\mid {\mathbf{x}}_{1:M},{\mathbf{y}}_{1:M-1})d{\mathbf{q}}_k.$$

The same Monte-Carlo procedure can be applied here.

2.4.2. EM Algorithm for GLMHS-DS: M-Step

Similarly, the expected complete log-likelihood in Equation 13 can be written as

$$\mathit{ECLL}=E_3+E_4+\mathit{const}.$$

where

$$E_3=\underset{k=1}{\overset{M-1}{\Sigma }}{E}_{P({\mathbf{q}}_{k+1}{\mathbf{q}}_k\mid \cdots )}\log P({\mathbf{x}}_{k+1},{\mathbf{q}}_{k+1}\mid {\mathbf{x}}_k,{\mathbf{q}}_k;\mathbf{A},\mathbf{V})$$ (17)

$$E_4=\underset{k=1}{\overset{M}{\Sigma }}\underset{c=1}{\overset{C}{\Sigma }}{E}_{P({\mathbf{q}}_k\mid \cdots )}\log P({\mathbf{y}}_k^c\mid {\mathbf{x}}_k,{\mathbf{H}}_k^c,{\mathbf{q}}_k;\{{\mu }_c,{\beta }_c,{\gamma }_c,{\mathbf{l}}_c\})$$ (18)

Here E₃ and E₄ contain different parameters. We can maximize E₃ to identify A and V, and maximize E₄ to identify {μ_c}, {β_c}, {γ_c}, and {l_c}. Note that Equation 18 is identical to Equation 11. Therefore the update of the parameters {μ_c}, {β_c}, {γ_c}, and {l_c} is the same as that in the M-step for the GLMHS-IS model.

The Maximization of E₃ with respect to A has a closed-form solution:

$$\begin{array}{cc}\hfill {\mathbf{A}}^{(i+1)}& =\left[\underset{k=1}{\overset{M-1}{\Sigma }}{E}_{P({\mathbf{q}}_{k+1}{\mathbf{q}}_k\mid \cdots )}\left(\begin{array}{c}\hfill {\mathbf{x}}_{k+1}\hfill \\ \hfill {\mathbf{q}}_{k+1}\hfill \end{array}\right){\left(\begin{array}{c}\hfill {\mathbf{x}}_k\hfill \\ \hfill {\mathbf{q}}_k\hfill \end{array}\right)}^T\right]{\left[\underset{k=1}{\overset{M-1}{\Sigma }}{E}_{P({\mathbf{q}}_k\mid \cdots )}\left(\begin{array}{c}\hfill {\mathbf{x}}_k\hfill \\ \hfill {\mathbf{q}}_k\hfill \end{array}\right){\left(\begin{array}{c}\hfill {\mathbf{x}}_k\hfill \\ \hfill {\mathbf{q}}_k\hfill \end{array}\right)}^T\right]}^{-1}\hfill \\ \hfill & =\left[\underset{k=1}{\overset{M-1}{\Sigma }}\left(\begin{array}{cc}\hfill {\mathbf{x}}_{k+1}{\mathbf{x}}_k^T\hfill & \hfill {\mathbf{x}}_{k+1}{\mathbf{q}}_{k\mid M}^T\hfill \\ \hfill {\mathbf{q}}_{k+1\mid M}{\mathbf{x}}_k^T\hfill & \hfill {\mathbf{W}}_{k+1,k\mid M}+{\mathbf{q}}_{k+1\mid M}{\mathbf{q}}_{k\mid M}^T\hfill \end{array}\right)\right]{\left[\underset{k=1}{\overset{M-1}{\Sigma }}\left(\begin{array}{cc}\hfill {\mathbf{x}}_k{\mathbf{x}}_k^T\hfill & \hfill {\mathbf{x}}_k{\mathbf{q}}_{k\mid M}^T\hfill \\ \hfill {\mathbf{q}}_{k\mid M}{\mathbf{x}}_k^T\hfill & \hfill {\mathbf{W}}_{k\mid M}+{\mathbf{q}}_{k\mid M}{\mathbf{q}}_{k\mid M}^T\hfill \end{array}\right)\right]}^{-1}\hfill \end{array}$$

The covariance V = diag(C_x, C_q) is a block-diagonal matrix where C_q denotes the covariance of the hidden state. To make the system identifiable, we fix C_q as the identity matrix. Based on the updated A⁽ⁱ⁺¹⁾, the solution to C_x also has a closed form:

$$\begin{array}{cc}\hfill {\mathbf{C}}_x^{(i+1)}& =\frac{1}{M-1}\underset{k=1}{\overset{M-1}{\Sigma }}{E}_{P({\mathbf{q}}_{k+1}{\mathbf{q}}_k\mid \cdots )}\left[({\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}^{(i+1)}{\mathbf{x}}_k-{\mathbf{A}}_{12}^{(i+1)}{\mathbf{q}}_k){({\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}^{(i+1)}{\mathbf{x}}_k-{\mathbf{A}}_{12}^{(i+1)}{\mathbf{q}}_k)}^T\right]\hfill \\ \hfill & =\frac{1}{M-1}\underset{k=1}{\overset{M-1}{\Sigma }}[({\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}^{(i+1)}{\mathbf{x}}_k){({\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}^{(i+1)}{\mathbf{x}}_k)}^T-{\mathbf{A}}_{12}^{(i+1)}{\mathbf{q}}_{k\mid M}{({\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}^{(i+1)}{\mathbf{x}}_k)}^T-({\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}^{(i+1)}{\mathbf{x}}_k){\mathbf{q}}_{k\mid M}^T{\mathbf{A}}_{12}^{{(i+1)}^T}+{\mathbf{A}}_{22}^{(i+1)}({\mathbf{W}}_{k\mid M}+{\mathbf{q}}_{k\mid M}{\mathbf{x}}_{k\mid M}^T){\mathbf{A}}_{22}^{{(i+1)}^T}]\hfill \end{array}$$

Note that each of the optimizations involved in the M-step for this model have unique solutions, although the marginal likelihood log P({y_k}|θ) may not be concave with respect to all of the elements of the parameter vector θ (Paninski, 2005). Thus initialization of the parameter search can play an important role, especially in the GLMHS-DS model, which has a few more parameters to describe the interaction of the kinematic state x_k with the hidden state q_k. We found that initializing the GLMHS-IS parameters to the GLM solution, and then initializing the GLMHS-DS parameters to the GLMHS-IS solution, led to reliable and accurate results.

2.5. Decoding

After all parameters in the model (GLMHS-IS or GLMHS-DS) are identified, we can use the model to decode neural activity and reconstruct the hand state. To make the decoding useful in practical applications, we focus on on-line “filtering” estimates, defined as the posterior distribution of the hand state conditioned on the previous and current spiking rate. Note that the exact estimation of the posterior distribution is intractable as the measurement equation is based on a non-linear Poisson model (Eqn. 3). To simplify the process, we approximate the posterior with a normal distribution whose mean and covariance we update with each time step. This allows us to use an efficient point process filter which is a nonlinear generation of the classical Kalman filter (Fahrmeir and Tutz, 1994; Brown et al., 1998; Truccolo et al., 2005). To use the point process filter in this situation, we combine the kinematic states x_k and the hidden states q_k to form a new state vector s_k. The procedure (omitted here) is similar to that described in Appendix A.

2.6. Goodness-of-Fit Analysis

A common way to perform goodness-of-fit analysis when spike trains are modeled in continuous time is to use the idea of Time Rescaling (Brown et al., 2002). Briefly, one would use the fitted point process rate function, and “rescale” the time axis. Under the assumption that the fitted model is “correct”, the rescaled spike train should be a homogeneous Poisson process.

However, for point processes modeled in discrete time, a different approach is needed. Recently, Brockwell (Brockwell, 2007) introduced a new method for conducting goodness-of-fit analysis for models in discrete time. In general, for continuous distributions, one can use Rosenblatt's Transformation (Rosenblatt, 1952) to map a continuous k-variate random vector X to one with a uniform distribution on a k-dimensional hypercube. Brockwell generalized this transformation for any vector X (either discrete, continuous or mixed) and showed that this new transformation of the vector X can still be mapped to a uniform distribution on [0, 1], allowing us to do goodness-of-fit even for discrete spike trains. In the context of neural spiking processes, this “generalized residual” is constructed as follows (Brockwell et al., 2007): For k = 1, …, M, calculate

$$\begin{array}{cc}\hfill {\stackrel{-}{r}}_k^{\left(c\right)}& =P\left({\mathbf{y}}_k^{\left(c\right)}\le N_k^{\left(c\right)}\mid {\mathbf{y}}_{1:k-1}^{\left(c\right)}=N_{1:k-1}^{\left(c\right)}\right)\hfill \\ \hfill & =\int P\left({\mathbf{y}}_k^{\left(c\right)}\le N_k^{\left(c\right)}\mid {\mathbf{x}}_k,{\mathbf{q}}_k\right)\mathit{dP}\left({\mathbf{x}}_k,{\mathbf{q}}_k\mid {\mathbf{y}}_{1:k-1}^{\left(c\right)}=N_{1:k-1}^{\left(c\right)}\right)\hfill \end{array}$$ (19)

and the left limits

$${\underset{-}{r}}_k^{\left(c\right)}=P\left({\mathbf{y}}_k^{\left(c\right)}<N_k^{\left(c\right)}\mid {\mathbf{y}}_{1:k-1}^{\left(c\right)}=N_{1:k-1}^{\left(c\right)}\right)$$ (20)

where $N_t^{\left(c\right)}$ is the spike count of the cth neuron at time t, and $N_{1:t-1}^{\left(c\right)}$ is the collection of spike counts up to t − 1. Using samples drawn from $P({\mathbf{x}}_k,{\mathbf{q}}_k\mid {\mathbf{y}}_{1:k-1}^{\left(c\right)}=N_{1:k-1}^{\left(c\right)})$ (essentially the prediction distribution up to the previous time step), we evaluate the Monte Carlo approximation to ${\stackrel{-}{r}}_k^{\left(c\right)}$ and ${\underset{-}{r}}_k^{\left(c\right)}$. With estimates of ${\stackrel{-}{r}}_k^{\left(c\right)}$ and ${\underset{-}{r}}_k^{\left(c\right)}$, draw independently $R_k^{\left(c\right)}~\mathit{Unif}\left({\underset{-}{r}}_k^{\left(c\right)},{\stackrel{-}{r}}_k^{\left(c\right)}\right)$ at each time k. Under the assumption of model correctness, the set of residuals $R_k^{\left(c\right)},k=1,\dots ,M$ should be uniformly distributed on [0, 1.] This procedure is done for all C neurons in the study.

It should be noted, however, that this method is stochastic in nature (meaning, we should expect slightly different results every time we execute this method). This is because there are two sources of randomness in this method: One is in the Monte Carlo samples used to evaluate the upper and lower limits (although this is not much of a problem since we expect some degree of convergence for larger sample sizes), and the other is in generating the residuals. It should also be noted that, while a goodness-of-fit procedure can provide us important information about a model's lack of fit, in many cases multiple models may “pass” a given goodness-of-fit test (indeed, this is the case here, as discussed further below). Therefore, to determine which model is most appropriate, further analyses, such as likelihood calculations or model selection procedures, need to be conducted. A detailed likelihood analysis is performed later in the paper.

3. Results

3.1. Identification

To both identify and verify our model, we divide our data into two distinct parts: a training set (to fit all necessary model parameters) and a testing set (to verify that the model fit is appropriate). In each dataset, we use the first 50 trials as our training set, with the next 50 trials as a testing set. Each trial was about 4-5 seconds long; with a bin size of 10ms, this results in about 400 to 500 observations for each trial, or a total size of 20000 to 30000 observations for the training set. This is a sufficient number for identification and modeling purposes. The typical number of iterations in each EM procedure is about 10 to 20.

3.1.1. GLMHS-IS Model

In the GLMHS-IS model, the hand kinematics are modeled independently of the common inputs (see Eqn. 1). This model is straightforward mathematically, as it enables us to fit parameters separately using the standard least squares method.

IPP case

Our first analysis involves measuring the goodness-of-fit in the GLMHS-IS IPP model (see Section 2.6). Based on the assumption of “model correctness”, the residuals constructed should be from a uniform distribution on [0, 1]. Here we calculate these residuals for each of our 50 training trials. We found that the residuals for most of the cells (around 90% in both datasets) are uniformly distributed (P-value > 0.05, Kolmogorov-Smirnov test).

We then analyze the CIF, ${\lambda }_k^c$, of the GLMHS-IS versus that of the classical GLM for IPP spike trains. In the GLMHS-IS, we take log ${\lambda }_k^c={\mu }_c+{\beta }_c^T{\mathbf{x}}_k+{\mathbf{l}}_c^T{\mathbf{q}}_{k\mid k}$, and in the GLM, log ${\lambda }_k^c={\mu }_c+{\beta }_c^T{\mathbf{x}}_k$. Note that μ_c, ${\beta }_c^T$ and ${\mathbf{l}}_c^T$ in the GLMHS models are fitted using the EM approach, while μ_c and ${\beta }_c^T$ in the classical GLM are fit through standard GLM methods. In both cases, we assume that these parameters are fixed quantities, and that x_k is known. We use the filtering estimates to obtain the approximate posterior distribution of q_k given the data up to time bin k, namely q_k ~ N(q_k|k, W_k|k); using this distribution assumption, we can calculate 95% confidence intervals for log ${\lambda }_k^c$ in the usual multiple regression manner, and then exponentiate to obtain the (asymmetric) confidence limits for ${\lambda }_k^c$.

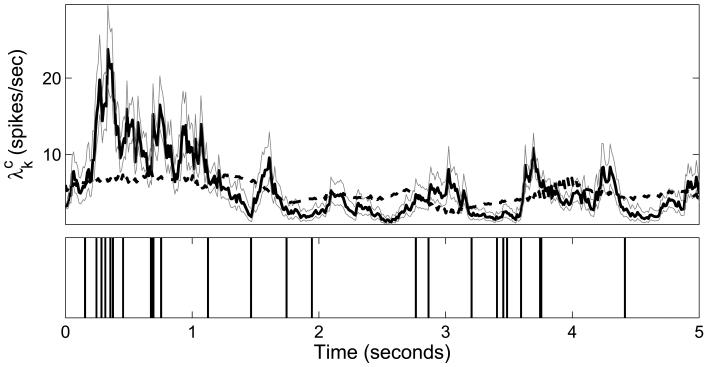
The CIFs of both models in one example trial are shown in Figure 2. We see from the figure that the confidence intervals are generally fairly “tight” around the estimated CIF. Also, we see that the GLMHS framework can better capture the significant variation of the spiking activity whereas the classical GLM appears to over-smooth the activity. For example, the CIF under our new model increases sharply when there is increased spiking activity (in the beginning of the trial, for example), while the classical GLM CIF remains relatively constant. It should be noted that, under this formulation, the CIF for the GLMHS model is a function of the spike values at each time k (through the calculation of q_k|k), while the CIF for the classical GLM is not (though the parameters in the model are still estimated from the spike values). This partially accounts for the apparently improved performance of the CIF in the GLMHS model.

Figure 2.

CIFs in the GLMHS-IS and GLM with IPP spike trains in one example trial. Upper plot: The thick black line denotes the CIF for the 50th neuron from Dataset 1 under the GLMHS-IS IPP Model with d = 4 with 95% confidence intervals (thin gray lines). The dashed black line denotes the CIF of the classical GLM. Here we see that the CIF for the GLMHS-IS model can capture more of the dynamics of the spike train when compared to the classical GLM. Lower plot: the original spike train.

We also calculate the Normalized Log-Likelihood-Ratios (NLLRs) in the testing part of each data set. This is for the purpose of cross-validation. The NLLR is calculated as:

$$\frac{1}{N\Delta t}{\log }_2\frac{L_d}{L_0}=\frac{1}{N\Delta t}({\log }_2{L}_d-{\log }_2{L}_0)$$

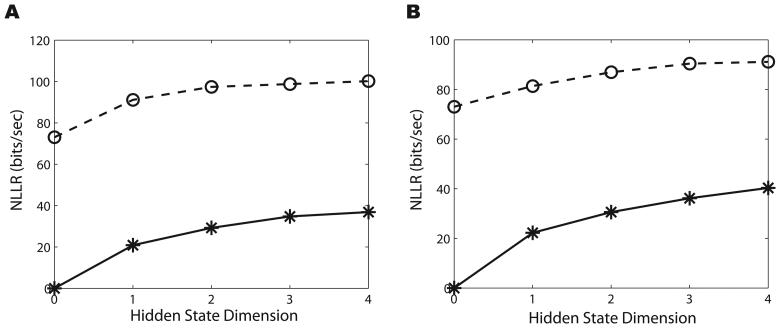
where L_d is the likelihood of the observed data under a d-dimensional GLMHS-IS model, L₀ is the likelihood under the classical GLM IPP model, N is the number of bins used to calculate the likelihood and Δt is the bin size. NΔt measures the time length of the data. Using base 2 units, the NLLR is measured in bits/sec. The results for the IPP case are shown as solid lines with stars in Figure 3. Here we see that the NLLR (computed on the test data) is increasing for all values of d (from 0 to 4) in both data sets.

Figure 3.

A. A comparison of the NLLRs for the GLMHS-IS models in the testing part of Dataset 1 when the spike train is modeled as an inhomogeneous Poisson process (solid line with stars) and when modeled as a non-Poisson process (dashed line with circles). The model is a classical GLM if the hidden dimension d = 0. We notice that the NLLR increases as d increases in both IPP and NPP cases. Also, we see the NLLR for the NPP case is higher than that for the IPP case. B. Same as A but for Dataset 2.

We use a standard Likelihood Ratio Test (LRT) to determine significance in the improvement since the models are nested (the GLMHS-IS model is equivalent to the classical GLM model if the hidden dimension d = 0). We found that the GLMHS-IS models provide significantly better representation than the classical GLM for all values of d (details omitted to save space). One can also use standard model-selection criterions such as the Bayesian Information Criterion (BIC) (Rissanen, 1989) to determine model significance. Lower values of the BIC indicate that the model is better when compared to another model. It was found that the BIC is a decreasing function with respect to the hidden dimension d. This indicates that larger hidden dimensions provide better representation on the neural activity and hand kinematics. Again, we emphasize that all the likelihood comparisons (in the above and in the following) are on the testing data. This indicates that the improvement in the model-fitting is effective as the result is already cross-validated.

NPP case

It is understood that including spike history terms is very important in the modeling of neural spiking processes (Brillinger, 1992; Paninski, 2004; Truccolo et al., 2005; Truccolo and Donoghue, 2007). In the non-Poisson process case, the logarithm of the CIF is a linear function of hand state, spike history, and hidden state; that is, log ${\lambda }_k^c={\mu }_c+{\beta }_c^T{\mathbf{x}}_k+{\gamma }_c^T{\mathbf{y}}_{k,N}^c+{\mathbf{l}}_c^T{\mathbf{q}}_k$. In our data analysis, we choose N = 10. This indicates that a neuron's current spiking activity is related to its spike values in the previous 100ms. Similar results were obtained as in the IPP case for both the goodness-of-fit and in the comparison of the CIF between the GLMHS-IS NPP model and the classical GLM model (the detail is omitted).

When calculating the NLLR in the NPP case, we fix L₀ to be the likelihood under the classical GLM IPP model as a baseline measure to compare the modeling improvement between IPP and NPP cases. The results for the NPP case are shown as dashed lines with circles in Figure 3. Here we see a similar trend as in the IPP case: NLLR is increasing with respect to d for each dataset. These results indicate that both IPP and NPP models with hidden inputs outperform the classical GLM model in the modeling of neural spiking processes. Furthermore, increasing the hidden dimension can provide a better representation. Finally, as a comparison between IPP and NPP models, we see that the NLLRs for the NPP are greater than for the IPP (significant jump between solid and dashed lines at d = 0 in Figure 3), suggesting that the NPP can better represent the nature of the neural activity than the IPP. Similar LRT and BIC analyses can be applied to quantify these results.

3.1.2. GLMHS-DS Model

In the GLMHS-DS model, the hand kinematics are allowed to influence the common inputs, and vice versa. While this idea is fairly straightforward, the mathematical approach involves more computations. We performed the same analysis as in the GLMHS-IS model. The goodness-of-fit results for the GLMHS-DS model were very similar to the previously discussed GLMHS-IS model, and are omitted to save space. Moreover, similar to the result in the GLMHS-IS case (Fig. 2) the CIF under the GLMHS-DS model can better characterize spiking activity than the classical GLM model. For example, the GLMHS-DS model can correctly capture certain spiking signals whereas the CIF of the GLM model seems to be over-smoothing the data.

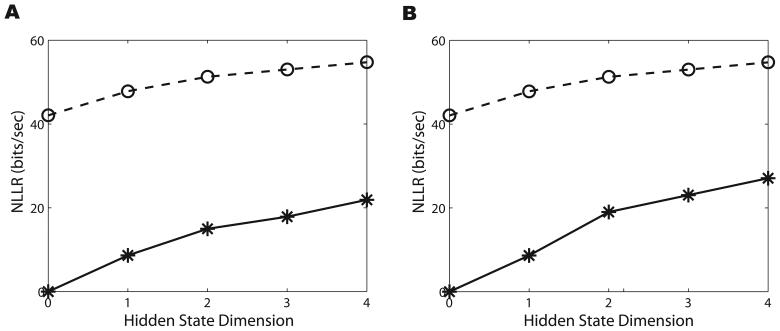
Figure 4 compares the NLLRs for both IPP and NPP cases under the GLMHS-DS model. Here we still see an increasing trend in the NLLRs with respect to d for each dataset. This indicates that the neural activity is better represented with the GLMHS-DS model for both the IPP and NPP cases. Consistent with our results in the GLMHS-IS model, the NLLRs for the NPP are greater than for the IPP, suggesting that the NPP can better represent the nature of the neural activity than the IPP.

Figure 4.

A. A comparison of the NLLRs for the GLMHS-DS models in the testing part of Dataset 1 when the spike train is modeled as an IPP (solid lines with stars) and when modeled as an NPP (dashed lines with circles). The model is a classical GLM if the hidden dimension d = 0. We observe that the NLLR increases with respect to d in both IPP and NPP cases. Also, we see the NLLR for the NPP case is higher than for the IPP case. B. Same as A but for Dataset 2.

3.2. Decoding

In the identification stage, we have used the EM algorithm to fit all necessary parameters in the model, and performed model diagnostics including goodness-of-fit analysis and likelihood calculations. Here we are interested in measuring the performance of our model in the decoding on testing data. In this stage, we reconstruct the hand state using the observed firing rates up to the current time. This “filtering” estimate would be desirable in practical on-line applications.

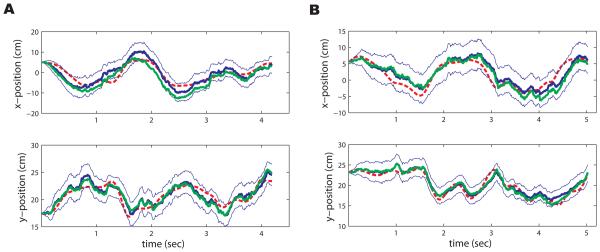
Figure 5 has an example for one trial in each of our datasets. Here we see that our new model is able to capture the true value of the hand kinematics with the 95% confidence intervals over time. Only in a few cases did the true hand kinematics stray outside of the confidence limits. This is observed both in the IPP (Fig. 5 A) and NPP (Fig. 5 B) cases. We quantify the decoding accuracy using a traditional 2-d Mean Square Error (MSE) in the units of cm², comparing the predicted hand trajectory to the true hand trajectory in the testing data (Wu et al., 2006). The results are summarized in Tables 1 (for GLMHS-IS models) and 2 (for GLMHS-DS models).

Figure 5.

A. True hand trajectory (dashed red), x- and y-position, of an example trial from dataset 1, and its reconstruction (solid blue) and 95% confidence region (thin solid blue) using the GLMHS-IS with d = 4 under the IPP case. The reconstruction by the classical GLM (solid green) is also shown here. B. Same as A except from another trial in dataset 2 in the NPP case with d = 1 in the model. In both cases, we see that the reconstructions from the GLMHS models perform well, and they are close to those from the classical GLM models.

Table 1.

Comparison of decoding accuracy (MSE in the units of cm²) between GLMHS-IS models and the classical GLM. The comparison is for both IPP and NPP cases in each of the two datasets. Numbers in the square brackets indicate the improvement by the NPP over the IPP. Numbers in parentheses indicate the improvement by the hidden state models over the classical GLM model.

Method	Dataset 1		Dataset 2
	IPP	NPP	IPP	NPP
classical GLM	9.17	8.61 [6%]	9.78	8.47 [13%]
d=1	8.66 (5%)	8.20 (5%)	7.91 (19%)	7.26 (14%)
d=2	8.41 (8%)	8.04 (7%)	8.11 (17%)	7.36 (13%)
d=3	8.50 (8%)	8.27 (4%)	7.79 (20%)	7.17 (15%)
d=4	7.77 (16%)	7.26 (16%)	7.70 (21%)	7.40 (13%)

From Table 1, we notice that, for all values of d, the MSE in the GLMHS-IS is better than in the classical GLM. Also, unlike the results in the linear case (Wu et al., 2009) where the MSE was always decreasing with respect to d, here we see that larger d does not always improve the decoding results. In Dataset 2, for example, the MSE is very consistent for all four dimensions. Table 2 summarizes the decoding results for the GLMHS-DS models. We found that overall the decoding here is more accurate than that in the GLMHS-IS models. For example, here there are more improvements larger than 10% in Dataset 1, and one improvement reaches 29% when d = 2 for the IPP case in Dataset 2 which is the maximum over all models. This suggests that there should be some direct interaction between the hand state and hidden state, and the interaction can help better characterize the dynamic systems and improve decoding performance.

Table 2.

Mean Squared Error (in the units of cm²) of GLMHS-DS models and the classical GLM for IPP and NPP cases in each of the two datasets. Numbers in the square brackets indicate of the improvement by the NPP over the IPP. Numbers in parentheses indicate the improvement by the hidden state models over the classical GLM model.

Method	Dataset 1		Dataset 2
	IPP	NPP	IPP	NPP
classical GLM	9.17	8.61 [6%]	9.78	8.47 [13%]
d=1	8.59 (6%)	8.27 (4%)	7.81 (20%)	7.31 (14%)
d=2	7.53 (18%)	7.40 (14%)	6.95 (29%)	6.40 (24%)
d=3	8.02 (13%)	8.00 (7%)	7.19 (26%)	6.80 (20%)
d=4	7.71 (16%)	7.39 (14%)	7.24 (26%)	6.93 (18%)

3.3. Comparison with the Linear State-Space Model with Hidden States

In (Wu et al., 2009), we proposed to add a multi-dimensional hidden state to a linear Kalman filter model. Here we refer to it as a KFHS (Kalman filer with hidden state) method. The KFHS shares many similarities to the GLMHS in this paper: 1) Both KFHS and GLMHS are in the framework of state-space models where the neural firing rate is the observation, and the hand kinematics and hidden state are the system state with a linear Gaussian transition over time. 2) Adding the hidden state improves the representation of the neural data (larger likelihoods in the hidden state models). In particular, the likelihood increases with respect to the dimension of the hidden state. 3) Adding the hidden state improves the decoding accuracy (lower mean squared errors). Based on the same datasets as in this study, the decoding accuracy using the KFHS is shown in Table 3 (reproducing the results in (Wu et al., 2009)). Comparing decoding results of the KFHS and the GLMHS (in Tables 1 and 2), we found that MSE in the KFHS is lower in some cases, whereas higher in the others (though the GLMHS models appear to often perform better than the classical Kalman filter).

Table 3.

Mean Squared Error (in the units of cm²) of KFHS models and the classical Kalman filter (KF) in each of the two datasets. Numbers in parentheses indicate the improvement by the hidden state models over the classical KF.

Method	Dataset 1	Dataset 2
classical KF	8.35	9.78
d=1	8.09 (3%)	8.37 (14%)
d=2	7.60 (9%)	8.23 (16%)
d=3	7.47 (11%)	7.61 (22%)

Though the main results are consistent, there are significant differences between these two methods which are worth emphasizing: 1) The KFHS assumes the neural firing is a continuous variable with a Gaussian distribution. The model can be identified using the conventional EM algorithm (Dempster et al., 1977). In contrast, the GLMHS is based on a more realistic and accurate non-linear discrete model of spike trains. The model is identified based on an approximate EM method (Smith and Brown, 2003). 2) In the KFHS, neural firing rates are described as a linear Gaussian model without spike history. In contrast, the firing rate in the GLMHS models can either include spike history (NPP model) or not (IPP model). 3) In the KFHS, it is necessary to have dependency between the hand kinematics and the hidden state, since we found empirically that the model can not be identified otherwise (the likelihood does not increase in the EM iteration). However, both the GLMHS-IS and GLMHS-DS can appropriately characterize the neural activity. 4) The hidden dimension in the KFHS can only vary from 1 to 3 before performance begins to decrease, whereas the hidden dimension in the GLMHS can be 4 or larger. 5) In the KFHS, higher hidden dimensions resulted in better decoding accuracy. Such a trend is much weaker in the GLMHS-IS and GLMHS-DS.

3.4. Analysis of the Hidden State

By adding a multi-dimensional hidden state to the classical GLM, we have obtained a better model fit as well as improved decoding. However, our understanding of the hidden state is still very limited as it is always unknown. Here we perform some rudimentary analysis to explore its role in neural coding by examining the non-stationarity and higher-order kinematics terms.

Non-stationarity check

It is widely known that neural activity in motor cortex may be highly non-stationary over time (Carmena et al., 2005; Kim et al., 2006; Chestek et al., 2007). Our recent study in the KFHS model indicated that each dimension of the hidden state decoded from neural activity has either a very weak or no trend at all over time. Results similar to the KFHS model are also obtained under our new GLMHS model. For example, fitting a linear regression to the 2-d GLMHS-IS model revealed R² values of .0001 and .0020, respectively. This suggests that the hidden states do not appear to capture the non-stationarity in the neural signals. Instead, the hidden state term is allowing us to properly account for overdispersion, i.e., higher variability than would be expected in the purely Poisson GLM model.

Higher-order kinematics check

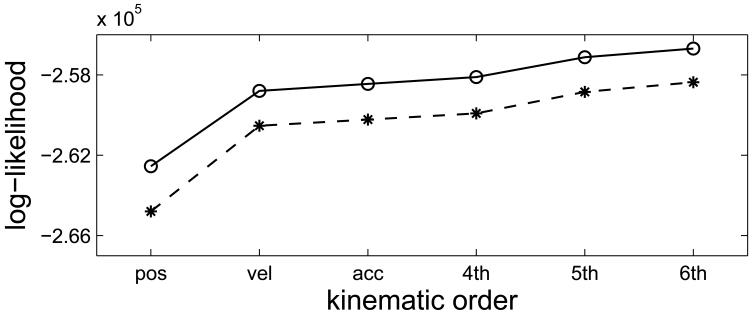
We have shown that adding a hidden state to the GLM model can better characterize the neuronal activity when the kinematics include position, velocity, and acceleration. The improvement is quantified by comparing the likelihood in each model. One may naturally hypothesize that the improvement might result from the fact that the neurons are not only tuned to position, velocity, and acceleration, but higher-order terms of the hand kinematic signal, and that the hidden state model is able to capture this higher-order information. To check on this, we use kinematics with various orders in the classical GLM and GLMHS models and compare their likelihoods. It was found that the likelihood in the GLMHS is still consistently larger than that in the GLM. As an example, the likelihood comparison in dataset 2 is shown in Figure 6 where the kinematic order varies from 1 (position only) to 6 (position, velocity, acceleration, plus 4th, 5th, and 6th order kinematics). It is apparent that the improvement in the GLMHS consistently holds over all kinematic orders. This result suggests that the hidden state represents information other than the higher-order kinematics.

Figure 6.

Log-likelihoods of the GLM (dashed line with stars) and the GLMHS-IS with d = 1 under the IPP case (solid line with circles) in dataset 2 where the kinematic order varies from 1 to 6. We see that the separation between the GLM and GLMHS is fairly constant for all kinematic orders.

4. Discussion

Motor cortical decoding has been extensively studied over the last two decades since the development of population vector methods (Georgopoulos et al., 1986; Moran and Schwartz, 1999), and indeed even earlier (Humphrey et al., 1970). Previous methods have focused on probabilistic representations between spiking activity and kinematic behaviors such as the hand position, velocity, or direction (Paninski et al., 2004; Brockwell et al., 2004; Truccolo et al., 2005; Sanchez et al., 2005; Wu et al., 2006). However, it was found that the neural activity may also relate to other states such as muscle fatigue, satiation, and decreased motivation (Carmena et al., 2005; Chestek et al., 2007; Truccolo and Donoghue, 2007). In this paper, we have proposed to incorporate a multi-dimensional hidden state in the commonly used generalized linear models, where the spike train can be characterized using an inhomogeneous Poisson process (IPP) or a non-Poisson process (NPP). The hidden term, in principle, can represent any (unobserved or unobservable) states other than the hand kinematics. We found that these hidden state models significantly improve the representation of motor cortical activity in two independent datasets from two monkeys. Moreover, the decoding accuracy can be improved by up to about 30% in some cases, compared to the standard GLM decoder. These results provide evidence that, by taking into account the various hidden effects that we do not measure directly during an experiment, we can design better online decoding methods, which in turn should prove useful in prosthetic design and in online experiments investigating motor plasticity. Consistent with our recent results in the linear case (Wu et al., 2009), and also related previous approaches due to (Brockwell et al., 2007) and (Yu et al., 2006, 2009; Santhanam et al., 2009), we found that the GLMHS models are able to better capture the over-dispersion, or extra “noise”, in real motor cortical spike trains than the classical GLM method. This suggests that the hidden state models could contribute to understand the uncertainty in neural data, which is a key problem in neural coding (Churchland et al., 2006a,b). Moreover, we think the same identification algorithms developed in this article can, in principle, be applied to other point process models, but the log-concavity of the likelihood function needs to be verified in each case.

A number of recent studies have emphasized similar points. For example, (Brockwell et al., 2007) incorporated a hidden normal variable in the conditional intensity function of a GLM-based model to address unobserved additional source of noise in motor cortical data. One major difference from our study is that these authors assumed that the noise term is independent over time and between neurons; in our case, the hidden noise term was assumed to have strong correlations both in time and between neurons, and even with the kinematic variables (in the GLMHS-DS model). It will be interesting to combine these approaches in future work. In addition, the model identification in (Brockwell et al., 2007) was based on Markov Chain Monte Carlo (MCMC) methods which are fairly computationally intensive; we used faster approximate EM methods, which might be easier to utilize in online prosthetic applications.

The use of correlated latent variables in the modeling of neural spiking processes was also previously examined in (Yu et al., 2006). They used latent variable models to examine the dynamical structure of the underlying neural spiking process in the dorsal premotor area during the delay period of a standard instructed-delay, center-out reaching task. The identification of the model also follows an EM framework. The main difference from this study is that they used Gaussian quadrature methods in the maximization of the expected log-likelihood in the M-step. In contrast, in our model the Hessian matrix is negative definite (therefore the function is strictly concave), allowing us to use an efficient Newton-Raphson approach for the maximization (see also (Paninski et al., 2009) for further discussion). More recently, these authors introduced Factor Analysis (FA; (Santhanam et al., 2009)) and Gaussian Process Factor Analysis (GPFA; (Yu et al., 2009)) methods for modeling these latent processes in the context of brain-machine interfaces. The GPFA is an extended version of multivariate methods such as Principal Component Analysis (PCA), in which temporal correlations are incorporated, much as we utilize a simple Gaussian autoregressive prior model for the kinematics x_k and hidden state q_k here. These authors used their methods, as we do here, to extract a lower-dimensional latent state to describe the underlying neural spiking process which can help account for over-dispersion and non-kinematic variation in the data. A few differences are worth noting: first, (Yu et al., 2009) use a simple linear-Gaussian model to model the (square-root transformed) spike count observations, while we have focused here on incorporating a discrete representation (including spike history effects) of the spike trains. (Santhanam et al., 2009) investigate a Poisson model with larger time bins than we used here and no temporal variability in their latent Gaussian effects, but found (for reasons that remain somewhat unclear) that the fully Gaussian model outperformed the Poisson model in a discrete (eight-target center-out) decoding task; this is the opposite of the trend we observed in section 3.3. Second, there are some technical computational differences: the general Gaussian process model used in (Yu et al., 2009) requires on the order of T³ time to perform each EM iteration, where T is the number of time bins in the observed data (note that T can be fairly large in these applications), whereas the state-space methods we have used here are based on recursive Markovian computations that only require of order T time (Paninski et al., 2009). Again, it will be very interesting to explore combinations of these approaches in the future.

One other technical detail is worth discussing here. In the definition of the CIF (Eqn. 5), one can also add interneuronal interactions in the history term (Brillinger, 1988, 1992; Paninski, 2004; Truccolo et al., 2005; Nykamp, 2007; Kulkarni and Paninski, 2007a; Pillow et al., 2008; Stevenson et al., 2009; Truccolo et al., 2009). However, this can significantly increase the computational burden, since now on the order of C² parameters must be fit, where C ~ 100 is the number of simultaneously observed cells. This large number of parameters could also generate instability in the model identification; see, e.g., (Stevenson et al., 2009) for further discussion of these issues. (Note that decoding in the presence of these interneuronal terms is quite straightforward, and can be done in real-time; the bottleneck is in the model identification, which may make these coupled multineuronal models somewhat less suitable for online decoding applications.) Thus, for simplicity, we set all interneuronal interaction terms to zero in this study, but we plan to explore these effects in more detail in the future.

In this study, the hidden dimension only varies from 1 to 4. When the dimension is larger, the EM identification procedure may become inefficient and unstable. Also, in the linear KFHS (Wu et al., 2009), we found that the model could not be identified by the EM algorithm if the kinematics and hidden state were assumed to evolve independently, or if the dimension of the hidden state is larger than 3. These problems may also be due to the iterative update in the EM algorithm. To better address these issues, we are exploring alternative approaches for the model identification. Based on the log-concavity of the likelihood function, a direct Laplace approximation method is attractive; see (Koyama et al., 2008, 2009; Paninski et al., 2009) for further details. Our preliminary results show that this Laplace method can lead to significant improvements in efficiency (gains in computational speed of approximately 2-4x compared to the EM method). Further investigation of these techniques will be conducted in the future. Finally, because of their accuracy and efficiency, the hidden-state models we have discussed here (both the KFHS and GLMHS) should be useful tools in on-line applications. An important next step will be to apply these new methods and to test their efficacy in real-time closed-loop experiments.

Appendix

A. Posterior Distributions in GLMHS-IS

The estimation of q_k|M, W_k|M, and W_k+1,k|M includes a forward (filtering) and a backward (smoothing) step. The “filtering” step computes the posterior of hidden state conditioned on the past and current observations. The computation is performed via a point process filter (Eden et al., 2004).

• For k = 2, ⋯ , M:

  $$\begin{array}{cc}\hfill {\mathbf{q}}_{k\mid k-1}& ={\mathbf{A}}_q{\mathbf{q}}_{k-1\mid k-1}\hfill \\ \hfill {\mathbf{W}}_{k\mid k-1}& ={\mathbf{A}}_q{\mathbf{W}}_{k-1\mid k-1}{\mathbf{A}}^T+{\mathbf{C}}_q\hfill \\ \hfill {\mathbf{W}}_{k\mid k}& =({\mathbf{W}}_{k\mid k-1}^{-1}+\underset{c=1}{\overset{C}{\Sigma }}{\mathbf{l}}_c^T\left({\lambda }_k^c\Delta t\right){\mathbf{l}}_c{)}_{{\mathbf{q}}_k={\mathbf{q}}_{k\mid k-1}}^{-1}\hfill \\ \hfill {\mathbf{q}}_{k\mid k}& ={\mathbf{q}}_{k\mid k-1}+{\mathbf{W}}_{k\mid k}^{-1}[\underset{c=1}{\overset{C}{\Sigma }}{\mathbf{l}}_c^T(y_k^c-{\lambda }_k^c\Delta t){]}_{{\mathbf{q}}_k={\mathbf{q}}_{k\mid k-1}}\hfill \end{array}$$

The “smoothing” step computes the posterior of hidden state conditioned on the entire observations. As the posterior distributions are normal, the computation follows a standard backward propagation (Haykin, 2001).

• For k = M − 1, ⋯ , 1:

  $$\begin{array}{cc}\hfill {\mathbf{J}}_k& ={\mathbf{W}}_{k\mid k}{\mathbf{A}}_q^T{{\mathbf{W}}_{k+1\mid k}}^{-1}\hfill \\ \hfill {\mathbf{q}}_{k\mid M}& ={\mathbf{q}}_{k\mid k}+{\mathbf{J}}_k({\mathbf{q}}_{k+1\mid M}-{\mathbf{A}}_q{\mathbf{q}}_{k\mid k})\hfill \\ \hfill {\mathbf{W}}_{k\mid M}& ={\mathbf{W}}_{k\mid k}+{\mathbf{J}}_k({\mathbf{W}}_{k+1\mid M}-{\mathbf{W}}_{k+1\mid k}){\mathbf{J}}_k^T\hfill \end{array}$$
• For k = M :

  $${\mathbf{W}}_{M,M-1\mid M}={\mathbf{W}}_{M\mid M}{\mathbf{J}}_{M-1}^T$$
• For k = M − 1, ⋯ , 2:

  $${\mathbf{W}}_{k,k-1\mid M}={\mathbf{W}}_{k\mid k}{\mathbf{J}}_{k-1}^T+{\mathbf{J}}_k({\mathbf{W}}_{k+1,k\mid M}-{\mathbf{AW}}_{k\mid k}){\mathbf{J}}_{k-1}^T$$

B. Newton-Raphson Method

We want to solve the equation

$$\underset{k=1}{\overset{M}{\Sigma }}{\int }_{{\mathbf{q}}_k}P({\mathbf{q}}_k\mid \cdots )[-{\lambda }_k^c\Delta t{\mathbf{V}}_k+y_k^c{\mathbf{V}}_k]d{\mathbf{q}}_k=0$$ (21)

where the vector,

$${\mathbf{V}}_k\left(\begin{array}{c}\hfill 1\hfill \\ \hfill {\mathbf{x}}_k\hfill \\ \hfill {\mathbf{y}}_{k,N}^c\hfill \\ \hfill {\mathbf{q}}_k\hfill \end{array}\right),\text{and}{\mathbf{y}}_{k,N}^c=\left(\begin{array}{c}\hfill y_{k-1}^c\hfill \\ \hfill ⋮\hfill \\ \hfill y_{k-N}^c\hfill \end{array}\right)$$

The integrand in Equation 21 includes two parts: The first one, $-{\lambda }_k^c\Delta t{\mathbf{V}}_k$, includes the density rate, but the second one, $y_k^c{\mathbf{V}}_k$, does not. The integration on the second part can be easily obtained:

$$\underset{k=1}{\overset{M}{\Sigma }}{\int }_{{\mathbf{q}}_k}P({\mathbf{q}}_k\mid \cdots )\left[y_k^c{\mathbf{V}}_k\right]d{\mathbf{q}}_k=\underset{k=1}{\overset{M}{\Sigma }}{y}_k^c\left(\begin{array}{c}\hfill 1\hfill \\ \hfill {\mathbf{x}}_k\hfill \\ \hfill {\mathbf{y}}_{k,N}^c\hfill \\ \hfill {\mathbf{q}}_{k\mid M}\hfill \end{array}\right)$$

where the equality holds as 1, x_k, and ${\mathbf{y}}_{k,N}^c$ are constant with respect to the integration, and by definition q_k|M = ∫q_k P(q_k| ⋯)q_kdq_k. Similarly, we can compute the integration on the first part:

$$\underset{k=1}{\overset{M}{\Sigma }}{\int }_{{\mathbf{q}}_k}P({\mathbf{q}}_k\mid \cdots )[-{\lambda }_k^c\Delta t{\mathbf{V}}_k]d{\mathbf{q}}_k=\underset{k=1}{\overset{M}{\Sigma }}[-\exp ({\mu }_c+{\beta }_c^T{\mathbf{x}}_k+{\gamma }_c^T{\mathbf{y}}_{k,N}^c)]\left[\exp ({\mathbf{l}}_c^T{\mathbf{q}}_{k\mid M}+\frac{1}{2}{\mathbf{l}}_c^T{\mathbf{W}}_{k\mid M}{\mathbf{l}}_c)\right]\Delta t\left(\begin{array}{c}\hfill 1\hfill \\ \hfill {\mathbf{x}}_k\hfill \\ \hfill {\mathbf{y}}_{k,N}^c\hfill \\ \hfill {\mathbf{q}}_{k\mid M}+{\mathbf{W}}_{k\mid M}{\mathbf{l}}_c\hfill \end{array}\right).$$

Denoting the sums

$$\{\begin{array}{ccc}\hfill {\mu }_c+{\beta }_c^T{\mathbf{x}}_k+{\gamma }_c^T{\mathbf{y}}_{k,N}^c& \hfill =\hfill & S_1\hfill \\ \hfill {\mathbf{l}}_c^T{\mathbf{q}}_{k\mid M}+\frac{1}{2}{\mathbf{l}}_c^T{\mathbf{W}}_{k\mid M}{\mathbf{l}}_c& \hfill =\hfill & S_2\hfill \\ \hfill {\mathbf{q}}_{k\mid M}+{\mathbf{W}}_{k\mid M}{\mathbf{l}}_c& \hfill =\hfill & S_3,\hfill \end{array}\phantom{\}}$$

we try to find the root of the function f with variables μ_c, β_c, γ_c, and l_c; that is,

$$\mathbf{f}\left(\begin{array}{c}\hfill {\mu }_c\hfill \\ \hfill {\beta }_c\hfill \\ \hfill {\gamma }_c\hfill \\ \hfill {\mathbf{l}}_c\hfill \end{array}\right)=\underset{k=1}{\overset{M}{\Sigma }}[-\exp \left(S_1\right)]\left[\exp \left(S_2\right)\right]\Delta t\left(\begin{array}{c}\hfill 1\hfill \\ \hfill {\mathbf{x}}_k\hfill \\ \hfill {\mathbf{y}}_{k,N}^c\hfill \\ \hfill S_3\hfill \end{array}\right)-\underset{k=1}{\overset{M}{\Sigma }}{y}_k^c\left(\begin{array}{c}\hfill 1\hfill \\ \hfill {\mathbf{x}}_k\hfill \\ \hfill {\mathbf{y}}_{k,N}^c\hfill \\ \hfill {\mathbf{q}}_{k\mid M}\hfill \end{array}\right)=0.$$ (22)

This system has a highly non-linear structure. There are no simple closed-form solutions for updating the parameters μ_c, β_c, γ_c, and l_c, c = 1, ⋯ , C. Here we use a standard Newton-Raphson method to search the root to the equation. Based on Equation 22, the Jacobian matrix for all parameters can be obtained as follows:

$$\begin{array}{cc}\hfill \mathbf{J}& =-\underset{k=1}{\overset{M}{\Sigma }}\exp (S_1+S_2)\Delta t\left(\begin{array}{cccc}\hfill 1\hfill & \hfill {\mathbf{x}}_k^T\hfill & \hfill {{\mathbf{y}}_{k,N}^c}^T\hfill & \hfill S_3^T\hfill \\ \hfill {\mathbf{x}}_k\hfill & \hfill {\mathbf{x}}_k{\mathbf{x}}_k^T\hfill & \hfill {\mathbf{x}}_k{{\mathbf{y}}_{k,N}^c}^T\hfill & \hfill {\mathbf{x}}_k{S}_3^T\hfill \\ \hfill {\mathbf{y}}_{k,N}^c\hfill & \hfill {\mathbf{y}}_{k,N}^c{\mathbf{x}}_k^T\hfill & \hfill {\mathbf{y}}_{k,N}^c{{\mathbf{y}}_{k,N}^c}^T\hfill & \hfill {\mathbf{y}}_{k,N}^c{S}_3^T\hfill \\ \hfill S_3\hfill & \hfill S_3{\mathbf{x}}_k^T\hfill & \hfill S_3{{\mathbf{y}}_{k,N}^c}^T\hfill & \hfill S_3{S}_3^T+{\mathbf{W}}_{k\mid M}\hfill \end{array}\right)\hfill \\ \hfill & =-\underset{k=1}{\overset{M}{\Sigma }}\exp (S_1+S_2)\Delta t\left[\left(\begin{array}{c}\hfill 1\hfill \\ \hfill {\mathbf{x}}_k\hfill \\ \hfill {\mathbf{y}}_{k,N}^c\hfill \\ \hfill S_3\hfill \end{array}\right){\left(\begin{array}{c}\hfill 1\hfill \\ \hfill {\mathbf{x}}_k\hfill \\ \hfill {\mathbf{y}}_{k,N}^c\hfill \\ \hfill S_3\hfill \end{array}\right)}^T+\left(\begin{array}{cccc}\hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill {\mathbf{W}}_{k\mid M}\hfill \end{array}\right)\right].\hfill \end{array}$$

J is negative definite. This is because for each term in the above sum 1) exponential term is always positive; 2) Δt > 0; 3) any matrix multiplied by its transpose must be semi-positive definite; 4) the matrix with covariance W_k|M in the last main diagonal is semi-positive definite. Finally, the variability in the kinematics and neural activity implies that the sum is nonsingular. This negative definiteness ensures fast convergence in finding the root of f.

Finally, the Newton-Raphson update on parameters μ_c, β_c, γ_c, and l_c is written as:

$${\left(\begin{array}{c}\hfill {\mu }_c\hfill \\ \hfill {\beta }_c\hfill \\ \hfill {\gamma }_c\hfill \\ \hfill {\mathbf{l}}_c\hfill \end{array}\right)}^{(i+1)}=\left(\begin{array}{c}\hfill {\mu }_c\hfill \\ \hfill {\beta }_c\hfill \\ \hfill {\gamma }_c\hfill \\ \hfill {\mathbf{l}}_c\hfill \end{array}\right)-{\mathbf{J}}^{-1}\mathbf{f}\left(\begin{array}{c}\hfill {\mu }_c\hfill \\ \hfill {\beta }_c\hfill \\ \hfill {\gamma }_c\hfill \\ \hfill {\mathbf{l}}_c\hfill \end{array}\right)$$ (23)

C. Posterior Distributions in GLMHS-DS

As in the GLMHS-IS, the estimation of q_k|M, W_k|M, and W_k+1,k|M includes a forward (filtering) and a backward (smoothing) step. As the hand state in the GLMHS-DS also follows a generative representation from the hidden state (Eqn. 14), more computations are required than that described in Appendix A.

Filtering

At first we define notation in the “filtering” step. For k = 2, ⋯ , M, let q_k|k−1 = E(q_k|x_1:k, y_1:k−1), W_k|k−1 = Cov(q_k|x_1:k, y_1:k−1) as the mean and covariance of the prior estimate, and q_k|k = E(q_k|x_1:k+1, y_1:k), W_k|k = Cov(q_k|x_1:k+1, y_1:k) as the mean and covariance of the posterior estimate. Then the recursive formula is as follows:

• For k = 2, ⋯ , M:

  $$\begin{array}{cc}\hfill {\mathbf{q}}_{k\mid k-1}& ={\mathbf{A}}_{22}{\mathbf{q}}_{k-1\mid k-1}+{\mathbf{A}}_{21}{\mathbf{x}}_k\hfill \\ \hfill {\mathbf{W}}_{k\mid k-1}& ={\mathbf{A}}_{22}{\mathbf{W}}_{k-1\mid k-1}{\mathbf{A}}_{22}^T+{\mathbf{C}}_q\hfill \\ \hfill {\mathbf{W}}_{k\mid k}& ={\left({\mathbf{W}}_{k\mid k-1}^{-1}+{\mathbf{A}}_{12}^T{\mathbf{C}}_x^{-1}{\mathbf{A}}_{12}+\underset{c=1}{\overset{C}{\Sigma }}\left({\lambda }_k^c\Delta t\right){\mathbf{l}}_c{\mathbf{l}}_c^T\right)}_{{\mathbf{q}}_k={\mathbf{q}}_{k\mid k-1}}^{-1}\hfill \\ \hfill {\mathbf{q}}_{k\mid k}& ={\mathbf{q}}_{k\mid k-1}+{\mathbf{W}}_{k\mid k}{\left[\underset{c=1}{\overset{C}{\Sigma }}({\mathbf{y}}_k^c-{\lambda }_k^c\Delta t){\mathbf{l}}_c+{\mathbf{A}}_{12}^T{\mathbf{C}}_x^{-1}({\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}{\mathbf{x}}_k-{\mathbf{A}}_{12}{\mathbf{q}}_{k\mid k-1})\right]}_{{\mathbf{q}}_k={\mathbf{q}}_{k\mid k-1}}\hfill \end{array}$$

The first two equations are naturally derived using the linear Gaussian transition of the hidden state (Eqn. 15). The last two equations are based on the measurement on firing rate (Eqn. 3) and hand state (Eqn. 14). The derivation of this posterior is similar to that in an adaptive point process filter (Eden et al., 2004) and is described as follows:

Using the basic probability rules, we have

$$\begin{array}{cc}\hfill P({\mathbf{q}}_k\mid {\mathbf{x}}_{1:k+1},{\mathbf{y}}_{1:k})& \propto P({\mathbf{y}}_k,{\mathbf{x}}_{k+1}\mid {\mathbf{q}}_k,{\mathbf{x}}_{1:k},{\mathbf{y}}_{1:k-1})P({\mathbf{q}}_k\mid {\mathbf{x}}_{1:k},{\mathbf{y}}_{1:k-1})\hfill \\ \hfill & \propto P({\mathbf{y}}_k\mid {\mathbf{q}}_k,{\mathbf{H}}_k,{\mathbf{x}}_k)P({\mathbf{x}}_{k+1}\mid {\mathbf{x}}_k,{\mathbf{q}}_k)P({\mathbf{q}}_k\mid {\mathbf{x}}_{1:k},{\mathbf{y}}_{1:k-1})\hfill \end{array}$$

Taking the logarithm, we have

$$\log P({\mathbf{q}}_k\mid {\mathbf{x}}_{1:k+1},{\mathbf{y}}_{1:k})=\log P({\mathbf{y}}_k\mid {\mathbf{q}}_k,{\mathbf{H}}_k,{\mathbf{x}}_k)+\log P({\mathbf{x}}_{k+1}\mid {\mathbf{x}}_k,{\mathbf{q}}_k)+\log P({\mathbf{q}}_k\mid {\mathbf{x}}_{1:k},{\mathbf{y}}_{1:k-1})+\mathit{const}.$$

We further assume the posterior P(q_k|x_1:k+1, y_1:k) follows a Gaussian distribution. Then

$$-\frac{1}{2}{({\mathbf{q}}_k-{\mathbf{q}}_{k\mid k})}^T{\mathbf{W}}_{k\mid k}^{-1}({\mathbf{q}}_k-{\mathbf{q}}_{k\mid k})=\underset{c=1}{\overset{C}{\Sigma }}({\mathbf{y}}_k^c\log {\lambda }_k^c-{\lambda }_k^c\Delta t)-\frac{1}{2}{({\mathbf{q}}_k-{\mathbf{q}}_{k\mid k-1})}^T{\mathbf{W}}_{k\mid k-1}^{-1}({\mathbf{q}}_k-{\mathbf{q}}_{k\mid k-1})-\frac{1}{2}{({\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}{\mathbf{x}}_k-{\mathbf{A}}_{12}{\mathbf{q}}_k)}^T{\mathbf{C}}_x^{-1}({\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}{\mathbf{x}}_k-{\mathbf{A}}_{12}{\mathbf{q}}_k)+\mathit{const}.$$

Taking derivative with respect to q_k on both sides, we have

$$-{\mathbf{W}}_{k\mid k}^{-1}({\mathbf{q}}_k-{\mathbf{q}}_{k\mid k})=\underset{c=1}{\overset{C}{\Sigma }}({\mathbf{y}}_k^c-{\lambda }_k^c\Delta t){\mathbf{l}}_c-{\mathbf{W}}_{k\mid k-1}^{-1}({\mathbf{q}}_k-{\mathbf{q}}_{k\mid k-1})+{\mathbf{A}}_{12}^T{\mathbf{C}}_x^{-1}({\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}{\mathbf{x}}_k-{\mathbf{A}}_{12}{\mathbf{q}}_k)$$ (24)

Let q_k = q_k|k−1 in Equation 24. Then,

$${\mathbf{q}}_{k\mid k}={\mathbf{q}}_{k\mid k-1}+{\mathbf{W}}_{k\mid k}{\left[\underset{c=1}{\overset{C}{\Sigma }}({\mathbf{y}}_k^c-{\lambda }_k^c\Delta t){\mathbf{l}}_c+{\mathbf{A}}_{12}^T{\mathbf{C}}_x^{-1}({\mathbf{x}}_{k+1}-{\mathbf{A}}_{11}{\mathbf{x}}_k-{\mathbf{A}}_{12}{\mathbf{q}}_{k\mid k-1})\right]}_{{\mathbf{q}}_k={\mathbf{q}}_{k\mid k-1}}$$

Taking the derivative with respect to q_k in Equation 24 and then let q_k = q_k|k−1, we have

$${\mathbf{W}}_{k\mid k}^{-1}={\mathbf{W}}_{k\mid k-1}^{-1}+{\mathbf{A}}_{12}^T{\mathbf{C}}_x^{-1}{\mathbf{A}}_{12}+\underset{c=1}{\overset{C}{\Sigma }}\left({\lambda }_k^c\Delta t\right){\mathbf{l}}_c{\mathbf{l}}_c^T{\mid }_{{\mathbf{q}}_k={\mathbf{q}}_{k\mid k-1}}$$

Smoothing

In the smoothing step, we estimate q_k|M, W_k|M, and W_k+1,k|M, which describe the distribution of the hidden state conditioned on entire recording of firing rate and hand kinematics. The procedure is the same as the smoothing recursion in Appendix A expect for the computation of q_k|M which results from the control input term in Equation 15. The derivation is fairly standard and can be briefly described as follows:

Use the probability rules,

$$\log P({\mathbf{q}}_{k+1},{\mathbf{q}}_k\mid {\mathbf{x}}_{1:M},{\mathbf{y}}_{1:M})=\log P({\mathbf{q}}_{k+1}\mid {\mathbf{q}}_k,{\mathbf{x}}_k)+\log P({\mathbf{q}}_k\mid {\mathbf{x}}_{1:k+1},{\mathbf{y}}_{1:k})-\log P({\mathbf{q}}_{k+1}\mid {\mathbf{x}}_{1:k+1},{\mathbf{y}}_{1:k})+\log P({\mathbf{y}}_{k+1}\mid {\mathbf{x}}_{1:M},{\mathbf{y}}_{1:M})$$ (25)

Based on the normality assumption, we have

$$\begin{array}{cc}\hfill {\mathbf{q}}_{k+1},{\mathbf{q}}_k\mid {\mathbf{x}}_{1:M},{\mathbf{y}}_{1:M}& ~N\left(\left(\begin{array}{c}\hfill {\mathbf{q}}_{k+1\mid M}\hfill \\ \hfill {\mathbf{q}}_{k\mid M}\hfill \end{array}\right),\left(\begin{array}{cc}\hfill {\mathbf{W}}_{k+1\mid M}\hfill & \hfill {\mathbf{W}}_{k+1,k\mid M}\hfill \\ \hfill {\mathbf{W}}_{k+1,k\mid M}^T\hfill & \hfill {\mathbf{W}}_{k\mid M}\hfill \end{array}\right)\right)\hfill \\ \hfill {\mathbf{q}}_{k+1}\mid {\mathbf{q}}_k,{\mathbf{x}}_k& ~N({\mathbf{A}}_{22}{\mathbf{q}}_k+{\mathbf{A}}_{21}{\mathbf{x}}_k,{\mathbf{C}}_q)\hfill \\ \hfill {\mathbf{q}}_k\mid {\mathbf{x}}_{1:k+1},{\mathbf{y}}_{1:k}& ~N({\mathbf{q}}_{k\mid k},{\mathbf{W}}_{k\mid k})\hfill \end{array}$$

Matching the linear term of q_k on both sides of Equation 25, we have

$${\mathbf{q}}_{k\mid M}={\mathbf{q}}_{k\mid k}+{\mathbf{J}}_k({\mathbf{q}}_{k+1\mid M}-{\mathbf{A}}_{22}{\mathbf{q}}_{k\mid k})-({\mathbf{W}}_{k\mid k}-{\mathbf{J}}_k{\mathbf{W}}_{k+1\mid k}{\mathbf{J}}_k^T){\mathbf{A}}_{22}^T{\mathbf{C}}_q^{-1}{\mathbf{A}}_{21}{\mathbf{x}}_k$$